1 Introduction

Mishra et al. [1] developed inventory models for deteriorating seasonal products considering price and stock dependent demand rate, and allowing both the complete and the partial backordering of shortages of a product. The deterioration rate is assumed to be controlled by a preservation technology investment. The decision variables considered in the models are the selling price, the ordering frequency, and the preservation technology investment. They determined the optimum values of the decision variables that maximized the total profit. The developed optimal policies had been illustrated with the numerical example problems. Priyamvada et al. [2] found some anomalies in Mishra et al. [1] models, in their solution procedures and also in the solutions to the numerical example problems. Then they modified their models and optimal solution procedures, and showed the benefit of their modifications with the solutions to the studied numerical example problems. However, we have found some erroneous derivations of mathematical expressions in Priyamvada et al. [2] models, including a flaw in the sales revenue function in case of partial backordering. Here we demonstrate these anomalies in obtaining the optimal solutions to the problem, and hence the models are modified further to get rid of these anomalies. Thereafter, the optimal solutions to three numerical example problems are found following the current updated models. Finally, we perform comparative studies of our updated models with the corresponding ones of Priyamvada et al. [2], on the optimal solutions to the numerical example problems. These comparative studies clearly highlight the potential significance of our modification of the models and the solution techniques.

2 Assumptions and Notation

The assumptions and notation used here are the same as in Priyamvada et al. [2].

2.1 Notation

2.1.1 Decision variables

\(n\) :

Ordering frequency (an integer number).

\(\alpha\) :

Cost of preservation technology investment per unit per unit time ($/unit/time unit).

\(p\) :

Selling price ($/unit).

2.1.2 Dependent decision variables

\(Q\) :

Ordering quantity (units)

\(D_{\Upsilon }\) :

Total number of products that become deteriorated during the interval [0,\({t}_{1}\)] (units)

2.1.3 Constant parameters

\({t}_{1}\) :

Time when the inventory level drops down to zero (time unit)

\(T\) :

Inventory cycle length (time unit)

\(\lambda (\alpha )\) :

Deterioration rate when there is an investment on preservation technology (units/time unit)

\({\lambda }_{0}\) :

Deterioration rate without preservation technology investment (units/time unit)

\(\delta\) :

Sensitive parameter of investment to the deterioration rate

\(\beta\) :

Stock dependent consumption rate parameter

\(D(p,t)\) :

Demand rate function is a function of instantaneous stock level \(I(t)\) and the selling price \(p\) (units/time unit).

D(p) :

Market demand (units/time unit).

\(a\) :

Demand scale

\(b\) :

Price sensitive parameter.

\(c\) :

Buying cost ($/unit).

\(d\) :

Deterioration cost ($/unit).

\(h\) :

Inventory holding cost ($/unit/time unit)

\(s\) :

Shortage cost ($/unit/time unit).

\({c}_{1}\) :

Unit opportunity cost due to lost sale, if the shortage is lost ($/unit).

\(A\) :

Ordering cost per order ($/order).

\(\eta\) :

Backordering parameter.

\(I(t)\) :

Inventory level at a time point t (units).

\(S(T/n)\) :

Maximum shortage level for complete backordering (units).

\(B(t)\) :

Backorder level at any time \(t\) for partial backordering (units).

\(L(t)\) :

Number of lost sales at any time \(t\) (units).

\(B(T/n)\) :

Maximum backorder level for partial backordering (units).

SR :

Sales revenue ($/time unit).

PC :

Purchase cost ($/time unit).

HC :

Holding cost ($/time unit).

SC :

Shortage cost ($/time unit).

LSC :

Lost sale cost ($/time unit).

DC :

Deterioration cost ($/time unit).

OC :

Ordering cost ($/time unit).

PTC :

Preservation technology cost ($/time unit).

TP :

Total profit of the selling season ($/time unit).

3 Demonstration of the anomalies

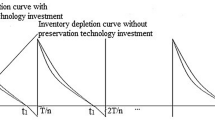
According to Mishra et al. [1], I(t), 0 ≤ t ≤ T/n, diminishes due to both the demand and the deterioration of the product within the period [0, \({t}_{1}\)], and finally drops to zero at t = \({t}_{1}\). Subsequently, shortages are permitted to happen in the period [\({t}_{1}\), T/n] and the whole demand during this time is assumed to be backordered both completely and partially.

The demand function \(D(p,t)\) is given by:

$$D\left( {p,t} \right) = \left\{ {\begin{array}{*{20}c} {D\left( p \right) + \beta I\left( t \right),} & {I\left( t \right) > 0} \\ {D\left( p \right),} & {I(t) \le 0} \\ \end{array} } \right.$$

\(D\left(p\right)=a-bp\) and 0 \(\le \beta \le 1\).

As in Priyamvada et al. [2], this research considers \(\lambda \left(\alpha \right)={\lambda }_{0 }{e}^{-\delta \alpha }.\)

3.1 The EOQ inventory model with complete backordering

Priyamvada et al. [2] modified the total profit function in this case as follows:

$$\begin{aligned} TP\left( {n,\alpha ,p} \right) & = SR - (PC + HC + SC + OC + PTC) \\ & \; = \frac{{p\beta D\left( p \right)\gamma ^{2} T^{2} }}{{2n}} + pD\left( p \right)T - cD\left( p \right)\gamma T - \frac{{cD\left( p \right)\left( {\lambda \left( \alpha \right) + \beta } \right)\gamma ^{2} T^{2} }}{{2n}} \\ & \quad - cD\left( p \right)T\left( {1 - \gamma } \right) - \frac{{hD\left( p \right)\gamma ^{2} T^{2} }}{{2n}} - nA - \alpha T + \frac{{sD\left( p \right)}}{n}\left( {2\gamma T^{2} - \gamma ^{2} T^{2} - T^{2} } \right) \\ \end{aligned}$$
(1)

However, the term \(\frac{sD\left(p\right)}{n}\left(2\gamma {T}^{2}{-\gamma }^{2}{T}^{2}-{T}^{2}\right)\) in (1) appears to be incorrect. Cancelling the terms \(-cD\left(p\right)\gamma T\) and \(cD\left(p\right)\gamma T\) in (1) and modifying the incorrect term, the correct profit function (rearranging the resultant terms) can be obtained as follows:

$$\begin{aligned} TP\left( {n,\alpha ,p} \right) = & p\beta D\left( p \right)\frac{{\gamma ^{2} T^{2} }}{{2n}} + pD\left( p \right)T \\& - cD\left( p \right)\left\{ {\left( {\lambda \left( \alpha \right) + \beta } \right)\frac{{\gamma ^{2} T^{2} }}{{2n}} + T} \right\} \\ & - hD\left( p \right)\left( {\frac{{\gamma ^{2} T^{2} }}{{2n}}} \right) - nA - \alpha T - \frac{{sT^{2} D\left( p \right)}}{{2n}}\left( {1 - \gamma } \right)^{2} \\ \end{aligned}$$
(2)

By equating the first partial derivative of \(TP\left(n,\alpha ,p\right)\) in (1) with respect to p to zero, they found the optimal value of p, \({p}^{*}\) as follows:

$${p}^{*}=\frac{2nbc\gamma T+bc{\gamma }^{2}{T}^{2}\left(\lambda \left(\alpha \right)+\beta \right)+2nbcT\left(1-\gamma \right)+hb{ \gamma }^{2}{T}^{2}+2naT-2bs{T}^{2}(2\gamma -{\gamma }^{2}-1)}{b\beta {\gamma }^{2}{T}^{2}+4nbT+b\beta {\gamma }^{2}{T}^{2}}$$
(3)

This formula for calculating \({p}^{*}\) seems to be incorrect. By equating the first partial derivative of \(TP\left(n,\alpha ,p\right)\) in (2) with respect to p to zero, we have found the correct value of \({p}^{*}\) as follows (derivation is shown in Appendix 1):

$${p}^{*}=\frac{b\{c\left(\lambda \left(\alpha \right)+\beta \right){\gamma }^{2}{T}^{2}+2cnT+h{\gamma }^{2}{T}^{2}+s{T}^{2}{\left(1-\gamma \right)}^{2}\}+2anT+a\beta {\gamma }^{2}{T}^{2}}{2b(\beta {\gamma }^{2}{T}^{2}+2nT)}$$
(4)

Note that although the terms in the denominators of (3) and (4) are the same, their numerators are different. The terms \(2bs{T}^{2}{(1-\gamma )}^{2}\) and \(bs{T}^{2}{(1-\gamma )}^{2}\) in the numerators of (3) and (4) respectively are different. Also, there is an extra term \(a\beta {\gamma }^{2}{T}^{2}\) in the numerator of (4).

Priyamvada et al. [2] demonstrated that Mishra et al. [1] profit functions in both the cases of complete and partial backordering were incapable of leading to the correct optimal solutions to the studied numerical example problems (since the total profits for examples 1 and 5 were found to be higher than the corresponding total sales revenue). Also, they reported that the value of \(\beta =0.2\) used in Mishra et al. [1] was inaccurate for all the cases in general. For the Mishra et al. [1] assumed parameter values of γ and T, Priyamvada et al. [2] showed that the value of \(\beta\) must be less than 0.025, (\(\beta\) < 0.025), and hence they solved all the numerical example problems with \(\beta\) = 0.02. So, we have also solved the studied numerical example problems with the same \(\beta\) value. Therefore, we have not included Mishra et al. [1] in our comparative study, since like-to-like comparison cannot be performed.

To show the potential significance of our revised version of Priyamvada et al. [2], we have performed a comparative study of our updated version of this model only with their original one, on the results of the studied numerical example problems 1 and 2. Although Priyamvada et al. [2] sales revenue function, SR is found to be correct, their calculated value of SR = $89,584.09 for example 1 seems to be incorrect. The correct value of SR for this example problem should be $91,586.63. Also, their calculated maximal total profits, $72,083.28 and $71,601.48 for examples 1 and 2 respectively seem to be incorrect, since we have found them as $71,364.11 and $70,899.41, by substituting their obtained optimal values of the decision variables in their profit function. The comparative optimal solutions of examples 1 and 2 obtained by Priyamvada et al. [2] (with the corrected maximal profits) and our modified version of it are given in Table 1.

Table 1 A comparative study of the results of the studied numerical example problems 1 & 2
Full size table

From Table 1 it can easily be seen that the profits are increased significantly by our revised model in this case of complete backordering. Besides, the values of the decision variables in our optimal solutions are different from the corresponding ones obtained by Priyamvada et al. [2]. Thus, our corrections of an erroneous mathematical expression in the model and hence the formula for obtaining the optimal value of p lead to the accurate optimal solution.

3.2 The EOQ inventory model with partial backordering

Considering the partial backordering of shortages Priyamvada et al. [2] developed the total profit function as follows:

$$\begin{aligned} TP\left( {n,\alpha ,p} \right) =& SR - (PC + HC + SC + LSC + OC + PTC) \\ \; =& p\beta D\left( p \right)\frac{{\gamma ^{2} T^{2} }}{{2n}} + \frac{{pD(p)T}}{n}\left[ {\left( {1 - \gamma } \right) - \frac{{\eta T}}{{2n}}\left( {1 - \gamma } \right)^{2} } \right] \\ \quad & - cD\left( p \right)\gamma T - \frac{{cD\left( p \right)\left( {\lambda \left( \alpha \right) + \beta } \right)\gamma ^{2} T^{2} }}{{2n}} - cD\left( p \right)T\left( {1 - \gamma } \right) \\ \quad & - \frac{{cD\left( p \right)\eta T^{2} }}{{2n}}\left( {1 - \gamma } \right)^{2} - hD\left( p \right)\left( {\frac{{\gamma ^{2} T^{2} }}{{2n}}} \right) - \frac{{sD\left( p \right)}}{{2n}}\left( {2\gamma T^{2} - \gamma ^{2} T^{2} - T^{2} } \right) \\ \quad& - nsD\left( p \right) + \frac{{sD\left( p \right)\eta T}}{2}\left( {1 - \gamma } \right) - \frac{{c_{1} D\left( p \right)\eta T^{2} }}{{2n}}\left( {1 - \gamma } \right)^{2} - nA - \alpha T \\ \end{aligned}$$
(5)

In the total profit function (5), they considered the sales revenue function, SR as follows:

$$SR=p\beta D\left(p\right)\frac{{\gamma }^{2}{T}^{2}}{2n}+\frac{pD(p)T}{n}\left[\left(1-\gamma \right)-\frac{\eta T}{2n}{\left(1-\gamma \right)}^{2}\right]$$

For example 5, substituting the values of the parameters and their obtained optimal values of the decision variables in their profit function, we have found the SR value as $5019.514271 and the maximal total profit as − 15,699.44. However, they showed the optimal total profit for this example problem as $70,512.81, which is greater than the sales revenue. All these anomalies clearly demonstrate that their solution procedure has failed in providing the accurate optimal solution to the problem.

Note that only the partial backorder level during the time \({t}_{1}\) to T/n is satisfied instead of the full demand. So, the partial backorder level at any time t, B(t) (instead of D(p)) is used in calculating the SR value in this period, where

$$B\left(t\right)=\frac{D\left(p\right)}{\eta }\left\{{e}^{-\eta \left(\frac{T}{n}-t\right)}-{e}^{-\eta \left(\frac{T}{n}-{t}_{1}\right)}\right\}, {t}_{1}\le t\le \frac{T}{n}$$

Thus, we have calculated the sales revenue function as follows:

$$SR=np{\int }_{0}^{{t}_{1}}\left(D\left(p\right)+\beta I\left(t\right)\right)dt+np{\int }_{{t}_{1}}^\frac{T}{n}B\left(t\right)dt$$
$$\Rightarrow SR\,=\,npD\left(p\right){t}_{1}+\frac{\beta npD\left(p\right)}{{\left(\lambda \left(\alpha \right)+\beta \right)}^{2}}\left[{e}^{\left(\lambda \left(\alpha \right)+\beta \right){t}_{1}}-{\left(\lambda \left(\alpha \right)+\beta \right)}{t}_{1}-1\right]+\frac{npD\left(p\right)}{\eta }\left[\frac{1}{\eta }\left(1-{e}^{-\eta \left(\frac{T}{n}-{t}_{1}\right)}\right)-\left(\frac{T}{n}-{t}_{1}\right){e}^{-\eta \left(\frac{T}{n}-{t}_{1}\right)}\right]$$

Setting, \({t}_{1}=\frac{\gamma T}{n}, 0<\gamma <1\) and applying Taylor series for small value of \(x\), we obtain

$$SR=pD\left(p\right)\gamma T+\beta pD\left(p\right)\frac{{\gamma }^{2}{T}^{2}}{2n}+\frac{pD(p){T}^{2}}{2n}{\left(1-\gamma \right)}^{2}\left\{1-\frac{\eta T}{n}\left(1-\gamma \right)\right\}$$

In (5) the term \(-\frac{cD\left(p\right)\eta {T}^{2}}{2n}{\left(1-\gamma \right)}^{2}\) should be \(\frac{cD\left(p\right)\eta {T}^{2}}{2n}{\left(1-\gamma \right)}^{2}\).

Also in (5), the term.

\(-\frac{sD\left(p\right)}{2n}\left(2\gamma {T}^{2}-{\gamma }^{2}{T}^{2}-{T}^{2}\right)-nsD\left(p\right)+\frac{sD\left(p\right)\eta T}{2}\left(1-\gamma \right)\) should be \(-\frac{sD\left(p\right){T}^{2}}{2n}{\left(1-\gamma \right)}^{2}\left\{1-\frac{\eta T}{n}\left(1-\gamma \right)\right\}\)

since this is a shortage cost, SC and it can be found as follows:

$$SC=ns{\int }_{{t}_{1}}^\frac{T}{n}B\left(t\right)dt=ns{\int }_{{t}_{1}}^\frac{T}{n}\frac{D\left(p\right)}{\eta }\left\{{e}^{-\eta \left(\frac{T}{n}-t\right)}-{e}^{-\eta \left(\frac{T}{n}-{t}_{1}\right)}\right\}dt$$
$$\Rightarrow SC =\frac{nsD\left(p\right)}{\eta }\left[\frac{1}{\eta }\left(1-{e}^{-\eta \left(\frac{T}{n}-{t}_{1}\right)}\right)-\left(\frac{T}{n}-{t}_{1}\right){e}^{-\eta \left(\frac{T}{n}-{t}_{1}\right)}\right]$$

Setting,\({t}_{1}=\frac{\gamma T}{n}, 0<\gamma <1\) and applying Taylor series for small value of \(x\), we find

$$SC=\frac{sD(p){T}^{2}}{2n}{\left(1-\gamma \right)}^{2}\left\{1-\frac{\eta T}{n}\left(1-\gamma \right)\right\}$$

By incorporating these corrections in (5), it can be modified as follows:

$$\begin{aligned} TP\left( {n,\alpha ,p} \right) = & pD\left( p \right)\gamma T + \beta pD\left( p \right)\frac{{\gamma ^{2} T^{2} }}{{2n}} + \frac{{pD\left( p \right)T^{2} }}{{2n}}\left( {1 - \gamma } \right)^{{2}} \left\{ {1 - \frac{{\eta T}}{n}\left( {1 - \gamma } \right)} \right\} \\ &- cD\left( p \right)\gamma T\left\{ {1 + \left( {\lambda \left( \alpha \right) + \beta } \right)\frac{{\gamma T}}{{2n}}} \right\} - cD\left( p \right)T\left( {1 - \gamma } \right)\left\{ {1 - \frac{{\eta T}}{{2n}}\left( {1 - \gamma } \right)} \right\} - hD\left( p \right)\left( {\frac{{\gamma ^{2} T^{2} }}{{2n}}} \right) \\ &- \frac{{sD(p)T^{2} }}{{2n}}\left( {1 - \gamma } \right)^{2} \left\{ {1 - \frac{{\eta T}}{n}\left( {1 - \gamma } \right)} \right\} - c_{1} D\left( p \right)\eta \left( {1 - \gamma } \right)^{2} \frac{{T^{2} }}{{2n}} - nA - \alpha T \\ \end{aligned}$$
(6)

Priyamvada et al. [2] found the optimal value of p, \({p}^{*}\) by equating the first partial derivative of \(TP\left(n,\alpha ,p\right)\) in (5) with respect to p to zero as follows:

$${p}^{*}=\frac{2{n}^{2}bc\gamma T+bcn{\gamma }^{2}{T}^{2}\left(\lambda \left(\alpha \right)+\beta \right)+2{n}^{2}bcT\left(1-\gamma \right)+nhb{\gamma }^{2}{T}^{2}+aT\left(\beta {\gamma }^{2}Tn+2n\left(1-\gamma \right)-nT{\left(1-\gamma \right)}^{2}\right)-2nbs{T}^{2}\left(2\gamma -{\gamma }^{2}-1\right)}{2nb\beta {\gamma }^{2}{T}^{2}+bT\left(2n-2n\gamma -nT-nT{\gamma }^{2}+2nT\gamma \right)}$$
(7)

However, this formula seems to be incorrect. The analogous formula we obtain by equating the first partial derivative of \(TP\left(n,\alpha ,p\right)\) in (6) with respect to p to zero as follows (derivation of this formula is given in Appendix 2):

$${p}^{*}= \frac{{bc\gamma }^{2}{T}^{2}\left(\lambda \left(\alpha \right)+\beta \right)+2nT(bc+a\gamma ){+\gamma }^{2}{T}^{2}(bh+a\beta ){+T}^{2}{\left(1-\gamma \right)}^{2}\left[\left\{1-\frac{\eta T}{n}\left(1-\gamma \right)\right\}\left(a+bs\right)+b\eta ({c}_{1}-c)\right]}{2b\gamma T(2n + \beta \gamma T)+2b{T}^{2}{\left(1-\gamma \right)}^{2}\left\{1-\frac{\eta T}{n}\left(1-\gamma \right)\right\}}$$
(8)

Using the updated version of the profit function (6) and the formula for calculating \({p}^{*}\) in (8), we have found the optimal solution to their numerical example problem 5. The comparative optimal solutions to this problem obtained by Priyamvada et al. [2] (with the corrected maximal profit) and our modified version of it is given in Table 2.

Table 2 A comparative study of the results of the studied numerical example problem 5
Full size table

From Table 2 it can easily be understood that the total profit is increased significantly by our updated version in this case of partial backordering. Besides, the values of the decision variables in our optimal solutions are different from their corresponding ones. Thus our corrections of erroneous mathematical expressions in the model, the sales revenue function and the formula for obtaining the optimal value of p, result in achieving the accurate optimal solution to the problem.

4 Managerial insight

Generally, production-operations managers deal with the maximization of profit by selling their products to customers. The correct maximization of that profit is dependent upon correct modelling of the problem, as well as on the available correct optimal solution technique to that model. This technical note demonstrates the incapability of the Priyamvada et al. [2] recently revised models and their erroneous solution techniques to them. Hence it presents the revised version of them in order to obtain the correct optimal solution to the concerned problem. It enables managers to not be misled with an erroneous solution to a relevant problem. Thus the technical note developed here helps the managers in finding the maximal profit solution to the problem correctly, by following this correct revised method.

5 Conclusion

We have found some anomalies in our analyses of the revised models of Priyamvada et al. [2] and demonstrated them. Their models have been rectified by taking into account these anomalies. The importance of the updated models and the optimal values of the variable p in obtaining optimal solutions to them are highlighted with the optimal solutions to numerical example problems. In both the cases of complete and partial backordering of demand, the maximal profits for all the studied numerical example problems obtained by our updated versions are found to increase significantly from Priyamvada et al. [2] corresponding ones. Thus, it has been demonstrated here that Priyamvada et al. [2] revised versions of Mishra et al. [1] models are still incapable of leading to the maximal profit solutions to the studied problems. Consequently, without refinement of Priyamvada et al. [2] models, they could be misleading to the industrial management and hence to the generation of inappropriate profit for a concerned organization. Therefore, our modifications of their models and the optimal values of the variable p in this study have provided a scope to the managers in obtaining the accurate maximal profit solution to the considered problem.