Abstract
This article presents a single-vendor and a single-buyer joint economic lot size (JELS) production-distribution inventory model with the prime aim on; the effect of the investment on ordering cost reduction, back order price discount and reduction on lead time. The produced items are delivered to the buyer by adopting a geometric shipment policy. Two continuous review models are developed by assuming that the lead time demand follows a normal distribution and distribution-free. Two types of investments are incorporated to reduce the ordering cost. They are (i) logarithmic investment function and (ii) power investment function. The minimax distribution free approach is adopted in the distribution-free model to find the optimal values of the decision variables by minimizing the expected annual total cost of the system. Numerical examples are given to validate the proposed models. Sensitivity analysis is also performed to analyze the behavior of the key parameters on lot size, ordering cost, backorder price discount, the number of shipments from the vendor to the buyer in one production run and the expected annual total cost of the proposed models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Success in the competitive business environment and optimization of performance anticipate an integrated policy as a new paradigm to be adopted by business organizations. Integrated policy is nothing but, the cost function consisting of both buyer total cost and vendor total cost. In today’s challenging environment, integration among the members in a supply chain is the key mantra for its success for all the entities in supply chain as it offers improved customer satisfaction and loyalty. It was observed by Lin [29] that the integrated inventory management system is a common practice in the global markets and the vendor and the buyer benefits economically. Several supply chain researchers captivated the integrated policy to study the effect of integration between a vendor and a buyer as it helps to shorten lead time and reduce the cost of inventory [9]. It also helps to identify problem areas; take decisive action and further reduce the cost to improve the final price; enables the system to meet unexpected disruptions. Many researchers analyzed the potential benefits of ordering time/cost reduction to inventory systems. Porteus [37] investigated the impact of capital investment in reducing ordering cost in the classical EOQ model. Business organizations have recognized the significance of prompt delivery of goods to customers as an instrument to grab the customers; a competitive weapon and as means of differentiating themselves in the market. Hoque [25] had revealed that lead time is approximately normally distributed around its mean value. But in reality, it is not always feasible to get enough data to estimate the probability density function of the lead time demand. So researchers have worked on developing integrated models in which the lead time demand is distribution-free. Giri and Sharma [12] had worked on JELS model with unequal geometric shipment policy for imperfect items as a geometric shipment policy might reduce the total cost of the integrated system. From the literature review, it is found that very few JELS models dealing with geometric shipment policy analyze the impact of distributions of lead time demand on the expected total cost of the integrated system. To the best of author’s knowledge, no integrated model dealing with geometric shipment policy have incorporated the effects of investment on ordering cost reduction and lead time. As reduction in lead time plays a vital role to improve customer loyalty by improving the on-time delivery of the products, the present study develops an integrated model by adopting a geometric shipment policy. It is assumed that an extra investment is made to reduce the ordering cost and lead time effectively. Two different types of investment functions are taken in to consideration in two different models. Firstly, we assume that the lead time demand follow a normal distribution. This assumption was relaxed and optimal policies are determined using minimax distribution-free approach. For the above said two cases, we incorporated two types of investment functions to reduce the ordering cost. In the distribution-free approach the first and second moments of the probability distribution of lead time demand are known and finite. Shortages are allowed and are partially backordered. The contribution of this article is to minimize the expected annual total cost of the integrated system by optimizing the number of shipments, first shipment quantity, ordering cost of the buyer, safety factor and the backorder price discount offered by the vendor to the buyer.
2 Literature review
Goyal [17] is among the pioneers who carried out works on integrated inventory model. Goyal’s model [17] was modified by Banerjee [2] in which a joint economic lot size model was considered by adopting a lot-for-lot policy. Goyal [18] presented a generalized model in which the lot-for-lot policy is relaxed and insisted that vendor’s economic production quantity must be an integral multiple of buyer’s order quantity. Lu [31] gave an optimal solution to the single-vendor single-buyer problem under the assumption that the items are supplied in integral number of equal shipments. But, Goyal [19] showed that a different shipment policy consisting of successive shipments increasing by a factor equal to the production rate divided by the demand rate gave a better solution. Hill [21] has discussed a generalized shipment policy in a single-vendor single-buyer production-inventory model. Hill [22] suggested a more general batching and shipping policy in which the successive shipment size of the first m shipments increase by a fixed factor and the remaining shipments are of equal size. Integrated production inventory model with unequal shipment size was developed by Giri and Sharma [11]. Later, several researchers [20, 24, 42, 44, 45] have developed integrated production-distribution inventory models by extending the idea of Goyal [18] and incorporating various realistic assumptions. It is often assumed by researchers that the demand is deterministic and shortages are not allowed. But it is not always suitable in a realistic environment. To fit in a more practical situation, Ben-Daya and Hariga [4] developed an integrated model by allowing shortages and considering stochastic demand. As globalization and technological advancement always creates anxiety in the trading system, lead time and ordering cost reduction are two key criteria that are to be focused the success of any business and have attracted considerable research attention. In a real-life situation, lead time cannot be treated as a constant it has to be treated as a variable. At this backdrop, much effort is being taken by enterprises to reduce lead time and earn customer satisfaction. Lead time reduction helps to reduce safety stock, loss due to out-of-stock and increase the competitive advantage of business. It is also clear that reduction in lead time could be achieved only by extra investments [39]. Lead time is controllable and has drawn the attention of many researchers to work on integrated models with investment on lead time reduction.
Hsu and Lee [26] revealed that lead time could be reduced by investing an additional amount on high-tech equipment, information technology, order expedite and logistics. The first attempt to formulate a probabilistic inventory model with lead time as decision variable was made by Liao and Shyu [32]. By treating the lead time as a decision variable, Pan and Yang [39] generalized Goyal’s model [18] and found that the joint total expected cost and lead time are less compared to that of Goyal’s model [18]. Later, Ouyang et al. [34] extended the model of Pan and Yang [39] by considering the lead time demand as stochastic. Researchers [13, 14, 23, 35] had worked on lead time reduction by formulating integrated production-inventory models in a single-vendor single-buyer supply chain environment. Glock [15, 16] has given a comprehensive review on JELS models. Sajadieh et al. [43] focused on stochastic lead time between the vendor and buyer.
In modern production management, ordering cost reduction is another criterion which should be focused for the success of any venture and have attracted much research attention. Efficient worker training, procedural changes, and hi-fi equipment acquisition enables ordering cost reduction. Porteus [37] first introduced and developed an EOQ model including the investment on set-up cost reduction. The influence of ordering cost reduction on modified continuous review inventory systems involving variable lead time and partial backorders was investigated by Ouyang et al. [33]. Later, Woo et al. [46] developed an integrated inventory model for a single vendor and multiple buyers with ordering cost/setup cost reduction. Zhang [47] extended Woo et al.’s [46] model by relaxing the assumption that the cycle times for all buyers and the vendor are the same. Later, some researchers [1, 6, 7, 27] addressed setup cost/ordering cost reduction inventory models under various assumptions. An integrated vendor-buyer inventory policy for a continuous review model with a random number of defective items and screening process gradually at a fixed screening rate in buyer’s arriving order lot was developed by [30].
In the current market scenario, the customer’s demands and preferences are changing very fast. So, customer satisfaction is paramount for an organization. Due to fluctuations in demand, it is not always possible to satisfy the demand of the customers completely. Some customers wait and backorder their demand, while, others may move to other vendor or to other brands of the same product. So, to motivate the customers to accept backorders, a buyer could offer a price discount on a stock-out item which leads to high customer loyalty. In order to reduce the cost of lost-sales and the holding cost which in turn minimizes the total inventory cost, it is highly imperative to control the backorder price discount. Researchers [5, 29, 36, 38, 40, 41] have focused on price discount offer by the buyer to the customers in order to increase the backorders. Certain organizations such as Procter and Gamble, Southwest Airlines, Nike, Disney, Nordstrom, Wal-Mart, McDonald’s, Marriot Hotels, and several Japanese and European companies are focused and work effectively towards the changing customer needs. They observed that the price discount offer increased the number of backorders [28]. They had also revealed that increase in the price discount increases the backorder ratio. So the discussion on the decision-making problem to find the optimal backorder ratio which minimizes the relevant inventory total cost is worth mentioning. A comparison of the present model with related existing models is given in Table 1.
The rest of the paper is organized as follows. Notations and assumptions needed for developing the models are presented in the next section. An integrated inventory model is developed in Sect. 4. The optimal solution procedure is presented in Sect. 5 by incorporating the two types of investment functions in the integrated inventory model. Further, models are extended in two ways: (i) lead time demand follows a normal distribution (ii) lead time demand is distribution free and by including the two types of investment functions in each model. An efficient algorithm is proposed to find the optimal solution. Numerical results are provided in Sect. 6. Sensitivity analysis with respect to various system parameters is carried out in Sect. 7. The paper is concluded with some remarks and future research directions in Sect. 8.
3 Notation and assumptions
To develop the proposed model, we adopt the following notations and assumptions.
3.1 Notation
- D :
-
Buyer’s expected demand rate in units per unit of time
- P :
-
Vendor’s production rate in units per unit of time, \(P>D\)
- \(A_{{0}}\) :
-
Buyer’s original ordering cost per order (before an investment is made)
- \(A_{v}\) :
-
Vendor’s setup cost per setup
- \(h_b\) :
-
Buyer’s holding cost per unit
- \(h_v\) :
-
Vendor’s holding cost per unit
- \(q_{i}\) :
-
Size of the \(i\mathrm{th}\) shipment
- Q :
-
Vendor’s production batch size
- \(\lambda\) :
-
Geometric growth factor
- \(T_{r}\) :
-
Transportation cost per shipment
- s :
-
Safety stock of the buyer
- X :
-
The lead time demand in units per unit of time, a random variable
- \(f_x(x)\) :
-
The probability density function (p.d.f) of X with finite mean DL and standard deviation \(\sigma \sqrt{L}\), where \(\sigma\) denotes the standard deviation of the demand in units per unit of time
- \(E(\cdot )\) :
-
Mathematical expectation
- \(x^{+}\) :
-
Maximum value of x and 0, i.e., \(x^{+} = \text {max}\{x,0\}\)
- \(\beta\) :
-
Fraction of the shortage backordered at the buyer’s end, \(0\le \beta <1\)
- \(\beta _{0}\) :
-
Upper bound of the backorder ratio, \(0\le \beta _{0} <1\)
- \(\pi _{0}\) :
-
Marginal profit (i.e., cost of lost demand) per unit
- r :
-
Reorder point of the buyer
Decision variables
- n :
-
Number of shipments
- \(A_{b}\) :
-
Buyer’s ordering cost per order
- \(q_{1}\) :
-
Size of the first shipment from the vendor to the buyer
- L :
-
Length of lead time for the buyer
- \(\pi _{x}\) :
-
Price discount offered on backorder by the vendor per unit, \(0\le \pi _{x} \le \pi _{0}\)
- k :
-
The safety factor.
3.2 Assumptions
-
1.
A single vendor provides a single product to a single buyer. The buyer orders a lot size of Q units and the vendor produces them with a finite production rate \(P~(P > D)\) in units per unit time in one setup. Produced items are supplied to the buyer in n unequal sized shipments.
-
2.
Shortages are allowed at the buyer’s point and they are partially backordered.
-
3.
The buyer adopts a continuous review inventory policy and places the order whenever the inventory level reaches the reorder level r.
-
4.
The reorder point r = the expected demand during lead time (DL) + safety stock (s), and \(s = k\) \(\times\) (standard deviation of lead time demand), i.e. \(r = DL + k\sigma \sqrt{L}\) [3].
-
5.
The lead time L consists of m mutually independent components. The \(i\mathrm{th}\) component has a normal duration \(b_i\), minimum duration \(a_i\), and crashing cost per unit time \(c_i\) such that \(c_1<c_2< \cdots <c_m.\) The components of lead time are crashed one at a time starting from the first component because it has the minimum unit crashing cost, and then the second component, and so on (see Ouyang et al. [35]).
-
6.
Let \(L_0=\sum _{i=1}^m b_i\), and \(L_i\) be the length of lead time with components \(1,2,\ldots , i\) crashed to their minimum duration, then \(L_i\) can be expressed as \(L_i=L_0-\sum _{j=1}^i (b_j-a_j),~i=1,2,\ldots ,m;\) and the lead time crashing cost per cycle R(L) is given by \(R(L)=c_i(L_{i-1}-L)+\sum _{j=1}^{i-1}c_j~(b_j-a_j),~ L\in [L_i,L_{i-1}]\) (see Ouyang et al. [35]).
-
7.
If a shortened lead time is requested then the extra costs incurred by the vendor will be fully transferred to the buyer. Therefore, lead time crashing cost is the buyer’s cost component.
-
8.
The transportation cost per unit from the vendor to the buyer is constant and independent of the ordering quantity.
4 Model development
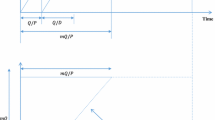
The joint economic lot size model is framed as follows and the diagrammatic representation can be seen in Figs. 1, 2 and 3. The vendor produces Q units at one set-up with a finite production rate P (\(P>D\)). As per the policy adopted by Darwish [8], items are delivered to the buyer in n unequal-sized shipments and the size of the \(i\mathrm{th}\) shipment within a batch is \(q_{i} = \lambda q_{i-1}=\lambda ^{i-1}q_{1}\), \(i=2,3,\ldots ,n\) and \(q_{1}\) is the lot size of the first shipment. Thus the size of the production lot is
and cycle length of the inventory is \(T = \frac{Q}{D}=\frac{q_{1}(\lambda ^{n}-1)}{D(\lambda - 1)}\).
4.1 Buyer’s perspective
It is assumed that as soon as the buyer’s inventory reaches the re-order level r, an order of size \(q_i\) is placed to the vendor at the \(i\mathrm{th}\) shipment. The vendor delivers these items after a constant lead-time L in n unequal-sized shipments. By assumption, since the safety factor k is related to the re-order point, k is considered a decision variable instead of r. The buyer receives a batch of \(q_{i}\) units in each shipment which could be utilized during the time period \(q_{i}/D\). So, the average inventory of the buyer during the time period \(q_{i}/D\) is \(q_{i}/2\) which gives the time-weighted inventory during a complete production cycle as
Hence the average inventory of the buyer is \(\frac{q_{1}^{2}(\lambda ^{2n}-1)}{2D(\lambda ^{2}-1)}/\frac{q_{1}(\lambda ^{n}-1)}{D(\lambda - 1)} = \frac{q_{1}(\lambda ^{n}+1)}{2(\lambda +1)}\). For each shipment the buyer incurs an ordering cost \(A_{b}\) and so the buyer’s ordering cost per cycle is \(nA_{b}\). In reality, owing to certain unpredictable situations, higher demand may cause a stock out situation for the buyer before the shipment arrives. Thus at the end of each cycle the expected shortage demand is given by \(E(X-r)^{+}\). Hence the expected number of back orders per cycle is \(\beta E(X-r)^{+}\) where \(\beta = \frac{\beta _{0}\pi _{x}}{\pi _{0}}\) (as in Lin [29]) and \(0\le \beta _{0} <1\), \(0\le \pi _{x}\le \pi _{0}\). So, \(\pi _{x}\) is treated as a variable. The expected shortage cost per unit time is
The expected net inventory level just before an order arrives is \(r-DL+(1-\beta )E(X-r)^{+}\) and hence the buyer’s expected holding cost per unit time is
In order to reduce the ordering cost from the original level \(A_{{0}}\) to the target level \(A_{b}\), a one-time capital cost investment \(I(A_{b})\) which is a function of the ordering cost is inevitable. Thus, the annual cost of such an investment is \(\tau I(A_{b})\), where \(\tau\) is the annual fractional cost of capital investment (e.g.,interest rate). In a competitive business environment lead time reduction is indispensable as it accelerates sales. So the lead time crashing cost per unit time is \(n R(L)/T = \frac{nD(\lambda - 1)R(L)}{q_{1}(\lambda ^{n}-1)}\), where R(L) is the lead time crashing cost for one cycle. Based on the above facts, buyer’s expected annual total cost per unit time is the sum of the investment opportunity cost, ordering cost, holding cost, transportation cost, stock-out cost and the lead time crashing cost and is given by
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\) and where \(G(\pi _{x})=\pi _{0}-\beta _{0}\pi _{x}+\frac{\beta _{0}\pi _{x}^{2}}{\pi _{0}}> 0\) as \(\frac{\pi _{0}}{\pi _{x}}> \beta _{0}(1-\frac{\pi _{x}}{\pi _{0}})>0\).
4.2 Vendor’s perspective
As soon as the vendor receives an order for Q units, he produces them at a rate \(P > D\) and supplies them in n unequal-sized shipments. When the production process is about to start, the vendor’s inventory level is zero and there are \(Dq_{1}/P\) units in the buyer’s inventory which is enough to satisfy the demand until the first shipment arrives. The vendor’s inventory level increases at a rate of \(P-D\) units and the total inventory level reaches the maximum height of \(Dq_{1}/P+(P-D)q_{1}(\lambda ^{n}-1)/(P(\lambda -1))\). Therefore average total inventory in the system is \(Dq_{1}/P+(P-D)(\lambda ^{n}-1)/(2P(\lambda -1))\).
Hence vendor’s average inventory = total system inventory - buyer’s average inventory.
Therefore, the vendor’s expected holding cost per unit time is \(h_{v} \left[ \frac{Dq_{1}}{P}+\frac{(P-D)q_{1}(\lambda ^{n}-1)}{2P(\lambda -1)}-\frac{q_{1}(\lambda ^{n}+1)}{2(\lambda +1)}\right]\). On the other hand, the vendor incurs \(A_{v}\) per set-up and as the production quantity for the vendor in a lot is Q units, the expected set-up cost per unit time is \(A_{v}D/Q\). Vendor’s expected annual total cost per unit time is the sum of the set-up cost and the holding cost and is given by
4.3 Integrated approach
The objective of this section is to determine the optimal values of the decision variables by minimizing the expected annual total cost per unit time of the integrated system which is the sum of the vendor’s expected annual total cost per unit time and the buyer’s expected annual total cost per unit time. Consequently the expected annual total cost per unit time of the integrated system is
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\).
Special cases: (i) When \(\lambda =1\) (equal-sized shipments), few terms of the total cost function becomes indeterminate. So, applying L’Hospital’s rule we get,
That is,
which is similar to the expected annual total cost per unit time of the integrated system of in Lin’s model [29] when \(T_{r}=0\).
(ii) When \(\lambda = \frac{P}{D}\) (Goyal policy), the expected annual total cost per unit time of the integrated system becomes
5 Optimal solution procedure
5.1 Investment in ordering cost reduction
In this section we study the effects of investment on ordering cost reduction by considering two different types capital cost investment functions. Here logarithmic and power functional forms which are convex and strictly decreasing functions as discussed by Porteus [37] are utilized.
Case(i) Logarithmic investment cost functional form
The capital investment \(I(A_{b})\) to reduce the ordering cost is considered as a logarithmic function of the ordering cost. That is,
where \(\delta\) is the percentage decrease in ordering cost \(A_{b}\) relative to per dollar increase in investment \(I(A_{b})\). Using Eq. (9) in (8) we get the expected annual total cost per unit time as
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\) and where the superscript L in EATCI denotes the logarithmic investment function case.
Case(ii) Power investment cost functional form
The capital investment \(I(A_{b})\) to reduce the ordering cost is considered as a power function of the ordering cost. That is,
where \(\alpha\) and \(\omega\) are constants.
Using Eq. (11) in (8) we get the expected annual total cost per unit time as
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\) and where the superscript P in EATCI denotes the power investment function case.
5.2 Lead time demand follows a normal distribution
As considered by Lin [29], let the lead time demand X follow a normal distribution with pdf \(f_{x}(x)\), finite mean DL and standard deviation \(\sigma \sqrt{L}\) so that \(r=DL+k\sigma \sqrt{L}\), \(E(X-r)^{+}=\int _r^{\infty }(x-r)f_{x}(x)dx=\sigma \sqrt{L}\psi (k)\), where \(\psi (k)\equiv \varphi (k)-k[1-\Phi (k)]>0\), \(\varphi (k)\) and \(\Phi (k)\) represent the standard normal probability density function (pdf) and cumulative distribution function respectively. Then the expected annual total cost per unit time given by Eqs. (10) and (12) can be rewritten as follows.
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\).
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\). Here the subscript N in \(EATCI^{L}\) and \(EATCI^{P}\) denotes the normal distribution case.
In both the logarithmic and power investment function cases, the optimal values of the decision variables are determined by minimizing the expected annual total cost per unit time given by Eqs. (13) and (14). Now let us consider the logarithmic investment function case and an analogous procedure can be applied to the other case.
It is observed that the expected annual total cost per unit time is convex with respect to each of the variable except L keeping other variables fixed (see Observation 1 in Appendix 1). Next, for a fixed n and \(L \in [L_{i}, L_{i-1}]\), the values of of the decision variables \(q_{1}\), k, \(A_{b}\), \(\pi _{x}\) are obtained by equating the corresponding first order derivatives of \(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) to zero. That is by setting Eqs. (32), (34) (36), and (38) to zero, the values of the decision variables \(q_{1}\), \(\pi _{x}\), \(A_{b}\) and \(\Phi (k)\) are as follows:
The value of k can be obtained from Eq. (18). As in the logarithmic investment cost functional case, it can be verified that for a fixed \(n, q_{1}, k, A_{b}, \pi _{x}\), \(EATCI_{N}^{P}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is concave in \(L \in [L_{i}, L_{i-1}]\). It can also be verified that \(EATCI_{N}^{P}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex with respect to each of the decision variable for a given set of the remaining variables. Therefore for a fixed n and \(L\in [L_{i}, L_{i-1}]\), the values of decision variables which minimizes the cost function is obtained by setting the respective first order partial derivatives of \(EATCI_{N}^{P}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) to zero. The closed form solutions of \(q_{1}, \pi _{x},\Phi (k)\) are similar to those obtained in the logarithmic investment cost functional case. In addition, buyer’s ordering cost is given as
We can establish the following algorithm to find the optimal values of the decision variables.
5.3 Algorithm
- Step 1 :
-
Set \(n=1\).
- Step 2 :
-
For every \(L_i\), \(i=1,2,\ldots ,m\) perform steps (2.1)–(2.4).
- Step 2.1:
-
Start with \(A_{bi}^{(1)}=A_{0}\), \(k_{i}^{(1)}=0\), \(\pi _{ix}^{(1)}=\pi _{0}\).
- Step 2.2:
-
Substitute \(A_{bi}^{(1)}\), \(k_{i}^{(1)}\), \(\pi _{ix}^{(1)}\) in Eq. 15 and evaluate \(q_{i1}^{(1)}\).
- Step 2.3:
-
Utilizing \(q_{i1}^{(1)}\) find the values of \(\pi _{ix}^{(2)}\) and \(A_{bi}^{(2)}\) from Eqs. (16) and (17) respectively.
- Step 2.4:
-
Now find the value of \(k_{i}^{(2)}\) from Eq. (18) by using \(q_{i1}^{(2)}\) and \(\pi _{ix}^{(2)}\).
- Step 2.5:
-
Repeat steps (2.1)–(2.4) until no change occur in the values of \(q_{i1}\), \(k_i\), \(A_{ib}\) and \(\pi _{ix}\). Denote the solutions by \((\bar{q}_{i1},\bar{\pi }_{ix},\bar{A}_{ib},\bar{k}_i)\).
- Step 3 :
-
Compare \(\bar{\pi }_{ix}\) and \(\bar{A}_{ib}\) with \(\pi _0\) and \(A_{0}\) respectively.
- Step 3.1:
-
If \(\bar{\pi }_{ix}<\pi _0\) and \(\bar{A}_{ib}<A_{0}\), then the solution found in Step 2 is optimal for the given \(L_i\). We denote the optimal solution by \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)\). i.e., \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)=(\bar{q}_{i1},\bar{\pi }_{ix},\bar{A}_{ib},\bar{k}_i)\). Go to step 4.
- Step 3.2:
-
If \(\bar{\pi }_{ix}\ge \pi _0\) and \(\bar{A}_{ib}<A_{0}\), then for this \(L_i\), letting \(\hat{\pi }_{ix}=\pi _0\), repeat step 2 to determine the new set \((\bar{q}_{i1},\bar{A}_{ib},\bar{k}_i)\) and denote the optimal solutions by \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)\). i.e., \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)=(\bar{q}_{i1},{\pi }_{0},\bar{A}_{ib},\bar{k}_i)\). Go to step 4.
- Step 3.3:
-
If \(\bar{\pi }_{ix}<\pi _0\) and \(\bar{A}_{ib}\ge A_{0}\), then for this \(L_i\), letting \(\hat{A}_{ib}= A_{0}\), repeat step 2 to determine the new set \((\bar{q}_{i1},\bar{\pi }_{ib},\bar{k}_i)\) and denote the optimal solutions by \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)\). i.e., \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)=(\bar{q}_{i1},\bar{\pi }_{ix},{A}_{b0},\bar{k}_i)\). Go to step 4.
- Step 3.4:
-
If \(\bar{\pi }_{ix}\ge \pi _0\) and \(\bar{A}_{ib}\ge A_{0}\), then for this \(L_i\), letting \(\hat{\pi }_{ix}=\pi _0\) and \(\hat{A}_{ib}= A_{0}\) repeat step 2 to determine the new set \(\bar{q}_{i1}\) and denote the optimal solutions by \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)\). i.e., \((\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i)=(\bar{q}_{i1},{\pi }_{0},{A}_{b0},\bar{k}_i)\). Go to step 4.
- Step 4 :
-
By using Eq. (13) find the corresponding expected total integrated cost \(EATCI_{N}^{L}(\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i,L_i,n)\) for \(i=1,2,\ldots ,m\).
- Step 5 :
-
Find \(\min \limits _{i=1,2,\ldots ,m}EATCI_{N}^{L}(\hat{q}_{i1}, \hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i,L_i,n)\) and denote it by \(EATCI_{N}^{L}(\hat{q}_{1(n)}, \hat{\pi }_{x(n)},\hat{A}_{b(n)}, \hat{k}_{(n)},L_{(n)},n)=\min \limits _{i=1,2,\ldots ,m}EATCI_{N}^{L}(\hat{q}_{i1}\), \(\hat{\pi }_{ix},\hat{A}_{ib}, \hat{k}_i,L_i,n)\) and \((\hat{q}_{1(n)}, \hat{\pi }_{x(n)},\hat{A}_{b(n)}, \hat{k}_{(n)},L_{(n)})\) are the optimal solutions for given n.
- Step 6 :
-
Replace n by \(n+1\) and repeat steps 2–5 to get \(EATCI_{N}^{L}(\hat{q}_{1(n)}, \hat{\pi }_{x(n)},\hat{A}_{b(n)}, \hat{k}_{(n)}\), \(L_{(n)},n)\).
- Step 7 :
-
If \(EATCI_{N}^{L}(\hat{q}_{1(n)}, \hat{\pi }_{x(n)},\hat{A}_{b(n)}, \hat{k}_{(n)},L_{(n)},n)\le EATCI_{N}^{L}(\hat{q}_{1(n-1)}, \hat{\pi }_{x(n-1)},\hat{A}_{b(n-1)}\), \(\hat{k}_{(n-1)},L_{(n-1)},n-1)\) then go to step 6 otherwise go to step 8.
- Step 8 :
-
Set \((\hat{q}_{1}, \hat{\pi }_{x},\hat{A}_{b}, \hat{k},\hat{L},\hat{n})=(\hat{q}_{1(n-1)}, \hat{\pi }_{x(n-1)},\hat{A}_{b(n-1)}, \hat{k}_{(n-1)},L_{(n-1)},n-1)\), and \(EATCI_{N}^{L}(\hat{q}_{1}, \hat{\pi }_{x},\hat{A}_{b}, \hat{k},\hat{L},\hat{n})\) is the minimum expected total integrated cost and \((\hat{q}_{1}, \hat{\pi }_{x},\hat{A}_{b}, \hat{k},\hat{L},\hat{n})\) is the set of optimal solutions.
5.4 Lead time demand is distribution free
In order to accommodate a more practical situation and as it is not always viable to get adequate distributional information regarding lead time, no assumption is made regarding the distribution function of the lead time demand X. Let the cumulative distribution function (C.D.F.) of X belong to the class \(\mathscr {F}\) of c.d.f.s with finite mean DL and standard deviation \(\sigma \sqrt{ L}\). As the probability distribution of X is unknown, the minimax distribution-free approach [34] is adopted here to find the optimal values of the decision variables. For each \((n, q_{1}, k, A_{b}, \pi _{x}, L)\), the minimax distribution-free approach helps to find the most unfavorable c.d.f. \(\Phi\) in \(\mathscr {F}\) and then the expected annual total cost function is minimized. Thus the problem is formulated as follows:
where
To facilitate further exploration we use the the following proposition asserted by Gallego and Moon [10].
Proposition 1
For any \(\Phi \in \mathscr {F}\),
Moreover the upper bound of the above equation is tight.
Using Proposition 1 and \(r=DL+k\sigma \sqrt{L}\) in Eqs. (10) and (12), problem (20) can be formulated as follows:
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\) and where \(K=(\sqrt{1+k^{2}}-k)/2\). and
subject to \(0< A_{b}\le A_{{0}}\), and \(0\le \pi _{x} \le \pi _{0}\). Here the subscript F in \(EATCI^{L}\) and \(EATCI^{P}\) denotes the distribution free case.
It is observed that the expected annual total cost per unit time is convex with respect to each of the variable except L keeping other variables fixed (see Appendix 1). Next, for a fixed n and \(L \in [L_{i}, L_{i-1}]\), the values of of the decision variables \(q_{1}\), k, \(A_{b}\), \(\pi _{x}\) are obtained by equating the corresponding first order derivatives of \(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) to zero. That is by setting Eqs. (42), (44), (46) and (48), to zero, the values of of the decision variables \(q_{1}\), k, \(A_{b}\), \(\pi _{x}\) are as follows:
where
As in the logarithmic investment cost functional case, it can be verified that for a fixed \(n, q_{1}, k, A_{b}, \pi _{x}\), \(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is concave in \(L \in [L_{i}, L_{i-1}]\). It can also be verified that \(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex with respect to each of the decision variable given a set of the remaining variables. Therefore for a fixed n and \(L\in [L_{i}, L_{i-1}]\), the values of decision variables which minimize the cost function are obtained by setting the respective first order partial derivatives of \(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) to zero. The closed form solutions of \(q_{1}, \pi _{x}, k\) are similar to those obtained in the logarithmic investment cost functional case. In addition, buyer’s ordering cost is given as
To find the optimal values of the decision variables we can utilize an algorithm similar to that of the logarithmic investment cost functional case.
6 Numerical results
In this section, to illustrate the above solution procedure we consider the adaptive parameters similar to that proposed by Lin [29]. The optimal values of the decision variables are obtained by using the solution procedure and the MATLAB software. \(D=200\) units/year, \(P = 1000\) units/year, \(A_{0} = \$ 200\)/order, \(A_v = \$1500\)/setup, \(T_{r}\)=$30 /shipment, \(h_b\) = $25/unit, \(h_v\) = $20/unit, \(\lambda\) = 1.5, \(\tau\) = 0.1, \(\sigma\) = 7 units per week, where 1 year = 52 weeks, the lead time has three components with data shown in Table 2 and the summarized information of the lead time components is given in Table 3.
Example 6.1
Assume that the lead time demand follows a normal distribution.
Case 1 : Logarithmic investment cost functional form
Letting \(\delta\) = 0.03 and \(A_{0} = \$ 200\)/order and applying the algorithm yields the result as in Table 4. To analyze the effects of ordering cost reduction and backorder price discount, optimal results of the no-investment and no-price discount policy are provided in the same table. From Table 4, it is clear that when no attempt is made to reduce the ordering cost and if price discount is not allowed then the expected total annual cost is \(\$4825\) when \(L=3\) weeks and the ordered units could be supplied in two shipments with an initial lot size of 81 units. But, if an additional cost of \(I(A_{b}) =\$ 183\) is spent then the expected total annual cost is reduced to \(\$4331\) when \(L=4\) weeks and the ordering cost reduces to \(\hat{A}_{b}=\$ 0.83\). This reveals that the system could earn an additional savings of \(\$494\) which is cost saving of \(10.24\%\).
Case 2 : Power investment cost functional form
Let \(\alpha = 2000\) and \(\omega = 0.01\). The optimal results are provided in Table 5. To analyze the effects of ordering cost reduction and backorder price discount, optimal results of the no-investment and no-price discount policy are provided in the same table. From the table it is clear that if an additional cost of \(I(A_{b}) =\$ 117\) is spent then the expected total annual cost is minimum when \(L= 4\) weeks and the ordering cost reduces to \(\hat{A}_{b}=\$ 0.50\). It is clear that the system could earn an additional savings of \(\$501\) which is cost saving of \(10.38\%\). Comparing Tables 4 and 5 it is observed that the optimal values of the first shipment size, backorder price discount, number of unequal sized shipments and the lead time are almost the same but the expected total annual cost is less in this case when compared to the logarithmic investment cost functional form. This is due to the power investment cost functional form adopted for the capital investment. It reveals that the integrated system could be benefited by more cost savings if power investment cost function is followed.
Example 6.2
Assume that the lead time demand is distribution free.
Case 1 : Logarithmic investment cost functional form
Let \(\delta\) = 0.03 and \(A_{0} = \$ 200\)/order. Consider the same data as in Example 6.1 and the assumptions proposed in Example 6.1, except that the probability distribution of the lead time demand is known. Suppose that the capital investment \(I(A_{b})\) for reducing the ordering cost is in the form of a logarithmic function. Letting \(\delta\) = 0.03 and \(A_{0} = \$ 200\)/order and by applying a computational algorithm similar to the normal distribution case, the optimal solutions obtained are presented in Table 6. To analyze the effects of ordering cost reduction and backorder price discount, optimal results of the no-investment and no-price discount policy are provided in the same table. From the table it is clear that if an additional cost of \(I(A_{b}) =\$ 159\) is spent then the expected total annual cost is minimum when \(L=3\) weeks and the ordering cost reduces to \(\hat{A}_{b}=\$ 1.67\). It is clear that the system could earn additional savings of \(\$383\) which is cost saving of \(7.26\%\).
Case 2 : Power investment cost functional form
Optimal results obtained are tabulated in Table 7. From the table it is clear that if an additional cost of \(I(A_{b}) =\$ 103\) is spent then the expected total annual cost is minimum when \(L=2\) weeks and the ordering cost reduces to \(\hat{A}_{b}=\$ 1.002\). It is clear that the system could earn an additional savings of \(\$390\) which is cost saving of \(7.39\%\). Comparing Tables 6 and 7 it is observed that the optimal values of the first shipment size, backorder price discount, number of unequal sized shipments and the lead time are almost the same but the expected total annual cost is slightly less in this case when compared to the logarithmic investment cost functional form. This is due to the power investment cost functional form adopted for the capital investment. Also the integrated system could be benefited by more cost savings if power investment cost function is followed.
Graphical representations of the optimal solutions for the above examples are given in Fig. 4. It is observed that when the distribution of the lead time demand is unknown then the expected total cost is minimum when \(L=3\) weeks.
7 Sensitivity analysis
In order to take decisions in an effective manner it is necessary to study the effect of changes in the values of the key parameters on the optimal solution. Sensitivity analysis is performed by changing one parameter at a time and keeping the other parameters of Examples 6.1 and 6.2 unaltered. Results are given in Tables 8 and 9 and the graphical interpretations are shown in Fig. 5. Following inferences and managerial implications are observed.
-
(1)
Consider the case when the lead time demand follows a normal distribution. As the value of \(\lambda\) increases, the number of shipments and the first shipment size decrease by a similar pattern for both the type of investment functions. Lead time remains unaltered.
-
(2)
Backorder price discount is slightly sensitive to the increase in the value of \(\lambda\) and is similar for both the type of investment functions.
-
(3)
Increase in the value of \(\lambda\) increases the ordering cost in the case of logarithmic investment function whereas it remain stable in the power investment function case and the cost is comparatively less than that of the previous case. Thus it implies that it is better to adopt a power investment cost function for reducing the ordering cost.
-
(4)
Consider the case when the lead time demand is distribution free. As the value of \(\lambda\) increases, the number of shipments and the lead time remains the same for both the type of investment functions. But the first shipment size decrease by a similar pattern for both the type of investment functions.
-
(5)
From Table 8, it is clear that the first shipment size and backorder price discount are slightly more in the distribution free case which results in the increase in the expected annual total cost of the integrated system.
-
(6)
Table 9 reveals that if the value of upper bound of the backorder ratio \(\beta _{0}\) increases, the expected annual total cost of the integrated system decreases in all the four cases. This results in an increase in the cost saving.
8 Conclusion
In this paper, two level production distribution inventory system consisting of a single-vendor and a single-buyer is developed. Two continuous review models are presented by assuming that the lead time demand follows a normal distribution in the first model and is distribution free in the second model. The main contribution of this study is that the joint total expected cost for the vendor-buyer integrated system is analyzed by adopting two different types of convex and decreasing investment functions to reduce the ordering cost when the items are delivered in unequal sized shipments. An algorithm is proposed for finding the optimal solutions. Numerical results reveal that the system could obtain a significant amount of savings when the lead time demand follows a normal distribution and the ordering cost could be reduced if power investment cost function is adopted. The impact of the parameters on the optimal solution are also analyzed for decision making references. This model can be extended by incorporating generalized investment functions to reduce the ordering cost and the lead time. This model could also be extended to analyze the effect of treating the geometric growth factor as a decision variable on the cost function.
References
Annadurai, K., Uthayakumar, R.: Ordering cost reduction in probabilistic inventory model with controllable lead time and a service level. Int. J. Manag. Sci. Eng. Manag. 5(6), 403–410 (2010)
Banerjee, A.: A joint economic-lot-size model for purchaser and vendor. Decis. Sci. 17(3), 292–311 (1986)
Ben-Daya, M.A., Raouf, A.: Inventory models involving lead time as a decision variable. J. Oper. Res. Soc. 45(5), 579–582 (1994)
Ben-Daya, M., Hariga, M.: Integrated single vendor single buyer model with stochastic demand and variable lead time. Int. J. Prod. Econ. 92(1), 75–80 (2004)
Chuang, B.R., Ouyang, L.Y., Lin, Y.J.: A minimax distribution free procedure for mixed inventory model with backorder discounts and variable lead time. J. Stat. Manag. Syst. 7(1), 65–76 (2004)
Chang, H.C., Ouyang, L.Y., Wu, K.S., Ho, C.H.: Integrated vendor-buyer cooperative inventory models with controllable lead time and ordering cost reduction. Eur. J. Oper. Res. 170(2), 481–495 (2006)
Coates, E.R., Sarker, B.R., Ray, T.G.: Manufacturing setup cost reduction. Comput. Ind. Eng. 31(1–2), 111–114 (1996)
Darwish, M.A.: Economic selection of process mean for single-vendor single-buyer supply chain. Eur. J. Oper. Res. 199(1), 162–169 (2009)
Dey, O., Giri, B.C.: Optimal vendor investment for reducing defect rate in a vendor-buyer integrated system with imperfect production process. Int. J. Prod. Econ. 155, 222–228 (2014)
Gallego, G., Moon, I.: The distribution free newsboy problem: review and extensions. J. Oper. Res. Soc. 44(8), 825–834 (1993)
Giri, B.C., Sharma, S.: Lot sizing and unequal-sized shipment policy for an integrated production-inventory system. Int. J. Syst. Sci. 45(5), 888–901 (2014)
Giri, B.C., Chakraborty, A., Maiti, T.: Consignment stock policy with unequal shipments and process unreliability for a two-level supply chain. Int. J. Prod. Res. 55(9), 2489–2505 (2017)
Glock, C.H.: A comment: “Integrated single vendor-single buyer model with stochastic demand and variable lead time’’. Int. J. Prod. Econ. 122(2), 790–792 (2009)
Glock, C.H.: Lead time reduction strategies in a single-vendor-single-buyer integrated inventory model with lot size-dependent lead times and stochastic demand. Int. J. Prod. Econ. 136(1), 37–44 (2012)
Glock, C.H.: The joint economic lot size problem: a review. Int. J. Prod. Econ. 135(2), 671–686 (2012)
Glock, C.H., Grosse, E.H., Ries, J.M.: The lot sizing problem: a tertiary study. Int. J. Prod. Econ. 155, 39–51 (2014)
Goyal, S.K.: An integrated inventory model for a single supplier-single customer problem. Int. J. Prod. Res. 15(1), 107–111 (1977)
Goyal, S.K.: “A joint economic-lot-size model for purchaser and vendor’’: a comment. Decis. Sci. 19(1), 236–241 (1988)
Goyal, S.K.: A one-vendor multi-buyer integrated inventory model: a comment. Eur. J. Oper. Res. 82(1), 209–210 (1995)
Goyal, S.K., Nebebe, F.: Determination of economic production-shipment policy for a single-vendor-single-buyer system. Eur. J. Oper. Res. 121(1), 175–178 (2000)
Hill, R.M.: The single-vendor single-buyer integrated production-inventory model with a generalised policy. Eur. J. Oper. Res. 97(3), 493–499 (1997)
Hill, R.M.: The optimal production and shipment policy for the single-vendor single-buyer integrated production-inventory problem. Int. J. Prod. Res. 37(11), 2463–2475 (1999)
Ho, C.H.: A minimax distribution free procedure for an integrated inventory model with defective goods and stochastic lead time demand. Int. J. Inf. Manag. Sci. 20(1), 161–171 (2009)
Hoque, M.A., Goyal, S.K.: A heuristic solution procedure for an integrated inventory system under controllable lead-time with equal or unequal sized batch shipments between a vendor and a buyer. Int. J. Prod. Econ. 102(2), 217–225 (2006)
Hoque, M.A.: A manufacturer-buyer integrated inventory model with stochastic lead times for delivering equal-and/or unequal-sized batches of a lot. Comput. Oper. Res. 40(11), 2740–2751 (2013)
Hsu, S.L., Lee, C.C.: Replenishment and lead time decisions in manufacturer-retailer chains. Transp. Res. Part E Logist. Transp. Rev. 45(3), 398–408 (2009)
Kim, S.L., Hayya, J.C., Hong, J.D.: Setup reduction in the economic production quantity model. Decis. Sci. 23(2), 500–508 (1992)
Kotler, P., Keller, K.L.: Marketing management, 12th edn. Prentice-Hall, Upper Saddle River (2006)
Lin, Y.J.: An integrated vendor-buyer inventory model with backorder price discount and effective investment to reduce ordering cost. Comput. Ind. Eng. 56(4), 1597–1606 (2009)
Hsien-Jen, L.I.N.: An integrated supply chain inventory model with imperfect-quality items, controllable lead time and distribution-free demand. Yugosl. J. Oper. Res. 23(1), 87–109 (2013)
Lu, L.: A one-vendor multi-buyer integrated inventory model. Eur. J. Oper. Res. 81(2), 312–323 (1995)
Liao, C.J., Shyu, C.H.: An analytical determination of lead time with normal demand. Int. J. Oper. Prod. Manag. 11(9), 72–78 (1991)
Ouyang, L.Y., Chen, C.K., Chang, H.C.: Lead time and ordering cost reductions in continuous review inventory systems with partial backorders. J. Oper. Res. Soc. 50(12), 1272–1279 (1999)
Ouyang, L.Y., Wu, K.S., Ho, C.H.: Integrated vendor-buyer cooperative models with stochastic demand in controllable lead time. Int. J. Prod. Econ. 92(3), 255–266 (2004)
Ouyang, L.Y., Wu, K.S., Ho, C.H.: An integrated vendor-buyer inventory model with quality improvement and lead time reduction. Int. J. Prod. Econ. 108(1), 349–358 (2007)
Ouyang, L.Y., Chuang, B.R., Lin, Y.J.: The inter-dependent reductions of lead time and ordering cost in periodic review inventory model with backorder price discount. Int. J. Inf. Manag. Sci. 18(3), 195 (2007)
Porteus, E.L.: Investing in reduced setups in the EOQ model. Manag. Sci. 31(8), 998–1010 (1985)
Pan, J.C.H., Hsiao, Y.C.: Inventory models with back-order discounts and variable lead time. Int. J. Syst. Sci. 32(7), 925–929 (2001)
Pan, J.C.H., Yang, J.S.: A study of an integrated inventory with controllable lead time. Int. J. Prod. Res. 40(5), 1263–1273 (2002)
Pan, J.C.H., Lo, M.C., Hsiao, Y.C.: Optimal reorder point inventory models with variable lead time and backorder discount considerations. Eur. J. Oper. Res. 158(2), 488–505 (2004)
Pan, J.C.H., Hsiao, Y.C.: Integrated inventory models with controllable lead time and backorder discount considerations. Int. J. Prod. Econ. 93, 387–397 (2005)
Pandey, A., Masin, M., Prabhu, V.: Adaptive logistic controller for integrated design of distributed supply chains. J. Manuf. Syst. 26(2), 108–115 (2007)
Sajadieh, M.S., Jokar, M.R.A., Modarres, M.: Developing a coordinated vendor-buyer model in two-stage supply chains with stochastic lead-times. Comput. Oper. Res. 36(8), 2484–2489 (2009)
Teng, J.T., Cárdenas-Barrón, L.E., Lou, K.R.: The economic lot size of the integrated vendor-buyer inventory system derived without derivatives: a simple derivation. Appl. Math. Comput. 217(12), 5972–5977 (2011)
Tsou, C.S., Fang, H.H., Lo, H.C., Huang, C.H.: A study of cooperative advertising in a manufacturer-retailer supply chain. Int. J. Inf. Manag. Sci. 20(12), 5–26 (2009)
Woo, Y.Y., Hsu, S.L., Wu, S.: An integrated inventory model for a single vendor and multiple buyers with ordering cost reduction. Int. J. Prod. Econ. 73(3), 203–215 (2001)
Zhang, T., Liang, L., Yu, Y., Yu, Y.: An integrated vendor-managed inventory model for a two-echelon system with order cost reduction. Int. J. Prod. Econ. 109(1), 241–253 (2007)
Acknowledgements
The work of authors are supported by Department of Science and Technology-Science and Engineering Research Board (DST-SERB), Government of India, New Delhi, under the grant number DST-SERB/SR/S4/MS: 814/13-Dated 24.04.2014.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Similar to the results proved in Lin [30] the convexity of the cost function is discussed.
Observation 1
\(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is concave in \(L \in [L_{i}, L_{i-1}]\) for a fixed \(n, q_{1}, k, A_{b}, \pi _{x}\).
Thus for a fixed \((n, q_{1}, k, A_{b}, \pi _{x})\), \(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is concave in \(L \in [L_{i}, L_{i-1}]\). Hence the minimum value of \(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) exists at the end points of the interval \([L_{i}, L_{i-1}]\).
Observation 2
\(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in n for a fixed \(k, q_{1}, L, A_{b}, \pi _{x}\).
where \(Y = \Bigl (A_{b}+\frac{A_{v}}{n}\Bigr ) +G(\pi _x)\sigma \sqrt{L}\psi (k)+R(L)+T_{r}\)
Observation 3
\(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in \(q_{1}\) for a fixed \(n, k, L, A_{b}, \pi _{x}\).
Observation 4
\(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in k for a fixed \(n, q_{1}, L, A_{b}, \pi _{x}\).
Observation 5
\(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in \(\pi _{x}\) for a fixed \(n, q_{1}, L, A_{b}, k\).
Observation 6
\(EATCI_{N}^{L}(n, q_{1}, k, \pi _{x}, \pi _{x}, L)\) is convex in \(A_{b}\) for a fixed \(n, q_{1}, L, \pi _{x}, k\).
Observation 7
\(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is concave in \(L \in [L_{i}, L_{i-1}]\) for a fixed \(n, q_{1}, k, A_{b}, \pi _{x}\).
Thus for a fixed \((n, q_{1}, k, A_{b}, \pi _{x})\), \(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is concave in \(L \in [L_{i}, L_{i-1}]\). Hence the minimum value of \(EATCI_{N}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) exists at the end points of the interval \([L_{i}, L_{i-1}]\).
Observation 8
\(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in n for a fixed \(k, q_{1}, L, A_{b}, \pi _{x}\),.
where \(Y = \Bigl (A_{b}+\frac{A_{v}}{n}\Bigr ) +G(\pi _x)\sigma \sqrt{L}K+R(L)+T_{r}\)
Observation 9
\(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in \(q_{1}\) for a fixed \(n, k, L, A_{b}, \pi _{x}\),.
Observation 10
\(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in k for a fixed \(n, q_{1}, L, A_{b}, \pi _{x}\).
Observation 11
\(EATCI_{F}^{L}(n, q_{1}, k, A_{b}, \pi _{x}, L)\) is convex in \(\pi _{x}\) for a fixed \(n, q_{1}, L, A_{b}, k\).
Observation 12
\(EATCI_{F}^{L}(n, q_{1}, k, \pi _{x}, \pi _{x}, L)\) is convex in \(A_{b}\) for a fixed \(n, q_{1}, L, \pi _{x}, k\).
Appendix 2
As the total cost function of the integrated system is highly non-linear, the convexity of the function for a given L is checked in the distribution free case when logarithmic investment function is adopted. For this case, the Hessian matrix H is given below. The leading principal minors \(H_{55}, H_{44}, H_{33}, H_{22}, H_{11}\) are positive and thus the hessian matrix is positive definite. Thus the solution obtained is globally optimum.
Rights and permissions
About this article
Cite this article
Latha, K.F.M., Kumar, M.G. & Uthayakumar, R. Two echelon economic lot sizing problems with geometric shipment policy backorder price discount and optimal investment to reduce ordering cost. OPSEARCH 58, 1133–1163 (2021). https://doi.org/10.1007/s12597-021-00515-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12597-021-00515-7