A Curve-Free Bayesian Decision-Theoretic Design for Phase Ia/Ib Trials Considering Both Safety and Efficacy Outcomes

Abstract

A curve-free, Bayesian decision-theoretic two-stage design is proposed to select biological efficacious doses (BEDs) for phase Ia/Ib trials in which both toxicity and efficacy signals are observed. No parametric models are assumed to govern the dose–toxicity, dose–efficacy, and toxicity–efficacy relationships. We assume that the dose–toxicity curve is monotonic non-decreasing and the dose–efficacy curve is unimodal. In the phase Ia stage, a Bayesian model on the toxicity rates is used to locate the maximum tolerated dose. In the phase Ib stage, we model the dose–efficacy curve using a step function while continuing to monitor the toxicity rates. Furthermore, a measure of the goodness of fit of a candidate step function is proposed, and the interval of BEDs associated with the best fitting step function is recommended. At the end of phase Ib, if some doses are recommended as BEDs, a cohort of confirmation is recruited and assigned at these doses to improve the precision of estimates at these doses. Extensive simulation studies show that the proposed design has desirable operating characteristics across different shapes of the underlying true toxicity and efficacy curves.

1 Introduction

As the first application of a new drug or drug combination to humans, a phase I oncology trial traditionally focuses on finding the safe dose or schedule of the medication. Such a trial usually is a single-arm, open label, sequential study involving a small number of patients. A principal goal of a phase I trial is to establish the recommended dose and/or schedule of an experimental drug for efficacy testing later. It is believed that the toxicity and efficacy of cytotoxic chemotherapies increase with dose; thus, the recommended dose is often selected as the maximum tolerated dose (MTD). A comprehensive review of the dose escalation methods for MTD in phase I cancer clinical trials can be found in Tourneau et al. [17].

Emerging targeted therapies, including monoclonal antibodies and immunotherapies, have distinct response outcomes from the chemotherapies. While it may be reasonable to assume monotonic toxicity with dose, the dose-limiting toxicity (DLT) may not exhibit at the therapeutic doses. Moreover, the efficacy may not follow monotonic patterns [6]. Therefore, methods that are optimal for the selection of MTD may not be appropriate for the determination of a recommended dose for targeted therapies [3]. These new therapies need alternative or complementary strategies to help the identification of dose ranges based on effect biomarkers, which could be target engagement, pharmaco-dynamics or disease progression biomarkers. The dose that demonstrates a certain level of biological effect measured by such a biomarker is considered a biological efficacious dose (BED), which should have a desirable efficacy performance while still safeguarding patients with an acceptable toxicity profile [14]. In a review of phase I trials that lead to a recommended phase II dose for molecularly targeted agents, Hansen et al. [7] observed that only 13% (22/161) of these trials use non-toxicity endpoints and that BEDs of molecularly targeted agents may not reach MTD in these phase I trials. Therefore, they replaced the DLT rate for a 3 + 3 design with an efficacy response rate and searched for a BED by modifying the 3 + 3 rule. Another commonly used dose target is the biological optimal dose (BOD), the optimal BED that has the highest efficacy among doses below the MTD [1].

To look for BOD, Thall and Cook [16] introduced EffTox, a Bayesian adaptive dose-finding design that models correlated binary efficacy and toxicity outcomes and incorporates the trade-off between efficacy and toxicity. Brock et al. [2] searched the PubMed on October 2016 for articles that cited Thall and Cook [16] and found that, among the 54 articles returned, only three used the EffTox design in clinical trials. This reflects the statement made by Thall [15]: “Bayesian models for early phase clinical trials have seen limited use in clinical practice”. We believe that, in general, parametric models and computational complexities are the primary barriers to widespread adoption of Bayesian designs.

Many researchers have started to develop and promote Bayesian designs that are relatively easy to understand and implement. One way is to adopt curve-free models for dose–response relations. For example, to identify the MTD, Fan et al. [5] proposed a Bayesian design that assumes only a monotonic relationship between dose and toxicity. However, for trials with both toxicity and efficacy outcomes, there is no simple curve-free assumption on the association between toxicity and efficacy. Therefore, instead of modelling the toxicity–efficacy relation, Ivanova [8], Fan and Chaloner [4], and Zhang et al. [19] modelled toxicity and efficacy as a single trinary response variable with three outcomes: no toxicity and no efficacy (no response), efficacy and no toxicity (success), and toxicity. Fan and Chaloner [4] adopted the continuation-ratio model and provided the analytic forms of its Bayesian optimal designs. However, their target dose is the most successful dose, different to BOD. To identify BOD, Sachs et al. [14] advocated the idea of a two-stage approach, in which stage 1 (Phase Ia) focuses primarily on toxicity to assess safety and tolerability as well as to establish the MTD, and stage 2 (Phase Ib) focuses primarily on efficacy to find a BED that is lower than the MTD. In this way, the complexity of joint modelling of the toxicity–efficacy association can be avoided by utilizing the marginal distributions of toxicity and efficacy sequentially. Zang and Lee [18] adopted the idea to identify the BOD, and their design assumes only that the (marginal) dose–toxicity relationship is monotonic and the (marginal) dose–efficacy relationship is unimodal or plateaued. A common thread that runs through these works is that the designs are curve free, that is, the dose–toxicity, dose–efficacy, and toxicity–efficacy relationships are not assumed to follow specific parametric curves.

While numerous trial designs for identifying the MTD or BOD have been proposed in the literature, designs for identifying the BEDs are limited. In this paper, we propose a two-stage, curve-free Bayesian design to identify the set of all BEDs in the dose domain of the study. Our two-stage approach is similar to Zang and Lee [18] but the goal is different: instead of finding the BOD, which is the optimal BED, we seek to identify all the BEDs. The reason for this goal is that the recommended phase II dose should be a decision that involves not only the statisticians but also the medical experts (such as the clinicians and pharmacologists). By providing a set of BEDs, the medical experts have the option of selecting a BED based on pharmacology and other clinical knowledge and experience to move forward to phase II trials, rather than relying solely on statistical criteria.

The disadvantage of a two-stage approach is that without utilizing the association between the toxicity and efficacy outcomes, a larger sample size may be required. However, this disadvantage can be minimized by using an efficient algorithm in the first stage. The algorithm proposed by Fan et al. [5] has been demonstrated to locate the MTD rapidly and robustly and so we adopt it in the first stage of our design. As for the second stage, because the goal is to identify all BEDs rather than the BOD, the grouping of doses, or the pooling of the samples at those doses, to estimate a single pooled efficacy rate should lead to an increased precision of the estimate. Based on this consideration, the efficacy curve is assumed to be unimodal or plateaued, and it is modelled nonparametrically by a step function. The dose selection in the second stage is based on the estimated step function and the posterior expected utilities.

Another practical issue is the selection of the single BOD from the multiple BEDs for phase II trials. Although a phase Ia/Ib trial does not aim to make statistical inferences on the efficacy of the selected dose(s), relatively large sample sizes on the selected doses (BEDs) could be required or essential for clinicians to make a good decision. To achieve that, stopping rules are implemented and the saved sample size can be used for a confirmation cohort. In our simulation studies, confirmation cohorts are guaranteed by lowering the maximal sample size of the first two stages.

Finally, the simplicity of the prior distributions and an intuitive way to specify the prior parameters are important for the adoption of a Bayesian method in actual trials. We choose the flexible beta priors for the toxicity/efficacy rates, which can be easily specified based on a preliminary guess of the toxicity/efficacy rates. The curve-free toxicity/efficacy models and less-informative priors can increase the robustness of the proposed design, so that errors in the initial prior specification can be quickly adjusted by the data. To facilitate the application of the proposed design, an R package has been developed and is available upon request.

The rest of our paper is organized as follows. Section 2 provides a description of the design, including the modelling of the dose-toxicity and dose–efficacy relationships, and dose selection rules based on Bayesian decision theory. In Sect. 3, we evaluate the operating characteristics of our design through simulation studies and sensitivity analysis. To promote the application of our design, a completed trial is simulated with complete details and presented in Sect. 4. Finally, we present a discussion in Sect. 5.

2 The General Design

We first describe the idea of the proposed design. It starts with identifying the safe doses. The Bayesian algorithm originally proposed by Fan et al. [5] for dose-finding or phase Ia trials, hereafter referred to as the FLW algorithm, is used to locate the MTD. Due to page limits, we cannot describe the FLW algorithm in detail here. In essence, the FLW algorithm assumes only a monotonic dose–toxicity relationship and estimates the MTD with an isotonic procedure that uses the observed as well as extrapolated toxicity data. Furthermore, it recommends the dose with the maximum posterior probability of being the MTD. Simulation studies provided by Fan et al. [5] show that the algorithm selects the target dose more frequently with fewer number of patients than other commonly used Bayesian methods; moreover, it is robust against prior misspecification. An R package that implements the FLW algorithm is available from the authors upon request.

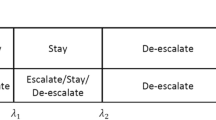
Once the MTD has been identified with sufficient confidence, in terms of the posterior probability of the recommended dose being the MTD exceeding a pre-set threshold, the phase Ib stage for the search of the BEDs begins. During the search, we continue to monitor the toxicity rates and update the MTD. In this stage, only the admissible doses, those not exceeding the current MTD, are considered in dose assignments. Because dose-finding trials typically have small sample sizes, the efficacy rate for each individual dose cannot be reliably estimated; therefore, we group the adjacent doses to obtain pooled estimates. Afterward, we approximate the unimodal dose–efficacy curve by a step function that divides the dose axis into three intervals/groups as illustrated in Fig. 1. The middle interval of the step function which maximizes a utility function will be recommended as the interval of BEDs. After the interval of BEDs has been recommended, a confirmation cohort is added to the trial to increase the precision of the estimate of the pooled efficacy rate of this interval. The point estimate, together with confidence intervals of the efficacy rate for each BED and of the pooled efficacy rate for all BEDs, can be provided to help clinicians select a dose to move forward to phase II trials.

Fig. 1

Plot of an efficacy curve with the minimum acceptable rate 0.30 and two-step function models: the best one in blue and another one in red

2.1 Modelling Toxicity and Efficacy Rates

Let the dose levels be indicated in discrete integers i for i = 1,…, m. Let ${P}_{T,i}$ and ${P}_{E,i}$ be the toxicity and efficacy rates, respectively, of dose i. We assume that the toxicity rates are monotonically non-decreasing, that is, ${P}_{T,1}\le {P}_{T,2}\le \dots \le {P}_{T,m}$; it follows that all doses not exceeding the current estimated MTD are admissible. The prior distribution of the toxicity rate at each dose level is taken to be independent beta distributions. Specifically, we have ${P}_{T,i}$ independently distributed as ${\text{Beta}}({\alpha }_{T,i}^{0}, {\beta }_{T,i}^{0})$ such that the means are monotonically non-decreasing: ${\mu }_{T,1}^{0}\le {\mu }_{T,2}^{0}\le \dots \le {\mu }_{T,m}^{0},$ where ${\mu }_{T,i}^{0}={\alpha }_{T,i}^{0}/\left({\alpha }_{T,i}^{0}+{\beta }_{T,i}^{0}\right).$ Note that the monotonically non-decreasing property will be preserved in the posterior means. Throughout, the superscript 0 is used to indicate that a parameter is associated with an initial prior distribution.

While it is reasonable to assume that the toxicity of an agent is monotonic and non-decreasing in dose, this assumption may not be tenable for the efficacy [6]. Therefore, we assume instead that the efficacy curve $f\left(s\right)$ is unimodal or plateaued: $f\left(s\right)$ increases at low dose levels and plateaus or even decreases at higher levels. It follows that the set of BEDs is an interval. Because our goal is to identify the interval of BEDs, rather than the BOD, we model the unimodal or plateaued efficacy curve using a step function, which is identified by an interval B = [l, r], $1\le l\le r\le m$ as follows:

$$\begin{array}{lll}{P}_{E,i} = \left\{\begin{array}{cc}\frac{1}{l-1}\sum_{j=1}^{l-1}{P}_{E,j} & \text{for }i<\mathrm{l}, \\ \frac{1}{r-\mathrm{l}}\sum_{j=\mathrm{l}}^{r}{P}_{E,j} & \text{for}\;l\le i\le r\\ \frac{1}{m-r-1}\sum_{j=r+1}^{m}{P}_{E,j}& \text{for }i>r. \end{array}\right.\end{array},$$

(1)

The efficacy rates of doses in the same range: to the left of, to the right of, or in the interval B, are modelled as the mean efficacy rate of all doses in the range.

The prior distribution of the efficacy rate at each dose level is taken to be independent beta distributions, that is, we have ${P}_{E,i}^{0}$ independently distributed as ${\text{Beta}}({\alpha}_{E,i}^{0}, {\beta}_{E,i}^{0})$ for i = 1,…,m. Similarly, we specify the initial prior distribution of the mean efficacy rate of an interval A of k doses, ${P}_{A}=\frac{1}{k}{\sum }_{i\in A}{P}_{E,i},$ as ${\text{Beta}}({\alpha}_{A}^{0}=\frac{1}{k}{\sum }_{i\in A}{\alpha}_{E,i}^{0}, \beta_{A}^{0}=\frac{1}{k}{\sum }_{i\in A}\beta_{E,i}^{0}).$ We defer the discussion of the specification of the prior parameters to Sect. 3.

2.2 Utility Functions

Let T_max be the maximum tolerable toxicity level and ${\mathrm{E}}_{min}$ be the minimum acceptable efficacy rate such that a BED should have its efficacy rate above it. Doses with tolerable toxicity and acceptable efficacy are BEDs. The goal of our design is to identify the interval of BEDs correctly and promptly. For an arbitrary interval B = [l, r], its utility of being the interval of BEDs is defined as follows.

Considering a dose i, if it is a BED, it should be included in B; if it is a non-BED, it should be excluded from B. Among all BEDs, the successful inclusion of a more efficacious dose should be given larger utility than that of a less efficacious dose. In contrast, among all non-BEDs, the successful exclusion of a less efficacious dose should be given larger utility than that of a more efficacious dose. The utility of interval B = [l, r] associated with dose i is defined as follows:

$$\begin{array}{ccc}{u}_{i}(B)& =& \left\{\begin{array}{cc}{1}_{\left\{{P}_{E,i}\ge {E}_{\min}\right\}}[a+{b(P}_{E,i}-{E}_{\min})]& \text{for }i\in B\\ {1}_{\{{P}_{E,i}<{E}_{\min}\}}[c+d{(E}_{\min}-{P}_{E,i})]& \text{for }i\notin B\end{array},\right.\end{array}$$

(2)

where 1_condition takes the value one if condition is true and zero otherwise. The positive constants a and b, which are associated with the BEDs, represent the weights for correct selection as BEDs and how much more efficacious it is than E_min, respectively. The positive constants c and d, which are associated with the non-BEDs, represent the weights for correct selection as non-BEDs and how much less efficacious it is than E_min, respectively. The total utility is the weighted sum of the utilities at all doses:

$$u\left(B\right)=\sum_{i=1}^{\text{MTD}}{w}_{i}*{u}_{i}\left(B\right).$$

(3)

An intuitive choice for the weight ${w}_{i}$ is the sample size at dose i, denoted ${n}_{i},$ but it can be chosen in other ways.

The utility function $u\left(B\right)$ is maximized when the interval B contains all and only BEDs. For any BED, say dose i,${u}_{i}(B)$ is at least one if it is in B and zero if not. Similarly, for any non-BEDs, say dose j,${u}_{j}(B)$ is zero if it is in B and at least one if not. To maximize the total sum of the utilities at all doses, the interval B must include all BEDs and exclude all non-BEDs.

When a prior distribution is added on ${P}_{E,i},$ the (Bayesian) utility associated with dose i is defined as the posterior expectation of ${u}_{i}\left(B\right), E\left[{u}_{i}\left(B\right)\right].$ Let ${n}_{e,i}$ be the number of efficacy outcomes among the ${n}_{i}$ patients treated at dose i. The posterior distribution of ${P}_{E,i}$ is ${\text{Beta}}({\alpha}_{E,i}={\alpha}_{E,i}^{0}+{n}_{e,i}, \beta_{E,i}=\beta_{E,i}^{0}+{n}_{i}-{n}_{e,i})$ and the expected utility at dose i is given by:

$$\begin{array}{ccc}E\left[{u}_{i}\left(B\right)\right]& =& \left\{\begin{array}{cc}\left(a-b\mathrm{*}{E}_{\min}\right)\left[1-{I}_{{E}_{\min}}\left({\alpha}_{E,i},{\beta}_{E,i}\right)\right]+\frac{b{\alpha}_{E,i}}{{\alpha}_{E,i}+{\beta}_{E,i}}\left[1-{I}_{{E}_{\min}}\left({\alpha}_{E,i}+1,{\beta}_{E,i}\right)\right]& \text{for }i\in B,\\ \left(c+d\mathrm{*}{E}_{\min}\right){I}_{{E}_{\min}}\left({\alpha}_{E,i},{\beta}_{E,i}\right)-\frac{d{\alpha}_{E,i}}{{\alpha}_{E,i}+{\beta}_{E,i}}{I}_{{E}_{\min}}\left({\alpha}_{E,i}+1,{\beta}_{E,i}\right)& \text{for }i\notin B,\end{array}\right.\end{array}$$

where ${I}_{{E}_{\mathrm{m}\mathrm{i}\mathrm{n}}}\left(\bullet ,\bullet \right)$ is the regularized incomplete beta function. It follows that there is an analytical expression for the expected total utility of an interval B:

$$E[u\left(B\right)]=\sum_{i=1}^{\text{MTD}}{w}_{i} ^{\ast} {E[u}_{i}\left(B\right)]$$

Let ${A}^{\ast}$ denote the interval which maximizes $E[u\left(B\right)]$ at the end of trial. Due to limited sample size, not all doses in ${A}^{\ast}$ are necessarily BEDs and so we need to exclude the non-BEDs as follows. First of all, because of the assumed unimodality of the dose–efficacy curve, any non-BEDs in the interval ${A}^{\ast}$ must be the lower or higher dose levels in ${A}^{\ast}.$ Let B be a subinterval of ${A}^{\ast}$ obtained by excluding one or more lower and/or higher dose levels in ${A}^{\ast},$ and let k be the number of doses in B. Next, we define the efficacy rate of B as the pooled efficacy rate ${P}_{B}=\frac{1}{k}{\sum }_{i\in B}{P}_{E,i},$ and we specify the initial prior distribution of P_B as the pooled beta prior distribution ${\text{Beta}}({\alpha}_{B}^{0}=\frac{1}{k}{\sum }_{i\in B}{\alpha}_{E,i}^{0}, \beta_{B}^{0}=\frac{1}{k}{\sum }_{i\in B}\beta_{E,i}^{0}).$ Upon the collection of data, the posterior distribution of P_B becomes ${\text{Beta}}({\alpha}_{B}={\alpha}_{B}^{0}+{\sum }_{i\in B}{n}_{e,i}, \beta_{B}=\beta_{B}^{0}+{\sum }_{i\in B}({n}_{i}-{n}_{e,i})),$ and the posterior probability that B is acceptable is given by $P\left({P}_{B}\ge {E}_{\min}\right)=1-{I}_{{E}_{\min}}\left({\alpha}_{B},\beta_{B}\right).$ Our design recommends the subinterval ${B}^{\ast}=[{l}^{\ast},{r}^{\ast}]$ that maximizes this posterior probability as the final interval of BEDs.

2.3 Dose Selection Rules

To use the sample size more efficiently, stopping rules are implemented at both stages. Let ${n}_{\text{min.mtd}}, {n}_{\text{max.mtd}}$ be the minimum and maximum sample sizes at the first stage for locating the MTD, and ${n}_{\min}{, n}_{\max}$ be the minimum and maximum samples sizes of the entire trial. In addition, ${n}_{\text{min.mtd}}\le {n}_{\text{max.mtd}}\le {n}_{\min}\le {n}_{\mathrm{m}\mathrm{a}\mathrm{x}}.$

At the beginning of a trial, phase Ia, we propose the following dose selection rules to locate the MTD quickly:

• (1) Start at the lowest dose and escalate until a toxicity outcome is observed or the highest dose is reached.

• (2) Use the FLW algorithm to locate the MTD and assign the next patient to the current MTD.

• (3) Step (2) is repeated until a pre-set sample size ${n}_{\text{min.mtd}}$ is reached. The dose assignment between sample size ${n}_{\text{min.mtd}}$ and ${n}_{\text{max.mtd}}$ follows the rules below:

  • (a) If the posterior probability of the first dose being overly toxic exceeds a threshold, the trial is terminated and we conclude that the MTD is below the first dose.

  • (b) Otherwise, if the posterior probability of the current MTD being the true MTD exceeds a threshold, we will begin to allocate the BED candidates to the patients.

  • (c) Otherwise, the current MTD is assigned to the next patient.

The parameter ${n}_{\text{min.mtd}}$ in Step (3) is designed to prevent incorrect early termination due to misspecified prior distributions (the conclusion “all doses are inadmissible” cannot be made before ${n}_{\text{min.mtd}}$ patients are treated), while the parameter ${n}_{\text{max.mtd}}$ is designed to ensure possible allocation of the BEDs to patients. One can set ${n}_{\text{min.mtd}}={n}_{\text{max.mtd}}$ to simplify the algorithm. The reason to allocate the MTD rather than BEDs at the beginning of the trial is to identify the MTD quickly, since patient safety should always be the first priority. Once the MTD is confidently located, phase Ib begins and patients will be allocated to BED candidates immediately.

The BED candidates are defined to be all the admissible doses in the interval of BEDs, ${B}^{\ast}=[{l}^{\ast},{r}^{\ast}]$ (as described in the end of Sect. 2.2) and its adjacent doses l* − 1 and r* + 1. To ensure patient safety, only admissible doses at or below the current MTD can be assigned to patients, and the MTD is updated throughout the entire trial using the FLW algorithm and observed data at all doses. Let ${q}_{1}$ be the pres-set threshold of the posterior probability of a dose being acceptable and ${q}_{2}$ be the threshold of the posterior probability of a dose being unacceptable. Each BED candidate is assigned to a patient until a minimum sample size ${n}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is reached and the following stopping rules apply:

• (1) If the current interval of BEDs, ${B}^{\ast},$ is very likely to be acceptable, that is, $P\left({P}_{{B}^{\ast}}\ge {E}_{\min}\right)\ge {q}_{1},$ the trial is terminated and we recommend ${B}^{\ast}$ as the interval of BEDs.

• (2) Otherwise, if all admissible doses are very likely to be unacceptable, that is, $P\left({P}_{E,i}<{E}_{\min}\right)\ge {q}_{2}$ for all $i\le {\text{MTD}},$ the trial is terminated and we conclude that there is no BED.

• (3) Otherwise, the trial is terminated until the maximum sample size ${n}_{\max}$ is reached. If the current interval of BEDs, ${B}^{\ast},$ is very likely to be unacceptable, that is, $P\left({P}_{{B}^{\ast}}<{E}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)\ge {q}_{2},$ we conclude that there is no BED; otherwise, we recommend ${B}^{\ast}$ as the interval of BEDs.

A flowchart of the proposed phase Ia/Ib design is presented in Fig. 2.

Fig. 2

Flowchart of CFBD

2.4 Confirmation Cohort

If at the end of trial, an interval  ${B}^{\ast}$= [l*, r*] is recommended as the BED interval, a confirmation cohort will be recruited to improve the efficiency of estimates. Each dose in the interval B will be assigned the same number of patients and this cohort is later referred to the confirmation cohort. After the confirmation cohort, the selection of the MTD and BED interval will be updated. In addition, the pooled efficacy rate for the updated interval  B* = [l*, r*] is empirically estimated by $\widehat{{P}_{{B}^{\ast}}}=\sum_{i={l}^{\ast}}^{{r}^{\ast}}{n}_{e,i}/\sum_{i={l}^{\ast}}^{{r}^{\ast}}{n}_{i}.$ The pooled efficacy rate is adopted rather than individual efficacy rate because of the small sample size at each individual dose. The size of the confirmation cohort depends on the desired efficacy and available resources. However, to detect a small difference from the target efficacy level E_min, it requires a large sample size at these BEDs. In addition, the goal of dose finding trials is to locate the good acceptable doses, not the precision of estimation. The confirmation cohort is only used to select one of these BEDs as the single dose to move to phase II trials.

3 Simulation Studies

Hereafter, we refer to our proposed design as CFBD, which stands for Curve-Free Bayesian Design. The CFBD is not the only curve-free Bayesian design in the literature, for example, Zack and Lee (2017) also proposed a curve-free Bayesian design (ZL) to identify the BOD. In our simulation studies, we compare the performance of CFBD to ZL because there are limited number of designs in the literature that seek to identify the BEDs, and ZL uses the same two-stage strategy and a similar curve-free Bayesian model. We would like to emphasize that the goals of CFBD and ZL are different and, as a result, the CFBD may outperform ZL in some scenarios simply because ZL was designed to identify the BOD rather than BEDs. In other words, our comparisons are not intended as a demonstration of the superiority of the CFBD; rather, the performance of ZL when used to identify the set of BEDs serves only as a benchmark.

3.1 Operating Characteristics

3.1.1 Simulation Settings

We examined the operating characteristics of the CFBD in six scenarios presented in Zang and Lee [18]. These scenarios, reproduced in Table 1 with the BEDs highlighted in bold, provide a variety of dose-efficacy curves: monotone increasing (scenarios 1 and 6), unimodal (scenarios 2 and 3), and increasing with a plateau (scenarios 4 and 5). Note that a step function would fit the dose-efficacy curve well in scenarios 4 and 5 but not apparently so in other scenarios. We simulated 5000 trials for each scenario, where the value of both the maximum tolerable toxicity rate, T_max, and the minimum acceptable efficacy rate, E_min, was 0.3.

Table 1 Six scenarios with its shape of efficacy curve; doses in bold are BEDs

In CFBD, we proposed the Beta distributions as the prior distributions of the toxicity and efficacy rates. Our choice of the parameters in the simulation studies was motivated by the following considerations. First of all, the values of the parameters should not be large, since a Beta(α, β) prior distribution has effective sample size r = α + β [12]. If r > n, where n is the sample size, the prior dominates posterior inferences, and vice versa. Therefore, unless there is reliable prior information, r should be fairly small so that any misspecified priors can be correctly updated with a small or moderate sample that is typical in Phase I trials. Secondly, a Beta(α, β) distribution is unimodal if and only if α > 1 and β > 1. As unimodal prior distributions are usually preferred, the parameters α⁰ and β⁰ of the Beta prior distributions should be larger than 1 if possible. Combining these two considerations, we should have α⁰ and β⁰ larger than but close to 1. However, this condition may not be satisfied at all dose levels, and so we require instead that it be at least satisfied at dose levels that are believed to be BEDs prior to the trial. Let ${\mu }_{E,i}^{0}$ and ${r}_{i}^{0}$ denote the mean and effective sample size, respectively, of a ${\text{Beta}}({\alpha}_{E,i}^{0}, \beta_{E,i}^{0})$ prior distribution for the efficacy rate at dose i. It is trivial to show that ${{\alpha}_{E,i}^{0}={r}_{i}^{0}\mu }_{E,i}^{0}$ and${{\alpha}_{E,i}^{0}={r}_{i}^{0}(1-\mu }_{E,i}^{0}),$ so that the equivalent condition is to have both ${{r}_{i}^{0}\mu }_{E,i}^{0}$ and ${{r}_{i}^{0}(1-\mu }_{E,i}^{0})$ greater than but close to 1 at the likely BEDs. In practice, these parameters can be specified in collaboration with clinicians based on their clinical experience and confidence level. Suppose that all efficacy rates of the BEDs are expected to be above E_min but below an upper bound of ${E}_{\max}(\ge {E}_{\mathrm{m}\mathrm{i}\mathrm{n}}).$ Let r be a multiplier such that $r{E}_{\min},{r (1-E}_{\min}),$$r{E}_{\max}$ and ${r (1-E}_{\max})$ are all larger than but close to 1. Then ${{\alpha}_{E,i}^{0}=r\mu }_{E,i}^{0}$ and ${{\beta}_{E,i}^{0}=r(1-\mu }_{E,i}^{0})$ ensure that the prior distributions are unimodal whenever ${{E}_{\min}\le \mu }_{E,i}^{0}\le {E}_{\max}.$ For now, ${\mu }_{E,i}^{0}$ is chosen to be equal to the actual efficacy rate at dose i; we will study the impact of misspecifications in Sect. 3.2. With E_min = 0.3 and E_max = 0.4 in our simulations, we have the effective sample size r = 4. Based on our earlier discussion, our prior information is as strong as that obtained from four treated patients.

The weights a, b, c, and d, which represent the rewards in the utility function defined in Eq. (2), are all set to 1, and the weights w_i used in the calculation of the total utility defined in Eq. (3) are given by the sample sizes, n_i, at the respective dose levels. The parameters of stopping rules for the simulated trials are given as follows. A trial should not be stopped when the sample size is small. The minimal and maximal sample size for MTD identification (phase Ia) are set as ${{n}_{\text{min.mtd}}=10, \;\mathrm{and}\;n}_{\text{max.mtd}}=30.$ In addition, it takes about 12 patients to have a power of 0.70 to test the hypothesis H₀: = ${{P}_{E,i}= E}_{\min}=$0.3 against H₁:P_E,i = 0.1 at a significance level of 0.1. Therefore, with 5 doses in our simulated trials, we set the minimum sample size to stop a trial early as ${n}_{\text{min.int}}=5\times 12=60.$ Although Zang and Lee [18] set the maximum sample size, ${n}_{\mathrm{m}\mathrm{a}\mathrm{x}.\mathrm{i}\mathrm{n}\mathrm{t}},$ as 150, we chose 100 instead to reflect the sample size constraint of actual phase I trials and reserved the remaining 50 for possible confirmation cohorts later. The size of the confirmation cohort per BED is chosen to be 10. Finally, the thresholds ${q}_{1}\, \mathrm{ a}\mathrm{n}\mathrm{d } \,{ q}_{2}$ for stopping rules defined in Sect. 2.3 are set to be 0.9.

3.1.2 Simulation Results

The simulation results are summarized in Tables 2 and 3. Recall that Zang and Lee [18] aim to identify the BOD (the BED with the highest efficacy rate) whereas CFBD aims to identify all BEDs. To facilitate comparisons, we compute the following summary statistics in Table 2:

• The percentage of trials that conclude that there is a target dose (%found), which is defined for CFBD as the percentage of trials recommending BEDs, and for ZL as the percentages of trials recommending a BOD.

• Within those trials recommending BEDs/BOD, the percentage of trials of which all recommended doses are truly admissible and acceptable (%correct).

• Within the trials recommending BEDs, the percentage of trials of which the sample pooled efficacy rate of the recommended BEDs is acceptable, i.e. confidence level of the pooled efficacy rate being above E_min (%success). This statistic is computed for CFBD only.

• The percentage of in-trial toxicities (%tox), the percentage of in-trial efficacies (%eff), and the average sample size over the 5000 simulated trials ($\stackrel{-}{n}$).

Table 2 The average sample size ($\stackrel{-}{n}$), the percentage of trials that recommend any BEDs/BOD (%found), within the trials recommending BEDs/BOD, the percentage that all the recommended doses are truly acceptable (%correct) and the percentage that sample pooled efficacy of the BEDs are acceptable (%success), and the percentages of in-trial toxicity (%tox) and efficacy (%eff) under the proposed Bayesian design (CFBD) and the design proposed by Zang and Lee (ZL)

Table 3 The selection percentages of MTD, BED interval limits: L*, U*, and patient allocation for all doses under CFBD; correct percentages are in bold

Additional summary statistics are provided in Table 3.

As seen from Table 2, CFBD performs very well in identifying the BEDs in most scenarios that have at least one BED. In scenarios 2 to 5, CFBD uses relatively fewer patients on average than ZL and yet has higher %found and %correct. Also, CFBD was able to recommend one or more BEDs in approximately 95% or more of the trials (%found) with at least 90% accuracy rate (%correct). In scenario 6, CFBD was able to detect the existence of BEDs 80.5% of the time, which is 16% more likely than ZL; however, the recommended doses are not very likely (less than 50%) to be all acceptable. An explanation for the low %correct is the existence of a boundary dose. Dose 4 has a high efficacy rate (0.4 compared to E_min = 0.3) and a toxicity rate that is close to being admissible (0.35 compared to T_max = 0.3). Due to the small sample size at dose 4, the toxicity rate of 0.35 cannot be distinguished from 0.30 and so CFBD often recommended dose 4 as a BED in the simulated trials. More specifically, dose 4 was often selected (29.4% of times) as the upper limit, U*, of the recommended interval of BEDs (see Table 3). If a toxicity rate of 0.35 is considered admissible, the percentage of trials that provided a correct recommendation would increase dramatically. It is observed that for all scenarios with BEDs (scenarios 2 to 6), the confidence level of the recommended BEDs being acceptable as a group (%success) is different from the true percentage of the recommended BEDs being all acceptable (%correct). This issue can be fixed by increasing the sample size in the confirmation cohort. However, the precision of efficacy estimation is not of interest in phase I trials and this issue can be deferred to phase II trials.

In scenario 1, where there is no BED, the percentage of trials in which CFBD did not recommend any dose (100 − %found) is comparable to that of ZL (93.4% versus 97.4%), but the former tended to stop the trials much later than the latter (an average of 67.0 versus 30.4 patients). This is due to the stopping rule n_min.int = 60 that is imposed on CFBD. If n_min.int = 10, the average sample size for CFBD drops to 26.7 while the percentage of trials in which CFBD did not recommend an interval remained at the high level (94.6%).

Overall, CFBD performs wells in terms of the average sample size and the percentage of good recommendation, regardless of the shape of the underlying efficacy curve.

3.2 Sensitivity Analysis

We conducted a sensitivity analysis to investigate the robustness of CFBD. There were two sets of simulations, one involving random errors and the other involving fixed errors in prior specifications. In the first set of simulations, we added random errors to the means of the Beta prior distributions, which were originally chosen to be equal to the true rates. Specifically, we set initial Beta mean toxicity and efficacy rate ${\mu }_{T,i}^{0}=(1+{\varepsilon }_{T,i}){P}_{T,i}$ and ${\mu }_{E,i}^{0}=(1+{\varepsilon }_{E,i}){P}_{E,i},$ where ${\varepsilon }_{T,i}$ and ${\varepsilon }_{E,i}$ are uniformly distributed between -50% and 50% of the corresponding true rates. All other settings were as described in the previous section. Table 5 summarizes the results, from which we see that CFBD is extremely robust: the operating characteristic of CFBD under misspecifications of parameter values, with random errors up to 50% of the true values, is nearly identical to that without misspecification. We attribute this robustness to adequate sample size, relatively weak prior information, and the curve-free approach. Recall that the minimum sample size of 60 patients was selected based on the consideration of power and significance level of a test of H₀:P_E,I = E_min (Sect. 3.1). Because every admissible dose in and around the interval of BEDs, rather than only the BOD, were assigned to the next cohort of patients, a given sample of patients would be fairly uniformly distributed among the admissible doses, such that an average of 12 or more patients were assigned to each admissible dose. Also recall that the parameters of the prior distributions were chosen such that the prior information is as strong as that obtained from four patients, translates into one-third of the average number of patients assigned to each admissible dose. This allows the data to correctly update the misspecified priors. Finally, without a parametric assumption on the dose–toxicity and dose–efficacy relationships, the data can freely correct any errors in the priors.

To investigate the robustness of CFBD to extremer misspecifications, we modified the original toxicity and efficacy scenarios in the second set of simulations. The (prior) toxicity rates were shifted such that the prior MTD is different from the true MTD, and the (prior) efficacy rates were also shifted or modified such that the prior set of BEDs and the true set of BEDs are disjoint (Table 4). All other settings remained the same as described in Sect. 3.1. The results are summarized in Table 5. Although the priors were very different from the true scenario, and the prior MTD and BEDs were completely different from the actual values, CFBD still performed reasonably well. In scenario 1, the only scenario with no BED, CFBD made the correct conclusion in 86.7% of simulated trials (100 − %found). For the scenarios with BEDs, CFBD was able to recommend one or more BEDs in 90% or more of the trials (%found) in scenarios 2 to 5, with at least 83% accuracy rate (%correct). In scenario 6, where there is a boundary dose (dose 4), CFBD under misspecified priors actually made a good recommendation (%found * %correct) slightly more often than CFBD under correct priors (42% vs. 39%). The reason is, the misspecified priors overestimated both toxicity and efficacy rates, which rendered the boundary dose inadmissible in more trials and thereby increased %correct, the percentage of trials that provided a correct recommendation within those trials recommending BEDs. Overall, in our simulation studies, CFBD still remains pretty robust with slightly larger sample size (less than 10 more on average) even with such greatly misspecified prior.

Table 4 Sensitivity analysis: fixed error priors with incorrect BED sets (disjoint with the true BED sets)

Table 5 Sensitivity analysis: average sample size ($\stackrel{-}{n}$), the percentage of trials that recommended any BEDs (%found), within the trial found BEDs, the percentage that recommended BEDs are acceptable (%correct) and the percentage that data suggest acceptable pooled efficacy (%success), and the percentages of in-trial toxicity (%tox) and efficacy (%eff) under correct priors, incorrect priors with random errors and with fixed errors

4 A Demonstration Based On Simulations Using Real Trial Data

A completed phase I trial conducted at the University of California at Los Angeles Medical Center [13] was used to demonstrate an application of the proposed CFBD. The purpose of the trial is to recommend the BOD of several doses of celecoxib combined with erlotinib at a fixed dose in patients diagnosed with advanced non-small-cell lung cancer (NSCLC). Celecoxib is a cyclooxygenase-2 (COX-2) inhibitor, which can regulate cellular proliferation, migration, and invasion. On the other hand, erlotinib is a highly specific epidermal growth factor receptor (EGFR) tyrosine kinase inhibitor (TKI), which has been shown to inhibit the growth of human cancer cells. Several studies by 2006, for example Krysan et al. [9], found that overexpression of COX-2 promotes EGFR-TKI resistance. The knowledge of COX-2 and EGFR in NSCLC and the interaction of their signalling pathways provided a unique way to inhibit tumour angiogenesis, invasion, and growth. Motivated by these findings, Reckamp et al. [13] conducted a combined trial to establish a BOD within 200, 300, 400, 600 and 800 mg of celecoxib administered with 150 mg of erlotinb. The BOD was determined at the lowest dose level (of celecoxib) showing optimal biological activity, defined as a maximal decrease in the level of urinary prostaglandin E-M (PGE-M), where no dose-limiting toxicity (DLT) occurred.

Twenty-two subjects were enrolled and 21 were evaluable for the determination of the BOD, toxicity and efficacy. There were no DLTs among the 21 subjects and thus a low toxicity profile is assumed. The adopted toxicity profile was modified slightly based on scenario 2, the lowest toxicity scenario in Table 1 in our previous simulation studies. The efficacy outcome was defined as a decline in urinary PGE-M of > 72%, which is known to improve overall survival. Based on the data of three patients per dose level, the sample mean of the decline percentages in urinary PGE-M at the five dose levels were around 9%, 8%, 65%, 84%, and 87%, respectively, with a sample standard deviation of less than 10%. In our illustration of CFBD, we assume the decline percentage follows a normal distribution with the mean 10%, 15%, 70%, 80%, 80%, and a standard deviation of 15% for all dose levels. The enlarged standard deviation and slightly different means are intended to reflect the uncertainty due to the small sample. The true efficacy rate, a probability of more than 72% decline in the urinary PGE-M, can then be calculated. Furthermore, the prior efficacy rates are based on the Emax curve [11]. The efficacy profile together with the toxicity profile is reported in Table 6.

Table 6 Demo trial: the selection percentages of MTD, BED interval limits: L*, U*, and patient allocation for all doses; average sample size ($\stackrel{-}{n}$), percentages of none and good BED selection (%none, %good), in-trial toxicity and efficacy rates (%tox, %eff); MTD and BED values are in bold

Different to Reckamp's phase I/II trial, our method is designed for phase Ia/Ib trials and our goal is to find all BEDs, that is, all admissible doses with sufficient efficacy. Because the sample size of Reckamp’s trial was much smaller than that used in the simulation studies presented in Sect. 3.1.2, we do not recruit any confirmation cohorts in the current simulated trials. In addition, to reflect the lower toxicity and higher efficacy rates in the actual trial, we set the maximal tolerable DLT rate as T_max = 0.20 and the minimal acceptable efficacy rate as E_min = 0.40. All other parameters remain the same as in Sect. 3. The summary statistics over 5000 simulated trials are reported in Table 6. The results show that CFBD is able to recommend at least one BED correctly 99.2% of time with an average of 61.8 patients. Within all in-trial patients, 57.1% of them had efficacy outcomes (> 72% decline in urinary PGE-M) and only 9.4% of them experienced DLTs. About 91% of patients are allocated at BEDs (400, 600, or 800 mg).

As a further illustration, we include here the details of one simulated trial. In the first stage, patients are enrolled one by one and are assigned the lowest dose (200 mg). If no DLT occurred, the next patient (cohort) is assigned the next higher dose level. The dose level continues to increase until the occurrence of a DLT. Once a DLT is observed, the FLW algorithm [5] is adopted to find the MTD, which will be assigned to the next patient (cohort). In this simulated trial, there is no DLT in the first five patients when the dose level is gradually increased from 200 to 800 mg. After including the data (no DLTs) from these five patients, the FLW algorithm recommends 800 mg as the MTD, which is given to the next patient. Since sixth patient did not experience DLT either, the FLW algorithm continues to recommend 800 mg as the MTD and so the seventh patient is treated at 800 mg. The procedure is repeated until the minimal sample size of stage one, 10, is reached. After the first 10 patients, no DLT ever occurred, and so there is sufficient evidence to conclude that 800 mg is the MTD. Stage one is concluded and its statistics are reported in Table 7.

Table 7 Demo trial: patient allocations and responses of one simulated trial

The trial now moves to the second stage to identify the BEDs. As described in Sect. 2.3, based on the prior information and data from stage one, the set of BEDs is found to be {600 mg, 800 mg} and thus the next cohort is treated at the BEDs and adjacently admissible doses: {400 mg, 600 mg, 800 mg}, with one patient per dose. After collecting the data from this cohort of 3 patients, the BED is updated and it remains the same. Therefore, the same doses (400, 600, and 800 mg) are assigned to the next cohort of three patients. This procedure is repeated until the minimal sample size of a trial, 60, is reached. The statistics of stage two are reported in Table 7. The BEDs turned out to be the same for all 17 cohorts in stage two in this particular simulated trial, but it is not the case in other simulated trials. After collecting data from 61 patients (10 from stage one and 17 × 3 = 51 from stage two), the evidence is sufficiently strong to conclude that 600 mg, 800 mg are the BEDs (see Sect. 2.3 for details). The trial is terminated before reaching the maximum sample size and recommends 600 mg and 800 mg for further phase II investigation.

5 Conclusion and Discussion

In this paper, we propose a curve-free Bayesian design for identifying the BEDs, assuming only a monotonic dose–toxicity relationship and a unimodal or plateau dose–efficacy relationship. We avoid the complexity of joint modelling of the toxicity–efficacy association by utilizing the marginal distribution approach. In addition to the identification of BEDs, a confirmation cohort is recruited to provide a better estimate of the efficacy/toxicity rates of the BEDs to facilitate the selection of a recommended dose to phase II trials.

Our design is motivated by the following considerations. First of all, parametric models are not necessarily better for small samples, which are typical in early phase clinical trials. Although parametric models provide increased power over nonparametric models, they are usually not robust in that small departures from an assumed model can have drastic effects on the performance of the related statistical inference procedures. On the other hand, nonparametric models, while robust, lack power in small samples to provide meaningful results. To achieve a balance between power and robustness, we adopt the curve-free approach: instead of assuming a parametric dose–response relationship, we assume that the dose-toxicity curve is monotonically increasing and the dose-efficacy curve is unimodal. Our simulation studies show that our design is robust under these weaker assumptions.

Secondly, if identifying the BEDs is of primary interest, it may not be necessary to model the association between toxicity and efficacy outcomes. With limited information on the agent under study in early phase clinical trials, the challenge of specifying a prior on the toxicity–efficacy association will likely discourage the use of Bayesian designs. Therefore, we adopt a simpler phase Ia/Ib approach that dispense with the modelling of the toxicity–efficacy association. The phase Ia stage of our design focuses on finding the MTD and toxicity is the primary outcome. Upon identifying the MTD, the phase Ib stage is initiated to search for the BEDs among doses not exceeding the MTD, and efficacy becomes the primary outcome. A disadvantage of our phase Ia/Ib approach is that, without utilizing the association between the toxicity and efficacy outcomes, a larger sample size may be required. This can be mitigated by implementing an algorithm that is capable of locating the MTD efficiently and accurately in the phase Ia stage, as was demonstrated in our simulation studies.

Thirdly, when identifying the BEDs is the goal, grouping doses could be a good idea since pooling the samples should lead to increased precision of estimated efficacy rate. Based on these considerations, we built the skeleton of CFBD.

Finally, the careful selection of prior distribution and its parameters fill the muscles of the CFBD. The well-known beta priors are chosen for toxicity/efficacy rates so that people can easily understand the models. In addition, the model-free efficacy curve and less-informative priors can increase the robustness of CFBD. Errors in the initial priors can be fixed quickly. Our simulation studies show the robustness of the proposed CFBD.

Several designs have been proposed for seamless phase I/II trials. One difference between phase Ia/Ib and phase I/II trials is that phase I/II trials requires statistical inferences on the efficacy of the selected dose, whereas phase Ia/Ib trials only recommend a likely dose range that has initial signals of biological activities beyond a target level; that is, a phase Ia/Ib trial is not required to establish the efficacy of a selected dose. The proposed CFBD in this paper is for one-agent phase Ia/Ib trials. Yet it can be easily extended to two-agent combination trials, under the assumptions that the dose-toxicity surface is marginally monotonic non-decreasing and the dose–efficacy surface is unimodal. In recent years, several dose-finding algorithms have been proposed to identify the maximum tolerated combination; however, adopting an efficient dose-finding algorithm in the first stage, such as that proposed by Lee et al. [10], is crucial to the success of the extension. To identify the set of best efficacious combinations, the dose–efficacy surface can be modelled using the equivalent of a step function in two-dimensional space and a similar utility function.