Hot Deformation Behaviors and Process Parameters Optimization of Low-Density High-Strength Fe–Mn–Al–C Alloy Steel

Abstract

The hot deformation behavior of low-density high-strength Fe–Mn–Al–C alloy steel at T = 900-1150 °C and $\dot{\varepsilon }$ = 0.01-10 s⁻¹ was studied by the Gleeble-3500 thermo-mechanical simulator. The rheological stress curve characteristics of the steel were analyzed through experimental data, and a physical constitutive model considering strain coupling was established. At the same time, the finite element software DEFORM was used to calculate the critical damage value of the steel, and the influence of T and $\dot{\varepsilon }$ on the maximum damage value was considered. By introducing the dimensionless parameter Zener–Hollomon, the critical damage model was established. Finally, the workability of the steel was evaluated by using the intuitive processing map technology. The results indicated that Fe–Mn–Al–C alloy steel is a positive strain rate-sensitive and a negative temperature-sensitive material, and the constitutive model considering physical parameters can well predict the rheological stress of the steel during hot deformation (R = 0.997). The critical damage factor of Fe–Mn–Al–C alloy steel varies with the change of T and $\dot{\varepsilon }$, and the range is 0.359-0.535. At the same time, the critical damage factor is more sensitive to $\dot{\varepsilon }$. At a constant T, the damage factor decreases with the increase of $\dot{\varepsilon }$. Based on the Prasad instability criterion, the dynamic material model processing map and the microstructure verification after thermal compression, the rheological instability characteristics of the steel are mainly mechanical instability and local plastic flow, and the stable deformation area is mainly characterized by dynamic recrystallization. The optimal hot working process window of the steel is 975-1050 °C/0.01-0.032 s⁻¹.

Graphical abstract

1 Introduction

The trend of material lightweight now is a promising scientific research field with the gradual growth of automotive industry. Fe–Mn–Al–C alloy steel owns capital performance, such as anti-corrosion, low density, etc. It can be applied in complicated working surroundings and other occasions, lighting, and safety area [1,2,3,4]. In the process of hot deformation, the material flow behavior is usually complex. The constitutive model is not only an important way to describe the plastic flow characteristics of materials, but also the key and foundation of solid mechanics and most analysis and calculation. At present, many researchers have constructed material constitutive models based on the Arrhenius equation, and the parameters in the equation are obtained by regression of experimental data [5, 6]. Although this method is simple, it does not take into account the influence of the hot working parameters on the physical properties of the material. It is necessary to establish the constitutive model by introducing physical parameters (self-diffusion coefficient, etc.) to Fe–Mn–Al–C alloy steel. The physical constitutive model combines macroscopic parameters (T and $\dot{\varepsilon }$, etc.) with physical basic parameters related to materials, which plays an important role in making the simulation results closer to the real situation. In addition, the internal damage of metal material accumulates continuously during the plastic forming process. When the damage value reaches the critical value, micro-cracks will occur in the material. Therefore, it is of positive significance to predict the time of cracks during the plastic forming of materials.

The processing map technology is widely used in the design and optimization of the hot deformation process of metal materials (magnesium alloy, aluminum alloy, titanium alloy, etc.) [7,8,9]. This technology aims to characterize the thermal workability of materials, taking into account the mechanical factors and irreversible thermodynamic factors during plastic deformation, which is helpful to obtain excellent products in the practical production field. Therefore, the establishment of a low-density high-strength Fe–Mn–Al–C alloy steel processing map is of great significance to the formulation and optimization of the hot forging process of the steel. At present, reports on Fe–Mn–Al–C alloy steel mainly focus on smelting, heat treatment, and mechanical properties, etc. For example, Zhang et al. [10] obtained Fe-25.7Mn-10.6Al-1.2C steel with micron austenite grains and a small number of submicron ferrite grains through a phase transition restraint recrystallization process, and the corresponding mechanical properties were also excellent. Li et al. [11] studied the effects of aging treatment and rolling on the tensile properties and microstructure of Fe-23.38Mn-6.86Al-1.43C steel. It was found that a good balance between dislocation recovery and κ-carbide precipitation was beneficial to rolling. The best tensile properties were obtained after aging at 450 ℃. However, the research reports on the hot deformation behavior of low-density high-strength Fe–Mn–Al–C alloy steel are not thorough enough. There is no research on the fracture damage of Fe–Mn–Al–C alloy steel and the prediction of the plastic flow of the steel during hot deformation by introducing a constitutive model of physical parameters.

In this paper, the hot deformation behaviors of Fe–Mn–Al–C alloy steel were mainly studied through thermal simulation compression experiments and metallographic observation. The flow stress curve characteristics of the steel were analyzed through experimental data, and a physical constitutive model considering strain coupling was established. At the same time, the critical damage value was calculated with the finite element software DEFORM, and the damage model was established, and the influencing factors of the critical damage factor were analyzed. Then the workability of the steel was evaluated with intuitive processing map technology and the optimum hot working process window was obtained. The research results can provide theoretical support for the determination of hot forging process parameters and the numerical simulation of hot forming of low-density high-strength Fe–Mn–Al–C alloy steel.

2 Experimental Procedures

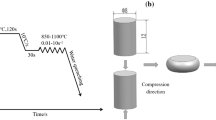
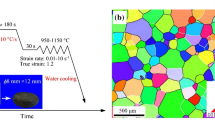
The material used in the experiment is Fe–Mn–Al–C alloy steel and the main chemical composition of the steel is given in Table 1. The hot compression sample is a cylinder of Φ8mm × 12 mm (Table 1), the surface of the sample is polished smoothly, and the two ends are parallel. A single-pass high-temperature compression experiment of the steel was performed on the Gleeble-3500 thermo-mechanical simulator. The experimental temperatures were 900, 950, 1000, 1050, 1100, and 1150 ℃, and the strain rates were 0.01, 0.1, 1, and 10 s⁻¹, respectively. The maximum height reduction rate was 60% (corresponding to the maximum true strain 0.92). The mica foils with high-temperature lubricants were affixed to the two end faces of the sample to reduce the friction and the non-uniformity of deformation. The sample was heated to 1200 °C at a rate of 10 °C/s, and then homogenized by holding 120 s, and then cooled to the set T at a rate of 5 °C/s. Before compression, keep the temperature at the set T for another 15 s to make the temperature difference between the inside and outside of the sample consistent. After compression, the sample was sprayed with water to cool down. Figure 1a shows the experimental process. Figure 1b shows the phase diagram of Fe–Mn–Al–C alloy steel. The compressed sample was split in half along the axial axis, and after sample preparation, grinding, polishing and etching. The etching solution was: 30% nitric acid alcohol solution (volume fraction). The microstructure images were collected on the LEXT OLS4000 laser confocal microscope and electron backscatter diffraction (EBSD). The sample was electropolished with 10% perchloric acid alcohol solution before EBSD was used for microstructure image collection. The parameters of electropolishing were set as follows: voltage 8 V, current 0.5A, and time 15 s.

Table 1 The chemical composition (mass fraction, %) and size of Fe–Mn–Al–C alloy steel for experiment

Fig. 1

Compression experiment process (a) and the phase diagram (b) of Fe–Mn–Al–C alloy steel

3 Results and discussion

3.1 Rheological behavior and physical constitutive model considering strain coupling

Figure 2a and b show the true stress-true strain curves of Fe–Mn–Al–C alloy steel at different temperatures and strain rates. Figure 2a and b show that the rheological stress behavior of the steel is mainly influenced by temperature and strain rate. The decrease of strain rate or increase of temperature will result in the decrease of rheological stress, which indicates that the steel is a positive strain rate-sensitive and negative temperature-sensitive material. The former is mainly due to the accelerated grain boundary mobility of dynamic recrystallization (DRX) at a higher temperature. At the same time, high temperature is beneficial to strengthen the softening effect and reduce the dislocation slip resistance [12,13,14,15]. The latter is mainly because the lower strain rate provides more time to promote DRX and dynamic recovery (DRV), leading to the work hardening effect less than the softening effect of the material, which shows that the rheological stress decreases with the decrease of strain rate. In addition, the Arrhenius equation was generally used to describe the relationship between rheological stresses, temperature and strain rate during the hot deformation of materials. To improve the accuracy and versatility of the constitutive model for hot deformation of materials, the Fe–Mn–Al–C alloy steel constitutive model was constructed by introducing physical parameters (self-diffusion coefficient D and Young’s modulus E), the relevant formulas of which are formulas (1)-(5):

$$E(T) = E_{0} \left( {1 + \frac{{T_{{\text{m}}} }}{{G_{0} }}\frac{{{\text{d}}G}}{{{\text{d}}T}} \cdot \frac{T - 300}{{T_{{\text{m}}} }}} \right)$$

(1)

$$D(T) = D_{0} \exp \left( { - \frac{{Q_{{{\text{sd}}}} }}{RT}} \right)$$

(2)

$$\frac{{\dot{\varepsilon }}}{D(T)} = B_{1} \left( {\frac{\sigma }{E(T)}} \right)^{{n_{1} }}$$

(3)

$$\frac{{\dot{\varepsilon }}}{D(T)} = B_{2} {\text{exp}}\left( {\frac{\beta \sigma }{{E(T)}}} \right)$$

(4)

$$\frac{{\dot{\varepsilon }}}{D(T)} = B\left[ {{\text{sinh}}\left( {\frac{\alpha \sigma }{{E(T)}}} \right)} \right]^{n}$$

(5)

where D(T) is the self-diffusion coefficient of the material expressed by temperature; D₀ is the diffusion constant of the material; Q_sd is the activation energy of self-diffusion (J·mol⁻¹); T is the temperature (K); R is the gas constant (8.314 J·(mol·K)⁻¹); σ is the stress (MPa); E(T) is Young’s modulus (GPa) of the material expressed by temperature; E₀ and G₀ are Young’s modulus (GPa) and shear modulus (GPa) at 300 K, respectively; T_m is the melting point (K); other parameters B, B₁, B₂, n, n₁, α and β are material constants, where α = β/n₁. n is the creep constant of the material, which is usually set as a fixed value of 5 for the sake of simple calculation, but this will reduce the prediction accuracy of the physical constitutive model [16]. The influence of technological parameters such as T and $\dot{\varepsilon }$ on its value is fully considered, and n is set as the material constant. The changes in the D and E with temperature were taken into account in the hot deformation constitutive model based on physics, which not only represents the rheological behavior of the steel but also reflects the physical properties of the steel.

Fig. 2

The true stress-true strain curves of Fe–Mn–Al–C alloy steel under different deformation conditions: a T = 1100 ℃; b $\dot{\varepsilon }$ = 1 s⁻¹

To build the constitutive model with physical parameters, the relevant material parameters [17,18,19] of Fe–Mn–Al–C alloy steel were substituted in formulas (1) and (2) to determine D and E of Fe–Mn–Al–C alloy steel at different T, $D(T) = 1.8 \times 10^{{{ - }5}} \exp \left( { - 270000/RT} \right)$ and $E(T) = [210 - 0.1083(T - 300)] \times 10^{3}$, respectively. After taking the natural logarithm of both sides of formulas (3) and (4) respectively, the relationship between $\ln [\dot{\varepsilon }/D(T)]$, $\sigma /E(T)$ and $\ln [\sigma /E(T)]$ can be obtained, differentiated them, and then obtained the expressions of n₁ and β: $\beta = \partial \ln [\dot{\varepsilon }/D(T)]/\partial [\sigma /E(T)]$ and $n_{1} = \partial \ln [\dot{\varepsilon }/D(T)]/\partial \ln [\sigma /E(T)]$. Taking true strain 0.3 as an example, the true stress–strain experimental data were substituted, β and n₁ were respectively determined by the slopes of fitting curves with the unary linear fitting of $\ln [\dot{\varepsilon }/D(T)] - \sigma /E(T)$ and $\ln [\dot{\varepsilon }/D(T)] - {\text{ln[}}\sigma /E(T)]$. As shown in Fig. 3a and b, the material parameters β and n₁ were obtained as β = 2677.217 and n₁ = 5.216 respectively, so α = β/n₁ = 513.270 can be determined. After taking the natural logarithms on both sides of formula (5), the relationship between $\ln [{\text{sinh(}}\alpha \sigma /E(T))]$ and $\ln [\dot{\varepsilon }/D(T)]$ was obtained:

$$\ln \left( {\frac{{\dot{\varepsilon }}}{D(T)}} \right) = n\ln \left[ {\sinh \left( {\frac{\alpha \sigma }{{E(T)}}} \right)} \right] + \ln B$$

(6)

Fig. 3

The linear relationship fitting of parameters of β a $\ln [\dot{\varepsilon }/D(T)] - \sigma /E(T)$, n1 b $\ln [\dot{\varepsilon }/D(T)] - {\text{ln[}}\sigma /E(T)]$ and n c $\ln [\dot{\varepsilon }/D(T)] - {\text{ln[sinh(}}\alpha \sigma /E(T))]$ of Fe–Mn–Al–C alloy steel

The formula (6) shows that there is a linear relationship between $\ln [{\text{sinh(}}\alpha \sigma /E(T))]$ and $\ln [\dot{\varepsilon }/D(T)]$, and the intercept lnB and the slope n can be obtained by unary linear regression. As shown in Fig. 3c, lnB and n were obtained as lnB = 34.495 and n = 3.919, respectively. Based on the constants α, lnB, n, and combined with formulas (1) and (2), the physical constitutive equation of Fe–Mn–Al–C alloy steel with true strain 0.3 was obtained:

$$\dot{\varepsilon } \cdot e^{{\frac{270000}{{RT}}}} = 1.7226 \times 10^{10} \left[ {{\text{sinh}}\left( {\frac{{513.27{\kern 1pt} \sigma }}{E(T)}} \right)} \right]^{3.919}$$

(7)

During the process of plastic deformation, the strain had an important influence on the high-temperature rheological behavior. The material parameters (α, n and lnB) under different strains are varied. The constitutive model constructed under a single strain cannot predict the rheological behavior of the entire material. In this regard, this paper introduced strain factors, so that the established physical constitutive model is suitable for all strain conditions, taking full account of the effect of strain on the material parameters. According to the above method, the values of α, n and lnB in the range of 0.05-0.92 and the strain interval of 0.05 (the strain interval of 0.9-0.92 was 0.02) were calculated. The results are shown in Table 2.

Table 2 Material parameters under different strains

Through the polynomial nonlinear fitting of the material parameters (α, n and lnB) under each true strain, it was found that the accuracy of the eighth-order nonlinear fitting was the best by comparison, as shown in Table 3. The eighth-order nonlinear fitting accuracy can better express the functional relationship between the true strain and each material parameter (see Fig. 4 and formula 8). The physical modeling above between these parameters and the strain can be called the eighth-order relationship. Many scholars [20,21,22,23] have used the above fitting method, the polynomial nonlinear fitting is used to establish the functional relationship between strain and material parameters, to establish the constitutive model of materials. The basic physical model of these relationships can be understood through the solving process of the above related parameters.

$$\left\{ \begin{gathered} \alpha (\varepsilon ) = U_{{8}} \varepsilon^{{8}} + U_{{7}} \varepsilon^{{7}} + U_{{6}} \varepsilon^{{6}} + U_{5} \varepsilon^{{5}} + U_{4} \varepsilon^{{4}} + U_{3} \varepsilon^{{3}} + U_{2} \varepsilon^{{2}} + U_{1} \varepsilon + U_{0} \hfill \\ n(\varepsilon ) = V_{8} \varepsilon^{{8}} + V_{7} \varepsilon^{{7}} + V_{6} \varepsilon^{{6}} + V_{5} \varepsilon^{{5}} + V_{4} \varepsilon^{{4}} + V_{{3}} \varepsilon^{{3}} + V_{2} \varepsilon^{{2}} + V_{1} \varepsilon + V_{0} \hfill \\ \ln B(\varepsilon ) = W_{8} \varepsilon^{{8}} + W_{7} \varepsilon^{{7}} + W_{6} \varepsilon^{{6}} + W_{5} \varepsilon^{{5}} + W_{4} \varepsilon^{{4}} + W_{3} \varepsilon^{{3}} + W_{2} \varepsilon^{{2}} + W_{1} \varepsilon + W_{0} \, \hfill \\ \end{gathered} \right.$$

(8)

Table 3 Comparison of fitting accuracy of material parameters

Fig. 4

The 8th polynomial fitting relationships among true strain, α a, lnB b, and n c

The coefficients obtained by the eighth-degree polynomial fitting are shown in Table 4. These parameters correspond to the entire thermal deformation process. After substituting the strain value into the function relation, the material parameters under the corresponding strain condition can be calculated, which also reflects the importance of these fitting parameters. The revised physics-based constitutive model (the strain coupling was considered) can be obtained by substituting the coefficient into formula (8) and embedding it into formula (5):

$$\sigma = \frac{E(T)}{{\alpha (\varepsilon )}}\ln \left\{ {\left( {\frac{{\dot{\varepsilon } \cdot {\text{exp(2}}{.7} \times 10^{5} {/}RT{)}}}{{1.8 \times 10^{{{ - }5}} B(\varepsilon )}}} \right)^{1/n(\varepsilon )} + \left[ {\left( {\frac{{\dot{\varepsilon } \cdot {\text{exp(2}}{.7} \times 10^{5} {/}RT{)}}}{{1.8 \times 10^{{{ - }5}} B(\varepsilon )}}} \right)^{2/n(\varepsilon )} + 1} \right]^{1/2} } \right\}$$

(9)

Table 4 The 8th polynomial coefficients of material parameters α, lnB and n

To verify the accuracy of the prediction model, the correlation analysis (correlation coefficient $R = \left[ {\sum\limits_{{{\text{i}} = 1}}^{n} {\left( {M_{{\text{i}}} - \overline{M}} \right)\left( {N_{{\text{i}}} - \overline{N}} \right)} } \right]/\left[ {\sqrt {\sum\limits_{{{\text{i}} = 1}}^{n} {\left( {M_{{\text{i}}} - \overline{M}} \right)^{2} } } \sqrt {\sum\limits_{{{\text{i}} = 1}}^{n} {\left( {N_{{\text{i}}} - \overline{N}} \right)}^{2} } } \right]$) and error test (average relative error $A_{RE} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\sum\limits_{{{\text{i}} = 1}}^{n} {\left| {(M_{{\text{i}}} - N_{{\text{i}}} )/M_{{\text{i}}} } \right|} } \right]/n \times 100{\text{\% }}$) of the predicted value (N) of the rheological stress and the experimental value (M) were carried out. The results as shown in Fig. 5, R is 0.997 and A_RE is only 3.85%. Figure 5d shows that the absolute error between N of the rheological stress and M is mostly within 18 MPa, which further shows that the constitutive model with physical parameters can accurately predict the rheological stress of low-density high-strength alloy steel. This model is suitable for the rheological behavior prediction of the steel during the hot deformation process.

Fig. 5

The correlation c and absolute error d between predicted and experimental values of the rheological stress model with physical parameters (a T = 1100 ℃; b $\dot{\varepsilon }$ = 1 s⁻¹)

3.2 Critical damage model and determination of maximum damage value

According to the principle of material ductile fracture, there is a fixed maximum tensile stress during the process of material ductile fracture [24, 25]. The damage factor is an important index to measure whether the material fails or not. The maximum tensile principal stress promotes the accumulation of stress and strain energy. The critical value C_max reached at the time of fracture is called the critical damage factor [26, 27].

$$C = \int_{0}^{{\overline{\varepsilon }_{f} }} {\frac{{\sigma_{T} }}{{\overline{\sigma }}}{\text{d}}} \overline{\varepsilon }$$

(10)

where C is the material damage factor; $\sigma_{T}$ is the maximum tensile stress; $\overline{\varepsilon }_{f}$ is the equivalent plastic strain; $\overline{\sigma }$ is the equivalent stress; ${\text{d}}\overline{\varepsilon }$ is the increment of equivalent strain.

To facilitate calculation, formula (10) was transformed into the sum of discrete steps, and the following can be obtained:

$$C = \int_{0}^{{\overline{\varepsilon }_{f} }} {\frac{{\sigma_{T} }}{{\overline{\sigma }}}\frac{{{\text{d}}\overline{\varepsilon }}}{{{\text{d}}t}}{\text{d}}} t = \int_{0}^{{t_{f} }} {\frac{{\sigma_{T} }}{{\overline{\sigma }}}\dot{\overline{\varepsilon }}{\kern 1pt} {\text{d}}t \cong } \sum\limits_{0}^{{t_{f} }} {\frac{{\sigma_{T} {\kern 1pt} \dot{\overline{\varepsilon }}{\kern 1pt} \Delta t}}{{\overline{\sigma }}}}$$

(11)

where $\dot{\overline{\varepsilon }}$ is the equivalent variable rate; $\Delta t$ is the time increment.

The ratio of damage increment to cumulative damage in per unit time $\Delta t$ is the damage sensitivity rate:

$$R_{{{\text{step}}}} = \frac{\Delta C}{{C_{{{\text{acc}}}} }}$$

(12)

where R_step is the damage sensitivity rate; C_acc is the current cumulative damage; $\Delta C$ is the damage increment in unit time increment.

When the damage factor C of the material accumulates to the critical value, it is considered that micro-cracks are formed, and then the damage factor remains unchanged and is no longer sensitive to deformation conditions. The rheological stress data collected from the hot compression tests and the physical constitutive model established were input into the finite element software DEFORM for numerical simulation analysis. Under high-temperature conditions, the plastic deformation of the workpiece was relatively large and the elastic deformation was usually negligible. Therefore, in the finite element simulation, the billet was set as a rigid plastic body and the indenter of the die was set as a rigid body. In order to improve the accuracy of the simulation, the material parameters were given to the die. A semi-symmetric specimen was used as the deformation model to shorten the finite element simulation time. Among them, it should be noted that the friction of the contact interface between the billet and the die was set as the shear-type and the value was 0.3 [28,29,30]. The convection coefficient of billet and air was set as 0.02 N/(s·mm ℃). The state of the simulation was transient. Since the damage of the compression was caused by the accumulated effect, the transient state simulation can better explain the correlation between the C(Δt) and the distribution of damage sensitivity points. Taking Fe–Mn–Al–C alloy steel at T = 950 ℃ and $\dot{\varepsilon }$ = 0.01 s⁻¹ as an example, the results are shown in Fig. 6a and b. It can be found from Fig. 6a that there are small cracks on the outer surface edge of the specimen in the physical test, and the central area is intact. And from Fig. 6b that the maximum damage value simulated by the software always appears at the outermost edge of the upsetting drum shape, that is, the free deformation zone of the material. The C_min always appears in the center of the billet, which is consistent with Fig. 6a experimental results.

Fig. 6

The damage distribution map about sample in 60% of height reduction at 950 ℃/0.01 s⁻¹ a and b and the damage value of the outermost edge of the sample under different $\dot{\varepsilon }$ at 950 ℃ c and 1050 ℃ d

In Fig. 6b, point P, the point with the C_max on the outermost side of the upsetting drum shape, was taken. In Fig. 6c and d, the result was obtained after point tracing of point P in the free deformation zone of materials under different T and $\dot{\varepsilon }$. When the deformation temperature of P is 950 ℃ and 1050 ℃, the damage value increases with the decrease of $\dot{\varepsilon }$. By comparing Fig. 6c and d, it can be concluded that under the condition of constant T, the critical damage value increases with the increase of true strain. The maximum damage value after the completion of the hot compression test was taken as the tracking object to further analyze the change of damage value with temperature. The results are shown in Fig. 7. Figure 7 shows that when the $\dot{\varepsilon }$ is constant, the maximum damage value is generally stable with the increase of T. Especially when the $\dot{\varepsilon }$ are 1 s⁻¹ and 10 s⁻¹, the maximum damage value does not change much. From the overall trend, the maximum damage value is more significantly affected by the $\dot{\varepsilon }$. When the T is constant, the maximum damage value decreases significantly with the increase of $\dot{\varepsilon }$, which is called the damage softening phenomenon [27, 31, 32]. The dislocation changes its slip plane mainly through cross-slip. When the $\dot{\varepsilon }$ increases, the dislocation proliferation rate increases, which will weaken the plastic deformation ability of the material and decrease the maximum damage value. At the same time, when the $\dot{\varepsilon }$ increases, the processing time decreases. And the heat conduction time between the material and the external environment is shortened, which is easy to cause the temperature rise, resulting in the material softening, and the maximum damage value is reduced.

Fig. 7

The C_max of the outermost edge of the sample at different T and $\dot{\varepsilon }$

Zener and Hollomon [33] studied the constitutive relationship of steel and found that the flow stress depends on temperature and strain rate. Therefore, they proposed the Zener-Hollomon (Z) parameter model (formula (13)) to characterize the comprehensive influence of T and $\dot{\varepsilon }$ on the flow stress. Considering the complicated relationship between the maximum damage value and T and $\dot{\varepsilon }$, the temperature compensated strain rate function (Z parameter) was introduced to further study the relationship.

$$Z = \dot{\varepsilon }{\kern 1pt} {\kern 1pt} {\text{exp[}}Q{/(}RT{)]}$$

(13)

where $\dot{\varepsilon }$ is the strain rate (s⁻¹); T is the deformation temperature (K); Q is the deformation activation energy (J·mol⁻¹). The Z parameter has been applied in many studies. Wang et al. [34] studied the effect of the Zener-Hollomon parameter on thermal deformation of CoCrFeMnNiC_0.5 high entropy alloy and found that with the lnZ increasing, the additions of carbon in solid solution effectively reduce the dislocation cross-slip. Li et al. [35] studied the isothermal compression tests of as-homogenized Mg-5.8Zn-0.5Zr-1.0Yb magnesium alloy and discussed the dynamic recrystallization kinetics of Mg-Zn-Zr-Yb magnesium alloy by introducing the Zener–Hollomon parameter. Aryshenskii et al. [36] used X-ray texture analysis, EBSD, and optical microscopy to evaluate the influence of the Zener-Hollomon parameter on substructure and texture evolution in iron-containing wrought aluminum alloys.

Since the thermal deformation process of metals was controlled by hot activation, the Arrhenius equation can be established [5, 37] to determine the hot activation energy Q:

$$\dot{\varepsilon } = A{\text{sinh(}}\alpha ^{\prime}\sigma {)}^{n^{\prime}} {\text{exp[}} - Q{/(}RT{)]}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} for{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} all{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} )$$

(14)

$$\dot{\varepsilon } = A_{1} \sigma^{{n_{1} ^{\prime}}} {\text{exp[}} - Q{/(}RT{)]}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\alpha \sigma < 0.8)$$

(15)

$$\dot{\varepsilon } = A_{2} {\kern 1pt} {\kern 1pt} {\text{exp(}}\beta {^{\prime}}\sigma {\text{)exp[}} - Q{/(}RT{)]}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {(}\alpha \sigma > {1}{\text{.2)}}$$

(16)

where A, A₁, A₂, β´ and α´ are constants related to materials and α´ = β´/n₁´. Take the natural logarithm of both sides of formulas (15) and (16):

$$\ln \dot{\varepsilon } = \ln A_{1} + n_{1} ^{\prime}\ln \sigma - Q{/(}RT{)}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$

(17)

$${\text{ln}}\dot{\varepsilon } = \ln A_{2} {\kern 1pt} {\kern 1pt} + \beta {^{\prime}}\sigma - Q{/(}RT{)}$$

(18)

The peak stress is an important basis for estimating maximum deformation load, die selection and equipment checking in actual production. According to Fig. 2, the peak stress σ_p of Fe–Mn–Al–C alloy steel can be determined, and then the relationship curve between $\ln \dot{\varepsilon } - {\text{ln}}\sigma_{{\text{p}}}$ and $\ln \dot{\varepsilon } - \sigma_{{\text{p}}}$ can be calculated and obtained, and linear regression can be performed. As shown in Fig. 8a and b, n₁´ = $\partial \ln \dot{\varepsilon }/\partial \ln \sigma_{{\text{p}}}$ = 7.945 and β´ = $\partial \ln \dot{\varepsilon }/\partial \sigma_{{\text{p}}}$ = 0.044 can be determined. According to α´ = β´/n₁´, α´ = 0.00554 can be obtained. Take the natural logarithm of both sides of formula (14) and write it into the following two forms:

$$\ln \dot{\varepsilon } = n^{\prime}\ln [\sinh (\alpha ^{\prime}\sigma )] + (\ln A - Q/RT)$$

(19)

$${\text{ln}}[\sinh (\alpha ^{\prime}\sigma )] = \frac{{\ln ({\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{\varepsilon }/A{\kern 1pt} {\kern 1pt} )}}{n^{\prime}} + \frac{Q}{{{\kern 1pt} {\kern 1pt} {\kern 1pt} n^{\prime}RT}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$

(20)

Fig. 8

Relationship maps of $\ln \dot{\varepsilon } - {\text{ln}}\sigma_{{\text{p}}}$ a and $\ln \dot{\varepsilon } - \sigma_{{\text{p}}}$ b and the relation curve of critical damage factor $C_{\max } - \ln Z$ c

Thus, the formula of hot deformation activation energy Q can be obtained:

$$Q = R\left[ {\frac{\partial \ln [\sinh (\alpha ^{\prime}\sigma )]}{{\partial (1000/T)}}} \right]_{{\dot{\varepsilon }}} {\kern 1pt} \left[ {\frac{{\partial \ln \dot{\varepsilon }}}{\partial \ln [\sinh (\alpha ^{\prime}\sigma )]}} \right]_{T}$$

(21)

Continue to take the relevant data under the peak stress σ_p condition as an example for substitution. By establishing the relationship between $\ln [\sinh (\alpha ^{\prime}\sigma_{{\text{p}}} )] - 1000/T$ and $\ln \dot{\varepsilon } - \ln [\sinh (\alpha ^{\prime}\sigma_{{\text{p}}} )]$, using the least square method for linear regression, $\partial {\text{ln}}[\sinh (\alpha ^{\prime}\sigma_{{\text{p}}} )]/\partial (1000/T)$ = 15.690 and $\partial {\text{ln}}\dot{\varepsilon }/\partial \ln [\sinh (\alpha ^{\prime}\sigma_{{\text{p}}} )]$ = 5.135 can be determined. Therefore, Q = 669.844 kJ·mol⁻¹ at peak stress according to formula (21). In addition, the critical ε rate for rheology or damage is related to the temperature, the critical ε rate is the function of T. Therefore, Q values are different at varied temperatures and strain rates. According to the above method, the activation energy Q of the steel under different T and $\dot{\varepsilon }$ conditions can be calculated, as shown in Table 5. Take the natural logarithm on both sides of the formula (13): $\ln Z = \ln \dot{\varepsilon }{\kern 1pt} + {\kern 1pt} Q{/(}RT{)}$. The corresponding lnZ value can be obtained from T and $\dot{\varepsilon }$ of Fe–Mn–Al–C alloy steel. According to the maximum damage value data of Fig. 7 and using the method of non-linear fitting, the $C_{\max } - \ln Z$ relation curve was established, see Fig. 8c, thus the critical damage model with Z parameter was obtained:

$$C_{\max } = 0.000541(\ln Z{\kern 1pt} ){\kern 1pt} {\kern 1pt}^{2} - 0.0741\ln Z + 2.915$$

(22)

Table 5 The activation energy Q under different temperatures and strain rates

This critical damage model considers the influence of the Z parameter on C_max after introducing T and $\dot{\varepsilon }$. Figure 8c shows that the area below the curve is the safe processing area of the steel, and the area above the curve is the vulnerable area, which reflects the high-temperature plastic deformation of Fe–Mn–Al–C alloy steel to a certain extent.

3.3 Process parameters optimization

3.3.1 Processing map of Fe–Mn–Al–C alloy steel

The processing map technology is an important tool for material processing technology design and optimization. It can analyze the safe and unsafe areas of plastic deformation of materials at different T and $\dot{\varepsilon }$ to achieve the purpose of avoiding defects and optimizing process parameters. According to the dynamic material model (DMM), the workpiece can be regarded as an energy dispersion during hot deformation, and the sum of the energy J dissipated during microstructure transformation and the energy G dissipated during plastic deformation is equal to the total energy P of the external input to the workpiece [38]: $P = \sigma \dot{\varepsilon } = J + G = \int_{0}^{\sigma } {\dot{\varepsilon }{\text{d}}} \sigma + \int_{0}^{{\dot{\varepsilon }}} {\sigma {\text{d}}\dot{\varepsilon }}$. $J = \int_{0}^{\sigma } {\dot{\varepsilon }{\text{d}}} \sigma$ and $G = \int_{0}^{{\dot{\varepsilon }}} {\sigma {\text{d}}\dot{\varepsilon }}$ are two complementary functions, respectively called power dissipation co-content and power dissipation.

Under a given strain and T, the dynamic response (dynamic constitutive equation) of the material to $\dot{\varepsilon }$ is $\sigma = K\dot{\varepsilon }^{m}$. K is a constant related to temperature; m is a strain rate sensitivity index, which determines the proportional relationship between the dissipation co-content J and the dissipation G in the material deformation [38, 39]. Prasad et al. [40] used the cubic spline function to fit the relationship between ln $\dot{\varepsilon }$ and ln, and derived the formula of strain rate sensitivity index m:

$$\left. {\frac{\partial J}{{\partial G}}} \right|_{{\varepsilon ,{\kern 1pt} T}} = \left. {\frac{{\dot{\varepsilon }{\kern 1pt} {\text{d}}\sigma }}{{\sigma {\kern 1pt} {\text{d}}\dot{\varepsilon }}}} \right|_{{\varepsilon ,{\kern 1pt} T}} = \left. {\frac{{\partial ({\text{ln}}\sigma )}}{{\partial (\ln \dot{\varepsilon })}}} \right|_{{\varepsilon ,{\kern 1pt} T}} = m$$

(23)

The co-content J of power dissipation can be described as [38, 40]:

$$J = \int_{0}^{\sigma } {\dot{\varepsilon }} {\text{d}}\sigma = \left( {\frac{m}{m + 1}} \right)\sigma \cdot \dot{\varepsilon }$$

(24)

When the material is in an ideal linear dissipation state, that is, when m = 1, the power dissipation co-content J reaches the maximum value J_max and J_max = $\dot{\varepsilon }$/2 = P/2. Since the relationship of J/J_max is closely related to the evolution of the microstructure of the material, Prasad et al. [41] defined the η as the power dissipation factor, to reveal the microscopic deformation of the material during the thermoplastic deformation process, where η = J/J_max. When the rheological stress of the material satisfies the above relationship, the expression of η can be derived as [39, 41]:

$$\eta = \frac{J}{{J_{{{\text{max}}}} }} = \left\{ \begin{gathered} 1{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J = J_{\max } {\kern 1pt} \hfill \\ \frac{2m}{{m + 1}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J < J_{\max } \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$$

(25)

where η represents the energy dissipation coefficient, which is a dimensionless parameter. For an ideal linear dissipative process, both m and η are equal to 1. For nonlinear dissipative processes, m and η are both less than 1. The 2D iso-line map where η varies with T and $\dot{\varepsilon }$ is called the power dissipation map.

According to the principle of maximum entropy, Prasad et al. [41] proposed the following conditions for material rheological instability:

$$\xi (\dot{\varepsilon }) = \frac{\partial \ln [m/(m + 1)]}{{\partial \ln \dot{\varepsilon }}} + m < 0$$

(26)

where ξ is the instability coefficient. When ξ is negative, it indicates that the plastic state of the material is unsteady, that is, instability may occur. The rheological instability map can be drawn by the change of $\xi (\dot{\varepsilon })$ with T and $\dot{\varepsilon }$. The processing map can be obtained by superimposing the ξ map and η map.

According to the rheological stress of Fe–Mn–Al–C alloy steel, the change curves of the energy dissipation coefficient with T under different strains and $\dot{\varepsilon }$ (Fig. 9a-c) and the 3D η map (Fig. 9d) were drawn. As can be seen from Figs. 9a-c, when $\dot{\varepsilon }$ is 0.01 s⁻¹, the energy dissipation coefficients at the late deformation stage (ε = 0.6-0.92) are all high, ranging from 0.23 to 0.40. Among them, the η value corresponding to 1000 ℃/0.01 s⁻¹ is the highest, which is 0.40. When $\dot{\varepsilon }$ is 0.1 s⁻¹, with the increase of strain, the energy dissipation coefficient fluctuates slightly with the change of T, and η is basically between 0.22 and 0.35. However, when $\dot{\varepsilon }$ are 1 s⁻¹ and 10 s⁻¹, the energy dissipation coefficient fluctuates greatly with T, and the variation law of η value under different strains is similar. As seen from the 3D η map (Fig. 9d), when the process parameters are 950-1100 ℃/0.01-0.1 s⁻¹, the area with the larger energy dissipation coefficient tends to expand with the increase of strain. The higher the η value is, the better the hot working performance of the material will be. According to the calculation $\xi (\dot{\varepsilon })$, the change curves of the instability parameters with T under different strains and $\dot{\varepsilon }$ (Fig. 10a-c) and the 3D ξ map (Fig. 10d) were drawn. Figure 10a-c show that the ξ value of low $\dot{\varepsilon }$ (0.01 s⁻¹ and 0.1 s⁻¹) is mostly higher than that of high $\dot{\varepsilon }$ (1 s⁻¹ and 10 s⁻¹). When the $\dot{\varepsilon }$ are 0.01 s⁻¹ and 0.1 s⁻¹, the instability parameter ξ is mostly positive, and the ξ value is lower than zero only at low temperatures (900-950 ℃). In addition, at $\dot{\varepsilon }$ of 1 s⁻¹ and 10 s⁻¹, the instability parameters show a downward trend with the increase of strain. This indicates that the possibility of unstable deformation of the steel increases under the condition of 1 s⁻¹ and 10 s⁻¹. When the $\dot{\varepsilon }$ is 10 s⁻¹, most of the instability parameters are negative when T is lower than 1000 ℃, and the lower T, the smaller the instability parameters are. This indicates that rheological instability is more likely to occur. The 3D ξ map (Fig. 10d) shows that the instability area is the largest when the strain is 0.92.

Fig. 9

Distribution of energy dissipation coefficient and 3D η map (d) of Fe–Mn–Al–C alloy steel at ɛ = 0.3 a, ɛ = 0.6 b and ɛ = 0.92 c

Fig. 10

Distribution of instability coefficient and 3D ξ map d of Fe–Mn-Al–C alloy steel at ɛ = 0.3 a, ɛ = 0.6 b and ɛ = 0.92 c

Figure 11a and b are the processing map of Fe–Mn–Al–C alloy steel obtained by superposition of ξ map and η map. When the strain is 0.6 (Fig. 11a), the instability area is mainly located in the upper left corner of the processing map, and the corresponding $\dot{\varepsilon }$ range gradually decreases with the increase of T. When the strain is 0.92 (Fig. 11b), the rheological instability region expands to the high T and high $\dot{\varepsilon }$ region, and the corresponding plastic conditions are 900-970 ℃/0.1-10 s⁻¹ and 970-1025 ℃/0.056-0.63 s⁻¹, respectively. From the change rule of the shaded area in Fig. 11, the rheological instability area changes mainly in the high $\dot{\varepsilon }$ area, and it gradually expands with the increase of strain. In addition, the energy dissipation coefficient in the processing map increases roughly with the increase of T and the decrease of $\dot{\varepsilon }$, and the value of η varies from 0.03 to 0.37. The best range of process parameters for the steel should be the areas with higher energy dissipation coefficients, and these areas are in the stable deformation zone. With the increase of strain, there is mainly a peak energy dissipation region (975-1050 ℃/0.01-0.032 s⁻¹) when ɛ = 0.92, and the peak η is 0.35. Fe–Mn–Al–C alloy steel is suitable for hot working in this region.

Fig. 11

Processing map of Fe–Mn–Al–C alloy steel at ɛ = 0.6 a and ɛ = 0.92 b

3.3.2 Microstructure verification of processing map

To verify the validity of the prediction results of the processing map above, it is necessary to observe the hot compression microstructure of the steel in combination with metallographic observation and analyze the microstructure of different deformation zones, to further determine and optimize the process parameter range of Fe–Mn–Al–C alloy steel during hot working. Figure 12a-c show the microstructure of the steel when T and $\dot{\varepsilon }$ are 950 ℃/10 s⁻¹, 900 ℃/0.1 s⁻¹, and 1000 ℃/0.1 s⁻¹, respectively. The area corresponding to these conditions is the rheological instability zone. The microstructure (Fig. 12a/a’) at 950 ℃/10 s⁻¹ presents the elongated coarse structure, and there are fine DRX grains at the grain boundary of the coarse structure, which appears in the form of a necklace. The microstructure uniformity of the whole deformation area is poor, which is easy to cause mechanical instability. The recrystallization temperature of Nb microalloyed steel is generally above 950-1000 ℃ [42, 43], which is consistent with the experimental results. It can be seen from Fig. 12a’ that the texture microstructure appears in the sample and their grain orientation is {0 0 1} < 1 1 1 > . This is accordant with the glide direction < 1 1 1 > of the Fe grains [4, 11, 44]. The microstructure (Fig. 12b) at 900 ℃/0.1 s⁻¹ shows local plastic flow, which is elongated and has poor homogeneity. This may be due to the thermal effect of deformation, which is easy to accumulate temperature in a large deformation zone with the shortening of deformation time. It is easy to cause local plastic flow phenomena and consequently decrease the mechanical properties of materials [6, 45]. The microstructure (Fig. 12c) under the condition of 1000 ℃/0.1 s⁻¹ has several relatively large elongated grains and many fine, equiaxed DRX microstructure. The microstructure uniformity is poor, which will cause mechanical instability. The appearance of large and small microstructures above will lead to uneven mechanical properties of materials.

Fig. 12

Microstructure of Fe–Mn–Al–C alloy steel under different T and $\dot{\varepsilon }$: a/a’ 950 ℃/10 s⁻¹; b 900 ℃/0.1 s⁻¹; c 1000 ℃/0.1 s⁻¹

Figure 13a/a’ and b/b’ are the optical microstructures and EBSD of the steel under the conditions of T and $\dot{\varepsilon }$ of 1000 ℃/0.01 s⁻¹ and 1050 ℃/0.01 s⁻¹, respectively, belonging to the microstructure of stable deformation region. The microstructures of the samples are taken out from the same position of the compression samples. DRX significantly occurred in the microstructure (Fig. 13a/a’) at 1000 ℃/0.01 s⁻¹, and the dynamic recrystallization average grain size under this condition was measured to be about 14 μm. The grain size is small and equiaxed, and the grain boundary is naturally curved. With the increase of T, the microstructure (Fig. 13b/b’) under the condition of 1050 ℃/0.01 s⁻¹ grew somewhat, and the degree of DRX was relatively high, and the microstructure distribution was relatively uniform. The dynamic recrystallization average grain size under this condition is about 19 μm, which is still in the category of fine grain. This is because high temperatures provide more energy to the microstructures. Some of the energy dissipated by the microstructures promote DRX development, and some of the energy dissipated by the microstructures fuel their growth [46]. To sum up, the rheological instability characteristics are found in the selected microstructure of the instability zone, mainly mechanical instability and local plastic flow, which will reduce the mechanical properties of the material and should be avoided in the hot working process. The microstructure corresponding to the peak area of energy dissipation is DRX, and the microstructure uniformity is good, which is conducive to hot working. The microstructure verification shows that the range of process parameters predicted by processing map technology is reliable. The best processing window of the steel is 975-1050 ℃/0.01-0.032 s⁻¹.

Fig. 13

Optical microstructures and EBSD f Fe–Mn–Al–C alloy steel under different T and $\dot{\varepsilon }$: a/a’ 1000 ℃/0.01 s⁻¹; b/b’ 1050 ℃/0.01 s⁻¹

4 Conclusion

• (1) Fe–Mn–Al–C alloy steel is a positive strain rate-sensitive and negative temperature-sensitive material, and its rheological stress decreases with the decrease of $\dot{\varepsilon }$ or the increase of T. The physical constitutive prediction model considering strain coupling is $\sigma = \frac{E(T)}{{\alpha (\varepsilon )}}\ln \left\{ {\left( {\frac{{\dot{\varepsilon } \cdot {\text{exp(2}}{.7} \times 10^{5} {/}RT{)}}}{{1.8 \times 10^{{{ - }5}} B(\varepsilon )}}} \right)^{1/n(\varepsilon )} + \left[ {\left( {\frac{{\dot{\varepsilon } \cdot {\text{exp(2}}{.7} \times 10^{5} {/}RT{)}}}{{1.8 \times 10^{{{ - }5}} B(\varepsilon )}}} \right)^{2/n(\varepsilon )} + 1} \right]^{1/2} } \right\}$, and the deviation is generally less than 18 MPa, and A_RE for all samples is only 3.85%, which indicates that the model can be used to predict the rheological stress of low-density high-strength alloy steel during hot deformation.

• (2) The critical damage factor of Fe–Mn–Al–C alloy steel was calculated and analyzed by the finite element software DEFORM simulation, and the critical damage model of the steel was established. The maximum damage value always appears in the free deformation zone of upsetting drum shape and the minimum damage value always appears in the difficult deformation zone of the billet. The critical damage factor is more sensitive to $\dot{\varepsilon }$. At a constant T, the damage factor decreases with the increase of $\dot{\varepsilon }$. The critical damage factor of the steel varies from 0.359 to 0.535 at different T and $\dot{\varepsilon }$, and its value changes with the process conditions.

• (3) The m, η and ξ were calculated by processing map technology, and the dynamic material model processing map was established. Combining the processing map with the verification of microstructure after hot compression, the steel rheological instability area was characterized by mechanical instability and local plastic flow, while the microstructure in the stable deformation area was characterized by DRX. The optimum hot working process window of the steel is 975-1050 ℃/0.01-0.032 s⁻¹.