An extended version of opportunity cost algorithm for communication decisions

Abstract

Decentralized Markov decision processes (DEC-MDPs) provide powerful modeling tools for cooperative multi-agent decision making under uncertainty. In this paper, we tackle particular subclasses of theoretic decision models which operate under time pressure having uncertain actions’ durations. Particularly, we extend a solution method called opportunity cost decentralized Markov decision process (OC-DEC-MDP) to handle more complex precedence constraints where actions of each agent are presented by a partial plan. As a result of local partial plans with precedence constraints between agents, mis-coordination situations may occur. For this purpose, we introduce communication decisions between agents. Since dealing with offline planning for communication increase state space size, we aim at restricting the use of communication. To this end, we propose to exploit problem structure in order to limit communication decisions. Moreover, we study two separate cases about the reliability of the communication. The first case we assume that the communication is always successful (i.e. all messages are always successfully received). The second case, we enhance our policy computation algorithm to deal with possibly missed messages. Experimental results show that even if communication is costly, it improves the degree of coordination between agents and it increases team performances regarding constraints.

1 Introduction

Many real world applications involve multiple agents acting together as a team under time pressure and uncertainty. Examples of such applications can be found in Mars exploration missions (Becker et al. 2003), disaster management problems (Nair et al. 2002), and decentralized detection of hazardous weather events (Kumar and Zilberstein 2009) …

The more suitable models capable of handling such problems are those studied in decision theory. These models are very expressive and are able to reason about the gain of action over time. They include decentralized Markov decision process (DEC-MDP) and decentralized partially observable Markov decision process (DEC-POMDP) (Oliehoek 2012). However, solving optimally these models was proven to be NEXP-complete (Bernstein et al. 2002).

For these reasons, subclasses of these models have been proposed which are more tractable. These subclasses are mainly derived based on dependencies between agents. For ones, agents are assumed transition independent and interactions are captured by complex non-additive rewards like transition independent DEC-MDP (TI-DEC-MDP) (Becker et al. 2003). For the others, agents are assumed to be transition dependent with simple rewards. Among them, we cite event driven interactions DEC-MDP (ED-DEC-MDP) (Becker et al. 2004) where dependencies are structured in the form of event-driven interactions and opportunity cost DEC-MDP (OC-DEC-MDP) (Beynier and Mouaddib 2005) where dependencies are interpreted by a precedence relation between agents. Another model resulting from the marriage between TI-DEC-MDP and ED-DEC-MDP is event driven interaction with complex rewards (EDI-CR) (Mostafa and Lesser 2009) where dependencies are in the form of event-driven interaction and for each agent a complex reward is assigned.

Another side of DEC-MDP is the communication issue. To deal with the lack of information between agents, communication has been introduced to improve decisions and thus improving the total cumulative reward (Goldman and Zilberstein 2004). Communication can be implicit or explicit (Goldman and Zilberstein 2003). Implicit, when communication actions affect the observations seen by another agent. Explicit, when there are designated communication actions and the language of communication is attached explicitly by the agent designer. Reasoning about communication can be offline at planning time (Mostafa and Lesser 2009; Melo et al. 2012; Spaan et al. 2006), or online during policy execution (Becker et al. 2009; Roth et al. 2005; Xuan et al. 2001). The latter is less complex in term of computational cost, but the former ensure a better long-term coordination. As communication cannot be free, a cost is associated that allows agents to reason about the gain in communicating.

In our work, we are interested in OC-DEC-MDP model which is capable of addressing temporal constraints, precedence constraints and uncertainty on actions’ durations. However, this model is suited to the case where agents have linear plans of their actions. This is a tight assumption regarding real world applications where agents’ actions may not be totally ordered. Hence, when considering partial local plans the solution proposed in Beynier and Mouaddib (2005, 2011) is not suited and need to be extended by handling other emerging problems as (i) which action to execute and (ii) when to execute it, instead of when to execute the beforehand known action in Beynier and Mouaddib (2005, 2011).

Moreover, as a consequence of partial local plans, agents have more than one path to accomplish their mission. Hence, the constrained agent may wait indefinitely for a predecessor action that will never be executed by the predecessor agent (when choosing a different path). This leads to a violation of the temporal constraints of the constrained action which leads to the total failure of agents’ mission.

Communication may handle problems resulting from partial local plans and improves the degree of coordination between agents. However, it induces a cost and considering it at planning time leads to an increase in state space size due to reasoning about all communication possibilities at each time step.

To alleviate this problem, we exploit problem structure (Melo et al. 2012; Mostafa and Lesser 2009) to define coordination points and introduce some heuristics. These heuristics allow efficient communication decisions that concern when to communicate, what to communicate and to whom communicate. A communicative version of OC-DEC-MDP was proposed in Beynier and Mouaddib (2010), but this version is once again suited to the case where agents’ actions are totally ordered. Applying heuristics proposed in Beynier and Mouaddib (2010) for partial local plans is not possible because both the problem structure and the decision problem are different from those considered in Beynier and Mouaddib (2010, 2011). The model of communication proposed in this paper is able to deal with specific problems arising from agents’ partial local plans on one side and precedence constraints among them on the other side.

Most of the works for planning for DEC-MDPs and DEC-POMDPs with communication assume that communication is instantaneous and without failure (Roth et al. 2005, 2007; Becker et al. 2009). Actually, instantaneous communication does not exist. Moreover, communication can fail temporarily and messages may be missed. In this case, the agent still has to select an action and its decision will be based only on its local information.

Since messages may be lost, an agent may wait indefinitely for a response which leads to a violation of its temporal constraints. For this purpose, we enhance our proposition to deal with missed messages. We propose to compute adaptive waiting times for each agent after which an agent chooses another action admitting that the message is lost en route. These adaptive waiting times depend on the state an agent might be in and regarding its temporal constraints.

The rest of the paper is organized as follows. In Sect. 2, we will motivate our concerns by an example. In Sect. 3, we will briefly introduce the OC-DEC-MDP model. Some related work will be discussed in Sect. 4. The extension of OC-DEC-MDP for partial local plans and communication decisions is given in Sect. 5. Afterward, we will detail the computation of the joint policy and how coordination between agents is ensured in Sect. 6. Experimental results are presented in Sect. 7. A comparative study will be discussed in Sect. 8. Section 9 concludes this paper.

2 Motivating example

The problem we treat can be motivated by scenarios of controlling the operation of multiple space exploration rovers, such as the ones used by NASA to explore the surface of Mars (Washington et al. 1999). Agents in such problems could take pictures, conduct experiments, and collect data under constraints (time, battery, memory …).

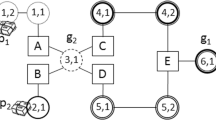
Figure 1 shows a simple problem involving a two-agent team whose objective is to execute their local plans. As agents’ local plans are partial each agent has to choose between two or more alternative actions. Depending on the current situation, alternative actions have different gains.

Fig. 1

Small mission graph presented by partial local plans of each agent

Despite local dependencies between actions, there is another type of dependencies between agents’ actions. For example, in Fig. 1, action J of agent 2 cannot be executed only when either actions H or I of the same agent are executed and action F of agent 1 is executed. Uncertainty results from actions’ durations. Indeed, an action can have several execution durations each of which is associated to a probability. These probabilities are obtained empirically (Witwicki and Durfee 2011). Moreover, the execution of each action is constrained by a temporal window that expresses the action’s earliest start time and latest end time. The successful completion of each action is associated to a value. The overall gain of the team is quantified by the cumulative values of completed actions.

Since the environment is dynamic and present constraints on actions’ execution, several unexpected situations can occur and thus need a change in agents’ plans. For example, agent 2 can choose to execute action I rather than action H and agent 1 can choose to perform action C rather than action B. In this case agent 1 will wait for action H from agent 2 that will never be executed. This conducts to a total failure of the mission.

Communication may handle these situations. Since communication in these domains is costly, it must be restricted. Several paths exist leading to the mission completion, but the goal is to find the global path which maximizes the overall gain of the group and avoiding the total failure of the mission. This path is interpreted by an optimal plan (policy) for each agent, which is calculated by resolving the appropriate DEC-MDP.

3 Background

OC-DEC-MDP represents the background of this work. In this section, we will present this model and its resolution algorithm.

3.1 Opportunity cost decentralized Markov decision process

OC-DEC-MDP model is proposed by Beynier and Mouaddib (2005, 2011), in order to handle temporal constraints where each action must be executed respecting a specific execution interval, precedence constraints where an action cannot be executed before the fulfillment of some actions of other agents and probabilistic actions’ durations. For n agents, this model is composed of n local MDPs. Each MDP is composed of fully ordered actions, factored states, transition function and reward function. Each component has to undergo a specific treatment based on temporal propagation (Bresina and Washington 2000) to take into account actions’ execution constraints. All agents’ actions are considered in one acyclic mission graph where nodes are actions and arcs are precedence constraints.

According to the type of problem studied and since communication between agents is not allowed, three types of states are identified: success states when the action respects its constraints, partial failure (PF) states when the action attempts to execute but its predecessors are not yet executed and total failure (TF) states when the action violates its constraints. OC-DEC-MDP was proven to be polynomial in the size of the state space. The construction of this model (and its resolution) rests on the assumption that the actions of each agent are totally ordered. This assumption means that the actions will be executed sooner or later. As a consequence of this representation, actions’ execution intervals must be large; otherwise, the probability of the total failure of one action execution on the execution of other actions is augmented (due to this chain representation). Consequently, the decision problem of each agent is alleviated. Indeed, each agent has to determine solely when to start an action.

The resolution of this model is based on an opportunity cost (OC). This measure is borrowed from the field of the economy (Wieser 1889). It is particularly introduced to handle precedence constraints. OC has been used for the first time in MDPs in (Mouaddib and Zilberstein 1998) and then extended to DEC-MDP in case of agents’ linear local plans in Beynier and Mouaddib (2005, 2011). The intuition behind using this cost is to allow each agent to take into account the effects of its own decisions on other agents in order to ensure coordination between agents.

Recently, a communicative version of OC-DEC-MDP is proposed in Beynier and Mouaddib (2010). Communication is introduced in order to handle mis-coordination between agents (interpreted by the number of partial failure states). Allowing agents to share information at planning time has for consequence an increase in the state and action spaces. In order to remedy to that, a set of heuristics is proposed. These heuristics consist in communicating the end time of previous successfully executed action, to agents who depend from it. A comparative study will be discussed in Sect. 8.

It is important to note that OC-DEC-MDP and communicative OC-DEC-MDP as defined, are not suited to the case where agents’ local plans are partially ordered which is more close to real world applications. In this latter, the local decision problem consists in two folds: what action to perform and when? which affects the resolution algorithm. Furthermore, the heuristics introduced in Beynier and Mouaddib (2010) to make communication possible cannot be applied in the case of partial local plans since an agent may choose to not execute a predecessor action.

The overall purpose of this work consists in extending OC-DEC-MDP and its policy computation to handle more complex precedence constraints. It is true that the reason behind introducing communication in Beynier and Mouaddib (2010) and this work is the same; reduce situations of mis-coordination, the way it is considered is different since the topology of the mission graph and decision problems are not the same. Situations of mis-coordination in Beynier and Mouaddib (2010) are interpreted by the PF state and result only from the fact that an action starts its execution before the completion of its predecessor. In this study, these situations result also from the fact that the predecessor agent may not execute the predecessor action at all. As we will see in Sect. 6.2, heuristics introduced in this paper are suited to the new topology of the mission graph where agents’ actions are partially ordered.

In the following subsection, we will explain the principle of OC algorithm according to (Beynier and Mouaddib 2011).

3.2 The principle of opportunity cost algorithm

The OC algorithm, like several other policy computation algorithms, starts with an initial policy which consists in the earliest starting time policy. This policy is then improved in several iterations until no further improvement is possible. Each iteration of this algorithm consists of two phases. The first phase is a computation of expected utilities, policies and OC values for each state based on the initial policy. The second one performs an update of the transition function based on the current policy found in the previous iteration in order to prepare to a new iteration of the algorithm. The reason behind updating transition probabilities is that these probabilities are computed based on the fixed initial policy.

To handle precedence constraints, opportunity cost algorithm starts from sink actions for which there is no successor (actions J and E according to the example of Fig. 1) rising to root actions (actions A and G from Fig. 1). The reason behind starting with leaf actions is that these actions have an opportunity cost equal to zero, since they don’t influence any other actions. For each state from which the current actions (sink actions, at first) can be executed, OC algorithm computes its expected utility, its policy, and opportunity cost values. These values (OC values) are then propagated to all possible predecessors’ states of other agents. At this moment, each agent can calculate its policy by considering its local rewards minus the propagated opportunity cost. From this new policy, the probability function is updated in order to run a new iteration of the algorithm.

4 Related work

In addition to the works in (Beynier and Mouaddib 2005, 2010, 2011), some other works exist in literature that concern planning for constrained actions using DEC-MDP and works on taking offline communication decisions. Marecki and Tambe (2007) improve the OC-DEC-MDP in term of speed and solution quality. Indeed, OC-DEC-MDP deals with discrete temporal constraints which result in a huge state space. The work in Marecki and Tambe (2007) deals with continuous temporal constraints in order to manipulate a value function over time rather than a separate value for each pair of action and time interval like in OC-DEC-MDP.

Another related work that handles execution constraints and making offline communication decisions is Mostafa and Lesser (2009). In order to make offline planning for communication tractable, interactions between agents are presented explicitly in EDI-CR model. This structure is exploited in order to define communication possibilities in advance and thus reducing the problem size. The work in Melo et al. (2012) also exploits interactions between agents in order to optimize communication decisions in DEC-POMDP. A key insight is that in domains with local interactions the amount of communication necessary for successful joint behavior can be heavily reduced, due to the limited influence between agents. This idea is exploited by deriving local POMDP models that optimize each agent’s communication behavior.

Most of approaches within communication in DEC-MDP and DEC-POMDP do not make any constraint on communication; rather, they assume instantaneous and successful communication. Recently, some works were realized considering constrained and stochastic communication where messages may be lost, corrupted or delayed.

Spaan et al. (2008) and Oliehoek and Spaan (2012) have been considered the problem of delayed communication by one or more time steps and uncertain successful communication (with a probability of success) within DEC-POMDP framework. Bayesian games were used in order to plan for DEC-POMDP with delayed communication. Matignon et al. (2012) introduced a new interaction-oriented resolution method for decentralized decision models that handles limited share of information and breaks in communication. This resolution method is based on distributed value function considering the latest time step where communication between agents succeeded. Message corruption, however, has received little attention in decentralized planning (Valtazanos and Steedman 2014).

Many approaches have been proposed to deal with uncertainties in scheduling, we cite (Lambrechts et al. 2008) where uncertainty is modeled by unavailability of resources and (Lazarova-Molnar and Mizouni 2010) which addressed uncertainties on task duration, task allocation and arbitrary on-the-fly decisions.

5 Problem description

The decision problem we consider is characterized by: $\left\langle { \propto ,A,C_{T} ,C_{P} ,\Delta ,R,C_{com} ,\Sigma } \right\rangle$, where:

• $\propto$ is a set of agents.

• A, is a set of actions.

• $C_{T} = \left\{ {\left[ {EST_{i} ,LET_{i} } \right], i = 1\ldots\left| A \right|} \right\}$ where, EST _i is a _i ’s earliest start time and LET _i is its latest end time.

• $C_{P} = \left\{ {EndoPred \cup ExoPred} \right\}$. Each action a _i has a set of endogenous predecessors [noted as $EndoPred(a_{i} )$] specifying the set of local actions that must be executed before a _i , and a set of exogenous predecessors [noted as $ExoPred(a_{i} )$], specifying the set of actions that must be executed before a _i by other agents.

• Each action a _i disposes of multiple possible execution durations each of which is associated to a probability. We note: $\Delta = \left\{ {\left( {d_{i} ,p_{i} } \right)| p_{i} = P\left( {duration = d_{i} } \right)} \right\}$.

• R, is a reward function. The successful execution of action a _i is awarded by a non-negative reward, R _i .

• C _com , is the communication cost.

• $\Sigma$, is the set of messages that can be sent by agents. The semantic of these messages is discussed in the next section.

We encode this decision problem by OC-DEC-MDP model. This latter is extended in order to take into account communication’s cost and language. As we mentioned in Sect. 3, the OC-DEC-MDP is known to be composed of a set of local MDPs, one for each agent. Each MDP is a tuple $\left\langle {S,A,P,R,\Sigma ,C_{com} } \right\rangle$, where S is a finite set of states and A is a finite set of actions including communication action. The dynamic of each MDP is maintained by a transition function P. R denotes the reward function and it is associated to a specific state. $\Sigma$ is a finite set of messages and C _com is the communication cost.

The modeling of constrained decision problem by OC-DEC-MDP is equivalent to construct each component of agent’s MDP. In the following, we describe this model construction.

5.1 Actions

Taking into account precedence constraints (local and global), uncertainty on actions’ durations and the strict execution temporal window, we compute for each action several possible start times and end times. We note ST _i and ET _i sets of possible start times and end times of action a _i , respectively. For example, for action B in Fig. 1, we obtain $ST_{B} = \left\{ {8,10,11,12} \right\}, ET_{B} = \left\{ {10,11,12,13,14,15} \right\}$.

5.2 States

Since action a _i has different start and end times, we can deduce different execution intervals in which a _i can be executed. These intervals constitute useful information for deciding about states’ transitions since it reveals when the action starts, when it ends, and how many time units it consumes. As we tackle communication decisions, the message constitutes useful information too for agents’ decisions. Hence, to satisfy Markov property, the state has to be factored and must encapsulate the last executed action a _i , its execution interval $\left[ {t_{i} ,{t_{t}}^{\prime } } \right]$ (where t _i is a possible start time of action a _i and ${t_{i}}^{\prime}$ is the associated end time), and the message $\Sigma$ if exists. Example, in Fig. 1 we obtain for action B: $\left\langle {B,\left[ {8,10} \right]} \right\rangle$, $\left\langle {B,\left[ {8,11} \right]} \right\rangle$, $\left\langle {B,\left[ {10,12} \right]} \right\rangle,$ $\left\langle {B,\left[ {10,13} \right]} \right\rangle$, $\left\langle {B,\left[ {11,13} \right]} \right\rangle$, $\left\langle {B,\left[ {11,14} \right]} \right\rangle$, $\left\langle {B,\left[ {12,14} \right]} \right\rangle$, $\left\langle {B,\left[ {12,15} \right]} \right\rangle$, $\left\langle {B,\left[ {8,10} \right],\Sigma } \right\rangle$, $\left\langle {B,\left[ {8,11} \right],\Sigma } \right\rangle$, $\left\langle {B,\left[ {10,12} \right],\Sigma } \right\rangle,$ $\left\langle {B,\left[ {10,13} \right],\Sigma } \right\rangle$, $\left\langle {B,\left[ {11,13} \right],\Sigma } \right\rangle$, $\left\langle {B,\left[ {11,14} \right],\Sigma } \right\rangle$, $\left\langle {B,\left[ {12,14} \right],\Sigma } \right\rangle$ and $\left\langle {B,\left[ {12,15} \right],\Sigma } \right\rangle$.

Note that not all states will contain messages because, as we will explain later, agents don’t communicate always at any state but communication is allowed at specific points. As in OC-DEC-MDP, three types of states are distinguished. Success state, the agent moves to such state when the action considered is executed successfully respecting its constraints. Partial failure (PF) state, when the agent attempts to execute an action having its exogenous predecessors not yet executed. Total failure (TF) state, when the action executed violates its temporal constraints.

5.3 Transition function

The transition function computes the transition probability from a state s _i associated to action a _i , to a resulting state s _i+1 associated to action a _i+1. The computation starts from the root of the mission graph to leaves.

Let s _i and s _i+1 be, respectively: $s_{i} = \left\langle {a_{i} ,I_{{a_{i} }} } \right\rangle , s_{i + 1} = \left\langle {a_{i + 1} ,I_{{a_{i + 1} }} } \right\rangle$.¹

$$P\left( {s_{i + 1} |s_{i} ,a_{i + 1} } \right) = P(I_{{a_{i + 1} }} )$$

This probability depends on the probability that action a _i+1 will be executed in the interval $I_{{a_{i + 1} }}$. Let $I_{{a_{i + 1} }} = \left[ {t_{i + 1} ,t_{i + 1}^{\prime } } \right].$ Hence:

$$P\left( {s_{i + 1} \left| {s_{i} ,a_{i + 1} } \right.} \right) = P\left( {start\left( {a_{i + 1} } \right) = t_{i + 1} } \right) \times P\left( {end\left( {a_{i + 1} } \right) = t_{i + 1}^{\prime} } \right)$$

(1)

This probability corresponds to the probability that the execution of a _i+1 starts at time t _i+1 and ends at time $t_{i + 1}^{\prime }$.

The first part of Eq. (1) depends on an initial policy, on one hand: if the initial policy of state s _i dictates the execution of a _i+1 at t _i+1, $P_{\pi } \left( {\pi \left( {s_{i} } \right) = (a_{i + 1} ,t_{i + 1} )} \right) = 1$, otherwise, this probability is equal to zero. On the other hand, $P\left( {start\left( {a_{i + 1} } \right) = t_{i + 1} } \right)$ depends on the probability that the exogenous predecessors of a _i+1 have finished their executions at a time inferior or equal to t _i+1.

The second part of Eq. (1) corresponds to the probability that a _i+1 consumes $d_{i + 1} = t_{i + 1}^{\prime } - t_{i + 1}$ time units which is given in problem statement ($P\left( {duration = d_{i + 1} = t_{i + 1}^{\prime } - t_{i + 1} } \right)$).

For example, in Fig. 1 the probability of transitioning from state $s_{A} = \left\langle {A,\left[ {6,8} \right]} \right\rangle$ to a resulting state $s_{B} = \left\langle {B,\left[ {8,10} \right]} \right\rangle$, is given by:

$$P\left( {s_{B} \left| {s_{A} ,B} \right.} \right) = P\left( {I_{B} = \left[ {8,10} \right]} \right) = P(start\left( B \right) = 8\left| {s_{A} } \right.) \times P(end\left( B \right) = 10\left| {s_{A} } \right.)$$

We suppose that the initial policy of agent 1 is to execute action B at time 8, $P_{\pi } \left( {\pi \left( {s_{A} } \right) = (B,8)} \right) = 1$. Hence:

$$P\left( {start\left( B \right) = 8\left| {s_{A} } \right.} \right) = 1$$

Since action B has not any exogenous predecessor, we don’t consider the probability that their exogenous predecessors have finished their executions.

From the problem statement, we have:

$$P\left( {end\left( B \right) = 10\left| {s_{A} } \right.} \right) = P\left( {d_{B} = 10 - 8} \right) = 0.2$$

Hence:

$$P\left( {s_{B} \left| {s_{A} ,B} \right.} \right) = 1 \times 0.2 = 0.2$$

Since we maintain the same model as in Beynier and Mouaddib (2011) (OC-DEC-MDP), where three types of states are introduced, we distinguish between three types of transition. Successful transition when action a _i+1 is executed in the interval $I_{{a_{i + 1} }} = \left[ {t_{i + 1} ,t_{i + 1}^{\prime} } \right]$ respecting its $EST_{i + 1}$ and $LET_{i + 1}$ ($EST_{i + 1} \le t_{i + 1} < t_{i + 1}^{\prime} \le LET_{i + 1}$). Partial failure transition when action a _i+1 starts its execution too early before all its predecessors have finished their executions. Total failure transition when action a _i+1 is executed in the interval $I_{{a_{i + 1} }} = \left[ {t_{i + 1} ,t_{i + 1}^{\prime } } \right]$ violating its $LET_{i + 1} (t_{i + 1}^{\prime } > LET_{i + 1} )$.

5.4 Reward function

The agent receives a reward which is a positive number for being in a success state. The partial failure state is associated to a reward equal to zero because no transition is done. As for the total failure state, the agent is penalized if such state occurs. This penalization consists in a negative number added to the loss in reward of all remaining actions reached from the failed action and executed by the same agent. If an agent opts to communicate, the communication cost is subtracted from the reward received.

5.5 Communication language

In our work, semantics are attached explicitly to messages. We propose three types of messages each of which with specific semantics. These semantics are explained in the next section.

6 Joint policy computation

This section is dedicated to the resolution of the model constructed in Sect. 5. We will first present how the original OC algorithm is extended to the case of partial local plan. Then, we will give and argument the proposed communication model and we will detail the joint policy computation according to our problem taking into account partial local plans and communication decision.

6.1 Opportunity cost algorithm for partial local plans

The adaptation of opportunity cost algorithm to handle partial local plan requires tackling two main issues. The first issue concerns two decision problems consisting in what action to execute and when to execute it, instead of the decision problem handled in original OC algorithm for total ordered actions where the decision problem concerns when to start the unique next action.

The second issue deals with when an action is considered to compute the expected utility, the policy and OC values (noted as ($V,\pi ,OC$), respectively) at planning time. Indeed and resulting from precedence constraints (local and global), tighter actions have to be defined so they can be evaluated ($V,\pi ,OC$), at planning time, at the same level. To do this, we transform local partial plans with exogenous precedence constraints into a unique acyclic mission graph and proceed to level decomposition of the mission graph. For each level, we define the set of nodes (actions) belonging to it.

6.1.1 Level decomposition

In order to apply OC algorithm the process of division must start from leaf nodes to root nodes.

We start with level $L_{k} \left( {k = 0} \right)$ containing leaf nodes (actions) that have no successors (neither exogenous nor endogenous). The next level L _k+1 contains predecessors of all nodes (actions) in L _k .

To compute the expected utility, the policy and OC values ($V, \pi ,OC$) for each action, two conditions (C ₁, C ₂) must hold in each level.

• C ₁: The ($V, \pi , OC$) values of an action a in level L _k are computed if actions having the same predecessor as a are in the same level L _k . Otherwise, the consideration of a is postponed to the next level.

• C ₂: The constrained action must be considered (OC computation) before its predecessor(s). Otherwise, the predecessor action(s) must be postponed to the next level.

6.1.2 Illustrating example

In this sub-section, we illustrate the process of level decomposition according to the example presented in Fig. 1.

In our example, we start by $L_{0} = \left\{ {J,E} \right\}$, (leaf nodes). L ₀ is checked for satisfying the two conditions (C ₁, C ₂), as C ₁ doesn’t hold for E (because the action D having the same predecessor C is not yet considered), E is postponed to level L ₁. L ₀ is then updated, $L_{0} = \left\{ J \right\}$. The next level L ₁ contains predecessors’ actions of nodes in L ₀ (J) with the postponed node from L ₀ (E). The result is $L_{1} = \left\{ {E,H,I,F} \right\}$. Level L ₁ will be checked, the two conditions don’t hold. C ₂ doesn’t hold for H (because C has as predecessor H is not considered) and C ₁ doesn’t hold for E (for the same reason cited above). Hence, H and E are postponed to level L ₂. The updated L ₁ is $L_{1} = \left\{ {I,F} \right\}$. Each time a level is updated, the remaining nodes will be newly checked. C ₁ doesn’t hold for I, this node will be postponed to level L ₂. Hence, the resulting level L ₁ contains only the node F($L_{1} = \left\{ F \right\}$)…

Like shown in Fig. 2, the leaf node E is postponed twice and is considered at level 2 instead of level 0 and level 1. Nodes H and I are postponed three times, from L ₁ to L ₄. Figure 2 describes also the process of OC algorithm as explained in Sect. 3.2.²

Fig. 2

The process of OC algorithm according to the example of Fig. 1

6.2 Communication model

We introduce communication decision to reduce mis-coordination caused by precedence relation. However, introducing communication at planning time leads to a significant increase in problem size. This latter concerns both action space and state space: when communication decision is always available, the action space increases dramatically because we add to every domain action decision a communication decision. The state space in turn increases since for every state, we need to distinguish between states with messages and states without messages captured in the factored state, and for each state with message we specify the possible content of the message so we can compute the respective values and policies.

To avoid this intractable increase in problem size, we take advantage of problem structure and introduce useful heuristics to specify when a communication decision is available, what should be communicated and to whom communicate. Note that these questions have already been raised in the literature (Beynier and Mouaadib 2010; Mostafa and Lesser 2009; Roth et al. 2005), but the relative answers (heuristics) we propose are specific to the problem we tackle.

In the following, we explain the heuristics we use to reduce the problem complexity.

6.2.1 H1: When to communicate?

To reduce action space, we exploit problem structure since the problem we tackle presents precedence relations between agents. This will limit information sharing at precedence points which we call coordination points. Moreover, communication decision is only available at the level of the constrained agent when it falls in PF state. Hence, for each PF state, a policy is computed which can dictate a communication action or no.

6.2.2 H2: To whom communicate?

In the case where the policy of a partial failure state dictates to communicate, the set of agents concerned with the communication are predecessor agents concerned by the partial failure. The reason behind imposing a heuristic for this communication issue is that to restrict the number of agents to whom the state space will be augmented by messages which are predecessor and constrained agents.

6.2.3 H3: What should be communicated?

In this study, we propose to attach explicitly the semantics of messages shared by agents in order to improve the global performances of the mission.

As in communication there are a sender (the constrained agent) and one or more receivers (predecessor agents) we will analyse the possible contents of messages for both the constrained agent and the predecessor agent(s).

At the level of constrained agent: the agent employs the query communication and asks its predecessor(s) for the action it needs, so it can continue its execution. Let a _i be the action belonging to the predecessor agent and needed by the constrained agent, the content of the message is $\Sigma = a_{i}$.

At the level of predecessor agent(s): no communication decision is available at this point for the predecessor agent(s). Hence, each time a predecessor agent receives an ask message, it should respond to the constrained agent (cooperative agents). Moreover, we assume at a first time that sent messages cannot be missed or corrupted and take one time unit for each direction (send → receive → respond, takes 2 time units). Then, we assume that the message may be missed in the transmission or in the receipt and we propose a mechanism to handle such a situation in Sect. 6.5.

The predecessor agent’s response depends on its current policy. Let the predecessor agent be in a state $\left\langle {a,\left[ {t,t^{\prime } } \right],\Sigma = a_{i} } \right\rangle$.

• If its current policy is different from the asked action a _i ($\pi \left\langle {a,\left[ {t,t^{\prime } } \right],\Sigma = a_{i} } \right\rangle \ne (a_{i} ,t_{i} )$), then the response message’s content is $\Sigma = \infty$. Note that this situation can illustrate both the case where the asked action will never be executed (because the agent responsible on it borrows a different path), or it cannot prevent its future policy.

• If its current policy corresponds to the asked action ($\pi \left\langle {a,\left[ {t,t^{\prime } } \right],\Sigma = a_{i} } \right\rangle = \left( {a_{i} ,t_{i} } \right)$ which means executing a _i at time t _i ), then the predecessor agent sends to the constrained agent the message containing, $\Sigma = val = \hbox{max} \left\{ {ET\left( {a_{i} ,t_{i} } \right)} \right\}$. This message consists in the greatest end time from the set ET of end times associated with (a _i , t _i ), since the predecessor agent cannot know the end time of its action before the execution phase.

6.3 OC computation

The opportunity cost is computed by the constrained agent and propagated to predecessors’ agents. Let action a _i be an exogenous predecessor of action a _j . Thus, OC values are computed by the agent who executes action a _j .

OC values are computed for each Δt which consists in the delay caused by each possible end time of action a _i on the start time of action a _j . These values consist in the difference between the expected utility (V) of the state associated to a _j when it starts its execution at t _j with no delay (at its first start time) and the expected utility of the state when its set of start times is restricted by a certain $\Delta t$, (Fig. 3). Formally:

$$OC(a_{j} ,\Delta t) = V^{\Delta t = 0} \left( {\left\langle {a_{j} ,\left[ {t_{j} ,t_{j} + d_{j} } \right]} \right\rangle } \right) - V^{\Delta t} \left( {\left\langle {a_{j} ,\left[ {t_{j} + \Delta t,\left( {t_{j} + \Delta t} \right) + d_{j} } \right]} \right\rangle } \right)$$

(2)

where $\left\langle {a_{j} ,\,\left[ {t_{j} ,t_{j} + d_{j} } \right]} \right\rangle ,\left\langle {a_{j} ,\left[ {t_{j} + \Delta t,\left( {t_{j} + \Delta t} \right) + d_{j} } \right]} \right\rangle$ are possible states associated to action a _j , V is the expected utility (value) of this state, t _j is the first possible start time of action a _j . The computation of V is explained later.

Fig. 3

The computation of opportunity cost

The computed OC values (for each Δt) are propagated to predecessor agent (the agent who executes action a _i ) who calculates in turn its policy taking into account the received OC values.

6.4 Policy computation

In this sub-section, we show how the value and the policy of each state are computed. The former is based on Bellman optimality principle (Bellman 1957) and the latter consists in an augmented Bellman equation in which an opportunity cost is introduced. This computation phase allows each agent to select the best action to execute in each state, considering its expected utility (value function), the opportunity cost induced on other agents and communication cost. In the following, we give the policy computation at the constrained agent side and at the predecessor agent side. We show the process of computation for two agents but it still applicable for any number of agents and each agent can be either predecessor or successor (with respect to the acyclic aspect).

6.4.1 Constrained agent

This agent can trigger communication. For this reason, we differentiate between the policy computation for each type of state.

• (a) Success State $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime } } \right]} \right\rangle$

  This state is associated to action a _i . The agent must decide about the next action to execute and when to execute it. To do this, the expected value of state s _i (V(s _i )) is calculated based on all actions’ values (Q) that can be reached from s _i .

  $$V\left( {s_{i} } \right) = R\left( {s_{i} } \right) + \mathop {\hbox{max} }\limits_{{p,t_{{i_{p} }} \ge {t_{i}^{\prime}} }} \left( {Q\left( {\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right)} \right)$$

  (3)

  where $p = 1\ldots m$ is the number of a _i ’s successors ($a_{{i_{p} }}$). $R(s_{i} )$ is the reward obtained for being in state s _i and it consists in the reward associated to the successful execution of action a _i given in the problem statement. $Q\left( {(a_{{i_{p} }} ,t_{{i_{p} }} ),s_{i} } \right)$ is the expected utility from executing action $a_{{i_{p} }}$ at time $t_{{i_{p} }} \ge t_{i}^{\prime }$. It is deduced from transition probabilities (success, PF and TF transitions) and the value of the resulting state.

  The policy of the state s _i is given by:

  $$\pi \left( {s_{i} } \right) = \mathop {\text{argmax}}\limits_{{p,t_{{i_{p} }} \ge t_{i}^{\prime} }} \left[ {Q\left( {\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right) - OC\left( {\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right)} \right]$$

  (4)

  where $OC\left( {(a_{{i_{p} }} ,t_{{i_{p} }} ),s_{i} } \right)$ is the opportunity cost from executing action $a_{{i_{p} }}$ at time $t_{{i_{p} }}$ induced on $a_{{i_{p} }}$‘s successors belonging to other agents.

• (b) Partial failure state $s_{i} = \left\langle {a_{i} ,\left[ {t,t + 1} \right],t_{i}^{\prime } } \right\rangle$ or $s_{i} = \left\langle {a_{i} ,\left[ {t + 1,t^{\prime}} \right],t_{i}^{\prime} ,\Sigma } \right\rangle$

  The components of the PF state are slightly different from those of the success state. In PF state we capture the last successfully executed action a _i , the PF interval $\left[ {t,t + 1} \right]$, Where t corresponds to the time where the agent tries to execute the next constrained action and t+1 is the time where it realizes that one or more predecessors have not been executed yet. We assume that it takes one unit of time to realize the PF, $t_{i}^{\prime }$ corresponds to the end time of a _i .

Since communication can be triggered at the partial failure state, the decision at this point differs based on the presence or not of messages. Hence, we distinguish between the policy computation of the two types of partial failure state (with and without messages).

• Partial failure state without message $s_{i} = \left\langle {a_{i} ,\left[ {t,t + 1} \right],t_{i}^{ \prime} } \right\rangle$, let a _i+1 be the action that leads to PF. We distinguish two scenarios

  • Wait some $\Delta t$ and try again the execution of a _i+1. However, it is not suitable for our case because, if repeated, this will violate the execution intervals of a _i+1 and leads to the total failure of the mission. This solution has been adopted in (Beynier and Mouaddib 2005, 2011).

  • The second scenario is to evaluate the gain between considering another successor action except a _i+1 (if exists in the partial plan) or communicate with the predecessor agent(s) asking for the enabling action(s). This scenario is more appropriate to our case since we introduce communication decision. Formally:

    $$V\left( {s_{i} } \right) = R\left( {s_{i} } \right) + \mathop {\hbox{max} }\limits_{{p - \left\{ {i + 1} \right\},t_{{i_{{p - \left\{ {i + 1} \right\}}} }} \ge t + 1}} \left( {Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right),V\left( {comm} \right)} \right)$$

    (5)

    where $R\left( {s_{i} } \right) = 0$, because, no reward is associated to PF state s _i . $p - \left\{ {i + 1} \right\}$ are all local successor actions of a _i except a _i+1 (causing the PF), $t_{{i_{{p - \left\{ {i + 1} \right\}}} }}$ is the time of executing a local successor action of a _i except a _i+1. $Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right)$ is the expected utility of executing a successor action of a _i except a _i+1 at time greater than or equal to t+1 (time of PF realization). $V\left( {comm} \right) = Q\left( {(a_{i + 1} ,t_{i + 1} ),s_{i} } \right) - C_{com}$, with $t_{i + 1} = \left( {t + 1} \right) + 2$ and C _com is the cost induced by the communication. Note that if $t + 1 \ge max\left\{ {ST_{{a_{i + 1} }} } \right\},$ $Q\left( {(a_{i + 1} ,t_{i + 1} ),s_{i} } \right) = 0$ because the agent could not retry to execute the action in question (a _i+1), there is no other possible start time for it.

    The policy is, then, given by:

    $$\pi \left( {s_{i} } \right) = \mathop {{\it{arg}} \hbox{max} }\limits_{{p - \left\{ {i + 1} \right\},t_{{i_{{p - \left\{ {i + 1} \right\}}} }} \ge t + 1}} \left( {Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right) - OC\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right),V\left( {comm} \right)} \right)$$

    (6)

• Partial failure state with message $s_{i} = \left\langle {a_{i} ,\left[ {t + 1,t^{\prime} } \right],t_{i}^{\prime} ,\Sigma } \right\rangle$

When the PF state contains a message, the decision about the next action to execute depends on the content of the message. When the message contains ∞, the agent must choose an alternative successor action of a _i except a _i+1. This corresponds to changing the path in its local partial plan. The agent must change the path in its local partial plan also when the message received contains a value (the greatest end time of the predecessor action) is greater than or equal to the maximum of possible start times of action a _i+1, since the agent may violate a _i+1′s temporal constraints.

When the value received is less than the maximum of possible start times of a _i+1, the agent can choose between changing the path or re-executing action a _i+1.

$$V\left( {s_{i} } \right) = R\left( {s_{i} } \right) + \mathop {\hbox{max} }\limits_{{p - \left\{ {i + 1} \right\},t_{{i_{{p - \left\{ {i + 1} \right\}}} }} \ge t^{\prime} }} \left( {Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right)} \right)\;if\;\Sigma = \infty\;or\;\Sigma = val \ge max\left\{ {ST_{{a_{i + 1} }} } \right\}$$

(7.1)

$$V\left( {s_{i} } \right) = R\left( {s_{i} } \right) + \mathop {\hbox{max} }\limits_{{\begin{array}{*{20}c} {p - \left\{ {i + 1} \right\},t_{{i_{{p - \left\{ {i + 1} \right\}}} }} \ge t^{\prime} } \\ {val \le t_{i + 1} < max\left\{ {ST_{{a_{i + 1} }} } \right\}} \\ \end{array} }} \left( {Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right),Q\left( {\left( {a_{i + 1} ,t_{i + 1} } \right),s_{i} } \right)} \right)\;if\;\Sigma = val < max\left\{ {ST_{{a_{i + 1} }} } \right\}$$

(7.2)

After computing the expected utility of state s _i , we move to the computation of its policy.

$$\pi \left( {s_{i} } \right) = \mathop {{\it{arg}} \hbox{max} }\limits_{{p - \left\{ {i + 1} \right\},t_{{i_{{p - \left\{ {i + 1} \right\}}} }} \ge t^{\prime} }} \left( {Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right) - \,OC\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right)} \right) if\; \Sigma = \infty \,or \,\Sigma = val \ge max \left\{ {ST_{{a_{i + 1} }} } \right\}$$

(8.1)

$$\pi \left( {s_{i} } \right) = \mathop {{\it{arg}} \hbox{max} }\limits_{{\begin{array}{*{20}c} {p - \left\{ {i + 1} \right\},t_{{i_{{p - \left\{ {i + 1} \right\}}} }} \ge t^{\prime} } \\ {val \le t_{i + 1} < max \left\{ {ST_{{a_{i + 1} }} } \right\}} \\ \end{array} }} \left( {Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right) - \,OC\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right),Q\left( {\left( {a_{i + 1} ,t_{i + 1} } \right),s_{i} } \right) - \,OC\left( {\left( {a_{i + 1} ,t_{i + 1} } \right),s_{i} } \right)} \right) \quad if\; \Sigma = val < max \left\{ {ST_{{a_{i + 1} }} } \right\}$$

(8.2)

where $R\left( {s_{i} } \right) = 0$ because s _i is a PF state. $p - \left\{ {i + 1} \right\}$ are all successor actions of a _i except a _i+1 (causing the PF). $t_{{i_{{p - \left\{ {i + 1} \right\}}} }}$ is the time of executing a local successor action of a _i except action a _i+1. $Q\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right)$ is the expected utility of executing a successor action of a _i except a _i+1 at time greater than or equal to $t^{\prime}$ (the time where the message is received). t _i+1is the time of re-executing a _i+1 after receiving a message containing a value greater or equal to the value received and inferior to the maximum of possible start times of a _i+1(in order to respect a _i+1′s temporal constraints). $Q\left( {\left( {a_{i + 1} ,t_{i + 1} } \right),s_{i} } \right)$ is the expected utility of executing action a _i+1 at time t _i+1. $OC\left( {\left( {a_{{i_{{p - \left\{ {i + 1} \right\}}} }} ,t_{{i_{{p - \left\{ {i + 1} \right\}}} }} } \right),s_{i} } \right)$ is the OC from executing $a_{{i_{{p - \left\{ {i + 1} \right\}}} }}$ at $t_{{i_{{p - \left\{ {i + 1} \right\}}} }}$ and $OC\left( {\left( {a_{i + 1} ,t_{i + 1} } \right),s_{i} } \right)$ is the OC from executing a _i+1 at t _i+1.

• c) Total failure state $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime} } \right],fail} \right\rangle$

From this state, no policy is calculated.

$$V\left( {s_{i} } \right) = - R\left( {s_{i} } \right) - \mathop \sum \limits_{{a_{ \ne i} \in EndoSuc(a_{i} )}} R\left( {s_{ \ne i} } \right)$$

(9)

where $- R\left( {s_{i} } \right)$ is the reward lost from failing the execution of action a _i . $\mathop \sum \limits_{{a_{ \ne i} \in EndoSuc(a_{i} )}} R(s_{ \ne i} )$ consists in the loss in reward of all remaining actions reached from the failed action a _i and executed by the same agent (called endogenous successors, $EndoSuc(a_{i} )$).

6.4.2 Predecessor agent

We recall that for this agent no policy for communication is computed. The agent must synchronize with the constrained agent if this latter triggers communication. As this agent has no constrained action, no PF state is treated.³

• (a) Success state $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime} } \right]} \right\rangle$ or $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime} } \right],\Sigma } \right\rangle$

  From a success state, the predecessor agent can choose between successor actions of action a _i .

  $$V\left( {s_{i} } \right) = R\left( {s_{i} } \right) - C_{com} + \mathop {\hbox{max} }\limits_{{p,t_{{i_{p} }} \ge t_{i}^{\prime} }} \left( {\left( {Q\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right)} \right)$$

  (10)

  When calculating the policy of this state, the agent must consider the opportunity cost induced on a _i ’s successors belonging to other agents.

  $$\pi \left( {s_{i} } \right) = \mathop {\text{argmax}}\limits_{{p,t_{{i_{p} }} \ge t_{i}^{\prime} }} \left[ {Q\left( {\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right) - OC\left( {\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right)} \right]$$

  (11)

  Note that when $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime} } \right]} \right\rangle$, C _com  = 0 and when $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime} } \right],\Sigma } \right\rangle$, C _com  = 2.

  R(s _i ) is the reward received for being in the state s _i and it consists in the reward associated to the successful execution of action a _i given in the problem statement. $Q\left( {\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right)$ is the expected utility from executing action $a_{{i_{p} }}$ at time $t_{{i_{p} }} \ge t_{i}^{\prime}$ from state s _i . $OC\left( {\left( {a_{{i_{p} }} ,t_{{i_{p} }} } \right),s_{i} } \right)$ is the opportunity cost from executing $a_{{i_{p} }}$ at time $t_{{i_{p} }}$ provoked on $a_{{i_{p} }}$‘s successors belonging to other agents.

• (b) Total failure state $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime} } \right],\Sigma ,fail} \right\rangle$ or $s_{i} = \left\langle {a_{i} ,\left[ {t_{i} ,t_{i}^{\prime} } \right],fail} \right\rangle$

  $$V\left( {s_{i} } \right) = - R\left( {s_{i} } \right) - \mathop \sum \limits_{{a_{ \ne i} \in EndoSuc(a_{i} )}} R\left( {s_{ \ne i} } \right) - C_{com}$$

  (12)

  Where $- R\left( {s_{i} } \right)$ is the reward lost from failing the execution of action a _i . $\mathop \sum \limits_{{a_{ \ne i} \in EndoSuc(a_{i} )}} R(s_{ \ne i} )$ consists in the loss in reward of all remaining actions reached from the failed action a _i and executed by the same agent (called endogenous successors, $EndoSuc(a_{i} )$). C _com is communication cost.

6.5 Dealing with missed messages

In this sub-section, we enhance our proposition to deal with missed messages. In such a case, an agent may wait indefinitely for a response which leads to a violation of its temporal constraints. To remedy to that, we augment partial failure states with adaptive waiting time $\Delta t$. This $\Delta t$ depends on the state an agent might be in and regarding its temporal constraints. Then, for each new partial failure state, the policy computation algorithm computes the corresponding policy.

According to Eq. 5, the policy of a partial failure state $s_{i} = \left\langle {a_{i} ,\left[ {t,t + 1} \right],t_{i}^{\prime} } \right\rangle ,$ is either to communicate or execute an alternative action of a _i+1 (execute one of a _i ’s successors except a _i+1). The value of communication in this case (the case of missed messages) is $V\left( {comm} \right) = Q\left( {\left( {a_{i + 1} ,t_{i + 1} } \right),s_{i} } \right) - C_{com}$, where $t_{i + 1} = \left( {t + 1} \right) + \Delta t$. $\Delta t$ corresponds to the waiting time after which the agent may re-execute a _i+1 or execute another action.

If after waiting $\Delta t$ time units there is no message received, the agent supposes that the message is missed either in transmission or in receipt phase, and still has to select an action (before violating its temporal constraints). Thus, we propose to compute $\Delta t$ based on the execution constraints of possible alternative action(s) of action a _i+1. We put,

$$\Delta t = \mathop {\hbox{max} }\limits_{{}} \left\{ {ST_{alter} } \right\} - t_{current}$$

where t _current corresponds to the end time of the PF state (t+1). $\mathop {\hbox{max} }\limits_{{}} \left\{ {ST_{alter} } \right\}$ corresponds to the greatest valid start time from the set of alternative action’s start times. We mean by ‘‘valid’’, the possible start time that does not violate the action’s temporal constraints extracted from all success states of alternative action of a _i+1. The reason behind choosing this value is that after waiting $\Delta t$ time units and no message is received, the agent still can select an action to execute (an alternative action on different path) respecting its temporal constraints. Figure 4 shows the development of partial failure states in the case of successful communication (case 1) with fixed time (equal to 2: 1 unit of time for sending and 1 unit of time for reception) and stochastic communication where messages may be lost (case 2).

Fig. 4

PF States in successful communication and communication with failure

Example According to the example presented in Sect. 2, $s = \left\langle {A,\left[ {8,9} \right],8} \right\rangle , s^{\prime } = \left\langle {A,\left[ {10,11} \right],8} \right\rangle$ are two PF states associated to action C when action H does not terminate its execution at times 8 and 10. The policy of states $s \,and\, s^{\prime}$ dictates to communicate and $\mathop {\hbox{max} }\limits_{{}} \left\{ {ST_{B} } \right\} = 12$(where $\mathop {\hbox{max} }\limits_{{}} \left\{ {ST_{B} } \right\}$ is the maximum of possible start times of action B- the alternative action of C of agent 1 extracted from B’s success states).

We have,

$$\Delta t = \mathop {\hbox{max} }\limits_{{}} \left\{ {ST_{B} } \right\} - t_{current}$$

Hence, For state s, we have:

$$\Delta t = 12 - 9 = 3$$

For state $s^{\prime}$, we have:

$$\Delta t = 12 - 11 = 1$$

The new states in which the agent will receive or not a message $\Sigma$ are: $s = \left\langle {A,\left[ {9,12} \right],8} \right\rangle$ or $s = \left\langle {A,\left[ {9,12} \right],8,\Sigma } \right\rangle$ and $s^{\prime} = \left\langle {A,\left[ {11,12} \right],8} \right\rangle$ or $\left\langle {A,\left[ {11,12} \right],8,\Sigma } \right\rangle$. For each state, the values and policies will be computed offline by our value and policy computation algorithms.

7 Results and discussion

Our experiments were directed towards performances and solution quality contrary to the work in Beynier and Mouaddib (2011) which is directed towards testing the scalability of the approach proposed. Indeed, OC-DEC-MDP has been shown to scale up (Beynier and Mouaddib 2011). Our main objective was the extension of this model to problems with partial local plans and raise issues resulting from this extension by proposing a rich model of communication.

We varied the number of agents and dependencies and we evaluated the consequences of adding communication in term of the global gain of agents. We mean by global gain the cumulative reward obtained by agents after executing their mission.

It is important to note that the type of problems we deal with suffers from the difficulty of obtaining random scenarios or instances whose policies actually dictate communication (Mostafa 2011). Randomly generated instances are not dependent enough to trigger communication. For this reason, during dependencies’ generation phase, the maximum of dependencies added was fixed empirically, so that we avoid the cycle. We recall that the mission graph must be acyclic. Moreover, we have followed some rules in order to insert a dependency. First of all, the constrained action must be in a level superior or equal to the level of the predecessor action in the mission graph. Second, in a given level, we must have at least one action with no exogenous precedence so that the agent can continue its execution. When generating our instances we assumed that the branching factor is equal to 2.

We generated three instances of problem:

• The first instance is composed of 15 tasks distributed among three agents,

• The second instance is composed of 21 tasks distributed among 4 agents and

• The third instance is composed of 40 tasks distributed among 6 agents.

The topology of each instance is given in Table 1 with the number of generated states after temporal propagation. The main parameters that affect an instance’s size materialized by the number of states are the number of actions of each agent, the number of dependencies (precedence relations) and the size of the temporal window. As we can see in Table 1, there is a growth in state space in the case of communication with failure compared to successful communication. This increase is interpreted by the fact that when considering missed messages, three types of states are considered after sending a message: PF state with $\Sigma = \infty$, PF state with $\Sigma = val$, and PF state without a message. This last state interprets the case where the constrained agent sends a query message and after waiting $\Delta t$ time units there is no response received (the message is missed). This is in contrast to successful communication where the state space is augmented by two types of states only: PF state with $\Sigma = \infty$ and PF state with $\Sigma = val$.

Table 1 The composition of each problem instance (case 1: successful communication, case 2: communication with failure)

It is important to note that without using heuristics proposed in Sect. 6.2, both state spaces’ size (case 1 and case 2) will be larger. Indeed, without any heuristic on communication issues and as a consequence of an offline communication, we must consider for each state its equivalent with a message.

For these instances, we conducted experiments which consist of two parts: in part 1, the aim is to show the necessity of communication particularly in case of tight temporal constraints to avoid total failure of the mission. In part 2, we computed the global gain of the agents when communication is free (upper bound global gain) and we measured the loss in global gain by introducing costly communication. For this part, the two cases of successful communication and communication with the possibility of missed messages are studied.

Simulations conducted were realized using JADE (Java Agent DEvelopment framework) (Singh et al. 2011; Prakash et al. 2014). After computing the policy of each agent (offline phase), we move to execute this joint policy (online phase using JADE). Each agent Ag has its local partial plan in which each action a _i has a list of exogenous predecessors $ExoPred(a_{i} )$, the list of all its possible states S with the corresponding policies $\Pi (S)$ and the resulting states such that $S,\Pi (S) \to S$. All this information (problem description and the computed policy) represent the entry of the online phase. When an agent observes its state, it executes the corresponding policy and it transits to one of its possible next states. To simulate the transition to a non-deterministic state, we proceed as usual in MDPs (Mostafa and Lesser 2009, Beynier and Mouaddib 2011) and we randomize among all possible resulting states. From the new resulting state, the agent executes once again its corresponding policy and so on. Each time the policy is executed, the corresponding reward is cumulated.

Part 1 Fig. 5 (a, b and c) shows that the cumulative reward when agents can communicate is always greater than the cumulative reward for the non-communicative case even for large temporal constraints. However, In case of tight intervals and without communication, the total failure of the mission is significant. This is due to the partial failure of constrained actions which leads to a violation of the tighter constraints. When communication is introduced the total failure did not occur because agents will always opt for a communication policy even if communication is costly. The loss in total expected utility induced from communication is less important than the total failure of the mission because in the case of tight intervals the next failure will eventually be a total failure instead of a partial failure in case of large constraints.

Fig. 5

Agent’s performance

As we can see in Fig. 5, the more the need for communication is increased (materialized by an increase in dependencies), the higher agents’ global gain is. The reason behind this increase is that agents assess the value of communicating before adopting a communication policy, so they find the best tradeoff between the utility of information received by communicating, communication cost, and the utility of other alternatives without communication, regarding their constraints.

The growth in the number of dependencies has two main results. It increases the need for communication, on one hand. On the other hand, it increments the number of execution intervals. Since agents are time constrained, the number of execution intervals that respect agents’ temporal window is restricted and the number of execution intervals that violate the temporal constraints is increased. In this case, communication seems to be a good choice for agents in order to avoid mis-coordination situations and the total failure of the mission, and thus agents’ performance will be improved.

Part 2 For the three instances, we executed the joint policy found offline and we computed the global gain by setting the communication cost equal to zero (free communication). This constitutes the best global gain that agents can obtain. Then, we added a communication cost (C _com  = 2) and we computed again the global gain of agents for the case where communication is successful, i.e. it consumes 2 time units, and when there is a possibility of missed messages. Moreover, we varied for each running instance the number of dependencies with respect to the acyclic property of the mission graph.

As shown in Fig. 6 (a, b and c) and Fig. 7 (a, b and c) there is a loss in cumulative reward when communication cost is introduced. Moreover, for each instance, when the number of dependencies increases, a loss in global gain is captured.

Fig. 6

The influence of the number of dependencies on the total gain in fixed time successful communication

Fig. 7

The influence of the number of dependencies on the total gain in stochastic communication: missed messages

The decrease in global reward is interpreted by the fact that communication is more solicited when dependencies are increased. As a consequence of increasing the need for communication, the associated cost is more considered.

When dealing with missed messages, we have observed a loss in cumulative reward comparing to the case of successful communication. This can be explained by the fact that the agent may not receive a response to its request. So, it is first penalized for communicating and will be obliged to choose an alternative action which has a less important reward than the first chosen action.

Experimental results demonstrate the effectiveness of heuristics introduced in order to take communication decisions leading to the possible best solution according to the problem constraints (temporal and precedence). These heuristics aim to reduce the problem size and optimizing information to share.

8 Comparative study

Several works have been done on communication in decision theoretic models, but the closest to ours is that of (Beynier and Mouaadib 2010). We try to highlight the similarities and differences between these two works in order to better understand how they stand in relation to each other. We recall that through this work, we are not trying to improve results finding in (Beynier and Mouaadib 2010) but our aim is to extend the proposed model to take into account partial local plans. As a consequence of this extension, some problems regarding coordination will take place. In order to raise these problems, we proposed a communication model specific to such mis-coordination situations.

The comparison between these two works is done in two fold. We compare, at first, between the topology of the mission graph, the decision model, and issues related to each model. Second, we detail and compare the two communication models proposed in order to handle issues specific to each work. Table 2 compares the topology of each mission graph.

Table 2 Comparison between the topology of mission graphs

As we can see in Table 2, the decision problem in (Beynier and Mouaadib 2010) deals with linear plans. This results in a reduction in solution space where there is one path in which each node is the sole action. Each action in the path has different possible schedules (because of its several durations). Our extension results in harder decision problem and larger solution space where there are different possible paths (partial plan). Each action in the path has different possible schedules (because of its several durations). This leads us to propose an adequate communication model (presented in Sect. 6.2) in order to deal with problems raised from partial plans.

We give in Table 3 a comparison between the two communication models. The following are the criteria we use for comparison:

• Aim: why introducing communication among agents.

• Communication action model: is communication action considered similarly to the domain level action or each action represents a different kind from the other?

• Decision problem: which are the decisions available to each agent at each decision step.

• Reasoning time: reasoning about communication can be done offline or online.

• AND/OR communication: communication actions can be chosen in combination with domain level actions or they may take the place of domain level actions.

• Who trigger communication: which agent initiates communication?

• When to communicate: this communication issue requires reasoning about the effects of communication on team behavior and expected global reward, at first. Second, if agents do not communicate at every time step, in which situations communication will be a good choice in order to maintain coordination.

• To whom communicate: in addition to deciding when communication is necessary, agents can also determine with whom they will share the information.

• Communication type: how communication is initiated, we consider three communication types (Xuan et al. 2001):

  • Tell, in this type, one agent decides to send a message to other agents voluntarily (information going outward). As a result, the sender will not know any information about the receiver.

  • Query, here, an agent asks one or more of its teammates for particular information which is useful to pursue its execution (information going inward).

  • Sync, this is a combination of the above two, in which all agents simultaneously communicate their local information with each other.

• Information flow: in each direction information will be sent.

• What to communicate: In an explicit communication, generally, agents can communicate any information that helps the receivers refine their beliefs over what the sender will do/has done.

• Value of communication: Deciding when to communicate in cooperative decentralized problems can be measured by the value of communication which refers to how an agent assesses the worth of a communication action. The value of communication can be defined as the net gain from communicating, which is the difference between the expected improvement in the agents’ performance and the costs associated with communication (Becker et al. 2009). It can be measured myopically or by considering the expected value of the state resulting from communication. Another approach may not calculate the value from communication. Rather, communication is triggered when a condition is met (Mostafa 2011).

• Solution method: how the joint policy is computed?

• After communication: refers to the influence of the message received on agents’ behaviors. In other words, how agents react after a communication round (reception of a message).

• Stochastic communication: dealing with missed, corrupted or delayed communication.

Table 3 Comparison between the two communication models

As we can see in Table 3, Communicative OC-DEC-MDP allows the agent to communicate the end time of a previous successfully executed action. The problem here is that the information sent is available when it is too late to the constrained agent to benefit from it. This results from the asynchronous execution of actions. Moreover, communication is used in one direction. This means that when the constrained agent arrives at the constrained action before its predecessor, it will be obliged to wait which may affect its temporal constraints and hence temporal constraints of depending agents (by propagation).

In this work and through the communication model proposed, we tried to fix these problems in addition to other emergent problems resulting from partially ordered actions. We have supposed that the constrained agent can ask for the action needed from other agents (when it falls in a PF state and its policy dictates the communication). By receiving a query, the predecessor agent is obliged to synchronize with the constrained agent. The language used in this work is chosen to take into account the possibility of receiving the query before deciding to execute the predecessor action or not (to deal with asynchronism). Furthermore, sharing information is doing in two ways (bi-directional communication), in order to maintain coordination. In fact, in Beynier and Mouaadib (2010) there is a decoupling between the agents because the predecessor agent decides to send information independently without considering if this is necessary for the constrained agent and if it really increases the global expected reward.

9 Conclusion

Modeling distributed real world applications using decentralized Markov Decision Processes requires a specific adaptation in order to take into account actions execution constraints.

In this paper, we aimed at extending a state of the art model OC-DEC-MDP which is proposed to take into account temporal and precedence constraints, and probabilistic actions’ durations in the case of linear local plans, to handle partial local plans and communication decisions.

In this type of problems, communication can only be beneficial in order to ensure coordination between agents. However, communication is expensive in terms of operational and computational costs and must be restricted.

The decision about the policy of each agent is based on the type of the state an agent might be in. It results from a tradeoff between the expected utility of the agent, its opportunity cost on other agents, and the value of communication.

In order to optimize communication decisions, we have proposed heuristics that concern when, what and with whom communicate. Since an agent depends from the others only when a precedence relation occurs between them, communication points are restricted in precedence constraint. The communication model we proposed considers that communication is triggered by the constrained agent after one partial failure state if its policy dictates to coordinate. We have considered three types of messages depending on the state of the agent. Moreover, it was supposed that the set of communicating agents is limited to the subset of agents that only depends from each other.

In this work, we have considered two cases: i) successful communication where messages are received after a fixed time, ii) fail communication where messages may be missed.

Our results have shown the effectiveness of the proposed approach. In fact, communication heuristics conducted us to the possible best solution according to the constraints.

A major inconvenient of OC-DEC-MDP is the large state space. One direction of future research is to reduce the size of this space by defining a representative subset of states where agents are likely to move in Marecki and Tambe (2007) handles the problem of the state space size by considering continuous time and thus dealing with value function over time for each action rather than a separate value for each action and execution interval. It will be interesting to increase the level of coordination by introducing communication among agents and measure its contribution on the overall gain. Another direction of future work is to consider constraints on communication such as defining a communication budget and then formalize exactly how much communication is allowed.