Introduction

An extreme rainfall of a definite duration has the greatest magnitude among many rainfalls of the same duration that occur in a single year. Hence, a gauged series of extreme rainfall of a specific duration contains as many numerical values of rainfall as the record length in years. Peculiar to a geographical location, the intensity of an extreme rainfall event (I) as a function of its duration (D) and its statistical frequency (F) is depicted by the intensity–duration–frequency (IDF) relationship, which is given in either a tabular or a diagrammatic form. The IDF relationship is needed to design various hydraulic structures, such as storm drainages, combined sewage systems of residential areas, and flood spillways of dams. The IDF relationship in a diagrammatic form consists of as many curves as the frequencies taken into consideration. Each curve presents the intensity of rainfall in mm/h units pouring onto a geographical point over a certain time period in minutes, having an average frequency in years, which is also called the average return period. Hence, the IDF relationship is a significant tool for the planning, design, and risk assessment stages in water resources engineering. The numerical values of an IDF relationship are determined by statistical frequency analyses applied on a significantly long series of gauged extreme rainfall records. The magnitude of the intensity of rainfall is inversely proportional to its duration and directly proportional to the frequency. Highly intense rainfalls are of short duration and the intensity gradually increases with increasing frequency (F). Statistical frequency analysis using suitable probability distributions is the common tool to relate the magnitude of extreme rainfalls to their frequencies (e.g., Bernard 1932; Hershfield 1961; Chow 1988; Koutsoyiannis et al. 1998; Dupont and Allen 2006; Asikoglu and Benzeden 2014).

In hydrometric studies, streamflow and rainfall are measured as point data in places where gauging stations are available. However, it is impossible to measure hydrologic data at every point on earth. Hence, hydraulic structures are not always optimally designed because of missing point measurements at their locations. Because hydrologic data are point-specific, they cannot directly be used in places away from the gauging stations, and they should be adapted to the points where they are needed. Similarly, determining the spatial distribution of rainfall over a specific drainage area from available point measurements is a common practice of utmost importance.

fOlofintoyeAs a pioneering contribution, Bernard (1932) developed an empirical equation in the form: \(i=\left(c1\bullet {T}^{c2}\right)/{t}^{c3}\) for the IDF relationship, where, c1, c2, and c3 are coefficients peculiar to a geographical region. Since then, various analytical expressions have been presented for different regions of the world. Froechlich (1995) presented rainfall intensity–duration equations for durations of 1 through 24 h for four geographical regions delineated by the United States Weather Bureau. He determined optimum parameter values for each one of four equations and gave the ratio of t‒h rainfall depth to 1-h rainfall depth for various frequencies. Bartual and Schneider (2001) applied frequency analyses on a series of many extreme rainfall events in the Alicante province of Spain, gauged between the years 1925 through 1992, by using the general extreme values (GEV) distribution for standard durations from 2 to 240 min, and developed nine different empirical equations for the IDF relationship. As a result of their work, they noted that three-parameter expressions were more meaningful for frequencies between 5 and 500 years. Yu et al. (2004) developed a regional IDF relationship for ungauged locations based on the scaling theory combining the Gumbel distribution and partial simple scaling hypothesis. Nhat et al. (2006) presented curves for the IDF relationship for the Yodo River basin and derived a generalized IDF formula. AlHassoun (2011) developed an empirical formula to estimate the rainfall intensity in the Riyad region of Saudi Arabia and showed a good match between the Gumbel method and the other analytical methods. Jaleel and Farawn (2013) obtained the IDF relationship for the Basrah province of Iraq by using Gumbel distribution and noted that maximum rainfall intensities exhibited high variability in short periods. Dourte et al. (2013) developed IDF relationships for the Indian peninsula and investigated the effects of variations in rainfalls on flows and groundwater replenishment. They noted that the updated IDF relationships revealed a significant change in rainfall characteristics as compared to the old relationships and reported increased rainfall intensities for all rainfall durations and frequencies. They concluded that severe rainfalls resulted in decreased groundwater replenishment and increased flows. Asikoglu and Benzeden (2014) used the two-parameter lognormal and Gumbel distributions in frequency analyses and obtained two types of IDF functions for the Aegean region of Turkey, based on the simple generalization procedure and the robust estimation procedure. These researchers compared the root mean squared error (RMSE) values of both procedures and reported that the former procedure yielded better rainfall intensity values than the latter. Rasel and Islam (2015) conducted a frequency analysis by applying the Gumbel and Log − Pearson − 3 distributions to derive the IDF relationship for Bangladesh by using the data of extreme rainfalls measured between 1974 and 2014. They calculated the IDF equation parameters for 2, 5, 10, 25, 50, and 100-year frequencies by non-linear multiple regression and reported high correlation coefficients for the resultant IDF equations. Liuzzo and Freni (2015) used climate change scenarios for the Sicilia Province and investigated the IDF relationships of extreme rainfalls for durations of 1, 3, 6, 12, and 24 h. They first conducted a trend analysis on all extreme rainfalls by the Mann‒Kendal method and determined decreasing‒increasing trends. Next, they used the outcomes of the trend analyses to devise an empirical equation for a climate scenario‒dependent IDF relationship. They noticed that decreasing and increasing trends influenced the intensity of extreme rainfalls with frequency. Hamaamin (2017) determined an IDF relationship for the Sulaimani province in Iraq, and achieved a determination coefficient of almost 1 for rainfall intensity values in the empirical equation, and hence indicated that the resultant empirical equation represented the actual values. There are several other research studies conducted in different regions of the world for generations of empirical rainfall intensity estimation equations and IDF curves (Bougadis and Adamowski 2006, Nhat et al. 2007, Trevor and Guillermo 2008, Omotosho and Oluwafemi 2009, Olofintoye et al. 2009, El−Sayed, 2011, Vivekanandan 2012, Antigha and Ogarekpe 2013, Al−anazi and El−sebaie, 2013, Chang et al. 2013, García−Marín et al. 2013, Wang et al. 2014, Akinsanola and Ogunjobi 2014).

Karahan et al. (2007) employed a genetic algorithm (GA) approach for rainfall intensity estimations and indicated that the GA method employing mean square error as the cost function could reliably be used to determine the IDF relationship. They also reported a good match for the measured and estimated values and applied this method for the IDF relationships in the GAP region of Turkey. These researchers stated that the GA method was an efficient tool to determine the mathematical model coefficients enabling it to represent the available data successfully (Karahan et al. 2008). Başakın et al. (2021a) developed an equation with the help of genetic programming (GP) using the information of the IDF relationships computed as the outcome of statistical frequency analyses to calculate intensities of extreme rainfalls for the Kayseri, Nevşehir, Niğde, and Yozgat provinces. They also used one of the empirical equations available in the literature for comparison with their model. They optimized the parameters of the empirical equation with the particle swarm optimization (PSO) scheme. In the end, they concluded that the equation derived by GP had higher accuracy than the equation obtained with PSO.

It is a known fact that algorithms such as GA and PSO can be employed to find the optimal values of the parameters of a predetermined mathematical expression. In order to obtain the best estimation accuracy, first a best model must be chosen and next the best values for the parameters of that model must be determined. Hence, with this objective in mind, the artificial bee colony programming (ABCP) was used in this study to obtain a model for the IDF relationship with high estimation accuracy. ABCP was introduced in 2012 by Karaboga et al. (2012) as a versatile means of machine learning. Golafshani and Ashour (2016) employed the ABCP method to predict the elasticity modulus of self-compacting concrete. Golafshani and Behnood (2018) applied the ABCP approach for predicting the elasticity modulus of recycled aggregate concrete. Boudardara and Gorkemli (2018) proposed the ABCP method in a robotic path planning problem. They later presented a new version of ABCP (Boudardara and Gorkemli 2020). Arslan and Ozturk (2019) provided an ABCP image descriptor for multi class texture classification. Prior to that, they used ABCP as a new tool for cancer data classification (Arslan and Ozturk 2018). Gorkemli and Karaboga (2019) proposed three new versions of ABCP to improve the convergence performance of the algorithm. Hara et al. (2018) proposed a modified ABCP method using semantic control crossover. Boudouaoui and Habbi (2018) made some structural modifications to the ABCP method. Arslan and Ozturk (2019) introduced a feature selection method based on ABCP for high-dimensional symbolic regression problems.

ABCP is a novel, evolutionary, and GP (Koza 1992)-like automatic programming and machine learning technique. It is based on the artificial bee colony (ABC) optimization algorithm (Karaboga 2005, 2010; Karaboga and Basturk 2007), which is inspired from the foraging behavior of honeybee swarms while the GP is an extension of GA. ABC is one of the most popular and widely used swarm intelligence based optimization algorithms for solving various types of problems from a wide spectrum of disciplines (Karaboga 2010, Bansal et al. 2013, Karaboga et al. 2014, Agarwal and Yadav 2019, Pooja and Shirmal 2020. Therefore, in this study, the ABCP model is proposed as a new and efficient approach to represent the numerical values of rainfall intensities over a wide range of frequencies from 2 to 10,000 years analytically. This range of frequencies resulted as the outcome of comprehensive regional statistical frequency analyses by the L-Moments method using 14 standard-duration-recorded series of extreme rainfalls carried out by Haktanir et al (2016). In the first phase of the study, nine different empirical equations available in literature for the IDF relationship were tested with the purpose of how well they represented the IDF relationship of the Inland Anatolia Region, as obtained by the L-Moments method. In the second phase, equations were developed by the ABCP approach for the same regionalized IDF relationship. In the last phase of the study, the performances of the nine empirical equations and the equations produced by the ABCP method were compared from the standpoint of their accuracies in representing the regionalized IDF relationship developed by the L-Moments method. These three stages are concisely explained in the following sections.

Hence, the main objective of this study was to quantitatively depict the regional IDF relationship peculiar to the Inland Anatolia Region, as determined by the outcome of comprehensive frequency analyses by the L-Moments method. This was done in a succinct analytical way to be obtained by the ABCP approach and to compare its accuracy against the accuracies of already used empirical equations, whose parameters were optimized based on the numerical values given by the L-Moments method.

Material and method

Research site

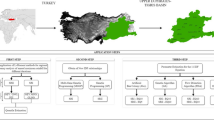
Seven geographical regions of Turkey and the positions of 31 meteorological stations in the Inland Anatolia Region, each having at least 30 years of gauged data, are shown in Fig. 1. Prior to this study, a regional frequency analysis by the L-Moments method was completed for the Inland Anatolia Region of Turkey by Haktanir et al. (2016). This study used the gauged series of successively increasing 14 standard − duration extreme rainfalls (AMR) with durations of 5, 10, 15, and 30 min, and 1, 2, 3, 4, 5, 6, 8, 12, 18, and 24 h at the 31 stations. Including the year 2010, all rainfall data were obtained from the General Directorate of Meteorology. Although there were more than 31 stations in this region, Haktanir et al. (2016) did not include those having record lengths shorter than 30 years in the frequency analyses, whose ultimate product was the regional IDF relationship consisting of many intensity values for 14 rainfall durations and for many frequencies ranging between 2 and 10,000 years. In the current study, a best-fit single mathematical model was searched for the regional IDF relationship obtained by Haktanir et al. (2016) as the outcome of comprehensive frequency analyses, based on a modified version of the L-Moments method.

Fig. 1
figure 1

Seven geographical regions of Turkey and locations of the meteorological stations in the Inland Anatolia Region, whose gauged data of 14 standard‒duration extreme rainfalls series, were used in determining the regional intensity‒duration‒frequency relationship for the Inland Anatolia Region by the L-Moments method

Full size image

The northern sections of the Inland Anatolia Region are surrounded by mountains reaching altitudes of 3000 m, which generally extend parallel to the Black Sea shoreline. The southern sections of the Inland Anatolia Region are surrounded by mountains with altitudes up to 3500 m, and they mostly lie parallel to the Mediterranean Sea coastline. The Inland Anatolia Region is a large plateau bordered by these rows of mountains in the North and South. Erciyes and Suphan are two independent volcanic mountains in this region. The mountain rows in the north and the south extend into the Eastern Anatolia Region where they intersect. The mountains in the western sections of the Inland Anatolia Region lie mostly perpendicular to the Aegean Sea coast. In brief, the Inland Anatolia Region constitutes a landlocked portion of Turkey and experiences a dominant terrestrial climate. Forests and woods sparsely exist in this region because of the harsh climate with less than average precipitation and steppes are common plant covers. There is less vegetable cultivation in this region compared to the other regions because of insufficient rainfalls and prevailing droughts. Yet, the major amount of precipitation occurs in spring, and severe storms produce considerable rainfalls of durations up to 24 h. Mostly cold-resistant food plants are cultivated in the Inland Anatolia Region. Potatoes, rye, green lentils, apples, and pears are the most common agricultural products.

Frequency analyses by L-Moments method

Statistical frequency analysis is developed to allow practitioners to make probabilistic predictions in the future. In addition, it is used to quantify the relationship between the magnitude and the probability of either exceedance or non-exceedance of hydrologic random variables. Commonly, frequency analyses in hydrology are applied for flood peaks and extreme rainfalls. The frequency analysis is done using a suitable probability distribution, and usually, one of three-parameter probability distributions of generalized normal (GNO), which is also known as the three-parameter log-normal, Pearson–3 (PE3), general extreme values (GEV), generalized logistic (GLO), and generalized Pareto (GPA) are used for this purpose. Estimation of the magnitudes of the parameters of a probability distribution using the observed series is an important stage of the frequency analysis and the conventional methods of moments and of maximum-likelihood are commonly used for this purpose. The L-Moments method has become recently popular because of its various merits.

The L-Moments method, which was originally put forth by Hosking (1990), and Hosking and Wallis (1997), is especially suitable for regional frequency analyses. The L-Moments of a random variable are some linear combinations of its probability-weighted moments, which were originally defined and presented to the statistics literature by Greenwood et al (1979). The L-Coefficients defined, as ratios of the L-Moments, which take values within − 1 and + 1, are able to depict the overall peculiarities of probability distributions, such as mean, variance, and skewness. There exist analytical relationships among the distribution parameters and the L-Coefficients peculiar to any probability distribution. Therefore, the parameters are computed using the estimates of the L-Coefficients calculated using the available recorded series. First, that particular three-parameter distribution most suitable to represent a homogeneous region from the frequency analysis standpoint is determined, based on the weighted average of the L-Coefficients computed for each station where gauged data exists. Ultimately, the regional growth curve is obtained, which is a curve relating the magnitude of the normalized random variable, whose mean is 1.0, to its probability of non-exceedance (Pnex). Growth curves usually are extended up to an average return period of 10,000 years. Aside from the regional growth curve, a meaningful regression equation relating the mean value of the random variable to a few explanatory variables, which are relevant geographical and meteorological characteristics of the homogeneous region, is obtained. The value taken from the growth curve is multiplied by the mean given by the regression equation to obtain the magnitude of the hydrologic variable at any geographical location in the region. The problem with 14 successively increasing standard − duration extreme rainfalls is more involved than a single hydrologic variable, like an annual flood peak. First, there are 14 growth curves. Second, more importantly, the parameters of each probability distribution suitable for each standard-duration extreme rainfalls series must be modified, so as to satisfy the divergence criterion, which emanates from the principle of conservation of mass (Haktanir et al. 2010). Detailed information about the L-Moments method to be applied to successively increasing standard − duration extreme rainfalls series can be found in Haktanir et al. (2016).

Artificial bee colony programming (ABCP) method

Since ABCP is based on the ABC algorithm, its basic steps are similar to those of ABC. However, while ABC can be employed to find optimal values for the parameters of a model, ABCP can be used to optimize the model and its parameters altogether (Karaboga et al. 2012; Gorkemli and Karaboga 2019). The basic steps of the ABCP are given below.

Initialization phase.

Repeat.

Employed Bee Phase.

Onlooker Bee Phase.

Memorize the best solution found so far.

Scout Bee Phase.

Until (Termination criteria are satisfied).

In ABCP, there are three foraging bee groups, namely, employed bees, onlooker bees, and scout bees, as in ABC. An employed bee has a food source in her mind and she leaves the hive to exploit it. When she returns to the hive, she performs some dances to give information about her food source to the onlookers. The onlooker bees wait in the hive and watch the employed bees’ dances. Considering these dances, an onlooker bee selects a food source and leaves the hive to exploit it. Every time an employed bee or onlooker bee goes to a source to exploit it, first, she searches for a better food source around the current one. If she finds a better food source, she starts to exploit it; otherwise, she continues to exploit the current source. In the colony of ABCP, the number of the employed bees is taken to be equal to the number of the onlooker bees. Since every employed bee has one food source, the number of the employed bees also equals the number of the food sources in the population. If the food source of an employed bee is exhausted, then this bee becomes a scout and randomly finds a new food source. In a cycle or iteration of the optimization process, the employed bee, onlooker bee, and scout bee phases are run orderly.

In ABCP, a food source refers to a tree structure based solution. A solution is given in tree form in Fig. 2 as an example. The mathematical formulation obtained from this solution is presented in Eq. 1, where \(a\) and f(a) refer to the independent and dependent variables, respectively. In a solution tree, there can be function nodes or terminal nodes. Function nodes can include some operators, like arithmetic functions, trigonometric functions, and logic operators. These nodes must have one or more operands. Terminal nodes cannot have any operands or any child nodes since they can only include some constants and input variables.

Fig. 2
figure 2

An exemplary solution by the ABCP approach in tree form

Full size image
$$f\left(a\right)=\left(a-\left(1+1\right)\right)\times \left(a\times a\right)$$
(1)

Although its basic optimization structure is similar to the ABC algorithm, some mechanisms cannot be directly used in ABCP, since the solutions are in tree form. For producing a candidate,\({v}_{i}\), from the current solution, xi, (the \(i\) th solution in the population), and the procedure summarized in Algorithm 1 below are used in the employed bee and onlooker bee phases.

Algorithm 1 Steps of the information sharing mechanism of the ABCP scheme.

figure a

In order to determine the quality of the solutions from their costs, Eq. 2 was used in this study, as was done by Karaboga and Ozturk (2012) and Gorkemli and Karaboga (2019),

$$fit\left({x}_{i}\right)=\frac{1}{1+f\left({x}_{1}\right)}$$
(2)

where, \(\mathrm{fit}\left({x}_{i}\right)\) is the quality of the solution \({x}_{i}\) and \(f({x}_{i})\) is the cost function value of this solution. After the employed bee phase, a probability of being selected by an onlooker is assigned to each food source according to its quality using Eq. 3 below.

$${P}_{1}=\frac{a\times fit\left({x}_{i}\right)}{fit\left({x}_{best}\right)}+\left(1-a\right)$$
(3)

where \(\alpha\) is a parameter assuming values between 0 and 1. In this study, 0.9 is taken, as the value of α. xbest is the best solution in the population.

Steps of the ABCP approach are given in Algorithm 2 below. The flowchart of the ABCP method is given in Fig. 3.

Fig. 3
figure 3

Flowchart of the ABCP method

Full size image

Algorithm 2 Basic steps of the ABCP scheme.

figure b

For more details about the ABCP method, interested researchers can read the publications by Karaboga et al. (2012) and Gorkemli and Karaboga (2019).

Empirical rainfall intensity − duration − frequency equations

IDF equations are the empirical formulas defining the relationship between the average intensity of an extreme rainfall as the dependent variable and rainfall duration and frequency as the independent variables. The ranges of rainfall duration and frequency are 5–1440 min and 2–10,000 years, respectively, in most countries. When the relevant publications to date were examined, it was seen that such empirical formulas for IDF could be analytically generalized by Eq. 4 below.

$$i\left(t,T\right)=\frac{A(T)}{B(t)}$$
(4)

The most common equations for the nominator of Eq. 4 are as follows:

$$\mathrm{A}(\mathrm{T}) =\mathrm{ a}\bullet \mathrm{Tb}$$
(5)

(Sherman, 1931; Bernard, 1932; Koutsoyionnis, 1994).

\(\mathrm{A}(\mathrm{T}) =\mathrm{ a }+\mathrm{ b}\bullet \mathrm{ln}(\mathrm{T}\)) (6).

(Koutsoyionnis, 1998)

$$\mathrm{A}(\mathrm{T}) =\mathrm{ a }+\mathrm{ b}\bullet [\mathrm{ln}(\mathrm{lnT})]$$
(7)

(Nhat et al. 2007).

While, the most common equations for the denominator of Eq. 4 are as follows:

$$\mathrm{B}(\mathrm{t}) = {\mathrm{t}}^{\mathrm{c}}$$
(8)

(Sherman, 1931; Bernard, 1932)

$$\mathrm{B}(\mathrm{t}) = ({\mathrm{t}}^{\mathrm{c}} +\mathrm{ d})$$
(9)

(Nhat et al. 2007)

$$B(t) = {(t + d)}^{c}$$
(10)

(Koutsoyionnis, 1998).

Combining A(T) and B(t), Lopcu (2007) presented the nine expressions given below, which were used in this study.

$$i=\left(a\bullet {T}^{b}\right)/{\left(t+c\right)}^{d}$$
(11)
$$i=\left(a\bullet {T}^{b}\right)/{t}^{c}$$
(12)
$$i=\left(a\bullet {T}^{b}\right)/\left({t}^{c}+d\right)$$
(13)
$$i=\left(a+b\bullet lnT\right)/{t}^{c}$$
(14)
$$i=\left(a+b\bullet lnT\right)/\left({t}^{c}+d\right)$$
(15)
$$i=\left(a+b\bullet lnT\right)/{\left(t+c\right)}^{d}$$
(16)
$$i=\left(a+b\bullet \left[ln\left(lnT\right)\right]\right)/{\left(t+c\right)}^{d}$$
(17)
$$i=\left(a+b\bullet \left[ln\left(lnT\right)\right]\right)/{t}^{c}$$
(18)
$$i=\left(a+b\bullet \left[ln\left(lnT\right)\right]\right)/\left({t}^{c}+d\right)$$
(19)

In these equations, i is the standard rainfall intensity (1/min); T is the frequency (years); t is the rainfall duration (min); and a, b, c, and d are the coefficients.

Implementations and results

Rainfall intensity–duration–frequency relationship

The IDF relationship used in this study has been developed by a modified version of the L-Moments method taking into consideration the ‘divergence criterion’ using the extreme rainfalls data observed at 31 meteorological gauging stations in Inland Anatolia Region. The final IDF relationship is a long table comprising values of intensity against so many durations and frequencies, which is also presented in the form of plots of so many points in a log–log scale graph. The summary of this study by Haktanir et al. (2016) can be phrased as follows:

  • Frequency analyses by the L-Moments method was separately conducted for 14 extreme rainfalls series with sequential durations from 5 min to 24 h.

  • At the very beginning, for each station, all of the 14 extreme rainfalls series were normalized by dividing each recorded rainfall value by the sample mean of that particular duration.

  • The incompatibility test was applied to all extreme rainfalls series of 31 stations from 5-min to 24-h durations of each station and it was checked if the incompatibility criterion (D statistic) was satisfied.

  • The homogeneity analyses were applied to all of the 14 extreme rainfalls series of 31 stations, and it was concluded that the Inland Anatolia Region was a single homogeneous region for all of 31 × 14 extreme rainfalls series.

  • The parameters of the GLO, GEV, GNO, PE3, and GPA distributions were computed using the average L-Coefficients. Following 500 synthetic simulations, the ZDIST statistics were computed for the GLO, GEV, GNO, PE3, and GPA distributions.

  • Because they had the smallest ZDIST statistics among the others, the most suitable distributions were: PE3 distribution for the 5 min, the GNO distribution for the 10 min and 15 min, the GEV distribution for the 30-min and 60-min series, and the GLO distribution for all of the other extreme rainfalls series between 120 and 1440 min.

  • The magnitudes of the coefficients of the significant explanatory variables of the multiple regression equation for the means of extreme rainfalls, which turned out to be rainfall duration, longitude, annual average precipitation, and annual average relative humidity, were computed. The average values yielded by the regression equation were multiplied by the magnitudes given by the growth curves of all of the extreme rainfalls series. Thus, the numerical values of the regional IDF relationship were obtained.

Empirical IDF equations and search for the best one for the regionalized IDF relationship

The numerical values of the regional IDF relationship obtained by Haktanir et al. (2016), as summarized above, were used in checking the accuracy of the common nine empirical equations to represent the regionalized relationship. The coefficients of Eqs. 11 through 19 were determined to define the regionalized relationship in the best way possible by its analytical form. The best numerical values of the a, b, c, and d coefficients in Eqs. 11 − 19 were determined so that each one of these equations come as close to the regional IDF relationship for the Inland Anatolia Region as possible with the Excel Solver tool aid. Next, to test the estimation accuracy of the equations with the best values for the coefficients, the mean square error (MSE) and determination coefficient (R2) were used as error statistics. For the Inland Anatolia Region, the best values of the coefficients of the nine equations and the error statistics are given in Tables 1 and 2. Although some of the equations were more successful, the resultant IDF relationships defined by these nine expressions yielded fairly accurate outcomes. Yet, Eq. 16, having the smallest MSE (0.4343) and the greatest R2 (0.995), was the best among them. The scatter plot of the rainfall intensities computed by Eq. 16 against the generalized rainfall intensities obtained by the frequency analyses by the L-Moments method for the Inland Anatolia Region is presented in Fig. 4.

Table 1 The numerical values of the coefficients of the nine empirical equations for the IDF relationship of the Inland Anatolia Region
Full size table
Table 2 The error statistics of the nine empirical equations for representing the IDF relationship obtained by the modified L-Moments method
Full size table
Fig. 4
figure 4

Scatter plot of Eq. 16, which was the best among the nine empirical equations for fitting the IDF relationship obtained by the L-Moments method for the Inland Anatolia Region

Full size image

At first glance, the rainfall intensities obtained by the regional frequency analyses and those computed by Eq. 16 seem to be close to each other. Considering the R2 values given in Table 2, Eqs. 11 and 12 yielded close outcomes, while Eqs. 13, 14, and 15 provided less accurate estimates. Yet, as seen in Table 2 and Fig. 4, Eq. 16 yielded intensities closest to those given by the regional IDF relationship. However, when the IDF relationship was plotted on a graph, in Fig. 5, it was visually observed that this empirical equation, Eq. 16, was not so successful in representing the overall IDF relationship. It can be observed in Fig. 5 that the IDF values obtained by the frequency analyses and those given by Eq. 16 do not reveal close conformity for all of the ranges of the frequencies. Equation 16 yielded successful outcomes for the frequencies of 2000, 5000, and 10,000 years, but was remarkably unsuccessful for shorter frequencies. The overall result is that even the best of these nine empirical equations available in the relevant literature for the IDF relationship is not able to define the regionalized IDF relationship accurately.

Fig. 5
figure 5

Graphical presentation of the numerical values obtained by the L-Moments method and the curves yielded by Eq. 16 with its optimized coefficients for the IDF relationship for Inland Anatolia Region for frequencies from 2 to 10,000 years

Full size image

Determination of the best-fit expression by the ABCP method for the regional IDF relationship

Other analytical expressions were developed by the ABCP approach, which would comply with the IDF relationship determined by the L-Moments method for the Inland Anatolia Region. For this purpose, experimental studies were conducted with different tree depths and different cost functions of the ABCP method. Since models with different structures could be achieved by using different error functions, three different cost functions, which are Eqs. 20, 21, and 22 below, were taken into consideration, and the ABCP scheme was run with the parameter values given in Table 3.

Table 3 Values of the parameters of the ABCP approach as applied to the IDF relationship of the Inland Anatolia Region
Full size table
$$\begin{array}{cc}{f}_{i}=\sum_{j-1}^{N}\left|{g}_{j}-{t}_{j}\right|& (1\mathrm{st cost function})\end{array}$$
(20)
$$\begin{array}{cc}{f}_{i}=\sum_{j-1}^{N}\left|{\mathrm{log}}_{10}\left({g}_{j}+1\right)-{\mathrm{log}}_{10}\left({t}_{j}+1\right)\right|& (2\mathrm{nd cost function})\end{array}$$
(21)
$$\begin{array}{cc}{f}_{i}=\sqrt{\frac{1}{N}\bullet \sum_{j=1}^{N}{\left({\mathrm{log}}_{10}\left({g}_{j}+1\right)-{\mathrm{log}}_{10}\left({t}_{j}+1\right)\right)}^{2}}& (3\mathrm{rd cost function})\end{array}$$
(22)

In these equations, gj represents the rainfall intensity obtained by the ABCP method, tj represents the rainfall intensity obtained by the L-Moments method (the target value), and N equals 168 (14 × 12) in this study. The first expression (Eq. 20) defines the model quality based on the sum of absolute values of differences between the target value (tj) of all cases and the model outcome (gj) (SAE: sum of absolute errors). Equation 20 is one of the most used cost functions in evolutionary computation based automatic programming applications (Koza 1992; Karaboga et al. 2012; Gorkemli and Karaboga 2019). In the other expressions (Eqs. 21 and 22), the target and model outcomes are assessed through logarithmic errors. Because the IDF relationship is always represented on graphs of logarithmic scales, the logarithmic error-based cost functions were considered in this study. While Eq. 21 was obtained by using a logarithmic function in Eq. 20, Eq. 22 provides a cost function that was formed by using root mean squared logarithmic error (RMSLE). In the cost function expressed by Eq. 22, large errors assume greater weights than the small errors.

Parameter settings: As given in Table 3, the colony size was taken as 500 and a total of 500,000 cost function assessments were considered as the termination criterion of an ABCP run. The t of the terminal set denotes the rainfall duration in minutes and T designates the frequency in years. R is a generated random number uniformly distributed within the interval: (− 1, 1). The “log” of the function set is a protected natural logarithm function. The function returns zero if the value to be processed is equal to zero; otherwise, the natural logarithm of the absolute value of the number to be processed is returned. Similarly, the protected version of the “/” function was used. In this function, if the denominator is equal to zero, the function returns 1; otherwise, the division operation is performed. Our studies were conducted by ABCP for simpler relationships with smaller tree depths. Therefore, initial and maximum tree depths were taken as equal to each other and their values were set as 2, 3, and 6.

The MSE and R2 error statistics were used to evaluate the accuracy of estimations by the ABCP approach, as done for the previously tried empirical equations. The mean, the standard deviation, the best, and the worst MSE error values obtained after 30 independent runs for each maximum depth of ABCP are given in Table 4. As seen in Table 4, the lowest MSE values for all depths were obtained by the first cost function. For structures with a maximum depth of 6, the MSE values of all three cost functions were close to each other. In experiments with the maximum depths of 2 and 3, the differences between the results of the 2nd and the 3rd cost functions and the 1st cost function increased. Generally, greater error values are observed in less deep trees than in deeper trees. However, the models with low depths may have simpler structures. The best models (solutions) obtained by ABCP for different maximum depths and different cost functions are presented in Table 5. The models given in Table 5 were obtained by ABCP. The models used in this study, given in Table, were simplified in order for the reader to understand them more easily. As seen in Table 6, Model 1 and Model 3 are similar in structure and have different coefficients. The reason for the coefficients in these two models being different stems from the fact that the cost functions are different. For the Inland Anatolia Region, the coefficients of the equations of the nine ABCP models and the error statistics are given in Tables 6 and 7. As seen in Table 6, these nine ABCP models for the Inland Anatolia Region have a different number of coefficients.

Table 4 Summaries of the MSE values obtained in 30 runs by the ABCP method, with three different maximum depths and three different cost functions
Full size table
Table 5 The analytical models obtained by the ABCP approach, with three different cost functions (CF) and three different maximum depths (MD)
Full size table
Table 6 The numerical values of the coefficients of nine ABCP-based models presented in Table 5
Full size table
Table 7 The error statistics of nine ABCP-based models for representing the IDF relationship obtained by the modified L-Moments method for the Inland Anatolia Region
Full size table

The best models of each cost function and the MSE and R2 values of these models are given in Table 6. Since rainfalls cannot be negative, in this study, the absolute values of the ABCP models were used when calculating the model outcomes. As seen from Tables 6 and 7, Model 7 of the 1st cost function, with a maximum depth of 6 yielded the lowest MSE (0.2129) and the greatest R2 (0.9979) values. The graphical presentations of the IDF relationships obtained by the ABCP method by three different cost functions and three different maximum depths of all models are given in Figs. 6, 7, and 8. The outcomes of the ABCP model for three different cost functions with a maximum depth of 2 and 3 are presented in Figs. 6 and 7. As seen in Figs. 6 and 7, the IDF values obtained by the L-Moments method had a poor fit to those yielded by any of the ABCP models with a maximum depth of 2 and 3. The ABCP model outcomes for three different cost functions with a maximum depth of 6 are presented in Fig. 8. As seen in this figure, the IDF values of the L-Moments method overlapped with the IDF values computed by this version of the ABCP models. As observed in Figs. 6, 7, and 8, the ABCP models with a maximum depth of 6 were more successful than the ABCP models with 2 and 3 maximum depths. According to Fig. 8, the estimations by Model 7 of the 1st cost function were greater than the L-Moments values for small frequencies like 2 and 5 years. Model 7 also yielded small deviations for the 10,000-year frequency. In Model 8, high estimation outcomes resulted for 3 h and longer rainfall durations for 5000- and 10,000-year frequencies. The results of Model 9 of the third cost function deviated from the L-Moments values for mid-term frequencies. Besides the graphical presentations of the results of Models 7, 8, and 9, the MSE and R2 values presented in Table 7 were investigated. As seen in Table 7, Model 7 of the third cost function, with a maximum depth of 6 had the highest R2 and the lowest MSE values. Hence, it can be stated that Model 7 yielded outcomes closest to the target values among nine ABCP models. Yet, Models 8 and 9 did not have remarkably high MSE values; thus, they can be used as an alternative to Model 7.

Fig. 6
figure 6

Graphical presentation of the numerical values obtained by the L-Moments method and the curves yielded by the ABCP model with maximum depth of 2 for the IDF relationship for the Inland Anatolia Region for frequencies from 2 to 10,000 years

Full size image
Fig. 7
figure 7

Graphical presentation of the numerical values obtained by the L-Moments method and the curves yielded by the ABCP model with maximum depth of 3 for the IDF relationship for the Inland Anatolia Region for frequencies from 2 to 10,000 years

Full size image
Fig. 8
figure 8

Graphical presentation of the numerical values obtained by the L-Moments method and the curves yielded by the ABCP model, with maximum depth of 6 for the IDF relationship for the Inland Anatolia Region for frequencies from 2 to 10,000 years

Full size image

In the last phase of the study, the best model obtained by the ABCP method was compared with the nine empirical equations considered herein. Among the nine empirical equations, Eq. 16 was determined to be the most appropriate one. Among the nine different models developed as different versions of the ABCP method, Model 7 was identified as the best model. Despite high R2 values by Eq. 16, it was visually observed in graphical form that that equation did not yield outcomes close to the actual values. When the results of Eq. 16 and Model 7 were compared with each other, it was observed that according to the IDF curves presented in Figs. 5 and 8, Model 7 produced by the ABCP method was more successful than empirical Eq. 16. Although the empirical equations available in literature were analytically simple expressions, they did not match the results of the L-Moments method, which is clearly noticeable to the naked eye when presented in graphical forms.

At the end of the study, in addition to the classical performance metrics, the nonparametric Kruskal − Wallis tests were also applied to all of the quantitative values given first by the regional frequency analyses by the L-Moments method and next by either those by the empirical equations or by those equations derived by the ABCP approach. The purpose of these tests was to check whether the predicted and actual values come from the same space (same population) (Başakın et al. 2020, 2021b; Özger et al 2020; Citakoglu 2021). The results of the Kruskal − Wallis tests are given in Table 8. As seen in Table 8, all models, the empirical equations, and the ABCP-produced ones passed the Kruskal − Wallis test at 95% significance level. Thus, the results of the empirical equations and the ABCP models come from the same population as those issued by the more accurate L-Moments approach. However, the ABCP method yields better accuracy than any of the empirical equations as summarized heretofore.

Table 8 The p-values of the null hypothesis (H0) of the Kruskal–Wallis test at 95% significance level and the decisions reached based on the magnitudes of the p-values
Full size table

Conclusions

In this study, an automatic programming method based on artificial bee colony programming (ABCP) was used to find the optimal model to define the (standardized rainfall intensity) − (rainfall duration) − (frequency) (IDF) relationship obtained for the Inland Anatolia Region of Turkey by the L-Moments method. Furthermore, an analytical expression was developed, which is more accurate than any of the empirical equations available in literature for the same purpose. Initially, the IDF relationship was investigated using each one of nine different empirical formulas. The comparison studies on these nine empirical equations with optimized values for their coefficients revealed that the one expressed by Eq. 16 showed the relatively best performance for the Inland Anatolia Region, for representing the IDF relationship (Table 1). However, as shown in Fig. 4, Eq. 16 exhibited an unsatisfactory performance for frequencies smaller than 2000 years and a seemingly high coefficient of determination was misleading. Then, ABCP, with three different cost functions and three different maximum depths, was used and new analytical expressions were generated for the present problem. The resultant best model obtained by ABCP was compared with the nine empirical formulas and the former was found to define the IDF relationship more accurately, as determined by the L-Moments method for the Inland Anatolia Region.

In analyses done by the ABCP method, by using three cost functions and three maximum depths, nine different models were produced for the relationship of rainfall intensity as the dependent variable and rainfall duration and frequency as the explanatory variables. The same comparison studies as the ones applied to those nine empirical equations revealed that Model 7, having the 1st cost function with a maximum depth of 6, yielded the lowest MSE and the highest R2 values. Hence, the ABCP method, recommended as an alternative technique for determining a single analytical expression for the IDF relationship, yielded highly accurate outcomes for the Inland Anatolia Region and Model 7, with the smallest MSE was appreciably better than the best empirical model.

In conclusion, the ABCP-based models can be used elsewhere in the world and will most probably quantify the regional IDF relationship more accurately than any of the conventionally used empirical formulas for places without rainfall measurements or with gauging records that are too short.

Conflicts of interest

The authors declare no competing interests.

Ethics approval

The authors paid attention to ethical rules in the study. There was no violation of ethics.

Consent for publication

If this study is accepted, it can be published in the Arabian Journal of Geosciences.