1 Introduction

Kirchhoff type shell theories are known for a long time. They have been successfully applied to a wide range of problems in structural mechanics. Applications vary from the dynamics of cell membranes [5, 10] to stress analyses of an aircraft fuselage. A continuum model typically predicts the deformed state of a body using tools from geometry and thermodynamics. In classical continuum mechanics, the geometry of the body remains frozen; three dimensional elasticity is an example of one such theory. Conventionally, Kirchhoff type shells are considered to be within the realms of classical continuum mechanics. This perspective stems from a purely displacement based formalism of these shells. An alternate approach to Kirchhoff shells is to consider the geometry of the mid-surface and its deformation as separate entities. From such a viewpoint, this shell theory contains non-classical aspects which cannot be found in classical continuum mechanics.

Srinivasa and Reddy [16] have classified non-local continuum models into two major groups; the first involves displacement as the primal field. In this class of models, non-locality is brought in by considering the energy contribution due to higher gradients or by averaging the conventional strains over a neighbourhood. Examples include higher gradient models and integral type non-local models of Eringen [7]. The second class of non-local models involves the introduction of additional variables other than displacement. These additional variables are in general tensor fields. Micropolar [17] and micromorphic theories [8] are representative examples from this class. In this class of models, the coupling between non-locality and deformation is through energy considerations (first and second laws of thermodynamics). This energetic coupling has led to limited success with the experimental characterization of the constitutive functions associated with non-local strains and tensorial internal variables. Recently, micro-continua based theories have been used to analyze the structural response of sandwich beams [11, 12]; these approaches try to relate the constitutive functions for the micro-degree of freedom from the unit cell response of the sandwich structure.

Following Srinivasa and Reddy [16], if we take a non-local theory as one involving higher gradients or additional (director like) degrees of freedom (other than displacements), a Kirchhoff type shell is indeed a non-local model in the following sense. It has curvature which is the second derivative of deformation. Moreover one may also define director fields (tangents and normal vectors) at each point of the mid-surface. However, it differs from the previously mentioned non-local models in a distinct way due to a kinematic coupling between the conventional displacement variables and the director degrees of freedom. This kinematic coupling is facilitated by the affine connection of the surface. Incorporating this affine connection into a computational scheme has always been difficult. As remarked in Simo et al., “it is apparent that objects such as Christoffel symbols, the second fundamental form, and covariant derivatives, which are not readily accessible in a computational framework, never appear explicitly”. Computational methods for shells often found a way to circumvent the explicit use of an affine connection and hence geometry; Dvorkin and Bathe [6] and Simo et al. [13] are representative examples. Arbind  et al. [1, 2] recently developed higher order models for tubes and rods using the notion of a moving frame. In these models, the centreline of the rod/tube is depicted using a curve with a suitable frame attached to it. Tensor quantities of interest are then described with respect to the frame. Equations of equilibrium are finally written down after a cross-sectional integration resulting in a system of ordinary differential equations for the displacement components of the centreline curve.

The goal of this article is to unravel the non-classical feature of Kirchhoff shells—a special class of models where a compatible geometry determines the deformation and vice verse. We reformulate the equations of Kirchhoff shell theory in a way that decouples geometry from deformation, thus admitting a generalization to scenarios where the evolving geometry and deformation contain non-overlapping information. Cartan’s method of moving frames is used for this purpose. The geometry of the mid-surface and deformation are combined in a compatible manner using the structure equations of Cartan. One should remember that such a reformulation does not bring in new physics; it only makes the geometry of the theory more transparent. This article is organized in the following sequence. The next section introduces differential forms and Cartan’s method of moving frames. Using these tools, the kinematics of a Kirchhoff type shell is then reformulated and the relationship of the present kinematics with defect mechanics is also elucidated. Section 3 discusses the equations of equilibrium pertaining to a stored energy functional for Kirchhoff type shells. Section 4 deals with a simple analytical solution where emphasis is placed on the use of structure equations. Some closing remarks are offered in Sect. 5.

2 Differential forms and kinematics of Kirchhoff shells

In this section, we collect a few basic results on differential forms which are required for the development of our approach. Although the following discussion is elementary, the importance of differential forms for our analysis makes this section essential; for more details, see [4]. The study of differential forms began with the work of H Grassmann; however it was E Cartan who exploited it more comprehensively for the study of geometry. Given a smooth manifold \(\mathcal {M}\), at any point \(x\in \mathcal {M}\), one may define the tangent space to \(\mathcal {M}\) as the set of all vectors tangent to curves passing though x; we denote this set by \(T_x\mathcal {M}\). An alternative picture is to think of tangent vectors as directional derivations of scalar valued functions defined on \(\mathcal {M}\). These two pictures are equivalent: while the former is geometric, the latter analytic. Given a coordinate system \((x^1,...x^n)\) in an open neighbourhood of \(\mathcal {M}\), it induces a basis on \(T_x\mathcal {M}\); we call it the coordinate basis and denote it by \(\{\partial _{x^1},...,\partial _{x^n}\}\). The vector space dual to \(T_x\mathcal {M}\) is denoted by \(T^*_x{\mathcal {M}}\); this vector space is also refereed to as the space of one-forms. For \(f:\mathcal {M}\rightarrow \mathbb {R}\), its differential \(\text{ d }f\) is understood as a one-form, which acts on a tangent vector v to produce the directional derivative of f in the direction of v. If one chooses the tangent vector to be the coordinate basis vector, then \(\text{ d }f(\partial _{x^i})=\partial _{x^i}f\), is the directional derivative of f in the \(x^i\) direction. On choosing f to be the ith coordinate function, one establishes the relationship \(dx^i(\partial _j)=\delta ^i_j\); this relation also establishes the duality between tangent vectors and one-forms. We call \(\{\text{ d }x^1,...,\text{ d }x^n\}\) the coordinate basis for \(T^*_x\mathcal {M}\).

A one-form may also be understood as an object that can be integrated along a curve to produce a real number. In particle mechanics, the work done by a point particle is the line integral of the forces acting on the particle as it traverses a curve. The force on the particle is identified as a one-form acting on the tangent vector (to the curve) to produce work. The degree of a differential form is defined as the dimension of the hyper-surface on which it must be integrated to produce a real number. In physics, a multitude of objects can be identified as differential forms; a classic example of a two-form is the magnetic field. At each point on \(\mathcal {M}\), a differential form can be defined as a multi-linear anti-symmetric map taking values in a vector space. Notice that differential forms can be vector valued as well. Differential forms of degree greater than one can be constructed using the wedge product. If \(\alpha\) and \(\beta\) are one-forms, then \(\alpha \wedge \beta\) is a two-form. The wedge product can be extended to forms of arbitrary degree. On a finite dimensional manifold, the highest degree of a scalar valued differential form that can be defined is equal to the dimension of the manifold. Differential forms of the highest degree are often called volume forms. For surfaces embedded in \(\mathbb {R}^3\), one can only define zero-, one- and two-forms.

Assigning a form of a certain degree smoothly to each point on \(\mathcal {M}\) defines a section of differential forms. Sections of one-forms are elements from the cotangent bundle; we denote it by \(T^*\mathcal {M}\). The notion of exterior derivative enables coordinate independent differentiation for differential forms. Exterior derivative is natural to differential forms in the sense that it does not require additional mathematical structure other than the smoothness of the manifold. The exterior derivative of a differential form \(\alpha\) is denoted by \(\text{ d }\alpha\). It takes a differential form of degree n to produce a form of degree \(n+1\). If \(\alpha\) and \(\beta\) are differential forms of degree m and n then,

$$\begin{aligned} \text{ d }(\alpha \wedge \beta )=\text{ d } \alpha \wedge \beta + \alpha \wedge (-1)^n\text{ d } \beta . \end{aligned}$$
(1)

It is also easy to verify that \(\text{ d } \text{ d } (\alpha )=0\) for any differential form \(\alpha\). Differential forms which satisfy the condition \(\text{ d } \alpha =0\) are called closed. If \(\alpha =\text{ d } \beta\) then, we say that \(\alpha\) is exact. Poincaré’s lemma establishes an important relationship between closed and exact forms.

The wedge product and the exterior derivative are natural operations with respect to pull-back. If \(\mathcal {M}\) and \(\mathcal {N}\) are differentiable manifolds and \(\varphi :\mathcal {M}\rightarrow \mathcal {N}\), the pull-back of \(\alpha \in T^*\mathcal {N}\) is denoted by \(\varphi ^*(\alpha ) \in T^{*}\mathcal {M}\). If \(\alpha ,\beta \in T^*\mathcal {N}\), the pull-back of their wedge product is given by,

$$\begin{aligned} \varphi ^*(\alpha \wedge \beta )=\varphi ^*(\alpha )\wedge \varphi ^*(\beta ). \end{aligned}$$
(2)

Similarly, the pull-back of the exterior derivative of \(\alpha\) is given by,

$$\begin{aligned} \varphi ^*{\text{ d }\alpha }=\text{ d }\varphi ^*(\alpha ). \end{aligned}$$
(3)

The above results are powerful; they can be exploited in finite deformation solid mechanics when formulated in terms of differential forms. One can forget the deformation map and work with differential forms as if they were defined on a given fixed manifold.

2.1 Moving frames

E Cartan developed the theory of moving frames to ascertain when two surfaces are geometrically equivalent; this equivalence is with respect to the symmetry group of the embedding space. This question also leads to the construction of a complete set of invariants characterizing a surface. This set of invariants is sufficient to determine the surface up to the symmetry group (rigid body motion for the Euclidean space). The following one dimensional case gives the general idea behind moving frames. Consider an interval \(I=[s_1,s_2]\subset \mathbb {R}\). AFootnote 1 curve p in \(\mathbb {R}^2\) is given by the map \(p:I\rightarrow \mathbb {R}^2\). We assume that the curve is parameterized by its arc length. The Frenet frame consisting of unit tangent and normal vectors completely determines the geometric properties of the curve p. For a regular curve in \(\mathbb {R}^2\), Frenet frame always exists. Quantities like arc length and curvature can be directly computed using the Frenet frame. Also notice that these quantities are invariant with respect to action on the Euclidean group (the symmetry group of \(\mathbb {R}^2\)) at p. An alternative way to think about it is to pull the Frenet frame back to the interval I; we denote the pull-back map by \(p^{*}\). To compute the pull-back frame, one has to think of the vectors of the Frenet frame as the value of a one-form (a vector-valued one-form). On an interval (curve), the degree of the volume form is one, which makes it convenient to identify one-forms with scalars. Geometric quantities may now be expressed in terms of these one-forms. Since pull-back commutes with exterior derivative and wedge product, the geometric information (scalar quantities like arc-length and curvature) contained in the frame is preserved. Now instead of working with the curve, one can work with the pulled back one-forms (frame); this gives an easy handle to manipulates the geometric information. Of course, the pulled back frame has to satisfy certain compatibility conditions for the existence of deformation, which are trivial in the one dimensional case (since integrability is trivial in one dimension). Figure 1 shows the curve p, its Frenet frame and the pull-back of the frame on to the interval \([s_1,s_2]\). If one finds an evolution rule for the one-forms associated with the Frenet frame, one may directly evolves the geometry. Moreover, if the geometry is compatible, one can also find a suitable deformation (up to rigid body motion), whose geometry is given by these one-forms. In the discussion above, we have largely argued based on the Frenet frame; it is well understood that there are curves for which the Frenet frame may not exist. But the Frenet frame is not the only available frame for a curve. Bishop [3] suggested multiple ways to define frame fields for a curve. A frame as such is indeed not that meaningful, only the geometric information they encode is important.

Fig. 1
figure 1

The Frenet fame of a regular curve in 2D and the pulled back frame to the interval [a, b]. One should note that we are actually pulling the one-forms associated with the frames

Full size image

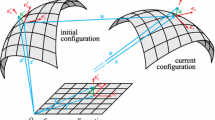
We now discuss the method of moving frames for a surface \(\mathcal {S}\) embedded in the three dimensional Euclidean space. A careful introduction to this subject can be found in [4, 9]. At any point on the surface, one can define two tangent vectors and a unit normal. The unit normal is unique but the tangent vectors are not. However, the vector space spanned by the tangent vectors is unique. We denote the normal vector by \(e_3\) and the tangent vectors by \(e_1\) and \(e_2\). The crux of a moving frame is in encoding the geometric information about the surface within the (pulled-back) differential of the frame.

Fig. 2
figure 2

A surface with its unit normal and tangent plane

Full size image

2.2 Affine connection of a surface

The Euclidean space has a natural parallelism; we say that two vectors are parallel if one is a scalar multiple of the other. On a surface, no such natural parallelism exists. However one can define parallel sections (vector fields) on a surface using the notion of parallel transport. It should be noted that parallel transport is an additional structure we place on a manifold. Many notions of parallelism may exist on a surface and each may lead to a corresponding notions of affine connection on the surface [15]. The Riemannian parallelism on a surface is a distinguished notion of parallel transport. It stems from the metric defined on the surface. Kirchhoff shells can be developed completely based on the parallel transport induced by the metric; this parallel transport is also the fundamental hypothesis behind Riemannian geometry. The hypothesis is that the length of a vector and angle between two vectors are preserved under parallel transport, i.e. the metric is preserved under parallel transport. It should also be mentioned that classical continuum mechanics is founded on the same hypothesis along with the flatness assumption. The infinitesimal version of this parallel transport defines an affine connection. Without the notion of a connection, it is not possible to differentiate tensor fields in a coordinate independent manner. This fact has been largely overlooked in many opaque continuum models dealing with internal variables and higher gradients. More specifically, it may not make sense to differentiate the strain tensor without the notion of an affine connection.

Using the method of moving frames, one can arrive at the notion of connection on the surface \(\mathcal {S}\). We call this notion of connection the Cartan connection, which corresponds to assigning a matrix of connection one-form (\(\omega _i^j\)) to each frame. The notion of Cartan connection predates the popularly known affine connection in terms of Christoffel symbols. It can be shown that Riemannian and Cartan connections on a surface are equivalent. The difference between these two notions is that one uses differential forms while the other depends on vector fields to describe the connection.

If \(\mathcal {F}=\{e_1,e_2,e_3\}\) is a frame defined on \(\mathcal {S}\), the connection matrix \(\omega\) is related to the differential of the frame in the following way,

$$\begin{aligned} \text{ d }e_i=e_j\omega _i^j. \end{aligned}$$
(4)

Since the frame \(\mathcal {F}\) is orthonormal, we have \(\omega _i^j=-\omega ^i_j\). The entries of the connection matrix are not real numbers but one-forms. The covariant derivative of a frame field with respect to another is given by,

$$\begin{aligned} \nabla _{e_i}e_j=e_k\omega ^k_j(e_i), \end{aligned}$$
(5)

\(\omega (e_i)\) denotes the action of the connection one-forms on the vector field \(e_i\). The relationship between the surface Christoffel symbols and the connection one-forms is also established by (5). It is easy to verify that the above definition satisfies the following properties,

$$\begin{aligned} \nabla _{e_i} (v+w)&=\nabla _{e_i} (v)+\nabla _{e_j} (w)\\ \nabla _{fe_i} (w)&=f\nabla _{e_i} (w)\\ \nabla _{e_i} (fw)&=f\nabla _{e_i} (w)+e_i(f)w \end{aligned}$$

for vector fields v, \(w\in T\mathcal {S}\) and \(f \in C^{\infty } (\mathcal {S})\). These properties define a covariant derivative on \(\mathcal {S}\). If \(w=w^ie_i\) is a vector field on \(\mathcal {S}\), then the covariant derivative of w in the direction of \(e_i\) may be expressed as,

$$\begin{aligned} \nabla _{e_i} w= \text{ d } w^j(e_i)e_j+e_kw^j\omega ^k_j(e_i). \end{aligned}$$
(6)

The last equation is just an application of the properties of covariant differentiation.

2.3 Surface theory via moving frames

Having introduced the notion of connection matrix in the last section, we introduce the metric and curvature tensors or the first and second fundamental forms of the surface in this section. The metric tensor is obtained by restricting the (3 dimensional) Euclidean metric on to the tangent space of the surface. Let \(p\in \mathcal {S}\subset \mathbb {R}^3\) be a point on the surface. We now fix an origin and basis vectors for the ambient space (Euclidean 3 dimensional space). The position vector of p is the vector connecting the origin and point p. We may indicate the point p by its position vector. Note that we use the same notation for an element from the set \(\mathcal {S}\) and its position vector, even though these are distinct entities. If we denote the basis vectors for the ambient Euclidean space by \(E_i\), \(i=1,2,3\), then the position vector can be written as,

$$\begin{aligned} p=f^1(\xi ^1,\xi ^2)E_1+f^2(\xi ^1,\xi ^2)E_2+f^3(\xi ^1,\xi ^2)E_3. \end{aligned}$$
(7)

Here, \(\xi ^\alpha\), \(\alpha =1,2\) are the coordinates of p in a chosen coordinate system and \(f^i\) are real valued functions. The important thing to observe here is that we can denote the same point \(p\in \mathcal {S}\) using the position vector or by its co-ordinates. It should be mentioned that the same point can have multiple co-ordinates depending on the coordinate chart applied to the surface. Even though the position vector can be expressed using multiple coordinate systems, the position vector as such is unique for a given point in \(\mathcal {S}\) The differential of the position vector is given by,

$$\begin{aligned} \text{ d }p=e_1\theta ^1+e_2\theta ^2. \end{aligned}$$
(8)

Here, \(\theta ^i\) are one-forms and \(e_i\) the tangent vectors from the frame \(\mathcal {F}\). We may refer to \(\theta ^i\) as deformation one-forms. Note that the differential of position does not have any component in the \(e_3\) direction. The quantity \(\text{ d }p\) is understood as a vector valued one-form; for higher clarity the following notation may be used: \(\text{ d }p=e_1\otimes \theta ^1+e_2\otimes \theta ^2\). However, we will stick to the notation introduced in (8). Moreover it should be noted that \(\text{ d }p\) is a \({1 \atopwithdelims ()1}\) tensor (second order). The volume (area) form associated with the deformation is given by,

$$\begin{aligned} J=\theta ^1\wedge \theta ^2. \end{aligned}$$
(9)

The first fundamental form I is a \({0 \atopwithdelims ()2}\) tensor; it can be computed as,

$$\begin{aligned} I=\text{ d }p.\text{ d }p. \end{aligned}$$
(10)

Note that, the dot ‘.’ in the above equation denotes the contraction of the vector part of \(\text{ d } p\) with itself using the metric tensor of the ambient Euclidean space; the co-vector (one form) part of \(\text{ d }p\) is left untouched. Using the orthonormality between the vectors \(e_1\) and \(e_2\), we arrive at

$$\begin{aligned} I=\theta ^1\otimes \theta ^1+\theta ^2\otimes \theta ^2. \end{aligned}$$
(11)

The last equation defines a symmetric covariant two-tensor which in turn defines the notions of length and angle between the tangent vectors on the surface. The second fundamental quantity is the curvature tensor of the surface denoted by II, also referred to as the second fundamental form. It describes how the unit normal changes as we move along the surface.

$$\begin{aligned} II=-\text{ d }e_3.\text{ d }p;\quad i=\{1,2\}. \end{aligned}$$
(12)

As in the definition of I, the dot ’.’ in the above equation is understood as the inner product in the ambient space. Using the definition of the connection matrix introduced in (4), we have

$$\begin{aligned} II=\omega ^1_3\otimes \theta ^1+\omega ^2_3\otimes \theta ^2. \end{aligned}$$
(13)

An immediate question that arises is about the relationship between the connection and deformation one-forms. The torsion free condition of the ambient space establishes this condition. Using exterior derivatives, this condition can be elegantly written as,

$$\begin{aligned} \text{ dd }p=0. \end{aligned}$$
(14)

If one uses a vector field perspective for connection, the above condition leads to the symmetry of the Christoffel symbols. Applying the exterior derivative to (8) leads to,

$$\begin{aligned} \begin{bmatrix} \text{ d }\theta ^1\\ \text{ d }\theta ^2\\ 0 \end{bmatrix} = \begin{bmatrix} 0 &{}\omega _1^2&{} \omega _1^3\\ -\omega _2^1&{} 0&{} \omega _2^3\\ -\omega _3^1&{} -\omega _3^2&{} 0\\ \end{bmatrix} \wedge \begin{bmatrix} \theta ^1\\ \theta ^2\\ 0 \end{bmatrix} \end{aligned}$$
(15)

The matrix multiplication indicated in the above equation uses the wedge product to combine the connection and deformation one-forms. The existence and symmetry of the second fundamental form follows from the third equation in (15). We also want the frame to be Euclidean: the surface to be embedded in an ambient space with zero curvature (flatness of the ambient space). This condition takes the form,

$$\begin{aligned} \text{ dd }e_i=0 \end{aligned}$$
(16)

Applying the exterior derivative to (4) leads to,

$$\begin{aligned} \begin{bmatrix} 0 &{}\text{ d }\omega _1^2&{} \text{ d }\omega _1^3\\ -\text{ d }\omega _2^1&{} 0&{} \text{ d }\omega _2^3\\ -\text{ d }\omega _3^1&{} -\text{ d }\omega _3^2&{} 0\\ \end{bmatrix}= \begin{bmatrix} 0 &{}\omega _1^2&{} \omega _1^3\\ -\omega _2^1&{} 0&{} \omega _2^3\\ -\omega _3^1&{} -\omega _3^2&{} 0\\ \end{bmatrix} \wedge \begin{bmatrix} 0 &{}\omega _1^2&{} \omega _1^3\\ -\omega _2^1&{} 0&{} \omega _2^3\\ -\omega _3^1&{} -\omega _3^2&{} 0\\ \end{bmatrix} \end{aligned}$$
(17)

The skew-symmetry of the connection matrix reduces the number of independent equations to just three. In contemporary differential geometry literature (15) and (17) are called Cartan’s structure equations. Together they contain the Gauss–Codazzi–Minardy equations often discussed in the theory of surfaces to establish the compatibility between the metric and curvature tensors.

From (15), one may note that \(\omega ^1_3\wedge \theta ^1+\omega ^2_3\wedge \theta ^2=0\). Applying Cartan’s lemma to the above equation, we conclude that there exists a symmetric matrix relating \(\omega ^1_3,\omega ^2_3\) and \(\theta ^1,\theta ^2\) in the following way,

$$\begin{aligned} \begin{bmatrix} \omega ^1_3\\ \omega ^2_3\\ \end{bmatrix} = \begin{bmatrix} a &{} b\\ b &{} c \end{bmatrix} \begin{bmatrix} \theta ^1\\ \theta ^2\\ \end{bmatrix} \end{aligned}$$
(18)

where a, b and c are real valued functions. Using (18), one can establish the symmetry of the second fundamental form.

2.4 Relationship with defect mechanics

From the previously discussed kinematics of Kirchhoff shells, the following differences vis-á-vis classical continuum mechanics are observed.

  1. 1.

    For a Kirchhoff type shell, there exist two tensorial quantities that completely describe the geometry of the shell. Contrast this with classical continuum mechanics where there is only one such quantity (the metric tensor); the flatness assumptionFootnote 2 renders the curvature tensor null.

  2. 2.

    The second major difference is that, in the current setup, the tensorial qualifiers of geometry co-evolve with the shell deformation in the ambient space. There is no analogue of such an evolution in classical continuum mechanics since the metric tensor is frozen or, in general, the geometry of the continuum body is frozen in time.

Even though the features as above are not found in classical continuum mechanics, it is prevalent in the mechanics of defects. Theories in defect mechanics are often considered within the broad umbrella of continuum mechanics, but beyond the scope of classical continuum theories. The continuum theory of dislocations [18, 19] is a good example, in which dislocations are modelled using the torsion tensor. This amounts to the following modification of the first structure equation (14),

$$\begin{aligned} \text{ dd }p=\tau \end{aligned}$$
(19)

In the above equation, \(\tau\) is a vector containing torsion two-forms as its entries. Similarly, if one needs to incorporate disclinations into the theory, the flatness assumption must be given up [20]. This leads to the following modification of the second structure equations (16),

$$\begin{aligned} \text{ dd }e_i=\Omega _i \end{aligned}$$
(20)

\(\Omega _i\) are called the curvature two-forms. Of course, additional compatibility conditions exist on \(\Omega\).

2.5 Reissner type shells

In the computational literature, Reissner type shells are often considered advantageous over Kirchhoff type shells since numerical solution schemes can be formulated with relative ease. Moreover, the former also incorporates shear deformation. Geometrically, Reissner type shells are quite distinct and their geometry is more complicated. In a Reissner type shell, the deformation of the mid-surface and the frame associated with the cross section are evolved independently with only an energetic coupling. No compatibility conditions are enforced between the differentials of the frame and the deformation. If we consider the cross sectional frame of a Reissner shell to be a valid moving frame, the lack of compatibility conditions between deformation and frame leads to a non-zero source term in the first structure equations. This may be interpreted as torsion of the embedding space. In addition, the source term in the second structure equation may imply that the embedding space has non-zero curvature. These geometric properties of a Reissner shell has gone unobserved since a computational mechanist is often interested in deformation and stress, and not particularly so in the geometry of the model.

3 Kinetics

Internal forces acting on the shell are given by,

$$\begin{aligned} n^i= t^i+s^ie^3;\quad i,j \in \{1,2\}. \end{aligned}$$
(21)

In the above equation, \(n^i\) and \(t^i\) are vectors and \(s^i\) is a scalar. The shear force acting at any point is given by \(s^i e^3\). In a Kirchhoff type shell, shear forces are not determined constitutively but are developed to enforce certain constraints. The constitutive rule for \(t^i\) is determined by introducing the surface stress tensor denoted by \(\sigma ^{ij}\). This stress tensor is conjugate to the first fundamental form. The tension tensor N is given by,

$$\begin{aligned} N^{ij}=\sigma ^{ij}+II^i_kM^{kj}. \end{aligned}$$
(22)

If we assume the existence of a stored energy functional, the constitutive rule for the surface stress tensor is given by,

$$\begin{aligned} \sigma ^{ij}=\frac{\partial W}{\partial I_{ij}}. \end{aligned}$$
(23)

The in-plane forces are then given by,

$$\begin{aligned} t^i=N^{ij}E_j; \quad i,j \in \{1,2\}. \end{aligned}$$
(24)

The bending moment tensor conjugate to the second fundamental form is given by,

$$\begin{aligned} M^{ij}=\frac{\partial W}{\partial II_{ij}}. \end{aligned}$$
(25)

Couples acting along the tangent vectors are denoted by,

$$\begin{aligned} m^i=M^{ij}E_i;\quad i,j \in \{1,2\}. \end{aligned}$$
(26)

Using the above quantities, the balance of linear momentum may be written as,

$$\begin{aligned} \frac{1}{J}(Jn^i)_{;i}+f=0 \end{aligned}$$
(27)

f is the externally applied surface force and \(n^i\) are internal forces generated by the shell to resist the external force. The balance of angular momentum may be written as,

$$\begin{aligned} \frac{1}{J}(Jm^i)_{;i}+(p_{,i} \times n^i)+l=0. \end{aligned}$$
(28)

Here, \(m^i\) and l are the internal and external couples. The derivatives in the first terms of (27) and (28) are understood as covariant derivatives, while the derivative in the second term of (28) is the usual directional derivative. This distinction is important, since \(m^i, n^i\) are one-forms (tangent objects) and p is a map between manifolds.

3.1 Stored energy function

The stored energy density of a shell involves contributions from bending and extension denoted by \(W_B\) and \(W_E\) respectively. The energy density of the shell is thus given by \(W=W_B+W_E\). We adopt the stored energy function proposed by Koiter for bending, which is quadratic in the second fundamental form,

$$\begin{aligned} W_B=\frac{Eh^3}{24(1-\nu ^2)} [(1-\nu ) \text {Tr}(II^2)+\nu \text {Tr}(II)^2], \end{aligned}$$
(29)

h is the thickness of the shell, E and \(\nu\) are respectively Young’s modulus and Poisson’s ratio. We set the energy associated with extension to zero \(W_E=0\). Using Cayley-Hamilton theorem, the above energy function can be rewritten as,

$$\begin{aligned} W_B=\frac{C_1}{2}H^2+C_2K. \end{aligned}$$
(30)

where, \(C_1\) and \(C_2=\) depend on material parameters, e.g. E, \(\nu\) and h. H and K are the mean and Gaussian curvatures respectively. These scalar invariants of the surface are given by,

$$\begin{aligned} H=\frac{1}{2}(a+c);\quad K=ac-b^2. \end{aligned}$$
(31)

We also ignore the second term in (30), since we do not expect a topological change; the second term adds only a constant to the energy. Finally the bending energy becomes,

$$\begin{aligned} W_B=\frac{C_1}{2}H^2. \end{aligned}$$
(32)

4 Applications of the present theory

We now apply the Kirchhoff type shell theory based on moving frames to analytically obtain a class of deformation in thin shells. The objective of the present section is to demonstrate the use of Cartan’s structure equations and kinematically close the deformation and connection one-forms. We also show how usual ideas from shell theory can be translated into the present setup (Fig. 2).

4.1 Pure bending of a thin elastic strip

Consider a thin rectangular elastic strip with one of its edges fixed. We assume a Cartesian coordinate system for the reference configuration of the thin strip. At the initial configuration, the longer and shorter edges are aligned along the x and y axes respectively. A bending moment is applied to the edge parallel to the fixed edge. This causes the strip bend in the form of a cylinder with its axis parallel to the fixed edge. Even though the deformation is relatively large, the state of strain in homogeneous with unit stretch and constant curvature. If one uses the method of moving frames to solve this problem, one has to resolve the five one-forms \((\theta ^1,\theta ^2,\omega ^1_3,\omega ^2_3, \omega ^2_1)\) which should be consistent with mechanical equilibrium and the two structure equations. Using a sequence of simple integrations along curves, one can then determine the frame and deformation from (4) and (8). We denote the frame of the reference configuration by \(E_i\); these are unit vectors along x, y and z directions. Depending on the coordinate system, \(E_1\) and \(E_2\) can be chosen but \(E_3\) is unique. Given that the strip is known to bend only in one direction and that it does not stretch, the deformation one-forms remain frozen as in the reference configuration. This leads to,

$$\begin{aligned} \theta ^1=dx;\quad \theta ^2=dy. \end{aligned}$$
(33)

For the determination of the deformed frame fields, one has to specify the connection one-forms. Again using the assumption of unidirectional bending, we conclude that \(\omega ^1_3\) is the only non zero unknown; all other connection one-forms reduce to zero. For the sake of avoiding multiple indices, we denote \(\omega ^1_3\) by \(\lambda\), which leads to the following expression for the matrix of connection one-forms,

$$\begin{aligned} \omega = \begin{bmatrix} 0 &{}0 &{}\lambda \\ 0 &{}0 &{}0\\ -\lambda &{}0 &{}0 \end{bmatrix}. \end{aligned}$$
(34)

The second fundamental form may now be computed as,

$$\begin{aligned} II=\lambda \otimes \theta ^1. \end{aligned}$$
(35)

Using the expression of the connection matrix in the first structure equation, we have,

$$\begin{aligned} \lambda \wedge \theta ^1=0. \end{aligned}$$
(36)

Applying Cartan’s lemma to the above equation leads to,

$$\begin{aligned} \lambda =a\theta ^1 \end{aligned}$$
(37)

for some real valued function a which may be dependent on both x and y. The other two relationships in the first structure equation become trivial for the assumed deformation and connection one forms. Using the above relationship in II, we arrive at,

$$\begin{aligned} II=a\theta ^1\otimes \theta ^1. \end{aligned}$$
(38)

Now the problem is to determine a from the second structure equation, mechanical equilibrium and boundary conditions. Using (34) in the second structure equation leads to,

$$\begin{aligned} \text{ d }\lambda =0. \end{aligned}$$

The above condition means that \(\lambda\) is a close one-form. From Poincaré’s lemma, we know that every closed form is exact, which means that there exists a real valued function \(\beta\) such that \(\lambda =\text{ d }\beta\). This real valued function can be interpreted as the angle by which the tangent vectors rotate during the deformation process. Now computing the exterior derivative of (37), we arrive at,

$$\begin{aligned} \text{ d }a\wedge \theta ^{1}+a\text{ dd }\theta ^1=0. \end{aligned}$$
(39)

From (33), we see that \(\text{ dd }\theta ^1=0\); using this result in the above equation leads to,

$$\begin{aligned} \text{ d }a\wedge \theta ^{1}=0. \end{aligned}$$
(40)

Now using the definition of the differential of a real valued function, we compute \(\text{ d }a=\frac{\partial a}{\partial x}\text{ d }x+\frac{\partial a}{\partial y}\text{ d }y\). Using it in the above equation, we have

$$\begin{aligned} \left( \frac{\partial a}{\partial x}\text{ d }x+\frac{\partial a}{\partial y}\text{ d }y\right) \wedge \text{ d }x=0. \end{aligned}$$
(41)

Using the properties of wedge product, we arrive at,

$$\begin{aligned} \frac{\partial a}{\partial y} \text{ d }y\wedge \text{ d }x=0. \end{aligned}$$
(42)

\(\text{ d }x \wedge \text{ d }y\) is the volume-form associated with the deformation which can never be zero, using which we conclude that

$$\begin{aligned} \frac{\partial a}{\partial y} =0. \end{aligned}$$
(43)

The above conclusion implies that a cannot vary along the y coordinate, i.e. \(a\) is a function only of the x coordinate. We now proceed to use mechanical equilibrium to arrive at the functional form of a. The mean curvature associated with the deformation can be computed as,

$$\begin{aligned} H=\frac{a}{2}. \end{aligned}$$
(44)

The bending moment tensor for II given in (35) leads to,

$$\begin{aligned} M=C_1a(\theta ^1\otimes \theta ^1) \end{aligned}$$
(45)

which yields \(m^1=C_1a\theta ^1\) and \(m^2=0\). The moment equilibrium equations and the definition of the covariant derivative then lead to,

$$\begin{aligned} \text{ d }a(E_1)\theta ^1=0 \implies \frac{\partial a}{\partial x} \theta ^1=0. \end{aligned}$$
(46)

From the above equation, we conclude that,

$$\begin{aligned} \frac{\partial a}{\partial x}=0. \end{aligned}$$
(47)

Combining (47) and (43), we conclude that a is a constant within the domain. By applying the boundary condition that \(m^1(e_1)=m\) at the free end, we have,

$$\begin{aligned} a=\frac{m}{C_1}. \end{aligned}$$
(48)

In the above equation, m is the moment applied at the free end. If we assume \(\nu =0\), we have \(C_1=\frac{Eh^3}{12}\). The relationship between the moment applied at the free-end and a may thus be written as \(m=\frac{12a}{Eh^3}\). Having computed the one-form \(\lambda\), we now proceed to compute the frame and position vector of the deformed configuration. These quantities are computed by integrating (4) and (8) along prescribed curves in the reference configuration. Let \(\Gamma (s)\), \(s\in [s_1,s_2]\subset \mathbb {R}\) be a curve in the reference configuration. The tangent vector to this curve is denoted by v. The frame of the deformed configuration may be computed using the following integral,

$$\begin{aligned} e_i(\Gamma (s))&=\int _{s_1}^{s}\text{ d }e_i(v)\nonumber \\&=\int _{s_1}^{s}e_j\omega ^j_i(v) \text{ d }s. \end{aligned}$$
(49)

To completely resolve the above integral, one must provide a condition on the frame at \(\Gamma (s_1)\), which is known from the fixed end of the cantilever strip. The frame at the fixed end is assumed to be \(\{e_x,e_y,e_z\}\) for all deformations. Similarly, to compute the position vector of a material point in the deformed configuration, we use the following integral,

$$\begin{aligned} p(\Gamma (s))-p(s_1)&=\int _{s_1}^{s}\text{ d }p(v)\nonumber \\&=\int _{s_1}^{s}e_1\theta ^1(v)+e_2\theta ^2(v) \text{ d }s. \end{aligned}$$
(50)

In the above equation, \(e_i\)’s are the values of the frame fields computed from the previous equation. If \(p(\Gamma (s_1))\) is known, then the above integral can be used to compute the position vector of any material point in the deformed configuration. (49) and (50) may be considered as the solution of a certain ordinary differential equation with initial conditions for the frame and position vector known from the fixed end of the cantilever strip. Now considering \(\Gamma\) to be straight lines along the x direction, the frame fields are computed as,

$$\begin{aligned} e_1&=\cos (ax)e_x-\sin (ax)e_z;\\ e_2&=e_y;\\ e_3&=\sin (ax)e_x+\cos (ax)e_z. \end{aligned}$$

Use of the above equation for the frame fields in (50) leads to the following expression for the position vector of the deformed configuration,

$$\begin{aligned} p=p_0+\frac{1}{a}(\sin (ax)e_x+(1-\cos (ax))e_z). \end{aligned}$$
(51)

In the last equation, \(p_0\) corresponds to points on the fixed boundary of the elastic strip which is of the form (0, y, 0) with \(y \in (0,w)\); w is the width of the strip. A plot of the deformed configuration for different values of a is given in Fig. 3. Using numerical simulations, Simo et al. [14], reported that a thin strip of length L bends to a full circle for a moment per unit width of \(m=\frac{24 \pi }{EL h^3}\) . Our current solution also predicts a circle for the same end moment per unit width.

Fig. 3
figure 3

Deformation of the elastic strip for different values bending moment per unit width. The frame fields are superimposed on the deformed configuration; the tangent vectors are represented by red and blue arrows, while the yellow vectors represent the unit normal. The triangulation on the deformed configuration is only a visual aid’; it has nothing to do with the solution procedure

Full size image

5 Conclusion

The structure equations for a surface were known for a long time; however, these equations were never used to solve boundary value problems to determine the deformation of thin shells. This article demonstrates the use of structure equations in solving simple boundary value problems. The key principle behind the entire discussion is to treat deformation and geometry of the surface as two separate entities given by a family of one-forms. Structure equations are then used to establish the compatibility between these one-forms. From such a perspective, we find that a Kirchhoff type shell has a non-classical aspect which, untraceable in classical continuum models, shares the salient features of defect mechanics. It is also found that topological defects like dislocations and disclinations may be brought into the formulation (2D and 3D) by adding appropriate source terms to the structure equations—an aspect we wish to deal with in a future study.