1 Introduction

1.1 Magnetic shape memory alloys

The interest of Magnetic Shape Memory Alloys (MSMAs) compared with the classical Shape Memory Alloys (SMAs) is their possible activation not only by stress and temperature actions but also by magnetic field. A model of rearrangement process of martensite platelets in a non-stoichiometric \(\hbox{Ni}_2\)MnGa MSMA single crystal under magnetic field and (or) stress actions has been recently proposed by the same authors in Gauthier et al. [17]. The aim of this following paper is to extend these works purpose to the anisothermal behavior when including the process of martensite reorientation platelets and phase transformation between austenite and martensite.

Presently, only single crystals show significant active properties but the single crystal manufacturing requires expensive costs and applicability problems for micro-systems devices or layer deposits. It is why so few practical applications appear all over the world. Nevertheless many researches are conducted on MSMA polycrystals. If they are conclusive, it will give more opportunities for real and practical applications based on MSMA. The model proposed in this paper is based on the Thermodynamics of Irreversible Processes (TIP) and an efficient internal variables choice in order to suggest a thermodynamical potential. In the first part of this paper, we will propose a general expression for the Gibbs free energy. This will be completed in a natural way with the Clausius-Duhem inequality and kinetics equations for the phase transformation and for the martensite platelets rearrangement. A particular attention will be paid to the prediction of the microstructure between the martensite variants (Mi,Mj) themselves and with the austenite mother phase A. The heat equation completes the magneto-thermo-mechanical model. In the final part, a comparison between experimental results and model predictions is done.

1.2 Modeling

Firstly, MSMA present the same properties as classical shape memory alloys but with the addition of a magnetic field sensibility. Several models are then devoted to the variant reorientation process. Some relatively old models are based on simple energy function [41, 42], energy minimization [14, 49, 50] or using a magnetic stress to disconnect mechanical and magnetic behaviours [32, 37, 48]. One of the first thermodynamic approach was built in OHandley [43], O’Handley et al. [44], Murray et al. [40] and the addition of internal variables in the thermodynamics of irreversible processes was proposed in Hirsinger [27], Hirsinger et al. [29], Creton and Hirsinger [13], Kiefer and Lagoudas [33], Kiefer et al. [34]

We can denote that other original approaches were studied using Preisach modeling [1], magneto-plasticity [38, 39], statistical [7, 21] and macroscopic with a constitutive equation [11].

Moreover, the stress-strain loops on single crystals showing the pseudoelasticity (austenite to one martensite variant), pseudoplasticity (i.e. reorientation of martensite platelets) have been studied intensively [9, 10, 30, 31, 47].

Very recently, [52, 53] gives in the frame of the thermodynamics of irreversible processes a model based on a micro-macro investigation. The thermomechanical model follows the Eshelby classical method where the single variant of martensite is considered as the inclusion in the mother austenitic phase. The thermodynamical driving force expression derived from the Gibbs free energy function permits to establish the kinetic equation. These authors model experimental curves of strain versus magnetic field under constant tensile and compressive loads due to Gans et al. [15].

A very interesting experimental study concerning the shape memory and martensitic deformation response of \(\hbox{Ni}_2\)MnGa single crystals is performed by Callaway et al. [8]. They establish the magnitude of detwinning stress levels on non-modulated martensite in \(\hbox{Ni}_{53} \hbox{Mn}_{25} \hbox{Ga}_{22}\) as a function of heat treatments and study the shape memory strains from constant load temperature cycling experiments for aged and unaged specimens. They underline a remarkable narrowing of the thermal hysteresis with increasing applied stress and a considerable two-way shape memory effect.

At last, [2] perform three-dimensional simulations of the microstructure and mechanical response of shape memory alloys undergoing cubic to tetragonal transitions (which is the case of Ni-Mn-Ga). They investigate how the stress-strain behavior changes as a function of strain rate.

Few papers relate the global modeling of MSMA including temperature, stress and magnetic field effects in the same formalism. The thermodynamical approach proposed in this paper is a relevant way to model the complex behaviour of MSMA in a global and macroscopic form.

2 Gibbs free energy expression associated with a magneto-thermo-mechanical loading

The Gibbs free energy G expression can be split into four parts: the chemical one G chem (generally associated with the latent heat of the phase transformation), the thermal one G therm (associated with the heat capacity), the mechanical one G mech and the magnetic one G mag .

$$ \begin{aligned} G(\underline{\Upsigma}, T, {\bf H}, z_o, z_1, \ldots, z_n, \alpha, \theta, \alpha_A ) &= G_{chem} (T,z_o) + G_{therm} (T)\\ & \quad+ G_{mech} (\underline{\Upsigma}, z_o, z_1, \ldots , z_n ) + G_{mag} ({\bf H}, z_o, \ldots , z_n, \alpha, \theta, \alpha_A) \end{aligned} $$
(1)

where the state variables are:

  • \(\underline{\Upsigma}\) the applied stress tensor,

  • H the magnetic field,

  • T the temperature, considered as homogeneous in the sample.

The internal variables are:

  • z o the austenite volume fraction,

  • z k the volume fraction of martensite variant Mk (\(k = 1 \ldots n\), i.e. the martensite presents n different variants),

  • α the Weiss domain proportion inside a martensite variant (see Fig. 1, [28]),

  • α A the Weiss domain proportion inside the austenite phase A,

  • θ the rotation angle of the magnetization vector M under the magnetic field H. Creton [12], Hirsinger et al. [29].

Fig. 1
figure 1

Representative elementary volume (REV) when the sample is composed by only two martensite variants M 1 and M 2 (z = z 1 and 1 − z = z 2) [28]

Full size image

The coupling between mechanic and magnetism is made by the choice of internal variables, for instance z i , and not by the addition of an interaction term G mech-mag in the free energy.

Let us examine the four terms of the Gibbs free energy expression.

2.1 Chemical energy expression

Under the natural hypothesis that all the chemical energies of the different martensite variants are the same, the chemical energy can be expressed as:

$$ \begin{aligned} \rho G_{chem} (T,z_o) &= z_o(u_{o}^{A}-Ts_{o}^{A}) + (1-z_o)(u_{o}^{M}-Ts_{o}^{M})\\ &= u_{o}^{M}-Ts_{o}^{M} + z_o \pi^{f}_{o}(T) \end{aligned} $$
(2)

with \(\pi^{f}_{o}(T) = \Updelta U - T \Updelta S, \Updelta U = u_{o}^{A} - u_{o}^{M}, \Updelta S= s_{o}^{A} - s_{o}^{M}\). \(u_{o}^{A}, u_{o}^{M}, s_{o}^{A}\) and s M o are respectively the internal energy of austenite, the internal energy of martensite, the entropy of austenite and entropy of martensite. ρ is the material density parameter.

2.2 Thermal energy expression

The expression of the thermal energy is chosen as:

$$ \rho G_{therm} = C_p \left[ {(T - T_o ) - T \cdot \ln\left( {{\frac{T}{{T_o }}}} \right)} \right] $$
(3)

This expression guarantees that the specific heat C p agrees with:

$$ C_p = - T {{\frac{{d^2 G_{therm}}}{{dT^2 }}}} $$
(4)

2.3 Mechanical energy general formulation

In this subsection, the mechanical energy of a (n + 1) phases system (one austenite, n martensite variants) is described. The key point of the chosen expression is how to describe the interactions ϕ it between the austenite and each variant of martensite and also the interaction between variants themselves. In a recent paper [45] Patoor et al. give a list of different interaction expressions of the literature.

For instance [51] choose:

$$ \phi _{it} (z_o, \ldots , z_n ) = Az_o (1 - z_o ) + {\frac{1} {2}}\mathop \Upsigma \limits_{k = 1}^n \mathop \Upsigma \limits_{\substack{\ell = 1 \ell \ne k}} ^n K_{k\ell } z_k z_\ell $$
(5)

and:

$$ \rho G_{mech} (\underline{\Upsigma}, z_o, z_1, \ldots, z_n) = - \underline{\Upsigma} :\left( {\mathop \Upsigma \limits_{k = 0}^n z_k \underline{E}_k } \right) -{\frac{1}{2}}\underline{\Upsigma} :\underline{\underline{S}} :\underline{\Upsigma} + \phi _{it} (z_o, \ldots , z_n ) $$
(6)

The elasticity compliance tensor \(\underline{\underline{S}}\) is chosen independent of the phase state. A and K kℓ are material interaction parameters. The Green Lagrange strain tensors E k will be defined in the next subsection through a study of the crystallography of the material.

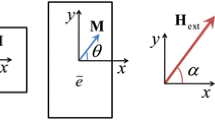
In the following, this paper considers the fact that a magnetic field H is applied in the x direction and a compressive stress is applied in the y direction (Fig. 2). The model works for other axis choice and also the orthogonality between stress and magnetization are not necessary conditions.

Fig. 2
figure 2

The MSM sample is subject to a compressive stress in the y direction and to a magnetic field in the x direction

Full size image

2.4 Crystallography of the Ni-Mn-Ga

The mother phase called austenite (A) exhibits a centered cubic structure called \(L_{2_1}\) (the lattice parameter a o is chosen equal to 5.82 Å). Depending on its composition, or stress level, the alloy can exhibit three different martensite phases:

  • the modulated five-layered martensite structure (Quadratic or tetragonal 5M),

  • the modulated seven-layered martensite structure (Monoclinic 7M),

  • the non-modulated quadratic phase (NMT)

The present paper is devoted to the most common Ni-Mn-Ga martensite e.g. 5M.

The austenite → martensite 5M phase transformation is a transformation of a cubic lattice A into a tetragonal lattice (M). The kinematics of this transformation is completely described by the second order tensor \(\underline{U}_i\), which is called the transformation stretch. In our case, there is three possible martensite variants (cf. Fig. 3). The three tensors are also given by:

$$ \underline{U}_1 = diag(\beta_c, \beta_a, \beta_a) \hbox {,} \,\underline{U}_2 = diag(\beta_a, \beta_c, \beta_a) \hbox {,} \,\underline{U}_3 = diag(\beta_a, \beta_a, \beta_c) $$
(7)

with \(\beta_a={\frac{a}{a_o}}, \beta_c={\frac{c}{a_o}}\). a o is the lattice parameter of cubic structure A, a and c are the lattice parameters of tetragonal structure M.

Fig. 3
figure 3

The three variants of martensite in a cubic to tetragonal transformation [5]

Full size image

By studying the nature of the interface between A and M, it can be proved that an exact interface between the parent phase A and a single variant of martensite Mi exists if and only if \(\underline{U} _i\) presents an eigenvalue λ2 = 1 with \(\lambda_3 \geq \lambda_2 \geq \lambda_1\) (cf. crystallographical theory of martensite—CTM—[4, 5, 23]). It is not the case for Ni-Mn-Ga alloys. For example, the alloy I (cf. [26]) presents lattice parameters a = 5.95 Å and c = 5.60 Å and so \(\lambda_2=\lambda_3=\beta_a=1.0188\) and \(\lambda_1=\beta_c=0.9589\).

Hence the alloy exhibits an austenite—twinned martensite microstructure represented on Fig. 4 [36]. It consists of two adjacent regions: in the first one, the austenite phase is present, the other one contains parallel bands of alternating layers of two martensite variants. According to Ball and James [3, 4] with the martensite variant pair (i, j), the compatibility equations are:

  • the twinning equation between the martensites i and j itself:

    $$ \underline{R}_{ij} \underline{U}_i - \underline{U}_j = {\bf a} \otimes {\bf n} $$
    (8)

  • the austenite/martensite interface equation:

    $$ \underline{R}_{ij} (\lambda \underline{R}_{ij} \underline{U}_i + (1-\lambda) \underline{U}_j) - \underline{1} = {\bf b} \otimes {\bf m} $$
    (9)
Fig. 4
figure 4

Austenite—twinned martensite microstructure [36]

Full size image

2.4.1 Determination of the solutions of the twinning equation for the variant pair (1,2)

The aim is to find the values a i and n i , solutions of the twinning Eq. (8). In a twodimensional case, there is only two couples of solutions (\(a_1, n_1\)) and (\(a_2, n_2\)). The algorithm to find the solutions is given in the paper of Hane [23] and also pp. 69–70 of the book of Bhattacharya [5]:

$$ {\bf a}_1={\frac{\sqrt{2}(\beta_a^2-\beta_c^2)}{\beta_a^2+\beta_c^2}} \left( \begin{array}{l} \beta_c\\ -\beta_a \\ 0 \\ \end{array} \right), \quad {\bf n}_1={\frac{1}{\sqrt{2}}} \left( \begin{array}{l} 1\\ 1 \\ 0 \\ \end{array} \right) $$
(10)

or

$$ {\bf a}_2={\frac{\sqrt{2}(\beta_a^2-\beta_c^2)}{\beta_a^2+\beta_c^2}} \left( \begin{array}{l} \beta_c\\ \beta_a \\ 0 \\ \end{array} \right), \quad {\bf n}_2={\frac{1}{\sqrt{2}}} \left( \begin{array}{l} 1\\ -1 \\ 0\\ \end{array} \right) $$
(11)

and also for (2,3) and (3,1)

2.4.2 Austenite-martensite interface

Given a matrix \(\underline{U}_i\) (i = 1 or 2) and vectors a, n that satisfy the twinning equation, we obtain a solution for the austenite-martensite interface equation using the following procedure.

$$ \begin{aligned} \delta &= {\bf a}_1 \underline{U}_1(\underline{U}_1^2-\underline{1})^{-1} {\bf n}_1\\ \eta &= tr(\underline{U}_{1}^2)-det(\underline{U}_{1}^2) - 2 + {\frac{||{\bf a}_1||^2}{2\delta}} \end{aligned} $$
(12)

The austenite-martensite interface equation has a solution if and only if:

$$ \delta \leq 2 \,\, \hbox{and},\,\, \eta \geq 0 $$
(13)
$$ \lambda = {\frac{1}{2}}\left(1-\sqrt{1+{\frac{2}{\delta}}}\right) $$
(14)
$$ C = (\underline{U}_{1}+\lambda {\bf n} \otimes {\bf a})(\underline{U}_{1}+\lambda {\bf a} \otimes {\bf n}) $$
(15)

\({\bf e}_1, {\bf e}_2, {\bf e}_3\) are the eigenvectors of C corresponding to the eigenvalues \(\lambda'_1 \leq \lambda'_2 \leq \lambda'_3\). Automatically, \(\lambda'_2=1\).

Therefore,

$$ \begin{aligned} {\bf b} &= {\frac{\sqrt{\lambda'_3}-\sqrt{\lambda'_1}}{\sqrt{\lambda'_3-\lambda'_3}}} \left( \sqrt{\lambda'_3(1-\lambda'_1)} {\bf e}_1 + k \sqrt{\lambda'_1(\lambda'_3-1)} {\bf e}_3 \right)\\ {\bf m} &= {\frac{1}{\sqrt{\lambda'_3-\lambda'_1}}} \left( -\sqrt{1-\lambda'_1} {\bf e}_1 + \sqrt{\lambda'_3-1} {\bf e}_3 \right) \end{aligned} $$
(16)

with k =  ±1, and evidently ||m|| = 1.

Moreover, Bhattacharya in [5] concludes that it is possible to form an austenite-martensite interface if and only if:

$$ \beta_c<1<\beta_a \qquad\beta_a^2+\beta_c^2 \leq 2 $$
(17)

The Ni-Mn-Ga alloy I fulfills these conditions. λ parameter can be calculated as:

$$ \lambda={\frac{1}{2}}\left(1 -\sqrt{1+{\frac{2(\beta_a^2-1)(\beta_c^2-1)(\beta_a^2+\beta_c^2)}{(\beta_c^2-\beta_a^2)^2}}} \right) $$
(18)

This formula constitutes an application (CC → tetragonal) of the general formula (14) and delivers λ = 0.3083 for the alloy I. In the paper, we will consider this alloy for numerical applications.

One must distinguish the strain tensors \(\underline{E}^{dtw}\) associated with the detwinning (M1 → M2 for example) to the strain tensor \(\underline{E}^{tr}\) associated with the phase transformation (A → (M1, M2)).

  • M1 → M2, in the non-linear kinematic theory:

    $$ \underline{E}^{dtw} = {\frac{1}{2}}(\underline{U}_2^2-\underline{U}_{1}^2) = diag( 0.0593, -0.0593, 0) $$
    (19)

  • A → (M1,M2), in the non-linear kinematic theory:

    $$ \begin{aligned} \underline{E}^{tr} &= {\frac{1}{2}}(\underline{U}_{tw}^2-\underline{1})\\ \hbox{with} \,\, \underline{U}_{tw} &= \lambda \underline{U}_2 + (1-\lambda)\\ \underline{U}_1 \hbox {so } \underline{E}^{tr} &=diag(-0.0224, 0.0004, 0.0190) \end{aligned} $$
    (20)

    Moreover, one can verify that the results are nearly the same for the kinematic non linear theory and the linear one (small deformation hypothesis).

2.5 Mechanical energy expression for a particular case

As said before, a compressive stress (σ < 0) is applied in the y direction, corresponding to the short axis of variant M2 (cf. Fig. 2, 5).

Fig. 5
figure 5

Different vector representation and 3D schematic view of austenite/twinned martensite interface

Full size image

The stress tensor can be written as:

$$ \underline{\Upsigma} = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & {\sigma} & 0 \\ 0 & 0 & 0 \\ \end{array} \right) $$
(21)

In this simple case, Eq. (6) of the mechanical energy expression is reduced to:

$$ \begin{aligned} \rho G_{mech}(\sigma ,z_o, z_1, z_2, z_3) &= - {\frac{\sigma}{2}} \left( (z_1+z_3) \left(\beta_a^2-1\right) + z_2 \left(\beta_c^2-1\right) \right)\\ &\quad- {\frac{1}{2}}{\frac{{\sigma^{2}}}{E}} +A z_o(1-z_o)+ K(z_1 z_2+z_1 z_3+z_2 z_3) \end{aligned} $$
(22)

with the following assumption:

$$ K_{12}=K_{21}=K_{13}=K_{31}=K_{23}=K_{32}=K $$
(23)

Moreover, we have to consider that:

$$ \mathop{\Upsigma} \limits_{k=0}^3 z_k = 1 $$
(24)

It means that there is only three z i as independent variables.

2.6 Magnetic energy expression

Remember that the magnetic field H is applied in the x direction. It means that:

$$ {\bf H}=H {\bf x} $$
(25)

In Gauthier et al. [18], the magnetic contribution to the Gibbs free energy was chosen as:

$$ \rho G_{mag}(H)=-\int\limits_0^{H} \mu_0 m.dH $$
(26)

where m is the magnetization of the sample in the x direction. Let \(m_1, m_2\) and m 3 be the magnetizations of the three martensite variants \(M_1, M_2\) and M 3 and m o be the magnetization of the austenite.

2.6.1 Magnetization of the martensite: easy magnetization direction

$$ m_1(H)=m_s(2\alpha(H)-1) $$
(27)

where m s is the saturation magnetization, and \(\alpha(H) \in [0,1]\) represents the proportion of Weiss domain inside the variant. The function α(H) is chosen as linear:

$$ 2\alpha(H)-1={\frac{\chi_a H}{m_s}} $$
(28)

2.6.2 Magnetization of the martensite: hard magnetization direction

$$ m_2(H)=m_3(H)=m_s \sin(\theta(H)) $$
(29)

where \(\theta(H) \in \left[-{\frac{\pi}{2}},{\frac{\pi}{2}}\right]\) represents the rotation angle of the magnetization vector. The function \(\sin(\theta(H))\) is also chosen as linear:

$$ \sin(\theta(H))={\frac{\chi_t H}{m_s}} $$
(30)

2.6.3 Magnetization of the austenite

The austenite is ferromagnetic. We consider in the present paper a temperature below the Curie temperature of the material. Its behavior is considered like the M 1 martensite variant:

$$ m_o(H)=m_s(2\alpha_A(H)-1) $$
(31)

where \(\alpha_A(H) \in [0,1]\) represents the proportion of Weiss domain inside the austenite variant. The function α A (H) is chosen linear:

$$ 2\alpha_A(H)-1={\frac{\chi_A H}{m_s}} $$
(32)

2.6.4 Global magnetic material behavior

A mixing rule is stated for the global magnetic material behavior:

$$ \begin{aligned} m(H) &= \mathop{\Upsigma} \limits_{k=0}^3 z_k m_k(H)\\ &= m_s \left[ z_o (2\alpha_A(H)-1) + z_1 (2\alpha(H)-1) + \,(z_2+z_3) (\sin(\theta(H))) \right] \end{aligned} $$
(33)

By using the Eq. (26), and by extending the integration of different parts of m.dH as it was done in the paper of Gauthier et al. [18], the following expression can be established:

$$ \begin{aligned} \rho G_{mag}(H,z_0,z_1,z_2,z_3,\alpha,\theta,\alpha_A) &= -\mu_0 m_S \left[ z_1 \left( (2\alpha-1)H -{\frac{m_S}{2\chi_a}}(2\alpha-1)^2 \right)\right.\\ &\quad +(z_2+z_3) \left( \sin(\theta) H-{\frac{m_S}{2\chi_t}} (\sin(\theta))^2 \right)\\ &\quad \left.+\, z_0\left( (2\alpha_A-1)H-{\frac{m_S}{2\chi_A}}(2\alpha_A-1)^2 \right) \right] \end{aligned} $$
(34)

Observation of experimental curves delivers that m s is not constant but function of the temperature. For ferromagnetism, the Weiss theory describes the m s temperature dependence by the following Eq. [54]:

$$ {\frac{m_s(T)}{m_o}}=\tanh \left[ {\frac{T_c m_s(T)}{m_o T}} \right] $$
(35)

where T c is the Curie temperature and m o the magnetization at 0 K. In order to simplify the model, the m o and T c values are kept the same for martensite and austenite phases.

2.7 Gibbs free energy expression

For a Ni-Mn-Ga single crystal presenting three variants of martensite and a mother phase, under thermal, magnetic loading and mechanical one, the Gibbs free energy expression can be:

$$ \begin{aligned} \rho G(H,\sigma,T,z_0,z_1,z_2,z_3,\alpha,\theta,\alpha_A) &= u_o^M-Ts_o^M + z_o (\Updelta U - T \Updelta S)\\ &\quad+C_p \left[ {(T - T_o ) - T \cdot \ln\left( {{\frac{T}{{T_o }}}}\right)} \right]\\ &\quad- {\frac{\sigma}{2}} \left( (z_1+z_3) \left(\beta_a^2-1\right) + z_2 \left(\beta_c^2-1\right) \right)\\ &\quad- {\frac{1}{2}}{\frac{{\sigma ^2 }}{E}} +A z_o(1-z_o)+ K(z_1 z_2+z_1 z_3+z_2 z_3)\\ &\quad-\mu_0 m_s(T) \left[ z_1 \left( (2\alpha-1)H -{\frac{m_s(T)}{2\chi_a}}(2\alpha-1)^2 \right)\right.\\ &\quad +(z_2+z_3) \left( \sin(\theta) H-{\frac{m_s(T)}{2\chi_t}} (\sin(\theta))^2 \right)\\ &\left. \quad +\, z_0\left( (2\alpha_A-1)H-{\frac{m_s(T)}{2\chi_A}}(2\alpha_A-1)^2 \right) \right] \end{aligned} $$
(36)

with \(\sum_{k = 0}^3 z_k=1\)

This expression is quite complicated but will be declined in some specific situations (pure magnetism loading, pure mechanical loading, pure thermal loading,\(\ldots\)) and a numerical resolution is achieved.

3 Clausius-Duhem inequality

3.1 Thermodynamical forces

In the classical frame of Thermodynamics of Irreversible Process, the total strain in y direction, the magnetization in x direction, and the entropy can be written as:

$$ \begin{aligned} \bullet\,\,\varepsilon \,&= \,-{\frac{{\partial \rho G}}{{\partial \sigma }}}= {\frac{\sigma}{E}}+{\frac{1}{2}} \left[ (z_1+z_3) \left(\beta_a^2-1\right) + z_2 \left(\beta_c^2-1\right) \right]\\ \bullet\,\, \mu_o m \,&=\,-{\frac{{\partial \rho G}}{{\partial H}}}= \mu_o m_s(T) \left[ z_o (2\alpha_A(H)-1) + z_1 (2\alpha(H)-1)+ (z_2+z_3) (\sin(\theta(H))) \right]\\ \bullet\,\, \rho s\,&=\,-{\frac{{\partial \rho G}}{{\partial T}}}=s_o^M + z_o \Updelta S + C_p \ln\left( {{\frac{T}{{T_o }}}}\right)\\ &\quad+\mu_0 {\frac{dm_s}{dT}} H \left[ z_1 (2\alpha-1) +(z_2+z_3)\sin(\theta) + z_0(2\alpha_A-1) \right]\\ &\quad- 2 \mu_0 m_s(T) {\frac{dm_s}{dT}} \left[z_1 {\frac{(2\alpha-1)^2}{2\chi_a}} +(z_2+z_3){\frac{\sin^2(\theta)}{2\chi_t}} + z_0{\frac{(2\alpha_A-1)^2}{2\chi_A}}\right] \end{aligned} $$
(37)

A magneto-thermal effect takes place in the entropy expression due to the temperature dependence of m s . This effect will be neglected in the present paper.

The thermodynamical forces associated with the progression of the Weiss domains widths α, α A and rotation angle θ are:

$$ {\frac{{\partial \rho G}}{{\partial \alpha_A }}}=0\; {\frac{{\partial \rho G}}{{\partial \alpha }}}=0\; {\frac{{\partial \rho G}}{{\partial \theta }}}=0 $$
(38)

The choice of the free energy expression confirms that the pure magnetic behavior is considered as reversible. Actually, the magnetization curves of the two martensite variants have no hysteresis on the Fig. 6 taken from Heczko [24].

Fig. 6
figure 6

Magnetization curves measured in easy (free sample) and hard (sample constrained by stress) magnetization directions [24]

Full size image

Finally, the thermodynamical forces associated with the z i martensite and austenite fractions are:

$$ \begin{aligned} \bullet\,\, \pi^{f}_{o}&=-{\frac{{\partial \rho G}}{{\partial z_o}}}=-\Updelta U + T \Updelta S - A (1-2z_o) +\mu_0 m_s(T) \left[\left( (2\alpha_A-1)H-{\frac{m_s(T)}{2\chi_A}}(2\alpha_A-1)^2 \right) \right]\\ \bullet\,\, \pi^{f}_{1}&=-{\frac{{\partial \rho G}}{{\partial z_1}}}={\frac{\sigma}{2}} \left( \beta_a^2-1 \right)- K(z_2+z_3) +\mu_0 m_s(T)\left( (2\alpha-1)H -{\frac{m_s(T)}{2\chi_a}}(2\alpha-1)^2 \right)\\ \bullet\,\, \pi^{f}_{2}&=-{\frac{{\partial \rho G}}{{\partial z_2}}}={\frac{\sigma}{2}} \left( \beta_c^2-1 \right)- K(z_1+z_3) +\mu_0 m_s(T) \left( \sin(\theta) H-{\frac{m_s(T)}{2\chi_t}} (\sin(\theta))^2 \right)\\ \bullet\,\,\pi^{f}_{3}&=-{\frac{{\partial \rho G}}{{\partial z_3}}}={\frac{\sigma}{2}} \left( \beta_a^2-1 \right)- K(z_1+z_2) +\mu_0 m_s(T) \left( \sin(\theta) H-{\frac{m_s(T)}{2\chi_t}} (\sin(\theta))^2 \right)\\ \end{aligned} $$
(39)

The mechanical behavior is highly irreversible, hence the Clausius-Duhem inequality has to be written:

$$ dD=-\rho dG-\mu_o m dH -\varepsilon d \sigma - s dT \geq 0 $$
(40)

where dD is the dissipation increment. This expression can be reduced to:

$$ dD=\pi^f_odz_o+\pi^f_1dz_1+\pi^f_2dz_2+\pi^f_3dz_3 \geq 0 $$
(41)

with \(\sum_{k = 0}^3 dz_k=0\)

3.2 Kinetic equations

The physical origin of the choice of the kinetic equations for phase transformation comes from the observations of the advance of a new phase in the mother phase by metallurgists such [35].

3.2.1 Example with two variants

In the previous inequality, three of the four variables are independent and the evolution depends on the configuration of the forces. For example, if the sample contains only two variants (\(z_o=z_3=0\)) during the evolution at constant temperature, then \(z=z_1=1-z_2\) and the Clausius-Duhem inequality becomes:

$$ \begin{aligned} dD&=\pi^f_1dz_1+\pi^f_2dz_2 \geq 0\\ dD&=(\pi^f_1-\pi^f_2)dz_1 \geq 0 \end{aligned} $$
(42)

An external loop, e.g. a complete rearrangement from z = 0 to z = 1 (path a) and from z = 1 to z = 0 (path b), is reported on Fig. 7. Rearrangement begins when \((\pi^f_1-\pi^f_2) \geq \pi_{cr}(T)\) for the path a and when \((\pi^f_1-\pi^f_2) \leq -\pi_{cr}(T)\) for the path b. After the rearrangement start, the behavior is modeled according to the following kinetic equations:

$$ \dot{\pi}^{f}_{1}-\dot{\pi}^{f}_{2} = \lambda \dot{z} \,\,\hbox{with:} \,\, \dot{z} = \dot{z}_1 = -\dot{z}_2 $$
(43)

λ is considered as a constant value in the present paper. But, in Gauthier et al. [18], the value of λ was considered depending on the previous strain history. The concept of memorized point was introduced and a difference appears between partial loops and major loops.

Moreover, π cr (T) is a function of the temperature as it was shown in Brinson [6] for classical SMA martensite reorientation and in Heczko and Straka [25] for MSMA. A linear dependence is used in this paper:

$$ \pi_{cr}(T)=\pi_{cr}^o+k_{cr}(A_S^o-T) $$
(44)
Fig. 7
figure 7

Thermodynamical force \([\pi^f_1-\pi^f_2](\sigma, \alpha, \theta)\) as a function of the M 1 martensite fraction \(z \in [0,1]\)

Full size image

3.2.2 Generalization to three variants and one austenitic phase

This concept of critical force π cr (T) and kinetic equation is generalized for three martensite variants and one austenite phase. The Fig. 8 represents the composition of a MSMA sample and the associated kinetics. c ij represents the transformation rate from M i into M j and the following relations are verified:

$$ \begin{aligned} \dot{z}_o &=c_{10}+c_{20}+c_{30}-c_{01}-c_{02}-c_{03}\\ \dot{z}_1 &=c_{01}+c_{21}+c_{31}-c_{10}-c_{12}-c_{13}\\ \dot{z}_2 &=c_{02}+c_{12}+c_{32}-c_{20}-c_{21}-c_{23}\\ \dot{z}_3 &=c_{03}+c_{13}+c_{23}-c_{30}-c_{31}-c_{32} \end{aligned} $$
(45)

c ij is defined by:

$$ \begin{aligned} c_{ij} &= 0 \quad\hbox{if}\,\,\pi^{f}_{j}-\pi^{f}_{i} < \pi_{cr}(T) \,\hbox{or}\, z_i=0\\ c_{ij} &= {\frac{1}{\lambda}}(\dot{\pi}^{f}_{j}-\dot{\pi}^{f}_{i})\quad \hbox{else} \end{aligned} $$
(46)
Fig. 8
figure 8

Schematic representation of kinetics

Full size image

Different values of λ are taking into account: λ A for austenite-martensite transformation and λ M for martensite reorientation.

4 Heat equation

As the phase transformation (austenite → martensite) is exothermal and the reverse one (martensite → austenite) endothermal, it can be useful to write an energy balance equation (heat equation).

In a classical way, the energy conservation principle induces the following equation:

$$ \rho \dot{u}(\varepsilon, m, s, z_o, \alpha , \theta) =-p_i+r_{ext}-div {\bf q} $$
(47)

where \(p_i= - \sigma \dot{\varepsilon}-\mu_0 H \cdot \dot{M}\) is the power of internal effort, r ext is the external heat contribution and q is the heat flux density vector.

According to the Legendre transformation:

$$ G=u-Ts-{\frac{\sigma \dot{\varepsilon}}{\rho}}-{\frac{\mu_0 H \cdot \dot{M}}{\rho}} $$
(48)

We can obtain:

$$ \rho \dot{G} = r_{ext}-div {\bf q} -\rho T\dot{s}- \rho s\dot{T} -\dot{\sigma} \cdot \varepsilon -\mu_0 \dot{H} \cdot M $$
(49)

On the other hand:

$$ \begin{aligned} \rho \dot{G} &={\frac{\partial {\rho G}}{\partial \sigma}} \dot{\sigma} + {\frac{\partial {\rho G}}{\partial H}} \dot{H} + {\frac{\partial {\rho G}}{\partial T}} \dot{T} + \sum_{i=0}^3 {\frac{\partial {\rho G}}{\partial z_i}} \dot{z}_i \\ &= -\varepsilon \dot{\sigma} - \mu_0 M \dot{H} -\rho s \dot{T}-\sum_{i=0}^3\pi^{f}_i \dot{z}_i \end{aligned} $$
(50)

The combination of Eqs. (49) and (50) gives:

$$ \sum_{i=0}^3\pi^{f}_i \dot{z}_i = -r_{ext}+div {\bf q}+\rho T\dot{s} $$
(51)

5 Parameters identification

Material parameters are strongly dependent on the alloy composition. A lot of different experimental curves are available in the literature but the alloy compositions are often different. The parameters indicated in this paper are then approximated but give a good idea of their size orders. The model’s parameters identification need different specific measurements, for instance X Ray for lattice parameter, differential scanning calorimetry for phase transformation temperatures, susceptibility measurement, Curie temperature and at last mechanical tests for young modulus and hardening curve slope.

5.1 Differential scanning calorimetry

A Differential Scanning Calorimetry gives informations about heat parameters. First, C p parameter could be found but is neglected in this paper. Second, the austenite start A s , austenite finish A f , martensite start M s and martensite finish M f temperatures can be found. Finally, the area under the curve corresponds to \(-\Updelta U\) parameter. As the model shows, we have to verify that \(A_f-A_s \approx M_s-M_f\). The model parameters are given by:

$$ \begin{aligned} \Updelta S &= {\frac{2\Updelta U}{A_s+M_s}} \\ A &= {\frac{-\Updelta S(A_s-M_s)}{2}} \\ \lambda_A &=-\Updelta S (A_f-M_s) \end{aligned} $$
(52)

5.2 Crystallographic measurements

Lattice parameters a o , a and c can be obtained from X-ray measurements.

5.3 Magnetic measurements

Magnetization versus magnetic field curves at different temperatures can be used to obtain the magnetic parameters \(T_c, m_{so}, \chi_t, \chi_a\) and χ A . AC susceptibility measurements are also used in the literature.

5.4 Mechanical measurements

Different reorientation curves (at different lower temperatures than A s ) could be used to obtain \(K, \pi_{cr}(T), \lambda_M\) and E. In this paper, K is neglected. The selected parameters are summarized in the Table 1.

Table 1 Selected material parameters
Full size table

6 Model efficiency

As the present model is developed within the framework of generalized standard materials [22], the thermodynamic admissibility must be checked. Hence, the dissipation must be positive whatever the magneto-thermo-mechanical loading. A numerical simulation was done with the help of the \(\hbox{Matlab/Simulink}^{\circledR}\) software. The inputs and outputs of the simulation are presented on the Fig. 9. The power of the modeling approach presented here is that either mechanical (pseudo-elasticity and martensite reorientation), thermal, and magnetic effects can be taken into account in the same numerical simulation. Some different cases will be considered in this section. Our experimental equipment does not allow to make anisothermal tests. It is why there is only prediction for Figs. 10, 11, 12, 13, 14. Concerning tests on Figs. 15 and 16, a comparison between modelling and experimentation is done.

Fig. 9
figure 9

Inputs and outputs of numerical simulations

Full size image
Fig. 10
figure 10

Simulation results of thermal action with or without magnetic field and mechanical stress

Full size image

6.1 Thermal effects

The Fig. 10 presents the strain and the volume fractions z i when the temperature is changing. The strain is about 2 % when a magnetic field is applied and is about 4 % when a mechanical stress is applied. No strain appears when neither magnetic field nor mechanical stress are applied and the martensite volume fractions z i (i = 1, 2, 3) are equal in this case.

6.2 Mechanical effects at high temperature

The Fig. 11 presents the strain when a mechanical compressive stress is applied at high temperature (the MSMA sample is in austenite phase without mechanical stress) representing the pseudo-elasticity. A first curve without applied magnetic field and a second curve with a magnetic field of 800 kA/m are superposed. Magnetic field effect on pseudo-elasticity appears to be insignificant.

Fig. 11
figure 11

Simulation results of mechanical action at high temperature (pseudoelasticity), with T = 320 K

Full size image

6.3 Mechanical effects at low temperature

The Fig. 12 presents the strain when a mechanical compressive stress is applied at low temperature (martensite phase) representing the martensite reorientation under a constant magnetic field of 800 kA/m. Two temperatures are chosen in order to present the temperature influence in the reorientation process. Two major results are shown. First, hysteresis width decreases when the temperature increases because the reorientation critical force decreases (see (44)). Second, the center of the hysteresis curve is shifted to the top of the graph when the temperature increases because the saturation magnetization decreases (see (35)) and so the magnetic field action too.

Fig. 12
figure 12

Simulation results of mechanical action at low temperature (martensite reorientation) under a constant magnetic field H = 800 kA/m

Full size image

6.4 Temperature influence on magnetization curves

The Fig. 13 presents the magnetization value when a magnetic field is applied at different constant temperatures. The magnetic field is first applied with positive values and next with negative values. At low temperature, the sample contains the three martensite variants with equal quantities, two knees appear corresponding to the magnetization saturations of easy and hard axis. This is the classical self-accommodated martensite magnetization curve. At low temperature, no reorientation process appears, therefore there is no hysteresis on this curve. At a higher temperature value but lower than the austenite start temperature (280 K), a reorientation of martensite variants generates an hysteresis on the curve. Finally, at 320 K, the MSMA is in austenite phase and the magnetization curve corresponds to the ferromagnetic behavior chosen for the austenitic phase. Let us denote that the magnetization at high field decreases when the temperature increase.

Fig. 13
figure 13

Simulation results of magnetization under magnetic action at different temperatures

Full size image

6.5 Magnetic effects under constant mechanical load at low temperature

The Fig. 14 presents the strain when a magnetic field is applied at different compressive stress levels at low temperature. These curves are very interesting to design actuators as it was done in Gauthier et al. [18]. Because the present paper is more generally written, the inner loops are taken into account in a simpler way than in Gauthier et al. [18] but the main characteristics are modeled. The influence on the stress to the strain progress is then as follow. Without stress, a reorientation appears just in one way when the magnetic is increasing but not when it is decreasing. With a stress greater than nearly 2.5 MPa, no reorientation due magnetic field is possible. Between these two extreme cases, a partial reorientation appears in both ways.

Fig. 14
figure 14

Simulation results of strain under magnetic action at different stress levels

Full size image

6.6 Temperature influence on magnetic action under constant mechanical load

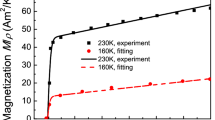
The Fig. 16 presents the strain when a magnetic field is applied with a constant stress of 1 MPa at different temperature levels. Experiments, taken from Straka and Heczko [46], corresponding to previous simulations are presented on the Fig. 15. The curves are drawn with a magnetic field applied with a negative sign then a positive one to show the maximum and minimum strains for the first cycle and for repeated cycles (useful in actuation applications).

At low temperature (T = 223 K), an increase of magnetic field generates a strain that is in part maintained when the magnetic field is canceled. At higher temperature (T = 288 K), a repeated actuation is possible and the range of strain increases with the temperature (T = 307 K). Some differences between experimental measurements and simulation results can be noticed but the shapes are in agreement : firstly, the magnetic field where reorientation begins decreases with the temperature due to the increase of critical force. Secondly, the reachable maximum strain decreases too because of the decrease of saturation magnetization.

Fig. 15
figure 15

Experimental results of strain and magnetization under magnetic action and constant stress (σ =  −1 MPa) at different temperature levels (taken from Straka and Heczko [46])

Full size image
Fig. 16
figure 16

Simulation results of strain and magnetization under magnetic action and constant stress at different temperature levels (σ =  −1 MPa)

Full size image

7 Conclusion

The purpose of this paper was to propose a full single crystal modeling of Magnetic Shape Memory alloys including the magneto-thermo-mechanical coupling. In the frame of the thermodynamics of irreversible processes, a model was proposed using a Gibbs free energy expression. As it can be seen on (36), the model is quite complicated and its use may be difficult. Nevertheless in practical applications and for specific conditions, some reductions can be made (isothermal process on 2D motions) and in such a case, the usefulness of the model is shown. For example, in the paper [19], an extension of the quasi-static isothermal model to the dynamical case was made, including the magnetic circuit creating the magnetic field and a dynamical load applied to the MSMA sample. A thermodynamic approach with hamiltonian modeling was used by the authors to design actuators [16] and new control laws [17].

Moreover, the thermodynamical approach proposed in this paper to model a specific MSMA can be easily extended to other materials, such as future MSMA monocristals and polycristals. Finally, this global model can be a basis to model MSMA in a Finite Element Analysis to design new mechanical structures for actuation and sensing applications.

Nota: A short version (7 pages) of this work [20] has been presented at ICEM14 in Poitiers (France), 5–9 july 2010.