Modelling Shape-Memory Effects in Ferromagnetic Alloys

Abstract

We develop a combined Ginzburg–Landau/micromagnetic model dealing with conventional and magnetic shape-memory properties in ferromagnetic shape-memory materials. The free energy of the system is written as the sum of structural, magnetic and magnetostructural contributions. We first analyse a mean field linearized version of the model that does not take into account long-range terms arising from elastic compatibility and demagnetization effects. This model can be solved analytically and in spite of its simplicity allows us to understand the role of the magnetostructural term in driving magnetic shape-memory effects. Numerical simulations of the full model have also been performed. They show that the model is able to reproduce magnetostructural microstructures reported in magnetic shape-memory materials such as Ni₂MnGa as well as conventional and magnetic shape-memory behaviour.

Introduction

Magnetic shape-memory effect (MSME) refers to a particular type of magnetostriction that originates from a rearrangement of twin-related variants induced by the application of a magnetic field [1]. This effect is usually associated with a martensitic transition taking place in materials with strong magnetostructural interplay driven by the magnetocrystalline anisotropy. Magnetic field-induced deformations in this class of materials are much larger than those attained in the case of the best conventional magnetostrictive materials such as Terfenol-D (Tb_0.27Dy_0.73Fe₂) and related rare-earth compounds.

The study of MSME started to receive increasing attention after O’Handley’s group reported in 1996 [2] deformations of ~0.2 % induced by moderate magnetic fields below 1 T in the Heusler alloy Ni₂MnGa. The authors suggested that the large response in strain in this material is the result of magnetic field-induced twin boundary motion. This is, to a large extent, the mechanism selected by the material in order to minimize Zeeman energy in the martensitic phase due to its large uniaxial magnetocrystalline anisotropy. While this paper certainly triggered intense research in this field, the same mechanism was already proposed 20 years earlier by Libermann and Graham [3] to explain the unusually large magnetostriction observed in Dy single crystals. However, this work received little attention, probably because the effect was observed at a quite low temperature of about 4 K.

The present paper deals with modelling conventional and MSMEs in ferromagnetic compounds based on a combined Ginzburg–Landau/micromagnetic free energy that incorporates the strong magnetostructural interplay responsible for the possibility of cross response to mechanical and magnetic fields. The paper is organized as follows. In “Basic Features” section, we introduce the general features associated with conventional shape-memory properties and compare them to those induced by a magnetic field. In “Modelling” section, we introduce the general model. Next, in “Linearized Mean Field Treatment” section, we derive and discuss a simple mean field linearized version of the model and in “Numerical Simulations” section, we present numerical simulations of the model. Finally, in “Summary and Conclusions” section, we summarize our main results and conclude.

Basic Features

Among the ferromagnetic alloys that are known to display magnetic shape-memory properties, most of them belong to the family of Heusler compounds [4, 5]. Ni₂MnGa is the prototypical material that undergoes a martensitic transition in its ferromagnetic phase with associated conventional and magnetic shape-memory properties. At high temperature, this Heusler alloy shows a B2 (Pm3m) nearest-neighbour ordered structure, and upon cooling next-nearest-neighbour order of the L2₁ (Fm3m) type develops. The L2₁-phase becomes ferromagnetic at a Curie temperature of T _c ≅ 380 K. The martensitic transition occurs at T _M ≅ 200 K towards a modulated 10 M crystallographic structure that, to a good approximation, is close to a tetragonal structure. The total magnetic moment is ~4.1 μ_B per formula unit, and is largely confined to the Mn-sites [6]. The magnetic anisotropy of the L2₁-phase is very weak. In contrast, the martensitic phase shows strong uniaxial anisotropy (two orders of magnitude larger than in the cubic phase) with easy axis along the short c-axis [7]. When the composition departs from the 2–1–1 stoichiometry by increasing the electron to atom ratio, e/a, the 14 M and non-modulated L1₂ martensites occur while the transition temperature increases. In contrast to modulated martensites, the non-modulated martensite has an easy plane perpendicular to the c-axis, which becomes the hard axis in this case (see Ref. [1]).

The martensitic transition is a diffusionless structural first-order transition between different crystalline phases, which is achieved by means of a dominant shear mechanism [8]. Due to the symmetry breaking taking place at the thermally induced martensitic transition, a single crystal of the high-temperature parent phase splits into a number of twin-related variants. These variants tend to form a complex heterophase such that no macroscopic change in shape occurs. The presence of an externally applied stress breaks variant-degeneracy, which results in a reduced number of favourable variants giving rise to a macroscopic deformation.

Certain materials undergoing a martensitic transition show a highly nonlinear and quasi-reversible¹ response to an applied stress, which provides them with the capacity of remembering their original shape after a severe deformation process. These materials are called shape-memory materials [8]. Specifically, the shape-memory effect refers to the fact that when these materials are mechanically deformed in the low-temperature martensitic phase, the deformation can be removed when the material is heated up above the reverse martensitic transition temperature. Usually, a warming process of few degrees is sufficient for the original shape (previous to the deformation) of the material to be recovered. In the high-temperature phase, the same systems display another unique property called superelasticity. It consists of the possibility of recovering, upon loading and unloading, a large strain (in some cases ≥10 %) associated with the stress- or strain-induced transformation. Indeed, these properties make this class of materials very attractive from a technological point of view, since they may function as sensors as well as actuators, and are promising candidates for smart materials [8, 9].

In some magnetic materials, including Ni₂MnGa, the large recoverable deformations can be induced by means of an applied magnetic field [10]. It is thus stated that these materials display magnetic shape-memory properties that are comparable to the corresponding conventional shape-memory properties, but with the magnetic field playing the role of mechanical stress. In the case of the MSME, the deformation is induced in the martensitic phase and it is associated with the field-induced rearrangement of twin-related variants through twin boundary motion. This mechanism becomes feasible when twin boundaries are highly mobile and the magnetocrystalline anisotropy is sufficiently high in order to restrict, as much as possible, the rotation of magnetic moments. Then, rearrangement of martensitic variants is promoted by the difference in Zeeman energy of neighbouring variants in such a way that their easy axis becomes aligned with the applied field. On the other hand, magnetic superelasticity² occurs when the martensitic transition can be induced by an applied magnetic field [1]. This requires a large-enough difference between the magnetic moments of the parent and martensitic phases such that an applied field strongly modifies their relative phase stability. The metamagnetic Ni–Mn–In Heusler alloy (and related compounds) is the prototypical material showing this property [12].

The possibility of a large magnetomechanical cross response in magnetic shape-memory alloys favours magnetic shape-memory properties as a consequence of the strong interplay between magnetism and structure. Such an interplay is driven by the change of structure taking place at the martensitic transition and leads to significant changes in the magnetic properties of the system. An interesting feature is the fact that the interplay shows up at two well-separated length scales [12]. At the scale of the martensitic variants, it is determined by the increase of magnetocrystalline anisotropy associated with the symmetry reduction occurring at the martensitic transition. At a more microscopic length scale (unit cell scale), it is controlled by the corresponding change in the effective magnetic exchange coupling. The change of magnetocrystalline anisotropy provides the basic mechanism for the MSME to occur [13, 14]. On the other hand, the change in the effective exchange induces a difference between the magnetic moments of the high- and the low-temperature phases, affecting their relative stability in the presence of an applied magnetic field. This effect is essential for magnetic superelasticity to be feasible [15, 16]. Application of a magnetic field stabilizes the phase with higher magnetization. Therefore, depending on specific features of the magnetostructural interplay, forward or reverse martensitic transition should be induced by application of a magnetic field depending on whether the martensite has a larger or a smaller magnetic moment than the parent phase. Materials displaying magnetic superelasticity are commonly denoted as metamagnetic shape-memory materials. From a practical point of view, the great advantage of magnetic superelasticity is that in addition to large field-induced deformations comparable to those attained by means of the field-induced variant reorientation mechanism, it enables to reach a much larger work output since the deformation occurs by magnetically inducing the magnetostructural transition [17].

At present, no materials showing simultaneously large magnetic shape-memory and large magnetic superelasticty effects have been found. This could be a consequence of the fact that concomitantly large changes of anisotropy and magnetization taking place at the martensitic transition seem to be incompatible in Heusler and related ferromagnetic alloys.

Modelling

In this section, we will present a model to describe shape-memory effects in ferromagnetic materials. Different approaches have been proposed to deal with ferroelastic and martensitic textures including models based on a combination of micromechanics and micromagnetic theories [18]. Among the most powerful and popular approaches, we can refer to the method based on sharp-interface minimizers first introduced by Ball and James [19] where compatibility is mathematically accounted through the Hadamard jump condition (or kinematic compatibility condition). This approach has been extended in order to incorporate magnetic degrees of freedom by James and Wuttig [20] who successfully applied the method to model magnetostrictive properties of the martensitic alloy Fe₇₀Pt₃₀. More recently, this approach has been used to model MSMEs in Heusler alloys (see for instance Refs. [21, 22]).

Concerning the phase field approach introduced by Khachaturyan [23, 24], it is formulated in terms of a free energy functional, which depends nonlinearly on morphological variables coupled to strain. Such variables have the role of identifying martensitic variants. In this approach, the inhomogeneous deformation associated with compatibility constraints is treated within the Eshelby local inclusion model. More recently, Zhang and Chen [25, 26] have extended this approach to the case of magnetic martensites by treating the magnetic degrees of freedom within the micromagnetic approach. Later on, the method has been used to analyse specific features of magnetic field-induced boundary motion [27] and related hysteresis effects [28], and to model MSME in a number of Heusler materials [29].

In the present paper, we approach the problem by combining a Ginzburg–Landau model for the structural degrees of freedom with a micromagnetic treatment of magnetism and magnetostructural interplay. The advantage of the Ginzburg–Landau method is that it can be formulated in terms of strains as the natural order parameters for the problem. When lattice integrity is imposed in the continuum limit through the St. Vénant condition (see for instance Ref. [30]), an elastic long-range effect explicitly arises, which is responsible for specific features of the obtained microstructures. The method has been successfully applied to deal with pure martensitic systems with different symmetries [31]. Here we show that by including magnetic degrees of freedom, the long-range term is modified due to the magnetostructural interplay. For the sake of simplicity, we will consider here a magnetostructural square-to-rectangular transition which mimics the 3-d cubic to tetragonal transition in, for instance, Ni₂MnGa. We will assume that the free energy of the system can be written as the sum of three contributions; the structural, the magnetic and the magnetostructural contributions. That is,

$$\begin{aligned} {\mathcal{F}} = F_\text{S} + F_\text{M} + F_\text{M-S}. \end{aligned}$$

(1)

Note that the last term accounting for the magnetostructural interplay is the essential term that will make the MSME possible.

Any distortion of the original square lattice can be described by means of the symmetry-adapted strains $e_1 = \frac{1}{2} (\varepsilon_{xx} + \varepsilon_{yy})$, $e_2 = \frac{1}{2} (\varepsilon_{xx} - \varepsilon_{yy})$ and $e_3 = \varepsilon_{xy}$, which account for changes of area, deviatoric distortions and shears, respectively. In the preceding expressions, $\varepsilon_{ij}$ are components of the linearized Lagrange strain tensor. For a square-to-rectangular transition $e_2 = e$ is the appropriate order parameter while $e_1$ and $e_3$ are non-symmetry breaking deformations (or non-order parameters). Taking into account symmetry considerations, the structural free energy can be expressed as the following Ginzburg–Landau functional,

$$\begin{aligned} F_\text{S}\,= \int \text{d}^2r \Bigg \{ &\frac{1}{2} A_2 e^2({\mathbf{r}}) + \frac{1}{4} B_2 e^4({\mathbf{r}}) + \frac{1}{6} C_2 e^6({\mathbf{r}}) \nonumber \\& + {} \frac{1}{2} A_1 e_1^2({\mathbf{r}}) + \frac{1}{2} A_3 e_3^2({\mathbf{r}}) - \sigma e({\mathbf{r}}) + \gamma |\nabla e({\mathbf{r}})|^2 \Bigg \} , \end{aligned}$$

(2)

where the integral is over the system area and $\gamma$ measures the energy cost of interfaces. $A_2$ is related to the elastic constant $C'$ and assumed to vary linearly with temperature as $A_2 = a (T - T^*)$, where $T^*$ is the low stability limit of the square phase. This elastic constant is small in martensitic materials. The coefficients $A_1$ ($= C_{11} + C_{12}$) and $A_3$ ($= 4C_{44}$) are related to the elastic constants associated with non-order parameters. Since the transition is expected to be first-order, $B_2 < 0$ and $C_2 > 0$. Here $\sigma$ is an externally applied stress that couples to the order parameter.

According to micromagnetic theory [32, 33], the pure magnetic contribution to the free energy is taken to be of the form

$$\begin{aligned} F_\text{M}\,=& \, D \int m_x^2({\mathbf{r}}) m_y^2({\mathbf{r}}) \text{d}^2r + J \int \left| \nabla {\mathbf{m}} ({\mathbf{r}}) \right| ^2 \text{d}^2r \nonumber \\& - {} \mu_0 M_\text{S} \int \left( \frac{1}{2} {\mathbf{H}}_\text{d} + {\mathbf{H}}_\text{ext}\right) \cdot {\mathbf{m}} \text{d}^2r, \end{aligned}$$

(3)

where ${\mathbf{m}} = {\mathbf{M}}/ M_\text{S}$ is the three-component³ unit magnetization vector and $M_\text{S}$ is the saturation magnetization. The first term corresponds to the anisotropy energy of the square lattice and thus only considers the in-plane components of the magnetization. It is minimized for ${\mathbf{m}}$ along x or y directions since the anisotropy coefficient D is assumed positive. The second term is the exchange energy which is determined by the spatial variation of the magnetization orientation. Therefore, J is an exchange stiffness constant. The third term includes the magnetostatic energy associated with the stray or demagnetizing field ${\mathbf{H}}_\text{d}$, and the Zeeman energy accounting for the coupling of the magnetization with an externally applied field ${\mathbf{H}}_\text{ext}$. The demagnetizing field ${\mathbf{H}}_\text{d}$ is created by the magnetization ${\mathbf{m}}({\mathbf r})$ itself throughout the system so that this results in long-range magnetic interactions. Such a potential is responsible for closing the magnetic field lines, which in turn is at the origin of the creation of vortices and magnetic domains. Its computation entails some difficulties such as time cost, which can be overcome here using Fourier transforms. The detailed computational method can be found in [25, 26].

Finally, the following magnetostructural term is assumed (see Ref. [32]),

$$\begin{aligned} F_\text{M-S}\,=&\,\kappa \int \left[ m_x^2({\mathbf{r}}) + m_y^2({\mathbf{r}})\right] e_1({\mathbf{r}}) \text{d}^2r \nonumber \\ & + {} \kappa \int \left[ m_x^2({\mathbf{r}}) - m_y^2({\mathbf{r}})\right] e({\mathbf{r}}) \text{d}^2r \nonumber \\ & + {} \kappa ' \int m_x({\mathbf{r}}) m_y({\mathbf{r}})e_3({\mathbf{r}}) \text{d}^2r, \end{aligned}$$

(4)

where $\kappa$ and $\kappa^{\prime}$ are magnetostrictive coefficients. Note that only the coupling of magnetization and strains at the minimum order allowed by symmetry has been considered. Actually, this term essentially determines the magnetocrystalline anisotropy of the martensitic phase.

In 2-d, if lattice integrity is assumed, the three strains $e_1$, $e_2 = e$ and $e_3$ are not independent. This can be taken into account by minimizing the preceding free energy under St. Vénant compatibility constraint [34, 35]. The contribution to the free energy from non-order parameters is a long-range term that can be written in Fourier space as

$$\begin{aligned} F_\text{nonOP}\,= & \,\frac{1}{4 \pi ^2} \int A_\text{c2}({\mathbf{k}})e({\mathbf{k}}) e(-{\mathbf{k}}) \text{d}{\mathbf{k}} \nonumber \\ & + {} \frac{\kappa }{4 \pi ^2} \int A_\text{c1}({\mathbf{k}})e({\mathbf{k}}) \int e^{i{\mathbf{{k}} \cdot {\mathbf{{r}}}}} \left[ m_x^2({\mathbf{r}}) + m_y^2({\mathbf{r}})\right] \text{d}{\mathbf{r}} \text{d}{\mathbf{k}} \nonumber \\ & + {} \frac{\kappa '}{8 \sqrt{2} \pi ^2} \int A_\text{c3}({\mathbf{k}})e({\mathbf{k}}) \int e^{i\mathbf{{k \cdot r}}} \left[ m_x^2(\mathbf{r}) m_y^2(\mathbf{r})\right] \text{d}\mathbf{r} \text{d} \mathbf{k}, \end{aligned}$$

(5)

where

$$\begin{aligned} A_\text{c1}({\mathbf{k}})= \frac{\left( k_x^2 - k_y^2\right) \left( k_x^2 + k_y^2\right) }{k^4 +\frac{8}{R}k_x^2k_y^2}, \end{aligned}$$

(6)

$$\begin{aligned} A_\text{c2}({\mathbf{k}})= & {} \frac{A_3}{2} \frac{\left( k_x^2 - k_y^2\right) ^2}{R k^4 + 8k_x^2k_y^2}, \end{aligned}$$

(7)

$$\begin{aligned} A_\text{c3}({\mathbf{k}})= \frac{\left( k_x^2 - k_y^2\right) k_x k_y}{\frac{R}{8} k^4 + k_x^2k_y^2}. \end{aligned}$$

(8)

$R = A_3/A_1$ is the ratio between the shear and the bulk moduli. Notice that this long-range term is minimized for $k_x = \pm k_y$ which explains the directionality of long-range correlations along the diagonals of the square lattice which are the soft directions due to the low value of $C^{\prime}$. It is worth noting that when the magnetostructural interplay vanishes, this long-range free energy reduces to the long-range free energy already reported for square-to-rectangle pure structural transitions [34], which is characterized by the kernel $\hat{U} = A_\text{c2} ({\mathbf{k}})$. When $\kappa$ is large, we expect ${\mathcal{F}}$ to be minimized for $m_x = \pm 1$ for $e < 0$ and $m_y = \pm 1$ for $e > 0$. In both cases, $e_1 = e_3 = 0$, and we thus expect this long-range contribution to be the dominant one. In this case, it is clear that the strength of the long-range interaction is proportional to $C_{44}$ and therefore increases with the elastic anisotropy (measured as the ratio $C_{44}/C'$).

The low-temperature ground state of the structural contribution to the total free energy corresponds to a homogeneously deformed lattice. In order to obtain a more realistic twinned structure, the self-accommodation process that makes the transition strain modulation (twinned structure) to be energetically favourable with respect to the single-domain structure must be taken into account. Such a process occurs when the martensitic phase nucleates within the parent (square) matrix and consists of preserving the lattice coherency at the parent-martensite interfaces, keeping such habit planes macroscopically undistorted. It has been shown [36] that this condition gives rise to an additional term in the long-range potential which depends on the strain at the phase boundary, and whose main interaction goes as $\sim \!\!1/|{\varvec{k}}|$, where k is the wave vector parallel to the boundary. The minimization of the structural free energy including this term leads to a new ground state consisting of a modulated twin pattern whose characteristic width $\lambda$ scales as $\lambda \sim \sqrt{L}$, where L is the width of the transformed region. This scaling is in agreement with available experiments (see for instance [37]).

Linearized Mean Field Treatment

The model presented in the preceding section gives a detailed mesoscopic description of the magnetostructural behaviour exhibited by ferromagnetic shape-memory materials. In particular, as it will be shown in the next section, the model reproduces properly fine details of the microstructure as well as the MSME. Before going into the results, we would like to gain some insight into the magnetic field-induced twin reorientation, that is at the origin of the large reversible strains observed in the MSME, and extend this case to include an externally applied stress. However, due to the significant number and complex interplay of the energetic contributions, the full model solution requires numerical simulations. In this sense, the output may be difficult to analyse with clarity, and the key physics underlying the intricate behaviour may remain hidden in the numerical computation. For this purpose, in the present section, we reduce the model within a simplified pseudo-mean field approximation that focuses on the main factors involved and omits secondary energetic contributions.

The magnetic field-induced strain under stress has been addressed by a large number of (pseudo-)phenomenological models (among others see Refs. [13, 14, 22, 38–42]). Most of them include explicitly dissipation terms occurring in twin reorientation to account for hysteresis in strain-magnetic field loops and deal with magnetostatic effects by means of approximate calculations of demagnetizing factors. In particular, Wang et al. [38] proposed a phenomenological constitutive model based on a variational approach of a pseudo-free energy that neglects exchange interactions. Kiefer and Lagoudas [39] introduced a micromechanical model aimed at studying magnetostrain curves under the effect of an additional bias magnetic field. Auricchio et al.  [40] considered a simple model, which is restricted to the limit of very strong magnetocrystalline anisotropy, so that no magnetization rotation is allowed inside each variant. They also neglected demagnetization effects. Chen et al.  [41] proposed a very versatile constitutive 3-dimensional model, where the calculation of the magnetostatic field is carried out properly by means of finite-element analysis. The model allows to take into account the effect of multi-axial stresses and rotating magnetic fields. The model reported by LaMaster et al.  [42] is formulated with only three adjustable parameters, and allows for 2-dimensional magnetic and stress fields.

Among the cited models, O’Handley’s model [13, 14] is worth mentioning as it can be fully solved analytically although it does not address the case of an applied stress. The present mean field model also allows analytical solutions and includes the effect of an externally applied stress. As we will see, the key results obtained by models in literature can be qualitatively reproduced by our approach.

The starting point for this simplified description is a spatially extended system with local Ising-like strains [43] accounting for the two rectangular twin-related deformed cells, being $e_2=\pm \bar{e}$. Since the magnetic field-induced twin reorientation occurs in the martensitic phase, the austenite phase and the martensitic transition described by the elastic Landau energy can be omitted. Moreover, long-range elastic interactions are substituted by a non-local structural term of the form of $F^\text{{MF}}_\text{S}=\frac{1}{2}C\langle e\rangle^2$, where $\langle e \rangle$ is the average deformation of the system, and $C>0$ is an effective modulus that accounts for the elastic response of the twinned phase to an applied force. The inverse of C is thus a good measure of the twin boundary mobility. If we denote by $1-\xi$ ($\xi$) the fraction of the system with deformation $\bar{e}$ ($-\bar{e}$), then $\langle e\rangle= (1 - 2\xi )\bar{e}$. In the absence of externally applied forces, $F^\text{{MF}}_\text{S}$ is minimized for $\xi =\frac{1}{2}$ which corresponds to a globally non-deformed system, thus accounting for an effective self-accommodation process.

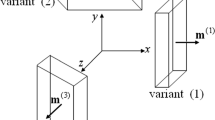
Associated with each deformed cell, a classical Heisenberg-like magnetic spin is also considered, with the easy-magnetization axis along the corresponding c-axis. The c-axis will be axis x(y) for variant $\bar{e}$ ($-\bar{e}$). In the general case, the spins will not be aligned with the c-axis but rather they are allowed to form an angle $\theta$ ($\phi$) in cells with strain $\bar{e}$ ($-\bar{e}$) (see Fig. 1). As pointed out by Kiefer and Lagoudas [39], such magnetization rotation inside the martensitic variants is known to be an important feature that favours the magnetic field-induced twin reorientation.

Fig. 1

Schematic description of the mean field approximation. For details see the text

The magnetic spins will only contribute to the free energy through the magnetostructural coupling $F^\text{MF}_\text{M-S}$ and the Zeeman energy $F^\text{MF}_{H_{\text{ext}}}$:

$$\begin{aligned} F^\text{MF}_\text{M-S}= & {} -\sum \kappa \langle e\rangle \left( M_x^2-M_y^2\right) \nonumber \\= & {} -\kappa V\bar{e}M_\text{s}^2\left[ \xi \cos (2\phi )+(1-\xi )\cos (2\theta )\right] \end{aligned}$$

(9)

and

$$\begin{aligned} F^\text{MF}_{H_{\text{ext}}} =& - \mu_0HM_\text{s}V\xi (\cos \alpha \sin \phi +\sin \alpha \cos \phi )\nonumber \\ &- {} \mu_0 HM_\text{s}V(1-\xi )(\cos \alpha \cos \theta -\sin \alpha \sin \theta ), \end{aligned}$$

(10)

where $\alpha$ is the angle between the x-axis and ${\mathbf{H}}_{\text{ext}}$.

We also consider a stress field $\sigma$ that favours deformation $\bar{e}$. Thus

$$\begin{aligned} F^\text{MF}_{\sigma_{\text{ext}}}=-\sum \sigma \langle e\rangle =-V(1-\xi )\sigma \bar{e}+V\xi \sigma \bar{e}=V\sigma \bar{e}(2\xi -1) . \end{aligned}$$

(11)

Since magnetostatic and exchange energies are not taken into account here, this approximation is not intended to study fine magnetic microstructure details such as internal magnetic stripes, which indeed will be obtained by numerical simulations of the full model. Notice that the full MSME cannot be strictly reproduced by the mean field approximation because the model cannot reproduce hysteresis effects and thus field-induced strains are directly recovered just after removing the external field.

The equilibrium solutions of the model are given by minimization of the total free energy $F^\text{MF}=F^\text{MF}_\text{S}+F^\text{MF}_\text{M-S}+F^\text{MF}_{H_{\text{ext}}}+F^\text{MF}_{\sigma_{\text{ext}}}$. Analytical solutions for different cases are summarized in the Table 1. Indeed, the model exhibits a general threshold in the magnetic field for the alignment of the magnetic spins which is given by $\mu_0 H_\text{c}\,=\,4\kappa M_\text{s}\bar{e}$. This threshold is also found in other models [13, 14, 38, 39].

Table 1 Solutions of the mean field model for $\alpha =0$ and $\frac{\pi }{2}$. $A=\frac{\mu_0H}{4\sqrt{2}\kappa M_\text{s}\bar{e}}$

Figure 2a, b (where we have set $\kappa =2.2\times 10^6$ and $C=1.8\times 10^5$, in arbitrary units) show the magnetic field dependence of $\xi$ and $\left\langle m_x\right\rangle$ for different constant applied stress fields, for a magnetic field orientation of $\alpha =0^o$. In this simple case, both the magnetic and stress fields favour the same variant, whose fraction is $(1-\xi )$. As a consequence, the larger the stress field, the lower the magnetic field needed to saturate both magnetization and strain. Notice that the magnitude of the saturation strain is directly related to the twin reorientation. Interestingly, while the magnetization always saturates at $\left\langle m_x\right\rangle =1$ (corresponding to the single magnetic domain), for low values of the stress field (black and red curves) the strain saturates at values $1-\xi <1$ ($\xi >0$) no matter how high the magnetic field is. This indicates that C is relatively large with respect to $\kappa$, since for certain range of the stress field the elastic energy prevails over the magnetostructural energy, and consequently, the complete magnetic field-induced twin reorientation cannot be accomplished.

Another interesting situation arises when the magnetic and the stress field are applied in such a way that each field favours a different strain variant respectively and hence operates against each other. This competing situation is shown in Fig. 2c, d where one can observe a nonlinear behaviour with the following trends: the larger the stress field, the higher the magnetic field needed to induce twin reorientation, and the lower the attainable saturation strain. Moreover, above a certain stress threshold (called blocking stress), the reorientation is inhibited regardless of the magnitude of the applied magnetic field. All these features are in agreement with the experimental observations [44–48] and with the models previously discussed. Note that, as indicated before, hysteretic effects associated with removal of the magnetic field cannot be reproduced by the present approximation.

In addition to the previously mentioned features, in Fig. 2c, d it can also be observed that the magnetic field required to fully align the magnetization in both variants is stress-independent. This was also obtained by Kiefer and Lagoudas [39]. In contrast, in Ref. [40] the inverse situation is found. It is the onset of the magnetic field-induced twin reorientation which seems to be stress-independent and thus no delay is found. Actually, according to the experiments quoted above, both thresholds do depend on stress. It is worth noting that in both models (as done in the present approximation), the calculation of the demagnetizing field is, at least, partially disregarded. Since it is involved in the magnetic domain wall motion occurring inside the twins (magnetic stripes), it may affect fine details of the behaviour as discussed here.

Figure 2e, f shows the magnetic field dependence of $\phi$ and $\left\langle m_x\right\rangle$ for $\alpha =0$° and $\alpha =45$°. The stress field is absent. They reveal that the saturation magnetic field is lowest for $\alpha =45$°, which is parallel to the twin boundaries. Notice that in the latter case (contrary to the case $\alpha =0$°), none of the strain variants is favoured, so that no magnetic field energy is spent in twin reorientation, but it is fully spent in reorienting the magnetization only. This is in agreement with the result obtained by O’Handley [13, 14]. Note that, the obtained dependence of the rotation angle $\phi$ on the magnetic field is qualitatively equivalent to that reported in Ref. [22].

Fig. 2

Panels a and b show the $\xi$ fraction and x-component of the average magnetization $\left\langle m_x\right\rangle$ respectively as a function of the magnetic field for different applied stress fields, for the case $\alpha =0$°. Panels c and d are analogous to a and b for $\alpha =90$°. Panels e and f show the orientation angle $\phi$ and $\left\langle m_x\right\rangle$ respectively as a function of the magnetic field for $\alpha =0$° and $\alpha =45$° in the absence of stress (Color figure online)

Figure 3 shows the dependence of $\left\langle m_x\right\rangle$ and $\left\langle e\right\rangle$ on an applied magnetic field for different sets of values for $\kappa$ and C. In this case, $\sigma =0$. It is intended to highlight the role of both the magnetostructural and elastic contributions and resembles again the general trends reported by O’Handley [13, 14]. Summarizing, there is a competition between the magnetostructural energy and the elastic energy: While the former maintains the magnetization aligned with the easy-magnetization axis determined by the magnetocrystalline anisotropy and thus favours the magnetic field twin reorientation, the latter penalizes the perturbation of the self-accommodated strain microstructure.

Fig. 3

Each panel shows the average magnetization $\left\langle m_x\right\rangle$ (black lines) and average strain $\left\langle e\right\rangle$ (red lines) as a function of the applied magnetic field. From panel to panel, magnetostructural constant $\kappa$ and elastic constant C are changed according to the offside axis. Specific values for $\kappa$ and C are also indicated in each panel for the sake of clarity. All values are in arbitrary units (Color figure online)

Numerical Simulations

In this section, we go back to the full model presented in “Modelling” section to study in detail structural and magnetic microstructures and shape-memory properties, which cannot be considered within the mean field approximation discussed in the previous section. Model parameters for our 2-d model have been taken from Ref. [49]. These parameters correspond to a situation of strong magnetoelastic interplay and high twin boundary mobility. For the simulations, we need dynamic equations for the magnetization and for the strain. Following the micromagnetic theory, the magnetization dynamics is governed by the Landau–Lifshitz–Gilbert (LLG) equation:

$$\begin{aligned} \left( 1+\alpha ^2\right) \frac{\partial {\mathbf{m}}}{\partial t}= & {} -\gamma_0{\mathbf{m}}\times {\mathbf{H}}_\text{eff} - \gamma_0\alpha {\mathbf{m}}\times \left( {\mathbf{m}} \times {\mathbf{H}}_\text{eff}\right) , \end{aligned}$$

(12)

where ${\mathbf{H}}_\text{eff}$ is a local effective magnetic field which, from micromagnetism arguments, is obtained as ${\mathbf{H}}_\text{eff}= -\frac{1}{\mu_0}\frac{\partial F}{\partial {\mathbf{m}}}$. According to LLG equation, the magnetization vectors make a damped precessional motion around ${\mathbf{H}}_\text{eff}$, with $\alpha$ the damping constant and $\gamma_0$ the gyromagnetic ratio (Even if the model is 2-d, assuming that magnetization is a 3-component vector with two components in-plane is important since it allows to consider a more realistic magnetization dynamics that takes into account precession of the magnetic vector around the applied magnetic field). In turn, the relevant strain field $e({\mathbf{r}})$ is allowed to evolve by means of a pure relaxational dynamics:

$$\begin{aligned} \frac{\partial e}{\partial t} = -\tau \frac{\delta F}{\delta e}. \end{aligned}$$

(13)

Note that magnetic and structural dynamics are not independent since they are coupled through the magnetoelastic term $F_\text{M-S}$ included in the total free energy F. To numerically solve the model, the system is discretized using the finite differences scheme onto a square mesh with periodic boundary conditions. Starting from randomly disordered configurations, the dynamical equations are iteratively applied until the system reaches a stabilized configuration (see Refs. [49, 50] for details).

At temperatures below the transition, martensitic twins develop and the magnetization vectors, hereafter referred to as spins, arrange in a configuration such as that shown in Fig. 4a. Assuming that almost all the spins lie in the $x-y$ plane, they can be characterized by their in-plane orientation given by the polar angle $\beta$, defined as the angle between the spin and the bottom border of the snapshot. Spins may take mainly four orientations: $\beta =0$°, $90$°, $180$° and $270$°, corresponding to dark red, dark blue, light red and light blue domains respectively in the figure, that result from the magnetostructural coupling, i.e., the magnetocrystalline anisotropy of the martensitic phase. Notice that a given strain variant couples energetically to two antiparallel orientations equivalently. The resulting four orientations combine in such a way that two types of magnetic domain walls appear:

• On one hand, as the arrows in the snapshot show, the change in the strain variant through the domain wall induces a $\Delta \beta =90$° in the spin orientation. Magnetostructural interactions bring magnetic domain walls to appear along the diagonal twin boundaries, thus forming $45$° angles with the spins. This is represented in the snapshot by the change of colour from blue to red. From these domain walls, the underlying structural configuration can be easily deduced.

• On the other hand, magnetic stripes appear within the twins (as indicated by same colour, different grades) as a result of the magnetostatic interactions. Magnetic stripes are characterized by a $\Delta \beta =180$° between spins belonging to nearest-neighbour stripes. It is worth noting that the width of the magnetic stripes and of all the magnetic domain walls is determined by the balance between exchange and magnetocrystalline anisotropy contributions. This kind of micromagnetic configuration shows excellent qualitative agreement with experimental observations, as it is shown in Fig. 4b.

Fig. 4

Comparison between a ${256\times 256}$ stable magnetic configuration obtained by numerical simulation (a) and an experimental micromagnetic structure observed in Co–Ni–Ga magnetic shape-memory alloy (b). Adapted from Ref. [51] (Color figure online)

Once we have obtained the right self-accommodated low-temperature magnetic and structural configurations, we can proceed to study the effect of both magnetic and stress fields on magnetization and strain respectively, and analyse the magnetic field-strain cross response in the case of the MSME. First, we focus on the conventional shape-memory effect which is shown in Fig. 5. It is illustrated by the evolution of the strain throughout the whole process, consisting of loading [(a)–(c)], unloading [(c)–(d)] and heating [(d)–(f)]. Selected snapshots of the microstructure are shown in representative points of the curve. Red and blue colours correspond to the two symmetry-allowed martensitic variants. Yellow colour stands for the austenite phase. The shape-memory effect takes place due to (i) the nonlinear stress–strain behaviour upon loading resulting from the stress-induced twin reorientation, which allows significant averaged (i.e. macroscopic) strain (about 4 % for this system); (ii) the retention of the single-domain configuration (and hence, of the macroscopic strain) upon unloading; and (iii) the occurrence of the reverse martensitic transition upon heating that brings the system back to zero macroscopic (and also zero microscopic) strain.

Fig. 5

Shape-memory effect. The snapshots show ${256\times 256}$ microstructural configurations at selected points of the curve. Arrows indicate the order of procedure of the simulation experiment. For details see the text (Color figure online)

Finally, we focus on the MSME, which is depicted in Fig. 6. Snapshots are micromagnetic configurations, with the same colour code as in Fig. 4. The starting point is precisely a self-accommodated magnetic and strain configuration [snapshot (a)], with approximately vanishing macroscopic strain. It is worth noting that the nonlinear magnetic field-strain behaviour resembles the stress–strain curve shown in Fig. 5. Looking at the evolution of the magnetic configurations [snapshots (a)–(d)], for a given range of the magnetic field, the Zeeman energy progressively causes the extinction of the magnetic stripes with magnetic moment opposite to the field [i.e. light red stripes in snapshot (b)], which are indeed energetically unfavourable. However, at this step the Zeeman energy is still not able to induce reorientation of all the spins perpendicular to the field [blue stripes, see snapshot (b)]. The way the system proceeds is twofold [see snapshot (c)]; on one hand, the spins adjacent to the twin boundary reorient easier than those in the non-favourable-twin bulk, so that the twin boundary moves forward and the favoured twin grows. This occurs because reorientation of boundary-adjacent spins is less penalized directly by the exchange and magnetostatic energies, and indirectly through the magnetostructural coupling in the Ginzburg–Landau free energy contribution, than in the case of the nucleation of favourable (red) magnetic domains within the bulk of non-favourable (blue) twins, which would require stronger externally applied magnetic fields. On the other hand, an interesting secondary effect of the extinction of the magnetic stripes within the favourable (red) twin variant takes place due to the fact that the magnetic stripes in the non-favourable (blue) twin variant are no longer supported by the magnetostatic energy and are progressively removed. In the present particular case, dark blue stripes are removed because of the extinction of light red stripes. Instead, light blue domains still survive since they are magnetostatic-favourable with dark red domains. Notice that the spins in the bulk of the vanishing stripes are reoriented parallel to the surviving domains and not to the magnetic field. That is to say, dark blue spins reorient and become light blue spins instead of dark red spins.

Above a given value of the magnetic field, the magnetization saturates (all the spins are aligned with the field), so that the system attains a single magnetic domain. In our present case, a single strain domain is also attained, which maximizes the achievable macroscopic strain and hence the MSME. Notice that once the single magnetic domain is reached, in contrast to the conventional shape-memory effect where the strain keeps increasing (at low rate) with the external stress, in the present case a further increase of the magnetic field has no effect on the strain. This is a consequence of the fact that the interplay of the strain with the magnetic field is mediated by the magnetization (the magnetostructural term). Hence, when the magnetization saturates and the strain arranges according to all the energetic contributions (the magnetostructural and elastic energies), the magnetostructural energy cannot keep decreasing despite an increase in the magnetic field. Notice that the ratio between the magnetostructural energy (magnetocrystalline anisotropy of the low-temperature phase) and the elastic energy (elastic constants) determines whether the system is able to undergo a full or partial magnetic field-induced twin reorientation. It is worth reminding that this result is in agreement with the results of the mean field model. After removing the magnetic field, the system remains macroscopically deformed. Then, an increase of temperature above the reverse martensitic transition allows to remove the strain so that the macroscopic austenitic state is recovered, which completes the magnetic shape-memory path.

Fig. 6

Magnetic shape-memory effect. The snapshots show 64 × 64 magnetic configurations at selected points of the curve. Arrows in the snapshots are depicted to show the orientation of the magnetic moments within each colour. The initial part of the curve, lying in the plane H-〈e〉 (and corresponding to the snapshots a–d) shows the nonlinear elastic response of the system to the magnetic field. When the magnetic field is removed, d–e, the system retains the macroscopic strain and the magnetic configuration. Upon heating, the backward martensitic transition is induced, so that, although the magnetic configuration is not modified (e–f), the system recovers the initial null strain. The initial small non-vanishing strain is due to the finite size of the simulation cell (Color figure online)

Summary and Conclusions

We have developed a magnetostructural model based on (i) a Ginzburg–Landau elastic free energy extended to include long-range anisotropic interactions, (ii) the micromagnetic theory and (iii) a term accounting for the magnetostructural interplay. A mean field approximation of the model is carried out which, among other effects, excludes both explicit long-range elastic and magnetic interactions. This treatment is intended to highlight the balance between the magnetostructural interplay and the elastic energy which is at the origin of the response of the system to externally applied magnetic and stress fields. Analytical solutions are obtained in particularly interesting cases such as selected magnetic field orientations. In general, it is found that the balance of the two energy terms plays a key role in determining the magnetic field-induced twin reorientation. The optimal orientation of the magnetic field to saturate the magnetization is parallel to the twin boundary, instead of favouring one of the martensitic variants.

To obtain a more accurate magnetostructural behaviour, numerical simulations of the full model have been performed. Simulations show that the model is able to reproduce several multiferroic features observed in real materials. In particular, the cooperation between the magnetostatic field and the magnetostructural coupling is crucial in order to understand fine details of the microstructure such as the particular arrangement of magnetic stripes within elastic twins. Also, when the latter term is strong enough, the magnetic field-induced twin reorientation that takes place in an a priori self-accommodated magnetoelastic system allows the MSME to occur. The evolution of the magnetic domains towards the single magnetic domain is not trivial: the magnetic interfaces which are parallel to the twin boundaries, and the magnetic stripes behave differently as has been discussed in detail.