1 Introduction

As recently introduced by Baykasoğlu and Akpinar (2015, 2017), Weighted Superposition Attraction algorithm (WSA) is a novel swarm intelligence-based metaheuristic algorithm, proposed to solve real-valued constrained and unconstrained optimization problems. WSA draws inspiration from the superposition of particles principle in physics. Solution vectors in WSA generate a superposition, which is followed by some of the agents (solution vectors), depending on the quality of the generated superposition.

As mentioned by Baykasoğlu and Akpinar (2015, 2017), WSA differs from other well-known methods including Genetic Algorithm (GA) (Holland 1975), Differential Evolution Algorithm (DE) (Storn and Price 1997), Ant Colony Optimization (ACO) (Dorigo et al. 1991), Particle Swarm Optimization (PSO) (Kennedy and Eberhart 1995) and new generation metaheuristics such as Firefly Algorithm (FA) (Yang 2008), Cuckoo Optimization Algorithm (Rajabioun 2011) and Bat Algorithm (BA) (Yang 2010) in several ways. One of the most striking differences of WSA is the utilization of anonymous intelligence of the agents. As to be clarified later, WSA generates a target point (superposition) by making use of the current population information. This target point is referred to as the superposition, which directs the agents towards its coordinates based on the quality (fitness) of the generated superposition. That is to say, superposition is an anonymous composition of the currently discovered points so far. Once the superposition is determined, agents explore the search space either by moving towards that point or by performing random walks.

The related literature includes some studies of WSA for a variety of optimization problems. In one of them, Baykasoğlu and Akpinar (2015) proposed making use of this new generation metaheuristic in constrained design optimization problems. In another work of the authors, Baykasoğlu and Akpinar (2017) employed WSA to solve real-valued unconstrained optimization problems including well-known mathematical functions. Resource constrained scheduling problem, which is a challenging combinatorial optimization problem, is solved by Baykasoğlu and Şenol (2016a) using WSA. A similar approach is applied to the Travelling Salesman Problem, which is another well-known challenging problem (Baykasoğlu and Şenol 2016b). The authors reported promising results, which are compared to the results of several state-of-the-art algorithms. Özbakır and Turna (2017) examined the performance of WSA in clustering problems. In the same study, the authors also introduced two new modifications of WSA, where in the former one, contributions of lower quality agents are eliminated and in the latter one, superposition is directly used as the best individual of the population. According to the reported results, both modifications of WSA and its canonical version show notable performance particularly in continuous and categorical data. Finally, Baykasoğlu and Ozsoydan (2018) tested WSA in dynamic optimization problems. According to the reported results, WSA is found as a competitive and a promising algorithm also in dynamically changing problems.

Although WSA has been shown to be successful in various optimization problems (Baykasoğlu and Akpinar 2015, 2017; Baykasoğlu and Şenol, 2016a, b; Özbakır and Turna 2017; Baykasoğlu and Ozsoydan 2018), the performance of WSA needs to be examined also in fundamental binary optimization problems, which is the main motivation of the present work.

In this respect, WSA is modified for binary spaces first. In the proposed modification, WSA does not require any transfer functions to convert real numbers to binary, whereas such functions are commonly used in approximation algorithms that are adapted to binary problems. Moreover, by making use of this approach, any type of variables can also be used along with binary variables. Additionally, a discrete step sizing function, which encourages population diversity at earlier iterations while intensifying the search towards the end, is adopted in the proposed WSA modification. Thus, premature convergence and local optima problems are attempted to be avoided.

Finally, the performance of the proposed binary WSA (bWSA) is examined by using some well-known binary optimization problems, including uncapacitated facility location problem (UFLP), 0–1 knapsack problem (0–1 KP) and the set union knapsack problem (SUKP). The obtained results are compared to the previously published results taken from the related literature. Comprehensive experimental study points out the superiority of bWSA in binary optimization problems.

The rest of the paper is organized as follows: benchmarking problems are formally defined in Sect. 2, detailed explanations of WSA and bWSA are introduced in Sect. 3. Finally, experimental study and concluding remarks are presented in Sects. 4 and 5, respectively.

2 Benchmarking problems

2.1 Uncapacitated facility location problem

Location problems have attracted notable attention from researchers because they have numerous applications in real world (Laporte et al. 2015). UFLP is a well-known type of location problems, where each customer is served by exactly one facility and facilities are assumed to have unlimited capacities (Cornuejols et al. 1990). Given a possible set of sites for establishing facilities and a set of customers at demand points, the aim here is to find the optimal locations for facilities to meet all demand such that the sum of facility opening costs and occurred shipment costs is minimized. UFLP can formally be formulated as given in the following (Eqs. 1–5).

$$minimize \mathop \sum \limits_{k \in K} \mathop \sum \limits_{l \in L} c_{kl} z_{kl} + \mathop \sum \limits_{k \in K} b_{k} y_{k}$$
(1)
$$\sum\limits_{k \in K}^{{{\text{s}} . {\text{t}} .}} {z_{kl} = 1,\quad } l \in L$$
(2)
$$z_{kl} \le y_{k} ,\quad k \in K\; {\text{and}}\;l \in L.$$
(3)
$$z_{kl} \in \left\{ {0,1} \right\},\quad k \in K\;{\text{and}}\;l \in L$$
(4)
$$y_{k} \in \left\{ {0,1} \right\},\quad k \in K$$
(5)

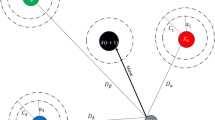
where K = {1, 2, …, n} is the possible locations for opening facilities, L = {1, 2, …, m} is the set of customers (demand points), bk is the cost of establishing a facility at the kth location,\(c_{kl}\) is the shipment cost between the facility opened at the kth location and the lth customer, zkl is a binary variable denoting whether the demand of the lth customer is fulfilled by the kth facility location (zkl = 1 if the lth customer is served by the facility opened at the kth location, zkl = 0 otherwise) and yk is another binary variable representing the status of a facility location (yk = 1 if a facility is opened at the kth location, yk = 0 otherwise). In this context, Eq. 1 represents the objective function to minimize the total cost. Equation 2 satisfies that each customer can exactly be served by only one facility. Equation 3 provides that customers can only be served by the opened facilities. Finally, Eqs. 4–5 impose restrictions on decision variables. An illustration for this problem is presented in Fig. 1.

Fig. 1
figure 1

An illustration for UFLP

Full size image

There are several exact solution techniques proposed for UFLP including a dual-based procedure (Erlenkotter 1978), a Lagrange relaxation (Barcelo et al. 1990), and a branch-and-bound method (Holmberg 1999). However, UFLP is shown to be an NP-hard problem and hence the solution time grows exponentially with the problem size. Therefore, making use of such exact solution approaches is limited only for small sized instances. In this regard, although exact solution methods guarantee optimality, they unfortunately have such limitations. On the other hand, metaheuristic algorithms do not guarantee optimality, however, they are easy to implement to any size of problem.

In the related literature, there are numerous publications focusing on location problems. Reporting them all is out of the scope of the present paper. Therefore, only the closely related ones and some state-of-the-art are mentioned here. In one of them, Jaramillo et al. (2002) employed GAs on several location problems. Tabu Search is another well-known method for solving UFLP (Al-Sultan and Al-Fawzan 1999; Sun 2006). Wang et al. (2008) introduced a multi-population-based parallel PSO that divides whole population into sub-populations for UFLP. Literature also includes other PSO implementations for this problem (Sevkli and Guner 2006; Guner and Sevkli 2008). In a more recent work, an Artificial Bee Colony (ABC) optimization algorithm was proposed by Kiran (2015). Tsuya et al. (2017) employed FA to solve UFLP. de Armas et al. (2017) and Della Croce et al. (2017a, b) reported deterministic and stochastic versions of UFLP. Hale and Moberg (2003) and Şahin and Süral (2007) presented comprehensive surveys for the related problem.

2.2 0–1 Knapsack problem (0–1 KP)

0–1 KP (Lin 2008) is the second benchmark problem used in the present study. 0–1 KP has many practical real world applications such as cargo loading, project funding selection, budget management, cutting stock, etc., (Kellerer et al. 2004). The aim in 0–1 KP is to maximize the knapsack profit such that the capacity of the knapsack is not exceeded. 0–1 KP can be formulated as in Eqs. 6–8.

$$maximize \mathop \sum \limits_{r \in R} p_{r} x_{r}$$
(6)
$$\sum\limits_{r \in R}^{{{\text{s}} . {\text{t}} .}} {w_{r} x_{r} \le C}$$
(7)
$$x_{r} \in \left\{ {0,1} \right\},\quad r \in R$$
(8)

where R = {1, 2, …, z} is the set of items, pr represents the profit the rth item, wr is the resource consumption of the rth item in the knapsack, C is the capacity of the knapsack, xr is a binary variable denoting whether the rth item is assigned to the knapsack (xr = 1 if the rth item is assigned, xr = 0, otherwise). In this regard, Eq. 6 is the objective function to maximize the profit of the knapsack. Equation 7 represents the capacity constraint. Finally, Eq. 8 imposes restrictions on the decision variables.

0–1 KP is shown to be an NP-hard problem (Kellerer et al. 2004). Although there exist some exact solution methodologies for 0–1 KP (Della Croce et al. 2017a, b), heuristic approaches are more commonly preferred due to similar reasons with those of UFLP’s. Shi (2006) proposed an improved modification of ACO for 0–1 KP. Shah-Hosseini (2008) employed an intelligent water drops algorithm to solve and extension of the 0–1 KP. Drake et al. (2014) used a genetic programming based on a hyper-heuristic for the same problem. A schema-guiding evolutionary algorithm was proposed by Liu and Liu (2009). A binary modification of PSO was employed by Li and Li (2009). Several bio-inspired algorithms were proposed to solve 0–1 KP (Bhattacharjee and Sarmah 2014; Feng et al. 2017). Zhou et al. (2016) used a complex-valued encoding in a metaheuristic algorithm. The same procedure was also adopted by Zhou et al. (2017) within another approximation algorithm, namely, Wind Driven Optimization algorithm. Bhattacharjee and Sarmah (2017) reported a survey focusing on swarm-based algorithms for knapsack problems.

2.3 Set union knapsack problem (SUKP)

SUKP is an extension of 0–1 KP (Goldschmidt et al. 1994; Kellerer et al. 2004; Arulselvan 2014). It comprises of a set of elements U = {1, …, n} and a set of items \(\aleph = \left\{ {1, \ldots ,m} \right\}\), where each item in set \(\aleph\) (i = 1, …, m) corresponds to a subset of elements, represented by Si, with a non-negative profit denoted by \(p: \aleph \to {\mathbb{R}}^{ + }\). Each of the elements has non-negative weight \(w: U \to {\mathbb{R}}^{ + }\) in SUKP. For an arbitrary subset \(A \subseteq \aleph\), total weight of the union of subset A is defined as \(W\left( A \right) = \mathop \sum \nolimits_{{e \in \cup_{{i \in A^{{S_{i} }} }} }} w_{e}\) and profit of A is denoted by \(P\left( A \right) = \mathop \sum \nolimits_{i \in A} p_{i}\). The aim is to find a subset of items \(\aleph^{*} \subseteq \aleph\) such that the total profit \(P\left( {\aleph^{*} } \right)\) is maximized and \(W\left( {\aleph^{*} } \right)\) does not exceed knapsack capacity. The problem is formally given by Eqs. 9–10, where we is the weight of the eth element in the union set of the selected items, pi is the profit of ith item in the subset A and C is the knapsack capacity.

$$maximize P\left( A \right) = \mathop \sum \limits_{i \in A} p_{i}$$
(9)
$$\begin{aligned} & {\text{s}}.{\text{t}}. \\ & W\left( A \right) = \mathop \sum \limits_{{e \in \cup_{{i \in A^{{S_{i} }} }} }} w_{e} \le C, A \subseteq \aleph \\ \end{aligned}$$
(10)

An illustration for the SUKP is depicted in Fig. 2. As one can see from this figure, there exist three items each with three elements. The item-1 contains the element-1 and the element-3, while the item-2 contains only the element-2. Finally, the item-3 contains the element-2 and the element-3. If the item-1 and the item-2 are included in the knapsack, the weights of all elements should be taken into account while evaluating the capacity constraint. Similarly, if the item-2 and the item-3 are assigned to the knapsack, only the element-2 and the element-3 should be considered, because, their union set is comprised of only these elements.

Fig. 2
figure 2

An illustration for set union knapsack problem

Full size image

SKUP has many practical applications including financial decision-making, database partitioning, data stream compression etc. (He et al. 2018). Although there are some SKUP-related publications in the literature, this problem deserves further research. Goldschmidt et al. (1994) proposed a dynamic programming procedure for SUKP. Lister et al. (2010) addressed dynamic character caching as SKUP. An important note, which is related to boundaries and a special case of SUKP, was presented by Arulselvan (2014). Riondato and Vandin (2014) solved SUKP in order to obtain an upper bound for frequent itemsets, which is closely related to data mining issues. Several approximation schemes for SUKP and related problems were presented by Taylor (2016). Su and Zhou (2016) presented a reduced modification of this problem. Diallo et al. (2017) modeled virtual machine selection problem in cloud computing systems as a SUKP. Finally, He et al. (2018) presented detailed discussions about this problem.

3 Weighted superposition attraction algorithm

Before introducing the proposed bWSA, canonical WSA (Baykasoğlu and Akpinar 2015, 2017) is first summarized.

3.1 Canonical WSA

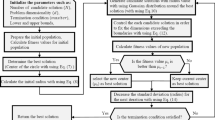
WSA is initialized with a predefined number of solutions. These solution vectors are referred to as artificial agents in WSA. Each artificial agent has its own position (coordinates) and an objective function value, representing the quality of the corresponding solution vector.

3.1.1 Initialization of WSA

This step consists of determining the values of the parameters used in WSA. The symbols of these parameters and related definitions are given below in Table 1. This nomenclature is used in the rest of the paper.

Table 1 Nomenclature for WSA
Full size table

3.1.2 Generating neighborhood solutions in WSA

The artificial agents in WSA move according to the guidance of the superposition vector. Therefore, the first step in neighborhood solution generation is to generate a superposition by making use of the current population information. Accordingly, WSA algorithm calculates the coordinates of the superposition as the weighted sum of the agents’ positions. In this respect, first, artificial agents are sorted according to their fitness values. The first rank is the fittest agent here. Next, weights of each agent are evaluated based on these ranks. Finally, weighted sum for each dimension is calculated as given in Algorithm 1. In this procedure, effects of the sorted agents on the generated superposition are exponentially decreased as their ranks increase. While the fittest individual has the greatest effect, lower quality solutions have minor effects. It should be noted here that effects the artificial agents on the generated superposition can be controlled by the user-supplied parameter τ.

Subsequent to generating the target vector (superposition), its fitness is evaluated and search directions of agents are determined as presented in Algorithm 2. It should be mentioned that this procedure is given for a minimization problem. According to this procedure, agents of which the fitness values are worse than that of the superposition’s, get attracted by the superposition vector. Additionally, if an agent is better than the superposition, then that agent might also move towards the coordinates of the supposition by a probability defined by \(e^{{f\left( i \right) - f\left( {\overrightarrow {tar} } \right)}}\). Otherwise, that agent performs a random walk. Finally, the positions of the agents for the next iteration are determined in regard to the formulation given in Eq. 11, where \(\left| {\vec{x}\left( {i,j} \right)^{t} } \right|\) represents the absolute value of the position vector of the ith artificial agent on dimension j at iteration t, and \(\overrightarrow {direct} \left( {i,j} \right)^{t} \in \left\{ { - 1,0,1} \right\}\). The mentioned procedure is formally given in Algorithm 3, where the parameter sl is also adaptively tuned. Updating of the sl for the next iteration is formulated in Eq. 12.

figure a
figure b
figure c
$$\vec{x}\left( {i,j} \right)^{t + 1} = \vec{x}\left( {i,j} \right)^{t} + sl^{t} \times \overrightarrow {direct} \left( {i,j} \right)^{t} \times \left| {\vec{x}\left( {i,j} \right)^{t} } \right|$$
(11)
$$sl^{t + 1} = \left\{ {\begin{array}{*{20}c} {sl^{t} - e^{{ - t/\left( {t + 1} \right)}} \times \varphi \times sl^{t} \quad if\quad rand() \le \lambda } \\ {sl^{t} + e^{{ - t/\left( {t + 1} \right)}} \times \varphi \times sl^{t} \quad if \quad rand() > \lambda } \\ \end{array} } \right.$$
(12)

Putting things together, subsequent to initialization of WSA algorithm, an iteration here is comprised of first, determination of the superposition and next, movement of all artificial agents in guidance of this generated superposition vector. Finally, at the end of an iteration, the best-found solution is updated if necessary. It is worth stressing that, although an adaptive step length is proposed in the canonical version of WSA, it not necessarily required in implementation. One can simply use a fixed step length that remains stationary throughout the search or any other step length controlling method can optionally replace this method.

3.2 The binary WSA

As mentioned above, a superposition in canonical WSA is generated by the weighted sum of the solution vectors for each dimension. However, in a binary space, this procedure is not practical. Therefore, in the present work, a recent method (Baykasoğlu and Şenol 2016a; Baykasoglu and Ozsoydan 2018), which is clarified in the following subsection, is adopted.

3.2.1 Generating binary superposition

In bWSA, agents are first sorted in regard to their fitness values (1st rank is the fittest) and weights are evaluated as in canonical WSA (Algorithm 1). Next, uniform random numbers rand() ∊  [0,1] are generated for each dimension. These random numbers are used as threshold values to determine the candidate agents that undergo roulette wheel selection. Thus, agents, whose weights are equal to or greater than these thresholds undergo roulette wheel procedure. Finally, the bit of the winner agent is chosen as the corresponding bit of the superposition vector. This procedure is followed for each of the dimensions. For a better understanding, an example with different weights for different τ values is presented in Table 2.

Table 2 A sample population for bWSA
Full size table

Let’s assume that τ is fixed to 0.7 and generated random numbers for each of the corresponding dimensions are 0.6, 0.3, 0.35, 0.4 and 0.9, respectively. Thus, for the first dimension, the first two agents undergo a roulette wheel, because, their weights are greater than or equal to 0.6. The bit of the winner agent (underlined and highlighted in bold) of this roulette wheel is transferred to the superposition vector (which is currently empty). The same procedure is performed for the remaining dimensions except for the last dimension. Since at least two candidates are required to perform a roulette wheel, the bit of the first agent for the last dimension is directly transferred to the superposition vector. Finally, the generated superposition is given in the last row of Table 2.

It should be stressed that the first agent is always a candidate for the roulette wheel procedure. It is also clear that transfer functions are not required here. Thus, one can directly use a binary population. Moreover, in parallel with WSA, behavior of bWSA can also be controlled via different values of τ. Lower values of τ encourages diversity, on the contrary, greater values of τ yield to a more elitist behavior.

3.2.2 Solution representation and generating neighbors in bWSA

A solution is represented by binary variables in bWSA. It is clear that the 1s in a solution string represent the opened facilities at the corresponding locations in UFLP. Therefore, the length of a solution string for UFLP is equal to the number of possible locations at which a facility can be established. Similarly, length of a solution string for 0–1 KP and SUKP is equal to the number of items that can be assigned to the knapsack. In parallel, 1s in a solution string for 0–1 KP and SUKP represent the included items in the knapsack.

In canonical WSA, agents move via \(\overrightarrow {direct}\) and \(\overrightarrow {gap}\) vectors. The parameters sl and φ control the speed of movements. However, since these vectors and parameters are not usable in binary spaces with their current forms, movements of agents are modified by making use of uniform-based crossover and bit-flipping procedures.

It should be recalled that artificial agents either move towards the coordinates of the superposition or they perform random walks. Let us first consider the random walks. In order to detect promising regions quickly, it is clear that a more diversified search is required at the beginning of the search. Additionally, it is known that an approximation algorithm should intensify to achieve better results. Therefore, the exponentially decreasing step length (Baykasoglu 2012; Baykasoğlu and Ozsoydan 2015) given in Eq. 12 is modified here for binary spaces. In this extension, the parameter \(sl^{t} \in \left[ {0,1} \right]\) is decreased for the next iteration by using the formula given in Eq. 13. Next, it is multiplied by the length of the solution string (dimension) and the obtained value is rounded up to obtain the total number of bits to flip, which shown by \(int\_sl^{t + 1}\) (Eq. 14). Finally, randomly selected \(int\_sl^{t + 1}\) bits of an agent are flipped.

$$sl^{t + 1} = sl^{t} - e^{{ - t/\left( {t + 1} \right)}} *\varphi *sl^{t}$$
(13)
$$int\_sl^{t + 1} = \lceil sl^{t + 1} \times D\rceil$$
(14)

Differently from canonical WSA, it is assumed here that initial step length is bounded by \(sl^{1} \in \left[ {0,1} \right]\). For example, if sl1 is set to 0.50, an agent performing a random walk flips 50% of its bits at the first iteration. An illustration for sl1 = 1.00 and for D = 50 with different φ values is presented in Fig. 3. As one can see from Fig. 3.a, greater values of φ give rise to steeper decrements in the continuous step length. Accordingly, randomly walking agents flip only a few bits throughout the second half of the search. On the other hand, φ = 0.01 yields to a late intensification. Therefore, a precise balance should be established to use this procedure efficiently.

Fig. 3
figure 3

Exponentially decreasing a continuous step length and b corresponding integer step length for different values of φ

Full size image

While moving an agent towards the superposition, a uniform-based crossover is employed in bWSA. In this procedure, uniform-based crossover rate (puxo) is defined first. This parameter represents the probability of taking a gene from the superposition vector. Accordingly, random numbers rand()∊ [0, 1] are generated for each dimension separately. If the generated random number for the corresponding bit is less than or equal to puxo, that dimension takes the value of the superposition’s. Otherwise, it is not changed. Thus, greater values of puxo induce faster movements towards the superposition. In the present study, puxo is assumed to remain stationary until the end of the run. The artificial agent movements in bWSA with respect to a minimization problem are presented in Algorithm 4. Finally, putting things together, bWSA is provided in Algorithm 5.

figure d

3.2.3 Handling infeasibilities

The first binary problem solved by bWSA is indeed obtained by excluding the capacity constraints from facility location problems. In other words, demands of all customers can be fulfilled by only a single opened facility in UFLP. It is also mentioned in the previous subsection that the number of the opened facilities is controlled by solution representations in bWSA. Therefore, this problem can be considered as an unconstrained binary optimization problem. Additionally, as mentioned by Kiran (2015), demand of a customer is always entirely fulfilled by the nearest opened facility.

figure e

On the other hand, 0–1 KP has a knapsack capacity constraint. In this regard, the penalizing function of Zou et al. (2011) (Eq. 15) is adopted for 0–1 KP. In this method, first, the maximization function of 0–1 KP (Eq. 6) is transformed into a minimization function by multiplying it by −1. Next, the penalty term \(\omega \times { \hbox{max} }\left( {0,g} \right)\) is appended to the objective function, where \(g = \mathop \sum \limits_{r \in R} w_{r} x_{r} - C\) and ω is a scalar that is fixed to 1020 in Eq. 15.

$$minimize\left( { - \mathop \sum \limits_{r \in R} p_{r} x_{r} + \omega \times { \hbox{max} }\left( {0,g} \right)} \right)$$
(15)

Finally, in SUKP, the repairing method presented by He et al. (2018) is employed. In this method, first, a quick sorting algorithm is used to sort the items in regard to their profit/weight ratios, taking the frequencies of elements separately for each item into account. Next, violating item(s) is (are) found by using this sorted list. After discarding them, a posterior procedure is peformed to detect any fitting item(s) to the remaining capacity. This procedure is presented in detail by He et al. (2018).

4 Experimental study

4.1 Fine tuning of the parameters in bWSA

bWSA has several parameters to tune. Allowed maximum number of iterations (maxiter) and population size (AA), which determine the number of consumed function evaluations (FEs), are two of these parameters. In order to perform fair comparisons with the literature and to keep FEs at an acceptable level, a balance between the parameters maxiter and AA is established. In this respect, performed preliminary trial tests show that higher quality solutions can be obtained, when maxiter and AA are fixed to 1000 and 20, respectively.

Another parameter that is denoted by τ ∊  [0,1] defines the search characteristic of bWSA. Therefore, a set of different values for τ ({0.1, 0.2, 0.3, …, 0.9}) is tested in preliminary work to observe the effects of this parameter. The preliminary empirical tests that have been performed based on medium-scaled instances show that bWSA achieves better results, when τ is fixed to 0.80.

The parameters φ and \(sl^{t} \in\) [0,1] have critical effects on random walks. It is further clear that the value of sl1 affects the succeeding step lengths. Therefore, one needs to define the initial step length sl1 and the speed of decrement (φ) to control the random walks in bWSA. According to the results of the preliminary tests, sl1 and φ are fixed to 0.4 and 0.008, respectively. Thus, while the agents flip 40% of their bits in the first generation, they flip only a single bit towards the end of the run.

The final parameter to tune in bWSA is the crossover rate (puxo ∊  [0,1]) that is used in uniform-based crossover while moving an agent towards the coordinates of the superposition. A set of different levels for puxo ({0.1, 0.2, 0.3, …, 0.9}) is tested. According to the same preliminary tests, puxo is fixed to 0.8.

4.2 Computational results

4.2.1 Results for UFLP

The performance of the bWSA in UFLP is tested in benchmarking instances taken from OR-Lib (http://people.brunel.ac.uk/~mastjjb/jeb/orlib/files/), for which the optimal solution is known. The attributes of these problems are presented in Table 3. Obtained results for UFLP are presented in Table 4. Columns of this table (best, worst, std. dev., hit) represent the best-found solution, the worst-found solution, standard deviance of the found solutions over 30 runs and the number of runs for which the optimum is found, respectively.

Table 3 Attributes of the used UFLP instances
Full size table
Table 4 Computational results for UFLP
Full size table

Results of bWSA are compared to the previously published results of the algorithms based on PSO and ABC. As one can see from Table 4, bWSA is capable of finding optimum solutions in all instances. Additionally, the highlighted results in Table 4 represent the instances, for which the hit numbers are greater than or equal to the hit numbers of other algorithms. In this respect, bWSA clearly outperforms CPSO of Sevkli and Guner (2006). Moreover, it can be concluded that the proposed algorithm is competitive considering the results of ABC, recently reported by Kiran (2015).

Finally, convergence graphs of bWSA for different instances are presented in Fig. 4. Since each problem has different optimum, plotting them on the same graph with an identical scale yields to disproportionality. Therefore, percentage gap values (Eq. 16) for the corresponding iteration are plotted in these figures. Each data point is the average over 30 runs.

$$gap\% = \left( {{\raise0.7ex\hbox{${\left( {z^{*} - opt} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {z^{*} - opt} \right)} {opt}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${opt}$}}} \right) \times 100$$
(16)
Fig. 4
figure 4

Gap % convergence graph of bWSA for instances a cap71–74, b 101–104 and c cap131–134

Full size image

It is clear from Fig. 4 that bWSA starts with greater gaps in larger-scaled instances. This is an expected result due to the adopted step size function. However, it is further clear from Fig. 4 that bWSA is capable of finding approximately same gap % values after performing only 50–100 iterations regardless of the difficulty of the problem. This demonstrates the convergence capability of the proposed approach.

4.2.2 Results for 0–1 KP

The performance of bWSA in 0–1 KP is tested first by using the standard benchmarks instances, which are denoted by \(f_{i} \left( {i = 1, \ldots ,10} \right)\) in Table 5. Next, the proposed approach is tested in randomly generated larger-scaled instances. All printed results are evaluated over 30 independent runs. The results of bWSA for the 10 commonly used benchmarks are presented in Table 5 of which the columns (f, opt., best, mean, worst, std. dev., gap %, hit) denote the instance index, optimum value, the best found solution, mean over 30 runs, the worst found solution, standard deviance, percentage gap (Eq. 16) and the number of runs, for which the optimum is found, respectively.

Table 5 Standard instances for 0–1 KP (Zou et al. 2011; Bhattacharjee and Sarmah 2014)
Full size table

As one can see from Table 5, bWSA is capable of finding optimum solution for each of the instances f1-10. Moreover, except for the instance f7, bWSA finds optimum solutions in all runs. However, it is apparent that the proposed approach finds sub-optimal results in a few runs of instance f7.

Secondarily, bWSA is tested in large-scaled 0–1 KP instances, which are generated according to the guidelines reported in Zou et al. (2011). Briefly, in this technique, profit and resource consumption parameters of the items are randomly generated as integer numbers according to some restrictions and the knapsack capacity is assumed to be fixed. It is clear that, although the optimum solutions of the instances f1-10 are known, an upper bound technique for the rest of the instances  f11-18 is required. In this respect, Dantzig upper bound (Pisinger and Saidi 2017) is employed in the present study. In Dantzig upper bound, the mathematical model is first relaxed. Thus, the LP-relaxed (fractional) 0–1 KP, where 0 ≤ xr ≤ 1 for all r = 1, 2, …, n. can be solved to optimality. Accordingly, items are sorted in regard to non-increasing order of profit/weight (\({\raise0.7ex\hbox{${p_{r} }$} \!\mathord{\left/ {\vphantom {{p_{r} } {w_{r} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${w_{r} }$}}\)) ratios. Next, sorted items are assigned to the knapsack until an item s does not fit into the knapsack. Finally, the optimum value of the LP-relaxed 0–1 KP can be found via Eq. 17. It is further known that if all profits are integers (as in the present case), this value can be floored and the Dantzig upper bound can be obtained as \(\lfloor z_{LP\_relaxed}^{*} \rfloor\).

$$z_{LP\_relaxed}^{*} = \mathop \sum \limits_{r = 1}^{s - 1} p_{r} + \left( {C - \mathop \sum \limits_{r = 1}^{s - 1} w_{r} } \right) \times \frac{{p_{r} }}{{w_{r} }}$$
(17)

The results for the rest of the problems f11–18 are presented in Table 6, of which the columns (f, number of items, Dantzig upper bound, best, mean, worst, std. dev., gap %) represent instance index, problem size, upper bound, the best found solution by the algorithm, mean over 30 runs, the worst found solution, standard deviance and the percentage gap (Eq. 16), respectively.

Table 6 Results for randomly generated larger-scaled instances for 0–1 KP
Full size table

It is clear in this case that \(\lfloor z_{LP\_relaxed}^{*} \rfloor\) replaces the opt in Eq. 16. As one can see from Table 6, obtained percentage gap values vary between 0.32% and 7.25% except for the instance f14. Particularly for extremely large-scaled instances with 1000–1500 items (f16-18), average gap appears to be approximately 4.09%, which can be considered as a promising performance. On the other hand, bWSA obtains lower quality solutions in f14. It is thought that this circumstance arises from the structure of the generated data, which has severe effects on the tightness of the instance. In such cases, occasionally the gap between the theoretical upper bound the best-found solution might dramatically increase.

Convergence graphs for gap % values of the used instances (except for f14) are presented in Fig. 5, where all plotted data points are the averages over 30 run. It is clear from this figure that bWSA can still converge to 0.00% gap if the algorithm is allowed to continue to search. This is due to the exponentially decreasing step size procedure. However, more challenging conditions are employed here and the algorithm is terminated when a fixed number of iterations is achieved. This criterion is defined regardless of the problem size. It is apparent from the curves in Fig. 5a (more horizontal looking) and Fig. 5b (more vertical looking).

Fig. 5
figure 5

Gap % convergence graph of bWSA for instances a f11–13 and b f14–18

Full size image

4.2.3 Results for SUKP

In order to test the performance of bWSA in SUKP, all instances presented by He et al. (2018) are used in the present work. The authors name those instances in the form of \(m\_n\_\alpha \_\beta\), where m is the number of items, n is the number of elements, α is the density of an element and \(\beta\) is a parameter to define the knapsack capacity. Three groups of instances are provided by He et al. (2018), where it is assumed that \(m > n\), \(m = n\), \(m < n\) for the first, for the second and for the third group of instances, respectively. The rest of the parameters are used exactly the same. All results, which are presented in Tables 7, 8, 9, are evaluated over 100 independent runs.

Table 7 Computational results of the first type of instances for SUKP
Full size table
Table 8 Computational results of the second type of instances for SUKP
Full size table
Table 9 Computational results of the third type of instances for SUKP
Full size table

In Tables 7, 8, 9, the Instance columns represent the attributes of the instance. The columns A-SUKP give the results obtained by the method proposed by Arulselvan (2014). Another column BABC is devoted to the results of the binary ABC of He et al. (2018), which was inspired by the study of Ozturk et al. (2015). A similar algorithm is denoted by ABCbin that is adopted from Kiran (2015). The other columns, GA and binDE are devoted to the results of GA and a binary modification of DE. All of these results are adopted from He et al. (2018). Finally, the columns bWSA are devoted to the results of the proposed approach.

As one can see from Tables 7, 8, 9, bWSA outperforms the rest of the algorithms in most of the instances. It is apparent that there are some ties particularly in smaller-scaled problems. However, it is further clear that the performance of bWSA is better than the compared algorithms particularly in large-scaled problems. This indeed shows that the proposed approach mostly obtains better solutions in SUKP regardless of the problem size. Additionally, it can be put forward that although similar mean values are obtained by each of the compared algorithms, generally speaking, standard deviance performance of bWSA is worse than the other algorithms’. This can be considered as a drawback for the proposed approach.

Putting things together, all conducted tests in the present work points out the efficiency of the proposed modification of bWSA in binary optimization problems.

5 Concluding remarks

The present study examines the performance of a new generation metaheuristic referred to as WSA in binary optimization problems. In this respect, WSA, which is already shown to be efficient in a variety of optimization problems, is first modified for stationary binary spaces. A specialized roulette wheel procedure is used for this modification. Additionally, uniform-based crossover and random bit flips are employed while generating a new solution. Thus, any transfer functions for converting real values to binary are not required in the proposed bWSA. Moreover, a systematically controlled step sizing procedure to put control on the search speed is adopted in bWSA. Step size, which is indeed the number of bits to be flipped, is exponentially decreased throughout generations. Thus, while bWSA performs a more diversified search at the initialization stage, it is encouraged for intensification around the found promising regions towards the end of a run.

The performance of bWSA is examined in some well-known binary optimization problems, including uncapacitated facility location problem, 0–1 knapsack problem and set union knapsack problem, which have numerous applications in real-life. Promising results point out the efficiency of the proposed bWSA. Extending the proposed modification for other combinatorial problems is scheduled as future work.