A vendor–buyer integrated inventory system with variable lead time and uncertain market demand

Abstract

In this paper, we consider a single-vendor single-buyer integrated inventory model in which the replenishment lead time is assumed to be a linear function of batch size, setup time, and transportation time. Both the vendor and the buyer are interested to invest in reducing the ordering cost. Shortages, if occur in buyer’s inventory, are partially backlogged with a certain limit of backorder price discount. The objective of the study is to derive the optimal decisions and the best investment policy by minimizing the expected annual total cost of the integrated system. The existence and uniqueness of the optimal solution are investigated and an efficient algorithm is designed to find the optimal solution of the proposed model numerically. We demonstrate the aids of reducing order-processing cost through numerical examples and show that it has significant effect on lot sizing decisions. It is also observed that transportation delay forces the buyer to stock more in order to defend the stock-out situation.

1 Introduction

In inventory management, lead time has always been an important factor to consider (Naddor 1966; Das 1975; Magson 1979; Foote et al. 1988). Lead time is defined as the duration of time between placing an order and receiving it. It has significant influence on logistics and supply chain management. Almost all integrated inventory models are developed based on the assumption that replenishment lead time is either zero or constant (Wee and Widyadana 2013; Das 2018) or a stochastic variable (Sajadieh and Jokar 2009; Zhou et al. 2012; Hossain et al. 2017) which is not subjected to control.

In many practical situations, however, lead time is controllable; that is, lead time can be shortened at the expense of an additional cost. Liao and Shyu (1991) were the first researchers to introduce variable lead time in stochastic inventory model. In their model, they assumed that the lead time can be decomposed into several components having different crashing costs for reducing to a specified minimum duration. Thereafter, a number of researchers have contributed significantly in controllable lead time literature (Dey and Giri 2014; Sarkar et al. 2015; Mandal and Giri 2015).

Although constant or deterministic lead time assumption follows JIT (just-in-time) philosophy, but it is not fitted in most of the modern complex setups where overseas, containerized, and air-freight transportation are involved. According to Tersine (1982), lead time involves order preparation time, order shipment/delivery time, set-up time, etc. Recognizing that manufacturing lead time is highly dependent on lot-size, Kim and Benton (1995) questioned on the assumption of fixed lead time and established a relationship between lot-size and lead time. They showed that significant savings can be occurred by considering the interrelationships between lot size and safety stock decisions. Hariga (1999) revisited Kim and Benton’s (1995) model to rectify the expression of the annual backorder cost, and proposed another relation for the revised lot-size. However, the above two models were considered only from buyer’s/manufacturer’s perspective. Ben-Daya and Hariga (2004) were the first researchers to consider lot-size dependent lead time in a vendor–buyer integrated supply chain model with stochastic demand. However, they assumed that the reorder points for all replenishment cycles are same. Hsiao (2008) improved this model by assuming that there are two different reorder points and service levels.

In reality, due to various reasons such as labor strike, bad weather, unavailability of raw materials, machine failure, human errors in counting, transcribing, etc., it is quite difficult for the vendor to deliver items timely to the buyer. As a result, the buyer faces the stock-out situation, in which case, customers’ demand is not fulfilled resulting in a financial loss for him/her. A stock-out situation not only disappoints customers but also makes doubt in customer’s mind about the storage capacity of the buyer. The unsatisfied customers may not turn up next time to meet their demand from the same buyer. Therefore, the buyer in this case loses the opportunity to earn some more profit. However, for fashionable goods such as certain brand gum shoes, hi-fi equipment, cosmetics and clothes, some customers may wait up to a certain period for backorder and some may not wait at all (Montgomery et al. 1973; Rosenberg 1979; Park 1982; Sarkar and Sarkar 2013; Aslani et al. 2017). Therefore, motivating the customers for backorder becomes a challenging problem for the buyers. Price discount on backordered items is a well-known policy which can motivate the customers for backorder as well as increase the rate of backorder (see Pan and Hsiao 2001; Lin 2010; Priyan and Uthayakumar 2014; Kurdhi et al. 2015).

Ordering cost reduction has become a key to business success and attracted considerable research attention recently. Ordering quantity, service level, and business competitiveness can be shown to possibly be influenced directly or indirectly via ordering cost control. Integrated vendor–buyer inventory models are generally developed considering constant ordering cost. However, in some practical situations, ordering cost can be controlled and reduced in various ways. It can be attained through worker training, procedural changes, specialized equipment acquisition, etc. Porteus (1985) first developed a framework for investing in reducing setup cost in an EOQ model. Subsequently, Affisco et al. (2002) investigated the investment in setup cost reduction and quality improvement for a joint supplier–customer system which produces defects at a known constant rate. Later, some researchers (Kim et al. 1992; Coates et al. 1996; Annadurai and Uthayakumar 2010; Lou and Wang 2013) developed setup/order cost reduction inventory models under various assumptions.

Many industries have been devoting efforts to improve customer service, control order frequencies and reduce costs with their business partners. In this regard, the following questions from managerial point of view may arise: What would be the optimal policy for an integrated vendor–buyer supply chain system if the lead time is dependent on production lot size, setup time and transportation time? What would be the appropriate price discount strategy, if adopted by the buyer during shortage period to secure customer demand, and what would be the right investment amount to reduce order processing cost? To find answers of these questions, in this paper, we model a continuous review inventory system. Unlike previous researches, we consider different replenishment lead times and reorder points for the shipments. We assume that the buyer offers backorder price discount to his customers with outstanding orders during the shortage period to secure customer orders. The backorder ratio is assumed to be a variable which is proportional to the backorder price discount offered by the buyer. We also assume that the order processing cost is a decreasing exponential function of capital expenditure. In this study, we assume that the long-term strategic partnership between the buyer and the vendor is well established and, therefore, the buyer and the vendor cooperate and share information with each other. The objective is to determine the optimal ordered quantity, safety factor, backorder price discount, the investment amount in ordering cost reduction, and the number of shipments by minimizing the annual total cost of the integrated system. The rest of the paper is organized as follows: Sect. 2 reviews the relevant literature. Notation and assumptions are given in Sect. 3. In Sect. 4, the proposed model is formulated mathematically. Section 5 describes the solution procedure of the model. Numerical results and sensitivity analysis are given in Sect. 6. Finally the paper is concluded in Sect. 7.

2 Literature review

During the last few decades, the concept of integrated vendor–buyer inventory management has attracted considerable attention of many supply chain researchers. The cooperation among vendors and buyers for improving the performance of the supply chain has been the key point of their researches. One of the primary models dealing with single-supplier single-buyer integrated inventory system was developed by Goyal (1976). Banerjee (1986) generalized Goyal’s model and presented a joint economic lot size model where the vendor produces order on lot-for-lot basis to fulfill the buyer’s order quantity under deterministic condition. Further, Goyal (1988) relaxed the lot-for-lot policy of the vendor to generalize Banerjee’s model. Later, Ha and Kim (1997) generalized Goyal’s (1988) model and developed an integrated lot-splitting model facilitating multiple shipments in small lots. Since then a lot of efforts have been made by the researchers (Cetinkaya et al. 2008; Kang and Kim 2010) to study the integrated vendor–buyer model under various assumptions. Yu and Dong (2014), and Braglia et al. (2016) made some advances in the integrated model under stochastic demand. Nouri et al. (2018) developed a compensation-based wholesale price contract to coordinate between retailer and seller in a two-echelon periodic review inventory system under a stochastic promotional and innovation efforts sensitive demand.

Most of the above mentioned works did not consider the issue of variable lead time and its relation to the production shipment schedule in terms of the number and the size of batches transferred from the vendor to the buyer. Liao and Shyu (1991) were the first researchers to introduce variable lead time in inventory model. In their model, they assumed that the lead time can be decomposed into several components having different crashing costs for reducing to a specified minimum duration. Ben-Daya and Raouf (1994) reconsidered Liao and Shyu’s (1991) model and established a more general model by taking both order quantity and lead time as decision variables without consideration of shortages. Ouyang et al. (1996) extended Ben-Daya and Raouf’s (1994) model to consider shortages in the inventory system. Later, Yang and Pan (2004), Ouyang et al. (2007), Li et al. (2011), Arkan and Hejazi (2012), Jha and Shanker (2013) and Mandal and Giri (2015) considered controllable lead time in integrated supply chain model to maximize benefits for all the participating players.

Glock (2012) extended Hsiao’s (2008) model by assuming that lead time can be reduced by crashing the setup time and transportation time. Zikopoulos (2017) studied a remanufacturing system and examined the advisability taking into account the stochastic remanufacturing lead-time under different scenarios regarding returns’ quality and demand for remanufactured products. Heydari et al. (2016) provided a new coordination mechanism based on the lead time crashing between a seller and a buyer in order to convince the buyer to change his decision variables and hence increase the profitability of the supply chain. Kazemi et al. (2016) developed a fuzzy lot-sizing model in which the effect of human learning with cognitive and motor capabilities are investigated. In their model, both demand and lead-time during the planning period were considered as fuzzy parameters. Yang et al. (2017) developed a newsvendor model to investigate inventory competition in a dual-channel supply chain and explored the delivery lead time decision in the direct channel. Hossain et al. (2017) developed a single-vendor single-buyer integrated inventory system with penalty cost for delivery lateness under generalized lead time distribution.

Some of the above works assumed that shortages, if occur, are either fully backlogged or completely lost; the issue of partial backlogging or partial lost sale is overlooked. However, in practice, there are some items especially fashionable goods such as certain brand gum shoes, hi-fi equipment, cosmetics and clothes for which a fraction of customers, during the shortage period, can wait for backorder up to a certain period while the other fraction can not wait at all. Ouyang et al. (1996) generalized Ben-Daya and Raouf’s (1994) model by considering mixture of backorder and lost sales. Ouyang and Chuang (2001) considered backorder rate as a control variable to generalize Ouyang et al.’s (1996) model. Kazemi et al. (2015) extended an existing EOQ inventory model with backorders in which they fuzzified both the demand and lead times. Cárdenas-Barrón et al. (2018) provided a correct mathematical formulation and solution of an inventory model with two backlog costs when the supplier offers a price discount to the buyer. Now-a-days, motivating the customers to wait for backorder is a challenging task for the buyers. Discount policy on backordered items can influence the customers for backorder as well as increase the backorder rate (Pan and Hsiao 2001, 2005; Chuang et al. 2004; Lee et al. 2006). Sarkar et al. (2015) studied an inventory model with quality improvement and backorder price discount under controllable lead time.

Most of the existing inventory models assume that order processing cost is fixed. In practice, order processing cost can be controlled and reduced through various efforts such as worker training, procedural changes and specialized equipment acquisition. In the literature, Porteus (1985) was the first author to introduce the concept of setup cost reduction. This development encouraged many researchers to examine setup/ordering cost reduction (see Keller and Noori 1988; Nasri et al. 1990; Kim et al. 1992; Paknejad et al. 1995). Chang et al. (2006) considered an integrated vendor–buyer model with controllable lead-time and ordering cost reduction. Zhang et al. (2007) analyzed a two-echelon integrated vendor-managed inventory system with ordering cost reduction. The capital investment in reducing buyer’s ordering cost is assumed to be a logarithmic function of the ordering cost. Huang (2010) developed an integrated inventory model to determine the optimal policy under conditions of order processing cost reduction and permissible delay in payments. Lou and Wang (2013) revisited Huang’s (2010) model to relax the dispensable assumption that the buyer’s interest earned is always less than or equal to its interest charged. Huang et al. (2010) developed a model to determine an optimal integrated vendor–buyer inventory policy under conditions of order processing time reduction and permissible delay in payments.

From the above literature review we found that many researchers focused on developing either setup cost or ordering cost reduction by assuming lead time as stochastic or controllable. However, no attempt has been made to consider integrated vendor–buyer inventory model with controllable order processing cost under variable lead time and backorder price discount. This paper intends to fill this gap in the literature. The position of the paper with respect to the existing literature is shown in Table 1.

Table 1 A comparison of the present model with some related works in the literature

3 Notation and assumptions

We use the following notation to develop the proposed model.

3.1 Notation

Symbols	Description
Decision variables
Q	Shipment size (units)
$k_{1}$	Safety factor of the first batch
$k_{2}$	Safety factor of the jth batch, $j=2,\ldots ,m$
$\pi _{x}$	Backorder price discount, $0\le \pi _{x}\le \pi _{0}$
W	Annual expenditure for reducing order processing cost
m	Number of deliveries from the vendor to the buyer
Parameters
D	Annual demand at the buyer (units/year)
P	Production rate, where $P=1/p$
S	Vendor’s setup cost per setup $(\$/$setup)
$A_{0}$	Buyer’s original order processing cost per order $(\$/$order)
$T_{s}$	Setup time including transportation time
$T_{t}$	Transportation time
$\epsilon$	Fraction of transportation time $T_{t}$ out of $T_{s}$, i.e, $\epsilon =T_{t}/T_{s}$
$h_{b}$	Unit holding cost at the buyer (${\$}$/unit/year)
$h_{v}$	Unit holding cost at the vendor (${\$}$/unit/year)
F	Transportation costs per shipment $(\$/$shipment)
$\pi _{0}$	Buyer’s marginal profit (${\$}$/unit)
$S_{1}$	Safety stock of the first batch
$S_{2}$	Safety stock of the jth batch, $j=2,\ldots ,m$
$r_{1}$	Reorder point of the first batch
$r_{2}$	Reorder point of the jth batch, $j=2,\ldots ,m$
$y_{1}$	Lead time demand of the first batch
$y_{2}$	Lead time demand of the jth batch, $j=2,\ldots ,m$
$g(y_{1})$	Probability density function of $y_{1}$
$g(y_{2})$	Probability density function of $y_{2}$
$\sigma$	Standard deviation of the lead time demand
$\delta _{0}$	Upper bound of backorder ratio
Functions
A(W)	Buyer’s order processing cost as a function of capital expenditure W
l(Q)	Buyer’s replenishment lead time as a function of shipment size Q
$\delta (\pi _{x})$	Backorder rate as a function of backorder price discount $\pi _{x}$
$EAC_{b}$	Expected annual cost for the buyer
$EAC_{v}$	Expected annual cost for the vendor
JEAC	Joint expected annual cost for the supply chain

We make the following assumptions to develop the proposed model:

• (i) A single-vendor single-buyer inventory system is considered for trading a single type of product.

• (ii) The buyer places an order of size mQ which the vendor produces with a finite production rate $P(>D)$ in a single setup but transfers the entire lot to the buyer over m deliveries of equal size.

• (iii) The buyer reviews his inventory continuously and plans for a replenishment whenever the inventory level drops to the reorder point r which is defined by $r=Dl(Q)+k\sigma \sqrt{l(Q)}$, where $Dl(Q)=$ expected demand during lead time, $k\sigma \sqrt{l(Q)}=$ safety stock.

• (iv) Lead time for receiving the first batch is proportional to batch size and fixed delay time due to machine setup time, and transportation time, i.e., $l(Q)=Qp+T_{s}$ (Kim and Benton 1995; Karmarker 1987). For the rest of the batches, replenishment lead time depends only on the transportation time $T_{t}$, because there will be sufficient inventory at the vendor for the jth batch ($j=2,\ldots ,m,$) (see Hsiao 2008).

• (v) Transportation time $T_{t}$ is a fraction of $T_{s}$ such that $T_{t}=\epsilon T_{s}$ (Glock 2012).

• (vi) Shortage is not allowed at the vendor but backorder is permitted at the buyer.

• (vii) The buyer provides backorder price discount to customers. The backorder ratio $\delta$ is considered as variable which is proportion to the backorder price discount $\pi _{x}$ offered by the buyer, where $\delta =\delta _{0}\pi _{x}/\pi _{0}, 0\le \delta _{0}<1$ and $0\le \pi _{x}\le \pi _{0}$. Therefore, if the backorder price discount $\pi _{x}$ is greater than the marginal profit $\pi _{0}$ then the buyer may decide against offering the price discount (see Pan and Hsiao 2005; Lin 2008).

• (viii) Order processing cost per shipment (A(W)) is assumed to be strictly decreasing function of capital expenditure. We take $A(W)=A_{0}e^{-aW},$ where $A_{0}$ is original order processing cost per shipment and a is the parameter which can be estimated using previous data.

4 Mathematical model

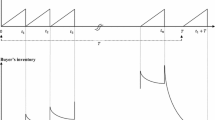
An equal-sized m-shipment policy for a single-vendor single-buyer supply chain is considered here. The buyer reviews his/her inventory continuously and places an order of size mQ whenever the inventory level falls to the reorder point. The vendor produces the total quantity mQ at one go and delivers it to the buyer over m shipments. The buyer receives the first batch after lead time l(Q) which is proportional to shipment size (Q), and delay time due to machine setup, and transportation time $(t_{s})$. However, for receiving the remaining $(m-1)$ batches, the replenishment lead time depends only on the transportation time $T_{t}$ because there will be sufficient units of the product at the vendor’s inventory for rest of the batches (see Hsiao 2008).

4.1 Buyer’s model

The buyer’s reorder point is the sum of expected lead time demand and safety stock. Therefore, the reorder point for the first batch is $r_{1}=Dl(Q)+S_{1}$, and for the jth batch ($j =2,3,\ldots$ m) is $r_{2}=DT_{t}+S_{2}$, where Dl(Q) and $DT_{t}$ are the expected lead time demands for the first batch and jth batch ($j =2,3,\ldots$ m), respectively, and $S_{1}=k_{1}\sigma \sqrt{l(Q)}$ and $S_{2}=k_{2}\sigma \sqrt{T_{t}}$ are the safety stocks for the first batch and jth batch ($j =2,3,\ldots$ m), respectively. Then, the buyer’s expected holding cost per unit time is given by (Ouyang et al. 2004; Pan and Hsiao 2005; Hsiao 2008)

$$\begin{aligned} h_{b}\left[ \frac{Q}{2}+\frac{1}{m}S_{1}+\frac{m-1}{m}S_{2}+(1-\delta )\left\{ \frac{1}{m}E_{1}+\frac{m-1}{m}E_{2}\right\} \right] \end{aligned}$$

Hence, the buyer’s expected annual cost is

$$\begin{aligned} EAC_{b}= & {} \frac{D}{mQ}[A(W)+mF]+h_{b}\Bigg [\frac{Q}{2}+\frac{1}{m}S_{1}+\left( 1-\frac{1}{m}\right) S_{2}+\left( \frac{1-\delta }{m}\right) \bigg \{E_{1} \\&+(m-1)E_{2}\bigg \}\Bigg ]+\frac{D}{mQ} [\pi _{x}\delta +\pi _{0}(1-\delta )]\left\{ E_{1}+(m-1)E_{2}\right\} +W \end{aligned}$$

(1)

where

$$\begin{aligned} E_{1}=\int _{r_{1}}^\infty (y_{1}-r_{1})g(y_{1})dy_{1} \end{aligned}$$

is the expected shortage in the first replenishment cycle, and

$$\begin{aligned} E_{2}=\int _{r_{2}}^\infty (y_{2}-r_{2})g(y_{2})dy_{2} \end{aligned}$$

is the expected shortage in the $j^{th}$ replenishment cycle, $j=2,\ldots ,m.$

In Eq. (1), the first, second, third and fourth terms represent respectively the order processing and shipment cost, holding cost, stockout cost, and annual expenditure to reduce order processing cost.

4.2 Vendor’s model

The vendor’s total cost includes setup cost and inventory holding cost. The vendor’s cycle time is $\frac{mQ}{D}$ and, therefore, setup cost per unit time is $\frac{DS}{mQ}$.

The vendor’s inventory is calculated as the difference of the vendor’s accumulated inventory and the buyer’s accumulated inventory (see Fig. 1). Therefore, the vendor’s average inventory is given by (Hsiao 2008):

$$\begin{aligned} \frac{Q}{2}\left[ m(1-Dp)-1+2Dp\right] \end{aligned}$$

Therefore, the vendor’s holding cost per unit time is

$$\begin{aligned} \frac{h_{v}Q}{2}\left[ m(1-Dp)-1+2Dp\right] \end{aligned}$$

Hence, the vendor’s total cost per unit time is

$$\begin{aligned} EAC_{v}=\frac{DS}{mQ}+\frac{h_{v}Q}{2}\left[ n\left( 1-Dp\right) -1+2Dp\right] \end{aligned}$$

(2)

Fig. 1

Inventory level diagrams for the vendor and the buyer

4.3 Joint annual cost

The joint expected annual cost of the supply chain is the sum of the buyer’s expected annual cost given by (1) and the vendor’s annual cost given by (2), i.e.,

$$\begin{aligned} JEAC= & {} \frac{D}{mQ}[A(W)+S+mF]+\Bigg \{h_{b}\left( 1-\delta \right) +\frac{D}{Q}[\pi _{x}\delta +\pi _{0}(1-\delta )]\Bigg \} \\&\quad \frac{1}{m}\{E_{1}+(m-1)E_{2}\}+h_{b}\left( \frac{Q}{2}+\frac{1}{m}(S_{1}+(m-1)S_{2})\right) +W \\&+\frac{h_{v}Q}{2}\left[ n\left( 1-Dp\right) -1+2Dp\right] \end{aligned}$$

(3)

Substituting $A(W)=A_{o}e^{-aW}$ and $\delta =\frac{\delta _{0}\pi _{x}}{\pi _{0}}$, Eq. (3) becomes

$$\begin{aligned} JEAC= & {} \frac{D}{mQ}\left[ A_{o}e^{-aW}+S+mF\right] +\Bigg \{\frac{D}{Q}\left[ \pi _{x} \left( \frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +\pi _{0}\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) \right] \\&+h_{b}\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) \Bigg \} \frac{1}{m}\{E_{1}+(m-1)E_{2}\} +h_{b}\left( \frac{Q}{2}+\frac{1}{m}(S_{1}+(m-1)S_{2})\right) \\&+W+\frac{h_{v}Q}{2}\left[ n\left( 1-Dp\right) -1+2Dp\right] \end{aligned}$$

(4)

Our objective is to minimize (4) subject to $0<\pi _{x}\le \pi _{0}.$

Let $R(m)=F+\frac{S}{m}>0,$ and $H(m)=h_{b}+h_{v}[m(1-Dp)-1+2Dp]>0.$ Then the above problem takes the form

$$\begin{aligned} \hbox {Minimize}\,JEAC&= \frac{D}{Q}\left[ \frac{A_{o}e^{-aW}}{m}+R(m)\right] +\frac{QH(m)}{2}+\frac{h_{b}}{m}(S_{1}+(m-1)S_{2}) \\ &\quad+\left[ h_{b}\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +\frac{D}{Q}\left( \pi _{0}-\delta _{0}\pi _{x} +\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) \right] \\&\quad \frac{1}{m}\{E_{1}+(m-1)E_{2}\}+W \\ \hbox {subject to}\quad&0<\pi _{x}\le \pi _{0}. \end{aligned}$$

(5)

5 Solution methodology

Assuming that the lead time demand is normally distributed, the expected shortage quantity of the first shipment is given by

$$\begin{aligned} E_{1}=\int _{r_{1}}^\infty (y_{1}-r_{1})g(y_{1})dy_{1}, \end{aligned}$$

(6)

where $g(y_{1})=\frac{1}{\sigma \sqrt{2\pi }}e^{-\frac{(y_{1}-\mu )^2}{2\sigma ^2}}$ for mean $\mu$ and standard deviation $\sigma .$

The expected shortage in the first replenishment cycle for a demand with mean Dl(Q) and standard deviation $\sigma \sqrt{l(Q)}$ during the lead time is given by

$$\begin{aligned} E_{1}=\int _{r_{1}}^\infty \frac{(y_{1}-r_{1})}{\sqrt{2\pi }\sigma \sqrt{l(Q)}}e^{-\frac{1}{2}\left( \frac{y_{1}-Dl(Q)}{\sigma \sqrt{l(Q)}}\right) ^2}dy_{1}. \end{aligned}$$

(7)

Taking $z=\frac{y_{1}-Dl(Q)}{\sigma \sqrt{l(Q)}}$ and $k_{1}=\frac{r_{1}-Dl(Q)}{\sigma \sqrt{l(Q)}},$ Eq. (7) reduces to

$$\begin{aligned} E_{1}=\sigma \sqrt{l(Q)}\int _{k_{1}}^\infty (z-k_{1})\phi (z)dz, \end{aligned}$$

(8)

where $\phi (z)$ is the standard normal probability density function.

Again, taking $\Psi (k_{1})=\int _{k_{1}}^{\infty }(z-k_{1})\phi (z)dz$, Eq. (8) further takes the form

$$\begin{aligned} E_{1}=\sigma \sqrt{l(Q)}\Psi (k_{1})=\sigma \sqrt{Qp+T_{s}}\Psi (k_{1}), \end{aligned}$$

(9)

Proceeding in a similar fashion, the expected shortage for the jth replenishment cycle $j=2,\ldots ,m,$ for a demand with mean $DT_{t}$ and standard deviation $\sigma \sqrt{T_{t}}$ during the lead time is given by

$$\begin{aligned} E_{2}=\int _{r_{1}}^\infty (y_{2}-r_{2})g(y_{2})dy_{2}=\sigma \sqrt{T_{t}}\Psi (k_{2}), \end{aligned}$$

(10)

where $\Psi (k_{2})=\int _{k_{2}}^{\infty }(z-k_{2})\phi (z)dz.$

Using (9) and (10), problem (5) can be reformulated as

$$\begin{aligned}&\hbox {Min}\,JEAC(Q,k_{1},k_{2},\pi _{x},W,m) \\&\quad =\frac{D}{Q}\left[ \frac{A_{o}e^{-aW}}{m}+R(m)\right] +\frac{QH(m)}{2}+h_{b}\left( \frac{1}{m}k_{1}\sigma \sqrt{Qp+T_{s}}+\frac{m-1}{m}k_{2}\sigma \sqrt{T_{t}}\right) \\&\qquad +\left[ h_{b}\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +\frac{D}{Q} \left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) \right] \\&\qquad \times \sigma \left[ \frac{1}{m}\sqrt{Qp+T_{s}}\Psi (k_{1})+\frac{m-1}{m}\sqrt{T_{t}}\Psi (k_{2})\right] +W\\ \hbox {subject to}\quad&0<\pi _{x}\le \pi _{0}. \end{aligned}$$

(11)

It is difficult to show that the cost function JEAC given in (11) is jointly convex with respect to the decision variables $Q,k_{1},k_{2},\pi _{x},W,$ and m. In order to find the optimal values of these decision variables numerically, we would follow a sequential search algorithm in which we search for the optimal value of one variable at a time. Before we outline the algorithm, we derive the following lemmas:

Lemma 1

For fixed values of$\pi _{x},k_{1},k_{2},W,$andm,  the cost functionJEACis convex with respect toQ, and the optimalQmust satisfy$\frac{\partial JEAC}{\partial Q}=0.$

Proof

Differentiating JEAC partially with respect to Q,  we get

$$\begin{aligned} \frac{\partial JEAC}{\partial Q}&= \frac{H(m)}{2}-\frac{D}{Q^2}\left[ R(m)+\frac{A_{o}e^{-aW}}{m}\right] +\frac{\sigma p}{2m\sqrt{Qp+T_{s}}} \\&\quad \left\{ h_{b}k_{1} +\Psi (k_{1})\left[ h_{b}\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +\frac{D}{Q}\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) \right] \right\} \\&\quad - \,\frac{\sigma D\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) }{mQ^2}\left[ \sqrt{Qp+T_{s}}\Psi (k_{1})+(m-1)\sqrt{T_{t}}\Psi (k_{2})\right] \\&= \frac{H(m)}{2}+\frac{1}{\sqrt{Qp+T_{s}}}\Bigg \{\frac{\sigma ph_{b}}{2m}\left( k_{1}+\Psi (k_{1})\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) \right) \\&\quad -\, \frac{\sigma p\Psi (k_{1})D\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) }{2m}\left( \frac{1}{Q}\right) \\&\quad -\,D\left( R(m)+\frac{A_{o}e^{-aW}}{m}+\frac{(m-1)\sigma \left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) \sqrt{T_{t}}\Psi (k_{2})}{m}\right) \left( \frac{\sqrt{Qp+T_{s}}}{Q^2}\right) \\&\quad -\,\frac{\sigma D\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) T_{s}\Psi (k_{1})}{m}\left( \frac{1}{Q^2}\right) \Bigg \} \end{aligned}$$

(12)

In order to write (12) in compact form, we use the following notations:

$$\begin{aligned} \Delta _{1}&= \frac{\sigma ph_{b}}{2m}\left( k_{1}+\Psi (k_{1})\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) \right)>0,\quad \Delta _{2}=\frac{\sigma p\Psi (k_{1})D\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) }{2m}>0,\\ \Delta _{3}&= D\left( R(m)+\frac{A_{o}e^{-aW}}{m}+\frac{(m-1)\sigma \left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) \sqrt{T_{t}}\Psi (k_{2})}{m}\right)>0,\\ \Delta _{4}&= \frac{\sigma D\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) T_{s}\Psi (k_{1})}{m}>0. \end{aligned}$$

Equation (12) then takes the form

$$\begin{aligned} \frac{\partial JEAC}{\partial Q}=\frac{H(m)}{2}+(Qp+T_{s})^{-\frac{1}{2}}\left\{ \Delta _{1}-\frac{\Delta _{2}}{Q}-\Delta _{3} \left( \frac{\sqrt{Qp+T_{s}}}{Q^2}\right) -\frac{\Delta _{4}}{Q^2}\right\} \end{aligned}$$

(13)

Let

$$\begin{aligned} U(Q)&= u_{1}(Q)u_{2}(Q),\hbox {where}\\ u_{1}(Q)&= (Qp+T_{s})^{-\frac{1}{2}}\\ u_{2}(Q)&= \Delta _{1}-\frac{\Delta _{2}}{Q}-\Delta _{3}\left( \frac{\sqrt{Qp+T_{s}}}{Q^2}\right) -\frac{\Delta _{4}}{Q^2} \end{aligned}$$

Then we have

$$\begin{aligned} \frac{\partial JEAC}{\partial Q}=\frac{H(m)}{2}+u_{1}(Q)u_{2}Q \end{aligned}$$

One can see that $u_{2}(Q)$ is an increasing function of Q for $Q>0.$

$$\begin{aligned} \hbox {Since}\,\lim _{Q\rightarrow 0^+}u_{2}(Q)\rightarrow -\infty \,\hbox {and}\,\lim _{Q\rightarrow +\infty }u_{2}(Q)\rightarrow \Delta _{1}>0, \end{aligned}$$

an unique value of $Q (=Q_{0a})$ exists which satisfies $u_{2}(Q_{0a})=0$ and $U(Q_{0a})=0.$

It is easy to see that $u_{1}(Q)$ is a decreasing function of Q for $Q>0$ and $u_{1}(Q)>0.$

For any $Q_{1}\in (0,Q_{0a}), Q_{2}\in (0,Q_{0a})$ and $Q_{1}<Q_{2},$ we have

$$\begin{aligned} u_{1}(Q_{1})>u_{1}(Q_{2})>0 \end{aligned}$$

and

$$\begin{aligned} 0>u_{2}(Q_{1})>u_{2}(Q_{2}) \end{aligned}$$

Hence,

$$\begin{aligned} u_{1}(Q_{1})u_{2}(Q_{1})<u_{1}(Q_{2})u_{2}(Q_{2})<0, \end{aligned}$$

i.e., $U(Q_{1})<U(Q_{2})<0$, which indicates that U(Q) is an increasing function of Q on the interval $(0,Q_{0a}).$

Thus, $\frac{\partial JEAC}{\partial Q}=\frac{H(m)}{2}+U(Q)$ is also an increasing function of Q on the interval $(0,Q_{0a}).$

$$\begin{aligned} \hbox {Since}\,\,\lim _{Q\rightarrow 0^+}\frac{\partial JEAC}{\partial Q}=-\infty , \frac{\partial JEAC}{\partial Q}\bigg |_{Q=Q_{0a}}=\frac{H(m)}{2}>0 \end{aligned}$$

and $\frac{\partial JEAC}{\partial Q}$ is an increasing function of Q on the interval $(0,Q_{0a})$, there exists a unique solution to the equation $\frac{\partial JEAC}{\partial Q}=0$ on the interval $(0,Q_{0a}).$

Let us suppose that the equation $\frac{\partial JEAC}{\partial Q}=0$ has a solution $Q_{0b}$ on the interval $(0,Q_{0b})$.

We know that

• (i) $\frac{\partial JEAC}{\partial Q}<0$ for $0<Q<Q_{ob}$.

• (ii) $\frac{\partial JEAC}{\partial Q}>0$ for $Q_{ob}<Q<Q_{oa}$.

• (iii) $\frac{\partial JEAC}{\partial Q}>0$ for $Q>Q_{0a}$. This is because $u_{1}(Q)>0, u_{2}(Q)>0$. Hence, $U(Q)=u_{1}(Q)u_{2}(Q)>0$ and $\frac{\partial JEAC}{\partial Q}=\frac{H(m)}{2}+U(Q)>0$.

This means that $\frac{\partial JEAC}{\partial Q}<0$ for $0<Q<Q_{0b}$ and $\frac{\partial JEAC}{\partial Q}>0$ for $Q>Q_{0b}.$

Thus, JEAC is convex in Q and the minimum value of JEAC occurs at the unique value $Q_{0b}.$

Equating $\frac{\partial JEAC}{\partial Q}$ equal to 0 and solving it, we have

$$\begin{aligned} Q=\sqrt{2D\frac{R(m)+\frac{1}{m}\left\{ A_{o}e^{-aW}+\sigma G(\pi _{x})\left[ \sqrt{Qp+T_{s}}\Psi (k_{1})+(m-1)\sqrt{T_{t}}\Psi (k_{2})\right] \right\} }{H(m)+\frac{\sigma p}{m\sqrt{T_{s}+Qp}}\left( h_{b}k_{1}+ \Psi (k_{1})\left[ h_{b}J(\pi _{x}) +\frac{D}{Q}G(\pi _{x})\right] \right) }} \end{aligned}$$

(14)

where $G(\pi _{x})=\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) , J(\pi _{x})=\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) .$

Hence, Lemma 1 is proved. $\square$

Lemma 2

For fixed value of$Q,\pi _{x},k_{2},W,$andm,  the cost function JEACis convex with respect to safety factor$k_{1}$and the optimal$k_{1}$must satisfy$\frac{\partial JEAC}{\partial k_{1}}=0.$

Proof

Differentiating JEAC partially with respect to $k_{1}$, we get

$$\begin{aligned} \frac{\partial JEAC}{\partial k_{1}}= & {} \frac{\sigma \sqrt{T_{s}+Qp}}{m}\left\{ h_{b} -\left[ h_{b}\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +\frac{D}{Q}\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) \right] \overline{\Phi }(k_{1})\right\} \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial ^2 JEAC}{\partial k_{1}^2}= & {} \sigma \left[ h_{b}\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +\frac{D}{Q} \left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) \right] \phi (k_{1})\sqrt{Qp+T_{s}} \end{aligned}$$

(16)

Clearly, $\frac{\partial ^2 JEAC}{\partial k_{1}^2}>0$. Hence the cost function in (11) is convex with respect to $k_{1} (>0).$

Setting $\frac{\partial JEAC}{\partial k_{1}}=0$ and solving for $k_{1}$, we obtain

$$\begin{aligned} \overline{\Phi }(k_{1})=\frac{h_{b}Q}{h_{b}Q\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +D\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) } \end{aligned}$$

(17)

Hence Lemma 2 is proved. $\square$

Lemma 3

For fixed value of$Q,\pi _{x},k_{1},W,$andm,  the cost function JEACis convex with respect to safety factor$k_{2}$and the optimal$k_{2}$must satisfy$\frac{\partial JEAC}{\partial k_{2}}=0.$

Proof

Proof is is similar to that of Lemma 2. Solving the first order optimality condition for $k_{2}$, we obtain

$$\begin{aligned} \overline{\Phi }(k_{2})=\frac{h_{b}Q}{h_{b}Q\left( 1-\frac{\delta _{0}\pi _{x}}{\pi _{0}}\right) +D\left( \pi _{0}-\delta _{0}\pi _{x}+\frac{\delta _{0}\pi _{x}^2}{\pi _{0}}\right) } \end{aligned}$$

(18)

Hence Lemma 3 is proved. $\square$

Lemma 4

For fixed value of$Q,k_{1},k_{2},W,$andm,  the cost functionJEACis convex with respect to$\pi _{x}$and the optimal$\pi _{x}$must satisfy$\frac{\partial JEAC}{\partial \pi _{x}}=0.$

Proof

Differentiating JEAC partially with respect to $\pi _{x}$, we get

$$\begin{aligned} \frac{\partial JEAC}{\partial \pi _{x}}= & {} \left\{ \frac{D}{Q} \left( \frac{2\delta _{0}\pi _{x}}{\pi _{0}}-\delta _{0}\right) -\frac{h_{b}\delta _{0}}{\pi _{0}}\right\} \sigma \Psi (k)\sqrt{Qp+T_{s}} \end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial ^2JEAC}{\partial \pi _{x}^2}= & {} \frac{2D\delta _{0}}{Q\pi _{0}}\sigma \Psi (k)\sqrt{Qp+T_{s}}>0 \end{aligned}$$

(20)

Hence the cost function JEAC is convex with respect to $\pi _{x} (\ge 0)$.

Setting $\frac{\partial JEAC}{\partial \pi _{x}}=0$ and solving for $\pi _{x}$, we obtain

$$\begin{aligned} \pi _{x}=\frac{1}{2}\left( \frac{h_{b}Q}{D}+\pi _{0}\right) \end{aligned}$$

(21)

Hence Lemma 4 is proved. $\square$

Lemma 5

For fixed value of$Q,k_{1},k_{2},\pi _{x},W,$andm,  the cost functionJEACis convex with respect toWand the optimalWmust satisfy$\frac{\partial JEAC}{\partial W}=0.$

Proof

The proof is straightforward as it easy to see that

$$\begin{aligned} \frac{\partial ^2JEAC}{\partial W^2}= & {} \frac{a^2DA_{o}e^{-aW}}{mQ}>0 \end{aligned}$$

(22)

Setting $\frac{\partial JEAC}{\partial W}=0$ and solving for W, we obtain

$$\begin{aligned} W=\frac{1}{a}\log \left( \frac{aDA_{o}}{mQ}\right) \end{aligned}$$

(23)

Hence Lemma 5 is proved. $\square$

It is obvious from expressions given in (17), (18), (21), and (23) that $k_{1}, k_{2}, \pi _{x}$ and W are not independent of each other; all are dependent on Q. To find the solution of the model, we adopt the solution algorithm proposed by Ben-Daya and Hariga (2004). First, the algorithm is initiated by setting $\pi _{x}=\pi _{0}$ and $W=0.$ Next, an initial value of Q is calculated by setting the stochastic parameter equal to zero in (14). These initial values are used to determine the corresponding values of $k_{1}, k_{2}, \pi _{x}$ and W using (17), (18), (21), and (23). This process is followed till a suitably stable solution is reached. It is to be noted here that if the updated value of $\pi _{x}$ is found to be greater than the initial value $\pi _{0}$, then the solution is not feasible. In this case, the updated value is rejected (see Pan and Hsiao 2005; Sarkar et al. 2015). The solution procedure can, therefore, be stated as given in the following algorithm:

5.1 Solution algorithm

Step 1 :

Set $JEAC^*=\infty , m=1$ and $\epsilon >0$ (a small positive number).

Step 2 :

Set $\pi _{x}=\pi _{0}, k_{1}=0, k_{2}=0, W=0$ and compute $Q_{0}$ from Eq. (14)

Step 2 :

Compute $k_{1}$ and $k_{2}$ from (17) and (18) using $Q_{0},\pi _{x},$ and $\Psi (k_{1})=\int _{k_{1}}^{\infty }(z-k_{1})\phi (z)dz$ and $\Psi (k_{2})=\int _{k_{2}}^{\infty }(z-k_{2})\phi (z)dz$.

Step 3 :

Compute $\pi _{x}$ from (21) using Q. If $\pi _{x}\ge \pi _{0},$ set $\pi _{x}=\pi _{0}.$

Step 4 :

Compute W from (23) using Q.

Step 5 :

Compute Q from (14) using $\pi _{x},k_{1},k_{2},$ and W.

If $|Q-Q_{0}|\le \epsilon ,$ compute $JEAC(Q,k_{1},k_{2},\pi _{x},W,m)$ using (11) and go to Step 6. Else, set $Q_{0}=Q$ and go to Step 3.

Step 6 :

If $JEAC^*\ge JEAC(Q,k_{1}, \pi _{x},W,m),$ set $JEAC^*=JEAC(Q,k_{1}, \pi _{x},W,m), Q^*=Q, \pi _{x}^*=\pi _{x}, k_{1}^*=k_{1},k_{2}^*=k_{2},W^*=W,$$m^*=m+1$ and go to Step 2. Else, $m^*=m-1$ and stop. The corresponding values of the control parameters for $m^*=m-1$ give the optimal solution.

6 Numerical results and sensitivity analysis

In this section, we demonstrate the proposed model using a numerical example. Table 2 provides the parameter-values which are used to illustrate the solution procedure of the developed model. Following the suggested algorithm, we obtain the results for the case when lead time demand follows normal distribution and backorder rate $\delta$ takes values 0.0, 0.5,  and 1. To demonstrate the impacts of investment in ordering cost reduction, we provide the optimal results in Table 3 for the models with and without investments. From Table 3, we see that the proposed model reduces the joint expected annual cost upto $5.16\%$. Thus the proposed model is more efficient than the fixed ordering cost model. Furthermore, for fully lost sale case ($\delta _{0}=0$), the joint expected annual cost is maximum, and for fully backlogged case ($\delta _{0}=1)$, it is minimum for both the models. On the other hand, from Table 3, it is also observed that a higher value of the upper bound of backorder ratio $\delta _{0}$ decreases the safety factor and the joint expected annual cost without affecting the number of shipments.

Table 2 Parameter-values

Table 3 Optimal results for different values of $\delta _{0}$

In the following, we investigate the sensitivity of key model-parameters on the optimal results:

• Effect of transportation cost

When the transportation cost varies from 20 to 640,  the optimal values of shipment size and number of shipments for both the models are shown in Fig. 2a, b. From Fig. 2a, b, the following observations are made:

• (i) The optimal shipment size for both the models gradually increases for increasing value of the transportation cost. However, the shipment size of the proposed model is always lower than that of fixed ordering cost model.

• (ii) The number of shipments decreases as the transportation cost increases.

The above two observations are not unexpected because, in practice, once the transportation cost increases then the buyer tries to reduce number of shipments by increasing the batch size.

• Effect of lead time variability

Figure 3a, b exhibits the effects of lead time variability on the optimal reorder point and safety stock. One can notice that there is a linear relationship between transportation delay and lead time. When the value of $t_{s}$ varies from 0.1 to 0.9, Fig. 3a, b shows that reorder point and safety stock increase almost linearly with increase in setup and transportation delay. Since the reorder point displays the level of inventory, it has a significant effect on the total cost. A higher reorder point indicates higher holding cost which results in an increase in the expected annual cost of the supply chain (see Fig. 3c).

• Effect of ordering cost reduction parameter

Figure 4 exhibits the effect of exponential ordering cost reduction parameter a on the optimal results. From Fig. 4, we see that ordering cost reduction investment W tends to increase for $a\in [0.002,0.005]$ and decrease for $a\in [0.006,0.2]$. However, the savings rate increases for $a\in [0.002,0.2]$ because the parameter a characterizes the ordering cost improvement rate of the related investment.

Fig. 2

Impact of transportation cost on shipment size and number of shipments aF versus Q, bF versus m

Fig. 3

Impact of lead time variability on optimal decisions a$t_{s}$ versus r, b$t_{s}$ versus S, c$t_{s}$ versus JEAC

Fig. 4

Impact of ordering cost reduction parameter $\alpha$ on optimal investment and savings

6.1 Managerial insights

In the business world, it is quite impossible to predict customers’ demand in advance. Therefore, the consideration of uncertain demand is appropriate across all industries. Additionally, when the demand is uncertain, lead time plays an important role. Because of economic uncertainty, companies are searching for alternative ways to stay competitive. Many industries would like to spend more money in order to improve customer service. In general, a buyer could offer a price discount on the stock-out item to secure more backorders; it may make the customers more willing to stay for the desired items. Through controlling price discount, a higher customer loyalty can be generated. In view of that, numerous companies such as Procter & Gamble, South west Airlines, Nike, Disney, Nordstrom, McDonald’s, Wal-Mart, Marriott Hotels, and several Japanese companies such as Canon, Sony, Toyota, and European companies such as Bang & Olufsen, IKEA, Club Med, Electrolux, Lego, Nokia, Tesco, focus on customers and are organized to respond effectively to changing customer needs. Certainly, these companies attempt to produce high customer loyalty so that, by price discount, they can raise the customer’s motivation to stay for backorder. Another important technique used along with the economic order quantity is the reorder point and safety stock. According to Chen (1998), the reorder point quantity reflects the level of inventory that triggers the placement of an order for additional units whereas the quantity associated with safety stock protects the company from stock-outs or backorders.

The following managerial implications of the proposed model can be derived based on the numerical results and effects of model-parameters on the optimal solution.

• An increased value of lead time demand deviation $\sigma$ increases the market demand uncertainty as well as out of stock probability. Therefore, when the lead time demand deviation is high, it is advisable to the supply chain manager to consider more safety stock. This safety stock will protect the system from the risk of stock-out when the lead time demand is high.

• If transportation delay starts to increase, the total cost of the supply chain will shoot rapidly. So, an operations manager must monitor for this condition. In practice, in order to minimize the transportation delay and ultimately the cost, WalMart has invested significantly on its distribution network.

• For higher transportation cost, it is advisable to the supply chain manager to reduce the number of shipments by increasing the shipment size.

• When the buyer’s holding cost is high, it is preferable to hold lesser safety stock.

• The ordering cost reduction investment will be beneficial especially to inventory systems where the buyer faces high ordering cost originally.

7 Conclusions

In this paper, a single-buyer single-vendor integrated model is developed for a single type of product. It extends the existing literature by including some realistic assumptions such as stochastic lead time demand, investment to reduce buyer’s ordering cost, and backorder price discount. Most of the existing works on integrated model assumes that lead time is constant or stochastic. However, in reality, lead time may not be constant as it depends on many factors such as setup time, transportation time, production time, etc. In this paper, we have considered lead time as a function of batch size, setup time, and transportation time. Further, we have tried to reduce the total supply chain cost by reducing the order processing cost. A numerical experiment is performed to examine the effects of variable lead time, backorder price discount, and reduction in ordering cost together on the optimal decisions of the integrated model.

Additionally, a sensitivity analysis is carried out to investigate the effect of major parameters on the optimal results. Our numerical study indicates that a high value of transportation cost increases the batch size but decreases the number of shipments in order to save the transportation cost. A higher transportation delay increases the buyer’s reorder point and safety stock to protect against shortages. We have shown graphically that the supply chain savings increases for increasing value of the parameter of exponential ordering cost reduction function. This indicates that the model with ordering cost reduction is superior to the model with fixed ordering cost.

There are several scopes of further research, e.g., one can consider imperfect production system at the vendor’s end. Also, it would be interesting to consider the present model with trade-credit financing.