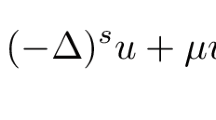Existence and Multiplicity of Solutions for Fractional $\kappa (\xi )$-Kirchhoff-Type Equation

Abstract

In this paper, we aim to tackle the questions of existence and multiplicity of solutions to a new class of $\kappa (\xi )$-Kirchhoff-type equation utilizing a variational approach. Further, we research the results from the theory of variable exponent Sobolev spaces and from the theory of space $\psi$-fractional ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$. In this sense, we present a few special cases and remark on the outcomes explored.

1 Introduction and Motivation

In this paper, we concern the following Kirchhoff’s fractional $\kappa (\xi )$-Laplacian equation

$$\begin{aligned} \left\{ \begin{array}{rcl} \mathfrak {M}\left( \displaystyle \int _{\Lambda }\frac{1}{\kappa (\xi )} \left| ^\textrm{H}\mathfrak {D}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d \xi \right) \textbf{L}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}\phi &{}=&{}\mathfrak {g}(\xi ,\phi ),\,\,\! in\!\,\,\Lambda =[0,T]\!\times [0,T], \\ \phi &{}=&{}0,\,\, on\,\,\partial \Lambda \end{array} \right. \nonumber \\ \end{aligned}$$

(1.1)

where

$$\begin{aligned} {\textbf{L}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}\phi =\,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{T}\left( \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )-2}~{^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}}\phi \right) , \end{aligned}$$

(1.2)

$^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{T}(\cdot )$ and $^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}(\cdot )$ are $\psi$-Hilfer fractional partial derivatives of order $\frac{1}{\kappa }<\mu < 1$ and type $0\le \nu \le 1$. Further, $\kappa = \kappa (\xi )\in C({\bar{\Lambda }})$, $1<\kappa ^{-}={\inf }_{\Lambda }~ \kappa (\xi )\le \kappa ^{+}={\sup }_{\Lambda }\kappa (\xi )<2$, ${\mathfrak {M}}(t)$ is a continuous function and ${\mathfrak {g}}(\xi ,\phi ):\Lambda \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is the Caratheodory function. Note that Eq. (1.2), is a generalization of $({\textbf{L}}^{\mu ,\nu ;\,\psi }_{\kappa }(\cdot )$ when $\kappa (\xi )=\kappa$ is a constant.

The Kirchhoff proposed a model given by equation

$$\begin{aligned} \rho \frac{\partial ^{2} u}{\partial t^{2}}- \left( \frac{\rho _{0}}{h}+ \frac{E}{2L}\int _{0}^{L} \left| \frac{\partial u}{\partial x}\right| ^{2} dx\right) \frac{\partial ^{2} u}{\partial x^{2}}=0, \end{aligned}$$

where $\rho , ~\rho _{0}, ~L, ~h,~ E$ are constants, which extends the classical D’Alembert’s wave equation.

The operator

$$\begin{aligned} \Delta _{p(x)} u:= {\textrm{div}}\left( |\nabla u|^{p(x)-2} |\nabla u| \right) \end{aligned}$$

is said to be the p(x)-Laplacian, and it becomes p-Laplacian when $p(x)=p$. The study of mathematical problems with variable exponents is very interesting. We can highlight the existence and multiplicity problem of the solution of p(x)-Laplacian equation, p(x)-Kirchhoff and p-Kirchhoff both in the classical and in the practical sense [2,3,4, 11, 12, 20,21,22, 24]. See also the problems involving fractional operators and the references therein [25, 26, 29, 30]. We can also highlight fractional differential equation problems with p-Laplacian using variational methods, in particular, Nehari manifold [6,7,8,9,10, 15, 16, 31].

In 2006, Correa and Figueiredo [4] investigated the existence of positive solutions to the class of problems of the p-Kirchhoff type

$$\begin{aligned} \left[ -M\left( \int _{\Lambda }\left| \nabla u \right| ^{p} d x\right) \right] ^{p-1} \Delta _{p} u&=f(x,u),\,\, \text{ in }\,\,\Lambda \nonumber \\ u&=0,\,\,\text{ on }\,\,\partial \Lambda , \end{aligned}$$

and

$$\begin{aligned} \left[ -M\left( \int _{\Lambda }\left| \nabla u \right| ^{p} d x\right) \right] ^{p-1} \Delta _{p} u&=f(x,u)+\lambda |u|^{s-2}u,\,\, \text{ in }\,\,\Lambda \nonumber \\ u&=0,\,\,\text{ on }\,\,\partial \Lambda , \end{aligned}$$

where $\Lambda$ is a bounded smooth domain of ${\mathbb {R}}^{N}$, $1<p<N$, $s\ge p^{*}=\dfrac{pN}{N-p}$ and M, f are continuous functions.

In 2010, Fan [21] considered the nonlocal p(x)-Laplacian Dirichlet problems with non-variational

$$\begin{aligned} -A(u) \Delta _{p(x)} u(x)= B(u) f(x,u(x))\,\,in\,\,\Lambda ,\,\,u|_{\partial \Lambda }=0, \end{aligned}$$

and with variational form

$$\begin{aligned} -a\left( \int _{\Lambda }\frac{1}{p(x)}\left| \nabla u \right| ^{p(x)} d x\right) \Delta _{p(x)} u(x)&=b\left( \int _{\Lambda } F(x,u) dx\right) f(x,u(x))\,\,\nonumber \\ \text{ in }\,\,\Lambda ,\,\,u|_{\partial \Lambda }=0, \end{aligned}$$

(1.3)

where

$$\begin{aligned} F(x,t)=\displaystyle \int _{0}^{t} f(x,s) ds, \end{aligned}$$

and a is allowed to be singular at zero. To obtain the existence and uniqueness of solutions for the problem (1.3), the authors used variational methods, especially Mountain pass geometry.

Problems involving Kirchhoff-type with variable and non-variable exponents are attracting attention and gaining prominence in several research groups for numerous theoretical and practical questions [13, 27, 32] and the references therein. On the other hand, it is also worth mentioning Kirchhoff’s problems with fractional operators, which over the years has been increasing exponentially [1, 23, 34]. The p(x)-Laplacian possesses more complex nonlinearity which raises some of the essential difficulties, for example, it is inhomogeneous.

Dai and Hao [11] discussed the existence of a solution for a p(x)-Kirchhoff-type equation given

$$\begin{aligned} -M\left( \int _{\Lambda }\frac{1}{p(x)}\left| \nabla u \right| ^{p} d x\right) div \left( |\nabla |^{p(x)-2} \nabla u \right)&=f(x,u)\,\, \text{ in }\,\,\Lambda ,\nonumber \\ u&=0,\,\,\text{ on }\,\,\partial \Lambda . \end{aligned}$$

Motivated by the ideas found in [4, 11, 21], we study the existence and multiplicity of solutions for problem (1.1) by supposing the following conditions:

($f_{0}$):

${\mathfrak {g}}: \Lambda \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ satisfies Caratheodory condition and

$$\begin{aligned} \left| {\mathfrak {g}}(\xi ,t)\right| \le c(1+|t|^{{\tilde{\zeta }}(\xi )-1}), \end{aligned}$$

(1.4)

where ${\tilde{\zeta }}\in C_{+}({\bar{\Lambda }})$ and ${\tilde{\zeta }}(\xi )<\kappa ^{*}_{\mu }(\xi )$ for all $\xi \in \Lambda$.

($C_{0}$):

there exists $m_{0}>0~ such ~that~ {\mathfrak {M}}(t)\ge m_{0}$.

($C_{1}$):

there exists $0<\omega <1$ such that $\widehat{{\mathfrak {M}}}(t)\ge (1-\omega ){\mathfrak {M}}(t)t$, where $\widehat{{\mathfrak {M}}}(t)=\displaystyle \int _{0}^{t} {\mathfrak {M}}(s)ds$.

($f_{1}$):

Ambrosetti-Rabinowitz condition i.e. there exist $T>0,\,\theta > \dfrac{\kappa ^{+}}{1-\omega }$ such that

$$\begin{aligned} 0<\theta ~G(\xi ,t)\le t {\mathfrak {g}}(\xi ,t),\,\,for\,\,all\,\,|t|\ge T, a. e. \,\xi \in \Lambda , \end{aligned}$$

(1.5)

where $G(\xi ,t):=\displaystyle \int _{0}^{t}{\mathfrak {g}}(\xi ,s)ds$.

$(f_2)$:

${\mathfrak {g}}(\xi ,t)=o(|t|^{\kappa ^{+}-1}), t\rightarrow 0, \text{ for }~ \xi \in \Lambda$ uniformly, where $\zeta ^{-} > \kappa ^{+}$.

($f_3$):

${\mathfrak {g}}(\xi ,-t)= -{\mathfrak {g}}(\xi ,t), \xi \in \Lambda , t\in {\mathbb {R}}$.

($f_4$):

${\mathfrak {g}}(\xi ,t) \ge c|t|^{\gamma (\xi )-1}$,  $t \rightarrow 0$ where $\gamma \in C_+ (\Lambda ), \kappa ^{+}< \gamma ^- \le \gamma ^+ < \dfrac{\kappa ^{-}}{1-\omega }$ for a.e. $\xi \in \Lambda$.

Our main results are the following:

Theorem 1.1

If ${\mathfrak {M}}$ satisfies ($C_{0}$) and

$$\begin{aligned} |{\mathfrak {g}}(\xi ,t)|\le c\left( 1+|t|^{{\widehat{\beta }} -1}\right) , \end{aligned}$$

(1.6)

where $1\le {\widehat{\beta }}<\kappa ^{-}$ then problem (1.1) has a weak solution.

Theorem 1.2

Assume that ${\mathfrak {M}}$ satisfies $({\textrm{C}}_{0})-({\textrm{C}}_{1})$ and ${\mathfrak {g}}$ satisfies ${ (f_0),(f_1),(f_2)}$. Then, problem (1.1) has a non-trivial solution.

Theorem 1.3

Assume that $({\textrm{C}}_{0})$, $({\textrm{C}}_{1})$, $({\textrm{f}}_0)$ and $({\textrm{f}}_1)$ hold and ${\mathfrak {g}}$ satisfies the condition $({\textrm{f}}_3)$. Then, problem (1.1) has a sequence of solutions $\{\pm \phi _k\}_{k=1}^{+\infty }$ such that ${\mathfrak {E}}(\pm \phi _k) \rightarrow +\infty$ as $k\rightarrow +\infty$.

Theorem 1.4

Assume that $(C_{0})$, $(C_{1})$, $(f_0)$, $(f_1)$, $(f_2)$ $(f_3)$ hold and ${\mathfrak {g}}$ satisfies the condition $(f_4)$. Then, problem (1.1) has a sequence of solutions $\{\pm v_k\}_{k=1}^{+\infty }$ such that ${\mathfrak {E}}(\pm v_k) <0$, ${\mathfrak {E}}(\pm v_k) \rightarrow +\infty$ as $k\rightarrow 0$.

The plan of the paper is as follows. In Sect. 2, we present some definitions on fractional derivatives and integrals, among others, and results on Sobolev spaces with variable exponents and $\psi$-fractional space. In Sect. 3, we dedicate ourselves to deal with the main contributions of the article, as highlighted above, i.e., Theorem 1.1, Theorem 1.2, Theorem 1.3 and Theorem 1.4.

2 Previous Results

In this section, we present a few essential definitions, lemmas and propositions to attack the main results of the article.

Let

$$\begin{aligned} C_{+}({\bar{\Lambda }})=\{ h~:~h\in C({\bar{\Lambda }}),~h(\xi )>1 ~\text{ for } \text{ any }~ \xi \in {\bar{\Lambda }}\}, \end{aligned}$$

and consider

$$\begin{aligned} h^{+}=\underset{{\bar{\Lambda }}}{\max }\,\,h(\xi ),~h^{-}=\underset{{\bar{\Lambda }}}{\,}\,{\min }\,h(\xi ) ~\text{ for } \text{ any } ~ h\in C({\bar{\Lambda }}) \end{aligned}$$

and

$$\begin{aligned} {\mathscr {L}}^{\kappa (\xi )}(\Lambda )=\left\{ \phi \in S(\Lambda ):\int _{\Lambda }\left| \phi (\xi )\right| ^{\kappa (\xi )}d \xi <+\infty \right\} \end{aligned}$$

with the norm

$$\begin{aligned} ||\phi ||_{{\mathscr {L}}^{\kappa (\xi )}(\Lambda )}=||\phi ||_{\kappa (\xi )}=\inf \left\{ \lambda >0~:~\int _{\Lambda }\left| \frac{\phi (\xi )}{\lambda }\right| ^{\kappa (\xi )}d \xi \le 1 \right\} , \end{aligned}$$

where $S(\Lambda )$ is the set of all measurable real function defined on $\Lambda$. Note that, for $\kappa (\xi )=\kappa$, we have the space ${\mathscr {L}}^{\kappa }$.

The $\psi$-fractional space is given by [6, 7]

$$\begin{aligned} {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )=\left\{ \phi \in {\mathscr {L}}^{\kappa (\xi )}(\Lambda )~:~\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| \in {\mathscr {L}}^{\kappa (\xi )}(\Lambda )\right\} \end{aligned}$$

with the norm

$$\begin{aligned} ||\phi ||=||\phi ||_{{\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )}=||\phi ||_{{\mathscr {L}}^{\kappa (\xi )}(\Lambda )}+\left\| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right\| _{{\mathscr {L}}^{\kappa (\xi )}(\Lambda )}. \end{aligned}$$

Denote by ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi ),0}(\Lambda )$ the closure of $C_{0}^{\infty }(\Lambda )$ in ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ).$

Next, we will present the definitions of Riemann-Liouville partial fractional integrals with respect to another function and of the fractional derivatives $\psi$-Hilfer for 3-variables. For a study of N-variables, see [5, 31].

Let $\theta =(\theta _{1},\theta _{2},\theta _{3})$, $T=(T_{1},T_{2},T_{3})$ and $\mu =(\mu _{1},\mu _{2},\mu _{3})$ where $0<\mu _{1},\mu _{2},\mu _{3}<1$ with $\theta _{j}<T_{j}$, for all $j\in \left\{ 1,2,3 \right\}$. Also put $\Lambda =I_{1}\times I_{2}\times I_{3}=[\theta _{1},T_{1}]\times [\theta _{2},T_{2}]\times [\theta _{3},T_{3}]$, where $T_{1},T_{2},T_{3}$ and $\theta _{1},\theta _{2},\theta _{3}$ are positive constants. Consider also $\psi (\cdot )$ be an increasing and positive monotone function on $(\theta _{1},T_{1}),(\theta _{2},T_{2}),(\theta _{3},T_{3})$, having a continuous derivative $\psi '(\cdot )$ on $(\theta _{1},T_{1}],(\theta _{2},T_{2}],(\theta _{3},T_{3}]$. The $\psi$-Riemann-Liouville fractional partial integrals of $\phi \in {\mathscr {L}}^{1}(\Lambda )$ of order $\mu$ $(0<\mu <1)$ are given by [5, 31]:

• 1-variable: right and left-sided

  $$\begin{aligned} {\textbf{I}}^{\mu ,\psi }_{\theta _{1}} \phi (\xi _{1})=\dfrac{1}{\Gamma (\mu )} \int _{\theta _{1}}^{\xi _{1}} \psi '(s_{1})(\psi (\xi _{1})- \psi (s_{1}))^{\mu -1} \phi (s_{1}) ds_{1},\,\,to\,\,\theta _{1}<s_{1}<\xi _{1} \end{aligned}$$

  and

  $$\begin{aligned} {\textbf{I}}^{\mu ,\psi }_{T_{1}} \phi (\xi _{1})=\dfrac{1}{\Gamma (\mu )} \int _{\xi _{1}}^{T_{1}} \psi '(s_{1})(\psi (s_{1})- \psi (\xi _{1}))^{\mu -1} \phi (s_{1}) ds_{1},\,\,to\,\,\xi _{1}<s_{1}<T_{1}, \end{aligned}$$

  with $\xi _{1}\in [\theta _{1},T_{1}]$, respectively.

• 3-variables: right and left-sided

  $$\begin{aligned}{} & {} {\textbf{I}}^{\mu ,\psi }_{\theta } \phi (\xi _{1},\xi _{2},\xi _{3})\\{} & {} \qquad =\dfrac{1}{\Gamma (\mu )\Gamma (\mu _{2})\Gamma (\mu _{3})} \int _{\theta _{1}}^{\xi _{1}} \int _{\theta _{2}}^{\xi _{2}} \int _{\theta _{3}}^{\xi _{3}} \psi '(s_{1})\psi '(s_{2})\psi '(s_{3}) (\psi (\xi _{1})- \psi (s_{1}))^{\mu _1-1}\\{} & {} \qquad \times (\psi (\xi _{2})- \psi (s_{2}))^{\mu _{2}-1} (\psi (\xi _{3})- \psi (s_{3}))^{\mu _{3}-1} \phi (s_{1},s_{2},s_{3}) ds_{3}ds_{2}ds_{1}, \end{aligned}$$

  to $\theta _{1}<s_{1}<\xi _{1}, \theta _{2}<s_{2}<\xi _{2}, \theta _{3}<s_{3}<\xi _{3}$ and

  $$\begin{aligned}{} & {} {\textbf{I}}^{\mu ,\psi }_{T} \phi (\xi _{1},\xi _{2},\xi _{3})\\{} & {} \qquad =\dfrac{1}{\Gamma (\mu )\Gamma (\mu _{2})\Gamma (\mu _{3})} \int _{\xi _{1}}^{T_{1}} \int _{\xi _{2}}^{T_{2}} \int _{\xi _{3}}^{T_{3}} \psi '(s_{1})\psi '(s_{2})\psi '(s_{3}) (\psi (s_{1})-\psi (\xi _{1}))^{\mu _1-1}\\{} & {} \qquad \times (\psi (s_{2})-\psi (\xi _{2}))^{\mu _{2}-1} (\psi (s_{3})-\psi (\xi _{3}))^{\mu _{3}-1} \phi (s_{1},s_{2},s_{3}) ds_{3}ds_{2}ds_{1}, \end{aligned}$$

  with $\xi _{1}<s_{1}<T_{1}, \xi _{2}<s_{2}<T_{2}, \xi _{3}<s_{3}<T_{3}$, $\xi _{1}\in [\theta _{1},T_{1}]$, $\xi _{2}\in [\theta _{2},T_{2}]$ and $\xi _{3}\in [\theta _{3},T_{3}]$, respectively.

On the other hand, let $\phi ,\psi \in C^{n}(\Lambda )$ be two functions such that $\psi$ is increasing and $\psi '(\xi _{j})\ne 0$ with $\xi _{j}\in [\theta _{j},T_{j}]$, $j\in \left\{ 1,2,3 \right\}$. The left and right-sided $\psi$-Hilfer fractional partial derivative of 3-variables of $\phi \in AC^{n}(\Lambda )$ of order $\mu =(\mu _{1},\mu _{2},\mu _{3})$ $(0<\mu _{1},\mu _{2},\mu _{3}\le 1)$ and type $\nu =(\nu _{1},\nu _{2},\nu _{3})$ where $0\le \nu _{1},\nu _{2},\nu _{3}\le 1$, are defined by [5, 31]

$$\begin{aligned}{} & {} {^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{\theta }\phi (\xi _{1},\xi _{2},\xi _{3})\nonumber \\{} & {} \qquad = {\textbf{I}}^{\nu (1-\mu ),\psi }_{\theta } \Bigg (\frac{1}{\psi '(\xi _{1})\psi '(\xi _{2})\psi '(\xi _{3})} \Bigg (\frac{\partial ^{3}}{\partial \xi _{1}\partial \xi _{2}\partial \xi _{3}}\Bigg ) \Bigg ) {\textbf{I}}^{(1-\nu )(1-\mu ),\psi }_{\theta } \phi (\xi _{1},\xi _{2},\xi _{3})\nonumber \\ \end{aligned}$$

(2.1)

and

$$\begin{aligned}{} & {} {^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{T}\phi (\xi _{1},\xi _{2},\xi _{3})\nonumber \\{} & {} \qquad = {\textbf{I}}^{\nu (1-\mu ),\psi }_{T} \Bigg (-\frac{1}{\psi '(\xi _{1})\psi '(\xi _{2})\psi '(\xi _{3})} \Bigg (\frac{\partial ^{3}}{\partial \xi _{1}\partial \xi _{2}\partial \xi _{3}}\Bigg ) \Bigg ) {\textbf{I}}^{(1-\nu )(1-\mu ),\psi }_{T} \phi (\xi _{1},\xi _{2},\xi _{3}),\nonumber \\ \end{aligned}$$

(2.2)

where $\theta$ and T are the same parameters presented in the definition of fractional integrals ${\textbf{I}}_{T}^{\mu ;\psi }(\cdot )$ and ${\textbf{I}}_ {\theta }^{\mu ;\psi }(\cdot )$.

Taking $\theta =0$ in the definition of ${^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{\theta }(\cdot )$, we have ${^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{0}(\cdot )$. During the paper we will use the following notation: ${^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{\theta } \phi (\xi _{1},\xi _{2},\xi _{3}):= {^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{\theta } \phi$, ${^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{T} \phi (\xi _{1},\xi _{2},\xi _{3}):= {^{{\textbf{H}}}{\mathfrak {D}}}^{\mu ,\nu ;\psi }_{T} \phi$ and ${\textbf{I}}_{\theta }^{\mu ;\psi }\phi (\xi _{1},\xi _{2},\xi _{3}):= {\textbf{I}}_{\theta }^{\mu ;\psi }\phi$.

Let $\theta =(\theta _{1},\theta _{2})$, $T=(T_{1},T_{2})$ and $\mu =(\mu _{1},\mu _{2})$. The relation

$$\begin{aligned}{} & {} \int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\left( {\textbf{I}}_{\theta }^{\mu ;\psi }\varphi \left( \xi _{1},\xi _{2}\right) \right) \phi \left( \xi _{1},\xi _{2}\right) {\textrm{d}}\xi _{2} {\textrm{d}}\xi _{1}\nonumber \\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\varphi \left( \xi _{1},\xi _{2}\right) \psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) {\textbf{I}}_{T}^{\mu ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) }\right) {\textrm{d}}\xi _{2} {\textrm{d}}\xi _{1}\nonumber \\ \end{aligned}$$

(2.3)

is valid.

One can prove Eq. (2.3) directly by interchanging the order of integration by the Dirichlet formula in the particular case Fubini theorem, i.e.,

$$\begin{aligned}{} & {} \int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\left( {\textbf{I}}_{\theta }^{\mu ;\psi }\varphi \left( \xi _{1},\xi _{2}\right) \right) \phi \left( \xi _{1},\xi _{2}\right) {\textrm{d}}\xi _{2} {\textrm{d}}\xi _{1}\\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\frac{1}{\Gamma \left( \mu _{1} \right) \Gamma \left( \mu _{2} \right) } \int _{\theta _{1}}^{\xi _{1}}\int _{\theta _{2}}^{\xi _{2}}\psi ^{\prime }\left( s_{1}\right) \psi ^{\prime }\left( s_{2}\right) \left( \psi \left( \xi _{1}\right) \right. \\{} & {} \qquad \quad \left. -\psi \left( s_{1}\right) \right) ^{\mu _{1} -1} \left( \psi \left( \xi _{2}\right) -\psi \left( s_{2}\right) \right) ^{\mu _{2} -1}\\{} & {} \qquad \quad \times \varphi \left( s_{1},s_{2}\right) {\textrm{ds}}_{2} {\textrm{ds}}_{1}\phi \left( \xi _{1},\xi _{2}\right) {\textrm{d}}\xi _{2} {\textrm{d}}\xi _{1}\\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\frac{1}{\Gamma \left( \mu _{1} \right) \Gamma \left( \mu _{2} \right) } \int _{\xi _{1}}^{T_{1}}\int _{\xi _{2}}^{T_{2}}\psi ^{\prime }\left( s_{1}\right) \psi ^{\prime }\left( s_{2}\right) \left( \psi \left( \xi _{1}\right) \right. \\{} & {} \qquad \quad \left. -\psi \left( s_{1}\right) \right) ^{\mu _{1} -1} \left( \psi \left( \xi _{2}\right) -\psi \left( s_{2}\right) \right) ^{\mu _{2} -1}\\{} & {} \qquad \quad \times \phi \left( \xi _{1},\xi _{2}\right) {\textrm{d}}\xi _{2} {\textrm{d}}\xi _{1}\varphi \left( s_{1},s_{2}\right) {\textrm{ds}}_{2} {\textrm{ds}}_{1}\\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\psi '(s_{1})\psi '(s_{2}) \varphi (s_{1},s_{2}){\textbf{I}}_{T}^{\mu ;\psi }\left( \frac{\phi \left( s_{1},s_{2}\right) }{\psi ^{\prime }\left( s_{1}\right) \psi '(s_{2}) }\right) {\textrm{ds}}_{2} {\textrm{ds}}_{1}. \end{aligned}$$

Theorem 2.1

Let $\psi (\cdot )$ be an increasing and positive monotone function on $[\theta _{1},T_1]\times [\theta _{2},T_2]$, having a continuous derivative $\psi '(\cdot )\ne 0$ on $(\theta _1,T_1)\times (\theta _2,T_2)$. If $0<\mu =(\mu _{1},\mu _{2}) <1$ and $0\le \nu =(\nu _{1},\nu _{2}) \le 1$, then

$$\begin{aligned}{} & {} \int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\left( ^{\textbf{H}}{\mathfrak {D}}_{\theta }^{\mu ,\nu ;\psi }\varphi \left( \xi _{1},\xi _{2}\right) \right) \phi \left( \xi _{1},\xi _{2}\right) \textrm{d}\xi _{2} \textrm{d}\xi _{1}\nonumber \\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\varphi \left( \xi _{1},\xi _{2}\right) \psi ^{\prime }\left( \xi _{1}\right) \psi ^{\prime }\left( \xi _{2}\right) \text { }^{\textbf{H}}{\mathfrak {D}}_{T}^{\mu ,\nu ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{\psi ^{\prime }\left( \xi _{1}\right) \psi ^{\prime }\left( \xi _{2}\right) }\right) \textrm{d}\xi _{2}\textrm{d}\xi _{1}\nonumber \\ \end{aligned}$$

(2.4)

for any $\varphi \in C^{1}$ and $\phi \in C^{1}$ satisfying the boundary conditions $\varphi \left( \theta _1,\theta _2\right) =0=\varphi \left( T_1,T_2\right)$.

Proof

In fact, using the Eq. (2.3), one has

$$\begin{aligned}{} & {} \int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\varphi \left( \xi _{1},\xi _{2}\right) \psi ^{\prime }\left( \xi _{1}\right) \psi ^{\prime }\left( \xi _{2}\right) \text { }^{\textbf{H}}{\mathfrak {D}}_{T}^{\mu ,\nu ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2})}\right) \textrm{d}\xi _{2}\textrm{d}\xi _{1} \\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\varphi \left( \xi _{1},\xi _{2}\right) \psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) {\textbf{I}}_{T}^{\gamma -\mu ;\psi }\text { }D_{T}^{\gamma ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) }\right) \textrm{d}\xi _{2}\textrm{d}\xi _{1} \\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) \\{} & {} \qquad \quad \left[ {\textbf{I}}_{\theta }^{\mu ;\psi } \text { }^{\textbf{H}}{\mathfrak {D}}_{\theta }^{\mu ,\nu ;\psi }\varphi \left( \xi _{1},\xi _{2}\right) +\frac{\left( \psi \left( \xi _{1}\right) -\psi \left( \theta _1\right) \right) ^{\gamma -1}\left( \psi \left( \xi _{2}\right) -\psi \left( \theta _2\right) \right) ^{\gamma -1} }{\Gamma \left( \gamma \right) }d_{j}\right] \\{} & {} \qquad \times \,{\textbf{I}}_{T}^{\gamma -\mu ;\psi }\text { }D_{T}^{\gamma ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) }\right) \textrm{d}\xi _{1} \textrm{d}\xi _{2} \text { }\\{} & {} \qquad \quad \left( \text {where }d_{j}=\left( \frac{1}{\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) }\frac{d}{\textrm{d}\xi _{1}}\frac{d}{\textrm{d}\xi _{2}}\right) {\textbf{I}}_{\theta }^{\left( 1-\nu \right) \left( 1-\mu \right) ;\psi }\varphi \left( \theta _1,\theta _2\right) \right) \\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) {\textbf{I}}_{\theta }^{\mu ;\psi }\text { } ^{\textbf{H}}{\mathfrak {D}}_{\theta }^{\mu ,\nu ;\psi }\varphi \left( \xi _{1},\xi _{2}\right) {\textbf{I}}_{T}^{\gamma -\mu ;\psi } \text { }\\{} & {} \qquad \quad D_{T}^{\gamma ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) }\right) \textrm{d}\xi _{2}\textrm{d}\xi _{1}\\{} & {} \qquad \quad \,+\frac{d_{j}}{\Gamma \left( \gamma \right) }\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) \left( \psi \left( \xi _{1}\right) -\psi \left( \theta _1\right) \right) ^{\gamma -1}\left( \psi \left( \xi _{2}\right) -\psi \left( \theta _2\right) \right) ^{\gamma -1}\nonumber \\{} & {} \qquad \quad \times \,{\textbf{I}}_{b-}^{\gamma -\mu ;\psi }\text { } D_{T}^{\gamma ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{\psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) }\right) \textrm{d}\xi _{2}\textrm{d}\xi _{1} \\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}{\textbf{I}}_{\theta }^{\mu ;\psi }\text { }^{\textbf{H}}{\mathfrak {D}}_{\theta }^{\mu ,\nu ;\psi }\varphi \left( \xi _{1},\xi _{2}\right) {\textbf{I}}_{T}^{-\mu ;\psi }\left( \frac{\phi \left( \xi _{1},\xi _{2}\right) }{ \psi ^{\prime }\left( \xi _{1}\right) \psi '(\xi _{2}) }\right) \textrm{d}\xi _{2}\textrm{d}\xi _{1} \\{} & {} \qquad =\int _{\theta _{1}}^{T_1}\int _{\theta _2}^{T_2}\text { }\left( ^{\textbf{H}}{\mathfrak {D}}_{\theta }^{\mu ,\nu ;\psi }\varphi \left( \xi _{1},\xi _{2}\right) \right) \phi \left( \xi _{1},\xi _{2}\right) \textrm{d}\xi _{2}\textrm{d}\xi _{1}, \end{aligned}$$

where $D_{T}^{\gamma ;\psi }(\cdot )$ is the $\psi$-Riemann-Liouville fractional derivative with $\gamma =\mu +\nu (1-\mu )$. $\square$

Proposition 2.2

[31] The spaces ${\mathscr {L}}^{\kappa (\xi )}(\Lambda )$ and ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ are separable and reflexive Banach spaces.

Proposition 2.3

[18] Set $\rho (\phi )=\displaystyle \int _{\Lambda }|\phi (\xi )|^{\kappa (\xi )}d \xi$. For any $\phi \in {\mathscr {L}}^{\kappa (\xi )}(\Lambda )$. Then,

• (1) For $\phi \ne 0,~|\phi |_{\kappa (\xi )}=\lambda$ if and only if $\rho \left( \frac{\phi }{\lambda }\right) =1,$

• (2) $|\phi |_{\kappa (\xi )}<1,~(=1;>1)$ if and only if $\rho (\phi )<1~(=1,>1),$

• (3) If $|\phi |_{\kappa (\xi )}>1,$ then $|\phi |^{\kappa ^{-}}_{\kappa (\xi )}\le \rho (\phi )\le |\phi |^{\kappa ^{+}}_{\kappa (\xi )},$

• (4) If $|\phi |_{\kappa (\xi )}<1,$ then $|\phi |^{\kappa ^{+}}_{\kappa (\xi )}\le \rho (\phi )\le |\phi |^{\kappa ^{-}}_{\kappa (\xi )},$

• (5) $\lim \nolimits _{k\rightarrow +\infty }|\phi _{k}|_{\kappa (\xi )}=0$ if and only if $\lim \nolimits _{k\rightarrow +\infty }\rho (\phi _{k})=0$

• (6) $\lim \nolimits _{k\rightarrow +\infty }|\phi _{k}|_{\kappa (\xi )}=+\infty$ if and only if $\lim \nolimits _{k\rightarrow +\infty }\rho (\phi _{k})=+\infty$.

Proposition 2.4

[17] If $\phi ,\phi _{k}\in {\mathscr {L}}^{\kappa (\xi )}(\Omega )$, $k=1,2,\ldots$ then the following statements are equivalent each other

• (1) $\lim _{k\rightarrow +\infty } |\phi _{k}-\phi |_{\kappa (\xi )}=0$;

• (2) $\lim _{k\rightarrow +\infty } \rho (\phi _{k}-\phi )=0$;

• (3) $\phi _{k}\rightarrow \phi$ in measure in $\Omega$ and $\lim _{k\rightarrow +\infty }\rho (\phi _{k})=\rho (\phi )$.

Proposition 2.5

[7, 8] For any $\phi \in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ there exists a positive constant c such that

$$\begin{aligned} ||\phi ||_{{\mathscr {L}}^{\kappa (\xi )}(\Lambda )}\le c\, \left\| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right\| _{{\mathscr {L}}^{\kappa (\xi )}(\Lambda )}. \end{aligned}$$

In this sense, we have that the norms $||\phi ||$ and $\left\| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right\| _{{\mathscr {L}}^{\kappa (\xi )}(\Lambda )}$ are equivalent in the space ${\mathcal {H}}^{\mu ,\nu ;\psi }_{\kappa (\xi )}(\Lambda )$, so let’s use $||\phi ||=\left\| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right\| _{{\mathscr {L}}^{\kappa (\xi )}(\Lambda )}$, for simplicity [7, 8].

Proposition 2.6

[31] Assume that the boundary of $\Lambda$ possess the property $\kappa \in C({\bar{\Lambda }})$ with $\kappa (\xi )<2.$ If $q\in C({{\bar{\Lambda }}})$ and $1\le h(\xi )\le \kappa ^{*}_{\mu }(\xi ),~ (1\le q(\xi )<\kappa ^{*}_{\mu }(\xi ))$ for $\xi \in \Lambda$ then there is a continuous (compact) embedding ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ) \hookrightarrow {\mathscr {L}}^{q(\xi )}(\Lambda ),$ whose $\kappa ^{*}_\mu =\dfrac{2 \kappa }{2-\mu {\kappa }}$.

We write

$$\begin{aligned} {\mathcal {I}}^{\mu ,\nu }(\phi )=\int _{\Lambda }\dfrac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi \end{aligned}$$

where meas $\left\{ \xi \in \Lambda ,\,\phi ^{+}>\theta \right\} >0$. We denote ${\mathcal {L}}^{\mu ,\nu }=({\mathcal {I}}^{\mu ,\nu })':{\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )\rightarrow \left( {\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )\right) ^{*}$ then

$$\begin{aligned} ({\mathcal {L}}^{\mu ,\nu } (\phi ,v))=\int _{\Lambda } \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )-2}\,\, ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \,\, ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}v\,\, d\xi \end{aligned}$$

for all $\phi ,v\in {\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )$.

Proposition 2.7

1.${\mathcal {L}}^{\mu ,\nu }:{\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )\rightarrow \left( {\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )\right) ^{*}$ is a continuous, bounded and strictly monotone operator;

2. ${\mathcal {L}}^{\mu ,\nu }$ is a mapping of type $(S_{+})$, i.e., if $\phi _{n}\rightharpoonup \phi$ in ${\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )$ and ${\overline{\lim }}_{n\rightarrow +\infty } ({\mathcal {L}}^{\mu ,\nu }(\phi _{n})-{\mathcal {L}}^{\mu ,\nu }(\phi ), \phi _{n}-\phi )\le 0$, then $\phi _{n}\rightarrow \phi$ in ${\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )$;

3. ${\mathcal {L}}^{\mu ,\nu }:{\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )\rightarrow \left( {\mathcal {H}}^{\mu , \nu ;\psi }_{\kappa (\xi )}(\Lambda )\right) ^{*}$ is a homeomorphism.

Proof

1. It is obvious that ${\mathcal {L}}^{\mu ,\nu }$ is continuous and bounded. For any $\xi ,y\in \Lambda$ [22, 28]

$$\begin{aligned} \left[ \left( |\xi |^{\kappa -2} \xi - |y|^{\kappa -2} y\right) (\xi -y) \right] \left( |\xi |^{\kappa }-|y|^{\kappa } \right) ^{(2-\kappa )/\kappa } \ge (\kappa -1)|\xi -y|^{\kappa } \end{aligned}$$

(2.5)

with $1<\kappa <2$ and

$$\begin{aligned} \left( |\xi |^{\kappa -2} \xi - |y|^{\kappa -2} y\right) (\xi -y) \ge \left( \frac{1}{2}\right) ^{\kappa }|\xi -y|^{\kappa }, \,\, \kappa \ge 2. \end{aligned}$$

(2.6)

2. From inequality (2.5), if $\phi _{n}\rightharpoonup \phi$ and ${\overline{\lim }}_{n\rightarrow +\infty } ({\mathcal {L}}^{\mu ,\nu }(\phi _{n})- {\mathcal {L}}^{\mu ,\nu }(\phi ),\phi _{n}-\phi )\le 0$, then $\lim _{n\rightarrow +\infty } \left( {\mathcal {L}}^{\mu ,\nu }(\phi _{n})-{\mathcal {L}}^{\mu ,\nu }(\phi ),\phi _{n}-\phi \right) =0$. In view of inequalities (2.5) and (2.6), $^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}$ goes in measure to $^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi$ in $\Lambda$, so we get a subsequence, satisfying $^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\rightarrow \,\, ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi$ a.e. $\xi \in \Lambda$. Using Fatou’s lemma, yields

$$\begin{aligned} {\underline{\lim }}_{n\rightarrow +\infty } \int _{\Lambda } \frac{1}{\kappa (\xi )} \, \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )} d\xi \ge \int _{\Lambda } \frac{1}{\kappa (\xi )} \, \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d\xi . \nonumber \\ \end{aligned}$$

(2.7)

From $\phi _{n}\rightharpoonup \phi$, yields

$$\begin{aligned} \lim _{n\rightarrow +\infty } ({\mathcal {L}}^{\mu ,\nu } (\phi _{n}),\phi _{n}-\phi )=\, \lim _{n\rightarrow +\infty } ({\mathcal {L}}^{\mu ,\nu } (\phi _{n}) -{\mathcal {L}}^{\mu ,\nu } (\phi ), \phi _{n}-\phi )=0. \nonumber \\ \end{aligned}$$

(2.8)

On the other hand, we also have

$$\begin{aligned}{} & {} \left( {\mathcal {L}}^{\mu ,\nu }(\phi _{n}),\phi _{n}-\phi \right) \nonumber \\{} & {} \quad =\int _{\Lambda } \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )-2}\,\, ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\,\, ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}(\phi _{n}-\phi ) d\xi \nonumber \\{} & {} \quad = \int _{\Lambda } \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )} d\xi - \, \int _{\Lambda } \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )-2}\,\, ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\,\, ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi d\xi \nonumber \\{} & {} \quad \ge \int _{\Lambda } \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )} d\xi - \int _{\Lambda } \Bigg ( \frac{\kappa (\xi )-1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )} d\xi \nonumber \\{} & {} \qquad + \frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d\xi \Bigg )\nonumber \\{} & {} \quad \ge \int _{\Lambda }\frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )} d\xi - \int _{\Lambda } \frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d\xi . \end{aligned}$$

(2.9)

Using the inequalities (2.7)–(2.9), it follows that

$$\begin{aligned} \lim _{n\rightarrow +\infty } \int _{\Lambda } \frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )} d\xi = \int _{\Lambda } \frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d\xi . \nonumber \\ \end{aligned}$$

(2.10)

From Eq. (2.10) it follows that the integral of the functions family $\left\{ \dfrac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )} \right\}$ possess absolutely equicontinuity on $\Lambda$. Since

$$\begin{aligned}{} & {} \frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\,\,-\,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}\nonumber \\{} & {} \qquad \le c\left( \frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n} \right| ^{\kappa (\xi )}+\frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} \right) \end{aligned}$$

(2.11)

the integrals of the family $\left\{ \dfrac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\,\,-\,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} \right\}$ are also absolutely equicontinuous on $\Lambda$ and therefore

$$\begin{aligned} \lim _{n\rightarrow +\infty } \int _{\Lambda } \frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\,\,-\,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d\xi =0. \end{aligned}$$

(2.12)

Using Eq. (2.12), one has

$$\begin{aligned} \lim _{n\rightarrow +\infty } \int _{\Lambda } \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi _{n}\,\,-\,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d\xi =0. \end{aligned}$$

(2.13)

From Proposition 2.4 and Eq. (2.13), $\phi _{n}\rightarrow \phi$, i.e., ${\mathcal {L}}^{\mu ,\nu }$ is of type $(S_{+})$.

3. By the strictly monotonicity, ${\mathcal {L}}^{\mu ,\nu }$ is an injection. Since

$$\begin{aligned} \lim _{||\phi ||\rightarrow +\infty } \frac{({\mathcal {L}}^{\mu ,\nu }\phi ,\phi ) }{||\phi ||} =\,\, \lim _{||\phi ||\rightarrow +\infty } \dfrac{ \displaystyle \int _{\Lambda }\left| \,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d\xi }{||\phi ||}=+\infty \end{aligned}$$

${\mathcal {L}}^{\mu ,\nu }$ is coercive, thus ${\mathcal {L}}^{\mu ,\nu }$ is a surjection in view of Minty-Browder theorem [35]. Hence ${\mathcal {L}}^{\mu ,\nu }$ has an inverse mapping $({\mathcal {L}}^{\mu ,\nu })^{-1}: \left( {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )\right) ^{*}\rightarrow {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$. Therefore, the continuity of $({\mathcal {L}}^{\mu ,\nu })^{-1}$ is sufficient to ensure ${\mathcal {L}}^{\mu ,\nu }$ to be a homeomorphism. If $f_{n},f \in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$, $f_{n}\rightarrow f$, let $\phi _{n}=({\mathcal {L}}^{\mu ,\nu })^{-1} (f_{n})$, $\phi =({\mathcal {L}}^{\mu ,\nu })^{-1} (f)$, then ${\mathcal {L}}^{\mu ,\nu }(\phi _{n})=f_{n}$, ${\mathcal {L}}^{\mu ,\nu }(\phi )=f$. So $\left\{ \phi _{n} \right\}$ is bounded in ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$. Without loss of generality, we can assume that $\phi _{n}\rightharpoonup \phi _{0}$. Since $f_{n}\rightarrow f$, then

$$\begin{aligned} \lim _{n\rightarrow +\infty } \left( {\mathcal {L}}^{\mu ,\nu }(\phi _{n}) - {\mathcal {L}}^{\mu ,\nu }(\phi _{0}),\phi _{n}-\phi _{0} \right) = \lim _{n\rightarrow +\infty } (f_{n},\phi _{n}-\phi _{0})=0. \end{aligned}$$

Since ${\mathcal {L}}^{\mu ,\nu }$ is of type $(S_{+})$, $\phi _{n}\rightarrow \phi _{0}$, we conclude that $\phi _{n}\rightarrow \phi$, so $({\mathcal {L}}^{\mu ,\nu })^{-1}$ is continuous. $\square$

Proposition 2.8

[22] (Hölder-type inequality) The conjugate space of ${\mathscr {L}}^{\kappa (\xi )}(\Lambda )$ is ${\mathscr {L}}^{q(\xi )}(\Lambda )$ where $\dfrac{1}{q(\xi )}+\dfrac{1}{\kappa (\xi )}=1$. For every $\phi \in {\mathscr {L}}^{\kappa (\xi )}(\Lambda )$ and $v\in {\mathscr {L}}^{q(\xi )}(\Lambda ),$ it follows that

$$\begin{aligned} \left| \int _{\Lambda }\phi vd \xi \right| \le \left( \frac{1}{\kappa ^{-}}+\frac{1}{q^{-}}\right) ||\phi ||_{\kappa (\xi )}||v||_{q(\xi )}. \end{aligned}$$

Definition 2.1

We say that $\phi \in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ is a weak solution of the problem (1.1), if

$$\begin{aligned}&{\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi \right) \int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )-2}~^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi ~^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}v d \xi \nonumber \\&\qquad =\int _{\Lambda }{\mathfrak {g}}(\xi ,\phi )v d \xi \end{aligned}$$

(2.14)

where $v\in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ).$

Define

$$\begin{aligned} \Phi (\phi )=\widehat{{\mathfrak {M}}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi \right) \,\,\,and\,\,\, \Psi (\phi )=\int _{\Lambda }G(\xi ,\phi )d \xi \end{aligned}$$

(2.15)

where

$$\begin{aligned} \widehat{{\mathfrak {M}}}(t)=\int _{0}^{t}{\mathfrak {M}}(s)ds,~G(\xi ,\phi )=\int _{0}^{\phi }{\mathfrak {g}}(\xi ,t)dt. \end{aligned}$$

The associated energy functional ${\mathfrak {E}}=\Phi (\phi )-\Psi (\phi ):{\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )\rightarrow {\mathbb {R}}$ to problem (1.1) is well defined. Note that ${\mathfrak {E}}\in C^{1}\left( {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ),{\mathbb {R}}\right) ,$ is a weakly lower semi-continuous and $\phi \in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ is a weak solution of the problem (1.1) if and only if $\phi$ is a critical point of ${\mathfrak {E}}$. Moreover, yields

$$\begin{aligned} {\mathfrak {E}}'(\phi )v&={\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi \right) \nonumber \\&\quad \int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )-2}~^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi ~^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}v d \xi \nonumber \\&\qquad -\int _{\Lambda }{\mathfrak {g}}(\xi ,\phi )vd \xi \nonumber \\&=\Phi '(\phi )v -\Psi '(\phi ),~~\forall v \in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ). \end{aligned}$$

(2.16)

Definition 2.2

We say that ${\mathfrak {E}}$ satisfies (PS) condition in ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ if any sequence $(\phi _{n})\subset {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ such that $\{{\mathfrak {E}}(\phi _{n})\}$ is bounded and ${\mathfrak {E}}'(\phi _{n})\rightarrow 0$ as $n\rightarrow +\infty ,$ has a convergent subsequence.

Lemma 2.9

If ${\mathfrak {M}}(t)$ satisfies (${\textrm{C}}_{0}$) and (${\textrm{C}}_{1}$), ${\mathfrak {g}}$ satisfies $({\textrm{f}}_{0})$ and ($f_1$), then ${\mathfrak {E}}$ satisfies (PS) condition.

Proof

Consider the sequence $\left\{ \phi _{n}\right\}$ in ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$, such that $|{\mathfrak {E}}(\phi _{n})|\le c$ and ${\mathfrak {E}}'(\phi _{n})\rightarrow 0$. Hence, one has

$$\begin{aligned}&c+||\phi _{n}||\ge {\mathfrak {E}}(\phi _{n})-\frac{1}{\theta }{\mathfrak {E}}'(\phi _{n})\phi _{n}\nonumber \\&\quad =\widehat{{\mathfrak {M}}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi \right) -\int _{\Lambda }G(\xi ,\phi _{n})d \xi \nonumber \\&\qquad -\frac{1}{\theta }{\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi \right) \int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi + \int _{\Lambda }\frac{1}{\theta }{\mathfrak {g}}(\xi ,\phi _{n})\phi _{n}d \xi \nonumber \\&\quad \ge (1-\omega ){\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi \right) t-\int _{\Lambda }G(\xi ,\phi _{n})d \xi \nonumber \\&\qquad -\frac{1}{\theta }{\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi \right) \int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d\xi + \int _{\Lambda } \frac{1}{\theta } {\mathfrak {g}}(\xi , \phi _n)\phi _n d\xi \nonumber \\&\quad \ge \left( \frac{1-\omega }{\kappa ^{+}}-\frac{1}{\theta }\right) {\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi \right) \int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi \nonumber \\&\qquad +\int _{\Lambda }\left( \frac{1}{\theta }{\mathfrak {g}}(\xi ,\phi _{n})\phi _{n}-G(\xi ,\phi _{n})\right) d \xi \nonumber \\&\quad \ge \left( \frac{1-\omega }{\kappa ^{+}}-\frac{1}{\theta }\right) m_{0}\int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi -c \nonumber \\&\quad \ge \left( \frac{1-\omega }{\kappa ^{+}}-\frac{1}{\theta }\right) m_{0}\left\| \phi _{n}\right\| ^{\kappa ^{-}}-c. \end{aligned}$$

(2.17)

So $\left\{ \left\| \phi _{n}\right\| _{\kappa (\xi )}\right\}$ is bounded. We assume that $\phi _{n}\rightharpoonup \phi$ (without loss of generality), then ${\mathfrak {E}}'(\phi _{n})(\phi _{n}-\phi )\rightarrow 0$. Thus, one has

$$\begin{aligned}&{\mathfrak {E}}'(\phi _{n})(\phi _{n}-\phi ) \nonumber \\&\quad ={\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi \right) \nonumber \\&\qquad \int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )-2}~^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}~^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}(\phi _{n}-\phi )d \xi \nonumber \\&\qquad -\int _{\Lambda }G(\xi ,\phi _{n})(\phi _{n}-\phi )\nonumber \\&\quad ={\mathfrak {M}}\left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )}d \xi \right) \nonumber \\&\qquad \int _{\Lambda }\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\right| ^{\kappa (\xi )-2}~^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}\, \left( ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi _{n}-\,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right) d \xi \nonumber \\&\qquad -\int _{\Lambda } {\mathfrak {g}}(\xi ,\phi _{n})(\phi _{n}-\phi ) d \xi \rightarrow 0.\nonumber \\ \end{aligned}$$

(2.18)

Using the condition $(f_{0})$, Proposition 2.6 and Proposition 2.8 it follows that

$$\begin{aligned} \int _{\Lambda }{\mathfrak {g}}(\xi ,\phi _{n})(\phi _{n}-\phi )d \xi \rightarrow 0. \end{aligned}$$

In this sense, we obtain

$$\begin{aligned}&{\mathfrak {M}}\int _{\Lambda } \left( \frac{1}{\kappa (\xi )} \left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } \phi _n \right| ^{\kappa (\xi )} d \xi \right) \\&\quad \int _{\Lambda }\left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi }\phi _n \right| ^{\kappa (\xi )-2}\, ^H{\mathfrak {D}}_+^{\mu ,\nu ;\,\psi } \left( ^H{\mathfrak {D}}_+^{\mu ,\nu ;\,\psi }\phi _n -\,\, ^H{\mathfrak {D}}_+^{\mu ,\nu ;\,\psi }\phi \right) d \xi \rightarrow 0. \end{aligned}$$

Using the condition $(C_0)$, yields

$$\begin{aligned} \int _{\Lambda } \left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi }\right| ^{\kappa (\xi )-2} {^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } }\phi _n \left( ^H{\mathfrak {D}}_+^{\mu ,\nu ;\,\psi } \phi _n -\,\,^H{\mathfrak {D}}_+^{\mu ,\nu ;\,\psi }\phi \right) d \xi \rightarrow 0 \end{aligned}$$

Finally, using Proposition 2.7, hence $\phi _n \rightarrow \phi$. Therefore, we complete the proof. $\square$

Since ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ is a reflexive and separable Banach space (see Proposition 2.2), there exist $\{\epsilon _j\}\subset {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ and $\{\epsilon _j^*\} \subset \left( {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )\right) ^*$ such that ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )=\overline{\text{ span }\{\epsilon _j: j=1,2,,\ldots \}},~~ \left( {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )\right) ^*=\overline{\text{ span }\{\epsilon _j^*:j=1,2,3,\ldots \}}$ and

$$\begin{aligned} <\epsilon _j,\epsilon _j^*>= {\left\{ \begin{array}{ll} 1~~\text {if}~~ i=j\\ 0~~\text {if}~~ i\ne j \end{array}\right. } \end{aligned}$$

Let’s use $\left( {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )\right) _j =\text{ span }\{\epsilon _j\}$, $Y_k =\oplus _{j=1}^{k} \left( {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )\right) _j$ and $Z_k =\overline{\oplus _{j=k}^{+\infty } \left( {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )\right) _j}$.

Lemma 2.10

[22] If $\mu \in C_+({\bar{\Lambda }})$, $\mu (\xi )<\kappa _{\mu }^{*} (\xi )$ for any $\xi \in {\bar{\Lambda }}$, denote

$$\begin{aligned} \beta _{k} =\sup \{|\phi |_{\mu (\xi )}: \vert |\phi \vert | =1, \phi \in Z_k\} \end{aligned}$$

(2.19)

then $\lim _{k\rightarrow +\infty } \beta _k =0$.

Lemma 2.11

[33] (Fountain Theorem) Assume

$(A_1)$:

X is a Banach Space, ${\mathfrak {E}} \in C^1(X,{\mathbb {R}})$ is an even functional. If for each $k=1,2,\ldots$ there exist $\rho _{k}> r_{k} >0$ such that:

$(A_2)$:

$\inf _{\phi \in Z_k, \vert |\phi \vert |=r_k} {\mathfrak {E}}(\phi ) \rightarrow +\infty$ as $k \rightarrow +\infty$.

$(A_3)$:

$\max _{\phi \in Y_k, ||\phi ||=\rho _{k}} {\mathfrak {E}}(\phi ) \le 0$.

$(A_4)$:

${\mathfrak {E}}$ satisfies (PS) condition for every $c>0$,

then ${\mathfrak {E}}$ has a sequence of critical values tending to $+\infty$.

Lemma 2.12

[33] (Dual Fountain Theorem) Assume $(A_{1})$ is satisfied and there is $k_0>0$ so that for each $k\ge k_{0}$, there exist $\rho _{k}> \gamma _k >0$ such that

$(B_1)$:

$\inf _{\phi \in Z_k,\vert |\phi \vert |=\rho _{k}}{\mathfrak {E}}(\phi )\ge 0$.

$(B_2)$:

$b_k =\max _{\phi \in Y_k,\vert |\phi \vert |=r_k} {\mathfrak {E}}(\phi ) <0$.

$(B_3)$:

$d_k =\inf _{\phi \in Z_k,\vert |\phi \vert |\le \rho _{k}} {\mathfrak {E}}(\phi ) \rightarrow 0$ as $k \rightarrow +\infty$.

$(B_4)$:

${\mathfrak {E}}$ satisfies $(PS)_c^*$ condition for every $c\in [d_{k_0}, 0)$.

Then ${\mathfrak {E}}$ has a sequence of negative critical values converging to 0.

Definition 2.3

We say that ${\mathfrak {E}}$ satisfies this $(PS)_c^*$ condition with respect to $(Y_n)$, if any sequence $\{\phi _{n_j}\}\subset {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$ such that $n_j \rightarrow +\infty$, $\phi _{n_j}\in Y_n$, ${\mathfrak {E}}(\phi _{n_J}) \rightarrow c$ and $({\mathfrak {E}}|_{Y_{n_j}})'(\phi _{n_j})\rightarrow 0$, contains a subsequence converging to a critical point of ${\mathfrak {E}}$.

Lemma 2.13

[11] Assume that $({\textrm{C}}_{0})$, $({\textrm{C}}_{1})$, $({\textrm{f}}_0)$ and $({\textrm{f}}_1)$ hold, then ${\mathfrak {E}}$ satisfies the $(PS)_{c}^{*}$ condition.

3 Main Results

In this section, we will address the main results of this paper, using variational techniques and results from Sobolev spaces with variable exponents and from the $\psi$-fractional space ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$, as discussed in the previous section.

Proof of Theorem 1.1

Using the inequalities (1.4) and (1.6), yields

$$\begin{aligned} \left| G(\xi ,t)\right|&=\left| \int _{0}^{t}{\mathfrak {g}}(\xi ,s)ds\right| \le \int _{0}^{t}|{\mathfrak {g}}(\xi ,s)ds\nonumber \\&\le c\int _{0}^{t}(1+|s|^{{\widehat{\beta }}-1})ds\nonumber \\&= c\int _{0}^{t}ds+c\int _{0}^{t}|s|^{{\widehat{\beta }}-1}ds\nonumber \\&\le c\left( |t|+|t|^{{\widehat{\beta }}}\right) \end{aligned}$$

(3.1)

and $\widehat{{\mathfrak {M}}}(t)\ge m_{0} t$. In this sense follows of (3.1)

$$\begin{aligned} {\mathfrak {E}}(\phi )&=\widehat{{\mathfrak {M}}} \left( \int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi \right) -\int _{\Lambda }G(\xi ,\phi )d \xi \\&\ge m_{0}\int _{\Lambda }\frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi -c\int _{\Lambda }|\phi |^{{\widehat{\beta }}}d \xi -c\int _{\Lambda }|\phi |d \xi \\&\ge \frac{m_{0}}{\kappa ^{+}}||\phi ||^{\kappa ^{-}}-c\left\| \phi \right\| ^{{\widehat{\beta }}}-c\left\| \phi \right\| \rightarrow +\infty , \end{aligned}$$

as $||\phi ||\rightarrow +\infty$. Since ${\mathfrak {E}}$ is weakly lower semi-continuous, ${\mathfrak {E}}$ has a minimum point $\phi$ in ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ),$ and $\phi$ is a weak solution of problem (1.1). $\square$

Proof of Theorem 1.2

Using Lemma 2.9, ${\mathfrak {E}}$ satisfies (PS) condition in ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )$. Since $\kappa ^{+}< \zeta ^{-} \le \zeta (\xi ) < \kappa _{\mu }^{*}(t)$, ${\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ) \hookrightarrow {\mathscr {L}}^{\kappa ^{+}}(\Lambda )$ then there exist $c>0$ such that

$$\begin{aligned} |\phi |_{\kappa ^{+}} \le c \Vert \phi \Vert , \phi \in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda ). \end{aligned}$$

(3.2)

Let $\epsilon >0$ such that $\epsilon c^{\kappa ^{+}} \le \dfrac{m_0}{2\kappa ^{+}}$. From the conditions $(f_0)$ and $(f_2)$, yields

$$\begin{aligned} G(\xi ,t) \le \epsilon |t|^{\kappa ^{+}} + c|t|^{\zeta (\xi )},(\xi ,t)\in \Lambda \times {\mathbb {R}}. \end{aligned}$$

(3.3)

Using the condition $(C_{0})$ and the inequality (3.3), yields

$$\begin{aligned} {\mathfrak {E}}(\phi )&\ge \frac{m_0}{\kappa ^{+}} \int _{\Lambda } \left| ^H {\mathfrak {D}}_{0+}^{\mu ,\beta , \psi } \phi \right| ^{\kappa (\xi )} d \xi - \epsilon \int _{\Lambda } |\phi |^{\kappa ^{+}} d \xi - c \int _{\Lambda } |\phi |^{\zeta (\xi )} d \xi \nonumber \\&\ge \frac{m_0}{\kappa ^{+}} \vert \vert \phi \vert \vert ^{\kappa ^{+}} - \epsilon c^{\kappa +} \vert \vert \phi \vert \vert ^{\kappa ^{+}} - c\vert \vert \phi \vert \vert ^{\zeta ^{-}}\nonumber \\&\ge \frac{m_0}{2\kappa ^{+}} \vert \vert \phi \vert \vert ^{\zeta ^{+}}-c\vert \vert \phi \vert \vert ^{\zeta ^{-}},&\end{aligned}$$

(3.4)

when $||\phi ||\le 1$.

Therefore, there exists $r>0,\delta >0$ such that, ${\mathfrak {E}}(\phi )\ge \delta >0$ for every $\vert \vert \phi \vert \vert =r$. From $(f_1)$, it follows that

$$\begin{aligned} G(\xi ,t) \ge c \vert t\vert ^{\theta }, ~\xi \in \Lambda , ~|t| \ge T. \end{aligned}$$

Consider the conditions (${\textrm{C}}_{0}$) and (${\textrm{C}}_{1}$). Note that the function $g(t)=\dfrac{\widehat{{\mathfrak {M}}}(t)}{t^{1/w-1}}$ is decreasing. So for all $t_{0}> 0$, when $t>t_0$, yields

$$\begin{aligned} g(t)\le g(t_0). \end{aligned}$$

In this sense, from $\dfrac{\widehat{{\mathfrak {M}}}(t)}{t^{1/w-1}}\le \dfrac{\widehat{{\mathfrak {M}}}(t_0)}{t^{1/w-1}}$, it follows that $\ln (\widehat{{\mathfrak {M}}}(t))\le \ln (\widehat{{\mathfrak {M}}}(t_0))-\dfrac{1}{1-w}\ln t-\dfrac{1}{1-w}\ln t_0$. Therefore, one has

$$\begin{aligned} \widehat{{\mathfrak {M}}}(t) \le \dfrac{\widehat{{\mathfrak {M}}}(t_0)}{t_{0}^{1/1-w}} t^{1/1-\omega } \le ct^{\frac{1}{1-\omega }},\,\, for\,\, t>t_{0} \end{aligned}$$

(3.5)

where $t_0>0$ (constant). For $w \in {\mathcal {H}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}(\Lambda )-\{0\}$ and $t>1$, yields

$$\begin{aligned} {\mathfrak {E}}(t w)&= \widehat{{\mathfrak {M}}} \left( \int _{\Lambda } \frac{1}{\kappa (\xi )}\left| t\, ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } w \right| ^{\kappa (\xi )} d \xi \right) - \int _{\Lambda } G(x,tw)d \xi \\&\le ct^{\frac{\kappa ^{+}}{1-\omega }} \left( \int _{\Lambda } \frac{1}{\kappa (\xi )}\left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } w \right| ^{\kappa (\xi )} d \xi \right) ^{\frac{1}{1-\omega }} - ct^{\theta } \int _{\Lambda } |w|^{\theta } d \xi -c\\&\quad \rightarrow -\infty ~~\text{ as }~~ t \rightarrow +\infty . \end{aligned}$$

due to $\theta > \dfrac{\kappa ^{+}}{1-\omega }$. Since ${\mathfrak {E}}(0)=0$, ${\mathfrak {E}}$ satisfies the conditions of the Mountain Pass Theorem. So ${\mathfrak {E}}$ admits at least one nontrivial critical point. $\square$

Now, we will use the Lemma 2.11 (Fountain Theorem) and Lemma 2.12 (Dual Fountain Theorem) to prove Theorem 1.3 and Theorem 1.4, respectively.

Proof of Theorem 1.3

Note that ${\mathfrak {E}}$ is an even function and satisfies (PS) condition (see condition $(f_3)$ and Lemma 2.9). Purpose here is proof that there is $\rho _{k}>\gamma _k >0$ (k large) such that (${\textrm{A}}_2$) and (${\textrm{A}}_3$) hold and, so use Lemma 2.11 (Fountain Theorem).

(${\textrm{A}}_2$) For any $\phi \in Z_k$, $\eta \in \Lambda$, $\vert |\phi \vert |$ = $\gamma _k$ = $\left( c\zeta ^{+}\beta _{k}^{\zeta ^+}m_{0}^{-1}\right) ^{\frac{1}{\kappa ^{-}-\zeta ^+}}$, it follows that

$$\begin{aligned} {\mathfrak {E}}(\phi )&= \widehat{{\mathfrak {M}}} \left( \int _{\Lambda } \frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } \phi \right| ^{\kappa (\xi )} d \xi \right) -\int _{\Lambda } {\mathfrak {g}}(\xi ,\phi )d \xi \\&\ge \frac{m_0}{\kappa ^{+}} \int _{\Lambda } \frac{1}{\kappa (\xi )}\left| ^{\textrm{H}}{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } \phi \right| ^{\kappa (\xi )} d \xi - c\int _{\Lambda } |\phi |^{\zeta (\xi )}d \xi -c\int _{\Lambda } |\phi |d \xi \\&\ge \frac{m_0}{\kappa ^{+}} \vert |\phi \vert |^{\kappa ^{-}} - c \vert |\phi \vert |^{\zeta (\eta )} -c \vert |\phi \vert |\\&\ge \vert |\phi \vert |^{\kappa ^{-}} -c\beta _k^{\zeta ^+} \vert |\phi \vert |^{\kappa ^{+}} -c\vert |\phi \vert |-c \\&= m_0 \left( \frac{1}{\kappa ^{+}}-\frac{1}{\zeta ^+}\right) \left( c\zeta ^+\beta _\kappa ^{\zeta ^+}m_0^{-1}\right) ^{\frac{\kappa ^{+}}{\kappa ^{+} -\zeta ^+}} -c\left( c\zeta ^+\beta _\kappa ^{\zeta ^+}m_0^{-1}\right) ^{\frac{1}{\kappa ^{-} -\zeta ^+}} -c \rightarrow +\infty \end{aligned}$$

as $\kappa \rightarrow +\infty$ and with $\kappa ^{+} <\zeta ^+, \kappa ^{-} >1$ and $\beta _{k} \rightarrow 0$.

(${\textrm{A}}_3$) Using $({\textrm{f}}_1)$, we have $G(\xi ,t) \ge c |t|^{\theta } -c$. Therefore, for any $w\in Y_k$ with $\vert |w \vert |= 1$ and $1< t =\rho _{k}$, yields

$$\begin{aligned} {\mathfrak {E}}(t w)&= \widehat{{\mathfrak {M}}} \left( \int _{\Lambda } \frac{1}{\kappa (\xi )}\left| t\,\, ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } w \right| ^{\kappa (\xi )} d \xi \right) - \int _{\Lambda } G(\xi ,t w)d \xi \nonumber \\&\le c\rho _{k}^{\frac{\kappa ^{+}}{1-\omega }} \left( \int _{\Lambda } \left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } \phi \right| ^{\kappa (\xi )} d \xi \right) ^{\frac{1}{1-\omega }} - c\rho _{k}^{\theta } \int _{\Lambda } |w|^{\theta }d \xi -c.&\end{aligned}$$

(3.6)

Note that, since $\theta > \dfrac{\kappa ^{+}}{1-\omega }$ and dim $Y_k = k$ holds, ${\mathfrak {E}}(\phi ) \rightarrow -\infty$ as $\vert |\phi \vert | \rightarrow +\infty$ for $\phi \in Y_k$. In this sense, using the Lemma 2.12 (Fountain theorem), we concluded the proof of Theorem. $\square$

Proof of Theorem 1.4

First, note that, using condition $(f_3)$ and Lemma 2.13, it follows that ${\mathfrak {E}}$ satisfies the conditions $(A_{1})$ and $(B_{4})$ (see Lemma 2.12-Dual Fountain Theorem).

($B_1$):

For any $v\in Z_k$, $\vert |v\vert |=1$, and $0<t<1$, yields

$$\begin{aligned} {\mathfrak {E}}(tv)&= \widehat{{\mathfrak {M}}} \left( \int _{\Lambda } \frac{1}{\kappa (\xi )}\left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } (tv) \right| ^{\kappa (\xi )} d \xi \right) - \int _{\Lambda } G(\xi ,tv)d \xi \nonumber \\&\ge \frac{m_0}{\kappa ^{+}} t^{\kappa ^{+}} \int _{\Lambda } \left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } v \right| ^{\kappa (\xi )} d \xi -\epsilon t^{\kappa ^{+}} \int _{\Lambda } |v|^{\kappa ^{+}} d \xi -c t^{\zeta ^-} \int _{\Lambda } |v|^{\zeta (\xi )} d \xi \nonumber \\&\ge \frac{m_0}{2\kappa ^{+}} t^{\kappa ^{+}} - {\left\{ \begin{array}{ll} c ~{\beta _{k}^{\zeta ^-}~t^{\zeta ^{-}}}~\text {if}~~ \Vert \phi \Vert _{\zeta (\xi )\le 1}\\ c ~{\beta _{k}^{\zeta ^+}~t^{\zeta ^{-}}}~\text {if}~~ \Vert \phi \Vert _{\zeta (\xi )> 1}. \end{array}\right. } \end{aligned}$$

(3.7)

Since $\zeta ^- > \kappa ^{+}$, without loss of generality taking $\rho _{k} =t$ with k (sufficiently large), for $v \in Z_k$ with $\vert | v\vert |= 1$, holds ${\mathfrak {E}}(tv) \ge 0$. In that sense, we have $\mathop {\inf }_{{\begin{array}{c}\phi \in Z_k,\vert |\phi \vert |=\rho _{k} \end{array}}} {\mathfrak {E}}(\phi ) \ge 0$ for k sufficiently large. Thus, the condition ($B_1$) is satisfied.

($B_2$):

For $v \in Y_k$, $\Vert v\Vert =1$ and $0<t<\rho _{k}<1$, yields

$$\begin{aligned} {\mathfrak {E}}(tv)&= \widehat{{\mathfrak {M}}} \left( \int _{\Lambda } \frac{1}{\kappa (\xi )}\left| t~ ^H{\mathfrak {D}} _{0+}^{\mu ,\nu ;\,\psi } v\right| ^{\kappa (\xi )} d \xi \right) -\int _{\Lambda }G(\xi ,tv) d \xi \\&\le c \left( \int _{\Lambda } \left| t~ ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } v\right| ^{\kappa (\xi )} d \xi \right) ^{\frac{1}{1-\omega }} -c \int _{\Lambda }\vert tv\vert ^{\gamma ^{(\xi )}} d \xi \\&\le c t^{\frac{\kappa ^{-}}{1-\omega }} \left( \int _{\Lambda } \left| ^H{\mathfrak {D}}_{0+}^{\mu ,\nu ;\,\psi } v\right| ^{\kappa (\xi )} d \xi \right) ^{\frac{1}{1-\omega }} -c t^{\gamma ^+} \int _{\Lambda } \vert v\vert ^{\gamma (\xi )} d \xi . \end{aligned}$$

Using the fact $\gamma ^+ <\dfrac{\kappa ^{-}}{1-\omega }$, there exists a $r_k \in (0,\rho _{k})$ such that ${\mathfrak {E}}(tv)<0$ when $t=r_{k}$. So, we obtain

$$\begin{aligned} b_k:=\mathop {\max }_{{\begin{array}{c}\phi \in Y_k,\\ \vert |\phi \vert |=r_k \end{array}}} {\mathfrak {E}}(\phi ) < 0. \end{aligned}$$

Thus, the condition $(B_{2})$ is satisfied.

(${\textrm{B}}_3$) Using the fact that $Y_k \cap Z_k \ne \emptyset$ and $r_k <\rho _{k}$, one has

$$\begin{aligned} d_k:=\mathop {\inf }_{{\begin{array}{c}\phi \in Z_k,\\ \vert |\phi \vert |\le \rho _{k} \end{array}}} {\mathfrak {E}}(\phi ) \le b_k:=\mathop {\max }_{{\begin{array}{c}\phi \in Y_k,\\ \vert |\phi \vert |=r_k \end{array}}} {\mathfrak {E}}(\phi ) <0. \end{aligned}$$

Using the inequality (3.7), for $v\in Z_k$, $\vert |v\vert | =1$, $0\le t\le \rho _{k}$ and $\phi =tv$, yields

$$\begin{aligned} {\mathfrak {E}}(\phi )={\mathfrak {E}}(tv) \ge - {\left\{ \begin{array}{ll} c ~{\beta _{k}^{\zeta ^-}~t^{\zeta ^{-}}}~\text {if}~~ \Vert \phi \Vert _{\zeta (\xi )}\le 1\\ c ~{\beta _{k}^{\zeta ^+}~t^{\zeta ^{-}}}~\text {if}~~ \Vert \phi \Vert _{\zeta (\xi )}> 1 \end{array}\right. } \end{aligned}$$

hence $d_k \rightarrow 0$ i.e. ($B_3$) is satisfied. Therefore, by means of Theorem 1.4, we conclude the proof. $\square$

4 A Special Problem and Comments

The following idea is to discuss some consequences of Theorem 1.1–Theorem 1.4. Consider the following fractional problem

$$\begin{aligned} \left( a+b\int _{\Lambda }\frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )} d \xi \right) ({\textbf{L}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}\phi&={\mathfrak {g}}(\xi ,\phi ),\,\, in\,\,\Lambda =[0,T]\times [0,T]\nonumber \\ \phi&=0 \end{aligned}$$

(4.1)

where

$$\begin{aligned} ({\textbf{L}}^{\mu ,\nu ;\,\psi }_{\kappa (\xi )}\phi =\,\,^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{T}\left( \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )-2}~{^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}}\phi \right) \end{aligned}$$

and a, b are two positive constants.

Let ${\mathfrak {M}}(t)=a+bt$ with $t=\displaystyle \int _{\Lambda }\frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi$. Note that, ${\mathfrak {M}}(t)\ge a>0$ and taking $\omega =\dfrac{4}{5}$, yields

$$\begin{aligned} \widehat{{\mathfrak {M}}}(t)=\int _{0}^{t} {\mathfrak {M}}(s)ds=at+\frac{b}{2}t^{2}\ge \frac{ 1}{2}\left( a+bt \right) t \ge \frac{ 1}{5}\left( a+bt \right) t=(1-\omega ) {\mathfrak {M}}(t)t. \end{aligned}$$

Therefore, the conditions $(C_{0})$ and $(C_{1})$ are satisfied. In this sense, as a consequence of Theorem 1.1, Theorem 1.2, Theorem 1.3 and Theorem 1.4, we have the following corollaries, namely:

Corollary 4.1

If ${\mathfrak {M}}$ satisfies $(C_{0})$ and $|{\mathfrak {g}}(\xi ,t)|\le {\mathcal {A}}_{1}+{\mathcal {A}}_{2} |t|^{\beta -1}$, where $1\le \beta <\kappa ^{-}$, then problem (4.1) has a weak solution.

Corollary 4.2

If ${\mathfrak {M}}$ satisfies $(C_{0})$ and $(C_{1})$, and f satisfies $(f_{0})$, $(f_{1})$ and $(f_{2})$, where $\zeta ^{-}>\kappa ^{+}$, then problem (4.1) has a nontrivial solution.

Corollary 4.3

Assume that the conditions $(C_{0})$, $(C_{1})$, $(f_{0})$, $(f_{1})$ and $(f_{3})$ hold. Then, problem (4.1) has a sequence of solutions $\left\{ \pm \phi _{k} \right\} _{k=1}^{+\infty }$ such that ${\mathfrak {E}}(\pm \phi _{k})\rightarrow +\infty$ as $k\rightarrow +\infty$.

Corollary 4.4

Assume that the conditions $(C_{0})$, $(C_{1})$, $(f_{0})$, $(f_{1})$, $(f_{3})$ and $(f_{4})$ hold. Then, problem (4.1) has a sequence of solutions $\left\{ \pm \phi _{k} \right\} _{k=1}^{+\infty }$ such that ${\mathfrak {E}}(\pm \phi _{k})\rightarrow +\infty$ as $k\rightarrow +\infty$.

Remark 1

Note that, we can take other functions with respect to ${\mathfrak {M}}(t)$ and t in Eq. (4.1) and get other versions of Kirchhoff-type problems, that is:

• ${\mathfrak {M}}(t)=a+bt$ with $t=\displaystyle \int _{\Lambda }\frac{1}{\kappa } \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa }d \xi$.

• ${\mathfrak {M}}(t)=bt$ with $t=\displaystyle \int _{\Lambda }\frac{1}{\kappa (\xi )} \left| ^{\textrm{H}}{\mathfrak {D}}^{\mu ,\nu ;\,\psi }_{0+}\phi \right| ^{\kappa (\xi )}d \xi$. Note that it also holds for $\kappa (\xi )=\kappa$.

• Note that, we only discuss the special cases above, starting from the particular choice of ${\mathfrak {M}}(t)=bt$, t and $\kappa (\xi )$. However, it is also possible to obtain and discuss other special cases, through the limits of $\beta \rightarrow 0$, $\beta \rightarrow 1$ and the function $\psi (\cdot )$.

Kirchhoff-type problems are of great interest, in particular, in recent years an approach involving fractional operators has gained prominence. After the results investigated above, some future questions can be addressed, namely:

• Discuss the same objectives of the present article for Kirchhoff-type problems with double phase.

• Another investigation possibility is to modify the problem boundary condition (1.1), to Neumann boundary.