Limit Cycle Bifurcations from a Quadratic Center with Two Switching Lines

Abstract

In this paper, we study limit cycle bifurcations for a differential system with two switching lines by using Picard–Fuchs equation. We obtain a detailed expression of the corresponding first order Melnikov function which can be used to get the upper bound of the number of limit cycles. It is worth noting that we greatly simplify the computation. Our results also show that the number of switching lines has essential impact on the number of limit cycles bifurcating from a period annulus.

1 Introduction and Main Results

Piecewise smooth differential systems have been studied extensively as they frequently appear in modeling many real phenomena. For instance, in control engineering [5], nonlinear oscillations [23] and biology [14], etc.. Moreover, these systems can exhibit complicated dynamical phenomena. Thus, in the past years, much interest from the mathematical community is seen in trying to understand their dynamical richness, especially the number of limit cycles.

There are many excellent papers studying limit cycle bifurcations of piecewise smooth differential systems with one switching line, see for example, [3, 7, 15,16,17,18,19, 27,28,29,30,31] and the references quoted there. Of course, there are also papers dedicated to study limit cycle bifurcations of piecewise smooth differential systems with multiple switching lines, see [2, 4, 6, 11, 13, 20, 21, 25, 26]. The methods used in the above papers are Melnikov function established in [10, 17] and averaging method developed in [1, 9, 19, 22]. The disadvantages of the above two methods are the complexity of calculation. Yang and Zhao [29] developed the Picard–Fuchs equation method to study the number of limit cycles of piecewise smooth differential systems with one switching line. Recently, a new development to multi-dimensional case of the averaging method on the upper bound was given in [12].

In this paper, our aim is to study limit cycle bifurcations of differential systems with two switching lines by using Picard–Fuchs equation. More precisely, we study the following integrable differential system under perturbations of piecewise polynomials of degree n

$$\begin{aligned} {\dot{x}}=y-2x^2-\eta , \ \ \ {\dot{y}}=-2xy, \end{aligned}$$

(1.1)

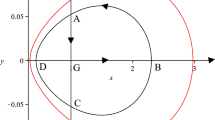
where $\eta$ is a real positive constant. System (1.1) has a unique center $G(0,\eta )$. See Fig. 1.

Fig. 1

The phase portrait of system (1.1)

The perturbed system of (1.1) with two vertical switching lines intersected at point $(0,\eta )$ is

$$\begin{aligned} \left( \begin{array}{c} {\dot{x}} \\ {\dot{y}} \end{array} \right) ={\left\{ \begin{array}{ll} \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^1(x,y) \\ -2xy+\varepsilon g^1(x,y) \end{array} \right) , \quad x>0,\ y>\eta ,\\ \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^2(x,y) \\ -2xy+\varepsilon g^2(x,y) \end{array} \right) ,\quad x>0,\ y<\eta ,\\ \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^3(x,y) \\ -2xy+\varepsilon g^3(x,y) \end{array} \right) ,\quad x<0,\ y<\eta ,\\ \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^4(x,y) \\ -2xy+\varepsilon g^4(x,y) \end{array} \right) ,\quad x<0,\ y>\eta , \end{array}\right. } \end{aligned}$$

(1.2)

where $0<|\varepsilon |\ll 1$,

$$\begin{aligned} f^k(x,y)=\sum \limits _{i+j=0}^na^k_{i,j}x^iy^j,\ \ g^k(x,y)=\sum \limits _{i+j=0}^nb^k_{i,j}x^iy^j,\ k=1,2,3,4. \end{aligned}$$

When $\varepsilon =0$, system (1.2) has first integrals

$$\begin{aligned} H^1(x,y)&=y^{-2}\Big (x^2-y+\frac{\eta }{2}\Big )=h, \ x>0,\ y>\eta ,\nonumber \\ H^2(x,y)&=y^{-2}\Big (x^2-y+\frac{\eta }{2}\Big )=h, \ x>0,\ y<\eta ,\nonumber \\ H^3(x,y)&=y^{-2}\Big (x^2-y+\frac{\eta }{2}\Big )=h, \ x<0,\ y<\eta ,\nonumber \\ H^4(x,y)&=y^{-2}\Big (x^2-y+\frac{\eta }{2}\Big )=h, \ x<0,\ y>\eta \end{aligned}$$

(1.3)

with integrating factor $\mu ^k(x,y)=y^{-3},\ k=1,2,3,4$ and a family of periodic orbits given by

$$\begin{aligned} L_h&=\{H^1(x,y)=h, x>0,\ y>\eta \}\cup \{H^2(x,y)=h, x>0,\ y<\eta \}\nonumber \\&\quad \cup \{H^3(x,y)=h, x<0,\ y<\eta \}\cup \{H^4(x,y)=h, x<0,\ y>\eta \}\nonumber \\&:=L^1_h\cup L^2_h\cup L^3_h\cup L^4_h, \ h\in \Sigma =\Big (-\frac{1}{2\eta },0\Big ). \end{aligned}$$

(1.4)

Obviously, $L_h$ approaches to the center $G(0,\eta )$ as $h\rightarrow -\frac{1}{2\eta }$ and an invariant curve $y=x^2+\frac{\eta }{2}$ as $h\rightarrow 0$, respectively. A, B, C and D are the intersection points of periodic orbit and switching lines $x=0$ and $y=\eta$. See Fig. 1.

Our main results are the following theorems.

Theorem 1.1

Let $0<|\varepsilon |\ll 1$ and the first order Melnikov function M(h) of system (1.2) is not zero identically. Then the number of limit cycles bifurcating from the period annulus around center $(0,\eta )$ is not more than $41n-23$ (counting multiplicity) for $n=1,2,3,\ldots$.

Theorem 1.2

Let $0<|\varepsilon |\ll 1$ and the first order Melnikov function M(h) of system (1.2) is not zero identically. If $f^1(x,y)=f^2(x,y)$, $g^1(x,y)=g^2(x,y)$, $f^3(x,y)=f^4(x,y)$ and $g^3(x,y)=g^4(x,y)$, then the number of limit cycles of system (1.2) bifurcating from the period annulus around center $(0,\eta )$ is not more than $9n-4$ (counting multiplicity) for $n=1,2,3,\ldots$.

Theorem 1.3

Let $0<|\varepsilon |\ll 1$ and the first order Melnikov function M(h) of system (1.2) is not zero identically. If $f^1(x,y)=f^4(x,y)$, $g^1(x,y)=g^4(x,y)$, $f^2(x,y)=f^3(x,y)$ and $g^2(x,y)=g^3(x,y)$, then the number of limit cycles of system (1.2) bifurcating from the period annulus around center $(0,\eta )$ is not more than $9n-6$ (counting multiplicity) for $n=1,2,3,\ldots$.

Remark 1.1

When $f^1(x,y)=f^2(x,y)=f^3(x,y)=f^4(x,y)$ and $g^1(x,y)=g^2(x,y)=g^3(x,y)=g^4(x,y)$, Gentes [8] studied the case of $n=2$ and proved that M(h) has at most 2 zeros. Xiong and Han [27] obtained that M(h) has at most n zeros under perturbation of polynomials of degree n.

Remark 1.2

From Lemmas 2.2, 4.1 and 5.1, we know that the first order Melnikov function of system (1.2) with two switching lines is more complicated than that of systems (4.1) and (5.1) with one switching line. Thus, the number of switching lines has essential impact on the number of limit cycles bifurcating from the quadratic center.

The rest of the paper is organized as follows: In Sect. 2, we will give detailed expression of the first order Melnikov function M(h) by using Picard–Fuchs equation. Theorems 1.1–1.3 will be proved in Sects. 3–5.

2 The Algebraic Structure of M(h) and Picard–Fuchs Equation

By Theorem 2.2 in [11] and Lemma 2.1 in [24], we know that the first order Melnikov function M(h) of system (1.2) is

$$\begin{aligned} M(h)= & {} \int _{L^1_h}y^{-3}[g^1(x,y)dx-f^1(x,y)dy]+ \int _{L^2_h}y^{-3}[g^2(x,y)dx-f^2(x,y)dy]\nonumber \\&\quad +\int _{L^3_h}y^{-3}[g^3(x,y)dx-f^3(x,y)dy]+\int _{L^4_h} y^{-3}[g^4(x,y)dx-f^4(x,y)dy]\nonumber \\ \end{aligned}$$

(2.1)

and the number of zeros of M(h) controls the number of limit cycles of system (1.2) if $M(h)\not \equiv 0$ in corresponding period annulus [9, 10].

For $h\in \Sigma$ and $i=0,1,2,\ldots ,j=0,1,2,\ldots$, we denote

$$\begin{aligned} \begin{aligned} I_{i,j}(h)&=\int _{L^1_h}x^iy^{j-3}dy,\ \ J_{i,j}(h)=\int _{L^2_h}x^iy^{j-3}dy,\\ {\tilde{J}}_{i,j}(h)&=\int _{L^3_h}x^iy^{j-3}dy,\ \ {\tilde{I}}_{i,j}(h)=\int _{L^4_h}x^iy^{j-3}dy. \end{aligned} \end{aligned}$$

Let $\Omega$ be the interior of $L^1_{h}\cup \overrightarrow{BG}\cup \overrightarrow{GA}$, see the black line in Fig. 1. Using Green’s Formula, we have for $i\ge 0$ and $j\ge -1$

$$\begin{aligned} \begin{aligned} \int _{L^1_{h}}x^iy^jdx&=\oint _{L^1_{h}\cup \overrightarrow{BG}\cup \overrightarrow{GA}}x^iy^jdx-\int _{\overrightarrow{BG}}x^iy^jdx\\&=j\iint \limits _\Omega x^{i}y^{j-1}dxdy-\eta ^j\int _{\overrightarrow{BG}}x^idx,\\ \int _{L^1_{h}}x^{i+1}y^{j-1}dy&=\oint _{L^1_{h}\cup \overrightarrow{BG}\cup \overrightarrow{GA}}x^{i+1}y^{j-1}dy =-(i+1)\iint \limits _\Omega x^{i}y^{j-1}dxdy. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \int _{L^1_{h}}x^iy^jdx=-\frac{j}{i+1}\int _{L^1_h}x^{i+1}y^{j-1}dy -\eta ^j\int _{\overrightarrow{BG}}x^idx. \end{aligned}$$

(2.2)

In a similar way, we have for $i\ge 0$ and $j\ge -1$

$$\begin{aligned} \int _{L^2_{h}}x^iy^jdx= & {} -\frac{j}{i+1}\int _{L^2_h}x^{i+1}y^{j-1}dy-\eta ^j\int _{\overrightarrow{GB}}x^idx,\nonumber \\ \int _{L^3_{h}}x^iy^jdx= & {} -\frac{j}{i+1}\int _{L^3_h}x^{i+1}y^{j-1}dy-\eta ^j\int _{\overrightarrow{DG}}x^idx,\nonumber \\ \int _{L^4_{h}}x^iy^jdx= & {} -\frac{j}{i+1}\int _{L^4_h}x^{i+1}y^{j-1}dy-\eta ^j\int _{\overrightarrow{GD}}x^idx. \end{aligned}$$

(2.3)

Therefore, we obtain from (2.1)–(2.3)

$$\begin{aligned} M(h)&=\sum \limits _{i+j=0}^nb^1_{i,j}\int _{L^1_h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^1_{i,j}\int _{L_h^1}x^iy^{j-3}dy\\&\quad +\sum \limits _{i+j=0}^nb^2_{i,j}\int _{L^2_h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^2_{i,j}\int _{L_h^2}x^iy^{j-3}dy\\&\quad +\sum \limits _{i+j=0}^nb^3_{i,j}\int _{L^3_h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^3_{i,j}\int _{L_h^3}x^iy^{j-3}dy\\&\quad +\sum \limits _{i+j=0}^nb^4_{i,j}\int _{L^4_h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^4_{i,j}\int _{L_h^4}x^iy^{j-3}dy\\&=\quad -\sum \limits _{i+j=0}^nb^1_{i,j}\left( \frac{j-3}{i+1}\int _{L_h^1}x^{i+1}y^{j-4}dy+\eta ^{j-3}\int _{\overrightarrow{BG}}x^idx\right) \\&\quad -\sum \limits _{i+j=0}^na^1_{i,j}\int _{L^1_h}x^iy^{j-3}dy\\&\quad -\sum \limits _{i+j=0}^nb^2_{i,j}\left( \frac{j-3}{i+1}\int _{L_h^2}x^{i+1}y^{j-4}dy+\eta ^{j-3}\int _{\overrightarrow{GB}}x^idx\right) \\&\quad -\sum \limits _{i+j=0}^na^2_{i,j}\int _{L^2_h}x^iy^{j-3}dy\\&\quad -\sum \limits _{i+j=0}^nb^3_{i,j}\left( \frac{j-3}{i+1}\int _{L_h^3}x^{i+1}y^{j-4}dy+\eta ^{j-3}\int _{\overrightarrow{DG}}x^idx\right) \\&\quad -\sum \limits _{i+j=0}^na^3_{i,j}\int _{L^3_h}x^iy^{j-3}dy\\&\quad -\sum \limits _{i+j=0}^nb^4_{i,j}\left( \frac{j-3}{i+1}\int _{L_h^4}x^{i+1}y^{j-4}dy+\eta ^{j-3}\int _{\overrightarrow{GD}}x^idx\right) \\&\quad -\sum \limits _{i+j=0}^na^4_{i,j}\int _{L^4_h}x^iy^{j-3}dy\\&=\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n{\tilde{a}}_{i,j}I_{i,j}(h) \\&\quad +\sum \limits _{i=0}^n{\tilde{a}}_{i}\int _{\overrightarrow{BG}}x^idx +\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n{\tilde{b}}_{i,j}J_{i,j}(h) +\sum \limits _{i=0}^n{\tilde{b}}_{i}\int _{\overrightarrow{GB}}x^idx\\&\quad +\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n{\tilde{c}}_{i,j}{\tilde{J}}_{i,j}(h) \\&\quad +\sum \limits _{i=0}^n{\tilde{c}}_{i}\int _{\overrightarrow{DG}}x^idx +\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n{\tilde{d}}_{i,j}{\tilde{I}}_{i,j}(h) +\sum \limits _{i=0}^n{\tilde{d}}_{i}\int _{\overrightarrow{GD}}x^idx,\\&=\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n\sigma _{i,j}I_{i,j}(h)+\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n\tau _{i,j}J_{i,j}(h)\\&\quad +\sum \limits _{i=0}^n{\tilde{a}}_{i}\int _{\overrightarrow{BG}}x^idx +\sum \limits _{i=0}^n{\tilde{b}}_{i}\int _{\overrightarrow{GB}}x^idx {+}\sum \limits _{i=0}^n{\tilde{c}}_{i}\int _{\overrightarrow{DG}}x^idx {+}\sum \limits _{i=0}^n{\tilde{d}}_{i}\int _{\overrightarrow{GD}}x^idx, \end{aligned}$$

where ${\tilde{a}}_{i,j}$, ${\tilde{b}}_{i,j}$, ${\tilde{c}}_{i,j}$, ${\tilde{d}}_{i,j}$, $\sigma _{i,j}$, $\tau _{i,j}$, ${\tilde{a}}_{i}$, ${\tilde{b}}_{i}$, ${\tilde{c}}_{i}$ and ${\tilde{d}}_{i}$ are arbitrary real constants and in the last equality we have used

$$\begin{aligned} {\tilde{I}}_{i,j}(h)=(-1)^{i+1}I_{i,j}(h),\ {\tilde{J}}_{i,j}(h)=(-1)^{i+1}J_{i,j}(h). \end{aligned}$$

The coordinates of B and D are $(\sqrt{\eta ^2h+\frac{\eta }{2}},\eta )$ and $(-\sqrt{\eta ^2h+\frac{\eta }{2}},\eta )$ respectively. Thus,

$$\begin{aligned} M(h)=\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n\sigma _{i,j}I_{i,j}(h) +\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n\tau _{i,j}J_{i,j}(h)+ \sum \limits _{i=0}^n\nu _i\eta ^{i+1}\Big (h+\frac{1}{2\eta }\Big )^{\frac{i+1}{2}},\nonumber \\ \end{aligned}$$

(2.4)

where $\nu _i$ is a real constant.

Lemma 2.1

If $i+j=n\ge 3$ and i is an even number, then

$$\begin{aligned} I_{i,j}(h)= & {} \frac{1}{h^{n-2}}\Big [{\tilde{\alpha }}_1(h)I_{0,1}(h) +{\tilde{\beta }}_1(h)I_{2,0}(h)+{\tilde{\varphi }}_{\frac{3}{2}n-\frac{7+(-1)^n}{4}}(h)\Big ],\nonumber \\ J_{i,j}(h)= & {} \frac{1}{h^{n-2}}\Big [{\tilde{\alpha }}_2(h)J_{0,1}(h) +{\tilde{\beta }}_2(h)J_{2,0}(h)+{\tilde{\psi }}_{\frac{3}{2}n-\frac{7+(-1)^n}{4}}(h)\Big ]. \end{aligned}$$

(2.5)

If $i+j=n\ge 3$ and i is an odd number, then

$$\begin{aligned} I_{i,j}(h)&=\frac{1}{h^{n-2}}\Big [{\tilde{\gamma }}_1(h)I_{1,0}(h) +{\tilde{\delta }}_1(h)I_{1,1}(h)+\sqrt{ h+\frac{1}{2\eta }}{\bar{\varphi }}_{\frac{3}{2}n-\frac{9-(-1)^n}{4}}(h)\Big ],\\ J_{i,j}(h)&=\frac{1}{h^{n-2}}\Big [{\tilde{\gamma }}_2(h)J_{1,0}(h) +{\tilde{\delta }}_2(h)J_{1,1}(h)+\sqrt{ h+\frac{1}{2\eta }}{\bar{\psi }}_{\frac{3}{2}n-\frac{9-(-1)^n}{4}}(h)\Big ], \end{aligned}$$

where ${\tilde{\varphi }}_{l}(h)$, ${\tilde{\psi }}_{l}(h)$, ${\bar{\varphi }}_{l}(h)$ and ${\bar{\psi }}_{l}(h)$ are polynomials in h of degrees at most l, and ${\tilde{\alpha }}_k(h)$, ${\tilde{\beta }}_k(h)$, ${\tilde{\gamma }}_k(h)$ and ${\tilde{\delta }}_k(h)$ are polynomials of h with

$$\begin{aligned}&\deg {\tilde{\alpha }}_k(h)\le n-\frac{3+(-1)^n}{2},\ \deg {\tilde{\delta }}_k(h)\le n-\frac{3-(-1)^n}{2},\\&\deg {\tilde{\beta }}_k(h),\deg {\tilde{\gamma }}_k(h)\le n-2,\ k=1,2. \end{aligned}$$

Proof

Without loss of generality, we only prove the first equality in (2.5). The others can be shown in a similar way. It follows from (1.3) that

$$\begin{aligned} -2x^2y^{-3}+2xy^{-2}\frac{\partial x}{\partial y}+y^{-2}-\eta y^{-3}=0. \end{aligned}$$

(2.6)

Multiplying (2.6) by $x^{i-2}y^{j}dy$, integrating over $L^1_h$ and noting that (2.2), we have

$$\begin{aligned} 2(i+j-2)I_{i,j}(h)=iI_{i-2,j+1}(h)-\eta iI_{i-2,j}(h)+2\eta ^{i+j-2}\Big (h+\frac{1}{2\eta }\Big )^{\frac{i}{2}}. \end{aligned}$$

(2.7)

Similarly, multiplying the first equality in (1.3) by $x^{i}y^{j-3}dx$ and integrating over $L^1_h$ yields

$$\begin{aligned} hI_{i,j}(h)=I_{i+2,j-2}(h)-I_{i,j-1}(h)+\frac{\eta }{2}I_{i,j-2}(h). \end{aligned}$$

(2.8)

Taking $(i,j)=(2,0),(3,-1)$ in (2.7), we obtain

$$\begin{aligned} I_{0,0}(h)= & {} \eta ^{-1}I_{0,1}(h)+\eta ^{-1}\Big ( h+\frac{1}{2\eta }\Big ),\nonumber \\ I_{1,-1}(h)= & {} \eta ^{-1}I_{1,0}(h)+\frac{2}{3}\eta ^{-1}\Big ( h+\frac{1}{2\eta }\Big )^\frac{3}{2}. \end{aligned}$$

(2.9)

From (2.8) we obtain

$$\begin{aligned} I_{0,2}(h)= & {} \frac{1}{h}\Big (I_{2,0}(h)-I_{0,1}(h) +\frac{\eta }{2}I_{0,0}(h)\Big ),\nonumber \\ I_{3,-1}(h)= & {} hI_{1,1}(h)+I_{1,0}(h)-\frac{\eta }{2}I_{1,-1}(h). \end{aligned}$$

(2.10)

Taking $(i,j)=(2,-1)$ in (2.7) and $(i,j)=(0,1)$ in (2.8), we have

$$\begin{aligned} I_{2,-1}(h)= & {} \eta I_{0,-1}(h)-I_{0,0}(h)-\eta ^{-2}\Big (\eta h+\frac{1}{2}\Big ),\nonumber \\ hI_{0,1}(h)= & {} I_{2,-1}(h)-I_{0,0}(h)+\frac{\eta }{2}I_{0,-1}(h). \end{aligned}$$

(2.11)

Eliminating $I_{0,-1}(h)$ in (2.11) and noting that (2.9), we get

$$\begin{aligned} I_{2,-1}(h)=\frac{1}{3}(2h+\eta ^{-1})I_{0,1}(h). \end{aligned}$$

(2.12)

In view of (2.7) and (2.8), we obtain

$$\begin{aligned} \left\{ \begin{array}{l} I_{0,3}(h)=\frac{1}{h}\Big (I_{2,1}(h)-I_{0,2}(h)+\frac{\eta }{2}I_{0,1}(h)\Big ),\\ I_{1,2}(h)=\frac{1}{h}\Big (I_{3,0}(h)-I_{1,1}(h)+\frac{\eta }{2}I_{1,0}(h)\Big ),\\ I_{2,1}(h)=I_{0,2}(h)-\eta I_{0,1}(h)+\eta h+\frac{1}{2},\\ I_{3,0}(h)=\frac{3}{2}I_{1,1}(h)-\frac{3}{2}\eta I_{1,0}(h)+\eta \Big (h+\frac{1}{2\eta }\Big )^\frac{3}{2},\\ I_{4,-1}(h)=2I_{2,0}(h)-2\eta I_{2,-1}(h)+h+\frac{1}{2\eta }. \end{array}\right. \end{aligned}$$

(2.13)

Now we prove the conclusion by induction on n. In fact, (2.13) implies that the conclusion holds for $n=3$. Suppose that the first equality in (2.5) holds for $i+j\le n-1\, (n\ge 4)$. If n is an even number, then, by (2.7) and (2.8), we have

$$\begin{aligned} {\mathbf {A}}\left( \begin{array}{c} I_{0,n}(h)\\ I_{2,n-2}(h)\\ I_{4,n-4}(h)\\ \vdots \\ I_{n-2,2}(h)\\ I_{n,0}(h) \end{array}\right) =\left( \begin{array}{c} \frac{1}{h}\left[ -I_{0,n-1}(h)+\frac{\eta }{2}I_{0,n-2}(h)\right] \\ \frac{1}{n-2}\left[ I_{0,n-1}(h)-\eta I_{0,n-2}(h)+\eta ^{n-2}\left( h+\frac{1}{2\eta }\right) \right] \\ \frac{1}{n-2}\left[ 2I_{2,n-3}(h)-2\eta I_{2,n-4}(h)+\eta ^{n-2}\left( h+\frac{1}{2\eta }\right) ^2\right] \\ \vdots \\ \frac{1}{2n-4}\left[ (n-2)I_{n-4,3}(h)-(n-2)\eta I_{n-4,2}(h)+2\eta ^{n-2}\left( h+\frac{1}{2\eta }\right) ^{\frac{n-2}{2}}\right] \\ \frac{1}{2n-4}\left[ nI_{n-2,1}(h)-n\eta I_{n-2,0}(h)+2\eta ^{n-2}\left( h+\frac{1}{2\eta }\right) ^{\frac{n}{2}}\right] \end{array}\right) ,\nonumber \\ \end{aligned}$$

(2.14)

where

$$\begin{aligned} {\mathbf {A}}=\left( \begin{matrix} 1&{} \quad -\frac{1}{h}&{} \quad 0&{} \quad \cdots &{} \quad 0&{} \quad 0&{} \quad 0\\ 0&{} \quad 1&{} \quad 0&{} \quad \cdots &{} \quad 0&{} \quad 0&{} \quad 0\\ 0&{} \quad 0&{} \quad 1&{} \quad \cdots &{} \quad 0&{} \quad 0&{} \quad 0\\ \vdots &{} \quad \vdots &{} \quad \vdots &{} \quad \vdots &{} \quad \vdots &{} \quad \vdots &{} \quad \vdots \\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0&{} \quad 1&{} \quad 0\\ 0&{} \quad 0&{} \quad 0&{} \quad \cdots &{} \quad 0&{} \quad 0&{} \quad 1 \end{matrix}\right) .\ \ \end{aligned}$$

Hence, the first equality in (2.5) holds.

Next we will discuss the degrees of ${\tilde{\alpha }}_1(h)$, ${\tilde{\beta }}_1(h)$ and ${\tilde{\varphi }}_l(h)$ in (2.5). If $(i,j)=(2,n-2),(4,n-4),\ldots ,(n-2,2),(n,0)$, then, in view of (2.14) and noting that n is an even number, we obtain

$$\begin{aligned} \begin{aligned} I_{i,j}(h)&=h\Big [\alpha ^{(n-1)}(h)I_{0,1}(h)+\beta ^{(n-1)} (h)I_{2,0}(h)+\varphi ^{(n-1)}(h)\\&\quad +\alpha ^{(n-2)}(h)I_{0,1}(h)+\beta ^{(n-2)}(h)I_{2,0}(h) +\varphi ^{(n-2)}(h)+\xi _{\frac{n}{2}}(h)\Big ]\\&:=\alpha ^{(n)}(h)I_{0,1}(h)+\beta ^{(n)}(h)I_{2,0}(h)+\varphi ^{(n)}(h), \end{aligned} \end{aligned}$$

where $\alpha ^{(n-s)}(h)$ and $\beta ^{(n-s)}(h)\ (s=1,2)$ are polynomials in h satisfying

$$\begin{aligned} \begin{aligned}&\deg \alpha ^{(n-1)}(h)\le n-2,\ \deg \beta ^{(n-1)}(h)\le n-3,\\&\deg \alpha ^{(n-2)}(h),\ \deg \beta ^{(n-2)}(h)\le n-4,\end{aligned} \end{aligned}$$

$\varphi ^{(n-1)}(h)$ is a polynomial of h satisfying $\deg \varphi ^{(n-1)}(h)\le \frac{3}{2}n-3$, $\varphi ^{(n-2)}(h)$ is a polynomial of h satisfying $\deg \varphi ^{(n-2)}(h)\le \frac{3}{2}n-5$ and $\xi _{\frac{n}{2}}(h)$ is a polynomial of h with degree at most $\frac{n}{2}$. Therefore,

$$\begin{aligned} \deg \alpha ^{(n)}(h), \deg \beta ^{(n)}(h)\le n-2,\ \deg \varphi ^{(n)}(h)\le \frac{3}{2}n-2. \end{aligned}$$

Similarly, we can prove that the conclusion holds for $(i,j)=(0,n)$.

If n is an odd number, we can prove the conclusion in a similar way. This ends the proof. $\square$

From (2.4) and Lemma 2.1, we obtain the algebraic structure of the first Melnikov function M(h) immediately.

Lemma 2.2

If $i+j=n>3$, then

(2.15)

where ${\varphi }_{l}(h)$ and ${\psi }_{l}(h)$ are polynomials of h of degrees at most l, and ${\alpha }_k(h)$, ${\beta }_k(h)$, ${\gamma }_k(h)$ and ${\delta }_k(h)$ are polynomials of h with

$$\begin{aligned}&\deg {\alpha }_k(h)\le n-\frac{3+(-1)^n}{2},\ \deg {\delta }_k(h)\le n-\frac{3-(-1)^n}{2},\\&\deg {\beta }_k(h),\deg {\gamma }_k(h)\le n-2,\ k=1,2. \end{aligned}$$

If $n=1,2,3$, then

(2.16)

where ${\varphi }_{l}(h)$ and ${\psi }_{l}(h)$ are polynomials of h of degrees at most l, and ${\alpha }_k(h)$, ${\beta }_k(h)$, ${\gamma }_k(h)$ and ${\delta }_k(h)$ are polynomials of h with

$$\begin{aligned} \begin{aligned} \deg {\alpha }_k(h), \deg {\delta }_k(h)\le 2,\ \ \deg {\beta }_k(h),\deg {\gamma }_k(h)\le 1,\ k=1,2. \end{aligned}\end{aligned}$$

The following lemma gives the Picard–Fuchs equations which the generators of M(h) satisfy.

Lemma 2.3

(i) The vector functions $\big (I_{0,1}(h),I_{2,0}(h)\big )^T$ and $\big (I_{1,0}(h),I_{1,1}(h)\big )^T$ respectively satisfy the Picard–Fuchs equations

$$\begin{aligned} \left( \begin{matrix} I_{0,1}(h)\\ I_{2,0}(h)\\ \end{matrix}\right) =\left( \begin{matrix} 2\big (h+\frac{1}{2\eta }\big )&{} \quad 0\\ h+\frac{1}{2\eta }&{} \quad h\\ \end{matrix}\right) \left( \begin{matrix} I'_{0,1}(h)\\ I'_{2,0}(h)\\ \end{matrix}\right) + \left( \begin{matrix} 0\\ -\frac{1}{2}(h+\frac{1}{2\eta })\\ \end{matrix}\right) \end{aligned}$$

(2.17)

and

$$\begin{aligned} \left( \begin{matrix} I_{1,0}(h)\\ I_{1,1}(h)\\ \end{matrix}\right) =\left( \begin{matrix} h+\frac{1}{2\eta }&{} \quad 0\\ 1&{} \quad 2h\\ \end{matrix}\right) \left( \begin{matrix} I'_{1,0}(h)\\ I'_{1,1}(h)\\ \end{matrix}\right) + \left( \begin{matrix} 0\\ -\sqrt{h+\frac{1}{2\eta }}\\ \end{matrix}\right) . \end{aligned}$$

(2.18)

(ii) The vector functions $\big (J_{0,1}(h),J_{2,0}(h)\big )^T$ and $\big (J_{1,0}(h),J_{1,1}(h)\big )^T$ respectively satisfy the Picard–Fuchs equations

$$\begin{aligned} \left( \begin{matrix} J_{0,1}(h)\\ J_{2,0}(h)\\ \end{matrix}\right) =\left( \begin{matrix} 2\big (h+\frac{1}{2\eta }\big )&{}\quad 0\\ h+\frac{1}{2\eta }&{}\quad h\\ \end{matrix}\right) \left( \begin{matrix} J'_{0,1}(h)\\ J'_{2,0}(h)\\ \end{matrix}\right) + \left( \begin{matrix} 0\\ \frac{1}{2}(h+\frac{1}{2\eta })\\ \end{matrix}\right) \end{aligned}$$

(2.19)

and

$$\begin{aligned} \left( \begin{matrix} J_{1,0}(h)\\ J_{1,1}(h)\\ \end{matrix}\right) =\left( \begin{matrix} h+\frac{1}{2\eta }&{} \quad 0\\ 1&{} \quad 2h\\ \end{matrix}\right) \left( \begin{matrix} J'_{1,0}(h)\\ J'_{1,1}(h)\\ \end{matrix}\right) + \left( \begin{matrix} 0\\ \sqrt{h+\frac{1}{2\eta }}\\ \end{matrix}\right) . \end{aligned}$$

(2.20)

Proof

We only prove the conclusion (i). Conclusion (ii) can be proved similarly. Since x can be regarded as a function of y and h, differentiating the first equation in (1.3) with respect to h, we get

$$\begin{aligned} \frac{\partial x}{\partial h}=\frac{y^2}{2x}, \end{aligned}$$

which implies

$$\begin{aligned} I'_{i,j}(h)=\frac{i}{2}\int _{L^1_h}x^{i-2}y^{j-1}dx. \end{aligned}$$

(2.21)

Hence,

$$\begin{aligned} I_{i,j}(h)=\frac{2}{i+2}I'_{i+2,j-2}(h). \end{aligned}$$

(2.22)

Multiplying both side of (2.21) by h and integrating over $L^1_h$, we have

$$\begin{aligned} hI'_{i,j}(h)=\frac{i}{i+2}I'_{i+2,j-2}(h)-I'_{i,j-1}(h)+\frac{\eta }{2}I'_{i,j-2}(h). \end{aligned}$$

(2.23)

On the other hand, by (2.2), we get for $i\ge 1$ and $j\ge -1$

$$\begin{aligned} I_{i,j}(h)= & {} \int _{L^1_h}x^{i}y^{j-3}dy= -\frac{i}{j-2}\int _{L^1_h}x^{i-1}y^{j-2}dx-\frac{i}{j-2} \eta ^{j-2}\int _{\overrightarrow{BG}}x^{i-1}dx\nonumber \\= & {} -\frac{i}{2(j-2)}\int _{L^1_h}x^{i-2}y^{j-2}(2hy+1)dy +\frac{\eta ^{i+j-2}}{j-2}\left( h+\frac{1}{2\eta }\right) ^\frac{i}{2}\nonumber \\= & {} -\frac{1}{j-2}\left[ 2hI'_{i,j}(h)+I'_{i,j-1}(h)-\eta ^{i+j-2} \left( h+\frac{1}{2\eta }\right) ^\frac{i}{2}\right] . \end{aligned}$$

(2.24)

Taking $(i,j)=(0,1)$ in (2.22) and noting that (2.12) we obtain

$$\begin{aligned} I_{0,1}(h)=2\left( h+\frac{1}{2\eta }\right) I'_{0,1}(h). \end{aligned}$$

From (2.24) we have

$$\begin{aligned} \left\{ \begin{array}{l} I_{2,0}(h)=hI'_{2,0}(h)+\frac{1}{2}I'_{2,-1}(h)-\frac{1}{2} \big (h+\frac{1}{2\eta }\big ),\\ I_{1,0}(h)=hI'_{1,0}(h)+\frac{1}{2}I'_{1,-1}(h) -\frac{1}{2\eta }\sqrt{h+\frac{1}{2\eta }},\\ I_{1,1}(h)=2hI'_{1,1}(h)+I'_{1,0}(h)-\sqrt{h+\frac{1}{2\eta }}. \end{array}\right. \end{aligned}$$

In view of (2.9) and (2.12) we obtain conclusion (i). The proof is completed. $\square$

Lemma 2.4

For $h\in \Sigma =(-\frac{1}{2\eta },0)$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} I_{0,1}(h)=-\sqrt{\frac{2}{\eta }}\sqrt{h+\frac{1}{2\eta }},\ \ I_{1,0}(h)=c_1\big (h+\frac{1}{2\eta }\big ),\\ I_{2,0}(h)=\frac{1}{2}h\ln \frac{1-\sqrt{ 2\eta h+1}}{1+\sqrt{2\eta h+1}}+\frac{1}{2}h\ln |h|-\frac{1}{2\eta }\sqrt{2\eta h+1}-c_2h-\frac{1}{4\eta },\\ I_{1,1}(h)=\frac{1}{2}\sqrt{|h|}\arctan \frac{2\eta h+\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}}-\sqrt{ h+\frac{1}{ 2\eta }}+\big (\frac{\pi }{4}-c_1\sqrt{2\eta }\big )\sqrt{|h|}+c_1 \end{array}\right. } \end{aligned}$$

(2.25)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} J_{0,1}(h)=-\sqrt{\frac{2}{\eta }}\sqrt{h+\frac{1}{2\eta }},\ \ J_{1,0}(h)=d_1\big (h+\frac{1}{2\eta }\big ),\\ J_{2,0}(h)=\frac{1}{2}h\ln \frac{1-\sqrt{2\eta h+1}}{1+\sqrt{2\eta h+1}}-\frac{1}{2}h\ln |h|-\frac{1}{2\eta }\sqrt{2\eta h+1}-d_2h+\frac{1}{4\eta },\\ J_{1,1}(h)=-\frac{1}{2}\sqrt{|h|}\arctan \frac{2\eta h+\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}}+\sqrt{ h+\frac{1}{ 2\eta }}-\big (\frac{\pi }{4}+d_1\sqrt{2\eta }\big )\sqrt{|h|}+d_1, \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.26)

where $c_i$ and $d_i$ ($i=1,2$) are real constants.

Proof

We only prove (2.25). (2.26) can be shown in a similar way. Since the coordinates of A and C are $(0,\frac{-\sqrt{2\eta h+1}-1}{2h})$ and $(0,\frac{\sqrt{2\eta h+1}-1}{2h})$, we have

$$\begin{aligned} I_{0,1}(h)=\int _{L^1_h}y^{-2}dy=-\sqrt{\frac{2}{\eta }}\sqrt{h+\frac{1}{2\eta }}. \end{aligned}$$

Inserting the above equality into the second equation in (2.17) gives the following first order linear differential equation

$$\begin{aligned} I_{2,0}(h)=hI'_{2,0}(h)-\frac{1}{2}\left( h+\frac{1}{2\eta }\right) -\frac{1}{\sqrt{2\eta }}\sqrt{h+\frac{1}{2\eta }}. \end{aligned}$$

(2.27)

Then, solving (2.27) gives $I_{2,0}(h)$ in (2.25).

It follows from the first equation in (2.18) that

$$\begin{aligned} I_{1,0}(h)=c_1\left( h+\frac{1}{2\eta }\right) , \end{aligned}$$

where $c_1$ is a real constant. Similar to solving $I_{2,0}(h)$, we obtain

$$\begin{aligned} I_{1,1}(h)=\frac{1}{2}\sqrt{|h|}\arctan \frac{2\eta h+\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}}-\sqrt{ h+\frac{1}{ 2\eta }}+c\sqrt{|h|}+c_1, \end{aligned}$$

(2.28)

where c and $c_2$ are real constants. Noting that $\lim \nolimits _{h\rightarrow -\frac{1}{2\eta }}I_{1,1}(h)=0$, we have $c=\frac{\pi }{4}-c_1\sqrt{2\eta }$. Then, substituting c into (2.28) yields $I_{1,1}(h)$ in (2.25). This completes the proof. $\square$

3 Proof of Theorem 1.1

In the following, we denote by $P_k(u)$, $Q_k(u)$, $R_k(u)$, $S_k(u)$ and $T_k(u)$ the polynomials of u with degree at most k and denote by $\#\{\phi (h)=0, h\in (\lambda _1,\lambda _2)\}$ the number of isolated zeros of $\phi (h)$ on $(\lambda _1,\lambda _2)$ taking into account the multiplicity.

Proof of Theorem 1.1

If $n>3$ is an even number, let ${\overline{M}}(h)=h^{n-2}M(h)$ for $h\in (-\frac{1}{2\eta },0)$, then ${\overline{M}}(h)$ and M(h) have the same number of zeros on $(-\frac{1}{2\eta },0)$. By Lemmas 2.2 and 2.4, we have

$$\begin{aligned} {\overline{M}}(h)&={\alpha }_1(h)I_{0,1}(h)+{\beta }_1(h)I_{2,0}(h) +{\gamma }_1(h)I_{1,0}(h)+{\delta }_1(h)I_{1,1}(h)\\&\quad +{\alpha }_2(h)J_{0,1}(h)+{\beta }_2(h)J_{2,0}(h)+{\gamma }_2(h)J_{1,0}(h) +{\delta }_2(h)J_{1,1}(h)\\&\quad +{\varphi }_{\frac{3}{2}n-\frac{7+(-1)^n}{4}}(h)+\sqrt{ h+\frac{1}{2\eta }}{\psi }_{\frac{3}{2}n-\frac{9-(-1)^n}{4}}(h)\\&:=P_{n-1}(h)\ln \frac{1-\sqrt{ 2\eta h+1}}{1+\sqrt{2\eta h+1}}+Q_{n-1}(h)\sqrt{|h|}\arctan \frac{2\eta h+\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}}\\&\quad +R_{n-1}(h)\ln |h|+S_{n-1}(h)\sqrt{|h|}+{\varphi }_{\frac{3}{2}n-2}(h)+\sqrt{ h+\frac{1}{2\eta }}{\psi }_{\frac{3}{2}n-2}(h). \end{aligned}$$

Let $t=\sqrt{h+\frac{1}{2\eta }}$, $t\in (0,\frac{1}{\sqrt{2\eta }})$, then ${\overline{M}}(h)$ can be written as

$$\begin{aligned} M_1(t)= & {} P_{n-1}(t^2)\ln \frac{1-\sqrt{ 2\eta }t}{1+\sqrt{2\eta }t}+Q_{n-1}(t^2)\sqrt{\frac{1}{2\eta }-t^2}\arctan \frac{2\eta t^2-\frac{1}{2}}{\sqrt{2\eta (1-2\eta t^2)}t}\\&\quad +R_{n-1}(t^2)\ln \left( \frac{1}{2\eta }-t^2\right) +S_{n-1}(t^2) \sqrt{\frac{1}{2\eta }-t^2}+T_{3n-3}(t). \end{aligned}$$

Hence, ${\overline{M}}(h)$ and $M_1(t)$ have the same number of zeros for $h\in (-\frac{1}{2\eta },0)$ and $t\in (0,\frac{1}{\sqrt{2\eta }})$. Suppose that $\Sigma _1=(0,\frac{1}{\sqrt{2\eta }})\backslash \{t\in (0,\frac{1}{\sqrt{2\eta }})|P_{n-1}(t^2)=0\}$. Then, for $t\in \Sigma _1$, we get

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\Big (\frac{M_1(t)}{P_{n-1}(t^2)}\Big )=\frac{2\sqrt{2\eta }}{2\eta t^2-1}\\&\quad +\frac{d}{dt}\left[ \frac{Q_{n-1}(t^2)\sqrt{\frac{1}{2\eta }-t^2}\arctan \frac{2\eta t^2-\frac{1}{2}}{\sqrt{2\eta (1-2\eta t^2)}t} +R_{n-1}(t^2)\ln \big (\frac{1}{2\eta }-t^2\big )+S_{n-1}(t^2)\sqrt{\frac{1}{2\eta }-t^2}+T_{3n-3}(t)}{P_{n-1}(t^2)}\right] \\ {}&\quad =\frac{P_{2n-2}(t^2)t\ln \big (\frac{1}{2\eta }-t^2\big )+Q_{2n-2}(t^2)t\sqrt{1-2\eta t^2}\arctan \frac{2\eta t^2-\frac{1}{2}}{\sqrt{2\eta (1-2\eta t^2)}t} +R_{2n-2}(t^2)t\sqrt{1-2\eta t^2}+S_{5n-4}(t)}{P^2_{n-1}(t^2)(2\eta t^2-1)}\\&\quad :=\frac{M_2(t)}{P^2_{n-1}(t^2)(2\eta t^2-1)}. \end{aligned} \end{aligned}$$

Let $\Sigma _2=(0,\frac{1}{\sqrt{2\eta }})\backslash \{t\in (0,\frac{1}{\sqrt{2\eta }})|P_{2n-2}(t^2)=0\}$, then we have for $t\in \Sigma _2$

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\left( \frac{M_2(t)}{P_{2n-2}(t^2)t}\right)&=\frac{d}{dt} \left[ \frac{Q_{2n-2}(t^2)t\sqrt{1-2\eta t^2}\arctan \frac{2\eta t^2-\frac{1}{2}}{\sqrt{2\eta (1-2\eta t^2)}t} +R_{2n-2}(t^2)t\sqrt{1-2\eta t^2}+S_{5n-4}(t)}{P_{2n-2}(t^2)t}\right] \\&\quad +\frac{4\eta t}{2\eta t^2-1}\\&=\frac{P_{4n-3}(t^2)t\sqrt{1-2\eta t^2}\arctan \frac{2\eta t^2-\frac{1}{2}}{\sqrt{2\eta (1-2\eta t^2)}t}+Q_{4n-3}(t^2)t\sqrt{1-2\eta t^2}+R_{9n-6}(t)}{P^2_{2n-2}(t^2)t^2(2\eta t^2-1)}\\&:=\frac{M_3(t)}{P^2_{2n-2}(t^2)t^2(2\eta t^2-1)}. \end{aligned} \end{aligned}$$

Similarly, let $\Sigma _3=(0,\frac{1}{\sqrt{2\eta }})\backslash \{t\in (0,\frac{1}{\sqrt{2\eta }})|P_{4n-3}(t^2)=0\}$, then we have for $t\in \Sigma _3$

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\left( \frac{M_3(t)}{P_{4n-3}(t^2)t\sqrt{1-2\eta t^2}}\right)&=\frac{d}{dt}\left[ \frac{Q_{4n-3}(t^2)t\sqrt{1-2\eta t^2}+R_{9n-6}(t)}{P_{4n-3}(t^2)t\sqrt{1-2\eta t^2}}\right] +\frac{2\sqrt{2\eta t}}{\sqrt{1-2\eta t^2}}\\&=\frac{P_{17n-10}(t)+Q_{8n-5}(t^2)t\sqrt{1-2\eta t^2}}{P^2_{4n-3}(t^2)t^2(1-2\eta t^2)\sqrt{1-2\eta t^2}}\\&:=\frac{M_4(t)}{P^2_{4n-3}(t^2)t^2(1-2\eta t^2)\sqrt{1-2\eta t^2}}. \end{aligned} \end{aligned}$$

Let $M_4(t)=P_{17n-10}(t)+Q_{8n-5}(t^2)t\sqrt{1-2\eta t^2}=0$. That is,

$$\begin{aligned} Q_{8n-5}(t^2)t\sqrt{1-2\eta t^2}=-P_{17n-10}(t). \end{aligned}$$

By squaring the above equation, we can deduce that $M_4(t)$ has at most $34n-20$ zeros on $(0,\frac{1}{\sqrt{2\eta }})$. Hence,

$$\begin{aligned} \begin{aligned} \# \left\{ M(h)=0, h\in \left( -\frac{1}{2\eta },0\right) \right\}&=\# \left\{ M_1(t)=0, t\in \left( 0,\frac{1}{\sqrt{2\eta }}\right) \right\} \\&\le 41n-23. \end{aligned} \end{aligned}$$

(3.1)

If $n=1,2,3$, it is easy to check that (3.1) also holds.

If n is an odd number, we can prove Theorem 1.1 similarly. This ends the proof of Theorem 1.1. $\square$

4 Proof of Theorem 1.2

If $f^1(x,y)=f^2(x,y)$, $g^1(x,y)=g^2(x,y)$, $f^3(x,y)=f^4(x,y)$ and $g^3(x,y)=g^4(x,y)$, then system (1.2) can be written as

$$\begin{aligned} \left( \begin{array}{c} {\dot{x}} \\ {\dot{y}} \end{array} \right) ={\left\{ \begin{array}{ll} \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^1(x,y) \\ -2xy+\varepsilon g^1(x,y) \end{array} \right) , \quad x>0,\\ \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^3(x,y) \\ -2xy+\varepsilon g^3(x,y) \end{array} \right) ,\quad x<0. \end{array}\right. } \end{aligned}$$

(4.1)

From Theorem 1.1 in [10, 17], we know that the first order Melnikov function M(h) of system (4.1) has the following form

$$\begin{aligned} \begin{aligned} M(h)&=\int _{L^1_h\cup L^2_h}y^{-3}[g^1(x,y)dx-f^1(x,y)dy]\\&\quad +\int _{L^3_h\cup L^4_h}y^{-3}[g^3(x,y)dx-f^3(x,y)dy] \end{aligned} \end{aligned}$$

and the number of zeros of M(h) controls the number of limit cycles of system (4.1) if $M(h)\not \equiv 0$ in corresponding period annulus.

For $h\in \Sigma$ and $i=0,1,2,\ldots ,j=0,1,2,\ldots$, we denote

$$\begin{aligned} \begin{aligned} U_{i,j}(h)=\int _{\Gamma _h}x^iy^{j-3}dy,\ \ {\tilde{U}}_{i,j}(h)=\int _{{\tilde{\Gamma }}_h}x^iy^{j-3}dy, \end{aligned} \end{aligned}$$

where $\Gamma _h=L^1_h\cup L^2_h$ and ${\tilde{\Gamma }}_h=L^3_h\cup L^4_h$. It is easy to get that ${\tilde{U}}_{i,j}(h)=(-1)^{i+1}{U}_{i,j}(h)$. Similar to (2.2), we get

$$\begin{aligned} \begin{aligned}&\int _{\Gamma _h}x^iy^jdx=-\frac{j}{i+1}\int _{\Gamma _h}x^{i+1}y^{j-1}dy,\\&\int _{{\tilde{\Gamma }}_h}x^iy^jdx=-\frac{j}{i+1}\int _{{\tilde{\Gamma }}_h}x^{i+1}y^{j-1}dy. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} M(h)= & {} \sum \limits _{i+j=0}^nb^1_{i,j}\int _{\Gamma _h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^1_{i,j}\int _{\Gamma _h}x^iy^{j-3}dy\\&\quad +\sum \limits _{i+j=0}^nb^3_{i,j}\int _{{\tilde{\Gamma }}_h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^3_{i,j}\int _{{\tilde{\Gamma }}_h}x^iy^{j-3}dy\\= & {} -\sum \limits _{i+j=0}^nb^1_{i,j}\frac{j-3}{i+1}\int _{\Gamma _h}x^{i+1}y^{j-4}dy -\sum \limits _{i+j=0}^na^1_{i,j}\int _{\Gamma _h}x^iy^{j-3}dy\\&\quad -\sum \limits _{i+j=0}^nb^3_{i,j}\frac{j-3}{i+1}\int _{{\tilde{\Gamma }}_h}x^{i+1}y^{j-4}dy -\sum \limits _{i+j=0}^na^3_{i,j}\int _{{\tilde{\Gamma }}_h}x^iy^{j-3}dy\\:= & {} \sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n{\bar{\sigma }}_{i,j}U_{i,j}(h), \end{aligned}$$

where ${\bar{\sigma }}_{i,j}$ are real constants.

Following the proof of Lemmas 2.1 and 2.2, we can get the following Lemma 4.1.

Lemma 4.1

, If $i+j=n>3$, then

$$\begin{aligned} M(h)=\frac{1}{h^{n-2}}\Big [\alpha _1(h)U_{0,1}(h)+{\beta _1}(h)U_{2,0}(h) +{\gamma _1}(h)U_{1,0}(h)+{\delta _1}(h)U_{1,1}(h)\Big ],\nonumber \\ \end{aligned}$$

(4.2)

where ${\alpha _1}(h)$, ${\beta _1}(h)$, ${\gamma _1}(h)$ and ${\delta _1}(h)$ are polynomials of h with

$$\begin{aligned} \begin{aligned}&\deg {\alpha _1}(h)\le n-\frac{3+(-1)^n}{2},\ \deg {\delta _1}(h)\le n-\frac{3-(-1)^n}{2},\\&\deg {\beta _1}(h),\deg {\gamma _1}(h)\le n-2. \end{aligned} \end{aligned}$$

If $n=1,2,3$, then

$$\begin{aligned} M(h)=\frac{1}{h}\Big [{\alpha _1}(h)U_{0,1}(h)+{\beta _1}(h)U_{2,0}(h) +{\gamma _1}(h)U_{1,0}(h)+{\delta _1}(h)U_{1,1}(h)\Big ],\nonumber \\ \end{aligned}$$

(4.3)

where ${\alpha _1}(h)$, ${\beta _1}(h)$, ${\gamma _1}(h)$ and ${\delta _1}(h)$ are polynomials of h with

$$\begin{aligned} \begin{aligned} \deg {\alpha }_1(h), \deg {\delta }_1(h)\le 2,\ \ \deg {\beta }_1(h),\deg {\gamma }_1(h)\le 1. \end{aligned} \end{aligned}$$

The following lemma gives the Picard–Fuchs equations which the generators of M(h) in (4.2) satisfy and can be proved by the method in Lemma 2.3.

Lemma 4.2

The vector functions $\big (U_{0,1}(h),U_{2,0}(h)\big )^T$ and $\big (U_{1,0}(h),U_{1,1}(h)\big )^T$ respectively satisfy the Picard–Fuchs equations

$$\begin{aligned} \left( \begin{matrix} U_{0,1}(h)\\ U_{2,0}(h)\\ \end{matrix}\right) =\left( \begin{matrix} 2\big (h+\frac{1}{2\eta }\big )&{}\quad 0\\ h+\frac{1}{2\eta }&{}\quad h\\ \end{matrix}\right) \left( \begin{matrix} U'_{0,1}(h)\\ U'_{2,0}(h)\\ \end{matrix}\right) \end{aligned}$$

(4.4)

and

$$\begin{aligned} \left( \begin{matrix} U_{1,0}(h)\\ U_{1,1}(h)\\ \end{matrix}\right) =\left( \begin{matrix} h+\frac{1}{2\eta }&{}\quad 0\\ 1&{}\quad 2h\\ \end{matrix}\right) \left( \begin{matrix} U'_{1,0}(h)\\ U'_{1,1}(h)\\ \end{matrix}\right) . \end{aligned}$$

(4.5)

From (4.5) and (4.6), we have for $h\in \Sigma =(-\frac{1}{2\eta },0)$

$$\begin{aligned} {\left\{ \begin{array}{ll} U_{0,1}(h)=-{\frac{2}{\eta }}\sqrt{h+\frac{1}{2\eta }},\ \ U_{1,0}(h)=e_1\big (h+\frac{1}{2\eta }\big ),\\ U_{2,0}(h)=\frac{1}{2}h\ln \frac{1-\sqrt{ 2\eta h+1}}{1+\sqrt{2\eta h+1}}-\frac{1}{2\eta }\sqrt{2\eta h+1}-e_2h,\\ U_{1,1}(h)=\big (\frac{\pi }{4}-e_1\sqrt{2\eta }\big )\sqrt{|h|}+e_1, \end{array}\right. } \end{aligned}$$

(4.6)

where $e_1$ and $e_2$ are real constants. Hence,

where ${\hat{P}}_{k}(h)$, ${\hat{Q}}_{k}(h)$, ${\hat{R}}_{k}(h)$ and ${\hat{S}}_{k}(h)$ are the polynomials of h with degree not more than k. Following the lines of the proof of Theorem 1.1, we can prove that M(h) has at most $9n-4$ zeros on $(-\frac{1}{2\eta },0)$. The Theorem 1.2 is proved.

5 Proof of Theorem 1.3

If $f^1(x,y)=f^4(x,y)$, $g^1(x,y)=g^4(x,y)$, $f^2(x,y)=f^3(x,y)$ and $g^2(x,y)=g^3(x,y)$, then system (1.2) can be written as

$$\begin{aligned} \left( \begin{array}{c} {\dot{x}} \\ {\dot{y}} \end{array} \right) ={\left\{ \begin{array}{ll} \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^1(x,y) \\ -2xy+\varepsilon g^1(x,y) \end{array} \right) , \quad y>\eta ,\\ \left( \begin{array}{c} y-2x^2-\eta +\varepsilon f^2(x,y) \\ -2xy+\varepsilon g^2(x,y) \end{array} \right) ,\quad y<\eta . \end{array}\right. } \end{aligned}$$

(5.1)

From Theorem 1.1 in [10, 17], we know that the first order Melnikov function M(h) of system (5.1) has the following form

$$\begin{aligned} M(h)= & {} \int _{\Upsilon _h}y^{-3}[g^1(x,y)dx-f^1(x,y)dy]\\&+\int _{{\tilde{\Upsilon }}_h}y^{-3}[g^2(x,y)dx-f^2(x,y)dy], \end{aligned}$$

where $\Upsilon _h=L^1_h\cup L^4_h$ and ${\tilde{\Upsilon }}_h=L^2_h\cup L^3_h$. Furthermore, the number of zeros of M(h) controls the number of limit cycles of system (5.1) if $M(h)\not \equiv 0$ in corresponding period annulus.

For $h\in \Sigma$ and $i=0,1,2,\ldots ,j=0,1,2,\ldots$, we denote

$$\begin{aligned} V_{i,j}(h)=\int _{\Upsilon _h}x^iy^{j-3}dy,\ \ {\tilde{V}}_{i,j}(h)=\int _{{\tilde{\Upsilon }}_h}x^iy^{j-3}dy. \end{aligned}$$

Noting that $\Upsilon _h$ and ${\tilde{\Upsilon }}_h$ are symmetric with respect to $x=0$, we get ${V}_{2l,j}(h)={\tilde{V}}_{2l,j}(h)=0$ for $l=0,1,2,\ldots$. Similar to (2.2), we have

$$\begin{aligned} \int _{\Upsilon _h}x^iy^jdx= & {} -\frac{j}{i+1}\int _{\Upsilon _h}x^{i+1} y^{j-1}dy-\eta ^j\int _{\overrightarrow{BD}}x^idx,\\ \int _{{\tilde{\Upsilon }}_h}x^iy^jdx= & {} -\frac{j}{i+1}\int _{{\tilde{\Upsilon }}_h} x^{i+1}y^{j-1}dy-\eta ^j\int _{\overrightarrow{DB}}x^idx. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} M(h)&=\sum \limits _{i+j=0}^nb^1_{i,j}\int _{\Upsilon _h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^1_{i,j}\int _{\Upsilon _h}x^iy^{j-3}dy\\&\quad +\sum \limits _{i+j=0}^nb^2_{i,j}\int _{{\tilde{\Upsilon }}_h}x^iy^{j-3}dx -\sum \limits _{i+j=0}^na^2_{i,j}\int _{{\tilde{\Upsilon }}_h}x^iy^{j-3}dy\\&=\sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j\ge -1 \end{array}}^n{\tilde{\sigma }}_{i,j}V_{i,j}(h)+ \sum \limits _{\begin{array}{c} i+j=0,\\ i\ge 0,j \ge -1 \end{array}}^n{\tilde{\tau }}_{i,j}{\tilde{V}}_{i,j}(h)\\ {}&\quad + \sum \limits _{i=0}^n{\tilde{\nu }}_i[(-1)^{i+1}-1]\eta ^{i+1} \left( h+\frac{1}{2\eta }\right) ^{\frac{i+1}{2}}, \end{aligned} \end{aligned}$$

where ${\tilde{\sigma }}_{i,j}$, ${\tilde{\tau }}_{i,j}$ and ${\tilde{\nu }}_i$ are real constants.

Lemma 5.1

If $i+j=n>3$, then

$$\begin{aligned} M(h)=\frac{1}{h^{n-2}}\Big [\gamma _1(h)V_{1,0}(h) +{\delta _1}(h)V_{1,1}(h)+\gamma _2(h){\tilde{V}}_{1,0}(h) +{\delta _2}(h){\tilde{V}}_{1,1}(h)\Big ],\nonumber \\ \end{aligned}$$

(5.2)

where ${\gamma _k}(h)$ and ${\delta _k}(h)$$(k=1,2)$ are polynomials of h with

$$\begin{aligned} \deg {\gamma _k}(h)\le n-2,\ \ \deg {\delta _k}(h)\le n-\frac{3-(-1)^n}{2},\ k=1,2. \end{aligned}$$

If $n=1,2,3$, then

$$\begin{aligned} M(h)=\frac{1}{h}\Big [\gamma _1(h)V_{1,0}(h) +{\delta _1}(h)V_{1,1}(h)+\gamma _2(h){\tilde{V}}_{1,0}(h) +{\delta _2}(h){\tilde{V}}_{1,1}(h)\Big ],\nonumber \\ \end{aligned}$$

(5.3)

where ${\gamma _k}(h)$ and ${\delta _k}(h)$$(k=1,2)$ are polynomials of h with

$$\begin{aligned} \deg {\gamma }_k(h)\le 1, \ \ \deg {\delta }_k(h)\le 2,\ k=1,2. \end{aligned}$$

Lemma 5.2

The vector functions $\big (V_{1,0}(h),V_{1,1}(h)\big )^T$ and $\big ({\tilde{V}}_{1,0}(h),{\tilde{V}}_{1,1}(h)\big )^T$ respectively satisfy the Picard–Fuchs equations

$$\begin{aligned} \left( \begin{matrix} V_{1,0}(h)\\ V_{1,1}(h)\\ \end{matrix}\right) =\left( \begin{matrix} h+\frac{1}{2\eta }&{}\quad 0\\ 1&{}\quad 2h\\ \end{matrix}\right) \left( \begin{matrix} V'_{1,0}(h)\\ V'_{1,1}(h)\\ \end{matrix}\right) + \left( \begin{matrix} 0\\ -2\sqrt{h+\frac{1}{2\eta }}\\ \end{matrix}\right) \end{aligned}$$

(5.4)

and

$$\begin{aligned} \left( \begin{matrix} {\tilde{V}}_{1,0}(h)\\ {\tilde{V}}_{1,1}(h)\\ \end{matrix}\right) =\left( \begin{matrix} h+\frac{1}{2\eta }&{}\quad 0\\ 1&{}\quad 2h\\ \end{matrix}\right) \left( \begin{matrix} {\tilde{V}}'_{1,0}(h)\\ {\tilde{V}}'_{1,1}(h)\\ \end{matrix}\right) + \left( \begin{matrix} 0\\ 2\sqrt{h+\frac{1}{2\eta }}\\ \end{matrix}\right) . \end{aligned}$$

(5.5)

From (5.5) and (5.6), we have for $h\in \Sigma =(-\frac{1}{2\eta },0)$

$$\begin{aligned} V_{1,0}(h)&={\hat{c}}_1\left( h+\frac{1}{2\eta }\right) ,\ \ {\tilde{V}}_{1,0}(h)={\hat{d}}_1\left( h+\frac{1}{2\eta }\right) ,\nonumber \\ V_{1,1}(h)&=\sqrt{|h|}\arctan \frac{2\eta h+\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}}\nonumber \\&\quad -2\sqrt{ h+\frac{1}{ 2\eta }}+\left( \frac{\pi }{2}-{\hat{c}}_1\sqrt{2\eta }\right) \sqrt{|h|}+{\hat{c}}_1,\nonumber \\ {\tilde{V}}_{1,1}(h)&=-\sqrt{|h|}\arctan \frac{2\eta h-\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}}\nonumber \\ {}&\quad -2\sqrt{ h+\frac{1}{ 2\eta }}-\left( \frac{\pi }{2}+{\hat{d}}_1\sqrt{2\eta }\right) \sqrt{|h|}+{\hat{d}}_1, \end{aligned}$$

(5.6)

where ${\hat{c}}_1$ and ${\hat{d}}_2$ are real constants. Hence,

$$\begin{aligned} M(h)= & {} \frac{1}{h^{n-2}}\big [{\gamma _1}(h)V_{1,0}(h)+{\delta _1}(h)V_{1,1}(h)+{\gamma _2}(h){\tilde{V}}_{1,0}(h)+{\delta _2}(h){\tilde{V}}_{1,1}(h)\big ]\\= & {} \frac{1}{h^{n-2}}\left[ {\gamma _1}(h){\hat{c}}_1\left( h+\frac{1}{2\eta }\right) +{\gamma _2}(h){\hat{d}}_1\left( h+\frac{1}{2\eta }\right) \right. \\&+{\delta _1}(h)\left( \sqrt{|h|}\arctan \frac{2\eta h+\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}}\right. \\&\left. -2\sqrt{ h+\frac{1}{ 2\eta }}+\left( \frac{\pi }{2}-{\hat{c}}_1\sqrt{2\eta }\right) \sqrt{|h|}+{\hat{c}}_1\right) \\&+{\delta _2}(h)\Big (-\sqrt{|h|}\arctan \frac{2\eta h-\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}} \\&\left. -2\sqrt{ h+\frac{1}{ 2\eta }}-\Big (\frac{\pi }{2}+{\hat{d}}_1\sqrt{2\eta }\Big )\sqrt{|h|}+{\hat{d}}_1\Big )\right] \\:= & {} {\check{P}}_{n-1}(h)\sqrt{|h|}\arctan \frac{2\eta h-\frac{1}{2}}{\sqrt{-2\eta h(2\eta h+1)}} \\&+\,{\check{Q}}_{n-1}(h)\sqrt{2\eta h+1}+{\check{R}}_{n-1}(h)\sqrt{|h|}+{\check{S}}_{n-1}(h), \end{aligned}$$

where ${\check{P}}_{n-1}(h)$, ${\check{Q}}_{n-1}(h)$, ${\check{R}}_{n-1}(h)$ and ${\check{S}}_{n-1}(h)$ are the polynomials of h with degree not more than $n-1$. Following the lines of the proof of Theorem 1.1, we get that M(h) has at most $9n-6$ zeros on $(-\frac{1}{2\eta },0)$. The Theorem 1.3 is proved.