Fuzzy optimization approach to component selection of fault-tolerant software system

Abstract

In developing software systems, a manager’s goal is to design software using limited resources and meet the user requirements. One of the important user requirements concerns the reliability of the software. The decision to choose the right software modules (components) becomes extremely difficult because of the number of parameters to be considered while making the decision. If suitable components are not available, then the decision process is further complicated with build versus buy decisions. In this paper, we have formulated a fuzzy multi-objective approach to optimal decision “build-or-buy” for component selection for a fault-tolerant modular software system under the consensus recovery block scheme. A joint optimization model is formulated where the two objectives are maximization of system reliability and minimization of the system cost with a constraint on delivery time. An example of developing a retail system for small-and-medium-size enterprises is used to illustrate the proposed methodology.

1 Introduction

Computers and software have become a significant part of modern society. It is virtually impossible to conduct many day to day activities without the aid of computer systems controlled by software. Software is involved in every aspect of modern society. Government, transportation, manufacturing, utilities, and almost every other sector that influences our way of life is affected directly or indirectly by software systems. As more dependence is placed on these software systems, it is essential that they operate in a reliable manner. Failure to do so can result in high monetary, property, or human loss. In developing software systems, a manager’s goal is to produce a software system within the limited resources and in accordance with the user requirements. One important user requirement concerns the reliability of the software. Good engineering practice is essential in the design of reliable software. The process is inherently more difficult in dealing with software than in the case of hardware. Software reliability engineering (SRE) is the “quantitative study of the operational behavior of software-based systems”. With SRE, one can deliver just enough reliability and avoid both excessive costs and development time.

Software development processes and methods have been studied for decades; despite that we still do not guarantee error-free software. One way of handling unknown and unpredictable software failures is through fault tolerance. Software fault-tolerance techniques are employed during the procurement, or development, of the software. They enable a system to tolerate software faults remaining in the system after its development. When a fault occurs, these techniques provide mechanisms to the software system to prevent system failure from occurring. There are two structural methodologies for a fault-tolerant system: Recovery Block Scheme and N-Version Programming. The basic mechanism of both the schemes is to provide redundant software to tolerate software failures. There are two optimization models for recovery block schemes, namely, independent recovery block and consensus recovery block. In this paper, we will discuss optimization models for the consensus recovery block. Fault tolerance improves system reliability, but incurs higher cost. Therefore, it is necessary to carry a trade-off between cost and reliability.

This paper discusses a framework that helps developers to decide whether to buy or build components of software architecture on the basis of cost and non-functional factors for a fault-tolerant modular software system. While developing software, components can be both bought as commercial off-the shelf (COTS) products, and probably adapted to work in the software system, or they can be developed in-house. This decision is known as “build-or-buy” decision. This decision affects the overall cost and reliability of the system. The growing availability of COTS components in the software market has concretized the possibility of building whole systems based on components. In this multitude, a recurrent problem is the selection of components that best fit the requirements. The development of component-based systems largely depends on the success of the selection process. COTS components have been growing rapidly as an emerging paradigm in software development. By COTS components, we mean commercial software packages with common purposes that are ready to be used in software development and application integration. If some COTS components are not available economically in the market, then these are developed within the organization and are known as in-house-built components.

Several optimization models of the COTS selection process exist in literature to achieve the different attributes of quality along with the objective of minimizing cost or keeping cost to a specified budgetary level. Berman and Ashrafi [2] formulated optimization model for reliability of modular software system. Cortellessa et al. [5] and [6] developed optimization models that supports “build-or-buy” decisions in selecting software components based on cost-reliability trade-off. Neubauer and Stummer [14] developed a two-phased decision support approach based on multi-objective optimization model for COTS selection of modular software system. Jha et al. [9] and [8] presented multi-objective optimization models for fault tolerant modular software system under consensus recovery block scheme. Kwong and Tang Mu [12] presented optimization model for determining the optimal selection of software components for component based software system development. Gupta et al. [7] presented cost reliability models for COTS selection in Fuzzy Environment.

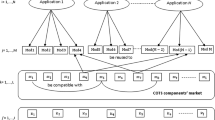
In this paper, the joint optimization of reliability and cost is considered while incorporating the build-or-buy approach for selection of components in designing a fault-tolerant modular software system under the consensus recovery block scheme. This paper discusses the issues related to reliability of software systems and cost produced by integrating COTS or in-house-built components. We have applied the fuzzy multi-objective approach to optimal decision “build-or-buy” for component selection for a fault-tolerant modular software system. A large software system has a modular structure to perform a set of functions with different modules having different alternatives for each module. For a COTS product, different versions are available for each alternative. A schematic representation of the software system is given in Fig. 1.

Fig. 1

Structure of software

A component is chosen for a module from a number of alternatives available to the software developer. COTS or in-house-built components may be selected. We are selecting the components for modules to maximize the system reliability by simultaneously minimizing the cost. The frequency with which the functions are used is not the same for all of them and not all the modules that the software has in its menu are called during the execution of a function. We assume that for all the alternatives available for a module, cost increases if higher reliability is desired. This is a realistic assumption, as COTS suppliers are ready to supply more reliable versions of the same component at a higher price. Purchase of high-quality COTS products can be justified by frequent use of the module. Hence, more than one version is available for alternatives of a module. Further, the best of testing efforts are required to improve the reliability of the in-house-built component. This leads to an increase in cost. The first optimization model (optimization model-I) of this paper maximizes the system reliability with simultaneously minimizing the overall system cost. The second optimization model (optimization model-II) considers the issue of compatibility between different alternatives of modules as it is observed that some COTS components cannot integrate with all the alternatives of another module. The models discussed are illustrated with a case study. The paper is organized as follows: Notations of the optimization models are discussed in “List of symbols”. Fuzzy Optimization models for the consensus recovery block scheme are discussed in Sect. 2. Solution of Fuzzy multi-objective optimization model is discussed in Sect. 3, a case study is illustrated in Sect. 4, and in Sect. 5, are the concluding remarks.

2 Optimization models

Consider software systems that are developed using modular techniques and are required to perform a set of functions. Each function is performed by different modules having different alternatives for each module. If a COTS component is selected, then different versions are available for each alternative and only one version will be selected for each alternative of a module. If a component is an in-house-built component, then the alternative of a module is selected. We assume that functionally equivalent and independently developed alternatives (i.e. in-house or COTS) for each module are available with an estimated reliability, cost and delivery time.

The first optimization model is developed for the following situations, which also holds good for the second model, but with additional assumptions related to compatibility among alternatives of a module. The following assumptions are common for the optimization models.

• 1. Software system consists of a finite number of modules.

• 2. Software system is required to perform a known number of functions. The program written for a function can call a series of modules $\left( {\le n}\right)$. A failure occurs if a module fails to carry out an intended operation.

• 3. Codes written for integration of modules do not contain any bug.

• 4. Several alternatives are available for each module. Fault-tolerant architecture is desired in the modules (it has to be within the specified budget). Independently developed alternatives (primarily COTS/-in-House components) are attached in the modules and work similar to the consensus recovery block scheme discussed in [11] and [3].

• 5. The cost of an alternative is the development cost, if developed in-house; otherwise it is the buying price for the COTS product.

• 6. Different in-house alternatives with respect to unitary development cost, estimated development time, average time to perform a test case and testability of a component are available.

• 7. Cost, reliability and development time of an in-house component can be estimated by using basic parameters of the development process, e.g., a component cost may depend on a measure of developer skills, or the component reliability depends on the amount of testing.

• 8. Different versions (COTS products) with respect to cost, reliability and delivery time of alternatives of a module are available.

• 9. Other than the available cost-reliability-delivery time versions of an alternative (only in case of COTS components), we assume the existence of a virtual version, which has a negligible reliability of 0.001 and zero cost and delivery time. These COTS components are denoted by index one in the third subscript of $x_{ijk}, c_{ijk}, d_{ijk} \, \mathrm{and} \, s_{ijk}$ for example, $s_{ij1}$ denotes the reliability of the first version of alternative $j$ for module $i$.

2.1 Model formulation

Let $S$ be a software architecture made of $n$ modules, with a maximum number of $m_i$ alternatives available for each module and each COTS alternative has different versions. The following are the constraints for optimization models.

2.1.1 Build versus buy decision

For each module $i$, if an alternative is bought (i.e., some $x_{ijk}=1)$, then there is no in-house development (i.e., $y_{ij}=0)$ and vice versa.

$$\begin{aligned} y_{ij} +\sum _{k=1}^{V_{ij}} {x_{ijk}} =1; \quad i=1,2,\ldots ,n; \quad j=1,2,\ldots ,m_i \end{aligned}$$

2.1.2 Redundancy constraint

The equation stated below guarantees that redundancy is allowed for both the build-and-buy components (i.e., in-house and COTS components).

$$\begin{aligned}&y_{ij} +\sum _{k=2}^{V_{ij}} {x_{ijk}}=z_{ij}\\&x_{ij1} +z_{ij} =1; \quad j=1,2,\ldots ,m_i\\&\sum _{j=1}^{m_i} {z_{ij}} \ge 1;\quad i=1,2,\ldots ,n \end{aligned}$$

2.1.3 Probability of failure-free in-house-developed component

The possibility of reducing the probability that the $j\mathrm{th}$ alternative of $i\mathrm{th}$ module fails by means of a certain amount of test cases (represented by the variable $N_{ij}^{tot})$. Cortellessa et al. [6] defined the probability of failure on demand of an in-house-developed $j\mathrm{th}$ alternative of $i\mathrm{th}$ module, under the assumption that the on-field users’ operational profile is the same as the one adopted for testing ([4]).

Basing on the testability definition, we can assume that the number $N_{ij}^{suc}$ of successful (i.e. failure-free) tests performed on $j{th}$ alternative of same module.

$$\begin{aligned} N_{ij}^{suc}&= \left( {1-\pi _{ij} } \right) N_{ij}^{tot};\quad i=1,2,\ldots ,n\quad \text{ and } \quad \\ j&= 1,2,\ldots ,m_i \end{aligned}$$

Let $A$ be the event “$N_{ij}^{suc}$ failure-free test cases have been performed” and $B$ be the event “the alternative is failure-free during a single run”. If $\rho _{ij}$ is the probability that the in-house developed alternative is failure-free during a single run given that $N_{ij}^{suc}$ test cases have been successfully performed, from the Bayes theorem, we get

$$\begin{aligned} \rho _{ij} =P(B/A)=\frac{P(A/B)P(B)}{P(A/B)P(B)+P(A/\overline{B})P(\overline{B})}. \end{aligned}$$

The following equalities come straightforwardly:

$$\begin{aligned}&{\bullet }\quad P(A/B)=1\qquad \qquad \qquad \qquad {\bullet }P(B)=1-\pi _{ij} \\&{\bullet }\quad P(A/\overline{B} )=(1-\pi _{ij})^{N_{ij}^{suc}}\qquad {\bullet }P(\overline{B})=\pi _{ij} \end{aligned}$$

Therefore, we have

$$\begin{aligned} \rho _{ij}&= \frac{1\!-\!\pi _{ij} }{\left( {1\!-\!\pi _{ij} } \right) \!+\!\pi _{ij} \left( {1-\pi _{ij} } \right) ^{N_{ij}^{suc} }}; \quad i =1,2,\ldots ,n\, \quad \text{ and }\\ j&= 1,2,\ldots ,m_i \end{aligned}$$

2.1.4 Reliability equation of both in-house and COTS components

As already mentioned, the reliability of COTS component $(s_{ij})$ is given by the vendor. Therefore, reliability $(r_{ij})$ of $j{th}$ alternative of $i{th}$ module of the software is given by

$$\begin{aligned} r_{ij}=\rho _{ij} y_{ij} +s_{ij} ;\quad i=1,2,\ldots ,n;\quad j=1,2,\ldots ,m_i, \end{aligned}$$

where

$$\begin{aligned} s_{ij}=\sum _{k=1}^{V_{ij}}{s_{ijk} x_{ijk} ;\quad i=1,2,\ldots ,n ; \quad j=1,2,\ldots ,m_i}. \end{aligned}$$

2.1.5 Delivery time constraint

The delivery time $(d_{ijk} )$ of the COTS components is given by the vendor and the development time of in-house component $\left( {t_{ij} +\tau _{ij} N_{ij}^{tot}}\right)$ is estimated by the software development team. To know their value precisely in a real world situation is a difficult task due to many factors involved in either developing or purchasing of the components. The delivery time $(T_{DT})$ for acquiring all the components (COTS orin-house) for the development of modular software system can be estimated using the following equation

$$\begin{aligned} \widetilde{T}_{DT}=\widetilde{T}_{SD} -\widetilde{T}_{IT}-\widetilde{T}_{ST} \end{aligned}$$

where $\sim$ on top of the notations above represents that they are fuzzy numbers. $(T_{SD})$ is the system development time, which is a function of integration testing time denoted by $(T_{IT})$, system testing time $(T_{ST)}$ and delivery time of acquiring the components $(T_{DT})$. The development team estimates these values in the early stage of software development. $(T_{SD})$ depend upon various factors such as testing strategies, testing environment, team constitution, market completion, vendors’ credentials, etc. The information and data needed to compute these either not available or partially available. This problem can be resolved by taking these values as fuzzy numbers.

It becomes arduous for the managers to determine the exact delivery time of acquiring the components for the development of modular software system. Therefore, the manager has to allow some level of tolerance to the delivery time constraint and the equation can be written as

$$\begin{aligned} \widetilde{T}_{DT}\le T_u \end{aligned}$$

The crisp form of the above delivery time constraint can then be written as following

$$\begin{aligned}&y_{ij} \left( {t_{ij} +\tau _{ij} N_{ij}^{tot}} \right) +\sum _{k=1}^{V_{ij}} {d_{ijk} x_{ijk}}\le T_u ;\\&\quad i=1,2,\ldots ,n;\quad j=1,2,\ldots ,m_i \end{aligned}$$

where $T_{u}$ is the tolerance level for the delivery time constraint and is decided by the manager.

2.2 Objective function

2.2.1 Reliability objective function

Reliability objective function maximizes the system quality (in terms of reliability) through a weighted function of module reliabilities. Reliability of modules that are invoked more frequently during use is given higher weights. Analytic Hierarchy Process can be effectively used to calculate these weights.

$$\begin{aligned} Maximize \ \widetilde{R} = \sum _{l=1}^L {f_l \prod _{i\in s_l } {\widetilde{R}_i}} \end{aligned}$$

where $R_i$ is the reliability of module $i$ of the system under the consensus recovery block scheme which is stated as follows:

$$\begin{aligned}&\widetilde{R}_i=1+\left[ \sum _{j=1}^{m_i } \frac{1}{^{(1-r_{ij} )^{z_{ij} }}}\left[ {\prod _{k=1}^{m_i } {(1-r_{ik} )^{z_{ik} }} } \right] \left[ {1-\left( {1-r_{ij} } \right) ^{z_{ij} }}\right] \right. \\&\quad \left. +\prod _{j=1}^{m_i } {\left( {1-r_{ij} } \right) ^{z_{ij} }}\right] \left[ {\sum _{j=1}^{m_i } {z_{ij} \left[ {\prod _{k=1}^{j-1} {P\left( {X_{ik} } \right) ^{z_{ik} }} } \right] } P\left( {Y_{ij}}\right) -1} \right] ;\\&\qquad i=1,2,\ldots ,n\\&P\left( {X_{ij} } \right) =\left( {1-t_1 } \right) \left[ {\left( {1-r_{ij} } \right) \left( {1-t_3 } \right) +r_{ij} t_2 } \right] \\&P\left( {Y_{ij} } \right) =r_{ij} \left( {1-t_2 } \right) . \end{aligned}$$

2.2.2 Cost objective function

Cost objective function minimizes the overall cost of the system. The sum of the cost of all the modules is selected from the “build-or-buy” strategy. The in-house development cost of the alternative $j$ of module $i$ can be expressed as $c_{ij} \left( {t_{ij} +\tau _{ij} N_{ij}^{tot} } \right)$

$$\begin{aligned} Minimize \ \widetilde{C} = \sum _{i=1}^n {\sum _{j=1}^{m_i } {\left( {\widetilde{c}_{ij} \left( {t_{ij} +\tau _{ij} N_{ij}^{tot} } \right) y_{ij} +\sum _{k=1}^{V_{ij} } {\widetilde{C}_{ijk} x_{ijk} } } \right) }} \end{aligned}$$

$\sim$ on the coefficients of objective functions represents that they are fuzzy numbers. The problem with reliability maximization and cost minimization objectives subject to delivery time and component selection constraints can be considered as a multiple objective problem of reliability and cost while solving with the fuzzy optimization.

2.3 Optimization model-I

Consensus Recovery Block achieving fault tolerance is used to run all the attached independent alternatives simultaneously and selecting the output by the voting mechanism. It requires independent development of independent alternatives of a program which the COTS components satisfy and a voting procedure. Upon invocation of the consensus recovery block, all alternatives are executed and their output is submitted by a voting procedure. Since it is assumed that there is no common fault, if two or more alternatives agree on one output then that alternative is designated as correct, otherwise, the next stage is entered. At this stage, the best alternative is examined by the acceptance test. If the output is accepted, it is treated as the correct one. However, if the output is not accepted, the next best alternative is subjected to testing. This process continues until an acceptable output is found or all outputs are exhausted.

The fuzzy multi-objective optimization model for component selection can be written as follows.

$$\begin{aligned} Maximize \,\widetilde{R} = \sum _{l=1}^L {f_l \prod _{i\in s_l } {\widetilde{R}_i}} \end{aligned}$$

$$\begin{aligned} Minimize\quad \widetilde{C} =\sum _{i=1}^n {\sum _{j=1}^{m_i } {\left( {\widetilde{c}_{ij} \left( {t_{ij} +\tau _{ij} N_{ij}^{tot} } \right) y_{ij} +\sum _{k=1}^{V_{ij} } {\widetilde{C}_{ijk} x_{ijk}}}\right) }} \end{aligned}$$

(P1)

subject to

$$\begin{aligned} X \in S&= \{{x_{ijk}\ \text{ and }\ \text{ y }_{ij} \text{ are } \text{ binary } \text{ variable/ }} \nonumber \\ \widetilde{R}_i&= 1+\left[ \sum _{j=1}^{m_i} \frac{1}{(1-r_{ij})^{z_{ij}}}\left[ {\prod _{k=1}^{m_i}{(1-r_{ik})^{z_{ik}}}} \right] \right. \nonumber \\&\times \left[ {1-\left( {1-r_{ij}}\right) ^{z_{ij}}} \right] + \left. \prod _{j=1}^{m_i} {\left( {1-r_{ij}}\right) ^{z_{ij}}} \right] \nonumber \\&\times \left[ {\sum _{j=1}^{m_i}{z_{ij}\left[ {\prod _{k=1}^{j-1} {P\left( {X_{ik} } \right) ^{z_{ik}}}}\right] }P\left( {Y_{ij}} \right) -1} \right] ;\nonumber \\&i=1,2,\ldots ,n\end{aligned}$$

(1)

$$\begin{aligned}&P\left( {X_{ij}}\right) = \left( {1-t_1 } \right) \left[ {\left( {1-r_{ij}} \right) \left( {1{-}t_3 } \right) {+}r_{ij} t_2 } \right] \end{aligned}$$

(2)

$$\begin{aligned}&P\left( {Y_{ij}}\right) =r_{ij}\left( {1-t_2}\right) \end{aligned}$$

(3)

$$\begin{aligned}&N_{ij}^{suc}=\left( {1-\pi _{ij}}\right) N_{ij}^{tot},\quad i=1,2,\ldots ,n \text{ and } \nonumber \\&j=1,2,\ldots ,m_i \end{aligned}$$

(4)

$$\begin{aligned}&\rho _{ij} =\frac{1-\pi _{ij}}{\left( {1-\pi _{ij}}\right) +\pi _{ij}\left( {1-\pi _{ij}} \right) ^{N_{ij}^{suc}}};\nonumber \\&i=1,2,\ldots ,n \quad \text{ and } \quad j=1,2,\ldots ,m_i\end{aligned}$$

(5)

$$\begin{aligned}&r_{ij} =\rho _{ij} y_{ij} +s_{ij} ;i=1,2,\ldots ,n \quad \text{ and } \quad \nonumber \\&j=1,2,\ldots ,m_i\end{aligned}$$

(6)

$$\begin{aligned}&y_{ij} +\sum _{k=1}^{V_{ij} } {x_{ijk} } =1; \quad i=1,2,\ldots ,n \quad \text{ and } \quad \nonumber \\&j=1,2,\ldots ,m_i\end{aligned}$$

(7)

$$\begin{aligned}&y_{ij} +\sum _{k=2}^{V_{ij}} {x_{ijk}} =z_{ij} ; \quad i=1,2,\ldots ,n\, \ \text{ and }\nonumber \\&j=1,2,\ldots ,m_i \end{aligned}$$

(8)

$$\begin{aligned}&x_{ij1} +z_{ij} =1\quad j=1,2,\ldots ,m_i\end{aligned}$$

(9)

$$\begin{aligned}&\sum _{j=1}^{m_i } {z_{ij} \ge 1; \quad i=1,2,\ldots ,n}\end{aligned}$$

(10)

$$\begin{aligned}&y_{ij} \left( {t_{ij} +\tau _{ij} N_{ij}^{tot}} \right) +\sum _{k=1}^{V_{ij} } {d_{ijk} x_{ijk}} \le T_u \} \end{aligned}$$

(11)

where $X$ is a vector of components $x_{ijk} ,y_{ij}, \ \text{ and } \ z_{ij} , i=1,\ldots ,n; j=1,\ldots ,m_i; k=1,\ldots ,V_{ij}$.

2.4 Optimization model-II

In a structured software design, functionality and data are arranged in software modules. Each module has a set of procedures, or methods, for accessing the encapsulated data. Modules can be treated as components, for example, taken from libraries, or implemented by different vendors. This raises the question of when two modules are compatible. Optimization model-II is an extension of optimization model-I. In optimization model-I, we assumed that all alternative COTS products of one module are compatible with the alternative COTS products of other modules. However, sometimes it is observed that some alternatives of a module may not be compatible with alternatives of other modules due to problems such as implementation, interfaces, and licensing [10]. Optimization model-II addresses this problem. It is done by incorporating additional constraints in the optimization models. This constraint can be represented as $x_{gsq}\le x_{hu_t c}$, which means that if alternative $s$ for module $g$ is chosen, then alternative $u_t, t=1,\ldots ,z$ has to be chosen for module $h$. We also assume that if two alternatives are compatible, then their versions are also compatible.

$$\begin{aligned}&x_{gsq}-x_{hu_t c} \le My_t,\quad q=2,\ldots ,V_{gs},\nonumber \\&\quad \text{ c }=2,\ldots ,V_{hu_t},\quad s=1,\ldots ,m_g\end{aligned}$$

(12)

$$\begin{aligned}&\sum {y_t=z\left( {V_{hu_t}-2} \right) } \end{aligned}$$

(13)

Constraints (1) to (11) are same for problem (P2). Constraints (12) and (13) make use of binary variable $y_t$ to choose one pair of alternatives from among different alternative pairs of modules. If more than one alternative compatible component is to be chosen for redundancy, constraint (13) can be relaxed as follows.

$$\begin{aligned} \sum {y_t \le z\left( {V_{hu_t}-2} \right) } \end{aligned}$$

(14)

Problem (P1) can be transformed to another optimization problem using compatibility constraint as follows. Therefore, optimization model-II can be written as follows:

$$\begin{aligned} Maximize\,\widetilde{R} = \sum _{l=1}^L {f_l \prod _{i\in s_l} {\widetilde{R}_i}} \end{aligned}$$

$$\begin{aligned} Minimize\, \widetilde{C}=\sum _{i=1}^{n}\sum _{j=1}^{m_i} {\left( {\widetilde{c}_{ij} \left( {t_{ij} +\tau _{ij} N_{ij}^{tot} } \right) y_{ij} +\sum _{k=1}^{V_{ij} } {\widetilde{C}_{ijk} x_{ijk}}} \right) } \end{aligned}$$

(P2)

subject to

$$\begin{aligned}&X\in S\\&x_{gsq}-x_{hu_{t}c} \le My_t,\quad q=2,\ldots ,V_{gs}, \\&\text{ c }=2,\ldots ,V_{hu_t},\quad s=1,\ldots ,m_g\\&\sum {y_t=z\left( {V_{hu_t}-2} \right) }. \end{aligned}$$

Crisp optimization techniques cannot be applied directly to solve the problems (P1) and (P2) since these methods provide no well defined mechanism to handle the uncertainties quantitatively. Hence we use fuzzy optimization approach to solve the problem.

3 Solution algorithm for fuzzy multi-objective optimization model

Most of our traditional tools of modelling are crisp, deterministic, and precise in character. However, for many practical problems, the input information is incomplete and unreliable. This results in the use of fuzzy multi-objective optimization method with fuzzy parameters. In the existing research related the software reliability, it is assumed that all the parameters of the problem are known precisely. Various objectives and restrictions set by the management and cost coefficients involved in the cost function are determined based on past experience and available database. This makes it difficult for the management to provide precise values of the various cost coefficients and objectives to be met. Moreover, changing customer specifications, lack of experience of the testing team or novelty, changing testing environment, complexity in the project involved, and emerging factors unknowable at the start of the project add imprecision and ambiguity to the above-mentioned definitions. It may also be possible that the management itself does not set precise values in order to provide some tolerance on these parameters due to competitive considerations. All this leads to uncertainty (fuzziness) in the problem formulation. Crisp mathematical programming approaches provide no such mechanism to quantify these uncertainties. Fuzzy optimization is a flexible approach that permits more adequate solutions of real problems in the presence of vague information, providing the well-defined mechanisms to quantify the uncertainties directly. The idea of fuzzy programming was first given by Bellman and Zadeh [1] and then developed by Tanaka et al. [15], Zimmermann [17].

The following algorithm specifies the sequential steps to solve fuzzy mathematical programming problems.

• Step 1. Compute the crisp equivalent of the fuzzy parameters using a defuzzification function. Same defuzzification function is to be used for each of the parameters. Here, we use the defuzzification function of the type $F_{2}(A)=\frac{\left( {a_l+2a_m +a_u}\right) }{4}$, where $a_l, a_m, a_u$ are the Triangular Fuzzy Numbers (TFN).

• Step 2. Incorporate the objective function of the fuzzifier min (max) as a fuzzy constraint with a restriction (aspiration) level. The above problem (P1) can be rewritten as

  $$\begin{aligned}&Find \quad X\\&subject \, to\\&R\left( X \right) =\sum _{l=1}^L {f_l \prod _{i\in s_l} {R_i}} \mathop \ge \limits _{\sim }R_0\\&C\left( X \right) \!=\!\sum _{i=1}^n {\sum _{j=1}^{m_i } {\left( {c_{ij} \left( {t_{ij} \!+\!\tau _{ij} N_{ij}^{tot}} \right) y_{ij} \!+\!\sum _{k=1}^{V_{ij} } {C_{ijk} x_{ijk}}} \right) }} \mathop \le \limits _{\sim } C_0\\&X\in S. \end{aligned}$$

  (P3)

  where $R_0$ and $C_0$ are defuzzified aspiration levels of system reliability and cost.

• Step 3. Define appropriate membership functions for each fuzzy inequality as well as constraint corresponding to the objective function. The membership function for the fuzzy parameters less than or equal to and greater than or equal to type are given as

  $$\begin{aligned} \mu _R (X)=\left\{ {\begin{array}{ll} 1;&{} \quad \quad R(X)\ge R_0 \\ \frac{R(X)-R_0^*}{R_0 -R_0^*};&{}\ \quad R_0^*\le R(X)<R_0\\ 0;&{}\quad \quad R(X)<R_0^*\\ \end{array}} \right. \!\!\!, \end{aligned}$$

  where $R_0$ is the aspiration level and $R_0^{*}$ is the tolerance levels to the fuzzy reliability objective function constraint.

  $$\begin{aligned} \mu _C (X)=\left\{ {\begin{array}{ll} 1;&{}\quad \ C(X)\le C_0 \\ \frac{C_0^{*}-C(X)}{C_0^{*}-C_0}; &{}\quad \ C_0 \le C(X)<C_0 ^{*} \\ 0; &{}\quad \ C(X)>C_0^{*} \\ \end{array}} \right. \!\!\!, \end{aligned}$$

  where $C_0$ is the restriction and $C_0^*$ is the tolerance level to the fuzzy budget constraint.

• Step 4. Employ extension principle to identify the fuzzy decision, which results in a crisp mathematical programming problem given by

  $$\begin{aligned}&Maximize\quad \quad \alpha \\&subject\, to\\&\mu _R (x)\ge \alpha , \\&\mu _C (x)\ge \alpha , \\&X\in S, \end{aligned}$$

  (P4)

  where $\alpha$ represents the degree up to which the aspiration of the decision-maker is met. The above problem can be solved by the standard crisp mathematical programming algorithms.

• Step 5. While solving the problem following steps 1-4, the objective of the problem is also treated as a constraint. Each constraint is considered to be an objective for the decision-maker and the problem can be looked as a fuzzy multiple objective mathematical programming problem. Further, each objective can have a different level of importance and can be assigned weight to measure the relative importance. The resulting problem can be solved by the weighted min max approach. The crisp formulation of the weighted problem is given as

  $$\begin{aligned}&Maximize\quad \quad \alpha \\&subject\,to \\&\mu _R (x)\ge w_1 \alpha , \\&\mu _C (x)\ge w_2 \alpha , \\&w_{1,}\, w_2 \ge 0,\quad w_{1} + w_2 =1. \end{aligned}$$

  (P5)

  If the constraints are fuzzy as well as crisp, then in the equivalent crisp mathematical programming problem, the original crisp constraints will not show any change as their tolerances are zero. The problem (P5) can be solved using the standard mathematical programming approach.

• Step 6. On substituting the values for $\mu _R (x)\text{ and } \mu _C(x)$ the problem becomes

  $$\begin{aligned}&Maximize \quad \quad \alpha \\&subject\, to \\&R(x)\ge R_0 -(1-w_1 \alpha )(R_0 -R_0^*) \\&C(x)\le C_0 +(1-w_2 \alpha )(C_0^*-C_0 )\\&\alpha \in \left[ {0,1} \right] \\&X\in S \\&w_{1,} w_2 \ge 0, w_{1} + w_2 =1. \end{aligned}$$

  (P6)

• Step 7. If a feasible solution is not obtained for the problem (P5) or (P6), then we can use the fuzzy goal programming approach to obtain a compromised solution given by Mohamed [13]. The method is discussed in detail in the case study.

4 Case study

In this section, a case study of component-based development is presented to illustrate the proposed methodology of optimizing the selection of software components for a modular software system. A local software system supplier planned to develop a software system for small and medium size retail organizers. Nine functional requirements of the system were identified, namely, sales, payment collection and authorization, shift-wise reporting and statistics, inventory control and movements, e-commerce, automatic updates, security and administration, business rules, financials and reporting. The software system development team of the company has defined three software modules, front office $(\text{ m }_{1})$, back office/ store $(\text{ m }_{2})$ and finance/ accounts $(\text{ m }_{3})$, that the retail software system needs to contain.

The front office $(\text{ m }_{1})$ module mainly provides the functions of sales, payment collection and authorization, shift-wise reporting and statistics. The back office/ store $(\text{ m }_{2})$ module mainly provides the functions of inventory control and movements, e-commerce, automatic updates, security and administration, while the finance/ accounts $(\text{ m }_{3})$ module provides business rules, financials and reporting.

A total of 18 COTS components available in markets were considered. Further the cost of building these components were also estimated as the software supplier can also build these components. The decision is to choose the right components for each software module so as to get a reliable software system at a minimum cost in the desired delivery time.

4.1 Data sets

The system consists of three modules; front office $(\text{ m }_{1})$, back office/store $(\text{ m }_{2})$ and finance/ accounts $(\text{ m }_{3})$. Each module provides different functional requirements mentioned in Table 1. A system is to be developed by integrating components/ alternatives which can be either COTS or the in-house-built components. The objective of this study is to select the optimal set of alternatives for each module so as to get a highly reliable retail software system. For each module, various alternatives are available, various COTS versions are available for each alternative of a module and an in-house alternative for each module can be built. The data set for COTS and in-house-developed components are given in Tables 2 and 3, respectively. Let $L=3,s_1 =\left\{ {1,2,3} \right\} ,s_2 =\left\{ {1,3} \right\} ,\text{ s }_{3} =\left\{ 2 \right\} ,f_{1} =0.5,f_{2} =0.3\, \text{ and }\, f_3 =0.2$. It is also assumed that $t_1 =0.01,t_2 =0.05\, \text{ and }\,t_3=0.01$.

Table 1 Functional requirements of a software system

Table 2 Data set for COTS components

Table 2 gives cost, reliability, and delivery time for the COTS components. The first column of Table 2 lists the three modules of the software system. The second column provides various alternatives for each module. Each alternative of a module has three versions. The third column provides the parameters of cost (in Kilo Euros, KE), reliability and delivery time (in weeks) for each version. Note that the cost of first version, i.e., the virtual versions for all COTS alternatives is zero and reliability is 0.001. This is done because “if in the optimal solution, for some module $x_{ij1} =1$, it implies corresponding alternative is not to be attached in the module”.

Table 3 Data set for in-house components

Table 3 shows the parameters that we have collected for in-house development of components. For each component, the average development time $t_{ij}$(in weeks) is given in the third column and the average time required to perform a single test $\tau _{ij}$(in weeks) is given in the fourth column, the unitary development cost $c_{ij}$ (KE per week) is given in the fifth column, finally the component testability $\pi _{ij}$ is given in the last column.

4.1.1 Assignment of weights

The assignment of weights is based on the expert’s judgment for the reliability and cost. Weights assigned for reliability and cost are 0.6 and 0.4, respectively.

4.1.2 Minimum and maximum levels of reliability and cost

Firstly, the triangular fuzzy reliability, and cost values are computed using fuzzy values of these parameters and then defuzzified using Heilpern’s defuzzifier (Table 4). If the available reliability and cost are specified as TFN, then the aspiration level and tolerance level can be given as follows:

Table 4 Aspiration and tolerance levels

4.2 Fuzzy goal programming approach

On solving the problem, we found that the problem (P6) is not feasible; hence the management goal cannot be achieved for a feasible value of $\alpha \in [0,1]$. Then, we use the fuzzy goal programming technique to obtain a compromised solution. The approach is based on the goal programming technique for solving the crisp goal programming problem given by Mohamed [13]. The maximum value of any membership function can be 1; maximization of $\alpha \in [0,1]$ is equivalent to making it as close to 1 as best as possible. This can be achieved by minimizing the negative deviational variables of goal programming (i.e., $\eta$) from 1. The fuzzy goal programming formulation for the given problem (P6) introducing the negative and positive deviational variables $\eta _j \text{ and }\rho _j$ is given as

$$\begin{aligned}&\text{ Minimize } \ u\\&\text{ subject } \text{ to }\\&\mu _{R} (X) +\eta _1-\rho _1 =1 \\&\mu _{ C} (X) +\eta _2 -\rho _2 =1\\&u\ge w_j *\eta _j ;\\&\eta _j *\rho _j =0;\quad \eta _j ,\rho _j \ge 0 \quad j=1,2\\&X\in S; \quad \alpha \in [0,1]; \quad w_1 ,w_2 \ge 0; w_1 \!+\!w_2 \!=\!1;\alpha =1-u \end{aligned}$$

(P7)

Therefore, solution of optimization model-I is obtained by solving problem (P7). And also solution of optimization model-II is obtained by solving problem (P7) with compatibility constraints.

4.3 Model solution

The model is solved using a software package called LINGO ([16]).

4.3.1 Optimization model-I

The optimal solution set so obtained for (P7) is optimal for optimization model-I. The solution to the model gives the optimal components selection for the software system along with the corresponding cost and reliability of the overall system under fuzzy environment.

Case 1: delivery time is assumed to be 3 weeks

At delivery time of 3 weeks, all COTS components are selected (Fig. 2). For the front office module, third version of the second alternative and second version of the third alternative are selected. For the back office module, third version of the first alternative and second version of the third alternative are selected. For the finance/accounts module, third version of the second alternative is selected. Since more than one alternative is selected for front office $(\text{ m }_{1})$ and back office $(\text{ m }_{2})$ modules, redundancy is allowed in these two modules. The overall system cost is 112.5 and system reliability is 0.742.

Fig. 2

Solution to optimization model-I (case 1)

Case 2: delivery time is assumed to be 5 weeks

As delivery time increases to 5 weeks along with COTS components, in-house-built component is also selected (Fig. 3). Redundancy is allowed for the first and second modules. For the back office module, two COTS components and an in-house-built component are selected. The overall system cost is reduced to 93 and system reliability is also improved and is 0.976.

As we can see from the solution given here, when delivery time increases from 3 to 5 weeks, there is a significant reduction in the overall cost and also there is a significant improvement in the reliability of the system. Also, the selected components are a combination of both COTS and in-house-built components. So, it is advisable to keep delivery time at 5 weeks and its corresponding solutions.

Fig. 3

Solution to optimization model-I (case 2)

4.3.2 Optimization model-II

To check compatibility amongst the alternatives of the modules, we have considered case no 2 of optimization model-I.

Case no 2: delivery time is assumed to be 5 weeks

We assume that the second alternative of third module is compatible with second and third alternatives of the first module as manager is interested in keeping the solution when delivery time is 5 weeks which according to him is the best decision Figs. 2, 3, 4.

Fig. 4

Solution to optimization model-II

It is observed that due to the compatibility condition, third alternative of first module is chosen as it is compatible with second alternative of third module. The overall system cost is 94 and system reliability is 0.96 (Fig. 4).

5 Conclusion

In this paper, we have developed a fuzzy multi-objective model that helps developers to decide whether to buy or build components for a fault-tolerant modular software system. This paper presented an optimization model for a consensus recovery block scheme. The component selection problem is formulated as a multi-objective programming problem and fuzzy goal programming technique is used to provide a feasible solution. Two optimization models for optimal selection of components were proposed. The first model was a bi-criteria optimization model based on decision variables indicating the set of structural components to buy or to build in order to maximize the software reliability with simultaneous minimization of the overall cost of the system. The second optimization model deals with the issue of compatibility amongst different COTS alternatives. The sensitivity analysis was performed on the delivery time constraint. A case study of retail system design was used to illustrate the proposed methodology in this paper. In the numerical example, it was observed that when delivery time was short, then all COTS components were selected and the overall reliability of the system was low. However, as the delivery time increased along with the COTS components, the in-house components were also selected, and there is a significant increase in the reliability of the system.