Introduction

Manufacturing engineering is about designing and optimizing manufacturing processes that transform raw materials or unfinished goods into desired products. It is responsible for ensuring the quality of the final product along with the safety and efficiency of the production lines. As the industry evolves, there is a growing interest in producing lighter and more sophisticated products with a lower carbon footprint and smaller or thinner components. This trend has led to the development of new manufacturing processes at lower scales, such as ultra-thin sheet metal forming, micro-milling, and thin wire drawing, where product dimensions are very small and loads are highly localized. In these situations, peculiar phenomena known as size effects occur, causing the strength of materials to become dependent on their geometric dimensions. These effects must be carefully considered in small-scale manufacturing processes to avoid unexpected performance issues. In the context of numerical simulation, such effects can be accurately reproduced using advanced theories based on gradient plasticity [1,2,3,4,5]. Unlike classical plasticity approaches which are based on the principle of local action, gradient-enhanced theories are capable of predicting non-uniform plastic deformations which correlate with size effects as experimentally observed [6, 7]. These theories have received a strong scientific interest in recent years and numerous gradient-enhanced models have been developed in the literature [8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Although providing an accurate description of complex size-dependent material behaviors [17, 21,22,23,24,25], these models generally involve a large number of material parameters, making their identification a non-trivial endeavor. The ability of such models to accurately predict the behavior of small-scale products is intricately tied to the relevance of the identification procedure and the available data used to identify the material parameters, particularly the internal length scales.

Although physical interpretations of some major gradient-enhanced material parameters have been proposed in the literature [26, 27], most of them still need to be calibrated using experimental data. Begley and Hutchinson [28], Yuan and Chen [6], and Abu Al-Rub and Voyiadjis [7] have shown that microindentation is an effective test for identifying the gradient-enhanced length scales. Alternative micro-scale tests, such as micro-bending [29] and micro-torsion [17], have also been investigated for parameter identification. However, as pointed out by Voyiadjis and Song [30], some important parameters, like the internal length scales, may not be intrinsic and can depend on the model, the loading conditions, the underlying deformation mechanisms, and the microstructural evolution. Therefore, it is generally necessary to identify the appropriate material parameters of a given gradient-enhanced model for each specific test condition, typically by defining an inverse problem based on a simulation and an optimization scheme. This problem poses three challenges. First, the number of material parameters to be identified is usually much larger than in the case of classical models. Second, experimental data are very limited due to the high cost and complexity of experiments at small scales. Third, the adoption of gradient-enhanced plasticity, like strain gradient plasticity, in the simulation dramatically increases the computation cost. As a result, the number of the simulations required to evaluate a given set of material parameters must be reduced as much as possible. These challenges constitute a significant obstacle to the deployment of gradient-enhanced models in industrial settings, despite the remarkable advancements in the development of increasingly accurate and industry-ready models. As a step towards overcoming this obstacle, the effectiveness of identification procedures used for classical plasticity must be evaluated in the context of gradient-enhanced plasticity assuming limited data conditions. This is the primary objective of the present paper, which is motivated by the notable lack of existing research on the subject in the literature.

In the framework of classical plasticity, material parameter identification by simulation-based inverse problem methodologies is an active topic, resulting in a rich toolbox of methodologies for engineers and researchers. Gradient-based optimization techniques have long been the cornerstone of this domain. These techniques utilize the derivatives of the objective function(s) to navigate the parameter space effectively. Over the years, various gradient-based algorithms have been developed and applied for material parameter identification. Examples of these algorithms include Conjugate Gradient [31], Levenberg-Marquardt [32,33,34], and Sequential Quadratic Programming [35] algorithms. Although widely used in material parameter identification, the performance of gradient-based optimization methods is sensitive to the initial guess of the parameters [36]. Furthermore, they are not well-suited for complex problems where the objective functions are not smooth or when their derivatives are computationally expensive to obtain. A more appropriate class of optimization techniques for this kind of problems is the class of direct search (or derivative-free) methods [37, 38]. Evolutionary methods [39], simplex approaches [40], and pattern search techniques [41] are typical examples of this class. Chakraborty and Eisenlohr [42] used the Nelder-Mead simplex algorithm [40] to determine the parameters of a crystal plasticity constitutive law based on nanoindentation experiments. Vaz et al. [43] used a particle swarm optimization algorithm to identify inelastic parameters for a deep drawing process. Agius et al. [44] implemented a multi-objective genetic algorithm (MOGA-II) for the search of a suitable set of material parameters of the Chaboche elastoplastic model for an aluminum alloy. Kapoor et al. [45] calibrated the parameters of a crystal plasticity model for a dual-phase titanium alloy within the framework of a genetic algorithm. Qu et al. [46] and Chaparro et al. [47] adopted a combination of a genetic and a gradient-based optimization method by using the results of the former as the initial guess for the latter. In an original work within the context of gradient-enhanced plasticity, Panteghini et al. [17] have applied the Coliny evolutionary algorithm to identify parameters of a distortion gradient plasticity model. The identification procedure has required several tens of thousands of finite element simulations. Despite their robustness, direct search methods generally require a large number of objective function evaluations to reach convergence [48]. This can be particularly costly in the context of gradient-enhanced plasticity, where a large number of material parameters are generally involved.

Considering the limitations of the aforementioned optimization approaches, alternative techniques based on the Response Surface Methodology (RSM) have gained attention in the realm of material parameter identification [49,50,51]. RSM enhances efficiency by approximating the objective function with a cheap-to-evaluate metamodel, also called surrogate model [51]. This approach enables material parameter identification to be carried out using the computationally efficient metamodel, bypassing the need for more resource-intensive simulations. Kakaletsis et al. [52] have demonstrated the suitability of machine learning-based (Gaussian process and neural network) metamodels to identify the constitutive parameters of soft materials. However, careful attention must be paid to the accuracy and reliability of the metamodel, as any inaccuracies can propagate into the material parameter identification process. Moreover, the initial dataset used to train the metamodel should be robust and representative to ensure that the approximation is valid across the parameter space of interest. This could be problematic for complex problems with little or no prior knowledge to guide the preparation of this dataset. A promising approach to overcome this difficulty is to apply the Bayesian optimization with an adaptive or infilling sampling strategy [53]. This approach starts with a probabilistic metamodel based on a minimal dataset and iteratively updates it using strategically chosen sampling points. This iterative sampling process allows for more oriented sampling in areas around the optimized solution, minimizing the number of objective function evaluations. Kuhn et al. [54] and Veasna et al. [55] have recently applied the Bayesian optimization strategy based on Gaussian process metamodels to identify the material parameters of complex crystal plasticity models. These authors have reported the promising outcomes of this strategy with respect to classical optimization techniques. Thanks to its efficiency, the Bayesian optimization has emerged as a powerful solution for various design problems [56]. Its application to gradient-enhanced plasticity has not yet been explored.

The present paper aims at investigating and comparing different optimization approaches, including evolutionary algorithm, response surface methodology, and Bayesian optimisation, for the identification of the material parameters of a recent flexible gradient-enhanced model developed by Jebahi et al. [5]. The choice of the objective functions will be discussed in detail. After the present introduction, the paper is organized as follows. Section “Inverse problem” presents the main features of the gradient-enhanced model used in this work and the inverse problem for material parameter identification. Section “Identification procedures” details the identification procedures to be investigated and compared in the paper. The associated results are discussed in Section “Results and discussions”. Finally, Section “Conclusion” presents some concluding remarks.

Inverse problem

The present investigation of material parameter identification is performed considering the recent gradient-enhanced crystal plasticity model developed in [5], which belongs to the most widely used class of strain gradient plasticity models in the literature. The main features of this model will be recalled in the next forthcoming subsection. Following this, the inverse problem associated with the identification of its material parameters is defined.

Table 1 Material parameters of the strain gradient crystal plasticity model, their reference values and ranges for the identification
Full size table

Constitutive model

A flexible Gurtin-type strain gradient crystal plasticity (SGCP) model, which has recently been developed in [5], is involved in this study. In this model, both displacement and plastic slip fields are considered as primary and controllable variables. As a consequence, it relies on two kinds of equilibrium equations, which are referred to hereafter as macroscopic and microscopic equilibrium equations. The macroscopic equilibrium equations as well as the associated boundary conditions are equivalent to those implied in traditional plasticity models and can be written as (static case):

$$\begin{aligned} \left\{ \begin{array}{rcll} \varvec{\nabla }\cdot \varvec{\sigma } &{} = &{} \varvec{0} &{} \hspace{0.5cm}\textrm{in}\hspace{0.5cm}\mathcal {V}\\ \varvec{\sigma }\cdot {\textbf {n}} &{} = &{} {{\textbf {t}}} &{} \hspace{0.5cm}\textrm{on}\hspace{0.5cm}\mathcal {S} \end{array}\right. \end{aligned}$$
(1)

where \(\mathcal {V}\) is the studied domain having as boundary \(\mathcal {S}\), \(\varvec{\sigma }\) is macroscopic (Cauchy) stress tensor, \(\varvec{n}\) is outward unit normal to \(\mathcal {S}\), \(\varvec{t}\) is macroscopic traction vector, and \(\varvec{\nabla }\cdot (*)\) is the divergence operator. The microscopic counterparts, which are associated with the plastic slips (viewed as primary variables), can be written as (static case):

$$\begin{aligned} \left\{ \begin{array}{rcll} \tau ^{\alpha }+\varvec{\nabla }\cdot \varvec{\xi }^{\alpha }-\pi ^{\alpha } &{} = &{} 0 &{} \hspace{0.5cm}\textrm{in}\hspace{0.5cm}\mathcal {V}\\ \varvec{\xi }^{\alpha }\cdot \varvec{n} &{} = &{} \chi ^{\alpha } &{} \hspace{0.5cm}\textrm{on}\hspace{0.5cm}\mathcal {S} \end{array}\right. \end{aligned}$$
(2)

where \(\tau ^{\alpha }\) is resolved shear stress on slip system \(\alpha \), \(\pi ^{\alpha }\) and \(\varvec{\xi }^{\alpha }\) are respectively microscopic stress scalar (work-conjugate to plastic slip \(\gamma ^{\alpha }\)) and microscopic stress vector (work-conjugate to plastic slip gradient \(\varvec{\nabla }\gamma ^{\alpha }\)), and \(\chi ^{\alpha }\) is microscopic traction scalar on slip system \(\alpha \). To solve the above equilibrium equations, constitutive laws governing the evolution of the involved macroscopic and microscopic stresses are required. These constitutive laws have been introduced in [5] assuming quadratic elastic strain energy and generalized power-law defect energy. Furthermore, to increase the flexibility of the proposed model, first- and higher-order dissipative processes are assumed to be uncoupled. For more details about the SGCP model, the reader is referred to the original paper [5]. Considering a 2D plane strain condition with only planar slip systems, the overall constitutive equations can be expressed in a simplified form as follows [5]:

$$\begin{aligned} \left\{ \begin{array}{l} {\displaystyle \varvec{\sigma }={\displaystyle \lambda \,\textrm{tr}\left( \varvec{\varepsilon }_{e}\right) \,{\textbf {I}}+2\,\mu \,\varvec{\varepsilon }_{e}}}\\ {\displaystyle {\displaystyle \varvec{\xi }^{\alpha }=X_{0}\,l_{en}^{n}\,\left[ \left| \varvec{s}^{\alpha }\cdot \varvec{\nabla }\gamma ^{\alpha }\right| ^{n-2}\,\varvec{s}^{\alpha }\otimes \varvec{s}^{\alpha }\right] \cdot \varvec{\nabla }\gamma ^{\alpha }+S_{\xi }^{\alpha }\,l_{dis}^{2}\,\left[ \frac{\dot{e}_{\xi }^{\alpha }}{\dot{\gamma }_{0}^{\alpha }}\right] ^{m}\,\frac{\varvec{\nabla }^{\alpha }\dot{\gamma }^{\alpha }}{\dot{e}_{\xi }^{\alpha }}}}\\ \pi ^{\alpha }={\displaystyle S_{\pi }^{\alpha }\,\left[ \frac{\dot{e}_{\pi }^{\alpha }}{\dot{\gamma }_{0}^{\alpha }}\right] ^{m}\,\frac{\dot{\gamma }^{\alpha }}{\dot{e}_{\pi }^{\alpha }}}\\ {\displaystyle \dot{S}_{\pi }^{\alpha }=\sum _{\beta =1}^{q}H_{\pi }\,\dot{e}_{\pi }^{\beta }\mathrm {\ ,\ \ \ }S_{\pi }^{\alpha }\left( 0\right) =S_{\pi 0}>0}\\ {\displaystyle \dot{S}_{\xi }^{\alpha }=\sum _{\beta =1}^{q}H_{\xi }\,\dot{e}_{\xi }^{\beta }\mathrm {\ ,\ \ \ }S_{\xi }^{\alpha }\left( 0\right) =S_{\xi 0}}\ge 0\\ {\displaystyle \dot{e}_{\pi }^{\alpha }=\left| \dot{\gamma }^{\alpha }\right| ,\ \ \ \dot{e}_{\xi }^{\alpha }=\left\| l_{dis}\,\varvec{\nabla }^{\alpha }\dot{\gamma }^{\alpha }\right\| }\\ {\displaystyle \alpha =1,\,2,\,...,\,q} \end{array}\right. \end{aligned}$$
(3)

where \(\lambda \) and \(\mu \) are the first and second Lamé elastic moduli, \(\varvec{\varepsilon }_{e}\) is elastic strain tensor, \(X_{0}\) is higher-order energetic slip resistance, \(S_{\pi 0}\) and \(S_{\pi }\) are respectively initial and current first-order dissipative slip resistances, \(S_{\xi 0}\) and \(S_{\xi }\) are respectively initial and current higher-order dissipative slip resistances, \(H_{\pi }\) and \(H_{\xi }\) are respectively first- and higher-order hardening moduli, \(l_{en}\) and \(l_{dis}\) are respectively energetic and dissipative length scales, n is defect energy index, \(\varvec{s}^{\alpha }\) is slip direction associated with slip system \(\alpha \), \(e_{\pi }^{\alpha }\) and \(e_{\xi }^{\alpha }\) are respectively first- and higher-order effective plastic strains for slip system \(\alpha \), \(\dot{\gamma }_{0}^{\alpha }>0\) is a constant strain rate representative of the flow rates of interest, \(m>0\) is a constant characterizing the rate-sensitivity of the considered material, and q is the total number of slip systems. In total, twelve material parameters are involved in system Eq. 3, as summarized in Table 1.

It is worth noting that the reference slip rate \(\dot{\gamma }_{0}^{\alpha }\) and the rate sensitivity parameter m are introduced in the model for the purpose of numerical regularization. These parameters are adjusted in such a way as to obtain a nearly elastic-plastic behavior, and consequently, they are not considered in the present identification study. Similarly, the elastic moduli (\(\lambda \) and \(\mu \)) are generally well-known for a given material and therefore are also excluded from this study. Finally, the defect energy index is deliberately set to \(n=2\) for the hardening behavior to be more consistent with common experimental observations. In summary, seven key parameters are involved in the proposed identification study, each crucial in defining the mechanical behavior of materials (Table 1).

Reference data

The present study of identification procedures is carried out based on a widely used benchmark in the context of gradient-enhanced models, which is the cyclic shear response of a constrained plate. In the absence of pertinent experimental data associated with this benchmark, synthetic numerical data, generated from presumed reference values of the SGCP model parameters (Table 1), are used as reference data for parameter identification. It is important to emphasize that these reference values are deliberately masked from the identification algorithms to ensure objectivity and reliability of the work findings. Although the identification of material parameters using real experimental data would be more interesting and challenging due to the presence of noise and the extent to which the constitutive model is valid, a well-posed problem using synthetic data does not entirely hinder the evaluation of the effectiveness of identification methods. The results of this study serve as a first step towards application in real settings.

Figure 1 presents the geometrical model associated with the considered benchmark. It consists of a simple 2D crystalline strip with \(h\times w\) dimensions and two symmetrically tilted slip systems with respect to \(\varvec{e}_{1}\) direction (\(\theta _{1}=-\theta _{2}=60{^\circ }\)). The strip is clamped at the bottom edge:

$$\begin{aligned} u_{1}(x_{1},0)=u_{2}(x_{1},0)=0 \end{aligned}$$
(4)

where \(u_{1}\) and \(u_{2}\) are displacements in \(\varvec{e}_{1}\) and \(\varvec{e}_{2}\) directions. The upper edge is subjected to a loading-unloading cycle of displacement in \(\varvec{e}_{1}\) direction:

$$\begin{aligned} u_{1}(x_{1},h)=h\varGamma \qquad \text {and}\qquad u_{2}(x_{1},h)=0 \end{aligned}$$
(5)

where \(\varGamma \) is the prescribed macroscopic shear strain which goes from 0 to 0.01 and back to 0. In addition to these classical boundary conditions, the upper and lower edges are also assumed to be passivated (no plastic slip on these edges):

$$\begin{aligned} \gamma ^{\alpha }(x_{1},0)=\gamma ^{\alpha }(x_{1},h)=0\qquad \text {for}\qquad \alpha =1,2 \end{aligned}$$
(6)

In order to model the infinite width of the strip in \(\varvec{e}_{1}\) direction, periodic boundary conditions are imposed on the left and right edges:

$$\begin{aligned} u_{i}(0,x_{2})&=u_{i}(w,x_{2})\qquad \text {for}\qquad i=1,2\end{aligned}$$
(7)
$$\begin{aligned} \gamma ^{\alpha }(0,x_{2})&=\gamma ^{\alpha }(w,x_{2})\qquad \text {for}\qquad \alpha =1,2 \end{aligned}$$
(8)

The simulation of the sheared strip is conducted using the commercial finite element code Abaqus/Standard. The aforementioned SGCP model is implemented in this code using a User-ELement (UEL) subroutine. The strip is discretized using 20 quadratic finite elements, representing a good compromise between accuracy and computation cost. Considering this number of elements, the duration of a typical simulation ranges from 60 to 90 minutes with a single core of the Intel Core i9-10900K CPU allocated for computation.

Fig. 1
figure 1

Illustration of a 2D crystalline strip of height h and of width w with two slip systems subjected to pure shear load

Full size image
Fig. 2
figure 2

(a) Reference macroscopic shear responses and (b) distribution of plastic shear strains along the strip thickness at the maximum prescribed macroscopic strain \(\varGamma =0.01\) for three different strip heights

Full size image
Fig. 3
figure 3

Illustration of the determination of the elastic limits from the macroscopic response

Full size image

Unlike when using classical (local) plasticity theories, the dataset required to identify the SGCP material parameters (particularly those defining size effects) must be generated considering more than one geometrical size of the strip. Accounting for the scarcity of data at small scales, only three strip configurations with different heights (\(h=8\mathrm {\,{mm}}\), \(10\mathrm {\,{mm}}\) and \(15\mathrm {\,{mm}}\)) are simulated, all using the same reference constitutive parameters as given in Table 1. The associated simulation results, in terms of macroscopic shear stress as a function of macroscopic shear strain, are used as reference data for identifying the SGCP material parameters (Fig. 2a). As can be observed in Fig. 2a, the initial yield and the hardening slope increase as the strip height decreases. These effects, known as size effects, are naturally captured by the SGCP model thanks to its ability to predict plastic deformation gradients, as illustrated in Fig. 2b. One may also combine macroscopic shear stresses and plastic strain distribution as reference data for the identification. The effectiveness of this strategy will be discussed later. It should be noted that the small oscillations observed at the elastic-plastic transition are due to the relatively large time step used in the simulations. While these oscillations can be eliminated by employing a smaller simulation time step, they were deliberately retained to mimic experimental artifacts, like noise in experimental data. An effective filtering technique is necessary to process them without compromising the identification process. As will be explained later, this is done by approximating the response curves using piecewise linear functions.

The objective of the inverse problem is then to identify from these reference macroscopic responses the seven adjustable constitutive parameters: higher-order energetic slip resistance \(X_{0}\), initial first- and higher-order dissipative slip resistance \(S_{\pi 0}\) and \(S_{\xi 0}\), first- and higher-order hardening modulus \(H_{\pi }\) and \(H_{\xi }\), energetic and dissipative length scales \(l_{en}\) and \(l_{dis}\). A large search space is covered with parameter bounds listed in Table 1.

Identification procedures

This section describes different identification strategies selected in this investigation for the identification of material parameters. First, different choices for the definition of objective functions are provided. Next, three optimization procedures, including evolutionary algorithm, response surface methodology and Bayesian optimization, are presented.

Objective functions

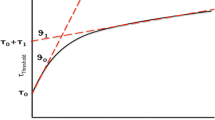
To solve the inverse problem inside an optimization framework, one first needs to define the objective functions that quantify the similarity between the simulation outputs and the observations. The inverse problem is solved by minimizing these objective functions, which must be carefully defined to ensure accurate identification of the material parameters. In this study, as the elastic and plastic behaviors are nearly linear, the macroscopic cyclic response of the sheared strip can be characterized by three representative stress scalars: the elastic limit during the loading stage, denoted as \(\sigma _{1}\); the flow stress at the maximum prescribed strain \(\varGamma =0.01\), denoted as \(\sigma _{2}\); and the elastic limit during the unloading stage, denoted as \(\sigma _{3}\). While the flow stress \(\sigma _{2}\) at \(\varGamma =0.01\) can easily be obtained, the extraction of the elastic limits (\(\sigma _{1}\) and \(\sigma _{3}\)) is more challenging, owing to the presence of small oscillations at the elastic-plastic transitions. To avoid the application of excessively small time steps for eliminating these oscillations, the two stresses are determined from the breakpoints of two-piecewise linear functions fitted on the elastic and plastic slopes of the macroscopic curves (Fig. 3). In the case of single-objective optimization, the objective function can then be defined as the Mean Squared Relative Error (MSRE) across all representative stresses (i.e., \(\sigma _{1}\), \(\sigma _{2}\) and \(\sigma _{3}\)) and strip configurations (i.e., different strip heights):

$$\begin{aligned} f=\frac{1}{3m}\sum _{i=1}^{m}\sum _{j=1}^{3}(\delta _{j}^{^{i}})^{^{2}} \end{aligned}$$
(9)

where m is the number of strip configurations used for the identification (\(m=2\) or 3 in this study), and \(\delta _{j}^{^{i}}\) is the relative error associated with the \(i^{th}\) strip configuration and the \(j^{th}\) representative stress:

$$\begin{aligned} \delta _{j}^{^{i}}=\frac{\sigma _{j}^{i}-\hat{\sigma }_{j}^{^{i}}}{\hat{\sigma }_{j}^{^{i}}} \end{aligned}$$
(10)

Here, \(\hat{\sigma }_{j}^{^{i}}\) and \(\sigma _{j}^{^{i}}\) represent respectively the reference and simulated stress values. This objective function is used in the comparative study of the optimization procedures.

To explore the possibility of incorporating strain field measurements into the identification process, an alternative definition of the objective function will be evaluated and compared with the formulation given by Eq. 9 in the Bayesian optimization framework:

$$\begin{aligned} f= \frac{1}{2} \left( \frac{1}{3m}\sum _{i=1}^{m}\sum _{j=1}^{3}(\delta _{j}^{^{i}})^{^{2}} + \frac{1}{mn} \sum _{i=1}^{m}\sum _{k=1}^{n}(\eta _{k}^{^{i}})^{^{2}} \right) \end{aligned}$$
(11)

where \(n=39\) is the number of finite element nodes along the strip thickness at which the plastic shear strains are measured (the nodes at the top and bottom boundaries, where boundary conditions are applied, are excluded), and \(\eta _{k}^{^{i}}\) is the relative error associated with the \(i^{th}\) strip configuration and the plastic shear strain at the \(k^{th}\) finite element node:

$$\begin{aligned} \eta _{k}^{^{i}}=\frac{(\gamma _{12}^p)_{k}^{i}-(\hat{\gamma }_{12}^p)_{k}^{^{i}}}{(\hat{\gamma }_{12}^p)_{k}^{^{i}}} \end{aligned}$$
(12)

Here, \((\hat{\gamma }_{12}^p)_{k}^{^{i}}\) and \(\gamma _{12}^p)_{k}^{i}\) represent respectively the reference and simulated plastic shear strain values. The objective function defined by Eq. 11 contains two parts: the first part controlling the relative error on the macroscopic shear stresses and the second part controlling the relative error on the plastic strain distribution. It should be noted that, in order to capture the full form of the plastic strain distribution, the latter is evaluated on a rather large number of points (\(n=39\)) along the strip thickness.

To explore the suitability of multi-objective optimization for the inverse problem being studied, two alternative definitions of multi-objective functions are also introduced and evaluated in the Bayesian optimization framework. In one definition, an objective function is defined for each strip configuration:

$$\begin{aligned} f^{^{i}}=\frac{1}{3}\sum _{j=1}^{3}(\delta _{j}^{^{i}})^{^{2}}\qquad \text {with}\qquad i=1,...,m \end{aligned}$$
(13)

In the second definition, an objective function is defined for each representative stress:

$$\begin{aligned} f_{j}=\frac{1}{m}\sum _{i=1}^{m}(\delta _{j}^{^{i}})^{^{2}}\qquad \text {with}\qquad j=1,2,3 \end{aligned}$$
(14)

Optimization outcomes obtained using these multi-objective functions will be compared with each other and with those obtained using single-objective function Eq. 9.

Optimization algorithms

This subsection briefly introduces the three selected optimization methods designed to address the inverse problem described earlier, namely evolutionary algorithm, response surface methodology based on Gaussian process metamodels and Bayesian optimization.

Evolutionary algorithm

Evolutionary algorithms refer to a class of stochastic optimization algorithms that employ mechanisms inspired by the principles of biological evolution, such as selection, recombination and mutation [39]. On the basis of how these nature-inspired operators are implemented, the class is categorized into different subclasses that include, but are not limited to, genetic algorithm, differential evolution, evolution strategy. In general, an evolutionary algorithm begins with a population of randomly generated candidate solutions called individuals. In each iteration, the individuals are evaluated and the best ones are selected based on the corresponding value of the objective function. The selected individuals, called parents, are then recombined and/or mutated to generate a new population. Through an iterative process involving multiple generations, the population evolves towards an optimal solution.

While a large number of evolutionary algorithms are available in the literature, they usually require a large population and, thus, a large number of objective function evaluations to obtain a good solution [57]. However, this configuration cannot be allowed in the context of gradient-enhanced plasticity because the computation cost associated to the evaluation of objective function is highly expensive. Consequently, it is crucial that the selected evolutionary algorithm is able to work effectively on a limited population size. Considering this requirement, the Covariance Matrix Adaptation Evolution Strategy (CMA-ES) algorithm is selected to represent the class of evolutionary algorithms in this study. CMA-ES is a stochastic derivative-free optimization algorithm for difficult (non-convex, noisy) optimization problems in continuous search spaces. It belongs to the evolution strategy subclass. Initially introduced by Hansen and Ostermeier in 2001 [58], CMA-ES is currently regarded as one of the state-of-the-art algorithms for black-box optimization. The algorithm has been shown to be effective with a small population [59, 60]. In addition, the majority of its internal parameters are autonomously adjusted by the algorithm rather than requiring user input. Using CMA-ES, Cauvin et al. [61] identified the parameters of a crystal plasticity model in an inverse analysis to reproduce the macroscopic stress-strain curves under uniaxial tension.

Figure 4 shows the flowchart of CMA-ES. During an i-th iteration, a population of size \(\lambda \) is sampled from a multivariate Gaussian distribution around a mean point \(m^{i}\) in the search space:

$$\begin{aligned} x_{k}^{i}=m^{i}+\sigma ^{i}z_{k}\qquad \text {with}\qquad z_{k}\sim \mathcal {N}(0,C^{i})\qquad \text {for}\qquad k=1,...,\lambda \end{aligned}$$
(15)

where \(\sigma ^{i}\) is a positive scalar called the step size and \(C^{i}\) is called the covariance matrix. Phenomenologically, \(C^{i}\) represents the direction along which the distribution is elongated while \(\sigma ^{i}\) indicates the extent to which the mutation should occur in that direction. The candidates are evaluated and sorted, and a number \(\mu \) of best candidates are selected (\(\mu <\lambda )\). The mean point, the step size and the covariance matrix for the next iteration are then updated based on the selected candidates. The mathematical formulations for the update can be found in the original paper [58]. Figure 5 demonstrates the principle of the CMA-ES for the optimization of a simple 2D function. The algorithm requires the user to provide the population size, the initial mean point and the initial step size. In this study, a population size \(\lambda =5\) is selected. An initial step size equal to one-fourth of the width of the search domain is set. At the start, five random candidates are evaluated and the one with the lowest objective is chosen for the initial mean point.

Fig. 4
figure 4

Flow chart of the CMA-ES algorithm

Full size image
Fig. 5
figure 5

Illustration of the CMA-ES algorithm for the minimization of a simple 2D function

Full size image

Response surface methodology

This approach implies the training of a metamodel that approximates the objective function for any given set of material parameters. Initially, a number of parameter sets are sampled in the search space and then evaluated by the simulation to construct the database that is required for the training. Given a fixed sample size and without any prior knowledge about the objective function landscape, the sample should be evenly distributed across the entire search space. In this study, the sampling is performed using the scrambled Sobol sequence [62,63,64]. This method has an advantage over the Latin Hypercube sampling in that one can incrementally add more points to an existing sample. When an increase of the sample size is needed to improve the accuracy of an existing metamodel, it allows to reuse data generated for the initial sample. This advantage is useful in the context of gradient-enhanced plasticity where the data generation is highly expensive.

Besides the classic choice of polynomial regression, various algorithms based on machine learning can be used for the metamodeling. Examples of these algorithms include radial basis functions [65], support vector machine [66], ensembles of decision trees [67], Gaussian Process (GP) [68], artificial neural network [69], optimal transport-based surrogate model [70] and proper generalized decomposition (PGD)-based regression [71]. When the data generation is expensive, it is crucial that the regression metamodel is able to give reliable predictions given a small dataset. In this context, GP regression [68] emerges as a viable option and is selected for this study. GP is known for its data-efficiency and its ability to handle high-dimensional data. In addition, as a non-parametric algorithm, it does not require the user to tune hyperparameters which are optimized directly on the dataset. Consequently, there is no need to divide the dataset into training and validation sets, and all data can be used for the training of the metamodel. One major drawback of GP is its poor scalability for large datasets. However, as the data in this study is limited, this concern is irrelevant. Indeed, GP is one of the most frequent metamodeling techniques in metamodel-based simulation optimization [72].

The idea of GP is to model a function f(x) as a stochastic process or a collection of random variables such that its values at any finite set of inputs follow a multivariate Gaussian distribution:

$$\begin{aligned}{} & {} \left( \begin{array}{c} f(x_{1})\\ f(x_{2})\\ \vdots \\ f(x_{n}) \end{array}\right) \sim \mathcal {N}(m(x),K)\qquad \text {with}\nonumber \\{} & {} K=\left[ \begin{array}{cccc} k(x_{1},x_{1}) &{} k(x_{1},x_{2}) &{} \cdots &{} k(x_{1},x_{n})\\ &{} k(x_{2},x_{2}) &{} \cdots &{} k(x_{2},x_{n})\\ &{} &{} \ddots &{} \vdots \\ &{} &{} &{} k(x_{n},x_{n}) \end{array}\right] \end{aligned}$$
(16)

where \(x_{i}\) is an input vector which is a set of material parameters in this study, m(x) is a mean function, and K is a symmetric covariance matrix. GP generalizes the multivariate Gaussian distribution to infinite dimensionality by introducing the covariance function \(k(x,x')\) such that k is large when x and \(x'\) is close to each other. This behavior reflects the similarity of the function f(x) at two adjacent inputs. In this study, the Radial Basic Function also known as Squared Exponential is used for the kernel :

$$\begin{aligned} k(x,x')=\sigma ^{2}\exp (-\frac{||x-x'||^{2}}{2l^{2}}) \end{aligned}$$
(17)

where ||.|| is the Euclidean distance, and \(\sigma \) and l are two hyperparameters. The prediction of a GP metamodel is a normal distribution conditioned on the observations in the training dataset. The mean and variance of the predicted distribution refers to the most probable predicted value and the associated uncertainty respectively.

At the start of this study, a GP metamodel has been trained to directly approximate the objective function defined in Eq. 9. However, the metamodel accuracy, when trained with a limited dataset, is insufficient to achieve a good optimized solution. The problem is related to the fact that the similarity between the simulated and reference macroscopic responses, originally characterized by a vector of different representative stresses, is compacted into an unique scalar. As a result, the information about the dependence of each representative stress on the material parameters, which is relatively monotonic and therefore easier to learn, is mixed together resulting in a scalar that is more complicated to predict. To overcome this issue, it is decided to train different GP models, each approximating a distinct representative stress from a strip configuration involved in the objective function. The mean predictions of these models are then aggregated using Eq. 9 to give a final metamodel approximating the objective. Finally, a gradient-based optimization algorithm is applied on the final metamodel for the search of the best parameter set. To avoid local minima, the optimization is performed with different initializations. The final solutions are validated by the simulation. This procedure is summarized in Figs. 6.

Fig. 6
figure 6

Flow chart of the identification procedure by GP-based RSM

Full size image

Bayesian optimization

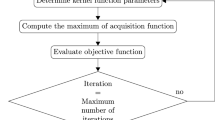
In the Bayesian optimization, GP probabilistic metamodels are constructed to approximate the objective function. Its flow chart is shown in Fig. 7. This algorithm distinguishes itself from other optimization approaches by two features : adaptive sampling strategy and acquisition function. During each iteration, the algorithm learns from previous evaluations to select new potential candidates to be evaluated next. At the beginning of the algorithm, only a small dataset is required, and the dataset is progressively enriched during the optimization. This principle allows to focus the sampling in regions where the objective is expected to be minimized. Consequently, the underlying surrogate model exhibits higher accuracy in proximity to the solutions as compared to conventional metamodel-based approaches, where the dataset is uniformly sampled throughout the search space. The criterion used to decide the new candidates to be evaluated and added to the dataset is based on the introduction of the acquisition function. Based on the predicted mean and uncertainty variance given by the probabilistic metamodel, the acquisition function is defined over the search space such that its value is high in regions near potential solutions. New samples are thus chosen in each iteration by maximizing the acquisition function. The resolution of these internal optimization problems is much simpler than the original problem as the acquisition function is cheap to evaluate and any gradient-based or evolutionary algorithms can be used. Compared to RSM, the incorporation of the uncertainty of the metamodel into the acquisition function allows to achieve an optimal balance between exploration (sampling in regions where the objective is unknown) and exploitation (sampling in regions where the objective is believed to be minimal), hence increasing the sampling efficiency. The principle of the Bayesian optimization is illustrated in Fig. 8. Each iteration can be summarized as follows:

  • Step 1: New solution candidates are selected by maximizing the acquisition function

  • Step 2: Evaluate the new candidates through the simulation

  • Step 3: Add the new candidates and their evaluation into the database

  • Step 4: Update the surrogate model and go for the next iteration.

Fig. 7
figure 7

Flow chart of the Bayesian optimization

Full size image
Fig. 8
figure 8

Illustration of the Bayesian optimization for the minimization of a simple 1D function

Full size image

For our inverse problem, we opt for the Expected Improvement which is a common acquisition function for a single-objective function. Its formulation is as follows:

$$\begin{aligned}{} & {} EI(x)=\left[ \mu (x)-f(x^{*})\right] \Phi (z)+\sigma (x)\varphi (z)\qquad \text {with}\nonumber \\{} & {} z=\frac{\mu (x)-f(x^{*})}{\sigma (x)}) \end{aligned}$$
(18)

where x is a sample in the search space, \(\mu (x)\) and \(\sigma (x)\) are respectively the mean and uncertainty variance predicted by the probabilistic GP metamodel, \(f(x^{*})\) is the objective at the current best solutions, and \(\Phi \) and \(\varphi \) are respectively the cumulative distribution function and the probability density distribution of the standard normal distribution. Furthermore, it is possible to handle multi-objective optimization in the framework of the Bayesian optimization with the Expected Hypervolume Improvement acquisition function [73]. It is based on the concept of the hypervolume indicator in multi-objective optimization which measures the volume of the dominated domain in the objective space [74]. By introducing this indicator, multi-objective optimization can be translated into single-objective optimization. Moreover, in order to take advantage of the capability of the computational system to run simulations in parallel, we opt for a batch version of the acquisition functions ins this study. It allows to determine more than one candidate to be evaluated in the next iteration before the metamodel is updated. Finally, the non-negative nature of the objective functions used in this study is carefully considered because a negative prediction by the metamodel (including the uncertainty range) will exaggerate the relevance of a solution and may mislead the sampling. However, it is not trivial to directly apply these constraints to the prediction of the GP metamodel. The author solution is to approximate and optimize instead the logarithm of the original objectives so that the new objectives can take positive and negative values. The fact that the logarithmic objective of an ideal solution is equal to negative infinity is not a concern as it is technically impossible to find in practice. Indeed, good parameter sets are found for a logarithmic objective less than -12 in this study.

Implementation

All identification procedures described in the previous subsection and summarized in Figs. 4, 6 and 7 are implemented in Python. The evaluation of material parameter sets is wrapped in a Python function that automatically sets up, runs simulations, and post-processes the results by making use of the Abaqus Scripting Interface. The evolutionary algorithm CMA-ES and the Bayesian optimization are applied using the pymoo [75] and Trieste [76] packages, respectively. Both packages provide an Ask-Tell interface, allowing for external evaluation of the objective function via Abaqus/Standard calculations. In the case of multi-objective Bayesian optimization, the Fantasizer function in Trieste is used to implement the batch version of the acquisition functions. In the above optimization procedures, the optimization loop is stopped after 200 objective function evaluations. Concerning the response surface methodology RSM, Gaussian Process metamodels are trained using the “GaussianProcessRegressor” class provided by the scikit-learn package [77].

Results and discussions

The three selected strategies for the identification of the SGCP constitutive parameters are investigated in this section. These strategies are first benchmarked using the same reference data and objective function to ensure an unbiased comparative assessment. The most effective strategy is then used to investigate the impact of other important identification aspects, namely the number of reference data and the choice of the objective function(s).

Comparison of optimization methods

For comparative evaluation, the three optimization methods described in Section “Optimization algorithms” are applied to solve the inverse problem defined in Section “Inverse problem”, taking into account a minimal set of reference data. Specifically, only two reference macroscopic shear responses corresponding to the two strip heights \(h=8\,\textrm{mm}\) and \(10\,\textrm{mm}\) are involved in the present subsection. The reference response corresponding to the strip height \(15\,\textrm{mm}\) is not used for the identification but is reserved for the validation of the identified parameters. The single-objective function given by Eq. 9 is used in the three optimization algorithms. To maintain consistency in the comparison, a population size of \(\lambda =5\) is set for the CMA-ES algorithm and a batch size of 5 is set for the Bayesian optimization. This implies that each iteration of both algorithms involves the same number of evaluations of the objective function. For the RSM, three datasets of different sizes (50, 100 and 200) are used for training of the GP metamodels. Data points are incrementally and quasi-randomly added using the scrambled Sobol sequence to generate datasets of various sizes. In order to quantify the efficiency and performance of the optimization algorithms under consideration, the Root Mean Squared Relative Error (RMSRE) is employed as an evaluation metric. For a given number of objective function evaluations, RMSRE is computed as the square root of the objective function Eq. 9 corresponding to the best solution. This metric provides a quantifiable measure of the mean discrepancy between simulation outputs and reference data.

Figure 9 presents the RMSRE evolution as a function of the number of evaluations, obtained with the three optimization strategies. For comparison purposes, results obtained with no special optimization technique are also provided in this figure. These results correspond to the best solutions obtained from various-sized quasi-random datasets. Remarkably, the three involved optimization procedures achieve errors less than \(1\%\) within a span of 200 evaluations, a distinct improvement over the best result (\(>7\%\) error) observed from a set of 200 quasi-randomly selected parameter combinations. This contrast not only underscores the importance of formal optimization techniques but also serves to caution against reliance on haphazard trial-and-error approaches for parameter identification.

From a macroscopic point of view, the obtained optimization results demonstrate the relevance and effectiveness of the selected optimization strategies for material parameter identification within a gradient-enhanced framework. However, upon closer inspection, the RSM and Bayesian techniques display superior effectiveness. Using fewer than 50 objective function evaluations, all three strategies show comparable performance, with RMSRE dropping rapidly as the number of evaluations increases. Beyond 50 evaluations, the evolutionary algorithm CMA-ES begins to exhibit large stagnation plateaus at \(2\%\) and \(1\%\) errors. No further improvement is observed after 130 evaluations. As will be discussed later, although the obtained errors seem to be small, the corresponding constitutive parameters may poorly predict size effects (i.e., the response of a new strip configuration with a different height), due to the limited number of reference data used for the optimization. The CMA-ES stagnation problem has already been reported in the literature [78] and is identified as a major limitation of population-based metaheuristic algorithms. This issue is particularly problematic when dealing with computationally demanding models, like those based on gradient-enhanced plasticity. On the contrary, the RSM and Bayesian procedures show smoother RMSRE evolution and provide better optimization results, achieving less than \(0.5\%\) errors at 200 evaluations.

Fig. 9
figure 9

RMSRE versus number of evaluations by different approaches for the case of one unique objective function

Full size image

Although sharing similarities, the closely matched performance levels obtained by the latter two procedures may seem counter-intuitive. Specifically, one would expect that the adaptive sampling strategy used in the Bayesian optimization would outperform the quasi-random sampling used in RSM optimization. This unexpected outcome can be attributed to the differences in the choice of the metamodel output between the two techniques. In the Bayesian optimization, the Gaussian process (GP) metamodel is trained to directly predict the final objective which has a complex form. This requires substantial training effort, although this is somewhat alleviated by the use of adaptive sampling. In contrast, the objective metamodel in RSM optimization is derived from individual stress metamodels, which are comparatively easier to construct even with quasi-random sampling, due to simpler relationships between each stress and the material parameters.

Figure 10 shows the macroscopic responses simulated with the best constitutive parameters obtained after 200 evaluations, using the three optimization methods. The CMA-ES obtained parameters reproduce accurately the two responses corresponding to strip heights \(h=8\,\textrm{mm}\) and \(10\,\textrm{mm}\), which are used as reference data for the identification process, explaining the obtained RMSRE of \(1\%\) at 200 evaluations. However, a relatively poor prediction of the response corresponding to \(h=15\,\textrm{mm}\) is obtained, showing poor prediction of size effects. Therefore, the reached RMSRE is not sufficient to correctly capture these effects, considering the minimal dataset of two responses used in the optimization process. On the contrary, all the macroscopic responses associated with the RSM and Bayesian methods are in very good agreement with the reference results for both the strip configurations used in the optimization process (\(h=8\,\textrm{mm}\) and \(10\,\textrm{mm}\)) and the strip configuration used for validation (\(h=15\,\textrm{mm}\)). Figure 11 shows the plastic shear strain profiles along the strip thickness at the end of the loading stage, obtained in the validation strip (\(h=15\,\textrm{mm}\)) using the reference and identified material parameters. The parameters identified by the CMA-ES algorithm are unable to reproduce accurately the reference distribution of plastic strains. In contrast, the parameters identified by the RSM and the Bayesian optimization are able to capture both the thickness of the boundary layers developed in the vicinity of the top and bottom boundaries and the maximum value of plastic shear strain. These results are consistent with the previous observations at the macroscopic level.

Fig. 10
figure 10

Simulated macroscopic responses with the identified constitutive parameters in comparison with the reference macroscopic responses

Full size image
Fig. 11
figure 11

Plastic strain profiles along the strip thickness at the maximum prescribed macroscopic strain \(\varGamma =0.01\) in the validation configuration (\(h=15\,\textrm{mm}\)) for different material parameter sets identified by CMA-ES, GP-based RSM and Bayesian optimization

Full size image

One may assume that the optimization algorithms have successfully identified the reference parameters. However, this is not the case as shown in Fig. 12, which displays the material parameter sets obtained by the three optimization techniques (the first seven axes). This figure also reveals that a single optimization technique can yield different values of optimized parameters, depending on the initial conditions. Using different initial quasi-random samples, different sets of material parameters are identified by the RSM method (green curves in Fig. 12). It was verified that all these parameter sets lead to an accurate prediction of the reference macroscopic responses. Therefore, the inverse problem under consideration admits more than one solution.

Examination of the different RSM-identified parameter sets (green curves in Fig. 12) reveals that the identified first-order parameters, namely the initial first-order dissipative slip resistance \(S_{\pi 0}\) and the first-order hardening modulus \(H_{\pi }\), are close to the reference ones, with no significant discrepancies. However, spectacular variations are observed in the higher-order parameters which are responsible for capturing size effects. Detailed analysis of these variations uncovers inter-dependencies between these higher-order parameters. For example, the products \(X_{0}\,l_{en}^{n}\) and \(S_{\xi 0}\,l_{dis}^{2}\) remain nearly constant across parameter sets (the last two axes in Fig. 12), even when the individual parameters vary. Importantly, these products closely match those calculated from the reference parameters, suggesting that size effects in the model are governed more by these combinations of parameters than by higher-order parameters individually. This observation suggests avenues for optimizing the number of parameters in the strain gradient crystal plasticity (SGCP) model used in this work [5].

Fig. 12
figure 12

Material parameter sets identified by CMA-ES, GP-based RSM and Bayesian optimization

Full size image

Overall, the present comparative study confirms the pertinence of the three selected optimization methods for the identification of the material parameters of gradient-enhanced models. Using only two reference responses to accommodate the limited data at small scales, all methods achieved less than \(1\%\) errors after a relatively low number of objective function evaluations (less than 200 evaluations). This number of evaluations is quite reasonable in the context of gradient-enhanced modeling. For comparison, the distortion gradient plasticity model of Panteghini and Bardella [17] required several tens of thousands of finite element simulations to identify its parameters using Coliny evolutionary algorithm. Among the tested methods, the RSM and Bayesian approaches demonstrate superior optimization capabilities with enhanced parameter identification. While both of them stand out as promising candidates to solve gradient-enhanced inverse problems, the Bayesian approach gains distinct prominence by employing adaptive sampling. Indeed, this allows for more effective optimization with no prior knowledge of the required number of objective function evaluations. The performance of this method is further investigated in the next subsection.

Bayesian optimization : influence of data and objective function(s)

The above subsection highlights the good performance of the Bayesian optimization for the identification of the SGCP model parameters within relatively precarious conditions, i.e., with a minimal set of two macroscopic reference results and a single-objective function. The present subsection aims at investigating how these conditions can influence the optimization behavior of the method.

Fig. 13
figure 13

RMSRE versus number of evaluations by the Bayesian optimization with and without considering the plastic strain distribution during the identification

Full size image
Fig. 14
figure 14

(a) Macroscopic responses and (b) plastic strain profiles along the strip thickness in the validation configuration (\(h=15\,\textrm{mm}\)) for material set identified by the Bayesian optimization considering plastic strain distribution

Full size image

To investigate the impact of the quantity of reference data, the following two scenarios are examined: (i) combining the previously considered macroscopic shear responses and the associated plastic strain distributions, and (ii) adding the macroscopic shear response of a third strip configuration (another strip height). In the first scenario, the same macroscopic responses of the two strip configurations used for the identification in Section “Comparison of optimization methods” (\(h=8\,\textrm{mm}\) and \(10\,\textrm{mm}\)) are used in combination with the associated plastic strain distributions along the strip thickness as reference data for the identification. For this purpose, the objective function defined by Eq. 11 is used (\(m = 2\)). Figure 13 compares the optimization results, specifically in terms of macroscopic stress RMSRE, with those previously obtained without accounting for the plastic strain distribution. The new scenario yields slower convergence rate, achieving more than \(1\%\) errors on the macroscopic shear stresses after 200 evaluations. This result may seem counter-intuitive, as it can be expected that including the distribution of plastic strains in the objective function would accelerate the convergence. The decline in convergence rate is due to increased complexity in the objective function, introducing additional challenges and nuances that the optimization algorithm must navigate, thereby compromising the optimization process. In a general manner, the objective function must be as simple as possible to maximize the performance. Figure 14 displays the simulated macroscopic stress responses and the plastic shear strain profiles for the validation configuration (\(h=15\,\textrm{mm}\)) using the identified constitutive parameters that take into account the reference plastic strain distribution. While there is an improved prediction of the maximum plastic strain value (as shown in Fig. 14b), the overall plastic shear strain distribution and the macroscopic stress responses are relatively poorly predicted compared to the results shown in Fig. 10c.

In the second scenario (2), the macroscopic shear response associated with the strip configuration of \(h=15\,\textrm{mm}\), which is previously used for the validation of the optimization results, is now considered as part of the reference data. The single-objective function is then evaluated from the responses of three strip configurations (\(h=8\,\textrm{mm}\), \(10\,\textrm{mm}\) and \(15\,\textrm{mm}\)), according to Eq. 9 with \(m=3\). Figure 15 compares the associated optimization results with those previously obtained considering two strip configurations (\(h=8\,\textrm{mm}\) and \(10\,\textrm{mm}\)). Even with only one added reference result, a substantial enhancement of the convergence rate is obtained. A level of \(0.5\%\) error is obtained with less than 50 objective function evaluations. The sets of identified parameters obtained with two and three reference data are compared in Fig. 16. The addition of more reference data reduces the number of possible solutions, leading to first-order (independent) parameters closer to their reference counterparts. As for higher-order parameters, due to inter-dependencies between them as detected in the above subsection, only the products \(X_{0}l_{en}^{n}\) and \(S_{\xi 0}l_{dis}^{2}\) are accurately predicted. Individually, these parameters still show differences with respect to the reference ones.

Another crucial factor influencing optimization performance is the definition of the objective function(s). Although primarily designed for single-objective optimization problems, the Bayesian optimization has recently been extended to handle multi-objective scenarios [73, 79]. Advanced Bayesian versions are capable of optimizing multiple conflicting objectives simultaneously while accounting for the trade-offs among them. The idea is to approximate the Pareto front which is the set of non-dominated solutions, where no objective can be improved without worsening another. To assess the performance of these multi-objective versions in identifying the SGCP model parameters, the two types of multi-objective functions defined by Eqs. 13 and 14 are tested. Figure 17 presents the associated optimization results in terms of RMSRE evolution as a function of the number of objective function evaluations. The result associated with single-objective optimization is also given, for comparison. Interestingly, the performance of multi-objective optimization is highly dependent on the definition of the objectives. Using multi-objective functions constructed based on the strip configurations, the RMSRE evolution stagnates after approximately 50 evaluations, yielding poor solution compared to single-objective approach. In contrast, multi-objective optimization based on the representative stresses Eq. 14 shows fast RMSRE convergence, surpassing its single-objective counterpart. Here, errors less than \(0.5\%\) are achieved after just 100 evaluations, compared to 200 in the single-objective case.

Fig. 15
figure 15

RMSRE versus number of evaluations by the Bayesian optimization using 2 and 3 reference macroscopic responses

Full size image
Fig. 16
figure 16

Material parameter sets identified by the Bayesian optimization using 2 and 3 reference macroscopic responses

Full size image

The disparity in performance between the considered types of multi-objective functions can be attributed to the underlying physics of the inverse problem at hand. Particularly, the involved SGCP model aims to capture the size effect, describing the dependence between material behaviors and geometric dimensions. When objectives are formulated based on individual strip configurations, the size effects are not inherently integrated into each function. As a result, capturing these effects accurately necessitates the concurrent minimization of all objectives. However, multi-objective optimization algorithm can explore paths where one objective is minimized while keeping another constant, diverting the search away from the ideal solution. On the contrary, when objectives are predicated upon each representative stress across all configurations, they intrinsically embed the size effects. This naturally prompts the algorithm to consider these crucial effects during every iteration, steering the optimization process more effectively toward the most desirable solution. In this case, multi-objective optimization can provide more accurate results with respect to its single-objective counterpart, as size effects on each representative stress can be more accurately reproduced (Fig. 17).

Fig. 17
figure 17

RMSRE versus number of evaluations by Bayesian optimization for the case of single-objective and the case of multi-objective with two different objective definitions

Full size image

Conclusion

The present paper investigated the effectiveness of three leading optimization techniques, including CMA-ES evolutionary algorithm, response surface methodology (RSM) and Bayesian optimization, in identifying the material parameters of a Gurtin-type strain gradient crystal plasticity model used to capture size effects. These techniques were tested using a minimal set of synthetic reference data to accommodate the scarcity of data at small scales.

The paper results show the effectiveness of the selected optimization methods within a gradient-enhanced framework. Good optimization results are obtained with relatively few evaluations of the objective function. Nevertheless, certain differences in their performance have been identified. The CMA-ES algorithm encounters stagnation issues beyond a certain number of evaluations. This poses a significant drawback, particularly in scenarios where computation cost is a pivotal concern. The RSM and Bayesian optimization emerge as superior alternatives. Each of these approaches presents unique advantages. The RSM enables the study of the overall landscape of the objective function and, thus, the identification of multiple solutions admitted by the inverse problem. Through the analysis of these solutions, it is possible to uncover sets of material parameters which act together as a combination. This possibility suggests a new tactic for optimizing the number of parameters in the strain gradient crystal plasticity models. Moreover, in situations where the objective functions are highly complex such that an effective metamodel cannot be obtained within a reasonable amount of data and the required number of objective function evaluations is unknown, the Bayesian optimization is demonstrated to be prominent thanks to the adaptive sampling strategy, making it a strong candidate for tackling complex gradient-enhanced inverse problems.

The interesting features of the Bayesian optimization approach motivated further investigation of its performance in relation with two key optimization aspects, namely the quantity of reference data and the formulation of the objective function(s). This investigation shows that incorporating strain field measurements into the identification process increases the complexity of the optimization problem. In contrast, adding more reference macroscopic data can considerably enhance the convergence rate. This result suggests the importance of the amount of experimental data for a consistent identification of the material parameters.

Furthermore, the type of objective function(s), whether single- or multi-objective, has a marked impact on optimization outcomes. Multi-objective functions that inherently capture underlying physics, like size effects, significantly enhance performance. However, poorly chosen objective functions can be detrimental, leading to less-performing optimization results with respect to the single-objective case.

In summary, the study highlights the promising features of the selected optimization techniques, particularly Bayesian optimization, in determining material parameters of advanced gradient-enhanced models when constrained by minimal data sets. Some versions of such advanced models are today sufficiently mature for industrial applications but are hindered by the scarcity of data allowing for an effective identification of their numerous parameters. The development of effective material parameter identification techniques tailored to these models helps overcome this limitation and enables broader application of such models in real engineering scenarios, such as the formability of small-scale components.