Modelling of shrinkage formation in casting by the phase field method

Abstract

Most commercial softwares simulating casting process use a scalar field to quantify the shrinkage on final parts. The repartition of this scalar is used to localize shrinkage in the part. In this work, the objective is to use a new approach to predict morphological information about size and shape of shrinkage: the phase field method. This method is based on a parameter order defining the alternating zones metal/gas. Starting with a uniform unit value of this scalar, the phase field equation is modified with a nucleation process predicting the growth of the air phase into the metal one still liquid. The coupling with the Navier-Stokes equation brings up some interesting non-dimensional parameters that affect shrinkage morphology. This is what we have tried to analyse after proposing the modified phase fields formalism. Even if we are not yet in the predictive stage, we present in the end of this paper a numerical/experimental comparison showing the potentiality of the developed approach.

Introduction

Porosity in castings is a major defect since it may have different effects on the deterioration of mechanical properties. Two types of defects are observed:

• The first one is the defect related to gas porosity (air entrapment) which is due to the turbulent flow when the die casting is filled. It also can be a consequence of die coating vaporization, or dissolved hydrogen rejection from metal during its solidification [1]. The microporosity increase can be associated with the dendritic arms growth that leads both to air entrapment and to hydrogen desorption in these voids. In permanent mould casting process, a vacuum system can be used to reduce this problem thanks to metal injection into the mould cavity under the quasi-vacuum conditions [2]. An example is shown in Fig. 1 (other figures could also be found in literature [3]).

  Fig. 1

  

  SEM micrographs of gas porosity and pore surface

• The second type is the shrinkage porosity induced by the densification occurring during the transformation from liquid to solid state. According to the default size we can deal with macroporosity or microporosity. This default is located in the hottest zones. This type of porosity depends on the solidification morphology (see Fig. 2 or [3]).

  Fig. 2

  

  SEM micrographs of shrinkage and dendrites

The defaults types are differentiated by their size, location and shape of the surface. Thus, porosity analysis and classification are achieved by microscope observation. The dispersion of shrinkage allows to define different morphology as shown in Fig. 3 (pipe shrinkage, centreline shrinkage or surface sink).

Fig. 3

Classification of shrinkage porosity [4]

In this study, we will focus only on shrinkage porosity induced by densification and its formation during the solidification process.

Most commercial softwares simulating casting process use a scalar field to quantify and localize the shrinkage on final parts.

Some of these commercial codes use the Niyama criterion (Ny) to detect shrinkage defects during solidification, which is defined as the local thermal gradient divided by the square root of the local cooling rate. As shown in Fig. 4, according to the diagram illustrating the relationship between the volume of shrinkage porosity and the Niyama criterion, the shrinkage formation can be estimated [5, 6].

Fig. 4

Schematic illustrating the Niyama Criterion to detect shrinkage porosity [6]

A more general approach is applied to Al-Cu and Al-Si alloys. Ch. Pequet, M. Gremaud, and M. Rappaz [7] have developed a numerical model to predict the microporosity, the macroporosity, and the pipeshrinkage formation during the solidification using a mushy-zone refinement method. In order to calculate the pressure drop in the mushy zone, they superimposed a fine and regular finite volume grid on the finite element grid used to calculate heat flows. Microporosity is formed in mushy zone. Macroporosity appears in the partially closed liquid regions which are connected to an open region via the mushy zone. Pipe shrinkage is obtained by integration of the calculated interdendritic fluid flow over the open-region boundaries.

In our work, we present a modelling approach for the formation of shrinkage during the cooling based on the phase field theory. The phase field approach allows to model free boundary problems without having to explicitly follow the complex interfaces that takes different forms during the evolution of the microstructure. This is done by the use of an order parameter. The phase field approach can be applied to a wide range of microstructure evolution problems related to very different processes by appropriately selecting physical or artificial variables. It has been successfully applied to many material processes such as alloy solidification [8], microstructural evolution of polycrystalline materials [9], crystalline nucleation [10], recrystallization process [11], dendritic growth [12], grain magnification and growth [13] among many others applications.

The main purpose of this paper consists to propose a numerical model of shrinkage formation during the cooling stage based on the phase field method and taking into accounts fluid dynamics as well as heat transfer. The filling stage simulation is not included in this work. In the beginning of this paper, we summarize the main idea of the phase field theory and we detail our contribution consisting to generate voids by a nucleation process. Then we present the coupled system resulting from the Cahn-Hilliard equations associated to the Navier-Stokes equations. A non-dimensionalization of the set of the obtained equations is also proposed. This allows to arise some non-dimensional parameters that we relate to the different kinds of voids distribution observed when making a parametric numerical study. Finally, a qualitative comparative study has been performed between our simulations and a gravity die casting part obtained in an instrumented mould.

Phase field model

Free energy of the system

The phase field model is formulated here for a binary mixture of two immiscible fluids (air and molten metal in liquid state) using the Cahn-Hilliard scattering function. The formulation starts from a free energy of the system $\mathcal {F}$ which is a function of fluids mixing composition.

$$ \begin{array}{@{}rcl@{}} \mathcal{F}=(C,\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}{C})=\int(\beta\psi({C})+\frac{\alpha}{2}|\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}{C}|^{2})d{\Omega} \end{array} $$

(1)

Here, C is the variable that describes the phase. It will be called in the following an order parameter. ψ(C) is a double-sink function that implies the only stable equilibrium values of C are + 1 for liquid or − 1 for air. A classical form of ψ which is used in most cases is defined by:

$$ \begin{array}{@{}rcl@{}} \psi=\frac{1}{4}(C+1)^{2}(C-1)^{2} \end{array} $$

(2)

However, other forms of ψ(C) can be found in the literature [14]. In our case, a non symmetric form is chosen in the numerical section, more suitable when the two phases are not in the same proportion. The choice of this function ensures that the values of C (+ 1 and − 1) are the stable equilibrium positions. α and β are the phase field parameters defining the free energy as proposed by Cahn & Hilliard in their original work in 1958 [15]. α is homogeneous to a force and β is homogeneous to an energy per unit volume, thus:

• $\sqrt {\alpha \beta }$: is the surface energy. We can consider that this quantity represents the surface tension between the two phases.

• $\sqrt {\frac {\alpha }{\beta }}$: is the liquid-air interface thickness. We are using a diffuse interface model. The transition between the liquid and the air is continuous with values of C ∈ [− 1,1].

By taking the variational derivative of the free energy $\mathcal {F}$ with respect to the order parameter C, we obtain:

$$ \begin{array}{@{}rcl@{}} \delta \mathcal{F}=\int(\beta\psi^{\prime}({C})-\alpha\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{2}C)\delta C d{\Omega} \end{array} $$

(3)

We define the chemical potential from the variational derivative of the free energy as:

$$ \begin{array}{@{}rcl@{}} \phi=\frac{\delta \mathcal{F}}{\delta C}=\beta\frac{\partial\psi}{\partial C}-\alpha {\Delta} C \end{array} $$

(4)

According to the Cahn-Hilliard formalism (see for example [16]), the diffusive flux in the evolution of C is proportional to the gradient of the cheminal potential:

$$ \begin{array}{@{}rcl@{}} \frac{dC}{dt}=-\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}. \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{J}} \text{with} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{J}}=-M \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}\phi \end{array} $$

(5)

$\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {J}}$ is the diffusive flux and M is the mobility (scalar in the case of isotropic separation mixture, and tensor in the case of non-isotropic separation).

Kinetic equations of volume defects

The evolution of the phase field variable C is deduced from the Eqs. 3, 4 and 5 and thus writes in the presence of a velocity field $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {v}}$ as:

$$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial t}+ \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}. \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C=\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}. (M \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} \phi) = \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}. (M \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} (\beta \frac{\partial \psi}{\partial C}-\alpha {\Delta} C)) \end{array} $$

(6)

The previous equation is conservative. It allows in several cases [17] to start with a mixture defined with C = 0 on a domain Ω. Over time, this domain is subdivided into alternating zones with C = 1 and C = − 1 while respecting the normality condition expressing that ${\int \limits }_{\Omega } C d{\Omega }$ is constant (the integral of C is conserved, i.e. the flux of C is assumed to be zero on the boundaries of Ω).

In our case of shrinkage formation during the cooling phase, we start with a liquid state (C= 1), then the density decreases according to the temperature. In most cases, the density is a decreasing function of temperature that can be experimentally identified for each material.

We can predict the global rate of the shrinkage formation during the cooling from the measured density evolution ρ(T). We assume in this work that: (i) there is no pressure effects on the density and that (ii) once the mould is filled, there is no alimentation of new liquid.

Our system starts from an initial state (in the beginning of the cooling phase) defined by:

$$ \begin{array}{@{}rcl@{}} \int C(t=0) d{\Omega}=|{\Omega}| ; \qquad C(t=0)=1 \end{array} $$

(7)

|Ω| is the volume of the mould cavity. At the end of the cooling phase, we have:

$$ \begin{array}{@{}rcl@{}} {\int}_{\Omega} C(t=\infty) d{\Omega}= C_{lim} |{\Omega}| \end{array} $$

(8)

The value of C_lim can be estimated from the experimental curve of ρ(T).

$$ \begin{array}{@{}rcl@{}} \frac {C_{lim} |{\Omega}|-|{\Omega}|}{|{\Omega}|}=C_{lim} - 1= 2\frac{\frac{1}{\rho({T_{f}})} - \frac{1}{\rho({T_{0}})}} {\frac{1}{\rho({T_{0}})}} \end{array} $$

(9)

T₀ is the initial temperature and T_f is a temperature below which the evolution of ρ with temperature does not create shrinkage but homogeneous part contraction. The temperatures in the previous expression allow to obtain a value of C_lim between − 1 and 1. In order to consider volume defect nucleation and growth, we introduce a source term S that affects the conservation of C during time. Equation 6 becomes non conservative and writes:

$$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial t} + v \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C = \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} . (M \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} (\beta \frac{\partial\psi}{\partial C} - \alpha {\Delta} C)) - S \end{array} $$

(10)

This approach was introduced in [18] in order to describe the formation of the polycrystalline phases in a metal. It will be used in our case based on a description of the phase field using a single variable C (and not using two variables C and η as in [18]). This approach is used here for the prediction of the void phase nucleation in the liquid.

In contrast to [19], we introduce the source term with a negative sign because we suppose that the void phase (defined by C = − 1) germinates in the liquid phase (defined by C = 1). So, the source term decreases the value of C.

The source term takes the form:

$$ S=\left\{ \begin{array}{l c l} 0 \quad\text{if}\quad C< C_{0} \quad\text{or}\quad R_{1}>P_{0}\\ R_{2}V_{g} \quad \text{if}\quad C\geq C_{0} \quad\text{and}\quad R_{1}<P_{0} \end{array} \right . $$

V_g is a nucleation velocity. C₀ is the critical order parameter of void nucleation, above which nucleation is authorized. It can takes for example the value 0. P₀ is a probability threshold that control the nucleation activation. It must be taken between 0 and 1. A simplest choice consists to fix it at 0.5. R₁ et R₂ are two random numbers generated uniformly between 0 and 1 that are independent from one time step to another. These two values are independently generated at any point of the continuous domain. With these elements, the source term S becomes defined at each material point of the Ω domain.

In order to reproduce a nucleation physics consistent with [7], where we suppose that the nucleation is assumed to occur far from the boundaries and located in the hottest zones, we propose the following form of V_g:

$$ \begin{array}{@{}rcl@{}} V_{g}=V_{g Max}\left[ \left( {\int}_{\Omega} C d{\Omega} - C_{lim}|{\Omega}| \right) \right]^{+} F(T) \end{array} $$

(11)

The notation [.]⁺ refers to the positive part ($\max \limits (.,0)$). F(T) is a user defined function that we propose under the following form:

$$ F(T)=\left \{ \begin{array}{l c l} 1 \quad\text{if}\quad T>(T_{max} -\delta T)\\ 0 \quad\text{otherwise} \end{array} \right. $$

In some previous works [19, 20], V_g is considered constant. However in our approach the proposed form (11) allows to:

• Adapt the nucleation velocity according to the integral of C on the domain. In fact the positive part of (${\int \limits } C d{\Omega } - C_{lim}|{\Omega }|$) allows to obtain a maximum nucleation rate at C = 1. This nucleation rate tends towards 0 when the system reaches the expected state verifying ${\int \limits } C d{\Omega } = C_{lim}|{\Omega }|$. We have chosen the linear dependency which is the simplest one, but other forms can be imagined.

• This form allows also via the F(T) function to locate voids nucleation in the hottest zones. T_max is the maximum temperature value recorded at each moment of the simulation and δT is a temperature gap set by the user that delimits the hottest zone.

To analyse the global effect of the source term, we can integrate the Eq. 6 on the volume Ω:

$$ \begin{array}{@{}rcl@{}} \frac{d}{dt} {\int}_{\Omega} C d{\Omega}= - {\int}_{\Omega} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}. \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{J}} - {\int}_{\Omega} S d{\Omega} \end{array} $$

(12)

This form assumes that there is no flux of C across the boundaries. The first term of the second member vanishes due to the conservative character of $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {J}}$. Knowing that:

$$ \begin{array}{@{}rcl@{}} C_{tot}={\int}_{\Omega} C d{\Omega} \end{array} $$

(13)

The Eq. 12 becomes:

$$ \begin{array}{@{}rcl@{}} \frac{dC_{tot}}{dt} =- {\int}_{\Omega} S d{\Omega} \end{array} $$

(14)

As S is numerically defined at each time step, this equation will control the conservation of C during the numerical integration.

The coupled system of equation

We consider here a system consisting of two-phases: metal and air. The Navier-Stocks equations has to be taken into account to get the kinematic fields. The velocity field is continuous from one phase to the other. It is denoted $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {v}}$ on each material point. The Cahn-Hillard and Navier-Stokes equations are coupled so that, the free energy generation by convection is at each time equal to the opposite of the kinematic energy generation by capillarity [21]. Thus an advection term is added to the source term of the Navier-Stockes equation containing the capillarity contribution which accounts for inter-facial forces as body forces:

$$ \begin{array}{@{}rcl@{}} \rho (\frac{\partial{\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}}}{\partial t} + \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} v)=- \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} P + {\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}}.(2\eta \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{D}})= - \rho g \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{z}} + \phi \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C \end{array} $$

(15)

Besides, the continuity equation is given by $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }}\cdot v =0$ in the metal phase. The thermo-physical properties such as the density ρ and the viscosity η will be expressed as continuous functions depending on the order parameter C. Simple mixture laws can be considered.

$$ \begin{array}{@{}rcl@{}} \rho (C) = \frac{1+C}{2}\rho_{liq} + \frac{1-C}{2} \rho_{air} \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \eta (C) = \frac{1+C}{2}\eta_{liq} + \frac{1-C}{2} \eta_{air} \end{array} $$

(17)

ρ_liq is the liquid density and ρ_air is the air density. Based on the volume-specific properties as a function of temperature, we can define ρ_liq as follows :

$$ \begin{array}{@{}rcl@{}} \rho_{liq}= \rho_{0} R(T) \end{array} $$

(18)

R(T) is a thermal dependent function verifying R(T₀) = 1, where ρ₀ is the value of ρ_liq at the reference temperature T₀. Thus:

$$ \begin{array}{@{}rcl@{}} \rho(C,T)=\frac{1+C}{2} \rho_{0} R(T) + \frac{1-C}{2} \rho_{air} \end{array} $$

(19)

Similarly, we write the viscosity as a function of the order parameter and the temperature according to:

$$ \begin{array}{@{}rcl@{}} \eta(C,T)=\frac{1+C}{2} \eta_{0} V(T) + \frac{1-C}{2} \eta_{air} \end{array} $$

(20)

η_air is the air viscosity and η_liq = η₀V (T) is the liquid viscosity (η_air << η_liq). η₀ is the liquid viscosity at a reference temperature. V (T) is a function that expresses the thermo-dependence: i.e, the viscosity variation as a function of the temperature verifying V (T₀) = 1.

To take into account the physics of the cooling during the post-fill stage of the casting process, the Naviers-Stockes and Cahen-Hillard equations must be coupled to the heat transfer equation (WLF or Arrhenius model can be used here for the function V (T)).

In its simplest form, the heat transfer equation can be written as follows:

$$ \begin{array}{@{}rcl@{}} \rho C_{p} (\frac{\partial T}{\partial t} + \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} T) = k {\Delta} T \end{array} $$

(21)

Where ρ is the density of the mixture, C_p is the specific heat capacity, and k is the thermal conductivity. All these parameters are dependent on the temperature and the order parameter C. Latent heat of phase change is not considered here but can be added with no major difficulties.

To solve such an equation, it is necessary to define correctly the boundary conditions and especially the heat convection coefficient between the metal and the mould. This was the object of a study which is not detailed here in which we did an instrumented casting setup that notes the real temperature in some points of the metal and the mould. A numerical simulation with an inverse identification allowed us to go up to the convection coefficient. However, in order to simplify the writing in numerical modelling section, the Dirichlet boundary conditions will be considered at the mould/part interface.

Summary of the equations

• Evolution of order parameter

  $$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial t} + \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}. \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C = \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}. (M \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} \phi ) - S \end{array} $$

  (22)

  Where $\phi = \beta \frac {\partial \psi }{\partial C } - \alpha {\Delta } C$

• The Naviers-Stokes equation neglecting the inertia term

  $$ \begin{array}{@{}rcl@{}} - \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} p + \eta {\Delta} u - \rho g \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{z}} + \phi \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C =0 ; \end{array} $$

  (23)

  associate to $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }}. \underset {{~}^{\boldsymbol {-}}}{\boldsymbol {v}} =0$ in the metal phase. Compressible behaviour is considered for the air phase.

• Heat transfer

$$ \begin{array}{@{}rcl@{}} \frac{\partial T}{\partial t} + \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} . \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} T = \frac{k}{\rho C_{p}} {\Delta} T \end{array} $$

(24)

Non-dimensionalization of the model equation

Several literature works present adimensionalization of Naviers-Stockes and Cahen-Hillard equations (see [16] for example). In most of these works, the characteristic velocity is defined as the ratio of the surface energy by the viscosity. As a result, the characteristic time is directly related to this velocity. In our work, we present another form of non-dimensionalization based on the mobility to define the characteristic time. The form that we propose does not allow to retrieve the classical dimensionless number such as the capillary number C_a and the bond number B_o. However it allows to obtain direct effect of non-dimensional parameters. We consider easier to interpret non-dimensional numbers in terms of counterpart forces.

In Eq. 6, the mobility M is homogenous to a diffusivity by volumic energy:

$$ \begin{array}{@{}rcl@{}} M \equiv \frac{[L]^{4}}{[F][t]} \equiv \frac{m^{4}}{N.s} \end{array} $$

(25)

Where L is a unit of characteristic length, F is a unit of force and t is a unit of time. β is equivalent to an energy per unit volume and is expressed in N/m². If we consider that L is a characteristic dimension of our geometry, then we can define the characteristic time by $\frac {L^{2}}{M \beta }$. The variables with ^∗ denotes the dimensionless quantity. According to the previous definitions, we can give the following choice:

• Dimensionless time : $t^{*} = t \frac {M \beta }{L^{2}}$

• Dimensionless operators : $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }}^{*} = L \underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }} ; \qquad {\Delta }^{*} = L^{2} {\Delta }$

• Dimensionless velocity : $v^{*} = \frac {v}{\frac {M \beta }{L}} ;$ $\quad \frac {M \beta }{L}$ is the characteristic velocity

• The interface thickness is defined by:

  $$ \begin{array}{@{}rcl@{}} \varepsilon = \sqrt{\frac{\alpha}{\beta}} \end{array} $$

  (26)

  It can be written in a dimensionless form as $\varepsilon ^{*} = \frac {\varepsilon }{L} = \frac {\sqrt {\frac {\alpha }{\beta }}}{L}$

• The dimensionless nucleation source term: $S^{*} = \frac {S L^{2}}{M \beta }$,

• The dimensionless nucleation rate: $V_{g Max}^{*} = V_{g Max} \frac {L^{2}}{M \beta }$

The other contributions in the source term R₁, R₂, F(T) and P₀ are already dimensionless.

Finally, the dimensionless Cahen-Hillard equation becomes:

$$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial t^{*}} + v^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{*} C = {\Delta}^{*} \phi^{*} - S^{*} = {\Delta}^{*} (\frac{\partial\psi}{\partial C} - \varepsilon^{*2} {\Delta}^{*} C ) - S^{*} \end{array} $$

(27)

Where, $\phi ^{*} = \frac {\phi }{\beta }$. It should be noted that this dimensionless equation is controllable with only two parameters:

• ε^∗: which represents the dimensionless interface thickness. This parameter has to be chosen according to the minimum size of the shrinkage and also in coherence with the size of the discretization elements.

• $V_{g Max}^{*}$: which controls the nucleation rate (this contribution is in S^∗).

For the Navier-Stokes equation, we define the dimensionless pressure as:

$$ \begin{array}{@{}rcl@{}} p^{*} = \frac{p L^{2}}{\eta_{0} M \beta} \end{array} $$

(28)

We consider that $\frac {\eta _{0} M \beta }{L^{2}}$ is the characteristic pressure.

By multiplying (23) by the term $\frac {L^{3}}{\eta _{0} M \beta }$, we obtain:

$$ \begin{array}{@{}rcl@{}} \left( \frac{1}{\eta_{0}} \frac{L^{2}}{M \beta} \right) \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} p &&= \frac{\eta}{\eta_{0}} L^{2} {\Delta} \left( \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \frac{L}{M \beta} \right)\\&&\quad- \left( \frac{\rho_{0} g L^{3}}{\eta_{0} \frac{M \beta}{L} L} \right) \frac{\rho}{\rho_{0}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{z}} + \frac{L^{2} \beta}{\eta_{0} \frac{M \beta}{L} L} \frac{\phi}{\beta} L \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C \end{array} $$

(29)

This equation arise two dimensionless numbers:

• 1. The first one is $G^{*} = \frac {\rho _{0} g L^{3}}{\eta _{0} \frac {M \beta }{L} L}$ which represents the ratio of the gravity forces by the viscous forces.

• 2. The second one is $P^{*} = \frac {L^{2} \beta }{\eta _{0} \frac {M \beta }{L} L}$ which represents the ratio of phase separation forces by viscous forces.

We keep voluntarily the denominator $\eta _{0} \frac {M \beta }{L}L$ without simplification to show the product of viscosity by a characteristic velocity by a characteristic time.

The final equation is then written as:

$$ \begin{array}{@{}rcl@{}} -\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{*} p^{*} + \eta^{*} {\Delta}^{*} v^{*} - G^{*} \rho^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{z}} + P^{*} \phi^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{*} C =0 \end{array} $$

(30)

Where, $\eta ^{*} = \frac {\eta }{\eta _{0}}$ and $\rho ^{*}= \frac {\rho }{\rho _{0}}$, are two functions that depend on C and temperature. They are equal to 1 for C = 1 and at reference temperature (T = T₀), where η₀ and ρ₀ are defined.

Finally the heat (24) becomes dimensionless when it is multiplied by $\frac {L^{2}}{M \beta }$. It writes:

$$ \begin{array}{@{}rcl@{}} \frac{\partial T}{\partial t^{*}}+v^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{*} T = D^{*} {\Delta}^{*} T \end{array} $$

(31)

$D^{*} = \frac {\frac {k}{\rho Cp}}{M \beta }$. This dimensionless quantity represents the ratio of a thermal diffusivity by the phase field diffusivity. It should be noted that the temperature remains with dimension. We can divide this equation by a characteristic temperature in order to have a dimensionless field, but that does not made a new significant dimensionless number. Beside, if we want to make this equation dependent on the C variable, we can say that: $D^{*} =\frac {[\frac {k}{\rho C_{p} }]_{C=1}}{M \beta } d^{*}(C)$ (with d^∗(C = 1) = 1) and we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial T}{\partial t^{*}}+ v^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{*} T = \frac{[\frac{k}{\rho C_{p} }]_{C=1}}{M \beta} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{*} (d^{*} (C) \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{*} T) \end{array} $$

(32)

Final set of dimensionless equations

The final set of equations is written after removing the asterix notation for simplification:

$$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial t} + \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C = {\Delta} (\frac{\partial \psi}{\partial C} - \varepsilon^{2} {\Delta} C) - S \end{array} $$

(33)

$$ \begin{array}{@{}rcl@{}} - \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} p + \eta (T, c) {\Delta} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} - G \rho (T, c) \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{z}} + P \phi \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C =0 \end{array} $$

(34)

$$ \begin{array}{@{}rcl@{}} \frac{\partial T}{\partial t} + \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} T = D {\Delta} T \end{array} $$

(35)

Numerical resolution

There are some difficulties related to the resolution of the Cahn-Hilliard equation. The first one consists to make possible an implicit resolution of the elliptic terms containing a non linear contribution. The second one is related to the fourth order derivative in the frame work of a classical low order P1 or Q2 finite element discretization. In most works dealing which such an equation (see for example [22, 23]), the fourth order derivative is reduced by introducing a new variable ζ = ΔC and by making a coupled resolution of a set of two second order equations where the second one is:

$$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial t} + v \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C = {\Delta} (\frac{\partial \psi}{\partial C}) - \varepsilon^{2} {\Delta} \zeta - S \end{array} $$

(36)

This is in some ways equivalent to a double application of the diffusion operator. In our approach, we keep the same idea but with a small difference which consists in making the substitution of the second variables before looking for its value. In this way, the fourth order terms could be treated in the frame work of an implicit resolution. Now let’s come back to the term ${\Delta } (\frac {\partial \psi }{\partial C})$ which cannot completely be resolved in an explicit strategy otherwise the elliptic character of the equation disappear. To avoid this, we make a splitting to introduce an ellipticity to the equation. We define the φ(C) function as:

$$ \begin{array}{@{}rcl@{}} \varphi(C) = \frac{\partial \psi}{\partial C} + C \end{array} $$

(37)

In the case where:

$$ \begin{array}{@{}rcl@{}} \psi(C) = \frac{1}{4} (C+1)^{2} (C-1)^{2} \end{array} $$

(38)

We have φ(C) = C³, and the order parameter equation becomes:

$$ \begin{array}{@{}rcl@{}} \frac{\partial C}{\partial t} + v \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C = - {\Delta} C - \varepsilon^{2} {\Delta} \zeta + {\Delta} \varphi(C) - S \end{array} $$

(39)

It must be noted that this splitting is valid for any choice of ψ.

At this stage, it is essential to address the question related to the choice of other forms of the function ψ. Even if in most works we use the symmetric form (38) where the unstable equilibrium is obtained for C = 0, we found suitable for the cases where our C_lim (defined in Eq. 9) is close to 1 to change the definition of ψ to a non symmetric form. The following form is proposed:

$$ \begin{array}{@{}rcl@{}} \psi(C) = \frac{C \left( 3 C^{3}-4 C_{lim} C^{2}-6 C+12 C_{lim} \right)}{12} \end{array} $$

(40)

That form defines the unstable equilibrium at C = C_lim. The related derivative is then given by:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \psi(C)}{\partial C} = (C_{lim}-C)(1-C)(1+C) \end{array} $$

(41)

The advantage of that expression is that it defines a generic writing allowing to regain the specific case of Eq. 38 by simply fixing C_lim = 0. In all cases, the expression of φ given by Eq. 37 remains unchanged and this is what we will use in the following.

Before solving the C evolution equation, a preliminary work consists to links the ζ variable to C.

In a weak form based on a finite element discretization, we can write:

$$ \begin{array}{@{}rcl@{}} {\int}_{\Omega} C^{*} \zeta d{\Omega} = {\int}_{\Omega} C^{*} {\Delta} C d{\Omega} \end{array} $$

(42)

A Galerkin discretization is used. It can be written as:

$$ \begin{array}{@{}rcl@{}} C(x) = \sum\limits_{i=1}^{n} N_{i} (x) C_{i} \end{array} $$

(43)

where n is the total number of interpolation functions and N_i are the interpolation functions.

The integration by part assuming zeros flux of C on the boundaries of Ω writes:

$$ \begin{array}{@{}rcl@{}} {\int}_{\Omega} C^{*} \zeta d{\Omega} = - {\int}_{\Omega} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C d{\Omega} \end{array} $$

(44)

The mass and the stiffness matrix are given by:

$$\underset{{~}^{=}}{\boldsymbol{M}}_{ij} = {\int}_{\Omega} N_{i}(x) N_{j} (x) d{\Omega}$$

$$\underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}}_{ij} = {\int}_{\Omega} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} N_{i}(x) \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} N_{j} (x) d{\Omega}$$

In our case, it is preferred to use the lumped form of the mass matrix.

The formulation (44) after simplification becomes:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{=}}{\boldsymbol{M}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\zeta}} = - \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{C}} \end{array} $$

(45)

then the formula used for the substitution writes:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\zeta}} = -\underset{{~}^{=}}{\boldsymbol{M}}^{-1} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{C}} = \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{L}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{C}}, \qquad \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{L}}= -\underset{{~}^{=}}{\boldsymbol{M}}^{-1} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}} \end{array} $$

(46)

Temporal discretization

The evolution (39) of C(x) is defined in space and time. A quasi-implicit method is used for temporal integration. We denote by C^t and C^t+δt the discrete values of C at two successive time steps t and t + δt. The iterative scheme is defined by:

$$ \begin{array}{@{}rcl@{}} \frac{C^{t+ \delta t} - C^{t}}{\delta t} &&+ \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} . \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C^{t+ \delta t} = - {\Delta} C^{t+ \delta t} - \varepsilon^{2} {\Delta} \zeta^{t+ \delta t} \\&&+ {\Delta} \varphi(C^{t}) - S^{t+ \delta t} \end{array} $$

(47)

The same space discretization used previously is again used for this equation. The velocity field is supposed known at this stage. The $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {v}} . \underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }} C$ term gives an advective character which requires an upwinding stabilization of the classical centred finite element interpolation:

$$ \begin{array}{@{}rcl@{}} \tilde{C}^{*}(x) = \sum\limits_{i=1}^{n} \left[ N_{i}(x)+ \frac{h}{2} \frac{\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}}{|| \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}||} \right] C_{i} \end{array} $$

(48)

h is the average size of each triangulation element.

Using the same previous discretization, the variational formulation writes:

$$ \begin{array}{@{}rcl@{}} \int C^{*} \frac{C^{t+ \delta t} - C^{t}}{\delta t} &&+ \int \tilde{C}^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}. \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C^{t+ \delta t} = \int \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C^{*} {\Delta} C^{t+ \delta t}\\&&+ \varepsilon^{2} \int \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} \zeta^{t+ \delta t} + \int \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C^{*} {\Delta} \varphi(C^{t})+ \int C^{*} S^{t+ \delta t}\\ \end{array} $$

(49)

The previously defined lumped mass matrix as well as the stiffness matrix can be used here. In addition, we define a new matrix by:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{G}}_{ij}= {\int}_{\Omega} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}}^{T} N_{i} \frac{h}{2} \frac{\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \otimes \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}}{||\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}}||} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} N_{j} d{\Omega} + \int N_{i}(x) \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} N_{j} d{\Omega} \end{array} $$

(50)

The Eq. 47 becomes:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{M}} \frac{C^{t+ \delta t} - C^{t}}{\delta t} &&+ \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{G}} C^{t+ \delta t} = \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}} {\Delta} C^{t+ \delta t} + \varepsilon^{2} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}} \zeta^{t+ \delta t} \\&&+ \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}} \varphi(C^{t}) + \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{M}} S^{t+ \delta t} \end{array} $$

(51)

Or after substitution:

$$ \begin{array}{@{}rcl@{}} (\mathbb{I} + \delta t \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{M}}^{-1} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{G}} &&- \delta t \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{L}} -\delta t \varepsilon^{2} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{L}}^{2}) C^{t+ \delta t} = \delta t \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{L}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\varphi}}(C^{t})\\&&- \delta t S^{t+ \delta t}+ C^{t} \end{array} $$

(52)

Where, $\mathbb {I}$ is the identity tensor. Let’s call $\mathbb {H} = \mathbb {I} + \delta t \underset {{~}^{\boldsymbol {=}}}{\boldsymbol {M}}^{-1} \underset {{~}^{\boldsymbol {=}}}{\boldsymbol {G}} - \delta t \underset {{~}^{\boldsymbol {=}}}{\boldsymbol {L}} -\delta t \varepsilon ^{2} \underset {{~}^{\boldsymbol {=}}}{\boldsymbol {L}}^{2}$ and $\mathbb {F} = \delta t \underset {{~}^{\boldsymbol {=}}}{\boldsymbol {L}} \underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\varphi }}(C^{t}) - \delta t S^{t+ \delta t}+ C^{t}$

To solve this problem, a normality condition has to be imposed with a Lagrange multiplier to ensure that the quantity ${\int \limits }_{\Omega } C d{\Omega }$ is congruent with the source term. We calculate at each time step $I_{c} = {\int \limits } C d{\Omega } = \underset {{~}^{\boldsymbol {-}}}{\boldsymbol {N}}^{T} C$. Initially it starts with the unit value, then it is given by $I_{c}^{t + {\Delta } t} = {I^{t}_{c}} - \delta t {\int \limits } S^{t+\delta t} d{\Omega }$.

The global system is finally given by:

$$ \begin{pmatrix} \mathbb{H} & \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{N}} \\ \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{N}}^{T} & 0 \end{pmatrix} \begin{pmatrix} C^{t+ \delta t} \\ \lambda \end{pmatrix} = \begin{pmatrix} \mathbb{F} \\ I_{c} \end{pmatrix} $$

Where λ is the Lagrange multiplier associated to the C integral conservation.

If we deal now with the kinematic problem, we assume that during the cooling stage there are no extreme solicitations that occur (such as contraction or high compression zone). In fact, the only flows that exist are related to the gravity or the phase separation. Thus we decide to solve the kinematic equation by penalizing the term $\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }} p$:

The penalized continuity equation is defined by:

$$ \begin{array}{@{}rcl@{}} div \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} \mathbb{I} + (1/\chi) \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} p = 0 \end{array} $$

(53)

Then we obtain:

$$ \begin{array}{@{}rcl@{}} - \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} p = \chi tr \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{D}} \mathbb{I} \end{array} $$

(54)

Where $\underset {{~}^{\boldsymbol {=}}}{\boldsymbol {D}} = \frac {\underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }} v + \underset {{~}^{\boldsymbol {-}}}{\boldsymbol {\nabla }} v^{T}}{2}$ and χ is a penalization parameter chosen generally equal to 10³ or 10⁴.

The equation then becomes:

$$ \begin{array}{@{}rcl@{}} \chi tr \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{D}} \mathbb{I} + \eta(T,C) {\Delta} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} - G \rho (T,C)\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{z}} + P \phi \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C = 0 \end{array} $$

(55)

The finite element formulation for this problem is written in 2D where the two components of the velocity field are v_x and v_z (respectively along the horizontal axis x and vertical axis z):

$$ \begin{array}{@{}rcl@{}} \mathbb{K} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} = \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{F}} \end{array} $$

(56)

$\mathbb {K}$ is the global finite element matrix derived from an assembly of the local stiffness matrix written on each element as Ωe:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{k}}^{e} = {\int}_{\Omega e} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{B}}^{T} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{A}} \begin{pmatrix} \lambda + 2 \eta & \lambda & 0 \\ \lambda & \lambda + 2 \eta & 0 \\ 0 & 0 & \eta \end{pmatrix} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{A}} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{B}} d {\Omega} e \end{array} $$

(57)

with:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{A}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ \end{pmatrix}, \qquad \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{B}} = \begin{pmatrix} \frac{\partial N_{1}}{\partial x} & 0 & \frac{\partial N_{2}}{\partial x} & 0 & \frac{\partial N_{3}}{\partial x} & 0\\ \frac{\partial N_{1}}{\partial z} & 0 & \frac{\partial N_{2}}{\partial z} & 0 & \frac{\partial N_{3}}{\partial z} & 0\\ 0 & \frac{\partial N_{1}}{\partial x} & 0 & \frac{\partial N_{2}}{\partial x} & 0 & \frac{\partial N_{3}}{\partial x} \\ 0 & \frac{\partial N_{1}}{\partial z} & 0 & \frac{\partial N_{2}}{\partial z} & 0 & \frac{\partial N_{3}}{\partial z} \\ \end{pmatrix} \end{array} $$

(58)

The right side is given by:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{F}} = G {\int}_{\Omega} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{N}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{N}}^{T}(\underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} C \phi) d {\Omega} - P {\int}_{\Omega} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{N}} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{N}}^{T} \rho \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{z}} d {\Omega} \end{array} $$

(59)

Finally, the heat transfer equation can be written using the same operators previously defined. The variational form:

$$ \begin{array}{@{}rcl@{}} {\int}_{\Omega} T^{*}\frac{\partial T}{\partial t} d {\Omega} + {\int}_{\Omega} T^{*} \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{v}} . \underset{{~}^{\boldsymbol{-}}}{\boldsymbol{\nabla}} T d {\Omega} = {\int}_{\Omega} T^{*} D {\Delta} T d {\Omega} \end{array} $$

(60)

corresponds to the discrete form:

$$ \begin{array}{@{}rcl@{}} \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{M}} \frac{T^{t+ \delta t} - T^{t}}{\delta t} + \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{G}} T^{t+ \delta t} + \underset{{~}^{\boldsymbol{=}}}{\boldsymbol{K}} T^{t+ \delta t} = 0 \end{array} $$

(61)

on which boundary conditions must be taken into account. This equation can be solved using a first order Euler implicit time integration scheme.

Analyse of non dimensional parameters influence

A 2D unit length square part is considered in this section. Simulations start when the mould is filled with a molten metal at temperature equal to 400^∘C. Dirichlet boundary conditions are applied to the interface with the mould (fixed temperature at the interface equal to 40^∘C). The parameter ε characterizing the interface thickness takes the value of 0.035 or 0.0033. The parameters G and P vary from 10⁴ to 10⁶. The Thermo-dependence is characterized by an Arrhenius like function defined by:

$$ V(T) = \exp[1000(1/T - 1/400)] $$

The function F(T) of Eq. 11 delimits the hottest zone by a difference from the maximum value equal to δT = 2^∘C. The V_gMax parameter is set to 10⁵. The probability threshold P₀ is fixed to 0.5. The C_lim value is chosen equal to 0.6, which is equivalent to a final voids proportion equal to 20%. Even if this value is not representative of a realistic distribution, it has been chosen to highlight well the parameters effects.

In the first Fig. 5 where ε = 0.035, we observe at different non-dimensional times the evolution of the system. In the beginning of the cooling, four void nuclei appear in the hottest zone. A coalescence is then observed which is favoured with the high value of the parameter P (10⁶). The induced kinematic is shown in the third column. The value of G = 10⁶ favours a rise of the formed cavity towards the upper part of the mould.

Fig. 5

Evolution of the system state during the cooling process: The first column represents the order parameter, the second one the interface metal/void, the third one the fluid phase velocity field and the final column the temperature field. Simulation done for P = G = 10⁶, D = 0.1

In order to observe the influence of the G and P parameters, four final morphologies are shown in Fig. 6 for a fixed parameter ε = 0.035.

Fig. 6

Different final voids repartitions according to the two parameters P and G with ε = 0.035 and D = 1

Two other parametric studies are presented in Figs. 7 and 8. To go down to a thinner void size, the parameter ε is decreased to 0.0033. To respect the conformity of the mesh regarding the interface thickness, a uniform size mesh with 368 000 finite elements has been used. Two values of non-dimensional conductivity are considered D = 1 and 10.

Fig. 7

Different final voids repartitions according to the two parameters P and G with ε = 0.0033 and D = 10

Fig. 8

Different final voids repartitions according to the two parameters P and G with ε = 0.0033 and D = 1

Regarding these figures, several conclusions can be done:

• The G parameter is the one who controls the rise of the voids to the upper zones of the part. Thus it is determinant to localize the vertical default distribution.

• The parameter ε determines the voids size at the end of the nucleation process (which corresponds in general to the first moment of the cooling stage). It defines the initial morphological size that evolves later under the kinematics effects.

• The parameter P controls the final size of the voids. A high value allows a mobility inducing coalescence.

• A rapid cooling (controlled by the D parameter) concentrates the defaults in the part core. A slow cooling may allow defaults to be located near the skin.

An example of experimental confrontation

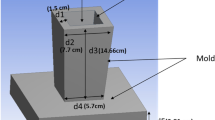
An example of mould providing almost 2D filling and cooling has been designed and used to produce hourglass-shaped parts. Such design localizes two hot zones who can communicate via a small constriction. The mould is presented in Fig. 9. The experimental set up is instrumented with k-thermocouples connected to a data acquisition system that measure metal and mould temperatures during filling and solidification phases. We can ensure then that the thermal predicted field by simulation is conform to the real one.

Fig. 9

Cast part design and thermocouples position

Five thermocouples have been installed (Fig. 9: Th A to Th E) and Fig. 10.

Fig. 10

The thermocouples location in the mould

Before casting, the mould is put into an oven at 150^∘C to ensure a homogeneous temperature repartition.

For each casting, a quantity of Zamak 5 was melted in the oven (450^∘C) and then casted. The part is ejected from the mould after one hour cooling.

In order to observe the shrinked zones, the part was cut according to the Fig. 11.

Fig. 11

Several cutting plans of the part

The shape of the shrinkage in some planes is shown in Fig. 12.

Fig. 12

Pictures of some planes showing macro-shrinkage formation

Our model has been applied to predict such defaults. A 2D symmetric mesh has been used based on 5000 finite elements. The simulation has been done with the following parameters: ε = 0.01 × the total height, G = 1.7.10⁶, P = 10⁶, V_gMax = 5.10⁴, C_lim = 0.8. Figures 13 and 14 shows respectively the velocity field and the temperature evolution during non-dimensional time. As the characteristic time of our model is related to the phase field parameters, it becomes difficult to determine it with direct experimental identification. Thus we used an inverse identification based on thermal fields confrontation. From this confrontation, we deduce that the ratio between the dimensional and dimensionless time is about 1500.

Fig. 13

The velocity field of the molten metal during non-dimensional time

Fig. 14

The Temperature field of the molten metal during time

The Fig. 15 shows the void morphology evolutions obtained from the phase-field model. The blue areas are considered as the voids (C = − 1) while the red regions are the liquid (C = 1). The shrinkage can be localized in the hottest zones. This figure illustrates that the formation of macro-shrinkage during cooling is qualitatively similar to the experimental observation.

Fig. 15

Order parameter evolution during time

Conclusion

A new void formation model based on the phase field framework is presented. It allows to model shrinkage formation during the cooling stage taking into account gravity and coalescence effects. The numerical method combines the discretization of the convective Cahn-Hilliard equation with the discretization of the Navier-Stokes equations coupled with heat transfer one.

The difficulty of such simulation lies in the couplings between the different mechanisms. An accurate modelling should include all the coupling that occurs during the cooling between flow, heat transfer, anisotropy, phase change, dependence of rheological or thermal parameters on kinetic variables, ...

Even if we success here to produce very reasonable qualitative results, a lot of efforts must be continued in order to determine perfectly all the multi-physics interdependency. In fact, if we just take the thermo-dependency law giving the viscosity as function of, temperature, no rheometer is today able to proceed under the processing conditions of our metal. Thus a convenient inverse approach development is required. To that is added the difficulty related to the identification of the phase field kinetic parameters, especially the mobility for which imaging technique is very probably unavoidable.