Introduction

Bent tubular parts are required in almost all industrial sectors. However, manufacturing of these parts, especially parts made of high strength steels, requires high bending forces that lead to large amounts of springback [1].

Several investigations were conducted to predict, compensate and reduce the springback in different profile bending processes. Gu et al. [2] established an FE (finite element) model for the NC-bending (numerical control bending) of thin-walled tubes and investigated the effects of geometry and process parameters on springback. The results showed that the springback angle increases with the increase of the bending angle. Jiang et al. [3] investigated the coupling effects of the material properties and bending angle on the springback angle of a titanium alloy tubes. They observed that any increase in the bending angle, yield stress, and hardening coefficient increase the springback angle, and any decrease in Young’s modulus, the hardening exponent, and the thickness anisotropy exponent leads to a decrease in springback angle. Al-Qureshi and Russo [4] developed an analytical model to predict the springback and residual stress distributions of thin-walled aluminium tubes by assuming an elastic-perfectly plastic material behaviour. A mathematical model which can consider the hardening behaviour of the steel tubes was proposed by El Megharbel et al. [5].

The most effective method to suppress springback is to reduce the bending moment. Wang and Hu [6] used the local induction heating to bend a pipe to a small bend radius. Hu [7] also developed an elasto-plastic solution to predict the springback under local induction heating. In recent years, stress superposition has been used as a useful method to reduce bending forces and springback. In the bend-rolling process, for instance, Tozawa and Ishikawa [8] combined bending with rolling. The results of their investigations showed that the flattening of the cross-section completely vanishes and springback is reduced. Nakamura et al. [9] combined a tube expansion and bending process. In this method, an internal tool is used to increase the diameter of the tube while simultaneously applying a bending moment resulting in a reduction of the applied bending forces. Another process is the Torque Superposed Spatial (TSS) bending process, which uses multiaxial stress superposition and allows bending profiles with arbitrary cross-sections to arbitrary 3D contours [10]. In the TSS bending process, a bending force reduction of about 20% was recorded by Becker et al. [11]. Free-form bending and spinning were combined by Hermes et al. [12] to produce tailored tubes with reduced bending moments as well as springback. In this so called incremental tube forming (ITF), the tube diameter is reduced by three spinning rolls while a bending roll applies a bending force. This results in a bending moment superposed into the forming zone to achieve the desired curvature. Initial studies showed a significant reduction of the bending moment in comparison to conventional bending methods. A process model was proposed for ITF by Becker et al. [13], which can predict the bending moment as well as the springback for a combination of diameter reduction and simultaneous bending. However, the interaction of the strains by spinning with strains from bending was not considered in their investigation. Becker and Tekkaya [14] showed that the wall-thickness of tubes can be controlled to some extent during manufacturing by varying specific process parameters. However, the influence that this alteration of wall-thickness has on the process forces has not been considered up until now. Additionally, the variation of the wall-thickness by using a mandrel has not yet been considered.

The aim of the current investigation is to develop an analytical model that can predict the bending moment and springback in incremental tube forming by considering both diameter and wall-thickness reduction together with interaction of the strains from spinning and bending. The analytical model predicts the bending stresses in the presence of radial and circumferential stresses. This model is validated using experimental and simulation data.

Process description

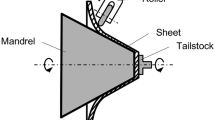
The forming tools of ITF include three spinning rolls, a bending roll, and a mandrel, as shown in Fig. 1. The spinning rolls can be moved radially into the tube and rotate around it, which leads to a reduction in tube diameter and press the material against the mandrel. By using the mandrel, the material flows into the axial direction of the tube. The thickness of the tube can be adjusted by controlling the axial position of the mandrel relative to the spinning rolls. Simultaneously, a bending force is applied by a bending roll to generate a curved tubular part.

Fig. 1
figure 1

Schematic of incremental tube forming with an internal mandrel

Full size image

Analytical solution for combined bending and spinning process

Here, an analytical solution is developed to predict the effect of the radial and circumferential stresses induced by the spinning process on the axial bending stresses. The solution can predict the effect of the diameter and thickness reductions on the axial bending stress. A finite element model was developed using ABAQUS/ Explicit to validate the distribution of the axial stress over the tube cross- section.

The combination of the spinning and bending process leads to a complex state of stress and strains. For an analytical investigation, it is assumed that if the spinning rolls spin at infinite rotational speed around the profile, the rolls would touch every part of the circumference of the tube in the forming zone at the same time. In this state, the spinning process can be replaced by a simple die, as shown also by Becker et al. [13], meaning that the whole cross-section experiences the diameter and thickness reduction at the same time (Fig. 2a). Additionally, it is assumed that the tube consists of several radial segments, placed at different distances from the bending plane (Fig. 2b). Thus, the stress state can be studied in each individual segment at an arbitrary distance from the horizontal symmetry plane, of which the stresses in the axial direction can be used to evaluate the stress distribution over the cross section of the tube as well as for calculating the bending moment. For the analytical calculations, an isotropic material with ideally plastic behaviour is investigated as well as isotropic material with linear hardening behaviour. The linear hardening behaviour can be represented by:

$$ {\sigma}_{\mathrm{y}}\left({\overline{\varepsilon}}_{\mathrm{p}}\right)={\sigma}_0\left(1+\alpha {\overline{\varepsilon}}_{\mathrm{p}}\right), $$
(1)

where, \( {\overline{\varepsilon}}_{\mathrm{p}} \) is the equivalent plastic strain, σ0 is the initial yield stress and α is a material hardening constant.

Fig. 2
figure 2

Simplifications (a) replacing the rolls with a die [13] (b) segmented cross-section of the tube

Full size image

Stress and strain states

The stress state is assumed to be three dimensional with zero shear stress components. The three normal stress components in an arbitrary element are σrr in the radial direction, σθθ in the circumferential direction and σzz in the axial direction.

The strain components are calculated from the shape change by bending and spinning, which include three components, namely εrr, sp, εθθ, sp and εzz, b. These strain components result from stresses in radial, circumferential and axial directions and can be calculated as:

$$ {\varepsilon}_{\mathrm{rr},\mathrm{sp}}=\frac{t_{1-}{t}_0}{t_0}, $$
(2)
$$ {\varepsilon}_{\uptheta \uptheta, \mathrm{sp}}=\frac{d_{1-}{d}_0}{d_0}, $$
(3)
$$ {\varepsilon}_{\mathrm{zz},\mathrm{b}}=\frac{y}{r_{\mathrm{m}}}, $$
(4)

where t0 and t1, are the initial and the reduced thickness respectively, d0 and d1 are the initial and the reduced outer diameter, respectively, rm is bending radius, and y is the distance of each segment from the horizontal symmetry plane of the tube. The parameter γ defines the ratio of the circumferential strain rate (diameter change by spinning) to the axial strain rate by bending, whereby the parameter η defines the ratio of the radial strain rate (thickness change by spinning) to the axial strain rate by bending. By assuming proportional loading, these ratios remain constant for each individual segment and, by additionally assuming linear strain paths, equal to the ratio of the final strains.

$$ \gamma =\frac{{\dot{\varepsilon}}_{\uptheta \uptheta, \mathrm{sp}}}{{\dot{\varepsilon}}_{\mathrm{zz},\mathrm{b}}}=\frac{\varepsilon_{\uptheta \uptheta, \mathrm{sp}}}{\varepsilon_{\mathrm{zz},\mathrm{b}}} $$
(5)
$$ \eta =\frac{{\dot{\varepsilon}}_{\mathrm{rr},\mathrm{sp}}}{{\dot{\varepsilon}}_{\mathrm{zz},\mathrm{b}}}=\frac{\varepsilon_{\mathrm{rr},\mathrm{sp}}}{\varepsilon_{\mathrm{zz},\mathrm{b}}} $$
(6)

Elastic loading

In the beginning of the forming process, considering the assumption of proportional loading, strains increase linearly from zero to the elastic limit. The components of the stress and strain tensors can be written as:

$$ \boldsymbol{S}=\left[\begin{array}{ccc}{\sigma}_{\mathrm{rr}}& 0& 0\\ {}0& {\sigma}_{\uptheta \uptheta}& 0\\ {}0& 0& {\sigma}_{\mathrm{zz}}\end{array}\right], $$
(7)
$$ \boldsymbol{\upvarepsilon} =\left[\begin{array}{ccc}{\varepsilon}_{\mathrm{rr}}& 0& 0\\ {}0& {\varepsilon}_{\uptheta \uptheta}& 0\\ {}0& 0& {\varepsilon}_{\mathrm{zz}}\end{array}\right]={\varepsilon}_{\mathrm{zz},\mathrm{b}}\left[\begin{array}{ccc}\eta -\upsilon -\upsilon \gamma & 0& 0\\ {}0& \gamma -\upsilon -\upsilon \eta & 0\\ {}0& 0& 1-\upsilon \gamma -\upsilon \eta \end{array}\right], $$
(8)

where, υ is the Poisson’s ratio in elastic loading. The stress-strain relation in the elastic part for an isotropic material can be written by:

$$ \boldsymbol{S}=2G\left[\frac{\upupsilon}{1-2\upsilon}\left( tr\boldsymbol{\upvarepsilon} \right)\boldsymbol{I}+\boldsymbol{\upvarepsilon} \right], $$
(9)

where, the constant G is known as the shear modulus and can be defined by Eq. (7).

$$ G=\frac{E}{2\left(1+\upsilon \right)} $$
(10)

Here, E is the Young’s modulus. By placing Eqs. (7) and (8) into Eq. (9), the stress components in elastic loading can be calculated as:

$$ {\sigma}_{\mathrm{rr}}=2G\left(1+\upupsilon \right){\eta \varepsilon}_{\mathrm{zz},\mathrm{b}}={E\eta \varepsilon}_{\mathrm{zz},\mathrm{b}}, $$
(11)
$$ {\sigma}_{\uptheta \uptheta}=2G\left(1+\upupsilon \right){\gamma \varepsilon}_{\mathrm{zz},\mathrm{b}}=E{\gamma \varepsilon}_{\mathrm{zz},\mathrm{b}}, $$
(12)
$$ {\sigma}_{\mathrm{zz}}=2G\left(1+\upupsilon \right){\varepsilon}_{\mathrm{zz},\mathrm{b}}=E{\varepsilon}_{\mathrm{zz},\mathrm{b}}. $$
(13)

During the elastic deformation, εzz, b increases from 0 to the value at the yield limit (\( {\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}\Big) \), where the yield criterion is satisfied by the stress state. By using the von Mises yield criterion, \( {\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}} \) at initial yield can be calculated by:

$$ {\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}=\frac{\pm {\sigma}_{\mathrm{y}}}{\sqrt{2}\mathrm{G}\left(1+\upsilon \right)\sqrt{{\left(1-\gamma \right)}^2+{\left(\eta -\gamma \right)}^2+{\left(\eta -1\right)}^2}}. $$
(14)

The stress components at yield can be determined by inserting Eq. (14) into Eqs. (11), (12) and (13). This results in:

$$ {\sigma}_{\mathrm{rr}}^{\mathrm{y}0}={\sigma}_{\mathrm{rr}}\left({\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}\right)=\frac{-\sqrt{2}{\eta \sigma}_{\mathrm{y}}}{\sqrt{{\left(1-\gamma \right)}^2+{\left(\eta -\gamma \right)}^2+{\left(\eta -1\right)}^2}}, $$
(15)
$$ {\sigma}_{\uptheta \uptheta}^{\mathrm{y}0}={\sigma}_{\uptheta \uptheta}\left({\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}\right)=\frac{-\sqrt{2}{\gamma \sigma}_{\mathrm{y}}}{\sqrt{{\left(1-\gamma \right)}^2+{\left(\eta -\gamma \right)}^2+{\left(\eta -1\right)}^2}}, $$
(16)
$$ {\sigma}_{\mathrm{zz}}^{\mathrm{y}0}={\sigma}_{\mathrm{zz}}\left({\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}\right)=\frac{\pm \sqrt{2}{\sigma}_{\mathrm{y}}}{\sqrt{{\left(1-\gamma \right)}^2+{\left(\eta -\gamma \right)}^2+{\left(\eta -1\right)}^2}}. $$
(17)

where, \( {\sigma}_{\mathrm{rr}}^{\mathrm{y}0} \), \( {\sigma}_{\uptheta \uptheta}^{\mathrm{y}0} \),\( {\sigma}_{\mathrm{zz}}^{\mathrm{y}0} \) are radial, circumferential and longitudinal stress components at initial yield, respectively.

Plastic loading

After reaching the initial yield point, and since the loading remains proportional, any changes in stresses depend on the hardening behaviour of the material. First, a linear hardening behaviour is considered as mentioned in the previous section. The stress components can be written as follows:

$$ \boldsymbol{S}=\left[\begin{array}{ccc}{\sigma}_{\mathrm{rr}}^{\mathrm{p}}+{\sigma}_{\mathrm{rr}}^{\mathrm{y}0}& 0& 0\\ {}0& {\sigma}_{\boldsymbol{\uptheta} \boldsymbol{\uptheta}}^{\mathrm{p}}+{\sigma}_{\uptheta \uptheta}^{\mathrm{y}0}& 0\\ {}0& 0& {\sigma}_{\mathrm{zz}}^{\mathrm{p}}+{\sigma}_{\mathrm{zz}}^{\mathrm{y}0}\end{array}\right]=\left[\begin{array}{ccc}{\sigma}_{\mathrm{rr}}& 0& 0\\ {}0& {\sigma}_{\uptheta \uptheta}& 0\\ {}0& 0& {\sigma}_{\mathrm{zz}}\end{array}\right], $$
(18)

where, \( {\sigma}_{\mathrm{rr}}^{\mathrm{p}} \), \( {\sigma}_{\uptheta \uptheta}^{\mathrm{p}} \) and \( {\sigma}_{\mathrm{zz}}^{\mathrm{p}} \) are added to the stress values at the initial yield point during plastic deformation due to the hardening.

For any points in the plastic region, the stress-strain relationship for a material with isotropic hardening can be described by the following constitutive equations [15]:

$$ {\dot{\boldsymbol{S}}}^{\mathrm{D}}=2G\left({\dot{\boldsymbol{\upvarepsilon}}}^{\mathrm{D}}-\frac{3G{\boldsymbol{S}}^{\mathrm{D}}\cdot {\dot{\boldsymbol{\upvarepsilon}}}^{\mathrm{D}}}{\sigma_{\mathrm{y}}^2\left(2G+\frac{2}{3}{\sigma}_{\mathrm{y}}^{\hbox{'}}\left({\overline{\boldsymbol{\varepsilon}}}_{\mathrm{p}}\right)\right)}{\boldsymbol{S}}^{\mathrm{D}}\right), $$
(19)
$$ tr\boldsymbol{S}=\frac{2G\left(1+\upsilon \right)}{\left(1-2\upsilon \right)} tr\boldsymbol{\upvarepsilon} . $$
(20)

where, SD and εD are deviatoric stress and strain tensors, σy and \( {\sigma}_{\mathrm{y}}^{\prime}\left({\overline{\varepsilon}}_{\mathrm{p}}\right) \) are yield stress and change of yield stress in respect to equivalent plastic strain \( \left({\overline{\varepsilon}}_{\mathrm{p}}\right) \). The equivalent plastic strain, \( {\overline{\varepsilon}}_{\mathrm{p}} \), can be written as [15]:

$$ {\overline{\varepsilon}}_{\mathrm{p}}=\underset{0}{\overset{t}{\int }}{\overline{\varepsilon}}_{\mathrm{p}}(t)=\frac{2G\left|{\dot{\boldsymbol{S}}}^{\mathrm{D}}\cdot {\dot{\boldsymbol{\upvarepsilon}}}^{\mathrm{D}}\right|}{\sigma_{\mathrm{y}}\left(2G+\frac{2}{3}{\sigma}_{\mathrm{y}}^{\hbox{'}}\left({\overline{\varepsilon}}_{\mathrm{p}}\right)\right)}, $$
(21)

where, \( \dot{\varepsilon_{\mathrm{p}}}(t) \) is equivalent plastic strain rate.

The strain rate tensor (\( \dot{\boldsymbol{\upvarepsilon}} \)) can be written as follows:

$$ \dot{\boldsymbol{\upvarepsilon}}=\left[\begin{array}{ccc}{\dot{\varepsilon}}_{\mathrm{rr}}& 0& 0\\ {}0& {\dot{\varepsilon}}_{\uptheta \uptheta}& 0\\ {}0& 0& {\dot{\varepsilon}}_{\mathrm{zz}}\end{array}\right]={\dot{\varepsilon}}_{\mathrm{zz},\mathrm{b}}\left[\begin{array}{ccc}\eta -{\upupsilon}_{\mathrm{p}}-{\upupsilon}_{\mathrm{p}}\gamma & 0& 0\\ {}0& \gamma -{\upupsilon}_{\mathrm{p}}-{\upupsilon}_{\mathrm{p}}\eta & 0\\ {}0& 0& 1-{\upupsilon}_{\mathrm{p}}\gamma -{\upupsilon}_{\mathrm{p}}\eta \end{array}\right], $$
(22)

where, parameter υp is the ratio of the transverse strain increment to axial strain increment during plastic deformation and can be determined by:

$$ {\upupsilon}_{\mathrm{p}}=\frac{0.5E+{\upsilon E}_{\mathrm{p}}}{E+{E}_{\mathrm{p}}}. $$
(23)

Here, Ep is the plastic tangent modulus. Derivation of Eq. (23) is given in the appendix.

Using Eqs. (7) and (22) in combination with Eqs. (19) and (20) results:

$$ \left\{\begin{array}{c}2{\dot{\sigma}}_{\mathrm{zz}}^{\mathrm{p}}-{\dot{\sigma}}_{\uptheta \uptheta}^{\mathrm{p}}-{\dot{\sigma}}_{\mathrm{rr}}^{\mathrm{p}}=2G\left[\left(1+{\upupsilon}_{\mathrm{p}}\right)\left(2-\gamma -\eta \right)-G\cdot A\cdot \left(2{\sigma}_{\mathrm{zz}}-{\sigma}_{\uptheta \uptheta}-{\sigma}_{\mathrm{rr}}\right)\right]{\dot{\varepsilon}}_{\mathrm{zz},\mathrm{b}},\\ {}2{\dot{\sigma}}_{\uptheta \uptheta}^{\mathrm{p}}-{\dot{\sigma}}_{\mathrm{zz}}^{\mathrm{p}}-{\dot{\sigma}}_{\mathrm{rr}}^{\mathrm{p}}=2G\left[\left(1+{\upupsilon}_{\mathrm{p}}\right)\left(2\gamma -1-\eta \right)-G\cdot A\cdot \left(2{\sigma}_{\uptheta \uptheta}-{\sigma}_{\mathrm{zz}}-{\sigma}_{\mathrm{rr}}\right)\right]{\dot{\varepsilon}}_{\mathrm{zz},\mathrm{b}},\\ {}{\dot{\sigma}}_{\mathrm{rr}}^{\mathrm{p}}+{\dot{\sigma}}_{\uptheta \uptheta}^{\mathrm{p}}+{\dot{\sigma}}_{\mathrm{zz}}^{\mathrm{p}}=\frac{2\mathrm{G}\left(1+\upupsilon \right)}{\left(1-2\upupsilon \right)}\left(1-2{\upupsilon}_{\mathrm{p}}\right)\left(\gamma +\eta +1\right){\dot{\varepsilon}}_{\mathrm{zz},\mathrm{b}},\end{array}\right. $$
(24)

with

$$ A=\frac{\left[\left(2{\sigma}_{\mathrm{zz}}-{\sigma}_{\uptheta \uptheta}-{\sigma}_{\mathrm{rr}}\right)\left(1-{\upupsilon}_{\mathrm{p}}\gamma -{\upupsilon}_{\mathrm{p}}\gamma \right)+\left(2{\sigma}_{\uptheta \uptheta}-{\sigma}_{\mathrm{zz}}-{\sigma}_{\mathrm{rr}}\right)\left(\gamma -{\upupsilon}_{\mathrm{p}}-{\upupsilon}_{\mathrm{p}}\gamma \right)+\left(2{\sigma}_{\mathrm{rr}}-{\sigma}_{\mathrm{zz}}-{\sigma}_{\uptheta \uptheta}\right)\left(\gamma -{\upupsilon}_{\mathrm{p}}-{\upupsilon}_{\mathrm{p}}\gamma \right)\right]}{\sigma_{\mathrm{y}}^2\left(2G+\frac{2}{3}{\sigma}_{\mathrm{y}}^{\prime}\left({\overline{\varepsilon}}_{\mathrm{p}}\right)\right)}. $$
(25)

Solving the above system of equations, the ratio of the radial, circumferential, and longitudinal stress increments to the increment of axial strain (caused by bending) in the range of plastic loading can be written as:

$$ \frac{{d\sigma}_{rr}^{\mathrm{p}}}{{d\varepsilon}_{\mathrm{zz},\mathrm{b}}}=\frac{-2}{3}G\left[\left(1+{\upupsilon}_{\mathrm{p}}\right)\left(1+\gamma -2\eta \right)-G\cdot A\cdot \left({\sigma}_{\mathrm{zz}}+{\sigma}_{\uptheta \uptheta}-2{\sigma}_{\mathrm{rr}}\right)-\frac{\left(1+\upupsilon \right)}{\left(1-2\upupsilon \right)}\left(1-2{\upupsilon}_{\mathrm{p}}\right)\left(\gamma +\eta +1\right)\right], $$
(26)
$$ \frac{{d\sigma}_{\uptheta \uptheta}^{\mathrm{p}}}{{d\varepsilon}_{\mathrm{zz},\mathrm{b}}}=\frac{2}{3}G\left[G\cdot A\cdot \left({\sigma}_{\mathrm{zz}}-2{\sigma}_{\uptheta \uptheta}+{\sigma}_{\mathrm{rr}}\right)-\left(1+{\upupsilon}_{\mathrm{p}}\right)\left(1-2\gamma +\eta \right)+\frac{\left(1+\upupsilon \right)}{\left(1-2\upupsilon \right)}\left(1-2{\upupsilon}_{\mathrm{p}}\right)\left(\gamma +\eta +1\right)\right], $$
(27)
$$ \frac{{d\sigma}_{\mathrm{zz}}^{\mathrm{p}}}{{d\varepsilon}_{\mathrm{zz},\mathrm{b}}}=\frac{2}{3}G\left[\left(1+{\upupsilon}_{\mathrm{p}}\right)\left(2-\gamma -\eta \right)-G\cdot A\cdot \left(2{\sigma}_{\mathrm{zz}}-{\sigma}_{\uptheta \uptheta}-{\sigma}_{\mathrm{rr}}\right)+\frac{\left(1+\upupsilon \right)}{\left(1-2\upupsilon \right)}\left(1-2{\upupsilon}_{\mathrm{p}}\right)\left(\gamma +\eta +1\right)\right]. $$
(28)

Eqs. (26)–(28) are ordinary differential equations, which in combination with Eq. (21) can be solved numerically with boundary conditions of \( {\sigma}_{\mathrm{rr}}^{\mathrm{p}}\left({\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}\right)=0 \), \( {\sigma}_{\uptheta \uptheta}^{\mathrm{p}}\left({\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}\right)=0 \), \( {\sigma}_{\mathrm{zz}}^{\mathrm{p}}\left({\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0}\right)=0 \). In plastic loading, εzz, b will change from \( {\varepsilon}_{\mathrm{zz},\mathrm{b}}^{\mathrm{y}0} \), which can be calculated by Eq. (17), to the final value, which can be calculated from Eq. (4).

It should be mentioned that solving of Eqs. (26)–(28) results in values of stress change with respect to the initial yield stresses during plastic deformation. The final stress values can be calculated by adding them to the values of the initial yield stresses as follows:

$$ {\sigma}_{\mathrm{rr}}={\sigma}_{\mathrm{rr}}^{\mathrm{p}}+{\sigma}_{\mathrm{rr}}^{\mathrm{y}0}, $$
(29)
$$ {\sigma}_{\uptheta \uptheta}={\sigma}_{\uptheta \uptheta}^{\mathrm{p}}+{\sigma}_{\uptheta \uptheta}^{\mathrm{y}0}, $$
(30)
$$ {\sigma}_{\mathrm{zz}}={\sigma}_{\mathrm{zz}}^{\mathrm{p}}+{\sigma}_{\mathrm{zz}}^{\mathrm{y}0}. $$
(31)

FEM model for combined bending and spinning

A finite element model of combined bending and spinning is established in ABAQUS/ Explicit. The model is used to validate the distribution of the calculated axial stress distribution over the cross-section. In order to reduce the computational time, the tube is modelled in two parts, as shown in Fig. 3. The first part which goes under plastic deformation is meshed with 8-node reduced integration solid elements (C3D8R). The second part is just for transferring the bending moment from bending roll to deformation zone. Linear 4-node reduced integration shell elements (S4R) are used for this purpose. The forming tools, such as spinning rolls, bending tool, and mandrel are modelled as rigid Part. A surface to surface contact is defined between the forming tools and the tube.

Fig. 3
figure 3

FEM model of incremental tube forming

Full size image

A case study to investigate the axial stress development

A numerical solution is presented to study the effect of superposed radial and circumferential stresses on the bending moment required for the generation of specific bending radii. The calculations are done for a hypothetical material with linear isotropic hardening, as shown in Fig. 4.

Fig. 4
figure 4

Linear material model for a numerical case study

Full size image

Eq. (31) gives the value of the axial stress for a segment at an arbitrary vertical distance from the neutral bending plane. For investigating the axial stress over the cross-section, this equation should be solved separately for each segment. However, to investigate how the axial stress is developed in the presence of radial and circumferential stresses, first, this equation is solved together with Eqs. (29) and (30) just for the single segments at inner and outer fibres. Figure 5 shows that the required axial stress is reduced dramatically in the presence of the superposed radial and circumferential stresses. The amount of the reduction depends on the magnitude of the superposed stresses.

Fig. 5
figure 5

Comparison of the longitudinal stress development in pure bending and presence of superposed radial and circumferential stresses

Full size image

The distribution of the axial stress over the cross-section with and without stress superposition is shown in Fig. 6. Depending on the position of the rolls, the axial stress over the cross-section can be changed. However, the average value of the axial stresses during one revelation of the spinning rolls, from the simulation results, is used as a comparison. It can be seen that both analytical and simulation results show a high reduction of axial stresses for all segments in the presence of superposed radial and circumferential stresses. However, there is a difference between the analytical and simulation values, which might be due to the initial assumptions. Two main assumptions were used in the analytical solution. First, the spinning rolls are replaced with a fixed die. Hence, the local plastification and the shear stresses, which can be induced by spinning, are neglected. Second, it is assumed that the strain increments are proportional. As a result, both spinning and bending processes are started at the same time. However, in the real process, the tube is first plastified by the spinning process and subsequently is influenced by the bending stresses. Hence, bending stresses only play a secondary role in plastifying the tube in the real process. These two assumptions in the analytical calculations lead to a deviation in the results, while the FE model is based on the real process and does not include mentioned simplifications.

Fig. 6
figure 6

Longitudinal stress distribution over the cross-section in presence of superposed radial and circumferential stresses

Full size image

Simplified analytical model

The method presented in the previous section needs a numerical solution of Eqs. (26)–(28). By neglecting the hardening effect, parameters α and υp will be 0 and 0.5, respectively. A comparison between the distribution of the axial stress over the cross-section for the case without and with different hardening constants (α) is shown in Fig. 7. The dashed lines show the result with neglected hardening. It can be seen that considering an elastic-ideally plastic material model leads to just a small deviation in the calculation of the axial stress distribution over the cross-section, which will depend on the position of the fiber from bending plane and also hardening constant. Considering the process and material parameters of the case study, the error in calculated axial stress at the outermost fiber is 10% and the error at the innermost fiber is 5%.

Fig. 7
figure 7

Effect of the assumptions for hardening behaviour

Full size image

Since the strain increments are proportional and that the strain paths are linear, the ratio of the principal strains during the loading process remains constant. By neglecting the work hardening behaviour, the solution presented in Section 3.3 can be simplified even more as is described in the following. When the loading process is started, the stresses will increase gradually from zero to the values that satisfy the initial yield criterion. It is expected that these values remain constant during plastic deformation when neglecting the hardening behaviour because of the normality rule, as shown in Fig. 8 for a plane stress case. In other words, by assuming proportional loading, linear strain paths, and elastic-ideally plastic material behaviour, it is sufficient to solely consider elastic loading and the yield criterion, which reduces the calculation effort to the equations presented Section 3.2.

Fig. 8
figure 8

Von Mises yield criteria in plane stress state

Full size image

Figure 9 compares the results of the elastic calculation using Eq. (17) with the one from numerical solution of the elastic-plastic calculation using Eq. (31), considering elastic-ideally plastic material behaviour. The presented stress distribution is virtually identical. It can be seen that when the stresses satisfy the yield criterion, then by continuing straining the material in the direction of the initial load path, the magnitudes of the stresses do not change after reaching the yield locus. Stresses at the initial yield point can be considered as final stresses and can directly be used to calculate the bending moment.

Fig. 9
figure 9

Effect of the assumption for proportional loading until yield locus

Full size image

Bending moment

The resulting bending moment M can be obtained by integrating the axial stress over the cross section of the tube:

$$ M=\underset{dA}{\int }{\sigma}_{\mathrm{zz}}(y)\cdot y\mathrm{d}A. $$
(32)

In Eq. (32), σzz not only depends on the distance of each segment from the neutral plane of the tube, but also to the value of the γ and η. The values of these two parameters are different for each segment, because of differences in the amount of εzz. In order to obtain a closed-form analytical model, these two strain ratios can be considered as constant values and equal to the values at \( y=\pm \frac{d_0}{4} \). By using these constant strain ratios, the distribution of axial stress will be linear over the cross-section and the bending moment can be written as follows:

$$ M=\frac{\pi \sqrt{2}}{4}\frac{t_1{\left({d}_1-{t}_1\right)}^3{\overline{\sigma}}_{\mathrm{y}}}{d_1}\left[\frac{1}{\sqrt{{\left(1+\gamma \right)}^2+{\left(\eta -\gamma \right)}^2+{\left(\eta +1\right)}^2}}-\frac{1}{\sqrt{{\left(1-\gamma \right)}^2+{\left(\eta -\gamma \right)}^2+{\left(\eta -1\right)}^2}}\right]. $$
(33)

Figure 10 compares the normalized bending moment based on the stress calculation from Eq. (31), which includes the hardening behaviour, with the normalized bending moment from Eq. (33), which include all the previously stated simplifications, for different values of diameter and thickness reduction as well as different bending radii. Eq. (33) is in a good agreement with the bending moment from Eq. (31).

Fig. 10
figure 10

Dependency of bending moment on diameter reduction (a), thickness reduction (b), and on the bending radius (c)

Full size image

Experimental validation

For the validation of the analytical model, experiments were carried out with the ITF machine IRU2590 (transfluid Maschinenbau GmbH) using a cold drawn steel tube (E235 + C). The standard tensile test was used for material characterisation according to DIN EN ISO 6892–1 (DIN (2009)). The results are shown in Fig. 11. This material shows a low uniform elongation before necking and low hardening.

Fig. 11
figure 11

Experimental and idealized true stress-true strain curve for E235 + C

Full size image

A comparison between experimental and analytical results for different thickness reductions and bending radii is given in Fig. 12. It can be seen that the experimental ITF results show a bending moment reduction up to 97%. The analytical model predicts a bending moment reduction up to 91%, whereby the calculated bending moment is lower at increased values of thickness reduction. This is in-line with the experimental results, which also show that the bending moment required to produce a specified radius is reduced when increasing the amount of thickness reduction. However, the absolute value of the predicted bending moment is still four to six times higher than the experimental values. The deviation between the analytical bending moment and the experimental values could be explained by the assumption of proportional loading and replacing of the spinning rolls by a fixed die in the analytical model.

Fig. 12
figure 12

Comparison of the analytical bending moment with experimental

Full size image

The bending moment from the analytical model can be used to calculate the unloaded bending radius after springback.

$$ \frac{1}{R_{\mathrm{U}}}=\frac{1}{R_{\mathrm{L}}}-\frac{M}{E\cdot I} $$
(34)

Here, RU is the unloaded bending radius, RL is the loaded bending radius, and I is the second moment of inertia of the tube cross-section. The springback ratio can be defined Eq. (35).

$$ S=\frac{R_{\mathrm{U}}-{R}_{\mathrm{L}}}{R_{\mathrm{L}}}\cdot 100\% $$
(35)

A comparison between the calculated springback ratio after unloading and experimental values is done in Fig. 13. It can be seen that, although deviations up to 15% exist in the calculation of the bending moment reduction, the deviation of the springback ratio is as low as 5%.

Fig. 13
figure 13

Comparison of the analytical springback ratio with experimental

Full size image

Conclusion

An analytical solution for the required bending moment during the combined loading in incremental tube forming (ITF) process is presented based on proportional loading and linear strain paths. Isotropic hardening and perfect plasticity are considered to describe the plastic material behaviour. It is observed that the calculated axial stresses for elastic-ideally plastic material behaviour are in a good agreement with the results of isotropic hardening behaviour. Based on these findings, a simplified analytical model is proposed that just uses the elastic loading step to calculate the stresses in combined axial, radial and circumferential loading. This model considers both thickness and diameter reduction to predict the bending moment and produces results in accordance with the more complex elastic-plastic analytical solution, developed in section 3.3, which can only be solved numerically.

The simplified analytical model is validated by experiments. It is shown that the analytical model for ITF process can predict the bending moment reduction up to 77–90% in comparison to conventional bending, where the experimental results show a reduction of 94–98%. However, the absolute value of the predicted bending moment is still three to four times higher than experimental values. Despite the deviation in the absolute values of bending moments, the amount of springback can be calculated with high accuracy (deviations of 5%), since the bending moments are small in ITF process. As an outlook, it is necessary to investigate the effects of non-proportional loading in future studies. As already mentioned, the tube is plastified first by spinning. Hence, the bending forces do not play any role in bringing the material from solid state to plastified state. It is also necessary to consider the deformation mode with spinning rolls in the further studies. Considering those two issues, initial assumptions are required to be modified and the deviations can be reduced.