Simulating squeeze flows in multiaxial laminates: towards fully 3D mixed formulations

Abstract

Thermoplastic composites are widely considered in structural parts. In this paper attention is paid to squeeze flow of continuous fiber laminates. In the case of unidirectional prepregs, the ply constitutive equation is modeled as a transversally isotropic fluid, that must satisfy both the fiber inextensibility as well as the fluid incompressibility. When laminate is squeezed the flow kinematics exhibits a complex dependency along the laminate thickness requiring a detailed velocity description through the thickness. In a former work the solution making use of an in-plane-out-of-plane separated representation within the PGD – Poper Generalized Decomposition – framework was successfully accomplished when both kinematic constraints (inextensibility and incompressibility) were introduced using a penalty formulation for circumventing the LBB constraints. However, such a formulation makes difficult the calculation on fiber tractions and compression forces, the last required in rheological characterizations. In this paper the former penalty formulation is substituted by a mixed formulation that makes use of two Lagrange multipliers, while addressing the LBB stability conditions within the separated representation framework, questions never until now addressed.

Introduction

Thermoplastic composites are preferred structural materials due to their excellent damage tolerance properties, shorter manufacturing cycles and ease of weldability. One of the precursor material to fabricate thermoplastic composite parts is an unidirectional (UD) prepreg which consists of aligned continuous fibers pre-impregnated with thermoplastic resin. In their melt state, UD prepreg can be viewed as inextensible fibers surrounded by an incompressible viscous matrix, and hence can be modeled as a transversally isotropic fluid [17]. These UD laminates are usually stacked in desired orientations to create a composite laminate.

Applied pressures during processing induce laminate deformation consisting of either squeeze flow of the matrix and fiber together or flow of the melt polymer through the fiber network. The squeeze flow behaviour of both unidirectional and multiaxial laminates has been studied in [4, 5, 12–16]. Due to the high viscosity of thermoplastic matrix and high fiber content of UD prepregs, the dominant material deformation occurs due to the squeeze flow. The squeeze flow behaviour of both unidirectional and multiaxial laminates has been studied in our former work [11], where a penalty formulation of the Ericksen fluid flow using an appropriate in-plane-out-of-plane separated representation.

Such separated representation was introduced and successfully applied for addressing problems defined in degenerated domains in which at least one of its characteristic dimensions is much smaller than the others. This is the case of laminates in which rich behaviors can occur in the thickness direction, needing for a fully 3D discretization. In that circumstances standard mesh-based discretization fail to address a rich enough out-of-plane representation. The use of an in-plane-out-of-plane separated representation makes possible to separate during the problem resolution the in-plane and out-of-plane problems allowing a extremely rich representation of 3D behaviors while keeping the computational complexity 2D (the one associated to the in-plane problem being the out-of-plane problem one-dimensional). This separated representation was considered in our former works [3, 6–8, 10].

In what follows we first address the penalty and mixed formulations of the Stokes flow in a narrow gap, that can be easily generalized to stratified flows. Then the flow of multi-axial laminates making use of the Ericksen fluid flow model at the ply level is considered. In this last case the penalty formulation related to both the fiber inextensibility and the flow incompressibility is substituted in favor of a mixed formulation making use of two Lagrange multipliers, the first related to the inextensibility constraint and the second one to the flow incompressibility. Such a richer description is needed to evaluate the fiber tension, crucial to predict defects related to its compression. On the other hand the rheological characterization of multiaxial laminates is performed by calculating the compression force to be applied for obtaining a given squeeze rate. For that purpose, it is important calculating the stress tensor in the fluid, and when using a penalty formulation the calculation of the pressure field remains a tricky issue. These facts justify the use of a mixed formulation instead of the penalized one previously considered in our former works, formulation that was retained in [11] for circumventing the issues related to the LBB stability condition.

3D modeling of stokes flow in narrow gaps

In-plane-out-of-plane separated representation

The in-plane-out-of-plane separated representation allows the solution of full 3D models defined in plate geometries with a computational complexity characteristic of 2D simulations. This separated representation allows independent representations of the in-plane and the thickness fields dependencies. The main idea lies in the separated representation of the velocity field by using functions depending on the in-plane coordinates x=(x,y), $\mathbf {P}_{i}^{j}(\mathbf {x})$, and others depending on the thickness direction z, $\mathbf {T}_{i}^{j}(z)$, according to:

$$\begin{array}{@{}rcl@{}} \left(\begin{array}{c}\mathbf{v}(\mathbf{x},z) \\p (\mathbf{x},z) \end{array}\right) &=&\left(\begin{array}{c} u (\mathbf{x},z) \\v (\mathbf{x},z) \\w (\mathbf{x},z)\\p (\mathbf{x},z) \end{array}\right) \approx \left(\begin{array}{c} \sum\limits^{N}_{i=1}{P_{i}^{1}}(\mathbf{x})\cdot {T_{i}^{1}}(z)\\ \sum\limits^{N}_{i=1}{P_{i}^{2}}(\mathbf{x})\cdot {T_{i}^{2}}(z)\\ \sum\limits^{N}_{i=1}{P_{i}^{3}}(\mathbf{x})\cdot {T_{i}^{3}}(z)\\ \sum\limits^{N}_{i=1}{P_{i}^{p}}(\mathbf{x})\cdot {T_{i}^{p}}(z) \end{array}\right) \\&=& \sum\limits_{i=1}^{N} \mathbf{P}_{i}(\mathbf{x}) \circ \mathbf{T}_{i}(z), \end{array} $$

(1)

where “ ∘” denotes the entry-wise or Hadamard’s product. When introduced into the flow problem weak form it allows the calculation of functions $P_{i}^{j}(\mathbf {x})$by solving the corresponding 2D equations and functions $T_{i}^{j}(z)$by solving the associated 1D equations, as described later.

The extraction of the velocity field from Eq. 1 writes

$$ \mathbf{v} (\mathbf{x},z) \approx \sum\limits_{i=1}^{N} \mathbf{P}^{v }_{i}(\mathbf{x}) \circ \mathbf{T}^{v }_{i}(z) = \left(\begin{array}{c} \sum\limits^{N}_{i=1}{P_{i}^{1}}(\mathbf{x})\cdot {T_{i}^{1}}(z)\\ \sum\limits^{N}_{i=1}{P_{i}^{2}}(\mathbf{x})\cdot {T_{i}^{2}}(z)\\ \sum\limits^{N}_{i=1}{P_{i}^{3}}(\mathbf{x})\cdot {T_{i}^{3}}(z) \end{array}\right), $$

(2)

which leads to a separated representation of the strain rate.

Remark 1

If a and b are vectors of the same dimension, vector c, defined from c = a∘b, has as components c _i = a _i ⋅b _i . If a and b are second order tensors with the same size, tensor c, defined from c = a∘b, has components c _{i j} = a _{i j} ⋅b _{i j} (no sum with respect to the repeated indexes). With a and b second order tensors of the same size it results a:b = c, with the scalar c given by c = a _{i j} ⋅b _{i j} considering sum with respect to the repeated indexes (Einstein’s summation convention).

Using this notation in Eq. 1, the velocity gradient ∇v(x,z) can be written as:

$$\begin{array}{@{}rcl@{}} \nabla \mathbf{v} &=& \left(\begin{array}{ccc} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} & \frac{\partial u}{\partial z} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{array} \right) \approx \sum \limits_{i=1}^{N} \left(\begin{array}{ccc} \frac{\partial {P_{i}^{1}}}{\partial x} & \frac{\partial {P_{i}^{1}}}{\partial y} & {P_{i}^{1}} \\ \frac{\partial {P_{i}^{2}}}{\partial x} & \frac{\partial {P_{i}^{2}}}{\partial y} & {P_{i}^{2}} \\ \frac{\partial {P_{i}^{3}}}{\partial x} & \frac{\partial {P_{i}^{3}}}{\partial y} & {P_{i}^{3}} \end{array} \right) \\ &&\circ \left(\begin{array}{ccc} {T_{i}^{1}} & {T_{i}^{1}} & \frac{\partial {T_{i}^{1}}}{\partial z} \\ {T_{i}^{2}} & {T_{i}^{2}} & \frac{\partial {T_{i}^{2}}}{\partial z} \\ {T_{i}^{3}} & {T_{i}^{3}} & \frac{\partial {T_{i}^{3}}}{\partial z} \end{array} \right) = \sum\limits_{i=1}^{N} \mathbb{P}_{i}(\mathbf{x}) \circ \mathbb{T}_{i}(z). \end{array} $$

(3)

The solution of full 3D Stokes problem within the in-plane-out-of-plane separated representation is revisited in the next sections.

Flow model

The Stokes flow model is defined in ${\Xi } = {\Omega } \times \mathcal {I}$, ${\Omega } \subset \mathbb {R}^{2}$ and $\mathcal {I} \subset \mathbb {R}$, and for an incompressible fluid, in absence of inertia and mass terms reduces to:

$$ \left\{ \begin{array}{l} \nabla \cdot \boldsymbol{\sigma} = \mathbf{0} \\ \boldsymbol{\sigma} = -p \mathbf{I} + 2 \eta \mathbf{D} \\ \nabla \cdot \mathbf{v} = 0 \end{array} \right. , $$

(4)

where σ is the Cauchy’s stress tensor, I the unit tensor, η the fluid viscosity, p the pressure (Lagrange multiplier associated with the incompressibility constraint) and the rate of strain tensor D defined as

$$ \mathbf{D} = \frac{\nabla \mathbf{v} + (\nabla \mathbf{v})^{T}}{2}. $$

(5)

The pressure in-plane-out-of-plane separated representation writes

$$ \ p=\sum\limits^{N}_{i=1}{P_{i}^{p}}(\mathbf{x})\cdot {T_{i}^{p}}(z) . $$

(6)

In what follows for the sake of notational simplicity the dependency of in-plane functions on x an the one of out-of-plane functions on z will be omitted.

The weak form of the coupled velocity-pressure Stokes problem, for both a test velocity v ^∗ and a test pressure P ^∗, the first vanishing on the boundary in which the velocity is prescribed, and assuming null tractions in the remaining part of the domain boundary, can be written as

$$ \int \limits_{\Omega \times \mathcal{I}} \left(- p \text{Tr}(\mathbf{D}^{\ast}) + 2\eta \mathbf{D}^{\ast} : \mathbf{D} \right) \ d \mathbf{x} \ dz= 0, $$

(7)

$$ \int \limits_{\Omega \times \mathcal{I}} - p^{\ast} \text{Tr}(\mathbf{D}) \ d \mathbf{x} \ dz= 0, $$

(8)

where Eqs. 7 and 8 make reference to the linear momentum and mass balances respectively.

Following the developments reported in the [Appendix], previous balances can be rewritten as

$$ 2 \eta \mathbf{D}^{\ast} : \mathbf{D} \!\approx\! \frac{\eta}{2} \sum\limits_{j=1}^{N} \sum \limits_{k=1}^{4} \left(\mathbb{A}_{jk}^{\ast} (\mathbf{x}) \!:\! \mathbb{B}_{jk} (z) \,+\, \mathbb{A}_{jk}(\mathbf{x}) : \mathbb{B}_{jk}^{\ast}(z) \right) , $$

(9)

$$ p \text{Tr}(\mathbf{D}^{\ast}) \approx \sum\limits_{i=1}^{N} {P_{i}^{p}}\cdot {T_{i}^{p}} \left(\frac{\partial P^{1}}{\partial x}T^{1} + \frac{\partial P^{2}}{\partial y}T^{2} +P^{3}\frac{\partial T^{3}}{\partial z}\right)^{*} , $$

(10)

and

$$ p^{*} \text{Tr}(\mathbf{D} )\approx \sum\limits_{i=1}^{N} (P^{p}\cdot T^{p})^{*} \left(\frac{\partial {P_{i}^{1}}}{\partial x}{T_{i}^{1}} \,+\, \frac{\partial {P_{i}^{2}}}{\partial y}{T_{i}^{2}} \,+\,{P_{i}^{3}}\frac{\partial {T_{i}^{3}}}{\partial z}\right) . $$

(11)

Separated representation constructor

The construction of the solution separated representation is performed incrementally, a term of the sum at each iteration. Thus, supposing that at iteration n−1, n≥1 and n≤N, the first n−1 terms of both velocity and pressure separated representations were already computed

$$ \mathbf{v}^{n-1} (\mathbf{x},z) = \sum\limits_{i=1}^{n-1} \mathbf{P_{i}^{v}}(\mathbf{x}) \circ \mathbf{T_{i}^{v}}(z), $$

(12)

$$ \ p^{n-1}(\mathbf{x},z) =\sum\limits^{n-1}_{i=1}{P_{i}^{p}}(\mathbf{x})\cdot {T_{i}^{p}}(z) , $$

(13)

the terms involved in the weak form Eqs. 7 and 8 are:

$$ \mathbf{D}^{\ast} : \mathbf{D}^{n-1} \,=\, \frac{1}{4} \sum\limits_{j=1}^{n-1} \sum \limits_{k=1}^{4} \left(\mathbb{A}_{jk}^{\ast} (\mathbf{x}) \!:\! \mathbb{B}_{jk} (z) \,+\, \mathbb{A}_{jk}(\mathbf{x}) \!:\! \mathbb{B}_{jk}^{\ast}(z) \right) , $$

(14)

$$ p^{n-1} \text{Tr}(\mathbf{D}^{\ast}) \!\approx\! \sum\limits_{i=1}^{n-1} {P_{i}^{p}}\cdot {T_{i}^{p}} \left(\frac{\partial P^{1}}{\partial x}T^{1} \!\,+\, \frac{\partial P^{2}}{\partial y}T^{2} \,+\,P^{3}\frac{\partial T^{3}}{\partial z}\right)^{*} , $$

(15)

and

$$\begin{array}{@{}rcl@{}} p^{*} \text{Tr}(\mathbf{D}^{n-1})&\approx& \sum\limits_{i=1}^{n-1} (P^{p}\cdot T^{p})^{*}\left(\frac{\partial {P_{i}^{1}}}{\partial x}{T_{i}^{1}} + \frac{\partial {P_{i}^{2}}}{\partial y}{T_{i}^{2}}\right.\\ &&\hspace*{6.5pc}\left.+{P_{i}^{3}}\frac{\partial {T_{i}^{3}}}{\partial z}\right), \end{array} $$

(16)

respectively. The indexes affecting test functions will be detailed below.

When looking for the improved velocity field v ⁿ(x,z) at iteration n

$$ \mathbf{v}^{n} (\mathbf{x},z) = \sum\limits_{i=1}^{n} \mathbf{P^{v}_{i}}(\mathbf{x}) \circ \mathbf{T^{v}_{i}}(z) = \mathbf{v}^{n-1}(\mathbf{x},z)+ \mathbf{P^{v}_{n}}(\mathbf{x}) \circ \mathbf{T^{v}_{n}}(z), $$

(17)

we consider the test function v ^∗(x,z)

$$ \mathbf{v}^{\ast} = \mathbf{P}^{v *} \circ \mathbf{T^{v}_{n}} + \mathbf{P}^{v}_{n} \circ \mathbf{T}^{v*} , $$

(18)

that implies

$$ \nabla \mathbf{v}^{\ast} = \mathbb{P}^{\ast} \circ \mathbb{T}_{n} + \mathbb{P}_{n} \circ \mathbb{T}^{\ast} . $$

(19)

When looking for the improved pressure field p ⁿ(x,z) at iteration n

$$ p^{n} (\mathbf{x},z) = \sum\limits_{i=1}^{n} {P_{i}^{p}}(\mathbf{x}) \cdot {T_{i}^{p}}(z) = p^{n-1}(\mathbf{x},z)+ {P_{n}^{p}}(\mathbf{x})\cdot {T_{n}^{p}}(z), $$

(20)

we consider the test function

$$ p^{\ast} = P^{p\ast} \cdot {T^{p}_{n}} + {P^{p}_{n}} \cdot T^{p\ast}. $$

(21)

In that case it results

$$\begin{array}{@{}rcl@{}} 4 \mathbf{D}^{\ast} : \mathbf{D}^{n} \!&=&\! \sum\limits_{j=1}^{n-1} \sum\limits_{k=1}^{4} \left(\mathbb{A}_{jk}^{\ast} (\mathbf{x}) \!:\! \mathbb{B}_{jk} (z) \,+\, \mathbb{A}_{jk}(\mathbf{x}) \!:\! \mathbb{B}_{jk}^{\ast}(z) \right) \\&& \,+\, \sum \limits_{k=1}^{4} \left(\mathbb{A}_{nk}^{\ast} (\mathbf{x}) \!:\! \mathbb{B}_{nk} (z) \,+\, \mathbb{A}_{nk}(\mathbf{x}) \!:\! \mathbb{B}_{nk}^{\ast}(z) \right), \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} p^{n} \text{Tr}(\mathbf{D}^{\ast}) \!&\approx&\! \sum\limits_{i=1}^{n-1} {P_{i}^{p}}\cdot {T_{i}^{p}} \left(\frac{\partial P^{1}}{\partial x}T^{1} \,+\, \frac{\partial P^{2}}{\partial y}T^{2} \,+\,P^{3}\frac{\partial T^{3}}{\partial z}\right)^{*} \\&&+ {P_{n}^{p}}\cdot {T_{n}^{p}}\left(\frac{\partial P^{1}}{\partial x}T^{1} \!+ \frac{\partial P^{2}}{\partial y}T^{2} \!+ P^{3}\frac{\partial T^{3}}{\partial z}\right)^{*},\\ \end{array} $$

(23)

and

$$\begin{array}{@{}rcl@{}} p^{*} \text{Tr}(\mathbf{D}^{n})\!&\approx&\! {\sum}_{i=1}^{n-1} (P^{p}\!\cdot\! T^{p})^{*} \left(\frac{\partial {P_{i}^{1}}}{\partial x}{T_{i}^{1}} \,+\, \frac{\partial {P_{i}^{2}}}{\partial y}{T_{i}^{2}} \,+\,{P_{i}^{3}}\frac{\partial {T_{i}^{3}}}{\partial z}\right)\\&&+ (P^{p}\!\cdot\! T^{p})^{*} \left(\frac{\partial {P_{n}^{1}}}{\partial x}{T_{n}^{1}} \,+\, \frac{\partial {P_{n}^{2}}}{\partial y}{T_{n}^{2}} \,+\,{P_{n}^{3}}\frac{\partial {T_{n}^{3}}}{\partial z}\right),\\ \end{array} $$

(24)

where

$$\begin{array}{@{}rcl@{}} &&\left(\frac{\partial P^{1}}{\partial x}T^{1} + \frac{\partial P^{2}}{\partial y}T^{2} +P^{3}\frac{\partial T^{3}}{\partial z}\right)^{*}\\&=& \left(\frac{\partial P^{1\ast}}{\partial x}{T^{1}_{n}} + \frac{\partial P^{2\ast}}{\partial y}{T^{2}_{n}} +P^{3 \ast}\frac{\partial {T^{3}_{n}}}{\partial z}\right)\\ &&+ \left(\frac{\partial {P^{1}_{n}}}{\partial x}T^{1\ast} + \frac{\partial {P^{2}_{n}}}{\partial y}T^{2 \ast} +{P^{3}_{n}}\frac{\partial T^{3 \ast}}{\partial z}\right), \end{array} $$

(25)

and

$$ (P^{p}\cdot T^{p})^{*} = P^{p\ast}\cdot {T^{p}_{n}} + {P^{p}_{n}}\cdot T^{p \ast}. $$

(26)

Thus the problem weak form Eqs. 7 and 8 writes at iteration n:

$$\begin{array}{@{}rcl@{}} \int \limits_{\Omega \times \mathcal{I}} &-&{P_{n}^{p}}\cdot {T_{n}^{p}} \left(\frac{\partial P^{1}}{\partial x}T^{1} + \frac{\partial P^{2}}{\partial y}T^{2} +P^{3}\frac{\partial T^{3}}{\partial z}\right)^{*} \ d \mathbf{x} \ dz \\&+& \int \limits_{\Omega \times \mathcal{I}} \frac{ \eta}{2} \left(\sum \limits_{k=1}^{4} \mathbb{A}_{nk}^{\ast} (\mathbf{x}) : \mathbb{B}_{nk} (z)\right.\\ &&\hspace*{3.5pc}\left.\vphantom{\sum \limits_{k=1}^{4}}+ \mathbb{A}_{nk}(\mathbf{x}) : \mathbb{B}_{nk}^{\ast}(z) \right) \ d\mathbf{x} \ dz \\&&= \int \limits_{\Omega \times \mathcal{I}} {\sum}_{j=1}^{n-1} {P_{i}^{4}}\cdot {T_{i}^{4}} \left(\frac{\partial P^{1}}{\partial x}T^{1} + \frac{\partial P^{2}}{\partial y}T^{2}\right.\\ &&\hspace*{7.5pc}\left.+P^{3}\frac{\partial T^{3}}{\partial z}\right)^{*} \ d \mathbf{x} \ dz \\&-& \int \limits_{\Omega \times \mathcal{I}} \frac{\eta}{2} \left({\sum}_{j=1}^{n-1} \sum \limits_{k=1}^{4} \left(\mathbb{A}_{jk}^{\ast} (\mathbf{x}) : \mathbb{B}_{jk} (z)\right.\right.\\ &&\hspace*{3.5pc}\left.\vphantom{{\sum}_{j=1}^{n-1}}\left.+ \mathbb{A}_{jk}(\mathbf{x}) : \mathbb{B}_{jk}^{\ast}(z) \right) \right) \ d\mathbf{x} \ dz , \end{array} $$

(27)

and

$$\begin{array}{@{}rcl@{}} \int \limits_{\Omega \times \mathcal{I}} \!&-&\! (P^{p}\cdot T^{p})^{*} \left(\frac{\partial {P_{n}^{1}}}{\partial x}{T_{n}^{1}} + \frac{\partial {P_{n}^{2}}}{\partial y}{T_{n}^{2}} +{P_{n}^{3}}\frac{\partial {T_{n}^{3}}}{\partial z}\right) \ d \mathbf{x} \ dz \\&=& \int \limits_{\Omega \times \mathcal{I}} {\sum}_{i=1}^{n-1} (P^{p}\cdot T^{p})^{*} \left(\frac{\partial {P_{i}^{1}}}{\partial x}{T_{i}^{1}} + \frac{\partial {P_{i}^{2}}}{\partial y}{T_{i}^{2}}\right.\\ &&\hspace*{7.5pc}\left. +{P_{i}^{3}}\frac{\partial {T_{i}^{3}}}{\partial z}\right) \ d \mathbf{x} \ dz. \end{array} $$

(28)

The extended weak forms Eqs. 27 and 28 become nonlinear because it involves the product of unknown functions P _n and T _n . Thus a linearization strategy becomes necessary, the simplest one being an alternating fixed point algorithm that proceeds as follows:

• 1. Assuming functions P _n (x) are known (arbitrarily chosen at the first iteration of the nonlinear iteration) matrices $\mathbb {A}_{jk}^{\ast }$ and $\mathbb {F}_{j}^{\ast }$, as well as functions $\left (\frac {\partial P^{1\ast }}{\partial x}{T^{1}_{n}} + \frac {\partial P^{2\ast }}{\partial y}{T^{2}_{n}} +P^{3 \ast }\frac {\partial {T^{3}_{n}}}{\partial z}\right )$ and P ^p∗ vanish. Being all functions depending on x known, integrals in Ω in Eqs. 27 and 28 can be calculated. Thus, it finally results in a one dimensional linear problem that involves the four scalar functions involved in T _n (z), ${T^{1}_{n}}(z)$, ${T_{n}^{2}}(z)$, ${T_{n}^{3}}(z)$ and ${T_{n}^{p}}(z)$.

• 2. Then, with the just computed function T _n (z), and with $\mathbb {B}_{jk}^{\ast }$, $\mathbb {G}_{j}^{\ast }$, T ^p∗ and $\left (\frac {\partial {P^{1}_{n}}}{\partial x}T^{1\ast } + \frac {\partial {P^{2}_{n}}}{\partial y}T^{2 \ast } +{P^{3}_{n}}\frac {\partial T^{3 \ast }}{\partial z}\right )$ vanishing, one can proceed to integrate Eqs. 27 and 28 in $\mathcal {I}$. It finally results in a two-dimensional linear problem for the unknown function P _n (x) that involves the four scalar functions ${P_{n}^{1}}(\mathbf {x})$, ${P_{n}^{2}}(\mathbf {x})$, ${P_{n}^{3}}(\mathbf {x})$ and ${P_{n}^{p}}(\mathbf {x})$.

• 3. The convergence is checked by comparing functions P _n and T _n between two consecutive iterations of the nonlinear solver. If both functions are small enough they are used to update both velocity and pressure fields

  $$ \left(\begin{array}{c}\mathbf{v}(\mathbf{x},z) \\p (\mathbf{x},z) \end{array}\right)= \sum \limits_{i=1}^{n} \mathbf{P}_{i}(\mathbf{x}) \circ \mathbf{T}_{i}(z). $$

  (29)

  If the convergence is not reached, one returns to step 1 with the calculated functions P _n to re-compute T _n

Because of the one-dimensional large scale variation present in the laminate thickness direction one can employ extremely detailed descriptions along the thickness direction without sacrificing the computational efficiency of the 3D solution procedure.

Flow in a laminate

Consider a laminate composed of $\mathcal {P}$ layers in which each layer involves a linear and isotropic viscous fluid of viscosity η _i , thus the extended Stokes flow problem in its weak form involves the dependence of the viscosity along the thickness direction.

If H is the total laminate thickness, and assuming for the sake of simplicity and without loss of generality that all the plies have the same thickness h, it results $h=\frac {H}{\mathcal {P}}$. Now, from the characteristic function of each ply χ _i (z), $i=1, {\cdots } , \mathcal {P}$:

$$ \chi_{i}(z) = \left\{ \begin{array}{ll} 1 & \text{if} \ (i-1)h \leq z < ih \\ 0 & \text{elsewehere} \end{array} \right. , $$

(30)

the viscosity reads

$$ \eta(\mathbf{x},z) = \sum \limits_{i=1}^{\mathcal{P}} \eta_{i} \cdot \chi_{i}(z) , $$

(31)

where it is assumed, again without loss of generality, that the viscosity does not evolve in the plane, i.e. η _i (x) = η _i .

This decomposition is fully compatible with the velocity-pressure separated representation (1) and with the in-plane-out-of-plane decomposition considered for solving Eqs. 27 and 28.

Ericksen fluid flow model in a laminate

The case of a prepreg ply reinforced by continuous fibres oriented along direction P ^T=(p _x ,p _y ,0), ∥P∥=1, is analyzed here. It is assumed that the thermoplastic resin exhibits Newtonian behaviour. Thus the velocity v(x,z) of the equivalent anisotropic fluid must satisfy the incompressibility and inextensibility constraints

$$ \nabla \cdot \mathbf{v} = 0, $$

(32)

and

$$ \mathbf{P}^{T} \cdot \nabla \mathbf{v} \cdot \mathbf{P} = 0, $$

(33)

respectively. Expression (33) can be rewritten using tensor notation as ∇v:a=0, where the second order orientation tensor a is defined from a = P⋅P ^T = P⊗P.

The orientation tensor a has only planar components (the out-of-plane fiber orientation can be neglected in the case of laminates), it is symmetric and of unit trace, i.e.

$$ \mathbf{a} = \left(\begin{array}{lll} a_{xx} & a_{xy} & 0 \\ a_{yx} & a_{yy} & 0 \\ 0 & 0 & 0 \end{array} \right) = \left(\begin{array}{ll} \mathcal{A} & \mathbf{0} \\ \mathbf{0}^{T} & 0 \ \end{array} \right) , $$

(34)

where $\mathcal {A}$ represents the plane component of the orientation tensor a, a _{x y} = a _{y x} (i.e. $\mathcal {A} = \mathcal {A}^{T}$) and a _{y y} =1−a _{x x} .

The simplest expression of the Ericksen’s constitutive equation [9] can be written in the compact form as follows

$$ \boldsymbol{\sigma} = -p \mathbf{I} + \tau \mathbf{a} + 2 \eta_{T} \mathbf{D} + 2 (\eta_{L}-\eta_{T}) (\mathbf{D} \cdot \mathbf{a} + \mathbf{a} \cdot \mathbf{D}) , $$

(35)

that is then introduced into the linear momentum balance

$$ \nabla \cdot \boldsymbol{\sigma} = \mathbf{0} . $$

(36)

In Eq. 35 p and τ represents respectively the Lagrange multipliers related to the incompressibility and inextensibility constraints, and η _L and η _T the longitudinal and transverse shear viscosities respectively.

By separating both the pressure and the fiber tension fields using an in-plane-out-of-plane-separated representation

$$ \ p(\mathbf{x},z) =\sum\limits^{N}_{i=1}{P_{i}^{p}}(\mathbf{x})\cdot {T_{i}^{p}}(z), $$

(37)

and

$$ \ \tau(\mathbf{x},z) =\sum\limits^{N}_{i=1}P_{i}^{\tau}(\mathbf{x})\cdot T_{i}^{\tau}(z), $$

(38)

it allows accurate calculations of both the fiber tension and the pressure field. This information can be used to predict either fibers buckling or forces acting on the squeezed boundary.

The weak form for a test velocity v ^∗(x,z) vanishing at the boundary in which velocity is prescribed, a test pressure p ^∗(x,z) and a test fiber tension τ ^∗(x,z), assuming null tractions in the remaining part of the domain boundary can be expressed as

$$ \hspace*{3pt}\int \limits_{\Omega \times \mathcal{I}} \mathbf{D}^{\ast} : \boldsymbol{\sigma} \ d\mathbf{x} \ dz = 0, $$

(39)

$$ \hspace*{3pt}\int \limits_{\Omega \times \mathcal{I}} p^{\ast} \mathbf{D} : \mathbf{I} \ d\mathbf{x} \ dz = 0, $$

(40)

and

$$ \hspace*{3pt}\int \limits_{\Omega \times \mathcal{I}} \tau^{\ast} \mathbf{D} : \mathbf{a} \ d\mathbf{x} \ dz = 0. $$

(41)

By introducing the Ericksen constitutive equation (35), Eq. 39 can be written as

$$\begin{array}{@{}rcl@{}} \int \limits_{\Omega \times \mathcal{I}} \mathbf{D}^{\ast} : \boldsymbol{\sigma} \ d\mathbf{x} \ dz &=& \int \limits_{\Omega \times \mathcal{I}} \mathbf{D}^{\ast} : \left( -p \mathbf{I} +\tau \mathbf{a} +\eta_{T} \mathbf{D}\right.\\ &&\left.+ \tilde{\eta} \left( \mathbf{D} \cdot \mathbf{a} + \mathbf{a} \cdot \mathbf{D} \right) \right)d \mathbf{x} \ dz= 0 , \end{array} $$

(42)

with $\tilde {\eta }=\eta _{L}-\eta _{T}$.

At this stage the in-plane-out-of-plane separated representation constructor of v(x,z), p(x,z) and τ(x,z) proceeds as described in the previous section.

Remark 2

If a = 0 this formulation reduced to one related to the Stokes flow problem.

Remark 3

Laminates can be addressed by associating with each ply the planar fiber orientation P _i (x), with its out-of-plane component vanishing, from which the associated orientation tensor a _i (x) results in a _i (x) = P _i (x)⊗P _i (x). Using again the characteristic function of the i-ply, χ _i (z), $i=1, {\cdots } , \mathcal {P}$, the orientation tensor in the laminate, a(x,z), can be expressed as

$$ \mathbf{a}(\mathbf{x},z)= \sum \limits_{i=1}^{\mathcal{P}} \mathbf{a}_{i}(\mathbf{x}) \chi_{i}(z). $$

(43)

Remark 4

If the fiber orientation is constant in each plane, then the laminate orientation tensor can be expressed as

$$ \mathbf{a}(z)= \sum \limits_{i=1}^{\mathcal{P}} \mathbf{a}_{i} \chi_{i}(z). $$

(44)

Revisiting fully penalized formulations.

Both Stokes and Ericksen flows have been successfully implemented by means of penalized formulations involving both, the pressure, p, and the fiber tension, τ. Such a penalized formulation leads to a problem that only involves the velocity field. Therefore, the aim is to clarify how the constitutive equation is modified when introducing two penalty parameters. For that purpose we consider:

$$ \nabla \cdot \mathbf{v}+\lambda p = \mathbf{D}: \mathbf{I} +\lambda p =0, $$

(45)

and

$$ \mathbf{D}: \mathbf{a}-\epsilon \tau = 0. $$

(46)

Where the coefficients λ and 𝜖 are chosen close to zero to ensure numerically incompressibility and fiber inextensibility. Both constraints are ensured as long as both penalty coefficients are small enough. Isolating p and τ from Eqs. 45 and 46, it results

$$ p = -\frac{1}{\lambda}\mathbf{D}:\mathbf{I} , $$

(47)

and

$$ \tau = \frac{1}{\epsilon}\mathbf{D}:\mathbf{a}. $$

(48)

If both pressure and fiber tension are penalized the constitutive equation reduces to,

$$ \boldsymbol{\sigma}=\frac{1}{\lambda}(\mathbf{I}\otimes \mathbf{I}):\mathbf{D}+\frac{1}{\epsilon}(\mathbf{a}\otimes\mathbf{a}):\mathbf{D}+2\eta\mathbf{D}, $$

(49)

where a very high effective viscosity acts along the fiber direction. This formulation was intensively considered in [1, 2, 10, 11] where a variety of results were presented and discussed, proving the potentiality of the approach. However neither fiber tension nor the pressure field were calculated because the penalty formulation does not allow an accurate post-calculation from the calculated velocity field and the penalty definitions Eqs. 47 and 48.

Numerical results

The numerical results discussed hereafter consider several cases starting from Stokes problem, then a single ply occupying the whole gap, then considering laminates composed of two plies with different relative orientations.

The main aim of this section is to show that there exists an in-plane-out-of-plane separated representation when both the pressure and the fiber tension have been introduced as Lagrange multipliers. Therefore, 3D finite element solvers for Stokes and Ericksen problems have been developed in order to check the accuracy of the separated representation solutions. The 3D-FEM solution will be taken as reference for validating the one involving a separated representation 3D-SR (SR refers to the in-plane-out-of-plane separated representation) calculated within the PGD framework.

The domain occupied by the laminate has length L, width W and thickness H, i.e. ${\Xi } = {\Omega } \times \mathcal {I}$, with Ω=[0,L]×[0,W] and $\mathcal {I} = [0,H]$, with x∈Ω and $z \in \mathcal {I}$.

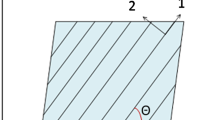
It is assumed that during compression, the upper wall moves down with a prescribed velocity V during the consolidation. Thus, mass conservation leads to significant velocity variations within Ω, e.g. the central point has a null in-plane velocity because of the symmetry condition whereas the in-plane velocity is maximal at the laminate lateral boundaries $\partial {\Omega } \times \mathcal {I}$. Moreover, when taking into account the through-thickness complex kinematics in multiaxial laminates, a sufficiently detailed solution is also required along the thickness direction to capture all its richness. Figure 1 depicts the laminate geometry as well as the squeezing conditions.

Fig. 1

Laminate geometry during compression molding of the laminate under prescribed velocity

Prescribed velocities are enforced at the top and bottom boundaries whereas null tractions apply on the lateral boundaries, i.e.:

$$ \left\{ \begin{array}{l} \mathbf{v} (x,y, z=0) = \mathbf{0} \\ \mathbf{v} (x,y,z=H) = (0,0,-V)^{T} \\ \boldsymbol{\sigma}(x=0,y,z) \cdot \mathbf{n}_{x} = \mathbf{0} \\ \boldsymbol{\sigma}(x=L,y,z) \cdot \mathbf{n}_{x} = \mathbf{0} \\ \boldsymbol{\sigma}(x,y=0,z) \cdot \mathbf{n}_{y} = \mathbf{0} \\ \boldsymbol{\sigma}(x,y=W,z) \cdot \mathbf{n}_{y} = \mathbf{0} \end{array} \right. , $$

(50)

where n _x =(1,0,0)^T and n _y =(0,1,0)^T.

Numerical results will be presented sometimes on the middle plane z = H/2, sometimes along the thickness at the intersection line between planes x = a and y = b, with a∈[0,L] and b∈[0,W].

Stokes flow

First the Stokes problem solution is addressed. Numerical issues as the ones related to the enforcement of the so-called LBB stability condition in the 3D-SR (in-plane-out-of-plane separated representation) will be deeply discussed. Viscosity is set to 1000 Pa⋅s and the compression velocity to V=1 m⋅s⁻¹. Two domains were addressed, the first perfectly cubic of length 1 m. The second flow problem was defined in the narrow gap of dimensions L×W×H=0.5×0.5×0.001 (all the lengths in meters) with a prescribed compression velocity of V=0.1 mm⋅s⁻¹. In this case the 3D flow problem solution could be approximated using the lubrication theory.

3D finite element solution

A standard stable 3D finite element discretization has been used for solving the Stokes problem in the cubic domain of unit size (L = W = H=1). The 3D-FEM solution will be taken as reference for evaluating the 3D solution making use of an in-plane-out-of-plane separated representation. A stable Q2/Q1 is considered for discretizing the 3D mixed formulation within the FEM framework.

Figure 2 depicts the three velocity components and the pressure field on the middle plane z = H/2. Because the problem symmetry the velocity components u(x,z) and v(x,z) vanish at x = L/2 and y = W/2 respectively. Moreover the component w remains, as expected, almost constant on the middle plane z = H/2. The pressure field exhibits a global maximum in the center of the middle plane of about 1669 P a.

Fig. 2

u(x,z = H/2) (top-left), v(x,z = H/2) (top-right), w(x,z = H/2) (bottom-left), and p(x,z = H/2) (bottom-right), associated with the solution of the Stokes problem using a stable 3D-FEM discretization

Figure 3 shows the different components of the velocity field as well as the pressure along the line defined as the intersection between planes x=0.625 and y=0.625. It can be noticed that boundary conditions are satisfied, with velocities u and v vanishing at z=0 and z = H, whereas velocity w vanishes at z=0 and corresponds to the compression velocity at z = H. Velocities u and v exhibit a parabolic profile along the thickness whose maximum is located at the middle plane z = H/2. Velocity w exhibit an almost cubic evolution along the thickness. The pressure field presents a minimum in the middle plane being maximum when approaching the upper and bottom walls.

Fig. 3

u(x=(0.625,0.625)^T,z) (top-left), v(x=(0.625,0.625)^T,z) (top-right), w(x=(0.625,0.625)^T,z) (bottom-left), and p(x=(0.625,0.625)^T,z) (bottom-right), associated with the solution of the Stokes problem using a stable 3D-FEM discretization

3D separated representation based solution

Now, the same problem is solved using a separated representation of both the velocity and pressure functions within the PGD framework. The in-plane functions were discretized using 2D Q2/Q1 approximations for the velocity and pressure fields respectively, whereas a 1D quadratic/linear was considered for approximating the velocity and pressure functions depending on the thickness coordinate respectively.

Figure 4 depicts the reconstructed velocity and pressure fields on the middle plane z = H/2. In the approximation of functions depending on the in-plane coordinates and those depending on the one related to the domain thickness, we considered meshes equivalent to the one considered in the 3D-FEM solution. Results are in perfect agreement to those obtained using the 3D-FEM. Despite the very coarse mesh considered the maximum gap in the pressure field was lower than 0.5 %.

Fig. 4

u(x,z = H/2) (top-left), v(x,z = H/2) (top-right), w(x,z = H/2) (bottom-left), and p(x,z = H/2) (bottom-right), associated with the solution of the Stokes problem using the in-plane-out-of plane separated representation

Figure 5 depicts the velocity and pressure profiles along the domain thickness at position x = y=0.625. Again the solution obtained within the PGD framework perfectly agrees with the reference solution obtained from the stable 3D finite element discretization previously presented.

Fig. 5

u(x=(0.625,0.625)^T,z) (top-left), v(x=(0.625,0.625)^T,z) (top-right), w(x=(0.625,0.625)^T,z) (bottom-left), and p(x=(0.625,0.625)^T,z) (bottom-right), associated with the solution of the Stokes problem using the in-plane-out-of plane separated representation

Moreover, in order to check the stability conditions (LBB) different choices were considered. First we considered Q2/Q2 approximations in the plane (that in 2D does not fulfill LBB stability conditions) whereas the one considered for the problem defined in the thickness was assured stable (quadratic/linear). It can be noticed in Fig. 6 that the resulting in-plane-out-of-plane approximation is not stable, and that the characteristic oscillations appear in the in-plane solution (in which stability fails).

Fig. 6

Velocity a pressure fields on the middle plane z=0.5 (top) and (bottom) solution along the thickness (x=(0.625,0.625)^T,z) when using the in-plane-out-of-plane separated representation with in-plane and thickness approximations Q2/Q2 and quadratic/linear respectively, for the functions involved in the velocity and pressure representation

We also check another approximation expected violating the LBB stability conditions, the one using a Q2/Q1 approximation in the plane for velocities and pressure respectively and quadratic/quadratic for functions depending on the thickness. The last is expected violating the LBB stability conditions. Figure 7 exhibits oscillations precisely in the pressure field along the thickness direction, that can be attributed to the wrong approximation choice for the functions depending of the thickness coordinate and involved in the velocity and pressure representation.

Fig. 7

Velocity a pressure fields on the middle plane z=0.5 (top) and (bottom) solution along the thickness (x=(0.625,0.625)^T,z) when using the in-plane-out-of-plane separated representation with in-plane and thickness approximations Q2/Q1 and quadratic/quadratic respectively, for the functions involved in the velocity and pressure representation

A first conclusion stressed from these numerical experiments is that when using in the separated representation approximations whose tensor product corresponds to 3D stable approximations (i.e. fulfilling the LBB condition) those separated approximations remain stable.

3D separated representation based solution in a narrow gap

The flow problem is now defined in a very narrow gap because is in these circumstances that the use of separated representations could be extremely advantageous because the use of a 3D finite element discretization could imply an extremely large number of elements in the case of degenerated 3D domains (e.g. plate-like) as discussed in [6]. As previously indicated now the domain L×W×H=0.5×0.5×0.001 (all the units in meters) being again the viscosity η=1000 Pa⋅s and the compression velocity applied at the upper wall V = 0.1 mm⋅s⁻¹.

Figures 8 and 9 depict velocities and pressure fields obtained using the in-plane-pot-of-plane separated representation in conjunction with stable approximations (Q2/Q1 in the plane and also quadratic/linear in the thickness). It is important to note that as expected from the lubrication theory pressure becomes constant all along the thickness.

Fig. 8

u(x=(0.33,0.333)^T,z) (top-left), v(x=(0.33,0.33)^T,z) (top-right), w(x=(0.33,0.33)^T,z) (bottom-left), and p(x=(0.33,0.33)^T,z) (bottom-right), associated with the solution of the Stokes problem in a narrow-gap using the in-plane-out-of plane separated representation

Fig. 9

u(x,z = H/2) (top-left), v(x,z = H/2) (top-right), w(x,z = H/2) (bottom-left), and p(x,z = H/2) (bottom-right), associated with the solution of the Stokes problem in a narrow-gap using the in-plane-out-of plane separated representation

Laminate composed of a single Ericksen ply.

The first test case consists of a laminate composed of a single ply described by the Ericksen constitutive equation, with the unidirectional continuous fiber reinforcement oriented along the x-coordinate axis. Thus, the reinforcement orientation is defined by P ^T=(1,0,0), implying the orientation tensor

$$ \mathbf{a} = \left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right). $$

(51)

The squeeze flow takes place within the narrow gap L = W=0.5 and H=10⁻³ (units in meters) being the fluid viscosities η _L =100 Pa⋅s and η _T =100 Pa⋅s. The squeezing rate was again V=0.1 mm⋅s⁻¹.

3D finite element solution

First it is solved the flow problem by using a stable 3D finite element discretization (Q2/Q1/Q1 for the velocity, pressure and tension respectively). The finite element solution will be considered as the reference one for checking the solutions obtained within the separated representation (PGD) framework.

Figure 10 depicts all the unknown fields, the three velocity components (u,v,w), the pressure p and the tension τ. As expected and because the symmetry, the velocity in the fibers direction vanishes (a constant value is not possible because the flow problem symmetry and on the other hand non constant velocities will imply extensibility that is not allowed in the Ericksen fluid model). Component w(x,z = H/2) is as expected constant and v(x,z = H/2) has a linear variation vanishing at y = W/2 because the flow problem symmetry. Both the pressure and the tension exhibit a parabolic profile, the first expected from the lubrication theory and the second quite intuitive because at y = W/2 the fibers resists a flow that in their absence will take place in the x-direction, and decrease until vanishing at y=0 and y = W. Figure 11 shows the velocity, pressure and tension profiles along the gap thickness at position x=(0.312,0.312)^T, that exhibit the expected behavior.

Fig. 10

u(x,z = H/2) (top-left), v(x,z = H/2) (top-right), w(x,z = H/2) (middle-left), p(x,z = H/2) (middle-right) and τ(x,z = H/2) (bottom) associated with the solution of the Ericksen fluid flow problem in a narrow-gap using a 3D stable finite element discretization

Fig. 11

u(x=(0.312,0.312)^T,z) (top-left), v(x=(0.312,0.12)^T,z) (top-right), w(x=(0.312,0.312)^T,z) (middle-left), p(x=(0.312,0.312)^T,z) (middle-right) and τ(x=(0.312,0.312)^T,z) (bottom), associated with the solution of the Ericksen fluid flow problem in a narrow-gap using a 3D stable finite element discretization

We proved from our numerical experiments that richer tension approximation do not satisfy the LBB stability conditions. Thus, approximating the tension in the same space than the pressure seems a safe choice.

3D separated representation based solution

Again an in-plane-out-of-plane separated representation of velocities, pressure and fiber tension was considered within the PGD framework. However, in the case of a single fluid layer, the Lagrange multiplier associated with the fiber tension is not coupled along the thickness direction, i.e. the tension at different z-coordinates are fully decoupled. Thus, no equation is found in order to compute the functions $T_{i}^{\tau }(z)$ and for this reason we considered the simplest choice of assuming they are the same that the ones used in the pressure separated representation, i.e.

$$ \ p(\mathbf{x},z) =\sum\limits^{N}_{i=1}{P_{i}^{p}}(\mathbf{x})\cdot {T_{i}^{p}}(z), $$

(52)

and

$$ \ \tau(\mathbf{x},z) =\sum\limits^{N}_{i=1}P_{i}^{\tau}(\mathbf{x})\cdot {T_{i}^{p}}(z), $$

(53)

Figures 12 and 13 presents similar results that the ones depicted in Figs. 10 and 11 when the 3D mixed formulation is solved by using a stable in-plane-out-of-plane separated representation within the PGD framework, considering Q2/Q1/Q1 approximations for the functions depending on the in-plane coordinates and also 1D quadratic/linear/linear for those depending on the z-coordinate. The obtained results are almost identical the the ones obtained by using the more experienced 3D finite element discretization discussed in the previous section.

Fig. 12

u(x,z = H/2) (top-left), v(x,z = H/2) (top-right), w(x,z = H/2) (middle-left), p(x,z = H/2) (middle-right) and τ(x,z = H/2) (bottom) associated with the solution of the Ericksen fluid flow problem in a narrow-gap using a 3D in-plane-out-of-plane separated representation

Fig. 13

u(x=(0.312,0.312)^T,z) (top-left), v(x=(0.312,0.12)^T,z) (top-right), w(x=(0.312,0.312)^T,z) (middle-left), p(x=(0.312,0.312)^T,z) (middle-right) and τ(x=(0.312,0.312)^T,z) (bottom), associated with the solution of the Ericksen fluid flow problem in a narrow-gap using a 3D in-plane-out-of-plane separated representation

Laminate composed of two Ericksen plies

The following test case consists of a laminate composed of 2 plies described by Ericksen constitutive equation. The ply dimensions are again L×W×H=0.5×0.5×10⁻³ (all units in meters) with a compression velocity applied at the upper wall V = 0.1 mm ⋅ s⁻¹, with the same viscosities that were employed previously. The fiber orientation in the bottom ply was given by P ^B=(1,0,0)^T whereas in the upper ply they were oriented along the y-direction, i.e. P ^U=(0,1,0)^T.

The discretization was carried out again using a stable 3D finite element approximation (Q2/Q1/Q1). The solution (velocity, pressure and tension) profiles though the thickness at position x=(0.33,0.33)^T are depicted in Fig. 14. As expected we obtain two parabolic profiles for the velocities u and v, the first vanishing in the bottom ply (because the fiber inextensibility and the flow problem symmetry) and exhibiting a parabolic profile in the upper ply; and the symmetric behavior for the velocity v. As expected the velocity component w evolves smoothly, the pressure remains almost constant, however, a peak in the tension is noticed at the plies interface.

Fig. 14

u(x=(0.33,0.33)^T,z) (top-left), v(x=(0.33,0.33)^T,z) (top-right), w(x=(0.33,0.33)^T,z) (middle-left), p(x=(0.33,0.333)^T,z) (middle-right) and τ(x=(0.33,0.33)^T,z) (bottom), associated with the solution of the two ply Ericksen fluid flow problem in a narrow-gap using a stable 3D finite element discretization

The origin of the tension peak is easy to understand. The parabolic profile of u(x,z) through the ply thickness z in the upper ply implies a shear rate and consequently a shear stress at the interface. However, at the interface the x-component of the traction T = σ⋅e _z (e _z being the unit vector defining the z-coordinate axis) computed at the bottom ply for equilibrating the shear stress associated to the parabolic profile in the upper-ply implies a non-null component xz of the rate of strain tensor, i.e. D _{x z} ≠0 (note that fiber tension τ is not involved in the expression of traction T). Thus the u velocity in the bottom ply cannot be exactly zero, there is a boundary layer located at the interface in which it activates the fiber tension. Because as just indicated the fibers tension do not communicate along the thickness, the tension singularity remains located at the interface level and does not propagate in the bottom ply. The same reasoning applies for the parabolic profile of v(x,z) in the bottom ply that implies a tension singularity in the upper ply at the interface neighborhood. By diminishing the viscosity the shear stress decreases and then the tension peaks. This tendency has been verified numerically.

Solving the same problem by using an in-plane-out-of-plane separated representation seems a tricky issue because the inevitable singularity that the Ericksen model induces at the plies interface when the orientation of fibers evolves from one ply to its contiguous one. Obviously we proved that if the different plies are oriented along the same direction no peak appears in the solution. The resulting solution in that case is the one associated with a single ply having the laminate thickness.

The solution for the considered case of two plies with different orientations is depicted in Fig. 15, that reveals all the expected tendencies, in particular the peak in the tension that now spreads a little bit more from the interface.

Fig. 15

u(x=(0.33,0.33)^T,z) (top-left), v(x=(0.33,0.33)^T,z) (top-right), w(x=(0.33,0.33)^T,z) (middle-left), p(x=(0.33,0.333)^T,z) (middle-right) and τ(x=(0.33,0.33)^T,z) (bottom), associated with the solution of the Ericksen fluid flow problem in a narrow-gap using an in-plane-out-of-plane separated representation

Due to these tension peaks when proceeding within the PGD framework the pressure solution is slightly polluted, revealing an almost constant value across the gap thickness a bit lower that the one obtained when using the 3D finite element discretization. For this reason we finally decided to consider a velocity-pressure mixed formulation whereas the tension is treated from a penalty formulation. In fact accurate pressure solutions are required in order to characterize the laminate behavior, however tension is only required for evaluating the defect risks related for example with compressive fiber tensions. Thus one could imagine that tension could be reconstructed from the velocity-pressure solution, and even if its accuracy is compromised it suffices for the purpose of evaluating defect risks. Figure 16 depicts the velocity and pressure solution where higher accuracy is noticed concerning the pressure field.

Fig. 16

u(x=(0.33,0.33)^T,z) (top-left), v(x=(0.33,0.33)^T,z) (top-right), w(x=(0.33,0.33)^T,z) (bottom-left) and p(x=(0.33,0.333)^T,z) (bottom-right) associated with the solution of the Ericksen fluid flow problem in a narrow-gap using an in-plane-out-of-plane separated representation with a penalized tension

Rheological characterization

In this section we address the rheological characterization of a laminate composed of the two Ericksen plies considered in the previous section. We consider different squeezing rates and for each one after calculating the velocity and pressure fields (from the stabilized and tension penalized in-plane-out-of-plane separated representation), tension σ⋅e _z is calculated on the upper plate and then the resultant of its normal component obtained. Figure 17 depicts the force/squeeze rate behavior, that as expected evolves linearly and from which one could extract an equivalent newtonian viscosity.

Fig. 17

Applied compression force versus squeeze rate for the two plies Ericksen laminate discussed in the previous section

Conclusions

A new numerical procedure is proposed to simulate the squeeze flow of multiaxial laminates, able to present resolution levels never envisaged until now. It is based on the use of an original in-plane-out-of-plane separated representation of the different unknown fields, that allows calculating extremely detailed 3D solutions while keeping the computational complexity characteristic of 2D problems. Thus, extremely high resolutions can be attained in the thickness direction, able to capture localized behaviors.

In this work we succeeded to solve mixed velocity-pressure-tension formulations within an in-plane-out-of-plane separated representation. In order to address multiaxial laminates involving tension localized behaviors, we proposed a mixed velocity-pressure with a penalized tension, that allowed very accurate velocity and pressure solutions, and a reasonable reconstructed tension, accurate enough for predicting risk of defects.

Appendix: A: Separated representation of the Stokes weak form

The efficient computer implementation of the separated representation constructor discussed in “Separated representation constructor” section needs a separated form of the flow problem expressed in a weak form (7). For that purpose we first consider the second term D ^∗:D, that takes into account expression (5) as follows

$$\begin{array}{@{}rcl@{}} 4 \mathbf{D}^{\ast} : \mathbf{D} &=& \nabla \mathbf{v}^{\ast} : \nabla \mathbf{v} + \nabla \mathbf{v}^{\ast} : (\nabla \mathbf{v})^{T} \\&&+ (\nabla \mathbf{v}^{\ast})^{T} : \nabla \mathbf{v} + (\nabla \mathbf{v}^{\ast})^{T} : (\nabla \mathbf{v})^{T}. \end{array} $$

(54)

The simplest choice of the test function v ^∗(x,z) is

$$ \mathbf{v}^{\ast}(\mathbf{x}, z) = \mathbf{P}^{\ast} (\mathbf{x}) \circ \mathbf{T}(z) + \mathbf{P}(\mathbf{x}) \circ \mathbf T^{\ast} (z), $$

(55)

from which the velocity gradient is:

$$ \nabla \mathbf{v}^{\ast} = \mathbb{P}^{\ast} \circ \mathbb{T} + \mathbb{P} \circ \mathbb{T}^{\ast}. $$

(56)

The choice of $\mathbb {P}$ and $\mathbb {T}$ in Eq. 56 is discussed in “Separated representation constructor” section.

Developing the first term in Eq. 54 (the other terms follow the same rationale) taking into account Eq. 3 results

$$ \nabla \mathbf{v}^{\ast} : \nabla \mathbf{v} \approx \left(\mathbb{P}^{\ast} \circ \mathbb{T} + \mathbb{P} \circ \mathbb{T}^{\ast} \right) : \left(\sum \limits_{j=1}^{N} \mathbb{P}_{j} \circ \mathbb{T}_{j} \right). $$

(57)

It is easy to note that if matrices $\mathbb {M}(\mathbf {x})$ and $\mathbb {N}(\mathbf {x})$ depend on the in-plane coordinates x, and matrices $\mathbb {U}(z)$ and $\mathbb {V}(z)$ depend on the out-of-plane coordinate z, we have

$$ \left(\mathbb{M} \circ \mathbb{U} \right) : \left(\mathbb{N} \circ \mathbb{V} \right) = \left(\mathbb{M} \circ \mathbb{N} \right) : \left(\mathbb{U} \circ \mathbb{V} \right). $$

(58)

Using this equality, Eq. 57 can be written as

$$\begin{array}{@{}rcl@{}} \nabla \mathbf{v}^{\ast} : \nabla \mathbf{v} &\approx& \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast} \circ \mathbb{P}_{j} \right) : \left(\mathbb{T} \circ \mathbb{T}_{j} \right)\right.\\ &&\left.+ \left(\mathbb{P} \circ \mathbb{P}_{j} \right) : \left(\mathbb{T}^{\ast} \circ \mathbb{T}_{j} \right) \right\}, \end{array} $$

(59)

and the other terms involved in Eq. 54 as

$$\begin{array}{@{}rcl@{}} \nabla \mathbf{v}^{\ast} : \left(\nabla \mathbf{v} \right)^{T} &\approx& \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T} \circ \mathbb{T}_{j}^{T} \right) \right.\\&&\left.+ \left(\mathbb{P} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T}^{\ast} \circ \mathbb{T}_{j}^{T} \right) \right\} , \end{array} $$

(60)

$$\begin{array}{@{}rcl@{}} \left(\nabla \mathbf{v} \right)^{\ast T} : \nabla \mathbf{v} &\approx& \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast T} \circ \mathbb{P}_{j} \right) : \left(\mathbb{T}^{T} \circ \mathbb{T}_{j} \right) \right.\\&&\left.+ \left(\mathbb{P}^{T} \circ \mathbb{P}_{j} \right) : \left(\mathbb{T}^{\ast T} \circ \mathbb{T}_{j} \right) \right\}, \end{array} $$

(61)

and

$$\begin{array}{@{}rcl@{}} \left(\nabla \mathbf{v} \right)^{\ast T} : \left(\nabla \mathbf{v} \right)^{T} &\approx& \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast T} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T}^{T} \circ \mathbb{T}_{j}^{T} \right) \right.\\&&\left.+ \left(\mathbb{P}^{T} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T}^{\ast T} \circ \mathbb{T}_{j}^{T} \right) \right\}. \end{array} $$

(62)

Thus, we finally obtain

$$\begin{array}{@{}rcl@{}} 4\mathbf{D}^{\ast} : \mathbf{D} \!&\approx&\! \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast} \circ \mathbb{P}_{j} \right) \!:\! \left(\mathbb{T} \circ \mathbb{T}_{j} \right) \,+\, \left(\mathbb{P} \circ \mathbb{P}_{j} \right) \!:\! \left(\mathbb{T}^{\ast} \circ \mathbb{T}_{j} \right) \right\} \\&&+ \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T} \circ \mathbb{T}_{j}^{T} \right)\right.\\ &&\hspace*{2.5pc}\left.+ \left(\mathbb{P} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T}^{\ast} \circ \mathbb{T}_{j}^{T} \right) \right\} \\&&+ \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast T} \circ \mathbb{P}_{j} \right) : \left(\mathbb{T}^{T} \circ \mathbb{T}_{j} \right)\right.\\ &&\hspace*{2.5pc}\left.+ \left(\mathbb{P}^{T} \circ \mathbb{P}_{j} \right) : \left(\mathbb{T}^{\ast T} \circ \mathbb{T}_{j} \right) \right\} \\&&+ \sum \limits_{j=1}^{N} \left\{ \left(\mathbb{P}^{\ast T} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T}^{T} \circ \mathbb{T}_{j}^{T} \right)\right.\\ &&\hspace*{2.5pc}\left.+ \left(\mathbb{P}^{T} \circ \mathbb{P}_{j}^{T} \right) : \left(\mathbb{T}^{\ast T} \circ \mathbb{T}_{j}^{T} \right) \right\} \\&=& \sum \limits_{j=1}^{N} \sum \limits_{k=1}^{4} \left\{ \mathbb{A}_{jk}^{\ast}(\mathbf{x}) : \mathbb{B}_{jk}(z) + \mathbb{A}_{jk}(\mathbf{x}) : \mathbb{B}_{jk}^{\ast}(z) \right\},\\ \end{array} $$

(63)

where ∀j, j=1,⋯,N

$$ \mathbb{A}_{jk}^{\ast} = \left\{ \begin{array}{ll} \mathbb{P}^{\ast} \circ \mathbb{P}_{j} ,& \mathrm{if } \ k=1\\ \mathbb{P}^{\ast} \circ \mathbb{P}_{j}^{T}, & \mathrm{if } \ k=2 \\ \mathbb{P}^{\ast T} \circ \mathbb{P}_{j}, & \mathrm{if }\ k=3\\ \mathbb{P}^{\ast T} \circ \mathbb{P}_{j}^{T}, & \mathrm{if }\ k=4 \end{array} \right. , $$

(64)

$$ \mathbb{B}_{jk} = \left\{ \begin{array}{ll} \mathbb{T} \circ \mathbb{T}_{j} ,& \mathrm{if } \ k=1 \\ \mathbb{T} \circ \mathbb{T}_{j}^{T} , & \mathrm{if } \ k=2 \\ \mathbb{T}^{T} \circ \mathbb{T}_{j} , & \mathrm{if } \ k=3 \\ \mathbb{T}^{T} \circ \mathbb{T}_{j}^{T}, & \mathrm{if } \ k=4 \end{array} \right. , $$

(65)

$$ \mathbb{A}_{jk} = \left\{ \begin{array}{ll} \mathbb{P} \circ \mathbb{P}_{j} ,& \mathrm{if } \ k=1 \\ \mathbb{P} \circ \mathbb{P}_{j}^{T}, & \mathrm{if } \ k=2 \\ \mathbb{P}^{T} \circ \mathbb{P}_{j}, & \mathrm{if } \ k=3 \\ \mathbb{P}^{T} \circ \mathbb{P}_{j}^{T}, & \mathrm{if } \ k=4 \end{array} \right. , $$

(66)

and

$$ \mathbb{B}_{jk}^{\ast} = \left\{ \begin{array}{ll} \mathbb{T}^{\ast} \circ \mathbb{T}_{j} ,& \mathrm{if } \ k=1 \\ \mathbb{T}^{\ast} \circ \mathbb{T}_{j}^{T} , & \mathrm{if } \ k=2 \\ \mathbb{T}^{\ast T} \circ \mathbb{T}_{j} , & \mathrm{if } \ k=3 \\ \mathbb{T}^{\ast T} \circ \mathbb{T}_{j}^{T}, & \mathrm{if } \ k=4 \end{array} \right. , $$

(67)

On the other hand, the first term in Eq. 7 can be expressed as:

$$ \text{Tr}(\mathbf{D}^{\ast}) \cdot \text{Tr}(\mathbf{D}) = \text{Tr}(\nabla \mathbf{v}^{\ast}) \cdot \text{Tr}(\nabla \mathbf{v}), $$

(68)

with

$$ \text{Tr}(\nabla \mathbf{v}) \approx \left(\sum \limits_{i=1}^{N} \mathbb{P}_{i} \circ \mathbb{T}_{i} \right) : \mathbf I. $$

(69)

Thus, a generic term in Eq. 68 can be written as

$$ \left(\left(\mathbb{P}^{\ast} \circ \mathbb{T} + \mathbb{P} \circ \mathbb{T}^{\ast} \right) : \mathbf{I} \right) \cdot \left(\left(\mathbb{P}_{j} \circ \mathbb{T}_{j} \right) : \mathbf{I} \right). $$

(70)

Now, by defining $\mathcal {V}(\mathbb {J})$ the vector form of the diagonal matrix $\mathbb {J}$, Eq. 70 results

$$\begin{array}{@{}rcl@{}} &&\left(\left(\mathbb{P}^{\ast} \circ \mathbb{T} + \mathbb{P} \circ \mathbb{T}^{\ast} \right) : \mathbf{I} \right) \cdot \left(\left(\mathbb{P}_{j} \circ \mathbb{T}_{j} \right) : \mathbf{I} \right) \\ &=& \left(\mathcal{V}(\mathbb{P}^{\ast} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{P}_{j} \circ \mathbf{I}) \right) : (\mathcal{V} (\mathbb{T} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{T}_{j} \circ \mathbf{I})) \\ &&+ \left(\mathcal{V}(\mathbb{P} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{P}_{j} \circ \mathbf{I}) \right) : (\mathcal{V} (\mathbb{T}^{\ast} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{T}_{j} \circ \mathbf{I})),\\ \end{array} $$

(71)

that allows finally casting the first term in the weak form (7) as

$$ \text{Tr}(\mathbf{D}^{\ast}) \cdot \text{Tr}(\mathbf{D}) \approx \sum\limits_{j=1}^{N} \mathbb{F}_{j}^{\ast} (\mathbf{x}) : \mathbb{G}_{j} (z) + \mathbb{F}_{j}(\mathbf{x}) : \mathbb{G}_{j}^{\ast}(z) $$

(72)

with

$$ \mathbb{F}^{\ast}_{j} = \mathcal{V}(\mathbb{P}^{\ast} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{P}_{j} \circ \mathbf{I}) , $$

(73)

$$ \mathbb{G}_{j} = \mathcal{V} (\mathbb{T} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{T}_{j} \circ \mathbf{I}), $$

(74)

$$ \mathbb{F}_{j} = \mathcal{V}(\mathbb{P} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{P}_{j} \circ \mathbf{I}), $$

(75)

and

$$ \mathbb{G}_{j}^{\ast} = \mathcal{V} (\mathbb{T}^{\ast} \circ \mathbf{I}) \otimes \mathcal{V}(\mathbb{T}_{j} \circ \mathbf{I}). $$

(76)