Introduction

Electromagnetic Material Forming (EMF) allows forming electrical conductive metallic materials at high strain rates. It uses pulsed magnetic fields to apply electromagnetic (Lorentz) body forces to shape sheet and tube metal parts. The magnetic field is generated by discharging into a coil high intensity currents pulsed from a high energy capacitor equipped with fast action switches. This kind of forming processes presents several advantages on classical low strain-rate forming processes, among which contact-free force application, process repeatability, and small duration can be cited. But the main interest lies in the fact that it enables to increase dramatically the forming limits classically reached with steady-state forming processes. The gain is all the more significant that the alloy in question has a low ductility at low strain rate. It also allows for the reduction of wrinkling and strongly limits the springback due to the forming operation. Thus, EMF processes are of great industrial interest for all types of industries, particularly concerning the weight reduction and multi-material assembly issues or for the design of complex geometry parts, thanks to a better formability of metallic alloys at high strain rate. We refer to [30] for a complete review of EMF.

From the industrial viewpoint, its implementation requires to determine many process parameters to achieve the proper geometry of the part to be formed; these parameters can be either related to the geometry of the electromagnetic forming device (geometries of the part and the coil) or related to the physical properties of the components embedded within the device, or even related to the chain generator-coil that pulses the discharged currents. Mastering the EMF requires a good knowledge of a domain of validity of these process parameters, which is often determined by the accumulated know-how of users. In this context, numerical simulations appear to be an effective way to explore parameter space, and therefore can limit a more expensive trial and error approach. Numerical parametric analysis may thus enable to improve and optimize these forming processes, but leads to the definition of optimization procedures that may turn out to be computationally very costly. Indeed, the often prohibitive numerical cost of the optimization procedure arises from the direct analysis run for each given set of parameters in order to evaluate the cost function and its optimality [4]. This iterative process leads to many assessments of the cost function and therefore to many direct computations of a given model. Since the numerical model may involve a structural analysis or the resolution of a Boundary Value Problem (BVP), this kind of approach may lead to a huge computation time, and we are led to limit as much as possible the number of parameters considered in the analysis, and therefore the size of the problem.

However, others approaches have been proposed to decrease the optimization computation time. Recently, procedures based on separated representations such as the Proper Generalized Decomposition (PGD) [3, 10, 26, 32] have proved to be particularly effective to reduce the complexity of problems exhibiting high dimensions, and circumvent the so-called curse of dimensionality. Indeed, while classical mesh-based methods like finite elements exhibit a complexity increasing exponentially with the number of dimensions, separated representations enable to alleviate this difficulty and shows a complexity scaling only linearly with the dimension of the problem. Introducing extra dimensions appears therefore much less penalizing with this approach. The Proper Generalized Decomposition enables a parametric resolution by introducing optimization parameters as extra-coordinates of the problem, and uses a separated representation to approximate the multidimensional solution. Consequently, the evaluation of the cost function does not require anymore a direct analysis, the computational effort being previously provided upstream of the optimization step. Thus, the optimization procedure reduces to a simple post-treatment of the multidimensional numerical solution, and can be done in real time on light computing devices. This decreases drastically the computation time allocated to the optimization procedure compared to classical approaches. PGD has already been used successfully in the framework of parametric analysis for the resolution of thermal problems, accounting for varying geometric [25] or material parameters [12, 23, 29], or related to boundary conditions [12, 18, 19]. PGD has also been used to solve stochastic problems [27], for the simulation of composites manufacturing [11], for thin structures [7] and in crack problems [20], in rheology and kinetic theory [3].

The aim of this paper is to take advantage of the Proper Generalized Decomposition to build a numerical tool dedicated to the optimization of the design of an electromagnetic compression device. This tool should allow to perform optimization procedures on this device at a much lower cost than that generated by conventional procedures coupled with mesh-based discretization methods. In this work, only the set of electromagnetic equations in quasistatics is solved on the electromagnetic compression device. The objective is to extract from the electromagnetic solution the Lorentz body forces. These body forces may afterwards be used as an input to any finite element code to perform the simulation of the mechanical stage of the process. It is well-known that EMF processes involve coupled multiphysical problems [14, 34, 35]; though a decoupled approach leads to introduce further simplifying assumptions, it may also enable (up to an accepted error of modeling) to view the coupled problem as a chain of different Boundary Value Problems, each associated to one physical phenomenon, and thus allows for a simplified approach and decoupling difficulties that can prove to be well-suited both for understanding occuring physical phenomena and for process optimization purposes. The study of coupling effects may afterwards be carried out if needed, but is not part of the scope of this work. It has to be emphazised that from the industrial viewpoint, it is of primary interest to have access to the Lorentz body forces defined on a parameter space. First, the Lorentz forces magnitude is a good indicator of the behavior of the part during the forming operation, and EMF users can either complete the numerical simulation by plugging their own mechanical solver or use their accumulated experimental know-how to relate the magnitude of these forces to the quality of the formed part. Second, these forces defined on a parameter space enable to compute efficiently sensitivities with respect to additional parameters, quantities of great interest for optimization purpose, without the need to run further computations. At last, defining the Lorentz forces on a parameter space allows to build a numerical chart and to evaluate the solution at a very low cost with respect to classical approaches.

The paper starts by recalling the principles of Electromagnetic Material Forming processes in section “Electromagnetic Material Forming”. Next, the problem considered in this work and the formulation of the set of electromagnetic equations in quasistatics in term of the magnetic vector potential are detailed. The bidimensional axisymmetric case is retained as usual in EMF modeling of compression devices [35]. Section “PGD” is devoted to the Proper Generalized Decomposition, basic principles [10, 12, 32] and the multidimensional weak form of the problem considered are presented. In this work, attention is focused on the generation of Lorentz body forces, the aim of the numerical tool built is to optimize the process parameters of the chain generator-coil and the geometrical parameters of the electromagnetic compression device with respect to the mechanical loading required to form the part. In section “Parametric modeling of the electrical loading”, we consider as a first step a parameterization of the discharged current through the decay time τ and its angular frequency ω. These two additional parameters can be related to more convenient quantities from the viewpoint of the user (capacitance, inductance and resistance), but it enables a more compact parameterization. Thus, this model leads to a five-dimensional numerical solution. In section “Parametric modeling of the geometry”, parameterization of the geometry of the electromagnetic compression device is carried out. We consider a multi-layered structure where the thicknesses of all layers are introduced as extra-coordinates in the considered problem. The numerical problem has then height dimensions. Though geometric parameters have already been treated in the 1D case within the framework of the PGD [25], it is shown here that some complications may arise in the axisymmetric case, and that the complexity of the computation may grows asymptotically as \(\mathcal {O}(m^{2})\) if we consider an m-layered structure. In order to illustrate possibilities offered by the multidimensional solution, an example of optimization procedure is carried out in section “Optimization procedure of the electromagnetic compression device”, in which we seek the geometrical configuration of the electromagnetic compression device maximizing the radial component of the resultant compression force applied on the part to be formed. For illustration purpose, the radial component of the resultant force is plotted on a part of the design space; it is shown that a minimum exists and is unique. This illustrates a first step towards the optimization of an electromagnetic compression device.

Electromagnetic Material Forming

Principles

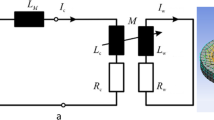
Electromagnetic Material Forming (EMF) is a high-speed forming technology that relies on the use of electromagnetic forces to form metallic workpieces at high strain rate [13, 16, 30]. Generally speaking, these processes use a magnetic coil as a “tool”. It consists in discharging a high intensity and oscillating current (Fig. 1a) into a coil using a high voltage capacitor bank with high-speed switches. This current, flowing within the coil, generates a pulsed magnetic field in the vicinity of coil windings. Providing the Faraday’s law saying that in the presence of a time-varying magnetic field any electrical conductive material is subjected to induced eddy currents, the interaction between the pulsed magnetic flux density and these eddy currents creates strong repulsive body forces called Lorentz forces. The resulting brief and intense mechanical loading accelerates and deforms the workpiece until it contacts a die giving it its final shape. Figure 1b shows a magnetic pulse crimping configuration, which is actually a special case of EMF processes. This configuration is required if we want to assemble a ring on a shaft, traditionally of circular cross-sections. The ring is accelerated and deforms until it contacts the shaft, achieving the crimping operation.

Fig. 1
figure 1

Electromagnetic material forming process

Full size image

The main interest to form at high strain rate lies in the fact that it improves the formability of metallic alloys, thus it allows to overcome traditional formability barriers that prevent a more widespread use of aluminium alloys in lightweight structural applications [16]. Usual strain rates reached with such processes are of the order of 103s−1. This impressive increase of ductility of metallic alloys results from the strain-rate sensitivity of the material constitutive’s response, as shown experimentally in [5] and [6]. EMF processes show as well many advantages with respect to classical low strain rate forming processes, such as the reduction of wrinkling in compression forming, reduction of springback due to the dynamics of contact with the forming die, high-productivity due to the high-speed forming operation, contact-free force application, high-repeatability [30].

Modeling

Electromagnetic Material Forming processes are coupled multiphysical problems. Electromagnetic, thermal and mechanical effects combine during the forming operation. Electromagnetic phenomena generate the mechanical loading (Lorentz body forces) on the workpiece, which deforms and heats due to the mechanical and electrical dissipations. Many authors have already studied the theoretical formulation of this strongly coupled problem [14, 28, 34, 35], and its numerical resolution with the finite element method [31, 33].

However in this kind of applications, all the couplings are not necessarily activated; thus it is commonly accepted to simplify the modeling by introducing some assumptions. First, the effective current frequencies being of the order of 10kHz, i.e. a characteristic length of the electromagnetic forming device being much smaller than the electromagnetic wavelength, the propagation is neglected [31, 33, 34]. Second, looking at the ratio of characteristic times of the different physical phenomena occuring during the process, many couplings may be neglected. Indeed, we can observe that for a classical aluminium (2xxx series for instance) the ratio of characteristic times related to magnetic and thermal phenomena is of the order of 5 · 10−3. Hence, magnetic and thermal phenomena can be solved separately. The decoupling between magnetic and mechanical effects is less evident as stated by many authors that pointed out the importance of this coupling [13, 33–35]. However, this coupling will be neglected in this work as stated in the introduction of this paper, so that the set of electromagnetic equations be solved independently. The approach followed here falls into a decoupled strategy of the resolution of the multiphysical problem, and attention will be focused in this work on electromagnetic effects.

The geometry considered is defined in the bidimensional axisymmetric case and is presented in Fig. 2. The domain Ω consists of a magnetic coil (Ω coil) surrounding the workpiece (Ω wp) of cylindrical shape, defining an electromagnetic compression device being plunged into a volume of air (Ω air). Hence, the domain Ω admits the following decomposition:

$$ \varOmega = \bigcup_{i} \varOmega_{i}\, ; \quad i = \{\text{coil},\text{wp},\text{air} \} $$
(1)

The boundary ∂ Ω of the domain Ω admits the decomposition:

$$ \partial \varOmega = \varGamma_{0} \cup \varGamma_{1} $$
(2)

where Γ 0 and Γ 1 stand for the part of the boundary for which Dirichlet and Neuman boundary conditions are respectively prescribed, see Fig. 2. A symmetry condition allows for limiting the domain of study, and helicity of the magnetic coil has been neglected.

Fig. 2
figure 2

Geometry of the computational domain

Full size image

It is usual to solve the set of electromagnetic equations by introducing potentials. Among them, the most popular is a formulation in term of the magnetic potential vector [31, 33, 35], using the third Maxwell’s equation stating the non-existence of magnetic charge:

$$ \mathbf{b} = \mathbf{curl} \;\mathbf{a} $$
(3)

where b denotes the magnetic flux density and a the magnetic vector potential. For bidimensional axisymmetric formulation, only the hoop component of the magnetic potential vector does not vanish:

$$ \mathbf{a}=a\mathbf{e}_{\theta} $$
(4)

It is thus easy to show that the total electric charge balance and the classical Coulomb gauge are automatically satisfied, therefore the initial boundary value problem considered in this work reads:

$$ \sigma \frac{\partial a}{\partial t} = \!\!\frac{1}{\mu}\left( \frac{\partial^{2} a}{\partial r^{2}} \,+\,\frac{1}{r}\frac{\partial a}{\partial r} \,-\,\frac{a}{r^{2}} +\frac{\partial^{2} a}{\partial z^{2}}\right) \,+\, j_{0} \quad \forall \mathbf{x} \in \varOmega $$
(5)
$$ a= 0 \qquad {\kern102pt} \forall \mathbf{x} \in \varGamma_{0} $$
(6)
$$ \frac{\partial a}{\partial n}= 0 \qquad {\kern95pt} \forall \mathbf{x} \in \varGamma_{1} $$
(7)
$$ a(r,z,t=0) = a_{0} \qquad {\kern50pt} \forall \mathbf{x} \in \varOmega $$
(8)

where σ refers to the electrical conductivity (vanishing in the air) and μ refers to the magnetic permeability of the medium. In this study, we consider the magnetic coil made of copper and the workpiece made of aluminium alloy, therefore the magnetic permeability in these media is almost equal to the vacuum permeability μ 0 = 4π · 107 H.m −1. Indeed, these materials are respectively diamagnetic and paramagnetic, for which the relative magnetic permeabilities are close to unity. Consequently, the initial boundary value problem Eqs. 5–8 is linear. The partial differential equation defined on the hoop component a of the magnetic potential vector is supplemented with appropriate initial (8) and boundary conditions. First, a symmetry condition is prescribed on Γ1 to restrict the domain of computation:

$$ \mathbf{n} \times \mathbf{h} = \mathbf{0} \quad \forall \mathbf{x} \in \varGamma_{1} $$
(9)

where h denotes the magnetic field and n the outward unit normal. The Eq. 9 combined with Eq. 3 and the following magnetic constitutive equation:

$$ \mathbf{b} = \mu \mathbf{h} $$
(10)

reduces to Eq. 7. Second, the magnetic potential vector vanishes on the symmetry axis [35] and tends to vanish far from the device, this leads to Eq. 6. Finally, a time-varying current density j 0 = j 0 e 𝜃 is prescribed within the coil, according to a damped sinusoid (Fig. 1a):

$$ j_{0} = \frac{I_{0}}{S} e^{-t/ \tau}\sin (\omega t) $$
(11)

where S denotes the cross-section of the windings, τ a decay time and ω the angular frequency of the pulsed current. The prescribing of a homogeneous distribution of the current density in each coil turn constitutes an approximation which is acceptable here given the intended applications involving a small dimension of coil turn and a sufficient mean radius of the coil, otherwise the total current should be applied in accordance to [33] and [35]. The Lorentz body forces are then computed in post-treatment from the magnetic flux density b and from induced eddy currents flowing within electrical conductive components of the device j = −σ ∂ a/∂ t, such that:

$$ \mathbf{f}= \mathbf{j} \times \mathbf{b} $$
(12)

PGD

The Proper Generalized Decomposition [10, 12, 26, 32] or PGD consists in seeking the solution of a boundary value problem in a separated representation. Let’s consider a field u depending of d coordinates (x 1,…,x d ) ∈ (Ω1×…×Ω d ), this approximation reads:

$$ u(x_{1},\ldots,x_{d})\simeq \sum\limits_{i=1}^{N} \prod\limits_{j=1}^{d} X_{i}^{(j)}(x_{j}) $$
(13)

In other words, if each dimension x j is discretized on a unidimensional mesh that consists of N j nodes, \(\mathbf {x}_{i}^{(j)}\in \mathbb {R}^{N_{j}}\) represents the vector of components \(X_{i}^{(j)}\left (x_{k}^{(j)}\right )\), with 1 ≤ k ≤ N j et 1 ≤ j ≤ d, so that Eq. 13 be rewritten as a sum of ranked-one tensor product:

$$ \mathbf{u} \simeq \sum\limits_{i=1}^{N} \mathbf{x}_{i}^{(1)} \otimes {\cdots} \otimes \mathbf{x}_{i}^{(d)} $$
(14)

The whole point of the PGD is to build a tensor product approximation basis in order to decouple the numerical integration of high dimensional model in each dimension. Indeed, working with functions of one variable leads to that the computational cost scales linearly with the number of dimensions of the problem, and no more exponentially as for mesh-based methods like finite elements, alleviating the so-called curse of dimensionality.

Functions \(X_{i}^{(j)}(x_{j})\) in Eq. 13 are unknown a priori. The solution procedure is based on a greedy algorithm and proceeds by successive enrichments. Let’s assume that the solution at enrichment step n is known, solution at enrichment step n+1 is given by:

$$ u^{n+1}=u^{n} + \prod\limits_{j=1}^{d} X_{n+1}^{(j)}(x_{j}) $$
(15)

Let’s now consider a tensor product approximation of the hoop component a of the magnetic potential vector (4) depending on coordinates (t, r, z, x 1,…,x m ) ∈ (Ω t × Ω r × Ω z × Ω1 × … × Ω m ), where (x 1,…,x m ) refer to m additional coordinates, and Ω in Eq. 1 being decomposed so that Ω = Ω r × Ω z , one gets:

$$ a^{n+1}=a^{n} + T(t)R(r)Z(z) \prod\limits_{i=1}^{m} X_{i}(x_{i}) $$
(16)

These m additional extra-coordinates refer to m additional parameters defined within the problem in order to carry out a parametric analysis, they can be related to initial or boundary conditions, geometrical, material or process parameters, etc. The computation of unknown functions at enrichment step n+1 is performed by invoking a multidimensional weak form of the initial boundary value problem; in the case of magnetodynamic, the weak form of the problem Eqs. 5–8 reads, accounting for m additional coordinates:

$$ \left\{ \begin{array}{lll} \text{Given the current density} j_{0} \, \in {\Omega}_{\text{coil}}, \\ \text{Find } a \! \in \! \mathcal{A}_{\text{ad}}, \! \text{ in} \!\left( {\Omega}_{t} \!\times \! {\Omega}_{r}\! \times \! {\Omega}_{z} \!\times \! {\Omega}_{1}\! \times \! \!{\ldots} \! \times \! {\Omega}_{m} \right)\! \text{ such that}, \\ \forall a^{\ast}\in \mathcal{A}_{\text{ad}}^{0} \\ \idotsint_{{\Omega}_{i}}{\int}_{{\Omega}_{t}} {\int}_{{\Omega}_{z}}{\int}_{{\Omega}_{r}} \Big(\sigma \frac{\partial a}{\partial t} \,a^{*} \,+\, \frac{1}{\mu} \left( \frac{\partial a}{\partial r} \frac{\partial a^{\ast}}{\partial r} \,+\, \frac{a a^{\ast}}{r^{2}} \,+\, \frac{\partial a}{\partial z} \frac{\partial a^{\ast}}{\partial z} \right) \\ {\kern90pt} - j_{0} \,a^{*} \Big) r \text{d}r \text{d}z \text{d}t \text{d}x_{1} {\ldots} \text{d}x_{m} =0 \\ a(r,z,t=0) = a_{0} \end{array}\right. $$
(17)

Notice that the term a a ∗/r arising in Eq. 17 makes the weak form of the magnetodynamic problem different with respect to that of the classical transient heat equation in the bidimensional axisymmetric case.

Test functions may be chosen as follows:

$$\begin{array}{@{}rcl@{}} a^{\ast} &=& T^{\ast}R(r)Z(z) \prod\limits_{i=1}^{m} X_{i}(x_{i}) + {\ldots} \\ &&+ T(t)R(r)Z(z) \prod\limits_{i=1}^{m-1} X_{i}(x_{i})X_{m}^{\ast}(x_{m}) \end{array} $$
(18)

With the trial and test functions given by Eqs. 16 and 18 respectively, the weak form Eq. 17 becomes a non-linear problem. From this viewpoint, the PGD is a method that transforms a linear problem into a sequence of non-linear problems. Therefore, it must be solved by means of a suitable iterative scheme. The simplest one is an alternated directions fixed-point algorithm, which was found particularly robust in this context. Computation of functions T(t),R(r),Z(z) and X i (x i ) (1 ≤ i ≤ m) is performed alternatively within the fixed-point loop.

Comment:

due to the parabolic nature of the problem Eqs. 5–8, the classical PGD algorithm may not converge if σ μ is too large. Therefore we use the so-called residual minimization approach. It can be shown that this approach leads to a monotonic convergence [26] and has proved to be robust, though much computational effort is required with respect to Galerkin-based PGD. The global stopping criterion for the computation of a n+1 at enrichment step n+1 is based on a residual relative L 2 error:

$$ \frac{\| \mathcal{R}\left(a^{n+1}\right) \|_{2}}{\| f \|_{2}} < \varepsilon $$
(19)

where f denotes the loading term.

Parametric modeling of the electrical loading

Formulation

We are first interested in the electrical loading parameterization, the objective being to allow for optimizing process parameters of the generator with respect to the mechanical loading required to form the part. It is here assumed that the generator is designed in such a way that the discharged current be expressed as a damped sinusoid:

$$ I(t) = I_{0}e^{-t/\tau} \sin(\omega t) $$
(20)

The decay time τ and the angular frequency ω are embedded as two additional coordinates, the PGD approximation consists thus of five dimensions and reads:

$$ a(t,r,z,\tau,\omega) \simeq \sum\limits_{i=1}^{N} T_{i}(t)R_{i}(r)Z_{i}(z)\tau_{i}(\tau){\Omega}_{i}(\omega) $$
(21)

PGD efficiency stems from the expression of all quantities in a separated form. Therefore, we are led to seek an expression of the pulsed current density j 0 of the form:

$$ j_{0}(t,\tau,\omega)= \sum\limits_{i=1}^{N_{j_{0}}} T_{i}(t) \mathcal{\tau}_{i}(\tau) {\Omega}_{i}(\omega) $$
(22)

One possibility among others [12] to express the current density with a separated form Eq. 22 is to build a PGD computation as follows:

$$ \mathcal{I}\left(\sum\limits_{i=1}^{N_{j_{0}}} T_{i}(t)\mathcal{\tau}_{i}(\tau) {\Omega}_{i}(\omega)\right)= f(t,\tau,\omega) $$
(23)
$$ \text{with } \!f(t,\!\tau,\!\omega) \,=\, \!\sum\limits_{j=1}^{N_{t}} {f_{t}^{j}} f_{\tau}^{j} f_{\omega}^{j};\quad \begin{array}{l} {f_{t}^{j}} = (I_{0}/S) \delta (t-t_{j}) \\ f_{\tau}^{j} = \exp(-t_{j}/\tau) \\ f_{\omega}^{j} = \sin(\omega t_{j}) \end{array} $$
(24)

where \(\mathcal {I}\) denotes the identity operator. The right-hand-side (24) is assessed by sampling the pulsed current density (11) on the time mesh. In other words, an L 2 projection is performed by invoking the PGD solver:

$$ {\int}_{\varOmega_{\omega}} {\int}_{\varOmega_{\tau}} {\int}_{\varOmega_{t}} \left( j_{0}(t,\tau,\omega)- f(t,\tau,\omega) \right) j_{0}^{\ast} \mathrm{d}t\mathrm{d}\tau \mathrm{d}\omega = 0 $$
(25)

looking for the approximation (22) of j 0 and accounting for a test function \(j_{0}^{\ast }\) defined analogously to Eq. 18. Besides, we expect that \(N_{j_{0}}\) be much smaller than N t . Another strategy would have been to perform a High Order SVD [24]. Afterwards, the resolution of the magnetodynamic problem (17) with the electrical loading parameterization (22) is performed as described in section “PGD”.

Results

Table 1 summarizes input data of the computation. The geometry of the device is set so that the half-length of the workpiece is 10−2m, its wall thickness 2 · 10−3m and its mean radius 8 · 10−3m. The side length of windings is 2 · 10−3m, the pitch is 4 · 10−3m and the mean radius of the coil is 11·10−3m.

Table 1 Input data
Full size table

The decomposition of the discharged current in separated representation is performed with 26 enrichments reaching a residual relative L 2 error ε of 10−3. The magnetodynamic analysis lasts one hour and need 200 enrichments to reach an error of 10−2. Figure 3 shows the Lorentz body forces magnitude applied on the workpiece (respectively on coil windings) at time t = 4 · 10−4s as a function of the decaying time (Fig. 3a) or the discharged current angular frequency (Fig. 3c) (respectively Fig. 3b and d). The post-treatment uses here the plugin developed by [8] allowing the export towards pxdmf file read with Paraview [2]. We observe as expected that the magnitude of Lorentz forces increases with that of the first current peak as the decay time grows. Varying the angular frequency shifts the first peak, the maximum magnitude of forces thus varies accordingly. PGD enables to build a multidimensional solution, leading to reduce the optimization procedure to a simple post-treatment of this solution.

Fig. 3
figure 3

Lorentz body forces magnitude (N.m −3) applied on the workpiece (resp. the coil) as a function of the decay time τ in Fig. 3(a) or the angular frequency ω in Fig. 3(c) (resp. in Fig. 3(b) and 3(d))

Full size image

The solution obtained with PGD solver has been validated against a solution obtained with the AC/DC module of Comsol [1]. A comparison performed on the magnitude of the Lorentz body forces for the following set of coordinates values (t = 1.07 · 10−4s, τ = 2 · 10−4s, ω = 2 · 104rad.s−1) shows a relative difference of about fifteen percents within the workpiece. Given the different meshes and numerical methods used for this comparison, this difference is found acceptable.

Parametric modeling of the geometry

Formulation

We are now interested in the parameterization of the geometry of the electromagnetic compression device, the objective being to allow for optimizing geometrical parameters of the workpiece and the coil with respect to the mechanical loading required to form the part. We consider the electromagnetic computational domain as a multi-layered structure, the thicknesses of all layers are introduced as additional parameters of the problem. Therefore five radial lengths denoted l i , 1 ≤ i ≤ 5 are introduced within the numerical problem, which has now eight dimensions. This parameterization is shown in Fig. 4.

Fig. 4
figure 4

Radial parameterization of the electromagnetic compression device

Full size image

The domain associated to the radial coordinate Ω r is thus mapped on a fixed parent domain for each layer, to which the coordinate s j is associated, so that:

$$ {\Omega}_{r} = \bigcup_{j=1}^{m} {\Omega}_{s_{j}} = \left[0,\sum\limits_{j=1}^{m} s_{j} \right] $$
(26)

The following change of variable is thus defined in each layer of the structure:

$$ r(s,l_{1},\ldots,l_{m})= \sum\limits_{p<j} l_{p} +l_{j}(s-(j-1)); \quad j-1\leq s \leq j $$
(27)

The PGD approximation is performed on the parent domain, accounting for extra-coordinates; the test function is defined analogously to (18):

$$ a^{n+1} = a^{n}+T(t)S(s)Z(z)\prod\limits_{i=1}^{m} L_{i}(l_{i}) $$
(28)
$$\begin{array}{@{}rcl@{}} a^{\ast} &=& T^{\ast}(t)S(s)Z(z)\prod\limits_{i=1}^{m} L_{i}(l_{i}) + {\ldots}\\ && + T(t) S(s)Z(z)\prod\limits_{i=1}^{m-1} L_{i}(l_{i}) L_{m}^{\ast}(l_{m}) \end{array} $$
(29)

The change of variable (27) implies that integral quantities involved within the weak form (17) are expressed as follows:

$$\begin{array}{@{}rcl@{}} &&{\int}_{{\Omega}_{t}} \int {\cdots} {\int}_{{\Omega}_{l_{i}}}{\int}_{{\Omega}_{z}}{\int}_{{\Omega}_{r}} (\cdots) r \text{d}r \text{d}z \text{d}l_{1} {\ldots} \text{d}l_{m} \text{d}t= \\ &&{\int}_{{\Omega}_{t}} \int \!\! {\cdots} \!{\int}_{{\Omega}_{l_{i}}}\!{\int}_{{\Omega}_{z}} \!\!\left( \sum\limits_{j=1}^{m}\! {\int}_{{\Omega}_{s_{j}}} \!\!(\cdots)\right.\\ &&\left.\times\left(\sum\limits_{p<j}\! l_{p} \!\,+\,l_{j}(s\! \! -\!(j\,-\,1))\!\right) l_{j} \text{d}s \right) \text{d}z \text{d}l_{1} {\ldots} \text{d}l_{m} \text{d}t \end{array} $$
(30)

The jacobian associated to cylindrical coordinates makes appear explicitly the change of variable within the integrand. In expression Eq. 30, the jacobian associated to the mapping on the parent domain has been easily computed as:

$$ \frac{\partial r}{\partial s}(s,l_{1}, \ldots,l_{m}) = l_{j} \:; \quad j-1 \leq s \leq j $$
(31)

Let’s now consider for instance the term (1 /μ)(∂ a /∂ r) (∂ a ∗/ ∂ r)r within the weak form Eq. 17, involving the derivative with respect to the radial coordinate. Introducing the change of variable (27), the PGD approximation Eq. 28 and the test function Eq. 29 in this term, and noting \(\langle \cdot , \cdot \rangle _{\varOmega _{x_{i}}}\) the inner \(L^{2}(\varOmega _{x_{i}})\) product, one gets:

$$\begin{array}{@{}rcl@{}} && {\int}_{{\Omega}_{t}} \int \cdots{\int}_{{\Omega}_{l_{i}}}{\int}_{{\Omega}_{z}}{\int}_{{\Omega}_{r}} \frac{1}{\mu} \frac{\partial a}{\partial r}\frac{\partial a^{*}}{\partial r}r \text{d}r \text{d}z \text{d}l_{1} {\ldots} \text{d}l_{m} \text{d}t \!= {\cdots} \\ &&\!= \sum\limits_{j=1}^{m} \sum\limits_{p<j} \langle T,T^{*} \rangle_{{\Omega}_{t}} \langle (1/\mu) S^{\prime},S^{\prime} \rangle_{{\Omega}_{s_{j}}} \langle Z, Z \rangle_{{\Omega}_{z}}\\ &&{\kern.3pc}\times \prod\limits_{i=1}^{m} \quad \!\!\!\left\langle \!\mathcal{H}(l_{p}) \mathcal{H} \!\left(\!l_{j}^{-1} \right)\! L_{i}, \!L_{i} \!\right\rangle_{{\Omega}_{l_{i}}}\\ &&\quad\!\!\,+\,\! \!\sum\limits_{j=1}^{m} \!\langle T,\!T^{\!\ast}\rangle\!_{{\Omega}_{t}} \!\langle \!(s\!\,-\,\!(j\!\,-\,\!1)\!) S , \!S \rangle_{{\Omega}_{s_{j}}} \! \langle Z, \!Z \rangle_{{\Omega}_{z}}\\ &&{\kern.4pc}\times \prod\limits_{i=1}^{m} \!\langle L_{i} , \!L_{i} \rangle_{{\Omega}_{l_{i}}} \!\!\,+\, \!\ldots\!\!\!\\ &&\quad\!\!+ \!\sum\limits_{j=1}^{m}\! \sum\limits_{p<j}\! \langle T,\!T \rangle_{{\Omega}_{t}} \langle \!(1\!/\!\mu) S^{\prime}\!,\!S^{\prime} \rangle_{{\Omega}_{s_{j}}} \langle Z, Z \rangle_{{\Omega}_{z}}\\ &&\quad\!\!\times \prod\limits_{i=1}^{m-1} \left\langle \mathcal{H}(l_{p}) \mathcal{H} \left(l_{j}^{-1} \right) L_{i}, L_{i}\right\rangle_{{\Omega}_{l_{i}}} \\ &&\quad \!\!\times \left\langle \mathcal{H}(l_{p}) \mathcal{H} \left(l_{j}^{-1} \right) L_{m}, L_{m}^{*} \right\rangle_{{\Omega}_{l_{m}}} \\ &&\quad \!\!+\sum\limits_{j=1}^{m} \langle T,T\rangle_{{\Omega}_{t}} \langle (s-(j-1)) S , S \rangle_{{\Omega}_{s_{j}}} \langle Z, Z \rangle_{{\Omega}_{z}} \\ &&\quad\!\!\times \prod\limits_{i=1}^{m-1} \langle L_{i} , L_{i} \rangle_{{\Omega}_{l_{i}}}\langle L_{m} , L_{m}^{*} \rangle_{{\Omega}_{l_{m}}} \end{array} $$
(32)

where \(\mathcal {H}(l_{p})\) denotes a presence function that is equal to l p if p = i, 1 otherwise. We observe that the number of terms grows asympotically as \(\mathcal {O}(m^{2})\) for a multi-layered domain constituted of m layers in the bidimensional axisymmetric case, as indicated by the double sum on j and p. Indeed, this decomposition is caused by the presence of the jacobian of the cylindrical coordinates in the integrand of the weak form. Thus, much more computational effort is required with respect to the unidimensional case [25]. Analogous developments are carried out for other terms of the weak form Eq. 17.

Comment:

A particular attention should be payed to the term a a ∗/r embedded within the weak form Eq. 17. Indeed, this term cannot be explicitly separated by introducing the change of variable (27). A first solution consists in multiplying the whole weak equation by the radius r. However, it squares the radius involved in the integrand (30) and so does the change of variable (27) for all terms in the weak form (except the term a a ∗/r), leading to a huge amount of operator splitting and thus to a large increase of computational effort. A second solution is to decompose it numerically in a separated form. Many solutions are available to perform such a decomposition: we can either perform a PGD to get the inverse of the radius in a separated form or use already implemented algorithms as PARAFAC (PARAllel FACtor analysis) [9, 21] that decomposes an array of dimension N (N ≥ 3) into the summation over the outer product of N vectors (a low-rank model). In other words, it decomposes an N-way array into a canonical tensor product approximation (14). Though the second solution using PARAFAC algorithm requires to build explicitly the N-way array of the inverse of the radius, it still appears much more computationally efficient than the first solution, and is hence used in this work.

Results

Table 2 summarizes the changing input data with respect to section “Results”. The computation lasts about two hours and needs 40 enrichments to reach an error ε of 10−2. Figure 5a and b show the Lorentz body forces isovalues generated on the device components at its first peak in time, for the two extremal cases of the gap value (l 3) between the workpiece and the coil. The results suggest as expected that their magnitude is greater when the gap is smaller.

Table 2 Input data
Full size table
Fig. 5
figure 5

Lorentz body forces (N.m −3) as a function of the gap (l 3) between the workpiece and the coil

Full size image

Then, it is interesting to investigate the evolution of the Lorentz forces magnitude applied either on the workpiece or on the coil while varying lengths of the structure layers. Figure 6 focuses on the workpiece and shows the evolution of these forces at their first extremum (associated to the first current peak) varying its thickness l 2 (Fig. 6a) and the gap magnitude l 3 (Fig. 6b). A best geometrical configuration appears for the length l 3 if we want to maximize the magnitude of Lorentz body forces applied on the workpiece; as previously stated, the smaller is l 3, the greater is the magnitude of body forces reached. The workpiece thickness l 2 does not seem at a first glance to have any signficative influence on body forces generated, because induced eddy currents only flow within a skin depth.

Fig. 6
figure 6

Lorentz body forces (N.m −3) applied on the workpiece as a function of lengths l 2 and l 3

Full size image

During the forming operation, coil windings are generally destroyed by the forces generated (unless a rigid coil is used). Therefore, we want to minimize the forces undergone by the coil so that it resists at least until the first current peak has passed. Indeed, a sufficient level of forces applied on the workpiece is required to achieve the proper geometry of the part to be formed. Figure 7 shows body forces applied on coil windings at their first peak varying the gap magnitude l 3 (Fig. 7a) and its thickness l 4 (Fig. 7b). A best geometrical configuration appears for both parameters if we want to minimize the magnitude of these forces; the greater are lengths l 3 and l 4, the smaller is the magnitude of forces applied on the coil. Their decrease with the gap l 3 is moderate and result from the remoteness with the workpiece; while for the second parameter, increasing l 4 leads to increase the winding cross-section, and thus decreases the current density flowing within the cross-section (even though it flows within the skin thickness of the conductor) for a given intensity provided by the generator. Consequently, lower induced eddy currents lead to lower Lorentz body forces.

Fig. 7
figure 7

Lorentz body forces (N.m −3) applied on the coil as a function of lengths l 3 and l 4

Full size image

Optimization procedure of the electromagnetic compression device

Sections “Parametric modeling of the electrical loading” and “Parametric modeling of the geometry” have illustrated the construction of a multidimensional solution with PGD, and possibilities offered for optimization purpose once this solution is available. To go further, an example of optimization procedure is carried out in this section. This optimization focuses on geometrical parameters; we seek the geometrical configuration of the electromagnetic compression device maximizing the radial component of the resultant compression force applied on the part. The design space considered is formed with design variables gathered in the following vector:

$$ \mathbf{x}^{T} = \{ t, l_{1}, l_{2}, l_{3}, l_{4} \} $$
(33)

The domain of feasability consists thus of five real dimensions (i.e. \(\mathbf {x}\in \mathbb {R}^{5}\)). The thickness of the fifth layer l 5 has been removed of the design problem since it does not fit into account within the geometrical optimization of the device, but need just to be as large as possible to limit influence of the Dirichlet boundary condition on the region of interest. Each dimension is bounded so that it leads to a constrained optimization problem with inequality-type constraints:

$$\begin{array}{@{}rcl@{}} &&{\kern-.65pc}t_{\min} \leq t \leq t_{\max} \\ &&{\kern-.65pc}l_{\min} \leq l_{i} \leq l_{\max}, \; 1 \leq i \leq 4 \end{array} $$
(34)

The optimization problem is thus written as follows:

$$ \min_{\mathbf{x}} \mathbf{F} \cdot \mathbf{e}_{r} \: ; \quad \mathbf{F} = 2 \pi h {\int}_{{\Omega}_{\text{wp}}} \mathbf{f} r \mathrm{d}r \quad \text{constrained with (34)} $$
(35)

where h denotes the half-length of the workpiece. Minimizing the radial component of the resultant force or maximizing its absolute value with respect to geometrical parameters is not necessarily the best criterion that will enable the best forming of the workpiece, because a numerical analysis of the mechanical stage of the process should be embedded into the optimization procedure to check it. However, this criterion appears to be a good indicator to characterize from the process viewpoint the performance of the chain generator-coil and thus that of the eletromagnetic compression device.

Many optimization algorithms are available to solve the problem Eq. 35 [4]. A first class of algorithms are descent methods, well-suited for convex problems, but it requires the computation of the gradient of the cost function. For non-convex optimization problems, zero-degree meta-heuristic methods allow to explore the domain of feasability without the need to compute gradients. Choosing the best suited algorithm to minimize Eq. 35 is not part of the scope of this work, which just aims at illustrating the possibilities made available by the multidimensional solution built with PGD. For illustration purpose and the computational cost of the evaluation of the cost function being very small here, a brute approach is chosen in order to build and plot the cost function on its design space. The cost function is thus evaluated without any intelligence at each node of the hypermesh of the design space, built with dimension meshes used for the PGD solver detailed in section “Results”. The time interval has been reduced to focus on the subrange t ∈ [20, 60] μs, containing the minimum sought. Other numerical values remain unchanged, and the length l 5 of the fifth layer is set to 7 · 10−3m.

The cost function is evaluated 12500 times, and the procedure lasts about one hour. Figure 8 shows isovalues smoothed by Paraview [2] of the radial component of the resultant force plotted on a part of the design space. We can observe that a minimum of the cost function Eq. 35 actually exists and is unique within the range defined. These isovalues show that this minimum is obtained for the smallest values of the gap l 3 and wire width l 4, as we could expect as explained in section “Results”, and for the largest values of the inner radius of the workpiece l 1 and of its thickness l 2. The largest value required for l 1 may be explained with the parameterization retained in Fig. 4: increasing l 1 also increases the coil windings radius, so does the magnetic flux generated and hence body forces. The largest value required for the thickness value l 2 can be explained from the form of the cost function (35).

Fig. 8
figure 8

Isovalues of the radial component of the resultant force applied on the workpiece in the sub-design space (l 1,l 2,l 3) respectively in axes (X, Y, Z) at time t = 5.3 · 10−5s and length l 4 = 2 · 10−3m

Full size image

Indeed, though body forces magnitude applied on the workpiece varies little with its thickness (see Fig. 6a), the integrand of Eq. 35 consists of the radial component of these body forces weighted with the radius, arising from cylindrical coordinates. This leads to increase the value of the integral when its upper limit increases as l 2 increases. Notice that increasing the workpiece thickness l 2 will make the forming more difficult, thus minimizing Eq. 35 is actually not the best criterion to perform the best forming of the workpiece. A better criterion would be to maximize the efficiency between input electrical energy and strain work undergone by the workpiece, but requires a mechanical analysis.

Figure 9 depicts the evolution of the radial component of the resultant force over a sub-range of the time interval, plotted for the best values of the remaining set of parameters (i.e. l i , 1 ≤ i ≤ 4). Points refer to the locations of the evaluation of the cost function, an extrapolation with a cubic spline is performed afterwards. The discharged current is superposed on the same graph, and we can observe a shift of about 20 microseconds between the maximum (actually the first peak) of the current and the minimum reached by the radial component of the resultant force. This delay arises from electromagnetic induction phenomenon which is not instantaneous, and depends on the magnetic diffusivity \(1/\sqrt {\mu \sigma }\).

Fig. 9
figure 9

Plot of the radial component of the resultant force over a sub-range of the time interval for the set of parameters l 1 = 7 · 10−3m, l 2 = 7 · 10−3m, l 3 = 2 · 10−3m, l 4 = 2 · 10−3m

Full size image

Once the cost function is known on the parameter space, its sensitivities with respect to design parameters can be easily computed by partial differentiation. Figures 10 and 11 show partial derivatives of the cost function with respect to lengths l 1 and l 3 respectively. Sensitivities are quantities of great interest for optimization, and enable to decouple sets of parameters of primary importance to parameters neglectable with respect to a given cost function.

Fig. 10
figure 10

Partial derivative of the radial component of the resultant force with respect to length l 1

Full size image
Fig. 11
figure 11

Partial derivative of the radial component of the resultant force with respect to length l 3

Full size image

Conclusion

In this work, a numerical tool dedicated to the optimization of the design of an electromagnetic compression device has been developed based on PGD. Attention has been focused on Lorentz body forces generated during the process by solving the set of electromagnetic equations in quasistatics, therefore following a decoupled approach for the resolution of the coupled multiphysical problem. The purpose of this numerical tool is to optimize process parameters related to the chain generator-coil and geometrical parameters of the electromagnetic compression device with respect to the mechanical loading required to form the part.

A first analysis has been performed with the parameterization of the electrical discharged current through its decay time and angular frequency, defining a five-dimensional numerical solution, in order to optimize the chain generator-coil for a given geometry of the device. Then, a parameterization of the geometry of the electromagnetic compression device has been carried out by considering the computational domain as a multi-layered structure, the thicknesses of all layers being accounted as optimization parameters and introduced as extra-coordinates. It has been shown that the parameterization of the radial coordinate in the bidimensional axisymmetric case leads to a decomposition into more operators than for space coordinate in a cartesian frame. More generally, the keypoint to perform parametric analyses with PGD lies in the fact to find appropriate changes of variables so that a separated form of the solution be kept, allowing to preserve the efficiency of the PGD solver. Finally, possibilities offered by the multidimensional solution have been shown on an example of optimization procedure, seeking the geometrical configuration maximizing the radial component of the resultant compression force applied on the workpiece. This illustrates a first step towards the optimization of an electromagnetic compression device.

PGD turns out to be a particularly attractive method for parametric analyses. Based on the separated representation of the solution, optimization parameters are added as extra-coordinates, and the high-dimensionality of complex problems can therefore be handled more easily than with mesh-based methods. The definition of the solution on a parameter space allows to build numerical charts, from which the solution for a particular set of parameters can be extracted at a very low cost. Thus several optimization procedures can be performed once this database has been built, and their computational cost are severly decreased with respect to traditional optimization approaches.