Introduction

Plates and shells are very common in nature and thus they inspired engineers that used both them from the very beginning of structural mechanics. Nowadays, plates and shells parts are massively present in most engineering applications.

This type of structural elements involves homogeneous and heterogeneous materials, isotropic and anisotropic, linear and non-linear. The appropriate design of such parts consists not only in the structural analysis of the parts for accommodating the design loads, but also in the analysis of the associated manufacturing processes because many properties in the final parts are induced by the forming process itself (e.g. flow induced microstructures). Thus, fine analyses concern both, the structural parts and their associated forming processes.

In general the whole design requires the solution of some mathematical models governing the evolution of the quantities of interest. These models consist of a set of partial differential equations combining general balance equations (mass, energy and momentum) and some specific constitutive equations depending on the considered physics, the last involving different material parameters. These complex equations (in general non-linear and strongly coupled) must be solved in the domain of interest.

When addressing plate or shell geometries the domains in which the mathematical models must be solved become degenerated because one of its characteristic dimensions (the thickness in the present case) is much lower than the other characteristic dimensions. We will understand the consequences of such degeneracy later. When analytical solutions are neither available nor possible because of the geometrical or behavior complexities, the solution must be calculated by invoking any of the available numerical techniques (finite elements, finite differences, finite volumes, methods of particles, ...).

In the numerical framework the solution is only obtained in a discrete number of points, usually called nodes, distributed in the domain. From the solution at those points, it can be interpolated at any other point in the domain. In general regular nodal distributions are preferred because they offer better accuracies. In the case of degenerated plate or shell domains one could expect that if the solution evolves significantly in the thickness direction, a large enough number of nodes must be distributed along the thickness direction to ensure the accurate representation of the field evolution in that direction. In that case, a regular nodal distribution in the whole domain will imply the use of an extremely large number of nodes with the consequent impact on the numerical solution efficiency.

When simple behaviors and domains were considered, plate and shell theories were developed in the structural mechanics framework allowing, through the introduction of some hypotheses, reducing the 3D complexity to a 2D one related to the problem now formulated by considering the in-plane coordinates.

In the case of fluid flows this dimensionality reduction is known as lubrication theory and it allows efficient solutions of fluids flows taking place in plate or shell geometries for many type of fluids, linear (Newtonian) and non-linear. The interest of this type of flow, taking place in plate and shell geometries, is not only due to the fact that it is involved in the manufacturing processes of plate and shell parts, but also due to the fact that many tests for characterizing material behaviors involve it.

However, as soon as richer physics are concerned by the models and the considered geometries differ of those ensuring the validity of the different reduction hypotheses, simplified simulations are compromised and they fail in their predictions.

In these circumstances the reduction from the 3D model to a 2D simplified one is not obvious, and 3D simulations appear many times as the only valid route for addressing such models, that despite the fact of being defined in degenerated geometries (plate or shell) they seem requiring a fully 3D solution. However in order to integrate such a calculations (fully 3D and implying an impressive number of degrees of freedom) in usual design procedures, a new efficient (fast and accurate) solution procedure is needed.

A new discretization technique based on the use of separated representations was proposed some years ago for addressing multidimensional models suffering the so-called curse of dimensionality, where standard mesh-based techniques fail [2]. The curse of dimensionality was circumvented thanks to those separated representations that transformed the solution of a multidimensional problem into a sequence of lower dimensional problems. The interested reader can refer to the recent reviews [6–8] and the references therein.

A direct consequence was separating the physical space. Thus in plate domains an in-plane-out-of-plane decomposition was proposed for solving porous media flow models in laminates [8], then for solving elasticity problems [5] and coupled multiphysics problems [9]. In those cases the 3D solution was obtained from the solution of a sequence of 2D problems (the ones involving the in-plane coordinates) and 1D problems (the ones involving the coordinate related to the plate thickness).

It is important emphasizing the fact that these approaches are radically different from standard ones. We propose a 3D solver able to compute the different unknown 3D fields without the necessity of introducing any hypothesis. The most outstanding advantage is that 3D solutions can be obtained with a computational cost characteristic of standard 2D solutions.

In this work we generalize the just referred approach for calculating the fully 3D solution of squeeze flows in different configurations, involving mono-layers and laminates of Newtonian and power-law fluids. Finally the approach will be generalized for considering more complex scenarios exhibiting different models through the laminate thickness. For this purpose we propose an efficient 3D solution of the Brinkman equation, again based on the use of an in-plane-out-of-plane separated representations of both the model and their involved unknown fields.

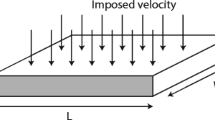
The squeeze flow of Newtonian or non-Newtonian fluids between two rigid parallel plates is relevant in many industrial problems including the moulding of fiber reinforced composites. Thermoplastic composite parts are often manufactured by compression moulding of concentrated suspensions of continuous aligned fibers, a process where squeeze flow takes place in reaction of the application of consolidation pressure. Squeeze flow induced by consolidation is an important stage of any fiber reinforced thermoplastic composite forming process. It allows the local redistribution by transverse elongation of the polymer/fiber mixture, which is very important for filling in the gaps between plies ensuring consolidation. The quality of bonding, through the healing process, of the different composite layers in laminates depends on the transverse squeeze flow mechanism. In addition excessive flow may lead to uncontrolled fiber motion and thus affect the mechanical properties of the part. It is therefore important to understand the squeeze flow behavior of thermoplastic composite laminates.

Squeeze flow has been used as an experimental method for rheological characterization [1, 11, 13, 21]. Many studies have been reported on the squeeze flow of Newtonian and non-Newtonian fluids between rigid parallel flat bodies with or without wall-slip concerning both experimental and numerical analyses, fundamentals and applications [3, 4, 12, 14–20, 22]. However it has been shown that flow should be monitored wherever possible (through appropriate visualization techniques) to get information about the real flow field during the squeezing. Experimental investigation of such a mechanism leads to practical difficulties due the small scale at which phenomena take place. Theoretical models can be used instead, however they have to be sophisticated enough to predict the real flow field and capture the actual fluid mechanics of laminate squeeze flow.

In the present work we focus on the squeeze flow occurring in composite laminates, pointing-out the limits of models based on the lubrication hypotheses, and proposing an alternative and novel route for solving very fine 3D models while preserving a computational complexity characteristic of lubrication based solutions. For this purpose we revisit in Section “Revisiting lubrication based descriptions” lubrication based modeling pointing-out its limits when addressing multilayered fluid flows as those encountered in composites laminates that seem requiring a fully 3D solution. In Section “Fully 3D modelling” we propose such a 3D efficient solution procedure based on the use of an in-plane-out-of-plane separated representation. The solutions of the 3D Stokes problem related to a Newtonian and a power-law fluid allow to conclude of the validity and limits of lubrication based solutions. Finally in Section “Brinkman’s model” we address the 3D solution of the Brinkman equations within the same framework opening new perspectives on the high fidelity solutions of 3D models defined in such degenerated geometries.

Revisiting lubrication based descriptions

Lubrication in a fluid monolayer

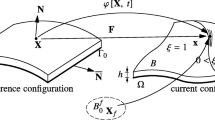
We assume a layer of a Newtonian fluid characterized by a viscosity η filling the domain Ξ = Ω × ℐ, where Ω ⊂ ℝ2 and ℐ = [−h/2, h/2] ⊂ ℝ. The layer thickness h is assumed very small with respect to the in-plane characteristic dimensions. We assume the thickness h being the same at each location x = (x, y) ∈ Ω. The layer is squeezed at a rate h ̇ . The resulting fluid flow is governed by the Stokes equations that allow calculating the velocity v = (u, v, w) and the pressure p(x, y, z) fields. Due to the very small thickness the lubrication hypotheses:

$$ \left \{ \begin{array}{l} \frac{\partial u}{\partial z} \gg \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial z} \gg \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial z} \gg \frac{\partial v}{\partial x} \\ \frac{\partial v}{\partial z} \gg \frac{\partial v}{\partial y}\\ w \approx 0 \end{array} \right. $$
(1)

can be considered into the Stokes equations, and proceeding as described in Appendix A, the fluid flow model results finally described from

$$ \dot h = -\frac{h^{3}}{12 \eta} \Delta p $$
(2)

that allows computing the pressure field p(x, y) that does not depend on the out-of-plane coordinate z. As soon as the pressure field is known, the velocity can be obtained by using (see Appendix A):

$$ \left\{ \begin{array}{ll}u=\frac{1}{2 \eta}\frac{\partial p}{\partial x}\left(z^2-\left(\frac{h}{2}\right)^{2}\right)\\ v=\frac{1}{2 \eta}\frac{\partial p}{\partial y}\left(z^2-\left(\frac{h}{2}\right)^{2}\right)\end{array} \right. $$
(3)

The reduction of the computational complexity is quite impressive because instead of solving the Stokes problem (involving the three momentum and the mass balances, all them defined in 3D, for determining the 3D velocity and pressure fields) one must only calculate the 2D pressure field from Eq. 2.

In order to address a more complex fluid rheology we consider a non-Newtonian described by the power-law constitutive equation

$$ \eta = K \cdot D_{eq}^{n-1} \cdot \mathbf D $$
(4)

where K and n are two material parameters, D the strain rate tensor and D e q the equivalent strain rate

$$ D_{eq} = \sqrt{2 \ (\mathbf D : \mathbf D) } $$
(5)

where ” : ” denotes the tensor product twice contracted. This viscosity law can describe Newtonian fluids n = 1 but also non-Newtonian fluids (rheothinning and rheothickening) for n ≠ 1.

As described in Appendix B, when considering the lubrication hypotheses (1) the velocity results

$$ \left \{ \begin{array}{l} u= \frac{\partial p}{\partial x}\frac{1}{K} \alpha^{(1-n)/n} \frac{n}{n+1} \cdot\left( |z|^{(1+n)/n} - \left(\frac{h}{2} \right)^{(1+n)/n} \right)\\ v= \frac{\partial p}{\partial y}\frac{1}{K} \alpha^{(1-n)/n} \frac{n}{n+1} \cdot\left( |z|^{(1+n)/n} - \left(\frac{h}{2} \right)^{(1+n)/n} \right) \end{array} \right. $$
(6)

with

$$ \alpha =\frac{1}{K} \sqrt{ (\nabla p)^{2}} $$
(7)

Now the flow rate q = (q x , q y ) can be computed from

$$ \left \{ \begin{array}{l} q_{x}(x,y) = \int \limits_{-h/2}^{h/2} u(x,y,z) \ dz \\ q_{y}(x,y) = \int \limits_{-h/2}^{h/2} v(x,y,z) \ dz\end{array} \right. $$
(8)

and the mass balance enforced

$$ \dot h = \nabla \cdot \mathbf q $$
(9)

that results in a second order non-linear partial differential equation that allows computing the 2D pressure field. Knowing the pressure field, the velocity can be obtained from Eq. 6.

Verifying lubrification hypotheses in multilayered laminates

In this section is verified the validity of the standard lubrication hypotheses in the case of multilayered laminates by assuming a simple dependence of the viscosity in the thickness coordinate η(z). Later we will consider that the reinforcement layers have a viscosity much bigger than the one related to the fluid layers as sketched in Fig. 1.

Fig. 1
figure 1

Composite laminate made of unidirectional prepregs separated by a pure matrix fluid

Full size image

Newtonian resin

First we consider a Newtonian resin that allows writing the momentum balance as

$$ \nabla p = \nabla(\eta \nabla \mathbf{v}) $$
(10)

that by introducing the standard lubrification hypotheses (1) leads to:

$$ \left \{ \begin{array}{l} \frac{\partial p}{\partial x}=\frac{\partial}{\partial z}\left(\eta \frac{\partial u}{\partial z}\right)\\ \frac{\partial p}{\partial y}=\frac{\partial}{\partial z}\left(\eta \frac{\partial v}{\partial z}\right) \end{array} \right. $$
(11)

with p = p(x, y) ≡ p(x).

By integrating in the thickness ℐ and taking into account the symmetry of the velocity field at z = 0, i.e. its derivative with respect to the coordinate z vanishes, we obtain:

$$ \left \{ \begin{array}{l} \frac{\partial p}{\partial x}\cdot \frac{z}{\eta} = \frac{\partial u}{\partial z}\\ \frac{\partial p}{\partial y}\cdot \frac{z}{\eta} = \frac{\partial v}{\partial z} \end{array} \right. $$
(12)

that can be integrated a second time in order to obtain the flow velocity components. For this purpose we consider a regular sequencing of resin and reinforcement layers with the same thickness and with viscosities η 1 and η 2 respectively, considering that both velocity components vanish at z = −h/2. As soon as the expression of the velocity components is available we can compute the flow rates q(x) and then enforce the mass balance ∇ · q = h ̇ to finally obtain a second order partial differential equation involving the pressure field p(x) defined in Ω.

The case of a 9-layer laminate of total thickness h = 0. 0104 m is analyzed. For the resin we considered the PEEK’s viscosity η 1 whereas for describing the rigid-like behavior of the reinforcement layers we considered a viscosity η 2 large enough, η 2 = 108 · η 1.

Once the pressure is known the velocity can be calculated from

$$ \left \{ \begin{array}{l} u=\frac{\partial p}{\partial x}\cdot \int_{-h/2}^{z} \frac{s}{\eta(s)}ds\\ v=\frac{\partial p}{\partial y}\cdot \int_{-h/2}^{z} \frac{s}{\eta(s)}ds \end{array} \right. $$
(13)

that is depicted in Fig. 2 and that clearly shows a unphysical solution where the ”rigid” layers are in fact flowing.

Fig. 2
figure 2

Velocity profile along the thickness in the case of a laminate involving a Newtonian fluid

Full size image

It is easy noticing that the large viscosity assumed in the reinforcement layers limits its shearing but accommodates an elongational flow that is not described within the standard lubrication hypotheses.

Power-law resin

In this section we analyze the validity of standard lubrification hypotheses in the case of a power-law fluid, even if we do not expect better conclusions than the ones derived from the analysis in the case of Newtonian fluids.

By following a similar procedure we obtain

$$ \left \{\begin{array}{l} u(z)=\frac{\partial p}{\partial x} \left(\sqrt{(\nabla p)^{2}}\right)^{(1-n)/n} \int \limits_{-h/2}^{z} \left(\frac{1}{K(s)}\right)^{1/n}\cdot s \cdot |s|^{(1-n)/n} ds\\ v(z)=\frac{\partial p}{\partial y} \left(\sqrt{(\nabla p)^{2}}\right)^{(1-n)/n} \int \limits_{-h/2}^{z} \left(\frac{1}{K(s)}\right)^{1/n}\cdot s \cdot |s|^{(1-n)/n} ds \end{array} \right. $$
(14)

where non-slipping boundary conditions were used. Then the flow rate can be calculated, and from it, by enforcing the mass balance, the equation governing the pressure field distribution that results in the preset case non-linear.

When considering the same problem just addressed, now taking a consistency parameter K in the reinforcement layers much bigger than the one considered in the resin ones, we obtain the velocity profile along the thickness direction shown in Fig. 3 that as in the Newtonian case seems completely unphysical by the same reasons.

Fig. 3
figure 3

Velocity profile along the thickness in the case of a laminate involving a power-law fluid

Full size image

Fully 3D modelling

We just proved than in the case of laminates composed of several layers of fluids with very different viscosities standard lubrication hypotheses fail for describing the flow kinematics. In that case fully 3D solutions seem compulsory. Even if there is no major conceptual difficulties in considering the fully 3D Stokes problem, from the numerical point of view the situation is radically different because we should consider a mesh fine enough for representing the viscosity evolution in the thickness direction and its induced effects on the flow kinematics. Such a discretization will imply an extremely large number of degrees of freedom to avoid too distorted elements in the mesh.

We proposed recently [5] an in-plane-out-of-plane separated representation that allows solving fully 3D models defined in plate geometries keeping a computational complexity characteristic of 2D simulations. This separated representation allows for independent representations of the in-plane and the thickness fields dependencies. The main idea lies in the separated representation of the velocity field according to:

$$ \mathbf{v}=\left(\begin{array}{c} u\\v\\w \end{array}\right) \approx \left(\begin{array}{c} \sum\limits^{i=N}_{i=1}X_{i}^{u}(x,y)\cdot Z_{i}^{u}(z)\\ \sum\limits^{i=N}_{i=1}X_{i}^{v}(x,y)\cdot Z_{i}^{v}(z)\\ \sum\limits^{i=N}_{i=1}X_{i}^{w}(x,y)\cdot Z_{i}^{w}(z) \end{array}\right) $$
(15)

that leads to a separated representation of the strain rate, that introduced into the Stokes problem weak form allows the calculation of functions X i (x, y) by solving the corresponding 2D equations and functions Z i (z) by solving the associated 1D equations. These 2D and 1D problems are derived considering a fixed point strategy for solving the resulting nonlinear problem. Functions depending on the z-coordinate are computed by assuming known the ones depending on the in-plane coordinates, and then the last are updated from the just calculated z-dependent functions. The iteration process continues until reaching convergence. For additional details the interested reader can refer to [5].

Because of the one-dimensional character of problems defined in the laminate thickness we can use extremely fine descriptions along the thickness direction without a significant impact on the computational efficiency.

In what follows we are considering the solution of the fully 3D Stokes problem in a laminate composed of a sequence of resin and reinforcement layers, the last ones represented thanks to a viscous enough pseudo-fluid. Later, in order to described more precisely the reinforcement layers, we will assume that the resin phase that impregnates the yarns of the reinforcement layers flows in a way that can be described by the usual Darcy’s model. In order to define a single model to be solved in the whole domain we combine the Stokes model that applies in the resin layers with the Darcy’s one applying in the fibrous layers. Both models can be coupled within the Brinkman’s model whose efficient solution will be addressed in Section “Brinkman’s model”.

Newtonian fluid

The Stokes model is defined in \(\Xi = \Omega \times \mathcal I\) and reads for an incompressible fluid:

$$ \left \{ \begin{array}{l} \nabla p = \nabla \cdot \left ( \eta \cdot \nabla \mathbf v \right ) \\ \nabla \cdot \mathbf v = 0 \end{array} \right. $$
(16)

To circumvent the issue related to stable mixed formulations (LBB conditions) within the separated representation used in what follows, we consider a penalty formulation that modifies the mass balance by introducing a penalty coefficient λ small enough

$$ \nabla \cdot \mathbf{v}+ \lambda \cdot p=0 $$
(17)

or more explicitly

$$ p= -\frac{1}{\lambda} \left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right) = - \frac{\nabla \cdot \mathbf v}{\lambda} $$
(18)

By replacing it into the momentum balance (first equation in (16)) we obtain

$$ \nabla(\nabla \cdot \mathbf{v})+\xi \Delta \mathbf{v}=0 $$
(19)

with ξ = η · λ. By developing it results

$$ \left(\begin{array}{c} \frac{\partial}{\partial x}\\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z} \end{array}\right) \left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right)+\xi \left(\begin{array}{c} \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} + \frac{\partial^{2} u}{\partial z^{2}} \\ \frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} + \frac{\partial^{2} v}{\partial z^{2}} \\ \frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} w}{\partial z^{2}} \end{array} \right)=0 $$
(20)

or

$$ \left(\begin{array}{c} \frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial}{\partial x}\frac{\partial v}{\partial y}+\frac{\partial}{\partial x}\frac{\partial w}{\partial z}\\ \frac{\partial}{\partial y}\frac{\partial u}{\partial x}+\frac{\partial^{2} v}{\partial y^{2}}+\frac{\partial}{\partial y}\frac{\partial w}{\partial z}\\ \frac{\partial}{\partial z}\frac{\partial u}{\partial x}+\frac{\partial}{\partial z}\frac{\partial v}{\partial y}+\frac{\partial^{2} w}{\partial z^{2}}\\ \end{array}\right)+ \xi \left(\begin{array}{c} \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} + \frac{\partial^{2} u}{\partial z^{2}} \\ \frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} + \frac{\partial^{2} v}{\partial z^{2}} \\ \frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} w}{\partial z^{2}} \end{array} \right)=0 $$
(21)

We consider again the fluid monolayer previously considered in the case of a Newtonian fluid with constant viscosity and take λ = 10−10. By comparing the 3D Stokes solution and the one obtained considering the lubrication hypotheses, the relative error is of about 0.7 %, validating the lubrication model in the case of a fluid monolayer of constant viscosity. The error related to the separated representation solution associated to the PGD solver with respect to a fully 3D finite element solution (computed on a mesh fine enough) was found lower than 0.1 %.

The fully 3D solution of the Stokes model seems particularly pertinent when addressing scenarios where the viscosity evolves in the thickness, as was the case when considering multilayered laminates.

When the multilayered laminate considered previously is solved by considering the fully 3D approach instead of the lubrication based 2D model we obtain the velocity profile depicted in Fig. 4. When comparing it with the one obtained within the lubrication framework the following conclusions can be stressed:

  1. 1.

    the solution obtained within the lubrication framework is very accurate when describing the squeeze flow of a Newtonian fluid monolayer with constant viscosity;

  2. 2.

    the solution obtained within the lubrication framework when addressing a laminate consisting of different layers of Newtonian fluids with very different viscosities is definitively wrong;

  3. 3.

    when lubrication approaches fail the only valuable alternative consists of solving the fully 3D Stokes problem. The efficient fully 3D solution is possible by applying the in-plane-out-of-plane separated representation.

Fig. 4
figure 4

Velocity profile related to the fully 3D Stokes solution in a multilayered laminate

Full size image

Note that the fully 3D solution was computed by using a mesh of Ω involving 3600 nodes and a mesh of ℐ consisting of 800 nodes uniformly distributed along the laminate thickness. An equivalent finite element description would require 3600 × 800 = 2880000 nodes, each one containing three degrees of freedom, the three velocity components. The separated representation solution addressed in Eq. 15 was computed in 3 minutes on a quad-core laptop, 2.3 Ghz per core. The separated solution involved 9 terms ( N = 9 in Eq. 15).

Power-law fluid

The Stokes model extended to power-law fluids reads:

$$ \left \{ \begin{array}{l} \nabla p = \nabla \cdot \mathbf T \\ \nabla \cdot \mathbf v = 0 \end{array} \right. $$
(22)

where the extra-stress tensor for power-law fluids writes:

$$ \mathbf T = 2 K \cdot D_{eq}^{n-1} \cdot \mathbf D $$
(23)

with D the strain rate tensor:

$$ \mathbf D=\left(\begin{array}{ccc} \frac{\partial u}{\partial x} & \frac{1}{2}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) & \frac{1}{2}\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right) \\ \frac{1}{2}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) & \frac{\partial v}{\partial y} & \frac{1}{2}\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right) \\ \frac{1}{2}\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right) & \frac{1}{2}\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right) & \frac{\partial w}{\partial z} \\ \end{array} \right) $$
(24)

and the equivalent strain rate D eq given by:

$$ D_{eq} = \sqrt{2 (\mathbf D : \mathbf D)} $$
(25)

where ” : ” denotes the tensor product twice contracted.

The solution is again carried out by using a penalty formulation. Moreover, at each iteration of the non-linear solver we must evaluate the equivalent strain rate, and write it in a separated form for enhancing the efficiency of the separated representation solver [5]. The simplest way for performing such decomposition

$$ D_{eq}^{n-1} \approx \sum\limits_{i=1}^{i=M} F_{i}(x,y) \cdot G_{i}(z) $$
(26)

consists of using a singular value decomposition. This decomposition is optimal but it requires a 3D reconstruction and data storage that can be too expensive from the computational point of view. Alternantives based on the use of discrete empirical interpolations (DEIM) are being developed to overcome this important drawback [10].

The solution related to n = 0. 49 and h = 0. 00104m. in a fluid monolayer was compared to the one previously obtained within the lubrication framework. Both solutions were in perfect agreement validating the simplified modeling based on the lubrication approach.

Then we consider the multilayered laminate previously addressed within the lubrification framework. The 3D solution is depicted in Fig. 5. The comparison of solutions obtained by using both approaches, the fully 3D and the one based on the use of the lubrication hypotheses, leads to following conclusions:

  1. 1.

    the solution obtained within the lubrication framework is very accurate when describing the squeeze flow of a power-law fluid monolayer;

  2. 2.

    the solution obtained within the lubrication framework when addressing a laminate consisting of different layers of power-law fluids with very different viscosities is definitively wrong;

  3. 3.

    when lubrication approaches fail the only valuable alternative consists of solving the fully 3D Stokes problem for power-law fluids. The efficient 3D solution is again possible by applying the in-plane-out-of-plane separated representation.

Fig. 5
figure 5

Velocity profile along the laminate thickness: the reduced strain rate around the mid-plane implies a greater viscosity and then lower velocities

Full size image

Brinkman’s model

As indicated before, in composites manufacturing processes resin located between fibers in the reinforcement layers also flows. A usual approach for evaluating the resin flow in such circumstances consists of solving the associated Darcy’s model. It is well known that Darcy-Stokes coupling at the interlayers generates numerical instabilities because the localized boundary layers whose accurate description requires very rich representations (very fine meshes along the laminate thickness).

In this section we propose to use the Brinkman model that allows representing in an unified manner both the Darcy and the Stokes behaviors. In order to avoid numerical inaccuracies we use a very fine representation along the thickness direction and for circumventing the exponential increase in the number of degrees of freedom that such a fine representation would imply when extended to the whole laminate domain, we consider again the in-plane-out-of-plane separated representation previously introduced.

The Brinkman model is defined by:

$$ \nabla p= \mu \cdot \mathbf K^{-1} \cdot \mathbf{v}+\eta \cdot \Delta \mathbf{v} $$
(27)

where μ is the dynamic viscosity, K the layer permeability tensor and η the dynamic effective viscosity.

In the zones where Stokes model applies (resin layers) we assign a very large isotropic permeability K = I (units in the metric system and I being the unit tensor) whereas in the ones occupied by the reinforcement, the permeability is assumed anisotropic, being several orders of magnitude lower, typically 10−8. Thus the Darcy’s component in Eq. 27 does not perturb the Stokes flow in the resin layers, and it becomes dominant in the reinforcement layers. Additionally by choosing this outstanding difference in permeability, representative of the one observed in liquid Resin Infusion process when highly porous distribution media are used, we also want to give the evidence that this type of problem can be addressed by the proposed approach.

In the numerical examples we consider again a 9-layer laminate alternating resin and unidirectional reinforcement layers. On the other hand the fibrous layers alternate the 0° and 90° directions as depicted in Fig. 6. The permeability component in the fiber direction is K / / = 10− 8 m 2, being the one related to the perpendicular directions one order of magnitude lower K ⊥ = 10−9 m 2. The viscosities involved in the Brinkman’s models are η = 200P a. s, and as usually considered η / μ = 2. Finally the penalty coefficient is fixed to λ = 10−9.

Fig. 6
figure 6

Model considered for solving Brinkman equations: Newtonian layer, unidirectional reinforcement aligned along the y-direction (90°) and unidirectional reinforcement aligned along the x-direction (0°)

Full size image

The resulting velocity profile along the thickness direction depends on the considered velocity component because the layers sequencing that alternates the x and y directions. Figures 7 and 8 depicts the velocity profiles u(x 1, z) and v(x 2, z) respectively, at positions x 1 = (L x , L y /2) and x 2 = (L x /2, L y ). We can notice that as expected when one velocity component is high in a fibrous layer, the other is low and vice-versa, because the differences of permeabilities induced by the fibers orientation. On the other hand because resin can flow from the resin layers to the fibrous ones and vice-versa the maximum velocity evolves along the z-coordinate as noticed in the previous figures. These mechanisms explain the noticed loss of symmetry of the velocity field along the thickness direction. This fact plenty justifies the 3D modeling, proving the limits of a lubrication approaches.

Fig. 7
figure 7

u(x = L x , y = L y /2, z) associated with the 3D Brinkman solution

Full size image
Fig. 8
figure 8

\(v(x=L_x/2,y=L_{y},z)\) associated with the 3D Brinkman solution

Full size image

Finally we compute the out-of-plane velocity component w(x = L x /2, y = L y /2, z) and compare it with the one obtained in the previous section by solving the Stokes equations. Both are depicted in Fig. 9. When considering the fully Stokes equation the velocity of the resin in the fibrous layers (modeled from a pseudo-fluid with large enough viscosity) was constant along the layer thickness (fibrous layers behave like a rigid solid) whereas in the case of the Brinkman model this velocity evolves inside the fibrous layer proving the existence of complex flow exchanges between the different layers.

Fig. 9
figure 9

Comparing the out-of-plane velocity component of both the 3D Brinkman and Stokes solutions

Full size image

Conclusion

In this paper we analyzed the validity of lubrication approaches for addressing squeeze flows in composite laminates. We considered different resin behaviors: Newtonian and shear thinning non-Newtonian fluids described by a power-law; and different configurations: monolayer or multilayered laminates. In the latter case we represented the fibrous layers by using two approaches: (i) a pseudo-fluid with a large enough viscosity within the Stokes framewotk or (ii) by taking into account the resin flow within the fibrous layers from a Darcy’s model. In the last case we considered the unified formulation due to Brinkman that combines both behaviors, the viscous one (Stokes) and the flow in porous media (Darcy).

When describing fibrous layers from a viscous enough pseudo-fluid the main conclusions are (for both Newtonian and power-law behaviors):

  1. 1.

    the solution obtained within the lubrication framework is very accurate when describing the squeeze flow of a fluid monolayer;

  2. 2.

    the solution obtained within the lubrication framework when addressing a laminate consisting of different layers of fluids with very different viscosities is definitively wrong;

  3. 3.

    when lubrication approaches fail the only valuable alternative consists of solving the fully 3D flow model. The efficient 3D solution is possible by applying the in-plane-out-of-plane separated representation.

Finally, the last section allowed considering finer descriptions based on a more realistic model of resin flow within the fibrous layers, consisting in the solution of the fully 3D Brinkman model that revealed a rich kinematics along the laminate thickness. This rich behavior requires a fine enough representation, that implies the necessity of using extremely fine discretizations in the thickness direction. This fact limits the applicability of standard 3D discretizations because the number of degrees of freedom increases too much, however when the solution is addressed by considering an in-plane-out-of-plane separated representation the fully 3D solution can be computed with a computational complexity characteristic of lubrication models (2D).