1 Introduction

Nowadays, glass fiber-reinforced polymer (GFRP) laminated composite structures sandwiched with honeycomb core are widely used in railway, marine, automotive, military, and exclusively in aerospace industries owing to their superior structural properties such as high specific stiffness, better-bending stiffness, and shear strength [1, 2]. The honeycomb sandwich composite consists of two thin face sheets and various types of core structures, such as honeycomb and foam [3]. Honeycomb sandwich composite structures, apart from being lightweight, is able to withstand out-of-plane shear and pressure load [1]. Also, the core structure transfers the load between the two face sheets, which results in a better load-carrying capacity of the composite sandwich structures [4]. Off late, nanomaterials are being employed as reinforcement in GFRP laminated honeycomb sandwich composites. Carbon nanotubes (CNTs) have received much attention due to their low density, extraordinary mechanical properties, thermomechanical properties and high permeability [5]. Several researchers have studied the effect of MWCNT reinforcement in the polymer matrix [6,7,8,9]. However, the use of CNT-reinforced polymer matrix is limited due to the difficulties associated with the proper dispersion of CNTs in the polymer matrix [10]. Several studies have reported the influence of the dispersion of CNTs on the mechanical properties of the polymer matrix. Garg et al. [11] inferred that functionalization process significantly improved the dispersion of CNTs, which consequently led to enhancement in mechanical properties; about 50% improvement in the flexural strength was found in the composite containing functionalized nanotubes as compared to the composites containing pristine CNTs. Chandra et al. [12] found that a low-viscosity dispersion medium for the dispersion of CNTs in foam-cored sandwich composites resulted in significant improvement in compressive strength. Along with laminated composites, CNTs have also been readily used in sandwich structures. Shifa et al. [13] evaluated the mechanical and electrical properties of CNT-reinforced sandwich composite structures and reported that the CNT-reinforced sandwich composite structure outperformed the unreinforced sandwich structure. In addition to experimental analysis, a large number of theoretical studies have also been conducted to explore the structural and mechanical behavior of CNT-reinforced sandwich composite structures. Chakraborty and Dey performed a nonlinear analysis to investigate the influence of volume fraction, gradation of CNTs and core thickness on the stability behavior of CNT-reinforced sandwich composites [14]. Bacciocchi and Tarantino [15] proposed an accurate and easily applicable tool to analyze the buckling response of sandwich plates with a honeycomb core and three-phase orthotropic skins based on the Reissner–Mindlin theory for laminated plates. Nijmi et al. [16] investigated the effect of carbon nanotubes and core wall thickness on the compressive and bending behavior of sandwich panels. The study concentrated on the construction of honeycomb sandwich panels reinforced with carbon nanotubes (CNT) using silicone moulding. Results showed that the compressive strength of honeycomb panels increased with an increase in CNT loading and wall thickness. The compressive strength of the sandwich panel containing 0.025 wt% CNT was 42 MPa, which was enhanced to 54 MPa for the panel containing 0.075 wt% CNT. Swetha et al. [17] carried out vibration analysis of hybrid honeycomb core sandwich composites with functional grade CNT reinforced polymer face sheets were varying under thermal environment conditions. Arunkumar et al. [18] performed analytical analysis of vibro-acoustic responses of graphene foam core and FG-CNT reinforced face sheets sandwich panels and developed the governing equation using the Hamilton principle. Praveen et al. [19] experimentally determined the shear properties of CNT-reinforced honeycomb cored sandwich plate in the corrugation (Gxz) and joining (Gyz) directions and found that the distribution of CNTs substantially influences the shear properties.

Different kinematic models viz. Classical Laminated Plate Theory (CLPT), First order Shear Deformation Theory (FSDT), Higher order Shear Deformation Theory (HSDT), etc. and different commercial finite element software such as Abacus, Ansys and Digimat-HC have been used to study the structural performance of honeycomb cored sandwich composites [20,21,22,23,24,25]. Although numerous work has been carried out to understand the mechanical and structural characteristics of CNT-reinforced honeycomb composites, however, there are a limited number of work where both numerical and experimental analysis of the aforementioned composites has been performed. In the present work, MWCNT reinforced honeycomb cored sandwich composite has been fabricated and the influence of various parameters on the bending characteristics, core shear strength and bending strength of the face sheet has been evaluated. The bending behavior of honeycomb-cored MWCNT-reinforced sandwich composite plate was investigated using an in-house finite element model based on HSDT and commercial Digimat-HC software. The accuracy of the FE models was validated by comparing the deflection values with existing literature and experimental three-point bending test results.

2 Theoretical Formulations

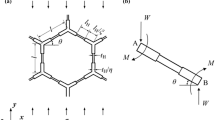
In the current section, numerical modeling of the bending behavior of a sandwich composite plate has been discussed. The sandwich plate consists of two stiff face-sheets at the top and bottom, sandwiched with one lightweight honeycomb core in the middle, as depicted in Fig. 1. The in-plane span length of the sandwich composite plate in the longitudinal and transverse direction is designated as ‘Sl’ and ‘Sw’, respectively, and the out of plane core thickness is designated as ‘hc’. It is important to note here that the developed mathematical formulations are presented in a brief form, detailed formulations can be found in the previous work of the authors [4].

Fig. 1
figure 1

Schematic diagram of honeycomb core sandwich structure

Full size image

2.1 Displacement Fields of the Composite Plate

The displacement fields for the top and bottom face sheets were derived based on Reddy’s HSDT model, as presented [10, 21]:

$$ \left\{ \begin{gathered} u_{{{\text{t}},{\text{b}}}} (x,y,z) \hfill \\ v_{{{\text{t}},{\text{b}}}} \left( {x,y,z} \right) \hfill \\ w\left( {x,y,z} \right) \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} u_{{{\text{mid\_}}{\kern 1pt} {\text{t,b}}}} \left( {x,y} \right) \hfill \\ \,v_{{_{{{\text{mid\_}}{\kern 1pt} {\text{t,b}}}} }} \left( {x,y} \right) \hfill \\ \;\;w_{{{\text{mid}}}} \left( {x,y} \right) \hfill \\ \end{gathered} \right\} + z\left\{ \begin{gathered} \phi_{x} \left( {x,y} \right) \hfill \\ \phi_{y} \left( {x,y} \right) \hfill \\ \quad 0 \hfill \\ \end{gathered} \right\} - \frac{{4z^{3} }}{{3h_{{\text{st,sb}}}^{2} }}\left\{ \begin{gathered} \chi_{x} \left( {x,y} \right) \hfill \\ \chi_{y} \left( {x,y} \right) \hfill \\ \quad 0 \hfill \\ \end{gathered} \right\}, $$
(1)

where, \({u}_{\mathrm{t},\mathrm{b}}\), \({v}_{\mathrm{t},\mathrm{b}}\) and \(w\) denote displacement fields with reference to x, y and z co-ordinates, respectively; \({u}_{{\mathrm{mid}}_{\_}\mathrm{t},\mathrm{b}}\), \({v}_{{\mathrm{mid}}_{\_}\mathrm{t},\mathrm{b}}\) and \({w}_{\mathrm{mid}}\) denote the midplane displacements with respect to x, y and z co-ordinates; \({\varphi }_{x}\) and \({\varphi }_{y}\) represent the rotation filed;\({\chi }_{x}\) and \({\chi }_{y}\) are high-order terms; \({h}_{\mathrm{st}}\mathrm{ and }{h}_{\mathrm{sb}}\) represent the thickness of the top and bottom orthotropic face sheet layer, respectively. The subscripts t and b represent the top and bottom face sheets, respectively.

The displacement fields for the core layer can be expressed as follows [27]:

$$ \left\{ \begin{gathered} U_{{{\text{core}}}} \hfill \\ V_{{{\text{core}}}} \hfill \\ w_{{{\text{core}}}} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} U_{o}^{{_{{{\text{core}}}} }} \hfill \\ V_{o}^{{_{{{\text{core}}}} }} \hfill \\ w_{o} \hfill \\ \end{gathered} \right\} + z\left\{ \begin{gathered} \lambda_{x}^{{{\text{Core}}}} \hfill \\ \lambda_{y}^{{{\text{Core}}}} \hfill \\ 0 \hfill \\ \end{gathered} \right\}, $$
(2)

where the displacement field of the core layer is represented with respect to the in-plane displacement of the top and bottom face sheets and \(z = - \left( {\frac{{h_{{{\text{st}}}} }}{2}} \right)\) and \(\left( {\frac{{h_{{{\text{sb}}}} }}{2}} \right)\). The details of mid-plane strain terms are illustrated in ref. [4].

2.2 Strain Fields

The in-plane strain field constituents of the top and bottom orthotropic face sheet with respect to the z-coordinates are as shown:

$$ \left\{ \begin{gathered} \left( {\varepsilon_{x}^{{}} } \right)_{{{\text{t,}}{\kern 1pt} {\text{b}}}} \hfill \\ \left( {\varepsilon_{y}^{{}} } \right)_{{{\text{t,}}{\kern 1pt} {\text{b}}}} \hfill \\ \left( {\gamma_{xy}^{{}} } \right)_{{{\text{t,}}{\kern 1pt} {\text{b}}}} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} (\varepsilon_{x}^{0} ) \hfill \\ (\varepsilon_{y}^{0} ) \hfill \\ (\gamma_{xy}^{0} ) \hfill \\ \end{gathered} \right\} + z\left\{ \begin{gathered} (\varepsilon_{x}^{1} ) \hfill \\ (\varepsilon_{y}^{1} ) \hfill \\ (\gamma_{xy}^{1} ) \hfill \\ \end{gathered} \right\} + z^{3} \left\{ \begin{gathered} (\varepsilon_{x}^{2} ) \hfill \\ (\varepsilon_{y}^{2} ) \hfill \\ (\gamma_{xy}^{2} ) \hfill \\ \end{gathered} \right\}. $$
(3)

The transverse shear strain constituents of the top and bottom orthotropic face sheet can be expressed as:

$$ \left\{ \begin{gathered} \left( {\gamma_{xz}^{{}} } \right)_{{{\text{t,}}{\kern 1pt} {\text{b}}}} \hfill \\ \left( {\gamma_{yz}^{{}} } \right)_{{{\text{t,}}{\kern 1pt} {\text{b}}}} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} \left( {\gamma_{xz}^{3} } \right) \hfill \\ (\gamma_{yz}^{3} ) \hfill \\ \end{gathered} \right\} + z\left\{ \begin{gathered} \left( {\gamma_{xz}^{4} } \right) \hfill \\ (\gamma_{yz}^{4} ) \hfill \\ \end{gathered} \right\} + z^{2} \left\{ \begin{gathered} \left( {\gamma_{xz}^{5} } \right) \hfill \\ (\gamma_{yz}^{5} ) \hfill \\ \end{gathered} \right\} + z^{3} \left\{ \begin{gathered} \left( {\gamma_{xz}^{6} } \right) \hfill \\ (\gamma_{yz}^{6} ) \hfill \\ \end{gathered} \right\}. $$
(4)

2.3 Constitutive Equation

The thermo-elastic stress–strain constitutive relationships for the top and bottom orthotropic face sheets with different layer orientations were derived using Hook’s law in terms of strains and stresses corresponding to laminate coordinates (x, y, z) as presented below:

$$ \left\{ {\sigma_{ij} } \right\} = \left[ {\overline{Q}_{ij} } \right]\;\left[ {\left\{ {\varepsilon_{ij} } \right\} - \Delta T\left\{ {\alpha_{ij} } \right\}} \right]. $$
(5)

The expanded form of Eq. (5) can be written as:

$$ \left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \tau_{xz} \hfill \\ \tau_{yz} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } & 0 & 0 \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } & 0 & 0 \\ {\overline{Q}_{16} } & {\overline{Q}_{26} } & {\overline{Q}_{66} } & 0 & 0 \\ 0 & 0 & 0 & {\overline{Q}_{44} } & {\overline{Q}_{45} } \\ 0 & 0 & 0 & {\overline{Q}_{45} } & {\overline{Q}_{55} } \\ \end{array} } \right]\left[ {\left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {\alpha_{x} } \\ {\alpha_{y} } \\ {\alpha_{xy} } \\ 0 \\ 0 \\ \end{array} } \right] \; \Delta T} \right], $$
(6)

where \(\overline{Q}_{ij}\) is the transformed material constants in the global x, y, z coordinate system, which can be expressed as a local coordinate system and transformation matrix, T1 in the following [28].

$$ \left[ {\overline{Q}_{ij} } \right] = \left[ {T_{1} } \right]\,\left[ {Q_{ij} } \right]\left[ {T_{1} } \right]^{T} , $$
(7)

where \(Q_{ij}\) can be found in reference [28].

The transformation matrix \(T_{1}\) is presented as:

$$ \left[ {T_{1} } \right] = \left[ {\begin{array}{*{20}c} {c^{2} } & {s^{2} } & {2cs} & 0 & 0 \\ {s^{2} } & {c^{2} } & { - 2cs} & 0 & 0 \\ { - cs} & {cs} & {c^{2} - s^{2} } & 0 & 0 \\ 0 & 0 & 0 & c & s \\ 0 & 0 & 0 & { - s} & c \\ \end{array} } \right], $$
(8)

where c = cosθ and s = sinθ; θ is the laminate orientation. Similarly, the thermal expansion coefficient also transformed into a global x, y, z coordinate system as presented below:

$$ \left[ {\begin{array}{*{20}c} {\alpha_{x} } \\ {\alpha_{y} } \\ {\alpha_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {c^{2} } & {s^{2} } & 0 \\ {s^{2} } & {c^{2} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\alpha_{1} } \\ {\alpha_{2} } \\ {\alpha_{12} } \\ \end{array} } \right]. $$
(9)

2.4 Governing Equation

The equation of equilibrium for bending analysis of the sandwich composite plate subjected to thermo-mechanical loading is obtained by using the minimum potential energy as presented below:

$$ \delta \left( {U - W} \right) = 0, $$
(10)

where, \(\delta\) is the variation symbol; \(\Pi = U\) is the total potential energy of the sandwich composite plate having volume, V and area, A.

2.4.1 Strain Energy

The total strain energy, U, can be obtained using the following expression:

$$ U = \frac{1}{2}\iint {\left\{ {\sum\limits_{k = 1}^{n} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\{ \varepsilon \}^{T} \left[ Q \right]^{k} \{ \varepsilon \} {\text{d}}z} } } \right\}}{\text{d}}x{\text{d}}y. $$
(11)

The strain energy for the bottom and face sheets induced due to axial deformation is rewritten by substituting the individual values of strain and stressed and presented in the following form:

$$ \begin{gathered} U_{{\text{t,b}}} = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{{ - \frac{B}{2}}}^{\frac{B}{2}} {\left\{ {\begin{array}{*{20}c} {\left( {\frac{{\partial \,u_{0} }}{\partial x}} \right)_{{\text{t,b}}} } \\ {\left( {\frac{{\partial \,v_{0} }}{\partial y}} \right)_{{\text{t,b}}} } \\ {\left( {\frac{{\partial \,u_{0} }}{\partial y} + \frac{{\partial \,v_{0} }}{\partial x}} \right)_{{\text{t,b}}} } \\ {\frac{{\partial \phi_{x} }}{\partial x}} \\ {\frac{{\partial \phi_{y} }}{\partial y}} \\ {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \\ {\frac{{\partial \chi_{x} }}{\partial x}} \\ \begin{gathered} \quad \;\frac{{\partial \chi_{y} }}{\partial y} \hfill \\ \frac{{\partial \chi_{x} }}{\partial y} + \frac{{\partial \chi_{y} }}{\partial x} \hfill \\ \end{gathered} \\ \end{array} } \right\}} }^{T} \times \left[ {\begin{array}{*{20}c} {A_{ij} } & {B_{ij} } & {E_{ij} } \\ {B_{ij} } & {D_{ij} } & {F_{ij} } \\ {E_{ij} } & {F_{ij} } & {H_{ij} } \\ \end{array} } \right]\; \times \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\partial \,u_{0} }}{\partial x}} \right)_{{\text{t,b}}} } \\ {\left( {\frac{{\partial \,v_{0} }}{\partial y}} \right)_{{\text{t,b}}} } \\ {\left( {\frac{{\partial \,u_{0} }}{\partial y} + \frac{{\partial \,v_{0} }}{\partial x}} \right)_{{\text{t,b}}} } \\ {\frac{{\partial \phi_{x} }}{\partial x}} \\ {\frac{{\partial \phi_{y} }}{\partial y}} \\ {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \\ {\frac{{\partial \chi_{x} }}{\partial x}} \\ \begin{gathered} \quad \;\frac{{\partial \chi_{y} }}{\partial y} \hfill \\ \frac{{\partial \chi_{x} }}{\partial y} + \frac{{\partial \chi_{y} }}{\partial x} \hfill \\ \end{gathered} \\ \end{array} } \right\}{\text{d}}x{\text{d}}y. \hfill \\ \hfill \\ \end{gathered} $$
(12)

The strain energy for bottom and face sheets induced due to transverse shear strain can be rewritten as presented below:

$$ \left( {U_{{\text{s}}} } \right)_{{\text{t,b}}} = \frac{1}{2}\int\limits_{{}}^{{}} {\int\limits_{{}}^{{}} {\left\{ {\begin{array}{*{20}c} {\frac{{\partial w_{0} }}{\partial x} + \phi_{x} } \\ {\frac{{\partial w_{0} }}{\partial y} + \phi_{y} } \\ { - \frac{4}{{h^{2} }}\chi_{x} } \\ { - \frac{4}{{h^{2} }}\chi_{y} } \\ \end{array} } \right\}} }^{T} \times \left[ {\begin{array}{*{20}c} {A_{11}^{s} } & {A_{12}^{s} } & {D_{11}^{s} } & {D_{12}^{s} } \\ {A_{21}^{s} } & {A_{22}^{s} } & {D_{21}^{s} } & {D_{22}^{s} } \\ {D_{11}^{s} } & {D_{12}^{s} } & {F_{11}^{s} } & {F_{12}^{s} } \\ {D_{21}^{s} } & {D_{22}^{s} } & {F_{21}^{s} } & {F_{22}^{s} } \\ \end{array} } \right] \times \left\{ {\begin{array}{*{20}c} {\frac{{\partial w_{0} }}{\partial x} + \phi_{x} } \\ {\frac{{\partial w_{0} }}{\partial y} + \phi_{y} } \\ { - \frac{4}{{h^{2} }}\chi_{x} } \\ { - \frac{4}{{h^{2} }}\chi_{y} } \\ \end{array} } \right\}\;{\text{d}}x{\text{d}}y. $$
(13)

The strain energy core layer of the sandwich plate can be written as:

$$ U_{{\text{c}}} = \frac{1}{2}\int\limits_{v} {\;\,\left\{ {\left\{ {\;\left( {\gamma_{yz} } \right){\kern 1pt}_{c}^{T} G_{yz}^{c} \;\left( {\gamma_{yz} } \right)_{{\text{c}}} \;} \right\} + \left\{ {\;\left( {\gamma_{xz} } \right)_{{\text{c}}}^{T} G_{xz}^{{\text{c}}} \;\left( {\gamma_{xz} } \right)_{{\text{c}}} \;} \right\}} \right\}{\text{d}}v} , $$
(14)

where \(G_{yz}^{{\text{c}}}\) and \(G_{xz}^{{\text{c}}}\) is the core layer shear modulus with reference to yz and xz axis of the core, respectively; \(\left( {\gamma_{xz} } \right)_{{\text{c}}}\) and \(\left( {\gamma_{yz} } \right)_{{\text{c}}}\) is the core layer shear strain of ith reference to yz and xz axis of the core, respectively, and is presented in the following Eqs. 15 and 16.

$$ \gamma_{xz} = \left( {\frac{{\partial w_{{\text{o}}} }}{\partial x}} \right) + \left( {\frac{{u_{{{\text{ot}}}} - u_{{{\text{ob}}}} }}{{h_{{\text{c}}} }} - \left( {\frac{{h_{{{\text{st}}}} + h_{{{\text{sb}}}} }}{{2h_{{\text{c}}} }}} \right)\phi_{x} + \left( {\frac{{h_{{{\text{st}}}} + h_{{{\text{sb}}}} }}{{6h_{{\text{c}}} }}} \right)\chi_{x} } \right), $$
(15)
$$ \gamma_{yz} = \left( {\frac{{\partial w_{{\text{o}}} }}{\partial y}} \right) + \left( {\frac{{v_{{{\text{ot}}}} - v_{{{\text{ob}}}} }}{{h_{{\text{c}}} }} - \left( {\frac{{h_{{{\text{st}}}} + h_{{{\text{sb}}}} }}{{2h_{{\text{c}}} }}} \right)\phi_{y} + \left( {\frac{{h_{{{\text{st}}}} + h_{{{\text{sb}}}} }}{{6h_{{\text{c}}} }}} \right)\chi_{y} } \right). $$
(16)

The total strain energy of the sandwich composite plate can be rewritten as follows:

$$ U = U_{{\text{t,b}}} + \left( {U_{{\text{s}}} } \right)_{{\text{t,b}}} + U_{{\text{c}}} . $$
(18)

2.4.2 Work Done

The work done, W, due to the combined external mechanical load and thermal forces can be expressed as:

$$ W = \iint {\{ d\}^{T} \{ F\} {\text{d}}x{\kern 1pt} {\text{d}}y} + \iint {\sum\limits_{k = 1}^{n} {\left( {\{ \varepsilon \}^{T} \left[ {\overline{Q}_{ij} } \right]^{k} \{ \varepsilon_{{{\text{th}}}} \} } \right)} }{\kern 1pt} {\text{d}}x{\text{d}}y, $$
(19)

where \(\varepsilon_{{{\text{th}}}}\) is the strain due to thermal forces.

2.5 Finite Element Formulation

The actual honeycomb cored sandwich composite plate was converted into small but finite, well-defined elements using the FEM. In the current study, a nine-node Lagragian plate element is utilized. Elastic properties are specified, boundary conditions and forces are applied at each element nodes.

For each element of the composite plate, the displacement vectors are expressed as:

$$ \{ d\} = \sum\limits_{i = 1}^{9} {[N_{i} } ]\{ (d_{i} )\} ;\quad (i = 1,\,2\,, \ldots 9), $$
(20)

where Ni is shape functions of the considered element.

The nodal DOF assigned to node ‘I’ can be written as [5]:

$$ \left. \begin{gathered} \left( {d_{i} } \right)_{t} = \left\{ {u_{0t1} ,v_{0t1} ,w_{1} ,\phi_{x1} ,\phi_{y1} ,\chi_{x1} ,\chi_{y1} , \cdots u_{0t9} ,v_{0t9} ,w_{9} ,\phi_{x9} ,\phi_{y9} ,\chi_{x9} ,\chi_{y9} } \right\}\,^{T} \hfill \\ \left( {d_{i} } \right)_{t} = \left\{ {u_{0b1} ,v_{0b1} ,w_{1} ,\phi_{x1} ,\phi_{y1} ,\psi_{x1} ,\chi_{y1} , \cdots u_{0b9} ,v_{0b9} ,w_{9} ,\phi_{x9} ,\phi_{y9} ,\chi_{x9} ,\chi_{y9} } \right\}\,^{T} \hfill \\ \end{gathered} \right\}. $$
(21)

The stiffness, \(k_{ij}^{e}\) of each element is computed using a three-point Gaussian quadrature and a strain displacement matrix generated at a particular node, as presented below:

$$ k_{ij}^{e} = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {[B]^{T} [D][B]\;[J]{\text{d}}\xi \;{\text{d}}\eta ,} } $$
(22)

where [B] is the strain displacement matrix. For predicting the global bending response of the sandwich composite plate, elemental stiffness matrices and load vectors are assembled in accordance with the requirements of nodal equilibrium and boundary conditions to get the global stiffness matrix and global load vector. The strain displacement matrix, [B] for the core layer and face sheets are illustrated in the reference [4].

The element nodal load vector due to the transverse load can be obtained as:

$$ [P_{e} ] = \iint {N_{i} [q]\,{\text{d}}x\,{\text{d}}y}. $$
(23)

The element nodal load vector due to the thermal load can be obtained as:

$$ [P_{e}^{{{\text{th}}}} ] = \iint {[B]^{T} \left\{ {F^{{{\text{th}}}} } \right\}\,{\text{d}}x\,{\text{d}}y}. $$
(24)

The elemental level stiffness metrics, \(k_{ij}^{e}\), displacement vector, d, element level nodal load vectors assembled to obtain the global stiffness matrix [K] and the global load vectors \(\{ P\}\) and \(\left\{ {P^{{{\text{th}}}} } \right\}\), can be written as:

$$ [K]\{ d\} = \{ P\} + \left\{ {P^{{{\text{th}}}} } \right\} $$
(25)

2.6 Finite Element Formulation Using Digimat-HC

In the current section, the procedure for three-point bending analysis of a sandwich composite with honeycomb core using Digimat-HC is described. In the first step, the core model parameters, such as the core type and core thickness were defined. Subsequently, microstructural parameters such as the cell geometry and material properties of the core were defined. In the second step, the parameters of face sheets (layers) were set such as the properties of the matrix material and fiber. In the third step, the parameters of the sandwich composite such as the number of layers of the face sheets and the core orientation were defined. The dimensions of the sandwich beam were specified, including the width, span length, and width of the loading pad. The load was then applied and finite element mesh refinement was defined. Finally, the loading type parameters such as the geometry of the sandwich beam and three-point bending test parameters were chosen and the analysis was performed and results were extracted. For a better understanding, the input parameters in the Digimat-HC software are presented in Table 1.

Table 1 Input parameters of the honeycomb structure in the Digimat-HC program
Full size table

3 Fabrication of Sandwich Composite Plate and Experimental Analysis

3.1 Fabrication of Sandwich Composites

The sandwich composite consists of three layers, i.e., one honeycomb core layer sandwiched by two top and bottom face sheets. MWCNT reinforced sandwich plates with honeycomb core were fabricated using uni-directional E-glass fiber and MWCNT dispersed in epoxy resin (LY-556) with suitable hardener (HY-951) as binder using vacuum-assisted hand lay-up technique. MWCNTs were procured from Shilpa Enterprises, Maharashtra, India. The MWCNTs were 99% pure with average length and diameter being 6 μm and 10–20 nm, respectively. Fabrication starts with dispersing the pre-determined loading of MWCNT (1.0 wt%) in acetone and sonicate for 1 h with a pulse duration of 1.5 s to de-agglomerate the CNTs (Fig. 2). The epoxy resin was then kept at a temperature of 60 °C for 1 h to reduce the viscosity of the polymer matrix. The CNTs were then mixed in the epoxy using a mechanical stirrer stirring at a speed of 200 rpm for about 20 min. Thereafter, the hardener in a ratio of 10:1 was mixed in the CNT-epoxy resin mixture and stirred for about 10 min with the help of a stick to ensure a proper mixture. Finally, the slurry (MWCNT/epoxy/hardener) was poured into the uni-directional E-glass fiber until the required number of layers for each face sheets i.e. three layers with orientation of [0°/90°/0°]S were stacked up. The detailed fabrication process flow is depicted in Fig. 3. After the required face sheets were made, the honeycomb core layer was fabricated using a custom-made honeycomb mold made from high carbon and high chromium steel. The honeycomb core was fabricated with similar steps for the bottom and top face sheets with two layers in [0°/90°] orientation and a layer thickness of 0.26 mm. The top and bottom face sheet and honeycomb core were bonded with araldite adhesive by cleaning the top surface with the help of acetone to ensure the proper binding between the core and the face sheet. Furthermore, the fabricated sandwich composites were kept in a hot air oven for 2 h to properly cure the sandwich composite plates, and samples were cut according to size for testing. Figure 4a illustrates the photograph of the honeycomb corrugated sheet, Fig. 4b, c depict the honeycomb core without and with nano-filler, respectively. The honeycomb core sandwich plate fabricated in this study is shown in Fig. 4d, e shows the line diagram of a single cell structure. The composite containing MWCNT reinforced honeycomb core is designated as CHC and the composite consisting of neat epoxy (without CNT) is designated as EHC (Table 2).

Fig. 2
figure 2

Schematic diagram depicting the preparation of MWCNT + Epoxy mixture

Full size image
Fig. 3
figure 3

Schematic diagram of the fabrication process of honeycomb core sandwich composites

Full size image
Fig. 4
figure 4

Schematic diagram of a honeycomb corrugated sheet, b honeycomb core without nano-fillers, c honeycomb core with nano-fillers, d honeycomb core sandwich plates, e single cell structure

Full size image
Table 2 The properties of E-glass fibre and epoxy [15]
Full size table

3.2 Bending Test and Microstructural Characterization

The properties of the honeycomb core sandwich composite structure under bending load was experimentally evaluated using three-point bending under various temperatures (30 °C, 60 °C, and 90 °C). The required number of bend test specimens was prepared in accordance with the dimensions (250 mm × 50 mm × 10 mm) specified in ASTM C393/C393M-20 standard. The test was carried out on a universal testing machine (UTM) with a maximum load of 30 kN (Fig. 5). The core shear strength (\(F_{{\text{s}}}^{{{\text{ult}}}}\)) and the face sheet bending stress (\(\sigma\)) were evaluated using the following expressions [24]:

$$ F_{{\text{s}}}^{{{\text{ult}}}} = \frac{{P_{\max } }}{{\left( {S_{{\text{w}}} + h_{{\text{c}}} } \right)h}}, $$
(26)
$$ \sigma = \frac{{LP_{\max } }}{{2h_{{\text{t}}} \left( {S_{{\text{w}}} + h_{{\text{c}}} } \right)h}}, $$
(27)

where, \(F_{{\text{s}}}^{{{\text{ult}}}}\), \(P_{\max }\), Sw, hc, and h donate ultimate core shear strength, maximum load, sandwich thickness, core thickness, and sandwich width, respectively. Face sheet bending stress is represented as \(\sigma\), L is the span length of the sandwich composite, and ht is face sheet thickness. The specimen dimensions of the fabricated honeycomb core sandwich composite structures are shown in Table 3.

Fig. 5
figure 5

Photograph depicting the three-point bending test of a fabricated sample

Full size image
Table 3 The specimen dimensions of the fabricated honeycomb core sandwich composite structures
Full size table

4 Results and Discussion

The bending behavior of a sandwich plate structure with a honeycomb core is computed numerically using an in-house finite element model based on HSDT and commercial Digimat-HC software. Accuracy of the developed FE model was validated by comparing the deflection values with existing literature and the results of experimental three-point bending tests. Further, various parametric studies are presented; such as the influence of various parameters on the bending characteristics, core shear strength and bending strength of the face sheet.

4.1 Validation Study

4.1.1 Numerical Validation

The validation study is a necessary step in a finite element numerical analysis. Hence, a validation study has been performed for a conventional sandwich composite plate, which consists of an isotropic softcore under sinusoidal distributed load (SSL), q (x, y) = 10,000 sin(πx/a) sin(πy/b) and simply supported edges (SSSS). The material properties are taken same as considered by Ye et al. [25] (Et = Eb = 20 GPa, Ef = Et = Eb, Gc = 40 MPa, υt = υb = υc = 0.3, ρt = ρb = 1400 kg/m3, ρc = 100 kg/m3, a = b = 2 m, ht = hb = 2 mm, hc = 50 mm, h = ht + hb + hc, hf = hb). The values of transverse central deflection for varying thickness ratio obtained via the model developed in this study are presented in Table 4. It can be observed that the results of this study are in good agreement with the results obtained by Ye et al. [30].

Table 4 Comparison of transverse central deflection under SSL
Full size table

In addition, the performance of the current model was also examined for thermal load. A laminated sandwich plate with the configuration of (00/Core/00) and SSSS end condition was considered and it was subjected to a sinusoidal load of ∆T = (T0 h) z (πx/a) sin(πy/b). The material properties are taken the same as considered by Zhen and Wanji [26] (E2 = 10 GPa, E1 = 15E2, G12 = 15E2, G23 = 0.3356E2, υ12 = 0.3, υ23 = 0.49, α2 = 10–6 K−1, α1 = 0.015α2, hc = 0.6 h). The values of non-dimensional central deflection (\(\overline{w }=(w)({\alpha }_{0}{T}_{0}h)\)) for varying thickness ratio obtained via the model developed in this study are presented in Table 5. It can be observed that the present results are in good agreement with the results of Refs. [31] and [32].

Table 5 Comparison of normalized central deflection under thermal load
Full size table

4.1.2 Experimental Validation

The effectiveness of the developed finite element formulation was demonstrated by comparing the numerical results with the experimental bending test results in terms considering clamped-free-clamped-free (CFCF) end condition, as shown in Fig. 5. The central deflection was determined experimentally by applying a flexural point load at the center of the specimen at a loading rate of 1 mm/min, and the central deflections were measured for loads varying from 10 to 40 kg at an interval of 5 kg. Furthermore, the central deflection of the sandwich composite plate was evaluated using the developed FE formulation and commercial Digimat-HC software with the same load, geometrical properties and material properties, as used in the experimental bending test. The central deflection values obtained by the experimental bending test, developed FEM model and Digimat-HC software is illustrated in Table 6. It can be noted that the central deflection values obtained via experimentation are in good agreement with the developed FEM model and Digimat-HC software. The deviation of experimental values from the developed FEM model varies in the range of 2.73–3.98%, whereas, from the Digimat-HC software, the experimental values deviate in the range of 2.32–4.88%.

Table 6 Central deflection values obtained by the experimental bending test, developed FEM model and Digimat-HC software
Full size table

4.2 Parametric Study

4.2.1 Effect of Temperature on Bending Behavior of Sandwich Composite Plate

It is well known that the surrounding temperature influences the bending behavior of the composites. Figure 6 illustrates the load–displacement curves of neat epoxy and CNT-reinforced honeycomb core composites at various temperatures. It can be observed that the maximum load-bearing capacity was exhibited by CNT-reinforced honeycomb sandwich composite at ambient temperature, 30 °C, which kept on decreasing with increasing temperature. However, irrespective of the test temperature, CNT-reinforced honeycomb sandwich composite exhibited far superior bending behavior as compared to the neat epoxy composite; displaying 8%, 21% and 12% higher load-bearing capacity at 30 °C, 60 °C and 90 °C, respectively. The MWCNT improves the bending behavior of honeycomb core sandwich composite due to the increase in viscosity of the matrix and strong interface bonding between CNTs and epoxy matrix [33]. The sandwich composites undergo three main failure modes, surface deformation, core shear, and indentation of the front sheet into the lattice core [34]. The load is carried primarily by the top face sheet, after which it is transferred to the core, which further carries the load until it reaches the bottom face sheet. Further increase in load is carried by the full structure until it reaches the peak load, and finally the core carries most of the load until the composite fails.

Fig. 6
figure 6

Load–displacement curves of neat epoxy and CNT-reinforced honeycomb core composites at various temperatures

Full size image

4.2.2 Effect of Temperature on Face Sheet Bending Stress and Core Shear Strength

The core shear strength and face sheet bending stress of the studied composites were calculated by using Eqs. (1) and (2), respectively and the obtained values are illustrated in Fig. 7. It can be clearly seen that the shear strength of the core and the bending stress of the face sheets follow the same trend, irrespective of the temperature and reinforcement. Furthermore, it was found that the core shear strength and face sheet bending stress of sandwich composites with CNT-reinforcement honeycomb core performed much better than the pure epoxy composite at all test temperatures. Also, the samples tested at 90 °C had substantial delamination and bent indicating the detrimental effect of high temperature on bending properties. When the test temperature increases, the properties of the composites decrease because high-temperature results in the collapse of a strong interface bond between the reinforcements and epoxy matrix.

Fig. 7
figure 7

Face sheet bending stress and core shear strength of CNT-reinforced and without reinforced honeycomb core sandwich composites

Full size image

4.3 Additional Numerical Examples

The validation study shows that the developed FE formulation and the commercial Digimat-HC software are capable of solving the bending problems of honeycomb-cored sandwich composite plates. Thus, to explore the applicability of the numerical models and improve the understanding of sandwich composite bending behavior, a few more examples such as examples of the influence of cell size thickness, height of the core and weight fraction of MWCNTs have been discussed in the subsequent sections. The numerical results have been computed by using Digimat-HC modeling software for sandwich composite under central transverse load with CFCF end conditions and material properties (Table 2) throughout the analysis unless otherwise noted. Further in the current numerical examples the weight fraction.

4.3.1 Effect of Cell Size Thickness and Height of the Core

At 500 N load, the experimentally determined values of maximum core shear strength and face sheet bending stress of CNT-reinforced honeycomb sandwich composite were 0.622 MPa and 25.95 MPa, respectively, whereas, the respective numerical values computed by Digimat-HC modeling software were 0.703 MPa, and 29.1 MPa (Fig. 8). Therefore, good agreement was found between the experimentally determined values and numerically computed values.

Fig. 8
figure 8

Numerical result of three-point bending test for honeycomb core sandwich composites for honeycomb core height, Ch = 10 and cell thickness, Tc = 0.5

Full size image

For the numerical analysis, the height of the core and thickness of the cell size were varied and the three-point bending test was performed under a load condition of 500 N. The configurations, dimensions and input parameters of the GFRP composite given as input to the Digimat-HC modeling software are mentioned in Table 7 and the computed result is presented in Table 8.

Table 7 Technical data of GFRP honeycomb core sandwich composite structure for the Digimat-HC program
Full size table
Table 8 Numerical results obtained using the Digimat-HC program for CNT-reinforced honeycomb core sandwich composite
Full size table

It can be noticed that the maximum face sheet bending stress is obtained for the composite having honeycomb core height, Ch = 5 and cell thickness, Tc = 1 (Fig. 9a) and minimum face sheet bending stress is obtained when the composite has honeycomb core height, Ch = 20 and cell thickness, Tc = 2. Similarly, the maximum core shear strength is obtained at honeycomb core height, Ch = 5 and cell thickness, Tc = 2 (Fig. 9b). Furthermore, it can be noted that the composites display the best amalgamation of core shear strength and face sheet bending stress, when the core height, Ch = 5. Also, as the height of the honeycomb core increases, core shear strength, and face sheet bending stress gradually decreases. However, upon increasing the cell size thickness, on one hand, face sheet bending stress decreases though marginally, but on the other hand, core shear strength increases significantly. So, based on the requirement, we can develop appropriate honeycomb core sandwich structures for different applications.

Fig. 9
figure 9

Numerical result of three-point bending test for honeycomb core sandwich composites for a honeycomb core height, Ch = 5 and cell thickness, Tc = 1, and b honeycomb core height, Ch = 5 and cell thickness, Tc = 2

Full size image

4.3.2 Effect of CNT Content on the Bending Deflection under Mechanical Load

To illustrate the effect of the weight fraction of CNTs on the normalized central deflection of the sandwich composite plate under UDL, normalized central deflection is evaluated for three different CNT loadings (wt%, 0, 0.05 and 0.1) under the UDL and CFCF boundary condition. The material properties of the randomly oriented MWCNT-reinforced glass fiber epoxy composite are evaluated using the Mori–Tanaka method as presented in the previous work of the authors [3, 28]. The result is presented in Table 9 and it can be observed that the deflection of the sandwich composites reduces as the weight fraction of MWCNT increases, irrespective of the thickness ratio. Therefore, it can be concluded that the addition of MWCNT reduces bending deflection, thereby increasing the stiffness of the structure. And, as expected, the deflection increases as the thickness ratio increases for all the considered weight fractions of MWCNT.

Table 9 Bending deflection of honeycomb cored sandwich composites for various weight fractions of MWCNT under UDL
Full size table

4.3.3 Effect CNT Content on the Bending Deflection Under Thermal Load

To illustrate the effect of the weight fraction of CNTs on the normalized central deflection of the sandwich composite plate subjected to the thermal load, normalized central deflection was evaluated for three different CNT loadings (0, 0.05 and 0.1 wt%) with SSSS boundary condition and temperature Tu = Tb = 373 K. The thermal material properties of the randomly oriented MWCNT-reinforced glass fiber epoxy composite were evaluated using the relations presented in the previous work of the authors [28, 29]. The deflections are normalized according to the formula \(\overline{w }=(w/h)\) and the results are presented in Table 10. It can be observed that as the weight fraction of CNTs increases, the deflection decreases irrespective of the thickness ratio.

Table 10 Normalized central deflection of honeycomb cored sandwich composites for various weight fractions of MWCNTs under thermal load
Full size table

4.3.4 Effect of Temperature Distribution on Deflection Under Uniformly Distributed Load

In addition to the above, the influence of temperature distribution on the normalized central deflection of a sandwich composite plate under a uniformly distributed load at various temperatures was studied. The temperature on the lower face sheet (Tu) was assumed to be 300 K, and the loading of CNTs was kept at 1.0 wt%. Further, the thickness ratio (a/h = 50, h = 0.005) and simply supported (SSSS) end condition were considered. The normalized central deflection results are presented in Fig. 10. It can be observed that the deflection increases as the temperature at the bottom face sheet increases. It can also be seen that the deflection monotonically increases as the ratio of the face sheet thickness (ht) to core thickness (hc) increases.

Fig. 10
figure 10

Effect of temperature distribution on a normalized central deflection of CNT reinforced sandwich plate subjected to uniform distributed load

Full size image

5 Conclusions

In the present work, the bending behaviour of honeycomb-cored multi-walled carbon nanotube (MWCNTS) reinforced sandwich composite plate was investigated using an in-house developed finite element model based on higher-order shear deformation theory and Digimat-HC software. Experimental tests were also conducted to further assert the accuracy of the developed models. Neat epoxy sandwich composite was also fabricated for the purpose of comparison. The findings of the study are summarized in the following observations and conclusions.

  • The central deflection values obtained via the three-point bending test were in good agreement with the developed FEM model and Digimat-HC software. The deviation of experimental values from the developed FEM model varied in the range of 2.73–3.98%, whereas, from the Digimat-HC software, the experimental values deviated in the range of 2.32–4.88%.

  • The maximum load-bearing capacity during the bending test was exhibited by CNT-reinforced honeycomb sandwich composite at ambient temperature, 30 °C, which kept on decreasing with increasing temperature. However, irrespective of the test temperature, the CNT-reinforced honeycomb sandwich composite exhibited far superior bending behaviour as compared to the neat epoxy composite; displaying 8%, 21% and 12% higher load-bearing capacity at 30 °C, 60 °C and 90 °C, respectively.

  • The MWCNT reinforced honeycomb core sandwich composite displayed the best amalgamation of core shear strength and face sheet bending stress, when the core height, Ch = 5. Also, as the height of the honeycomb core was increased, core shear strength and face sheet bending stress gradually decreased. However, upon increasing the cell size thickness, on one hand, face sheet bending stress decreased though marginally, but on the other hand, core shear strength increased significantly. So, based on the requirement, an appropriate honeycomb core sandwich structure can be developed for different applications.