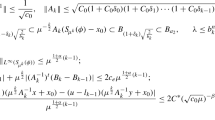A Best Possible Maximum Principle and an Overdetermined Problem for a Generalized Monge-Ampère Equation

Abstract

This paper investigates a P-function associated with solutions to boundary value problems of some generalized Monge-Ampère equations in bounded convex domains. It will be shown that P attains its maximum value either on the boundary or at a critical point of any convex solution. Furthermore, it turns out that such P-function is actually a constant when the underlying domain is a ball. Therefore, our results provide a best possible maximum principle in the sense of L. Payne. As an application, we will use these results to study an overdetermined boundary value problem. More specifically, we will show solvability of this overdetermined boundary value problem forces their P-function to be a constant.

1 Introduction

We recall the notion of “best possible maximum principle” introduced by L. Payne a few decades ago [7, 8]. A function P that depends on solutions and their derivatives of a boundary value problem on bounded domains is said to satisfy a best possible maximum principle if P satisfies the weak maximum principle for every bounded domain $\Omega$, and if there is a special domain on which it is a constant. As an example, let u satisfy

$$\begin{aligned} \Delta u=1\ \ \hbox {in}\ \ \Omega ,\ \ u=0\ \ \hbox {on}\ \ \partial \Omega . \end{aligned}$$

The function

$$\begin{aligned} P=|Du|^2-\frac{2}{n}u \end{aligned}$$

satisfies

$$\begin{aligned} \Delta P=2\sum _{i,j=1}^nu_{ij}^2-\frac{2}{n}\ge 2\sum _{i=1}^nu_{ii}^2-\frac{2}{n}\ge \frac{2}{n}(\Delta u)^2-\frac{2}{n}=0, \end{aligned}$$

where $u_i=\frac{\partial u}{\partial x_i},$ $u_{ij}=\frac{\partial ^2 u}{\partial x_i\partial x_j}.$ It follows that P attains its maximum value on $\partial \Omega$. If $\Omega$ is a ball of radius R centered at the origin, we have

$$\begin{aligned} u=\frac{|x|^2-R^2}{2n}. \end{aligned}$$

The corresponding function $P=|Du|^2-\frac{2}{n}u$ is a constant in $\Omega$.

In [2], the following problem is discussed. Let $\Omega \subset {\mathbb {R}}^n$ be a bounded convex domain, and let u be a convex solution to the boundary value problem

$$\begin{aligned} \textrm{det}(D^2u)=1\ \ \hbox {in}\ \ \Omega ,\ \ u=0\ \ \hbox {on}\ \ \partial \Omega . \end{aligned}$$

Corresponding to this solution, consider the function

$$\begin{aligned} P=\sum _{i,j=1}^n\frac{\partial \textrm{det}(D^2u)}{\partial u_{ij}}u_iu_j-2u. \end{aligned}$$

In [2], the authors prove that P satisfies a best possible maximum principle. Similar problems are discussed in [6, 9].

Let $\Omega \subset {\mathbb {R}}^n$ be a bounded convex domain. For a smooth function u we have

$$\begin{aligned} \textrm{det}(D^2u)=\frac{1}{n}\Bigl (T_{(n-1)}^{ij}(D^2u)u_i\Bigr )_j, \end{aligned}$$

where $T_{(n-1)}(D^2u)=[T_{(n-1)}^{ij}(D^2u)]$ is the adjoint of the Hessian matrix $D^2u$. Here and in what follows sub-indices denote partial differentiation, and the summation convention from 1 to n over repeated indices is in effect.

In the present paper, we find a best possible maximum principle relative to the following generalized Monge-Ampère equation. With $p>1$, we consider the boundary value problem

$$\begin{aligned} \frac{1}{n}\Bigl (T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_i\Bigr )_j=1\ \ \hbox {in}\ \ \Omega ,\ \ \ u=0\ \ \ \hbox {on}\ \ \ \partial \Omega . \end{aligned}$$

(1)

Note that this generalization of the Monge-Ampère operator is similar to the p-Laplacian as the generalization of the Laplacian [13]. For a discussion of problems related to Monge-Ampère operators we refer to [1, 4, 5].

Problem (1) in case of $p=2$ has been discussed in [2]. From now on we concentrate on the case $p>1$, $p\not =2$. We suppose $u\in \Phi$, where

$$\begin{aligned} \Phi = \{u\in C^1_0(\Omega )\cap C^2(\partial \Omega ),\ u\ \hbox {is strictly convex and smooth whenever}\ |Du|>0.\} \end{aligned}$$

Let $u_m=\min _\Omega u(x)=u(x_0)$. Clearly, $|Du|=0$ at $x_0$ only. We say that u is smooth in ${\mathcal {O}}$ if it is at least $C^4$ in ${\mathcal {O}}$.

Note that the matrix $D^2u$ is positive definite where $|Du|>0$. We say that $u\in \Phi$ is a solution to (1) if

$$\begin{aligned} -\frac{1}{n}\int _\Omega T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_i\phi _j\, dx=\int _\Omega \phi \, dx\ \ \ \forall \phi \in H^1_0(\Omega ). \end{aligned}$$

We claim that

$$\begin{aligned} \lim _{x\rightarrow x_0}T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_iu_j=0. \end{aligned}$$

Indeed, let

$$\begin{aligned} \Omega ^t=\{x\in \Omega : u(x)<t\},\ \ \ u_m<t<0. \end{aligned}$$

If we multiply (1) by $(t-u)^+$ and we integrate over $\Omega$ we find

$$\begin{aligned} \int _{\Omega ^t}T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_iu_j\, dx=n\int _{\Omega ^t}(t-u)\, dx\le n|\Omega ^t|\sup _{\Omega ^t}(t-u). \end{aligned}$$

It follows that

$$\begin{aligned} \frac{1}{|\Omega ^t|}\int _{\Omega ^t}T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_iu_j\, dx\le n\sup _{\Omega ^t}(t-u)=n(t-u_m). \end{aligned}$$

As $t\rightarrow u_m$, the claim follows.

Define the P-function

$$\begin{aligned} P=\frac{p-1}{p}T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_iu_j-u,\ \ x\not =x_0, \end{aligned}$$

(2)

and $P(x_0)=-u_m$.

Our first result is the following

Theorem 1.1

Let $\Omega$ be a bounded convex domain. If $u\in \Phi$ is solution to Problem (1), the function P defined as in (2) attains its maximum value either on the boundary $\partial \Omega$ or at the point where $Du=0$. Moreover, if $\Omega$ is a ball then P is a constant.

By using Theorem 1.1, we shall discuss the following overdetermined problem. Let $u\in \Phi$ be a solution to Problem (1). Furthermore, if $u_m=\min _\Omega u(x)$, suppose there is some constant c such that

$$\begin{aligned} {{\mathcal {H}}}_{(n-1)}|Du|^{n(p-1)+1}=c\ \ \hbox {on}\ \ \partial \Omega ,\ \ \frac{p-1}{p}c\ge -u_m, \end{aligned}$$

(3)

where ${{\mathcal {H}}}_{(n-1)}$ is the Gauss curvature of $\partial \Omega$.

Theorem 1.2

If there is a solution $u\in \Phi$ to problem (1) which satisfies the additional condition (3), then the function P defined as in (2) is a constant in $\Omega$.

Overdetermined problems for second order linear and quasilinear equations were discussed more than fifty years ago in the seminal papers [12, 15].

In case of $n=2$, we shall prove the analogous of Theorem 1.1 for the minimum. Similar results are proved in [3]. As an application, we will prove Theorem 1.2 without the restriction $\frac{p-1}{p}c\ge -u_m$.

2 A Best Possible Maximum Principle

Recall that, where $|Du|>0$, the operator $T_{(n-1)}^{ij}(D^2u)$ is divergence free (see, for example, [10, 11]), that is

$$\begin{aligned} \Bigl (T_{(n-1)}^{ij}(D^2u)\Bigr )_i=0,\ \ \ j=1,\cdots ,n. \end{aligned}$$

(4)

Moreover, since $T_{(n-1)}(D^2u)$ is the adjoint of the Hessian matrix $D^2u$, we have

$$\begin{aligned} T_{(n-1)}(D^2u)D^2u=I\textrm{det}(D^2u), \end{aligned}$$

(5)

where I is the $n\times n$ identity matrix. On using these facts, after some computation one finds

$$\begin{aligned} \frac{1}{n}\Bigl (T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_i\Bigr )_j=(p-1)|Du|^{n(p-2)}\textrm{det}(D^2u). \end{aligned}$$

Therefore, Equation (1) for $x\in \Omega$ such that $|Du|>0$, can be written as

$$\begin{aligned} \textrm{det}(D^2u)=\frac{1}{p-1}|Du|^{n(2-p)}. \end{aligned}$$

(6)

Proof of Theorem 1.1

Let $x_0\in \Omega$ be the point where $Du=0$, and let $u_m=u(x_0)$. Arguing by contradiction, let ${\tilde{x}}\in {\Omega {\setminus } \{x_0\}}$ be a point such that

$$\begin{aligned} \begin{aligned}&P({\tilde{x}})=\frac{p-1}{p}T_{(n-1)}^{ij}(D^2u({\tilde{x}}))|Du(\tilde{x})|^{n(p-2)}u_i({\tilde{x}})u_j({\tilde{x}})-u({\tilde{x}})\\&>\max \Bigl [\frac{p-1}{p}\max _{x\in \partial \Omega }\bigl (T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_iu_j\bigr ),-u_m\Bigr ]. \end{aligned} \end{aligned}$$

Choose $0<\tau <1$ close enough to 1 so that

$$\begin{aligned} \begin{aligned} P({\tilde{x}})&=\frac{p-1}{p}T_{(n-1)}^{ij}(D^2u({\tilde{x}}))|Du(\tilde{x})|^{n(p-2)}u_i({\tilde{x}})u_j({\tilde{x}})-\tau u({\tilde{x}})\\&>\max \Bigl [\frac{p-1}{p}\max _{x\in \partial \Omega }\bigl (T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_iu_j\bigr ),-\tau u_m\Bigr ]. \end{aligned} \end{aligned}$$

Then, also the function

$$\begin{aligned} \tilde{P}(x)=\frac{p-1}{p}T_{(n-1)}^{ij}(D^2u)|Du|^{n(p-2)}u_iu_j-\tau u \end{aligned}$$

attains its maximum value at some point ${\bar{x}}\in {\Omega {\setminus } \{x_0\}}$. We show that this cannot happen.

On using the equations (5) and (6) we find

$$\begin{aligned} T_{(n-1)}(D^2u)=\frac{1}{p-1}|Du|^{n(2-p)}(D^2u)^{-1}, \end{aligned}$$

where $(D^2u)^{-1}$ is the inverse matrix of $D^2u$. Therefore, if $[u^{kl}]= (D^2u)^{-1}$ we have

$$\begin{aligned} p{\tilde{P}}= u^{kl}u_ku_l-p\tau u. \end{aligned}$$

We compute

$$\begin{aligned} p{\tilde{P}}_i= u^{kl}_iu_ku_l +2 u^{kl}u_{ki}u_l-p\tau u_i. \end{aligned}$$

Since

$$\begin{aligned} u^{kl}u_{ki}=\delta ^{l}_i\ \ \ \hbox {(the Kronecker delta)} \end{aligned}$$

we find

$$\begin{aligned} p{\tilde{P}}_i= u^{kl}_iu_ku_l+(2-p\tau )u_i,\ \ \ i=1,\cdots ,n. \end{aligned}$$

(7)

Further differentiation yields

$$\begin{aligned} p{\tilde{P}}_{ii}= u^{kl}_{ii}u_ku_l +2 u^{kl}_iu_{ki}u_l+(2-p\tau )u_{ii}. \end{aligned}$$

We note that our equation (1) is invariant under a rigid rotation. Let us make a suitable rotation around the point ${\bar{x}}$ such that $D^2u$ has a diagonal form at this point. With some abuse of notation, ${\tilde{P}}_i$ denote derivatives of ${\tilde{P}}$ with respect to the new variables. Then,

$$\begin{aligned} p{\tilde{P}}_{ii}= u^{kl}_{ii}u_ku_l +2 u^{il}_iu_{ii}u_l+(2- p\tau )u_{ii},\ \ \ i=1,\cdots ,n. \end{aligned}$$

Clearly, also $(D^2u)^{-1}$ will have a diagonal form at ${\bar{x}}$. Furthermore, for i fixed we have $u^{ii}u_{ii}=1.$ Multiplying by $u^{ii}$ the equation in above and adding from $i=1$ up to $i=n$ we get

$$\begin{aligned} pu^{ii}{\tilde{P}}_{ii}= u^{ii}u^{kl}_{ii}u_ku_l +2 u^{il}_iu_l+n(2- p\tau ). \end{aligned}$$

(8)

By (5) and (6) we find

$$\begin{aligned} |Du|^{n(2-p)}(D^2u)^{-1}=(p-1)T_{(n-1)}(D^2u). \end{aligned}$$

(9)

Hence, since the matrix $T_{(n-1)}(D^2u)$ is divergence free, we have

$$\begin{aligned} \Bigl (|Du|^{n(2-p)}u^{il}\Bigr )_i=0,\ \ \ l=1,\cdots ,n, \end{aligned}$$

from which we find (recall that we are adding over repeated indices)

$$\begin{aligned} u^{il}_i=n(p-2)|Du|^{-2}u_{ik}u_ku^{il}=n(p-2)|Du|^{-2}\delta _k^lu_k=n(p-2)|Du|^{-2}u_l. \end{aligned}$$

Therefore,

$$\begin{aligned} u^{il}_iu_l=n(p-2). \end{aligned}$$

(10)

Insertion of this equation into (8) yields

$$\begin{aligned} pu^{ii}{\tilde{P}}_{ii}= u^{ii}u^{kl}_{ii}u_ku_l +n(2p-2-p\tau ).\end{aligned}$$

(11)

Now we evaluate the quantity $u^{ii}u^{kl}_{ii}u_ku_l$. Unfortunately, our computations are quite long. Since $[u^{kl}]$ is the inverse matrix of $[u_{kl}]$, we have

$$\begin{aligned} u^{kl}_i=-u^{km}u^{lq}u_{mqi}. \end{aligned}$$

Differentiating with respect to $x^i$ we find

$$\begin{aligned} u^{kl}_{ii}=(u^{ks}u^{mj}u^{lq}+u^{km}u^{ls}u^{qj})u_{sji}u_{mqi}-u^{km}u^{lq}u_{mqii}. \end{aligned}$$

Since $D^2u$ has a diagonal form at ${\bar{x}}$, from the latter equation we find (here we do not add with respect to i, k or l)

$$\begin{aligned} u^{kl}_{ii}=2u^{kk}u^{jj}u^{ll}u_{ijk}u_{ijl}-u^{kk}u^{ll}u_{klii},\ \ i,k,l=1,\cdots ,n. \end{aligned}$$

Multiplying by $u^{ii}$ and adding from $i=1$ up to $i=n$ we get

$$\begin{aligned} u^{ii}u^{kl}_{ii}=2u^{ii}u^{jj}u^{kk}u^{ll}u_{ijk}u_{ijl}-u^{ii}u^{kk}u^{ll}u_{iikl}. \end{aligned}$$

(12)

To evaluate the last quantity in (12), let us differentiate Equation (6) with respect to $x^k$. We find

$$\begin{aligned} \frac{\partial \textrm{det}(D^2u)}{\partial u_{ij}}u_{ijk}=\frac{n(2-p)}{p-1}|Du|^{n(2-p)-2}u_{ks}u_s,\ \ \ k=1,\cdots ,n. \end{aligned}$$

By (9) we have

$$\begin{aligned} \frac{\partial \textrm{det}(D^2u)}{\partial u_{ij}}=T_{(n-1)}^{ij}(D^2u)=\frac{1}{p-1}|Du|^{n(2-p)}u^{ij}. \end{aligned}$$

By the last two equations we find

$$\begin{aligned} \frac{1}{p-1}|Du|^{n(2-p)}u^{ij}u_{ijk}=\frac{n(2-p)}{p-1}|Du|^{n(2-p)-2}u_{ks}u_s. \end{aligned}$$

Simplifying we get

$$\begin{aligned} u^{ij}u_{ijk}=n(2-p)|Du|^{-2}u_{ks}u_s. \end{aligned}$$

Further differentiation with respect to $x^l$ yields

$$\begin{aligned} u^{ij}u_{ijkl}+u^{ij}_lu_{ijk}=n(2-p)\big [-2|Du|^{-4}u_{ll}u_lu_{kk}u_k+|Du|^{-2}u_{ksl}u_s+|Du|^{-2}u^2_{ll}\delta ^k_{l}\bigr ]. \end{aligned}$$

Note that we are using the condition that $D^2u$ has a diagonal form at the point ${\bar{x}}$. Since $u^{ij}_l=-u^{ii}u^{jj}u_{ijl}$ (with i and j fixed), by the previous equation we find

$$\begin{aligned} \begin{aligned}u^{ii}u_{iikl}&=u^{ii}u^{jj}u_{ijk}u_{ijl}+n(2-p)\big [-2|Du|^{-4}u_{ll}u_lu_{kk}u_k\\&+|Du|^{-2}u_{ksl}u_s+|Du|^{-2}u^2_{ll}\delta ^k_{l}\bigr ]. \end{aligned} \end{aligned}$$

(13)

Insertion of (13) into (12) leads to

$$\begin{aligned}\begin{aligned} u^{ii}u^{kl}_{ii}&=2u^{ii}u^{jj}u^{kk}u^{ll}u_{ijk}u_{ijl}-u^{ii}u^{jj}u^{kk}u^{ll}u_{ijk}u_{ijl}\\&+n(p-2)\big [-2|Du|^{-4}u_lu_k+|Du|^{-2}u^{kk}u^{ll}u_{kls}u_s+|Du|^{-2}\delta ^k_{l}\bigr ].\end{aligned} \end{aligned}$$

Simplifying we find

$$\begin{aligned}\begin{aligned} u^{ii}u^{kl}_{ii}&=u^{ii}u^{jj}u^{kk}u^{ll}u_{ijk}u_{ijl}+n(p-2)\big [-2|Du|^{-4}u_lu_k\\&+|Du|^{-2}u^{kk}u^{ll}u_{kls}u_s+|Du|^{-2}\delta ^k_{l}\bigr ].\end{aligned} \end{aligned}$$

Multiplying by $u_ku_l$ (and adding with respect to k and l) we get,

$$\begin{aligned} u^{ii}u^{kl}_{ii}u_ku_l =u^{ii}u^{jj}\bigl (u^{kk}u_{ijk}u_k\bigr )^2-n(p-2) +n(p-2)|Du|^{-2}u^{kk}u^{ll}u_{kls}u_ku_lu_s. \end{aligned}$$

Inserting this equation into (11) we find

$$\begin{aligned} pu^{ii}{\tilde{P}}_{ii}= u^{ii}u^{jj}\bigl (u^{kk}u_{ijk}u_k\bigr )^2+np(1-\tau ) +n (p-2)|Du|^{-2}u^{kk}u^{ll}u_{kls}u_ku_lu_s.\nonumber \\ \end{aligned}$$

(14)

Let us evaluate the first quantity of the right hand side in (14). By using the inequality

$$\begin{aligned} \sum _{i=1}^na_i^2\ge \frac{1}{n}\Bigl (\sum _{i=1}^na_i\Bigr )^2,\ \ \ a_i\in {\mathbb {R}}, \end{aligned}$$

with $a_i=b_i(\sum _kc_{ik})$ we find

$$\begin{aligned} \sum _{i}b_i^2\Bigl (\sum _{k}c_{ik}\Bigr )^2\ge \frac{1}{n} \Bigl (\sum _{i,k}b_ic_{ik}\Bigr )^2. \end{aligned}$$

Hence,

$$\begin{aligned} \sum _{i,j}u^{ii}u^{jj}\Bigl (\sum _ku^{kk}u_{ijk}u_k\Bigr )^2\ge \sum _{i}(u^{ii})^2\Bigl (\sum _ku^{kk}u_{iik}u_k\Bigr )^2 \ge \frac{1}{n}\Bigl ( \sum _{i,k}u^{ii}u^{kk}u_{iik}u_k\Bigr )^2. \end{aligned}$$

Since

$$\begin{aligned} u^{ii}u^{kk}u_{iik}=-u^{ik}_i, \end{aligned}$$

on using (10) we find

$$\begin{aligned} u^{ii}u^{kk}u_{iik}u_k=-u^{ik}_iu_k=-n(p-2). \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{i,j}u^{ii}u^{jj}\Bigl (\sum _ku^{kk}u_{jki}u_k\Bigr )^2\ge n(p-2)^2. \end{aligned}$$

(15)

Insertion of (15) into (14) yields

$$\begin{aligned} \begin{aligned} pu^{ii}{\tilde{P}}_{ii}&\ge n(p-2)^2+np(1-\tau ) +n (p-2)|Du|^{-2}u^{kk}u^{ll}u_{kls}u_ku_lu_s. \end{aligned} \end{aligned}$$

(16)

To finish, we must evaluate the last quantity of the right hand side in (16). This is easy. By (7), at ${\bar{x}}$ (the point of maximum of ${\tilde{P}}$) we have

$$\begin{aligned} 0= u^{kl}_iu_ku_l+(2-p\tau )u_i,\ \ \ i=1,\cdots ,n, \end{aligned}$$

whence,

$$\begin{aligned} u^{kk}u^{ll}u_{kli}u_ku_l=(2-p\tau )u_i. \end{aligned}$$

Multiplying by $u_i$ and adding from $i=1$ up to $i=n$ we find

$$\begin{aligned} |Du|^{-2}u^{kk}u^{ll}u_{kli}u_ku_lu_i=2-p\tau . \end{aligned}$$

Insertion of this equation into (16) yields

$$\begin{aligned} pu^{ii}{\tilde{P}}_{ii}\ge n(p-2)^2+np(1-\tau )+n (p-2)(2-p\tau ). \end{aligned}$$

After simplification we get

$$\begin{aligned} u^{ii}{\tilde{P}}_{ii}\ge n(p-1)(1-\tau )>0, \end{aligned}$$

contradicting the assumption that ${\bar{x}}$ is a point of maximum for ${\tilde{P}}$. It follows that P must attain its maximum value either on the boundary $\partial \Omega$ or at the point where $Du=0$.

Now consider the case $\Omega$ is a ball of radius R, centered at the origin. If $u=u(r)$, $r=|x|$, we may assume $u_1=u'$, $u_i=0,\ \ 2\le i\le n.$ Then,

$$\begin{aligned} D^2u=\textrm{diag}\Bigl \{u'',\frac{u'}{r},\cdots ,\frac{u'}{r}\Bigr \}. \end{aligned}$$

Therefore, Equation (6) reads as

$$\begin{aligned} u''\Bigl (\frac{u'}{r}\Bigr )^{n-1}=\frac{1}{p-1}(u')^{n(2-p)}, \end{aligned}$$

or

$$\begin{aligned} (u')^{n(p-1)-1}u''=\frac{r^{n-1}}{p-1}. \end{aligned}$$

Integrating we find

$$\begin{aligned} u'=r^\frac{1}{p-1}. \end{aligned}$$

Integrating again and using the condition $u(R)=0$ we find

$$\begin{aligned} u(r)=\frac{p-1}{p}\Bigl (r^\frac{p}{p-1}-R^\frac{p}{p-1}\Bigr ). \end{aligned}$$

Recall that our P-function reads as

$$\begin{aligned} P=\frac{1}{p}u^{ij}u_iu_j-u, \end{aligned}$$

where $[u^{ij}]$ is the inverse matrix of $[u_{ij}].$ Then,

$$\begin{aligned} P=\frac{1}{p}\frac{1}{u''}(u')^2-u=\frac{p-1}{p}r^\frac{p}{p-1}-\frac{p-1}{p}\Bigl (r^\frac{p}{p-1}-R^\frac{p}{p-1}\Bigr )=\frac{p-1}{p}R^\frac{p}{p-1}. \end{aligned}$$

Hence P is a constant, and the theorem is proved.

3 An Overdetermined Problem

Proof of Theorem 1.2

We note that (see [14])

$$\begin{aligned} T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l=\mathcal{H}_{(n-1)}|Du|^{n(p-1)+1}\ \ \hbox {on}\ \ \partial \Omega , \end{aligned}$$

where ${{\mathcal {H}}}_{(n-1)}$ is the Gauss curvature of $\partial \Omega$. Therefore, we can write condition (3) as

$$\begin{aligned} T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l=c\ \ \hbox {on}\ \ \partial \Omega ,\ \ \frac{p-1}{p}c\ge -u_m. \end{aligned}$$

(17)

By Theorem 1.1, the maximum of the function P is either $\frac{p-1}{p}c$ (attained on $\partial \Omega$) or $-u_m$ (attained where $Du=0$). Hence, since $\frac{p-1}{p}c\ge -u_m$, we have

$$\begin{aligned} P(x)=\frac{p-1}{p}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l-u\le \frac{p-1}{p} c,\ \ \forall x\in \Omega . \end{aligned}$$

(18)

Recall that $x_0$ is the point of minimum for u, and that $u_m$ is the minimum value of u. For $u_m\le t<0$ we define

$$\begin{aligned} \Omega _t=\{x\in \Omega :\ t\le u(x)<0\}. \end{aligned}$$

Clearly, $\Omega _{u_m}=\Omega .$ Moreover we have

$$\begin{aligned} \partial \Omega _t=\partial \Omega \cup \Sigma _t,\ \ \ \ \Sigma _t=\{x\in \Omega :\ u(x)=t\}. \end{aligned}$$

Let $e=(e^1,\cdots ,e^n)$ be the exterior unit normal to $\partial \Omega _t$. On $\partial \Omega _t$ we have $u_k=|Du|e^k$. Therefore, using Equation (1) we find

$$\begin{aligned} \begin{aligned}&\int _{\Omega _t}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_lu_k\, dx=t\int _{\Sigma _t} T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_l e^k\, d\sigma \\&+\int _{\Omega _t} (-u)\Bigl (T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_l\Bigr )_k\, dx\\&=t\int _{\Sigma _t} T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)-1}u_lu_k\, d\sigma +n\int _{\Omega _t} (-u)\, dx. \end{aligned} \end{aligned}$$

On $\Sigma _t$ we have (see [14])

$$\begin{aligned} T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l=\mathcal{H}_{(n-1)}|Du|^{n(p-1)+1}, \end{aligned}$$

where ${{\mathcal {H}}}_{(n-1)}$ is the Gauss curvature of $\Sigma _t$. Hence,

$$\begin{aligned} \int _{\Omega _t}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_lu_k\, dx=t\int _{\Sigma _t}{{\mathcal {H}}}_{(n-1)}|Du|^{n(p-1)}\, d\sigma +n\int _{\Omega _t} (-u)\, dx.\nonumber \\ \end{aligned}$$

(19)

On noting that

$$\begin{aligned} \int _{\Sigma _t}{{\mathcal {H}}}_{(n-1)}\, d\sigma =n\omega _n\ \ \ \ (\omega _n=\ n-\hbox {measure of the unit sphere}), \end{aligned}$$

and that

$$\begin{aligned} \lim _{t\rightarrow u_m}|Du|=0, \end{aligned}$$

we have

$$\begin{aligned} \lim _{t\rightarrow u_m}\int _{\Sigma _t}{{\mathcal {H}}}_{(n-1)}|Du|^{n(p-1)}\, d\sigma =0. \end{aligned}$$

Hence, by (27) we find

$$\begin{aligned} \lim _{t\rightarrow u_m}\int _{\Omega _t}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_lu_k\, dx=n\int _{\Omega } (-u)\, dx, \end{aligned}$$

(20)

and

$$\begin{aligned} \int _{\Omega }T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_lu_k\, dx=n\int _{\Omega } (-u)\, dx. \end{aligned}$$

(21)

Now we use a sort of Pohozaev identity. We find

$$\begin{aligned} \begin{aligned}&\int _{\partial \Omega _t}x^ie^iT_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l\, d\sigma \\&\quad =\int _{\partial \Omega _t}x^iu_i T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ke^l\, d\sigma \\&\quad =\int _{\Omega _t}\Bigl (x^iu_iT_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_k\Bigr )_l\, dx\\&\quad =\int _{\Omega _t}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_lu_k\, dx\\&\qquad +\int _{\Omega _t}x^iu_{il}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_k\, dx\\&\qquad +\int _{\Omega _t}x^iu_i\Bigr (T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_k\Bigr )_l\, dx. \end{aligned} \end{aligned}$$

(22)

Since

$$\begin{aligned} u_{il}T_{(n-1)}^{kl}(D^2u)=\textrm{det}(D^2u)\delta ^{k}_i=\frac{|Du|^{n(2-p)}}{p-1}\delta ^{k}_i \end{aligned}$$

we have

$$\begin{aligned}\begin{aligned}&\int _{\Omega _t}x^iu_{il}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_k\, dx=\frac{1}{p-1}\int _{\Omega _t}x^iu_i\, dx\\&\quad =\frac{t}{p-1}\int _{\Sigma _t}x^i e^i\, d\sigma +\frac{n}{p-1}\int _{\Omega _t}(-u)\, dx\\&\quad =\frac{nt}{p-1}|\Omega \setminus \Omega _t|+\frac{n}{p-1}\int _{\Omega _t}(-u)\, dx. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \lim _{t\rightarrow u_m}\int _{\Omega _t}x^iu_{il}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_k\, dx=\frac{n}{p-1}\int _{\Omega }(-u)\, dx. \end{aligned}$$

(23)

Finally, on using Equation (1) once more we find

$$\begin{aligned} \begin{aligned}&\int _{\Omega _t}x^iu_i\Bigr (T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_k\Bigr )_l\, dx=n\int _{\Omega _t}x^iu_i\, dx\\&=n^2t|\Omega \setminus \Omega _t|+n^2\int _{\Omega _t}(-u)\, dx. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{t\rightarrow u_m}\int _{\Omega _t}x^iu_i\Bigr (T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_k\Bigr )_l\, dx= n^2\int _{\Omega }(-u)\, dx. \end{aligned}$$

(24)

Hence, letting $t\rightarrow u_m$ in (22) and using (21), (23) and (24) we find

$$\begin{aligned} \begin{aligned}&\int _{\partial \Omega }x^ie^iT_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l\, d\sigma \\&\quad =n\int _{\Omega } (-u)\, dx+\frac{n}{p-1}\int _{\Omega }(-u)\, dx+n^2\int _{\Omega }(-u)\, dx\\&\quad =n\Bigl (n+\frac{p}{p-1}\Bigr )\int _\Omega (-u)\, dx. \end{aligned} \end{aligned}$$

(25)

On the other hand, using condition (17) we find

$$\begin{aligned} \int _{\partial \Omega }x^ie^iT_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l\, d\sigma =c\int _{\partial \Omega }x^ie^i\, d\sigma =cn|\Omega |. \end{aligned}$$

From this equation and (24) it follows that

$$\begin{aligned} c|\Omega |=\Bigl (n+\frac{p}{p-1}\Bigr )\int _\Omega (-u)\, dx. \end{aligned}$$

(26)

Using (21) and (26) we get

$$\begin{aligned} \begin{aligned}&\int _\Omega \Bigl [P(x)-\frac{p-1}{p}c\Bigr ]dx\\&\int _{\Omega }\Bigl [\frac{p-1}{p}T_{(n-1)}^{kl}(D^2u)|Du|^{n(p-2)}u_ku_l-u-\frac{p-1}{p}c\Bigr ]\, dx\\&=\int _{\Omega }\Bigl [\frac{p-1}{p}n(-u)-u-\frac{p-1}{p}c\Bigr ]\, dx\\&=\frac{p-1}{p}\Bigl [\Bigl (n+\frac{p}{p-1}\Bigr )\int _{\Omega }(-u)\, dx-c|\Omega |\Bigr ]=0. \end{aligned} \end{aligned}$$

This together with (18) shows that $P(x)=\frac{p-1}{p}c$ in $\Omega$.

The theorem is proved.

4 The Case $n=2$

Theorem 4.1

Let $\Omega \subset {\mathbb {R}}^2$ be a bounded convex domain. If $u\in \Phi$ is a solution to Problem (1) in $\Omega$, the function P defined as in (2) for $n=2$ attains its minimum value either on the boundary $\partial \Omega$ or at the point where $Du=0$.

Proof

Let $x_0\in \Omega$ be the point where $Du=0$, and let $u_m=u(x_0)$. Arguing by contradiction, let ${\tilde{x}}\in {\Omega {\setminus } \{x_0\}}$ be a point such that

$$\begin{aligned} \begin{aligned} P({\tilde{x}})&=\frac{p-1}{p}T_{(1)}^{ij}(D^2u({\tilde{x}}))|Du(\tilde{x})|^{2(p-2)}u_i({\tilde{x}})u_j({\tilde{x}})-u({\tilde{x}})\\&<\min \Bigl [\frac{p-1}{p}\min _{x\in \partial \Omega }\bigl (T_{(1)}^{ij}(D^2u)|Du|^{2(p-2)}u_iu_j\bigr ),-u_m\Bigr ]. \end{aligned} \end{aligned}$$

Choose $1<\tau <2-\frac{1}{p}$ with $\tau$ close enough to 1 so that

$$\begin{aligned} \begin{aligned} P({\tilde{x}})&=\frac{p-1}{p}T_{(1)}^{ij}(D^2u({\tilde{x}}))|Du(\tilde{x})|^{2(p-2)}u_i({\tilde{x}})u_j({\tilde{x}})-\tau u({\tilde{x}})\\&<\min \Bigl [\frac{p-1}{p}\min _{x\in \partial \Omega }\bigl (T_{(1)}^{ij}(D^2u)|Du|^{2(p-2)}u_iu_j\bigr ),-\tau u_m\Bigr ]. \end{aligned} \end{aligned}$$

Then, also the function

$$\begin{aligned} {\tilde{P}}(x)=\frac{p-1}{p}T_{(1)}^{ij}(D^2u)|Du|^{2(p-2)}u_iu_j-\tau u \end{aligned}$$

attains its minimum value at some point ${\bar{x}}\in {\Omega {\setminus } \{x_0\}}$. Choose $\tau$ such that $\tau <2-\frac{1}{p}$. We show that this cannot happen.

Let us write ${\tilde{P}}$ as

$$\begin{aligned} p {\tilde{P}}= u^{kl}u_ku_l-p\tau u. \end{aligned}$$

(27)

We perform a rigid rotation around ${\bar{x}}$ so that $D^2u$ has a diagonal form at this point. By the same computation as in the proof of Theorem 1.1 we find Equation (14) with $n=2$, that is,

$$\begin{aligned} pu^{ii} {\tilde{P}}_{ii}= u^{ii}u^{jj}\bigl (u^{kk}u_{ijk}u_k\bigr )^2+2p(1-\tau )+2(p-2)|Du|^{-2}u^{kk}u^{ll}u_{kls}u_ku_lu_s. \end{aligned}$$

(28)

To evaluate the last quantity in (28) we differentiate $\tilde{P}$ with respect to $x^s$. Since ${\bar{x}}$ is a point of minimum, by (27) we find

$$\begin{aligned} u^{kl}_su_ku_l+2u^{kl}u_{ks}u_l-p\tau u_s= & {} 0, \\ u^{kl}_su_ku_l+(2-p\tau )u_s= & {} 0. \end{aligned}$$

Recalling that $D^2u$ has a diagonal form, from the latter equation we find

$$\begin{aligned} u^{kk}u^{ll}u_{kls}u_ku_l=(2-p\tau )u_s. \end{aligned}$$

(29)

If we multiply by $u_s$ we get

$$\begin{aligned} |Du|^{-2}u^{kk}u^{ll}u_{kls}u_ku_lu_s=(2-p\tau ). \end{aligned}$$

Inserting this into (27) we find

$$\begin{aligned} pu^{ii} {\tilde{P}}_{ii}= u^{ii}u^{jj}\bigl (u^{kk}u_{ijk}u_k\bigr )^2+2p(1-\tau )+2(p-2)(2-p\tau ). \end{aligned}$$

(30)

To finish, we must evaluate the first quantity in (30). From Equation (1) with $n=2$ we find (recall that $D^2u$ is assumed to be diagonal at ${\bar{x}}$)

$$\begin{aligned} u^{ii}u_{iik}=2(2-p)|Du|^{-2}u_{kk}u_k,\ \ \ k=1,2. \end{aligned}$$

Putting $2(2-p)|Du|^{-2}:=\alpha$ we have the two equations

$$\begin{aligned} \begin{aligned}&u^{11}u_{111}+u^{22}u_{122}=\alpha u_{11}u_1\\&u^{11}u_{112}+u^{22}u_{222}=\alpha u_{22}u_2.\end{aligned} \end{aligned}$$

(31)

Moreover, from (29) we have the two more equations

$$\begin{aligned} \begin{aligned}&(u^{11})^2u_{111}u_1^2+2u^{11}u^{22}u_{112}u_1u_2+(u^{22})^2u_{122}u_2^2=(2-p\tau )u_1\\\\&(u^{11})^2u_{112}u_1^2+ 2u^{11}u^{22}u_{122}u_1u_2+(u^{22})^2u_{222}u_2^2=(2-p\tau )u_2. \end{aligned} \end{aligned}$$

(32)

The system of four equations (31)-(32) is linear with respect to $u_{111}, u_{112}, u_{122}$ and $u_{222}$, and the determinant of the coefficients is equal to $(u^{11}u^{22})^2S^2$, where

$$\begin{aligned} S=u^{11}u_1^2+u^{22}u_2^2. \end{aligned}$$

By elementary computation we find

$$\begin{aligned}{} & {} \begin{aligned} u_{111}&=\frac{1}{u^{11}S^2}\Bigl [(2-p\tau )\bigl (u^{11}u_1^3-3u^{22}u_1u_2^2\bigr )+\alpha u_{11}(u^{22})^2u_1u_2^4\\&\quad +2\alpha u_{22}(u^{22})^2 u_1u_2^4+3\alpha u_{11}u^{11}u^{22}u_1^3u_2^2\Bigr ], \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \begin{aligned} u_{112}&=\frac{1}{u^{11}S^2}\Bigl [(2-p\tau )\bigl (3u^{11}u_1^2u_2-u^{22}u_2^3\bigr )+\alpha u_{22}(u^{22})^2u_2^5\\&\quad -\alpha u_{22}u^{11}u^{22} u_1^2u_2^3-2\alpha u_{11}(u^{11})^2u_1^4u_2\Bigr ], \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned}{} & {} \begin{aligned} u_{122}&=\frac{1}{u^{22}S^2}\Bigl [(2-p\tau )\bigl (3u^{22}u_1u_2^2-u^{11}u_1^3\bigr )+\alpha u_{11}(u^{11})^2u_1^5\\&\quad -\alpha u_{11}u^{11}u^{22} u_1^3u_2^2-2\alpha u_{22}(u^{22})^2u_1u_2^4\Bigr ], \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned}{} & {} \begin{aligned} u_{222}&=\frac{1}{u^{22}S^2}\Bigl [(2-p\tau )\bigl (u^{22}u_2^3-3u^{11}u_1^2u_2\bigr )+\alpha u_{22}(u^{11})^2u_1^4u_2\\&\quad +2\alpha u_{11}(u^{11})^2 u_1^4u_2+3\alpha u_{22}u^{11}u^{22}u_1^2u_2^3\Bigr ]. \end{aligned} \end{aligned}$$

(36)

We start computing $u^{kk}u_{11k}u_k$. On using (33) and (34) we find

$$\begin{aligned} \begin{aligned}&u^{11} u_{111}u_1+u^{22} u_{112}u_2\\&\quad =\frac{1}{S^2}\Bigl [(2-p\tau )\bigl (u^{11}u_1^4-3u^{22}u_1^2u_2^2\bigr )+\alpha u_{11}(u^{22})^2u_1^2u_2^4\\&\qquad +2\alpha u_{22}(u^{22})^2 u_1^2u_2^4+3\alpha u_{11}u^{11}u^{22}u_1^4u_2^2\\&\qquad +(2-p\tau )\Bigl (3u^{22}u_1^2u_2^2-\frac{(u^{22})^2}{u^{11}}u_2^4\Bigr )+\alpha u_{22}\frac{(u^{22})^3}{u^{11}}u_2^6\\&\qquad -\alpha u_{22}(u^{22})^2 u_1^2u_2^4-2\alpha u_{11}u^{11}u^{22}u_1^4u_2^2\Bigr ]\\&\quad =\frac{1}{S^2}\Bigl [(2-p\tau )\Bigl (u^{11}u_1^4-\frac{(u^{22})^2}{u^{11}}u_2^4\Bigr )+\alpha u_{11}(u^{22})^2u_1^2u_2^4\\&\qquad +\alpha u_{22}(u^{22})^2 u_1^2u_2^4+\alpha u_{11}u^{11}u^{22}u_1^4u_2^2+\alpha u_{22}\frac{(u^{22})^3}{u^{11}}u_2^6\Bigr ]. \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} u^{11}u_1^4-\frac{(u^{22})^2}{u^{11}}u_2^4=\frac{1}{u^{11}}\Bigl ((u^{11})^2u_1^4-(u^{22})^2u_2^4\Bigr )=\frac{S}{u^{11}}\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr ). \end{aligned}$$

we get

$$\begin{aligned} \begin{aligned}&u^{11} u_{111}u_1+u^{22} u_{112}u_2\\&\quad =\frac{1}{S^2}\Bigl [(2-p\tau )\frac{S}{u^{11}}\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr )+\alpha u_{11}(u^{22})^2u_1^2u_2^4\\&\qquad +\alpha u_{22}(u^{22})^2 u_1^2u_2^4+\alpha u_{11}u^{11}u^{22}u_1^4u_2^2+\alpha u_{22}\frac{(u^{22})^3}{u^{11}}u_2^6 \Bigr ]. \end{aligned} \end{aligned}$$

(37)

Since

$$\begin{aligned} u_{11}(u^{22})^2u_1^2u_2^4+u_{11}u^{11}u^{22}u_1^4u_2^2=u_{11}u^{22}u_1^2u_2^2 S, \end{aligned}$$

and

$$\begin{aligned} u_{22}(u^{22})^2 u_1^2u_2^4+u_{22}\frac{(u^{22})^3}{u^{11}}u_2^6=\frac{1}{u^{11}}u_{22}(u^{22})^2u_2^4 S. \end{aligned}$$

by (43) we get

$$\begin{aligned} \begin{aligned}&u^{11} u_{111}u_1+u^{22} u_{112}u_2\\&\quad =\frac{1}{S^2}\Bigl [(2-p\tau )\frac{S}{u^{11}}\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr )+\alpha u_{11}u^{22}u_1^2u_2^2 S\\&\qquad +\alpha \frac{1}{u^{11}}u_{22}(u^{22})^2u_2^4 S \Bigr ]\\&\quad =\frac{1}{S}\Bigl [(2-p\tau )\frac{1}{u^{11}}\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr )\\&\qquad +\alpha \Bigl (u_{11}u^{22}u_1^2u_2^2+ \frac{1}{u^{11}}u_{22}(u^{22})^2u_2^4 \Bigr )\Bigr ]. \end{aligned} \end{aligned}$$

(38)

We find

$$\begin{aligned} u_{11}u^{22}u_1^2u_2^2 +\frac{1}{u^{11}}u_{22}(u^{22})^2u_2^4 =\quad \frac{1}{u^{11}}u^{22}u_2^2\bigl (u_{11}u^{11}u_1^2+u_{22}u^{22}u_2^2\bigr ). \end{aligned}$$

(39)

Recalling that $D^2u$ is diagonal, we have $u_{11}u^{11}=u_{22}u^{22}=1$. Therefore, from (39) we get

$$\begin{aligned} u_{11}u^{22}u_1^2u_2^2 +\frac{1}{u^{11}}u_{22}(u^{22})^2u_2^4 =\quad \frac{1}{u^{11}}u^{22}u_2^2|Du|^2. \end{aligned}$$

Insertion of the latter result into (38) yields

$$\begin{aligned} u^{11} u_{111}u_1+u^{22} u_{112}u_2=\frac{1}{Su^{11}}\Bigl ((2-p\tau )\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr ) +\alpha u^{22}u_2^2|Du|^2 \Bigr ).\nonumber \\ \end{aligned}$$

(40)

Now we compute $u^{kk}u_{22k}u_k$. By using (35) and (36) (or changing the index 1 and 2 in (40)) we find

$$\begin{aligned} u^{11} u_{122}u_1+u^{22} u_{222}u_2=\frac{1}{Su^{22}}\Bigl ((2-p\tau )\bigl (u^{22}u_2^2-u^{11}u_1^2\bigr ) +\alpha u^{11}u_1^2|Du|^2 \Bigr ).\nonumber \\ \end{aligned}$$

(41)

Finally, let us compute $u^{kk}u_{12k}u_k$. By using (34) and (35), we find

$$\begin{aligned} \begin{aligned}&u^{11} u_{112}u_1+u^{22} u_{122}u_2\\&\quad =\frac{1}{S^2}\Bigl ((2-p\tau )\bigl (3u^{11}u_1^3u_2-u^{22}u_1u_2^3\bigr )+\alpha u_{22}(u^{22})^2u_1u_2^5\\&\qquad -\alpha u_{22}u^{11}u^{22} u_1^3u_2^3-2\alpha u_{11}(u^{11})^2u_1^5u_2\\&\qquad +(2-p\tau )\bigl (3u^{22}u_1u_2^3-u^{11}u_1^3u_2\bigr )+\alpha u_{11}(u^{11})^2u_1^5u_2\\&\qquad -\alpha u_{11}u^{11}u^{22} u_1^3u_2^3-2\alpha u_{22}(u^{22})^2u_1u_2^5\Bigr ). \end{aligned} \end{aligned}$$

After some simplification we find

$$\begin{aligned} \begin{aligned}&u^{11} u_{112}u_1+u^{22} u_{122}u_2\\&\quad =\frac{1}{S^2}\Bigl ((2-p\tau )2\bigl (u^{11}u_1^3u_2+u^{22}u_1u_2^3\bigr )-\alpha u_{22}(u^{22})^2u_1u_2^5\\&\qquad -\alpha u_{22}u^{11}u^{22} u_1^3u_2^3-\alpha u_{11}(u^{11})^2u_1^5u_2-\alpha u_{11}u^{11}u^{22} u_1^3u_2^3\Bigr ). \end{aligned} \end{aligned}$$

Further simplification and use of the equations $u_{11}u^{11}=u_{22}u^{22}=1$ yields

$$\begin{aligned} \begin{aligned}&u^{11} u_{112}u_1+u^{22} u_{122}u_2\\&\quad =\frac{1}{S}\Bigl ((2-p\tau )2u_1u_2-\alpha u_1u_2|Du|^2\Bigr ). \end{aligned} \end{aligned}$$

(42)

By using (40), (41) and (42) we find

$$\begin{aligned} \begin{aligned}&u^{ii}u^{jj}\Bigl (u^{kk} u_{ijk}u_k\bigr )^2\\&\quad =\frac{1}{S^2}\Bigl [\Bigl ((2-p\tau )\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr ) +\alpha u^{22}u_2^2|Du|^2\Bigr )^2\\&\qquad +\Bigl ((2-p\tau )\bigl (u^{22}u_2^2-u^{11}u_1^2\bigr ) +\alpha u^{11}u_1^2|Du|^2 \Bigr )^2\\&\qquad +2u^{11}u^{22}\Bigl ((2-p\tau )2u_1u_2-\alpha u_1u_2|Du|^2\Bigr )^2\Bigr ]. \end{aligned} \end{aligned}$$

If we expand the powers in above and use the equations

$$\begin{aligned} \begin{aligned}&2\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr )^2+8u^{11}u^{22}u_1^2u_2^2=2S^2,\\\\&\bigl (u^{22}u_2^2|Du|^2\bigr )^2+\bigl (u^{11}u_1^2|Du|^2\bigr )^2+2u^{11}u^{22}\bigl (u_1u_2|Du|^2\bigr )^2=S^2|Du|^4,\\\\&2\bigl (u^{11}u_1^2-u^{22}u_2^2\bigr )\bigl (u^{22}u_2^2-u^{11}u_1^2)|Du|^2-8u^{11}u^{22}u_1^2u_2^2|Du|^2=-2S^2|Du|^2. \end{aligned} \end{aligned}$$

we find

$$\begin{aligned} u^{ii}u^{jj}\Bigl (u^{kk} u_{ijk}u_k\bigr )^2=2(2-p\tau )^2+\alpha ^2|Du|^4-2\alpha (2-p\tau )|Du|^2. \end{aligned}$$

Since $\alpha |Du|^{2}=2(2-p)$, we have

$$\begin{aligned} \alpha ^2|Du|^4-2\alpha (2-p\tau )|Du|^2=4p(2-p)(\tau -1). \end{aligned}$$

Therefore,

$$\begin{aligned} u^{ii}u^{jj}\bigl (u^{kk} u_{ijk}u_k\bigr )^2=2(2-p\tau )^2+4p(2-p)(\tau -1). \end{aligned}$$

Inserting the latter result into (30), after simplification we find

$$\begin{aligned} u^{ii} P_{ii}=2(1-\tau )\bigl [p(2-\tau )-1\bigr ]. \end{aligned}$$

Since $1<\tau <2-\frac{1}{p}$ we have $p(2-\tau )-1>0$ and $u^{ii} P_{ii}<0$, contradicting the assumption that ${\bar{x}}$ was a point of minimum. The theorem is proved.

If $n=2$, we prove Theorem 1.2 by using the following condition

$$\begin{aligned} {{\mathcal {H}}}_{(1)}|Du|^{2(p-1)+1}=c\ \ \hbox {on}\ \ \partial \Omega , \end{aligned}$$

(43)

where c is some positive constant and ${{\mathcal {H}}}_{(1)}$ is the curvature of the boundary $\partial \Omega$.

Theorem 4.2

Let $\Omega \subset {\mathbb {R}}^2$ be a bounded convex domain. If there is a solution $u\in \Phi$ to problem (1) in $\Omega$ which satisfies the additional condition (43), then the function P defined as in (2) with $n=2$ is a constant in $\Omega$.

Proof

If $\frac{p-1}{p}c\ge -u_m$, then the conclusion follows by Theorem 1.2. So, in what follows, we suppose $\frac{p-1}{p}c< -u_m$. By Theorem 4.1, the function P has its minimum value on $\partial \Omega$. Therefore

$$\begin{aligned} \frac{p-1}{p}T_{(1)}^{kl}(D^2u)|Du|^{2(p-2)}u_ku_l-u\ge \frac{p-1}{p} c,\ \ \forall x\in \Omega . \end{aligned}$$

(44)

By the same computation as in the proof of Theorem 1.2 we find (21) with $n=2$, that is,

$$\begin{aligned} \int _{\Omega }T_{(1)}^{kl}(D^2u)|Du|^{2(p-2)}u_lu_k\, dx=2\int _{\Omega } (-u)\, dx. \end{aligned}$$

(45)

On the other hand, by the Pohozaev identity (26) for $n=2$ we have

$$\begin{aligned} c|\Omega |=\Bigl (2+\frac{p}{p-1}\Bigr )\int _\Omega (-u)\, dx. \end{aligned}$$

(46)

Using (45) and (46) we get

$$\begin{aligned} \begin{aligned}&\int _{\Omega }\Bigl [P(x)-\frac{p-1}{p}c\Bigr ]dx=\int _{\Omega }\Bigl [\frac{p-1}{p}T_{(1)}^{kl}(D^2u)|Du|^{2(p-2)}u_ku_l-u-\frac{p-1}{p}c\Bigr ]\, dx\\&\quad =\int _{\Omega }\Bigl [\frac{p-1}{p}2(-u)-u-\frac{p-1}{p}c\Bigr ]\, dx=\frac{p-1}{p}\Bigl [\Bigl (2+\frac{p}{p-1}\Bigr )\int _{\Omega }(-u)\, dx-c|\Omega |\Bigr ]=0. \end{aligned} \end{aligned}$$

This result together with (44) shows that $P(x)=\frac{p-1}{p}c$ in $\Omega$.

The theorem is proved.