Stationary Sets and Asymptotic Behavior of the Mean Curvature Flow with Forcing in the Plane

Abstract

We consider the flat flow solutions of the mean curvature equation with a forcing term in the plane. We prove that for every constant forcing term the stationary sets are given by a finite union of disks with equal radii and disjoint closures. On the other hand for every bounded forcing term tangent disks are never stationary. Finally in the case of an asymptotically constant forcing term we show that the only possible long time limit sets are given by disjoint unions of disks with equal radii and possibly tangent.

1 Introduction

Mean curvature flow is one of the simplest and yet most interesting geometric evolution equation. In order to deal with formation of singularities or rough initial data several notions of generalized solutions have been proposed. Among them we mention Brakke’s solutions in the varifold sense [7], level-set solutions in the viscosity sense [10, 15], De Giorgi’s minimal barriers [12] and the flat flows solutions constructed by the minimizing movements method [2, 21]. Each method has its own advantages and drawbacks. For instance Brakke’s theory fails to provide unique solutions, but yields a satisfactory partial regularity theory, see also [19]. On the contrary, the viscosity level-set method provides uniqueness and global existence, but it is not so convenient as far as regularity is concerned. Indeed in this framework one may construct singular solutions where the evolving hypersurfaces become sets with nonempty interior, the so called fattening phenomenon. This phenomenon can occur even if the initial set is regular after a positive time, see [5]. De Giorgi’s minimal barriers provide essentially the same solutions as the level-set method, see [4]; within this approach the fattening phenomenon is related to the fact that minimal and maximal solutions may be different, see [5]. Flat flow solutions are also defined globally in time. They are always given by evolving boundaries of sets and may not be unique whenever the level-set solution experiences the fattening phenomenon. However, level-set solutions, De Giorgi’s minimal barriers and flat flows all coincide with the classical solutions as long as the latter exist.

In this paper we focus on the flat flow approach for the mean curvature equation with a time dependent forcing term in the plane, i.e.,

$$\begin{aligned} V_t = -k_{E_t} + f(t) \qquad \text {on } \, \partial E_t \end{aligned}$$

(1.1)

with an arbitrary initial datum under the assumption that the forcing term f is uniformly bounded, i.e.,

$$\begin{aligned} \sup _{t \ge 0} |f(t)| \le C_0. \end{aligned}$$

(1.2)

Here $k_{E_t}$ stands for the curvature of the boundary of $E_t$ with respect to the orientation given by the outward normal. For the precise definition of flat flow see the beginning of Sect. 2.

The existence of flat flow solutions for the equation (1.1) in any dimension and their relations with the De Giorgi’s barriers and the level-set solutions has been investigated in [9]. In this paper we further elaborate on the properties of flat flow solutions in two dimensions focusing on the following issues: how the flat flow selects a solution when the fattening phenomenon occurs, the characterization of sets that are stationary when f is constant and the long time behavior of solutions.

1.1 Flat Flow as a Selection Principle

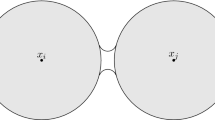
Here we consider a particular situation where the initial set is given by two tangent disks of equal radii $D_r(x_1)$ and $D_r(x_2)$. It is well known that in this example the level-set solution develops instantaneously a nonempty interior. When $f(t)\equiv 1/r$ the minimal barrier solution of (1.1) is stationary, while the maximal barrier solution becomes a connected set containing a ball centered at the origin with a time dependent radius, see [5]. It is an interesting problem to look for a selection principle among the possible admissible behaviors. One such principle can be obtained by adding to the forcing term a small stochastic perturbation. This has been investigated in [14] where the perturbation considered is of the form $\varepsilon \,dW$, with W a standard Brownian motion. The authors show that when $\varepsilon$ goes to zero the corresponding motion converges with probability 1/2 to the maximal barrier solution and with probability 1/2 to the minimal one. In this paper we prove that any flat flow instantaneously connects the two tangent disks with a thin neck and keeps enlarging the neck at least for a short time interval, thus showing that the flat flow somehow picks the behavior of the maximal barrier solution. The precise statement is as follows.

Theorem 1.1

Let $E_0 \subset {\mathbb {R}}^2$ be a union of two tangent disks $E_0 = D_r(x_1) \cup D_r(x_2)$ and let $(E_t)_t$ be a flat flow of (1.1) starting from $E_0$ and assume that (1.2) holds. There exist $\delta >0$, $\eta$ $\in (0, r)$ and $c>0$ such that for every $t \in (0,\delta )$ the set $E_t$ contains a dumbbell shaped simply connected set which in turn contains the disks $D_{\eta }(x_1)$ and $D_{\eta }(x_2)$ and a ball centered at the origin of radius t. In particular for every $t \in (0,\delta )$

$$\begin{aligned} |E_t \setminus E_0| \ge c\,t^3. \end{aligned}$$

This theorem is also relevant for the second issue we want to deal with, i.e., the characterization of stationary sets, as it shows that the union of two equal tangent disks is not stationary for the flat flow.

1.2 Characterization of Stationary Sets

When the forcing term $f\equiv c_0$ equation (1.1) can be regarded as the gradient flow of the following energy

$$\begin{aligned} {\mathcal {E}}(E)=P(E)-c_0|E|, \end{aligned}$$

(1.3)

where P(E) stands for the perimeter of E and |E| for its Lebesgue measure. Therefore one might think that $E_0$ is stationary for the flow if and only if it is critical for the energy (1.3), i.e., it satisfies $k_{E_0}=c_0$ on $\partial E_0$ in a weak sense. Indeed if $E_0$ is stationary then it also critical, while the converse is certainly true when $E_0$ is smooth, i.e., is given by a union of finitely many disks with equal radii and mutually disjoint closures (see [13] for a characterization of critical sets in any dimension, even in the nonsmooth case). However, Theorem 1.1 shows that the two notions do not coincide since the union of two tangent disks of equal radii is critical as it has constant mean curvature in the weak sense, but not stationary. Here we show that a set E is stationary for the flow (1.1) when $f \equiv c_0$ if and only if it is a union of disks with radius $r = 1/c_0$ with positive distance to each other. More precisely we have the following.

Theorem 1.2

Assume $E_0 \subset {\mathbb {R}}^2$ is a bounded set of finite perimeter. Then $E_0$ is stationary (see Definition 3.1) for the flow (1.1) with $f \equiv c_0 >0$ if and only if there are points $x_1, \dots , x_N$ such that $|x_i -x_j| > 2r$ for $i \ne j$, with $r = 1/c_0$, and

$$\begin{aligned} E_0 = \bigcup _{i =1}^N D_r(x_i). \end{aligned}$$

The fact that any stationary set is a union of disjoint disks follows from a sharp quantitative version of the Alexandrov theorem in the plane, see Lemma 3.2, while the fact that the disks must be at positive distance apart is a consequence of Theorem 1.1.

We remark that the same type of classification holds true in the framework of level-set solutions, as recently shown in [16, Theorem 4.7]. The general n-dimensional case remains open also for the viscosity solutions, see [17].

1.3 Long Time Behavior

We now address the long time behavior of the flat flow under the assumption that the forcing term is asymptotically constant, namely that it satisfies

$$\begin{aligned} \int _0^\infty |f(s) -c_0|^2\, ds <\infty . \end{aligned}$$

(1.4)

In the next theorem our goal is to characterize the possible limit sets and we show in particular that the asymptotically stationary sets are given once again by a union of disjoint disks, which however can be tangent. Precisely we show that either, up to a diverging sequence $t_j$ of times, the area of $E_{t_j}$ blows up or the sets $(E_t)_t$ converge up to a translation in the Hausdorff sense to a disjoint union of disks with equal radii.

Theorem 1.3

Assume $E_0 \subset {\mathbb {R}}^2$ is a bounded set of finite perimeter. Let $(E_t)_t$ be a flat flow of (1.1) starting from $E_0$ and assume (1.2) and (1.4) with $c_0 >0$, and

$$\begin{aligned} \sup _{t >0} |E_t| < \infty . \end{aligned}$$

Then there exist $N\in {\mathbb {N}}$ and $x_i(t):(0,+\infty )\rightarrow {\mathbb {R}}^2$, with $i=1,\dots ,N$ and $|x_i(t) -x_j(t)| \ge 2/c_0$ for $i \ne j$, such that, setting $F_t = \cup _{i=i}^N D_{1/c_0}(x_i(t))$

$$\begin{aligned} \lim _{t\rightarrow \infty }\,\sup _{x\in E_t\Delta F_t}d_{\partial F_t}(x)=0. \end{aligned}$$

We stress here the fact that the initial set $E_0$ in the above theorem is an arbitrary bounded set of finite perimeter without further regularity assumption. It is plausible that in Theorem 1.3 the convergence holds not just up to translation.

Previous results dealt with special classes of sets in any dimension such as convex or star-shaped initial sets, see for instance [3, 20]. We also mention [23] where the long-time behavior of the discrete Euler implicit scheme for the volume preserving mean curvature flow is addressed for any arbitrary bounded initial set with finite perimeter. The long time behavior of the forced mean curvature flow in the context of viscosity level-set solutions was also investigated in [16, 17] where it is shown that under certain assumptions the solutions converge to a stationary solution of the level-set equation. The problem of classifying the latter is open in general.

We now show that it is indeed possible to obtain as a limit of the flow (1.1) a union of essentially disjoint disks such that at least two of them are tangent. To this end we take G to be the ellipse

$$\begin{aligned} G = \{ (x_1,x_2) \in {\mathbb {R}}^2 : \, a^2 x_1^2 + x_2^2 < 1 \} \qquad \text {with } \, a>1 \end{aligned}$$

and we show the following theorem.

Theorem 1.4

Let $e_1 = (1,0)$ and G as above. Denote by $\rho = \frac{1}{\sqrt{a}}$ the radius such that $|D_\rho | = |G|$. The volume preserving mean curvature flow $(E_t)_t$, starting from

$$\begin{aligned} E_0 = (G - \rho e_1 ) \cup (G + \rho e_1 ), \end{aligned}$$

is well defined in the classical sense for all $t >0$ and converges exponentially fast to the union of two tangent disks

$$\begin{aligned} E_t \rightarrow (D_\rho - \rho e_1 ) \cup (D_\rho + \rho e_1 ). \end{aligned}$$

Note that Theorem 1.4 shows that a flat flow of (1.1) may converge to tangent disks. Indeed the classical solution of the flow in Theorem 1.4 is well defined and smooth for all times and we may write it in the form (1.1) with $f(t) =-\int _{\partial E_t}k_{E_t}$ and the flat flow agrees with it. Moreover, by the exponential convergence we have that f(t) satisfies (1.4).

We note that in Theorem 1.4 the flow $(E_t)_t$ remains smooth and diffeomorphic to a union of two disks. Only the limit set is non-smooth (Fig. 1).

Fig. 1

The union of two ellipses converges to the union of two tangent disks

2 Notation and Preliminary Results

Since the results of this section hold in any dimension we state them in full generality and we will go back to the planar case in the next sections.

Given a set $A \subset {\mathbb {R}}^n$ the distance function $d_A : {\mathbb {R}}^n \rightarrow [0,\infty )$ is defined as usual

$$\begin{aligned} d_A(x) := \inf _{y \in A} |x - y| \end{aligned}$$

and we denote the signed distance function by ${\bar{d}}_A : {\mathbb {R}}^n \rightarrow {\mathbb {R}}$,

$$\begin{aligned} {\bar{d}}_A(x) := {\left\{ \begin{array}{ll} - d_{{\mathbb {R}}^n \setminus A}(x) , \,\,\text {for }\, x \in A \\ d_A(x) , \,\, \text {for }\, x \in {\mathbb {R}}^n \setminus A. \end{array}\right. } \end{aligned}$$

Then clearly it holds $d_{\partial A} = |{{\bar{d}}}_A|$.

For a set of finite perimeter $E \subset {\mathbb {R}}^n$ we denote its perimeter by P(E) and recall that for regular enough set it holds $P(E) = {\mathcal {H}}^{n-1}(\partial E)$ [1, 22]. For a measurable set |E| denotes its Lebesgue measure. We denote by $H_E$ the sum of the principal curvatures of E, while in the planar case we write $k_E$. We denote the disk with radius r centered at x by $D_r(x)$ and in the higher dimensional case we write $B_r(x)$ instead.

We consider solutions of (1.1) constructed via the minimizing movement scheme. We fix a small time step $h>0$ and a bounded set of finite perimeter $E_0 \subset {\mathbb {R}}^n$, which is our initial set $E^{h,0} = E_0$. We obtain a sequence of set $(E^{h,k})_{k=1}^\infty$ by iterative minimizing procedure, where $E^{h,k+1}$ is a minimizer of the functional ${\mathcal {F}}_k(E; E^{h,k})$ defined as

$$\begin{aligned} {\mathcal {F}}_k(E; E^{h,k}) = P(E) + \frac{1}{h} \int _E {\bar{d}}_{E^{h,k}} \, dx - {{\bar{f}}}(kh) |E|, \end{aligned}$$

(2.1)

where ${\bar{d}}_{E^{h,k}}$ is the signed distance defined above and ${{\bar{f}}}(kh) = \frac{1}{h}\int _{kh}^{(k+1)h} f(s)\, ds$. We define the approximate flat flow $(E_t^h)_{t > 0}$ by

$$\begin{aligned} E_t^h = E^{h,k}, \qquad \text {for } \, (k-1)h < t \le k h \end{aligned}$$

(2.2)

and we set ${{\bar{f}}}(t)={{\bar{f}}}(kh)$ for $(k-1)h < t \le k h$. Any cluster point of $E_t^h$ as h goes to zero is called a flat flow for the equation (1.1).

We warn the reader that in the above definition it is understood that we identify $E^{h,k}$ with its set of its points of density 1 so that there is no ambiguity in the definition of ${\bar{d}}_{E^{h,k}}$.

Recall that if $E_0$ and f are smooth then any flat flow coincide with the classical solution of (1.1) as long as the latter remains smooth, see [9].

In general, the problem (2.1) does not admit a unique minimizer and thus there is no unique way to define the approximate flat flow $(E_t^h)_{t > 0}$. Also the flat flow may not be unique when fattening occurs. However, as we mentioned in the introduction, in the case when the initial set and the forcing term are smooth, the flat flow is unique for a short time interval and agrees with the classical solution.

Even if there is no uniqueness, the approximate flat flow satisfies the following weak comparison principle, see for instance the proof of Lemma 6.2 in [8].

Proposition 2.1

Assume $f_1, f_2:[0,\infty ) \rightarrow {\mathbb {R}}$ satisfy (1). Let $E_0, F_0$ be two bounded sets of finite perimeter and let $(E_t^h)_t$ be an approximate flat flow with forcing term $f_1$ starting from $E_0$ and $(F_t^h)_t$ an approximate flat flow with forcing term $f_2$ starting from $F_0$.

• (i) If $F_0 \subset E_0$ and $f_1 > f_2$, then for every $t>0$ it holds $F_t^h \subset E_t^h$.

• (ii) If $E_0 \subset {\mathbb {R}}^n \setminus F_0$ and $-f_2 > f_1$, then for every $t>0$ it holds $E_t^h \subset {\mathbb {R}}^n \setminus F_t^h$.

We need preliminary results on the structure of the approximate flat flow constructed via (2.1). We note that if $E^{h,k+1}$ is a minimizer of ${\mathcal {F}}_{k}(\cdot , E^{h,k})$ then it is a $\Lambda$-minimizer of the perimeter, see for instance [24], with $\Lambda \le C/h$, see [22] for the definition of $\Lambda$-minimizer. Then it follows that $\partial E^{h,k+1}$ is $C^{1,\alpha }$-regular for all $\alpha \in (0,1)$ up to a singular set $\Sigma$ with Hausdorff dimension at most $n-8$, see [22]. Then the Euler–Lagrange equation

$$\begin{aligned} \frac{{\bar{d}}_{E^{h,k}}}{h} = -H_{E^{h,k+1}} + {\bar{f}}(kh) \qquad \text {on } \, \partial E^{h,k+1}\setminus \Sigma , \end{aligned}$$

(2.3)

which holds in the weak sense, implies that $\partial E^{h,k+1}\setminus \Sigma$ is $C^{2,\alpha }$-regular and satisfies (2.3) in the classical sense.

Lemma 2.2

Assume that $(E^{h,k})_k$ is a sequence obtained via minimizing movements (2.1) starting from a bounded set of finite perimeter $E_0$ and assume that the forcing term satisfies (1.2). Then there is a constant $C_1$ such that for every $k = 0,1,2, \dots$

$$\begin{aligned} \sup _{x \in E^{h,k+1} \Delta E^{h,k}} d_{\partial E^{h,k}}(x) \le C_1 \sqrt{h}. \end{aligned}$$

Moreover, there are constants $C_2>1$ and $c_1>0$ such that for every $k =1,2,3, \dots$ it holds

$$\begin{aligned} |E^{h,k+1} \Delta E^{h,k}| \le C_2 \left( l P( E^{h,k}) + \frac{1}{l} \int _{E^{h,k+1} \Delta E^{h,k}} |{{\bar{d}}}_{E^{h,k}}(x)| \, dx \right) \end{aligned}$$

for any $0< l < c_1 \sqrt{h}$.

Proof

The first claim follows from the argument of the proof of [24, Proposition 3.2] and thus we omit it. The second claim follows from an argument similar to [24, Proposition 3.4] and we only sketch it. We write

$$\begin{aligned} |E^{h,k+1} \Delta E^{h,k} |= & {} | \{x \in E^{h,k+1} \Delta E^{h,k} : |{{\bar{d}}}_{E^{h,k}}(x)|\ge l\}| \\&\quad + |\{x \in E^{h,k+1} \Delta E^{h,k} : |{{\bar{d}}}_{E^{h,k}}(x)| < l\}|. \end{aligned}$$

We estimate the first term as

$$\begin{aligned} | \{x \in E^{h,k+1} \Delta E^{h,k} : |{{\bar{d}}}_{E^{h,k}}(x)|\ge l\} | \le \frac{1}{l} \int _{E^{h,k+1} \Delta E^{h,k}} |{{\bar{d}}}_{E^{h,k}}(x)| \, dx. \end{aligned}$$

For the second term we use Vitali covering theorem to choose a finite family of disjoint balls $(B_l(x_i))_{i=1}^N$, with $x_i \in \partial E^{h,k}$, such that

$$\begin{aligned} \{x \in {\mathbb {R}}^n : |{{\bar{d}}}_{E^{h,k}}(x)| < l\} \subset \cup _{i=1}^N B_{5l}(x_i). \end{aligned}$$

Since $E^{h,k}$ is a minimizer of ${\mathcal {F}}_k(E; E^{h,k-1})$, we have the density estimates [24, Corollary 3.3]. Thus by the relative isoperimetric inequality we have for every $i = 1, \dots , N$

$$\begin{aligned} |B_l(x_i)| \le C ({\mathcal {H}}^{n-1}(\partial E^{h,k} \cap B_l(x_i))^{\frac{n}{n-1}}\le C l \, {\mathcal {H}}^{n-1}(\partial E^{h,k} \cap B_l(x_i)). \end{aligned}$$

Therefore

$$\begin{aligned} \begin{aligned} |\{x \in E^{h,k+1} \Delta E^{h,k} : |{{\bar{d}}}_{E^{h,k}}(x)| < l\}|&\le \sum _{i=1}^N |B_{5l}(x_i)| \le 5^n \sum _{i=1}^N |B_{l}(x_i)| \\&\le Cl \sum _{i=1}^N {\mathcal {H}}^{n-1}(\partial E^{h,k} \cap B_l(x_i)) \le C l \, P(E^{h,k} ). \end{aligned} \end{aligned}$$

$\square$

In the next proposition we list useful properties of the flow in the case when the forcing term satisfies only (1.2).

Proposition 2.3

Let $(E_{t}^h)_t$ be an approximate flat flow starting from a bounded set of finite perimeter $E_0$ and assume that the forcing term satisfies (1.2). Then the following hold:

• (i) For every $T>0$ there is $R_T>0$ such that $E_t^h \subset B_{R_T}$ for every $t \le T$.

• (ii) There is $C_3$, depending only on $E_0$ and f, such that for every $T >0$ it holds

  $$\begin{aligned} P(E_T^h) \le C_3^{1+T} \end{aligned}$$

  for h sufficiently small.

• (iii) For every $h< s<t <T$ with $t-s >h$ and h sufficiently small, it holds $|E_t^h \Delta E_s^h| \le C_T \sqrt{t-s}$, where the constant $C_T$ depends on T.

• (iv) There exists a subsequence $(h_l)_l$ converging to zero such that $(E_t^{h_l})_t$ converges to a flat flow $(E_t)_t$ in $L^1$ in space and locally uniformly in time, i.e., for every T

  $$\begin{aligned} \sup _{h_l< t \le T }|E_t^{h_l} \Delta E_t| \rightarrow 0 \qquad \text {as } \, h_l \rightarrow 0. \end{aligned}$$

Proof

The claim (i) follows by applying Proposition 2.1 to $E_t^h$ and $F_t^h$, where the latter is approximate flat flow starting from $B_R$, such that $E_0 \subset B_R$, and with constant forcing term $f_2 \equiv \sup _t f(t) +1$. Then $E_t^h \subset F_t^h$. It is easy to check that the sets $(F_t^h)_{t \le T}$ are balls whose radii satisfy $r(t) \le C(1+T)$ for $t \le T$.

Let us prove (ii). By the minimality of $E^{h,k+1}$ we have ${\mathcal {F}}_{k}( E^{h,k+1}; E^{h,k}) \le {\mathcal {F}}_{k}( E^{h,k}; E^{h,k})$ which implies

$$\begin{aligned} P(E^{h,k+1}) + \frac{1}{h} \int _{E^{h,k+1}} {\bar{d}}_{E^{h,k}} \, dx - {{\bar{f}}}(kh) |E^{h,k+1}| \le P(E^{h,k}) + \frac{1}{h} \int _{E^{h,k}} {\bar{d}}_{E^{h,k}} \, dx - {{\bar{f}}}(kh) |E^{h,k}|. \end{aligned}$$

We write this as

$$\begin{aligned} \frac{1}{h} \int _{E^{h,k+1} \Delta E^{h,k}} |{\bar{d}}_{E^{h,k}}| \, dx + P(E^{h,k+1}) \le P(E^{h,k}) + {{\bar{f}}}(kh) (|E^{h,k+1}| - |E^{h,k}|). \end{aligned}$$

(2.4)

By (1.2) we simply estimate ${{\bar{f}}}(kh) (|E^{h,k+1}| - |E^{h,k}|) \le C_0 |E^{h,k+1} \Delta E^{h,k}|$. Then we use the second statement in Lemma 2.2 with $l = {\hat{C}} h$, where ${\hat{C}}$ is a large constant to deduce

$$\begin{aligned} |E^{h,k+1} \Delta E^{h,k}| \le C h \, P(E^{h,k}) + \frac{1}{2C_0 h} \int _{E^{h,k+1} \Delta E^{h,k}} |{\bar{d}}_{E^{h,k}}| \, dx. \end{aligned}$$

Therefore we deduce from these two inequalities and from (2.4) that

$$\begin{aligned} \frac{1}{2h} \int _{E^{h,k+1} \Delta E^{h,k}} |{\bar{d}}_{E^{h,k}}| \, dx + P(E^{h,k+1}) \le (1+ C \, h ) P(E^{h,k}). \end{aligned}$$

(2.5)

By iterating the inequality $P(E^{h,k+1}) \le (1+ C \, h ) P(E^{h,k})$ we get

$$\begin{aligned} P(E^{h,k}) \le (1+ C \, h )^{k-1} P(E^{h,1}) = \left( (1+ C \, h )^{1/h}\right) ^{(k-1)h} P(E^{h,1}) \le C^{(k-1)h}\, P(E^{h,1}). \end{aligned}$$

Finally we use (2.4) for $k=0$ and have

$$\begin{aligned} P(E^{h,1}) \le P(E_{0}) + {{\bar{f}}}(0) (|E^{h,1}| - |E_{0}|). \end{aligned}$$

(2.6)

By (i) we may estimate $|E^{h,1}| \le |B_{2R}|$ for h sufficiently small, where we recall that $B_R$ is the ball containing $E_0$. Therefore $P(E^{h,1}) \le P(E_0) + C$ and we obtain the claim (ii)

The claim (iii) follows from argument similar to [24, Proposition 3.5] so we only point out the main differences. Let k, m be such that $s \in (kh, (k+1)h]$ and $t \in ((k+m)h, (k+m+1)h]$. Note that $mh \le 2(t-s)$. We may estimate the quantity $|E_t^h \Delta E_s^h|$ by applying the second statement of Lemma 2.2 with $l = c_1\frac{h}{2\sqrt{t-s}}$, (2.5) and the part (ii) to get

$$\begin{aligned} \begin{aligned} |E_t^h \Delta E_s^h|&\le \sum _{i=1}^m |E^{h,k+i+1} \Delta E^{h,k+i}|\\&\le \sum _{i=1}^m C \left( \frac{h}{\sqrt{t-s}} P( E^{h,k+i}) + \frac{\sqrt{t-s}}{h}\int _{E^{h,k+i+1} \Delta E^{h,k+i}} |{{\bar{d}}}_{E^{h,k+i}}(x)| \, dx \right) \\&\le \sum _{i=1}^m C \left( \frac{h}{\sqrt{t-s}}P( E^{h,k+i}) + \sqrt{t-s}\big ((1+ C \, h ) P( E^{h,k+i}) - P( E^{h,k+i+1}) \big ) \right) \\&\le C\sqrt{t-s} \, \sup _{t\le T}P(E_t^h) + \sqrt{t-s} P(E^{h,k+1}) \le C_T \sqrt{t-s}. \end{aligned} \end{aligned}$$

Similarly (iv) follows from the proof of [24, Theorem 2.2]. $\square$

When in addition we assume that the forcing term satisfies (1.4) we obtain estimates which are more uniform with respect to time. To this aim we define the following quantity which plays the role of the energy

$$\begin{aligned} {\mathcal {E}}(E) := P(E) -c_0 |E|, \end{aligned}$$

(2.7)

where $c_0$ is the constant appearing in (1.4).

Proposition 2.4

Let $(E_{t}^h)_t$ be an approximate flat flow starting from a bounded set of finite perimeter $E_0$ and assume that the forcing term satisfies (1.2) and (1.4). Then, if h is sufficiently small, the following hold:

• (i) For every $\varepsilon >0$ there is $T_\varepsilon$ such that for every $T_\varepsilon< T_1 < T_2$, with $T_2 \ge T_1+h$, we have the following dissipation inequality

  $$\begin{aligned} c \int _{T_1}^{T_2}\int _{\partial E_t^h} (H_{E_t^h} - {{\bar{f}}}(t-h))^2 \, d{\mathcal {H}}^{n-1}dt + {\mathcal {E}}(E_{T_2}^h )\le {\mathcal {E}}(E_{T_1-h}^h) + \varepsilon \sup _{T_1-h \le t \le T_2} P(E_{t}^h). \end{aligned}$$

• (ii) If $\sup _{t \ge 0} | E_t^h| < \infty$, then $\sup _{t \ge 0} P(E_t^h) < \infty$.

• (iii) If $\sup _{t \ge 0} | E_t^h| < \infty$, there exists a constant $C_4$ such that $|E_t^h \Delta E_s^h| \le C_4 \sqrt{t-s}$ for every $h< s <t$ with $t-s >h$.

Proof

To prove (i) we begin with (2.4). This time we estimate the last term in (2.4) as

$$\begin{aligned} {{\bar{f}}}(kh) (|E^{h,k+1}| - |E^{h,k}|) \le c_0(|E^{h,k+1}| - |E^{h,k}|) + |{{\bar{f}}}(kh) -c_0| \, |E^{h,k+1} \Delta E^{h,k}|. \end{aligned}$$

We use the second estimate in Lemma 2.2 with $l = {\hat{C}}\, |{{\bar{f}}}(kh) -c_0| h$, where ${\hat{C}}$ is a large constant and h is sufficiently small, to deduce

$$\begin{aligned} |{{\bar{f}}}(kh) -c_0| \, |E^{h,k+1} \Delta E^{h,k}| \le C |{{\bar{f}}}(kh) -c_0|^2 h \, P(E^{h,k}) + \frac{1}{2 h} \int _{E^{h,k+1} \Delta E^{h,k}} |{\bar{d}}_{E^{h,k}}| \, dx. \end{aligned}$$

Therefore we have by (2.4) that

$$\begin{aligned} \frac{1}{2 h} \int _{E^{h,k+1} \Delta E^{h,k}} |{\bar{d}}_{E^{h,k}}| \, dx + {\mathcal {E}}(E^{h,k+1} )\le {\mathcal {E}}(E^{h,k}) + C |{{\bar{f}}}(kh) -c_0|^2 h \, P(E^{h,k}), \end{aligned}$$

where ${\mathcal {E}}$ is defined in (2.7).

Let us fix $\varepsilon >0$. Since we assume (1.4), there exists $T_\varepsilon$ such that

$$\begin{aligned} \int _{T_\varepsilon }^\infty (f(t) -c_0)^2\, dt \le \frac{\varepsilon }{C}, \end{aligned}$$

(2.8)

where C is a constant to be chosen later. Let $T_2> T_1 > T_\varepsilon$ and let j, m be such that $T_1 \in (jh, (j+1)h]$ and $T_2 \in ((j+m)h, (j+m+1)h]$. We iterate the previous inequality from $k= j$ to $k = j+m$ and obtain

$$\begin{aligned} \begin{aligned}&\sum _{k=j}^{j+m} \frac{1}{2 h} \int _{E^{h,k+1} \Delta E^{h,k}} |{\bar{d}}_{E^{h,k}}| \, dx + {\mathcal {E}}(E_{T_2}^h ) \\&\quad \le {\mathcal {E}}(E_{T_1-h}^h) +C\left( \sup _{T_1-h \le t \le T_2} P(E_{t}^h) \right) \left( \int _{T_1-h}^{T_2} |{{\bar{f}}}(t) -c_0|^2 \,dt \right) \\&\quad \le {\mathcal {E}}(E_{T_1-h}^h) +C\left( \sup _{T_1-h \le t \le T_2} P(E_{t}^h) \right) \left( \int _{T_\varepsilon }^{\infty } |f(t) -c_0|^2 \,dt \right) \\&\quad \le {\mathcal {E}}(E_{T_1-h}^h) + \varepsilon \left( \sup _{T_1-h \le t \le T_2} P(E_{t}^h) \right) , \end{aligned} \end{aligned}$$

(2.9)

where the last inequality follows from (2.8).

Arguing as in the proof of [24, Lemma 3.6], we deduce that there is a constant $c>0$, depending only on the dimension, such that

$$\begin{aligned} c\, h \int _{\partial E^{h,k+1}} \left( \frac{{\bar{d}}_{E^{h,k}}}{h}\right) ^2 \, d {\mathcal {H}}^{n-1} \le \int _{E^{h,k+1} \Delta E^{h,k}} \frac{|{\bar{d}}_{E^{h,k}}|}{h} \, dx. \end{aligned}$$

Therefore by the Euler–Lagrange equation (2.3) we have

$$\begin{aligned} \begin{aligned} \sum _{k=j}^{j+m} \frac{1}{h} \int _{E^{h,k+1} \Delta E^{h,k}} |{\bar{d}}_{E^{h,k}}| \, dx&\ge c \sum _{k=j}^{j+m} h \int _{\partial E^{h,k+1}} \left( \frac{{\bar{d}}_{E^{h,k}}}{h}\right) ^2 \, d {\mathcal {H}}^{n-1}\\&= c \sum _{k=j}^{j+m} h \int _{\partial E^{h,k+1}} \left( H_{E^{h,k+1}} - {{\bar{f}}}(kh)\right) ^2 \, d {\mathcal {H}}^{n-1}\\&\ge c \int _{T_1}^{T_2} \int _{\partial E_{t}^h} \left( H_{E_{t}^h} - {{\bar{f}}}(t-h)\right) ^2 \, d {\mathcal {H}}^{n-1} dt . \end{aligned} \end{aligned}$$

Thus we have the claim (i) by (2.9).

To show (ii) we fix $0<\varepsilon < 1/2$, $T > T_\varepsilon$ and apply the part (i) with $T_1 = T_\varepsilon +h$ and $T_1+h<T_2 = t \le T$ to deduce

$$\begin{aligned} {\mathcal {E}}(E_{t}^h )\le {\mathcal {E}}(E_{T_\varepsilon }^h) + \varepsilon \sup _{T_\varepsilon \le s \le T} P(E_{s}^h). \end{aligned}$$

We recall that ${\mathcal {E}}(E) = P(E) - c_0 |E|$ and that we assume $\sup _{t> 0}|E_t^h| <\infty$. Therefore from the above inequality, recalling that $P(E_t^h)\le C_\varepsilon$ for all $t<T_\varepsilon +1$ by Proposition 2.3 (ii), we get

$$\begin{aligned} P(E_{t}^h ) \le C_\varepsilon + c_0\sup _{t> 0}|E_t^h|+\varepsilon \sup _{T_\varepsilon \le s \le T} P(E_{s}^h) \end{aligned}$$

for every $T_\varepsilon < t\le T$. Thus, since $\varepsilon < 1/2$ we deduce that

$$\begin{aligned} \sup _{T_\varepsilon \le t \le T} P(E_{t}^h) \le 2\big (C_\varepsilon + c_0\sup _{t> 0}|E_t^h|\big ). \end{aligned}$$

The claim (ii) follows from the fact that T was arbitrary.

Finally the proof of (iii) follows from the proof of Proposition 2.3 (iii), noticing that now the constant $C_T$ is in fact independent on T thanks to the bound on the perimeters provided by (ii). $\square$

Remark 2.5

If $(E_t^h)_t$, $E_0$ and f are as in Proposition 2.4, and if we assume

$$\begin{aligned} \sup _{t \ge 0} | E_t^h| \le C, \end{aligned}$$

then Proposition (i) and (ii) imply that the energy ${\mathcal {E}}(E_t^h)$ is asymptotically almost decreasing. More precisely, for every $\varepsilon >0$ there is $T_\varepsilon$ such that for $t>s>T_\varepsilon$ it holds

$$\begin{aligned} {\mathcal {E}}(E_t^h) \le {\mathcal {E}}(E_s^h) + C \varepsilon , \end{aligned}$$

(2.10)

with $T_\varepsilon$ and C independent of h. This inequality implies in particular that there exists

$$\begin{aligned} \lim _{t\rightarrow +\infty }{\mathcal {E}}(E_t^h) . \end{aligned}$$

Moreover, from the proof of Proposition 2.4 we have also that if h is sufficiently small and $\sup _{0<t <T} | E_t^h| \le C$ for some $T>0$, then there exists a constant ${\tilde{C}}$, independent of h, such that $\sup _{0<t <T} P(E^h_t) \le {\tilde{C}}$.

3 Stationary Sets and Proof of Theorem 1.1

In this section we go back to the two dimensional setting. We study critical sets of the isoperimetric problem and stationary sets for the flow (1.1). A set of finite perimeter E is critical for the isoperimetric problem if its distributional mean curvature is constant.

We define stationary sets for the equation (1.1) as follows.

Definition 3.1

Assume that the forcing term f in (1.1) is constant, i.e., $f \equiv c_0>0$. A set of finite perimeter $E_0$ is stationary if for any flat flow $(E_t)_t$ starting from $E_0$ it holds

$$\begin{aligned} \sup _{0\le t \le T} |E_t \Delta E_0| = 0 \end{aligned}$$

for every $T>0$.

We begin by proving the sharp quantitative version of the Alexandrov’s theorem in the plane.

Lemma 3.2

Let $M>0$ and let $E \subset {\mathbb {R}}^2$ be $C^2$-regular with $P(E) \le M$. There exist a constant $C_M$ and points $x_1, x_2, \dots , x_N$, with $|x_i -x_j| >2$, such that for $F = \cup _{i=1}^N D_1(x_i)$ it holds

$$\begin{aligned} \sup _{x\in E\Delta F}d_{\partial F}(x) \le C_M \Vert k_E-1 \Vert _{L^1(\partial E)} \end{aligned}$$

(3.1)

and

$$\begin{aligned} | P(E) - 2\pi N| \le C_M \Vert k_E-1 \Vert _{L^1(\partial E)} . \end{aligned}$$

(3.2)

Moreover, there exists $\varepsilon _0>0$ such that if $\Vert k_E-1 \Vert _{L^2(\partial E)} \le \varepsilon _0$ then E is $C^1$-diffeomorphic to the disjoint union of N disks.

Proof

Assume that $\Vert k_E-1 \Vert _{L^1(\partial E)} \ge \varepsilon _0$ for a small $\varepsilon _0$ to be chosen later. Since $\Vert k_E\Vert _{L^1(\partial E)}<\infty$, E has finitely many connected components $E_i$, $i=1,\dots ,N$. If $P(E)\ge 2\pi N$, then $|P(E)-2\pi N|\le M$, hence (3.2) follows with a sufficiently large constant. Otherwise, using Gauss-Bonnet theorem,

$$\begin{aligned} 2\pi N-P(E)\le \sum _{i=1}^N\int _{\partial E_i}(|k_E|-1)\,d{\mathcal {H}}^1\le \Vert k_E-1\Vert _{L^1(\partial E)}, \end{aligned}$$

hence (3.2) follows with $C_M=1$. Since $P(E_i)\le M$ for every i, there exist points $x_i$ such that $E_i\subset D_M(x_i)$. Therefore $\sup _{x\in E_i\Delta D_1(x_i)}d_{\partial D_1(x_i)}(x)$ is smaller than M. Hence $\sup _{x\in E\Delta F}d_{\partial F}(x)\le M$ and (3.1) holds with a sufficiently large constant.

Assume now that $\Vert k_E-1 \Vert _{L^1(\partial E)} \le \varepsilon _0$ for a small $\varepsilon _0$. Let us fix a component $E_i$ of E and denote $l = P(E_i)$. Let us first prove that there is ${x}_i$ such that

$$\begin{aligned} \sup _{x\in E_i \Delta D_1(x_i)}d_{\partial D_1(x_i)}(x) \le C \Vert k_E-1 \Vert _{L^1(\partial E)} \qquad \text {and} \qquad |l - 2 \pi | \le \Vert k_E-1 \Vert _{L^1(\partial E_i)} .\nonumber \\ \end{aligned}$$

(3.3)

It is not difficult to see that the claim follows from (3.3).

We claim first that $E_i$ is simply connected. Indeed, let $\Gamma _0$ be the outer component of $\partial E_i$ for which it holds $\int _{\Gamma _0} k_E \, d {\mathcal {H}}^1 = 2 \pi$. Then it follows from $\Vert k_E-1 \Vert _{L^1(\partial E)} \le \varepsilon _0$ that

$$\begin{aligned} 2 \pi - {\mathcal {H}}^1(\Gamma _0) = \int _{\Gamma _0} (k_E -1) \, d {\mathcal {H}}^1 \le \int _{\partial E} |k_E-1| \, d {\mathcal {H}}^1 \le \varepsilon _0. \end{aligned}$$

This yields $P(E_i) \ge {\mathcal {H}}^1(\Gamma _0) \ge 2 \pi - \varepsilon _0$. Then

$$\begin{aligned} \int _{\partial E_i} k_E \, d {\mathcal {H}}^1 = \int _{\partial E_i} (k_E -1) \, d {\mathcal {H}}^1 + P(E_i) \ge P(E_i) - \int _{\partial E} |k_E-1| \, d {\mathcal {H}}^1 \ge 2 \pi - 2\varepsilon _0. \end{aligned}$$

Therefore when $\varepsilon _0 < \pi$ we conclude that $\int _{\partial E_i} k_E \, d {\mathcal {H}}^1$ is positive. Since $E_i$ is connected, this implies that it is simply connected.

Since the boundary $\partial E_i$ is connected we may parametrize it by unit speed curve $\gamma : [0, l] \rightarrow {\mathbb {R}}^2$, $\gamma (s) = (x(s),y(s))$ with counterclockwise orientation. Define $\theta (s) := \int _{0}^s k_E(\gamma (\tau )) \, d \tau$ so that $\theta (0) = 0$ and $\theta (l) = 2 \pi$. Then

$$\begin{aligned} |\theta (s) - s| \le \Vert k_E-1 \Vert _{L^1(\partial E_i)} \qquad \text {for all }\, s \in [0,l]. \end{aligned}$$

(3.4)

In particular, for $s = l$ (3.4) implies

$$\begin{aligned} |\theta (l) - l|= |2 \pi - l| \le \Vert k_E-1 \Vert _{L^1(\partial E_i)} \end{aligned}$$

which is the second inequality in (3.3).

By possibly rotating the set E we have

$$\begin{aligned} x'(s) = - \sin \theta (s) \qquad \text {and} \qquad y'(s) = \cos \theta (s) . \end{aligned}$$

In particular, (3.4) implies

$$\begin{aligned} |x'(s) + \sin s| \le \Vert k_E-1 \Vert _{L^1(\partial E_i)} \qquad \text {and} \qquad |y'(s) - \cos s| \le \Vert k_E-1 \Vert _{L^1(\partial E_i)} \end{aligned}$$

for all $s \in [0,l]$. Therefore there are numbers a and b such that

$$\begin{aligned} |x(s) - a - \cos s| \le C \Vert k_E-1 \Vert _{L^1(\partial E_i)} \qquad \text {and} \qquad |y(s) - b - \sin s| \le C \Vert k_E-1 \Vert _{L^1(\partial E_i)}\nonumber \\ \end{aligned}$$

(3.5)

for all $s \in [0,l]$. Therefore we obtain from $|l - 2 \pi | \le \Vert k_E-1 \Vert _{L^1(\partial E)}$ that

$$\begin{aligned} |x(s) - a - \cos (2 \pi s /l )|\le & {} C \Vert k_E-1 \Vert _{L^1(\partial E_i)}\qquad \text {and}\\ \qquad |y(s) - b - \sin (2 \pi s /l )|\le & {} C \Vert k_E-1 \Vert _{L^1(\partial E_i)} , \end{aligned}$$

which gives the first inequality in (3.3) for ${x}_i = (a,b)$.

Note that from (3.5) it follows that if $\Vert k_E - 1 \Vert _{L^2(\partial E)}$ is small, then $\gamma (s)$ is close in $C^{1,\alpha }(0,l)$ to the parametrization $(a+\cos (2 \pi s /l ), b+\sin (2 \pi s /l ))$ of $\partial D_1( x_i)$. Hence $E_i$ is $C^{1,\alpha }$-close to $D_1({x}_i)$.

$\square$

The following lemma is based on a comparison argument.

Lemma 3.3

Assume $E_0 \subset {\mathbb {R}}^2$ is $C^2$-regular set with $P(E_0) \le M$ and let $(E_t^h)_t$ be the approximate flat flow starting from $E_0$. If $E_0$ is close to a disjoint union of N disks with radius one, i.e., there exists $F = \cup _{i=1}^N D_1(x_i)$, with $|x_i - x_j| \ge 2$ for $i \ne j$, such that

$$\begin{aligned} \sup _{x \in E_0 \Delta F}d_{\partial F}(x) \le \delta , \end{aligned}$$

then for $\delta >0$ small enough it holds

$$\begin{aligned} \sup _{x \in E^h_t\Delta F} d_{\partial F}(x) \le 5\delta ^{1/4} \qquad \text {for all }\, t \in (0,\sqrt{\delta }) \end{aligned}$$

for all $h >0$ small.

Proof

Let F be the union of disks as in the assumption and define

$$\begin{aligned} F_- := \{ x \in F : d_{{\mathbb {R}}^2 \setminus F}(x) > \delta ^{1/4}\} \qquad \text {and} \qquad F_+ := \{ x \in {\mathbb {R}}^2 : d_F(x) < \sqrt{\delta } \} . \end{aligned}$$

Then clearly $F_- \subset F \subset F_+$ and by the assumption $\sup _{x \in E_0 \Delta F} d_{\partial F}(x) \le \delta$ it holds $F_- \subset E_0 \subset F_+$.

Let $(F_t^h)_t$ be the approximate flat flow with the constant forcing term $f = -\Lambda$, where $\Lambda := C_0 +1$, with $C_0$ as in (1.2), starting from $F_-$. Then by Proposition 2.1 it holds $F_t^h\subset E_t^h$ for all $t>0$. Note that $F_-$ is a union of disks with radius $R = 1 -\delta ^{1/4}$ and with positive distance to each other. It is easy to see that $(F_t^h)_t$ is decreasing, i.e., $F_t^h \subset F_s^h$ for $t >s$ and therefore it is enough to study the evolution of a one single disk $D_{R}$, because the flow $(F_t^h)_t$ is the union of them. If now $(\tilde{F}_t^h)$ is the approximate flat flow starting from $D_{R}$ with the forcing term $f = -\Lambda$ then it is not difficult to see that for $t \in (kh, (k+1)h]$ the set $\tilde{F}_t^h$ is a concentric disk with radius $r_{k+1}$ and by the Euler–Lagrange equation (2.3) it holds

$$\begin{aligned} \frac{ r_{k+1} - r_k}{h} = -\frac{1}{r_{k+1}}-\Lambda . \end{aligned}$$

Therefore, it holds

$$\begin{aligned} r_{k+1} - r_k \ge -(\Lambda +2) h. \end{aligned}$$

for all $k = 0,1,2,\dots$ for which $r_{k+1} \ge 1/2$. By adding this over $k=0,1,\dots , K$ with $\sqrt{\delta }/h \le K \le 2\sqrt{\delta }/h$ and recalling that $r_0 = R = 1 -\delta ^{1/4}$ we obtain

$$\begin{aligned} r_K \ge r_0 -2\sqrt{\delta }(\Lambda +2) \ge 1 - 2\delta ^{1/4}, \end{aligned}$$

when $\delta$ is small. This implies $\sup _{x \in D_R \setminus \tilde{F}_t^h} d_{\partial D_R}(x) \le 2 \delta ^{1/4}$ for $t \in (0, \sqrt{\delta })$ and thus by the previous discussion

$$\begin{aligned} \sup _{x \in F \setminus F_t^h}d_{\partial F}(x) \le 2\delta ^{1/4} \qquad \text {for } \, t \in (0, \sqrt{\delta }). \end{aligned}$$

Since $F_t^h\subset E_t^h$ we have

$$\begin{aligned} \sup _{x \in F \setminus E_t^h}d_{\partial F}(x) \le 2 \delta ^{1/4} \qquad \text {for } \, t \in (0, \sqrt{\delta }). \end{aligned}$$

(3.6)

We need yet to show that

$$\begin{aligned} \sup _{x \in E_t^h \setminus F}d_{\partial F}(x) \le 5 \delta ^{1/4} \qquad \text {for } \, t \in (0, \sqrt{\delta }). \end{aligned}$$

(3.7)

Denote $\Gamma = \{x \in {\mathbb {R}}^2 \setminus F :d_{\partial F}(x) = 5\, \delta ^{1/4} \}$. Fix $x \in \Gamma$ and denote the disk $D_r(x)$ with $r = 4 \, \delta ^{1/4}$. Then by $E_0 \subset F_+$ and $D_r(x) \subset {\mathbb {R}}^2 \setminus F_+$ we have $E_0 \subset {\mathbb {R}}^2 \setminus D_r(x)$ if $\delta$ is sufficiently small. Let $(G_t^h)_t$ be the approximate flat flow starting from $D_r(x)$ with the constant forcing term $f = -\Lambda$. Arguing as above we deduce that for $t \in (kh, (k+1)h]$ the set $G_t^h$ is disk with radius $r_{k+1}$, i.e., $G_t^h = D_{r_{k+1}}(x)$ and

$$\begin{aligned} \frac{ r_{k+1} - r_k}{h} = -\frac{1}{r_{k+1}}-\Lambda \ge - \delta ^{-1/4} - \Lambda \end{aligned}$$

for $k = 0,1,\dots$ for which $r_{k+1} \ge \delta ^{1/4}$. By adding this over $k=0,1,\dots , K$ with $\sqrt{\delta }/h \le K \le 2\sqrt{\delta }/h$ and recalling that $r_0 =r = 4\, \delta ^{1/4}$ we obtain

$$\begin{aligned} r_K \ge r_0 - 2 \sqrt{\delta } (\delta ^{-1/4} + \Lambda ) \ge 4 \, \delta ^{1/4} - 3 \, \delta ^{1/4} = \, \delta ^{1/4}, \end{aligned}$$

when $\delta$ is small. In other words $D_{\delta ^{1/4}}(x) \subset G_t^h$ for all $t \in (0, \sqrt{\delta })$. Since $E_0 \subset {\mathbb {R}}^2 \setminus D_r(x)$ Proposition 2.1 yields

$$\begin{aligned} E_t^h \subset {\mathbb {R}}^2 \setminus G_t^h \subset {\mathbb {R}}^2 \setminus D_{ \delta ^{1/4}}(x) \end{aligned}$$

for all $0<t \le \sqrt{\delta }$. By repeating the same argument for all $x \in \Gamma$ we conclude that the flow $E_t^h$ does not intersect $\Gamma$ for any $t \in (0,\sqrt{\delta })$. This implies (3.7). $\square$

In the next lemma we show that if $E_0$ is stationary then necessarily it is a disjoint union of disks, i.e., a critical set of the isoperimetric problem.

Lemma 3.4

Assume $E_0 \subset {\mathbb {R}}^2$ is a bounded set of finite perimeter. If $E_0$ is stationary according to Definition 3.1 then it is a disjoint union of disks with equal radii.

Proof

Let us fix $T>1$ and $\varepsilon >0$ and let $(E_t^h)_t$ be an approximate flat flow starting from $E_0$. Then for any $\delta >0$ it holds by Definition 3.1 and by Proposition 2.3 that

$$\begin{aligned} \sup _{h< t \le T} |E_t^h \Delta E_0| \le \delta \end{aligned}$$

(3.8)

for small h. Now the forcing term satisfies trivially the assumption (1.4) and therefore the left hand side of (2.8) is always zero. Then from the proof of Proposition 2.4 (i) we get that for every h sufficiently small

$$\begin{aligned} c \int _{2h}^{T}\int _{\partial E_t^h} (k_{E_t^h} - c_0)^2 \, d{\mathcal {H}}^{1}dt + {\mathcal {E}}(E_{T}^h )\le {\mathcal {E}}(E_{h}^h). \end{aligned}$$

Recall that ${\mathcal {E}}(E) = P(E) - c_0 |E|$. By (3.8) it holds $|E_T^h \Delta E_h^h| \le 2\delta < \frac{\varepsilon }{c_0}$. Therefore we have

$$\begin{aligned} c \int _{2h}^{T}\int _{\partial E_t^h} (k_{E_t^h} - c_0)^2 \, d{\mathcal {H}}^{1}dt + P(E_T^h) \le P(E_h^h) + \varepsilon . \end{aligned}$$

Finally by (2.6) and (3.8) we obtain

$$\begin{aligned} P(E_h^h) \le P(E_0) + c_0( |E_{h}^h| - |E_0| ) \le P(E_0) + c_0 \delta \le P(E_0) + \varepsilon . \end{aligned}$$

Hence,

$$\begin{aligned} c \int _{2h}^{T}\int _{\partial E_t^h} (k_{E_t^h} - c_0)^2 \, d{\mathcal {H}}^{1}dt + P(E_T^h) \le P(E_0) + 2\varepsilon . \end{aligned}$$

By (3.8) it holds $|E_T^h \Delta E_0| \le \delta$. Therefore by the lower semicontinuity of the perimeter it holds $P(E_0) \le P(E_T^h) + \varepsilon$ when $\delta$ and h are small. Therefore we have

$$\begin{aligned} c \int _{2h}^{T}\int _{\partial E_t^h} (k_{E_t^h} - c_0)^2 \, d{\mathcal {H}}^{1}dt \le 3\varepsilon . \end{aligned}$$

By the mean value theorem there is $t <T$ such that

$$\begin{aligned} \Vert k_{E_t^h} - c_0\Vert _{L^2} \le C \sqrt{\varepsilon }. \end{aligned}$$

Since by Proposition 2.4$\sup _{t\ge 0}P(E^h_t)\le M$ for some M independent of h, from the previous inequality and from Lemma 3.2 it follows that there are points $x_1, \dots , x_N$, with $|x_i - x_j| \ge 2r$, where $r = \frac{1}{c_0}$, such that for the set $F= \cup _{i=1}^N D_r(x_i)$ it holds

$$\begin{aligned} \sup _{x \in E_t^h \Delta F} d_{\partial F}(x) \le C \sqrt{\varepsilon }. \end{aligned}$$

Thus by (3.8) it holds

$$\begin{aligned} |E_0 \Delta F| \le C \sqrt{\varepsilon }. \end{aligned}$$

Note that the points $x_i$ might depend on t and on h but the radius r and the number of disks N does not. Therefore we conclude that the set $E_0$ is arbitrarily close to a union of essentially disjoint disks. This implies that the set $E_0$ itself is a union of essentially disjoint disks with radii $r = \frac{1}{c_0}$. $\square$

For a set $E \subset {\mathbb {R}}^2$ we denote its Steiner symmetrization with respect to $x_1$-axis by $E^s$, see [1, 22]. Steiner symmetrization decreases the perimeter and preserves the area. Moreover, in the case of equality $P(E^s) = P(E)$ it is well known that for smooth set E every vertical section of E is an interval [22, Theorem 14.4]. We also notice that if the set $E_0$ is Steiner symmetric with respect to $x_1$-axis, i.e. $E_0 = (E_0)^s$, then Steiner symmetrization also decreases the dissipation term in (2.1). This follows rather directly from Fubini’s theorem and we leave the details for the reader. Hence, we have the following observation.

Remark 3.5

If $E_0$ is Steiner symmetric with respect to $x_1$-axis, then every minimizer E of ${\mathcal {F}}_0(\cdot ; E_0)$ has the property that every vertical section is an interval. In particular, every component is simply connected.

Proof of Theorem 1.1

Without loss of generality we may assume that

$$\begin{aligned} E_0 = D_1(-e_1) \cup D_1(e_1) \end{aligned}$$

where $e_1 = (1,0)$. Let us now fix a small $h>0$ and consider the minimization problem (2.1) which gives a sequence of sets $(E^{h,k})_{k=1}^\infty$ and thus an approximate flat flow $(E_t^h)_t$.

Let us fix $\varepsilon _0>0$. Then for $\delta$ small enough we have by Lemma  3.3 that for $k \le \frac{\delta }{h}$ it holds

$$\begin{aligned} \left( D_{1-\varepsilon _0}(-e_1) \cup D_{1-\varepsilon _0}(e_1)\right) \subset E^{h,k} \subset \left( D_{1+\varepsilon _0}(-e_1) \cup D_{1+\varepsilon _0}(e_1)\right) , \end{aligned}$$

(3.9)

when h is small. Moreover, by Lemma 2.2 it holds

$$\begin{aligned} \left( D_{1-C_1\sqrt{h}}(-e_1) \cup D_{1-C_1\sqrt{h}}(e_1) \right) \subset E^{h,1}. \end{aligned}$$

(3.10)

Let us improve the above estimate and show that the set $E^{h,1}$ contains a large simply connected set. To be more precise, we denote the rectangle $R^h_{\eta } = (-2C_1 \sqrt{h}, 2C_1 \sqrt{h}) \times (-\eta h^{1/4},\eta h^{1/4})$ and prove that for $\eta >0$ small, independent of h, it holds

$$\begin{aligned} \left( D_{1-C_1\sqrt{h}}(-e_1) \cup D_{1-C_1\sqrt{h}}(e_1)\right) \cup R^h_{\eta } \subset E^{h,1}. \end{aligned}$$

(3.11)

We argue by contradiction assuming that $\partial E^{h,1} \cap (-2C_1 \sqrt{h}, 2C_1 \sqrt{h}) \times (-\eta h^{1/4},\eta h^{1/4})$ is non-empty. We denote the rectangle $R^h_{3 \eta } =(-2C_1 \sqrt{h}, 2C_1 \sqrt{h}) \times (-3\eta h^{1/4}, 3 \eta h^{1/4})$ and define

$$\begin{aligned} \tilde{E}^{h,1} =E^{h,1} \cup R^h_{3 \eta }. \end{aligned}$$

Recall that by Remark 3.5 every vertical section of $E^{h,1}$ is an interval and that (3.10) holds. By using these two properties a simple geometric argument shows that any component containing one of the two disks in (3.10), say $G^1$, has the property that ${\mathcal {H}}^1(\partial G^1 \cap R^h_{3 \eta })$ is greater than $2 \eta h^{1/4}$. We have then the following estimate

$$\begin{aligned} P(\tilde{E}^{h,1}) \le P(E^{h,1}) - \eta h^{1/4} , \end{aligned}$$

(3.12)

when h is small. We also have

• (i) $\big | |\tilde{E}^{h,1}| - |E^{h,1}| \big | \le |R^h_{3 \eta }| = 24 C_1 \eta h^{\frac{3}{4}}$

• (ii) $|{\bar{d}}_{E_0}(x)| \le 10 \eta ^2\sqrt{h}$ for all $x \in R^h_{3 \eta } \setminus E_0$.

It follows from (i), (ii) and $\sup _t |f(t)| \le C_0$ that

$$\begin{aligned} \begin{aligned} \frac{1}{h} \int _{\tilde{E}^{h,1}}&{\bar{d}}_{E_0} \, dx - {{\bar{f}}}(h) |\tilde{E}^{h,1}| \\&\le \frac{1}{h} \int _{E^{h,1}} {\bar{d}}_{E_0} \, dx - {{\bar{f}}}(h) |E^{h,1}| + \frac{1}{h} \int _{R^h_{3\eta } \setminus E_0} {\bar{d}}_{E_0} \, dx + C_0 \big | |\tilde{E}^{h,1}| - |E^{h,1}| \big | \\&\le \frac{1}{h} \int _{E^{h,1}} {\bar{d}}_{E_0} \, dx - {{\bar{f}}}(h) |E^{h,1}| + C \eta ^3 h^{1/4} \end{aligned} \end{aligned}$$

when h is small. Therefore using (3.12) and the above inequality we may estimate

$$\begin{aligned} \begin{aligned} {\mathcal {F}}(\tilde{E}^{h,1};E_0)&\le {\mathcal {F}}(E^{h,1};E_0) - \eta h^{1/4} + C \eta ^3 h^{1/4} < {\mathcal {F}}(E^{h,1};E_0) \end{aligned} \end{aligned}$$

when $\eta >0$ is small enough. This contradicts the minimality of $E^{h,1}$ and we obtain (3.11).

We continue by constructing a barrier set $G_h$ (see Fig. 2) and prove that $G_h \subset E^{h,k}$ for every $k \le \delta /h$. The barrier $G_h$ can be seen as a discrete version of a minimal barrier to the flow. See e.g. [14] for a similar construction in a continuous setting. For $h\ge 0$ we define $\varphi _h : (-3\varepsilon _0, 3 \varepsilon _0) \rightarrow {\mathbb {R}}$ as

$$\begin{aligned} \varphi _h(s) = 3 \varepsilon _0 - \sqrt{9 \varepsilon _0^2 - s^2} + h \end{aligned}$$

and define the set

$$\begin{aligned} G_{\varphi _h} := \{(x_1,x_2) \in {\mathbb {R}}^2 : x_1 \in (-3\varepsilon _0, 3 \varepsilon _0) , \,\, |x_2| < \varphi _h(x_1) \} , \end{aligned}$$

which is ’the neck’. We define the barrier set as

$$\begin{aligned} G_h = \left( D_{1-2\varepsilon _0}(-e_1) \cup D_{1-2\varepsilon _0}(e_1)\right) \cup G_{\varphi _h}. \end{aligned}$$

The barrier set $G_h$ is open and connected and we have the estimate on the curvature at the neck

$$\begin{aligned} {for every }\, x \in \partial G_h \setminus ({\bar{D}}_{1 -2\varepsilon _0}(-e_1) \cup {\bar{D}}_{1 -2\varepsilon _0}(e_1) )\,\, {it holds }\, k_{G_0}(x) = -\frac{1}{3 \varepsilon _0}.\nonumber \\ \end{aligned}$$

(3.13)

Moreover, we notice that when h is small then by (3.11) it holds

$$\begin{aligned} G_h \subset E^{h,1} \end{aligned}$$

In fact, (3.11) implies that

$$\begin{aligned} \inf _{{\mathbb {R}}^2 \setminus E^{h,1}} d_{G_h}(x) \ge c\, h^{1/4} \end{aligned}$$

(3.14)

for small $c>0$.

Fig. 2

The boundary of $\partial E^{h,k}$ lies outside of the barrier set $G_h$

Let us define

$$\begin{aligned} \rho _k := \inf _{{\mathbb {R}}^2 \setminus E^{h,k}} d_{G_h}(x) \end{aligned}$$

for $k=1,2,\dots$ and $\rho _0 := 0$. We claim that for every $k \le \frac{\delta }{h}$ it holds

$$\begin{aligned} \rho _{k+1} - \rho _k \ge 2h \qquad \text {or} \qquad \rho _{k+1} \ge \frac{\varepsilon _0}{2} \end{aligned}$$

(3.15)

when h is small.

We prove (3.15) by induction and notice that for $k=0$ the inequality (3.15) is already proven since (3.14) implies $\rho _1 \ge c\, h^{1/4}$. Let us assume that (3.15) holds for $k-1$ and prove it for k. Let us assume that $\rho _{k+1} < \frac{\varepsilon _0}{2}$. The induction assumption and $\rho _1 \ge c\, h^{1/4}$ yields $\rho _{k} \ge c\, h^{1/4}$. On the other hand by Lemma 2.2 it holds $\sup _{E^{h,k+1} \Delta E^{h,k}} d_{\partial E^{h,k}} \le C_1\sqrt{h}$ and therefore $\rho _{k+1} >0$.

Let $x_{k+1} \in \partial E^{h,k+1}$ and $y_{k+1} \in \partial G_h$ be such that $|x_{k+1}-y_{k+1}| = \min _{x \in \partial E^{h,k+1}} d_{G_h}(x) = \rho _{k+1}$. By (3.9) it holds $x_{k+1} \notin D_{1-\varepsilon _0}(-e_1) \cup D_{1-\varepsilon _0}(e_1)$ and therefore by $\rho _{k+1} < \frac{\varepsilon _0}{2}$ we have

$$\begin{aligned} y_{k+1} \in \partial G_h \setminus ({\bar{D}}_{1 -2\varepsilon _0}(-e_1) \cup {\bar{D}}_{1 +2\varepsilon _0}(e_1) ). \end{aligned}$$

Then (3.13) yields

$$\begin{aligned} k_{G_h}(y_{k+1}) = -\frac{1}{3 \varepsilon _0}. \end{aligned}$$

Since $x_{k+1}$ is a point of minimal distance $k_{E^{h,k+1}}(x_{k+1}) \le k_{G_h}(y_{k+1}) = -\frac{1}{3 \varepsilon _0}$. By taking $\varepsilon _0$ smaller, if needed, we have by the Euler–Lagrange equation (2.3) and by $\sup _{t>0}|f(t)| \le C_0$ that

$$\begin{aligned} \frac{ {\bar{d}}_{E^{h,k}}(x_{k+1})}{h} = -k_{E^{h,k+1}}(x_{k+1}) + {{\bar{f}}}(kh) \ge \frac{1}{3 \varepsilon _0} -C_0\ge 2. \end{aligned}$$

(3.16)

The inequality (3.16) and $G_h \subset E^{h,k}$ imply that $x_{k+1} \notin E^{h,k}$ and $y_{k+1} \in E^{h,k}$. Thus there is a point $z_{k+1}$ on the segment $[x_{k+1},y_{k+1}]$ such that $z_{k+1} \in \partial E^{h,k}$. Since $y_{k+1} \in \partial G_h$ it holds $|z_{k+1}-y_{k+1}| \ge \rho _{k}$ and by (3.16) we have $|x_{k+1}-z_{k+1}|\ge {\bar{d}}_{E^{h,k}}(x_{k+1}) \ge 2h$. Therefore because $z_{k+1}$ is on the segment $[x_{k+1},y_{k+1}]$ we have

$$\begin{aligned} \rho _{k+1} = |x_{k+1}-y_{k+1}| = |x_{k+1}-z_{k+1}| + |z_{k+1}-y_{k+1}| \ge 2h + \rho _{k}. \end{aligned}$$

Thus we have (3.15).

Let us conclude the proof. By adding (3.15) together for $k=0,1,2, \dots , K$ with $K \le \delta /h$ we deduce that for $\delta$ small it holds

$$\begin{aligned} \inf _{{\mathbb {R}}^2 \setminus E_t^h} d_{G_h}(x) \ge t \qquad \text {for all }\, t \in (h,\delta ]. \end{aligned}$$

(3.17)

In particular $G_h \subset E_t^h$. Let $h_l\rightarrow 0$ be any sequence such that $\sup _{h_l< t\le \delta }|E^{h_l}_t\Delta E_t|\rightarrow 0$, see Proposition 2.3. By (3.17) we get

$$\begin{aligned} \inf _{{\mathbb {R}}^2 \setminus E_t} d_{G_0}(x) \ge t \qquad \text {for all }\, t \in (0,\delta ]. \end{aligned}$$

This inequality implies, in particular, that $E_t$ contains a ball centered at the origin with radius t for all $t \in (0,\delta )$ and that

$$\begin{aligned} |E_t \setminus E_0| \ge c\,t^3. \end{aligned}$$

This is the second statement of Theorem 1.1. The inequality (3.17) implies that

$$\begin{aligned} \{ x \in {\mathbb {R}}^2 : d_{G_h}(x) <t \} \subset E_t^h \qquad \text {for all }\, t \in (h,\delta ]. \end{aligned}$$

Passing to the limit as above, along the subsequence $h_l$, we deduce

$$\begin{aligned} \{ x \in {\mathbb {R}}^2 : d_{G_0}(x) <t \} \subset E_t \qquad \text {for all}\, t \in (0,\delta ]. \end{aligned}$$

The first claim follows from the fact that $\{ x \in {\mathbb {R}}^2 : d_{G_0}(x) <t \}$ is open and simply connected. $\square$

We conclude this section by explaining how Theorem 1.2 follows from Theorem 1.1.

Proof of Theorem 1.2

First, it is easy to see that if $E_0$ is a union of disks with equal radius and with positive distance to each other, then $E_0$ is stationary according to the Definition 3.1. If $E_0$ is stationary then by Lemma 3.4 it is critical, i.e., finite union of essentially disjoint disks $D_r(x_i)$, with $r=1/c_0$ and $i=1,\dots ,N$. We need to show if $i\not =j$ then $|x_i-x_j|>2/c_0$. If by contradiction there are two tangential disks, say $D_r(x_1)$ and $D_r(x_2)$, then we define $F_0 = D_r(x_1) \cup D_r(x_2)$. Let $(E_t)_t$ be a flat flow starting from $E_0$ and let $h_l\rightarrow 0$ be a sequence such that $|E^{h_l}_t\Delta E_t|\rightarrow 0$ and $|F^{h_l}_t\Delta F_t|\rightarrow 0$, where $(F_t)_t$ is a flat flow starting from $F_0$ with forcing term $g = c_0 -\varepsilon$. Then by Proposition 2.1$F_t ^{h_l}\subset E_t^{h_l}$ for all $t>0$ and $h_l$, hence $F_t \subset E_t$. By Theorem 1.1 we have that there exist $\delta , c>0$ such that for all $t\in (0,\delta )$

$$\begin{aligned} |F_t \setminus F_0| \ge c\,t^3. \end{aligned}$$

This implies

$$\begin{aligned} |E_t \setminus E_0| \ge c\,t^3 \end{aligned}$$

and therefore $E_0$ is not stationary. $\square$

4 Proofs of Theorems 1.3 and 1.4

Proof of Theorem 1.3

First, by scaling we may assume that $c_0 =1$ in the assumption (1.4).

Let $(E_t^h)$ be an approximate flat flow which converges, up to a subsequence, to $(E_t)_t$. We simplify the notation and denote the converging subsequence again by h. From the assumption $\sup _{t >0} |E_t|= M$ and from Proposition 2.3 (iv) it follows that for every $T>0$ there is $h_{ T}$ such that up to subsequence of h it holds

$$\begin{aligned} \sup _{0< t<T} |E_t^h| \le 2M \qquad \text {for all } \, 0<h<h_{ T}. \end{aligned}$$

Then Remark 2.5 yields that there exists a constant ${\tilde{C}}$ independent of h and T such that for $0<h<h_T$

$$\begin{aligned} \sup _{0<t<T} P(E_t^h) \le \tilde{C}. \end{aligned}$$

The dissipation inequality in Proposition 2.4 and the above volume and perimeter bounds imply

$$\begin{aligned} \int _{T_0}^{T} \int _{\partial E_t^h} (k_{E_t^h} - {{\bar{f}}}(t-h))^2 \, d {\mathcal {H}}^1 dt \le C \end{aligned}$$

for some $T_0>0$ for every $T > T_0$. Then the assumption (1.4) (recall that $c_0 = 1$) yields

$$\begin{aligned} \int _{T_0}^{T} \int _{\partial E_t^h} (k_{E_t^h} - 1)^2 \, d {\mathcal {H}}^1 dt \le C . \end{aligned}$$

for some $T_0$ large and for every $T > T_0$ and $0<h<h_T$. In particular, if we denote $I_j = [(j-1)^2, j^2]$ for $j =1,2,\dots , k < \sqrt{T}$ then it holds

$$\begin{aligned} \int _{I_j} \int _{\partial E_t^h} (k_{E_t^h} - 1)^2 \, \, d {\mathcal {H}}^1 dt \le C \end{aligned}$$

for j large. Let us fix a small $\varepsilon >0$. From the previous inequality we obtain that there exists $j_\varepsilon$ such that, if $j_\varepsilon \le j\le \sqrt{T}$ and $0<h<h_T$ there exists $T_{h,j}$ such that

$$\begin{aligned} (j-1)^2 \le T_{h,j} \le j^2, \qquad \text {and } \qquad \Big \Vert k_{E_{T_{h,j}}^h} - 1\Big \Vert _{L^2(E_{T_{h,j}}^h)} \le \varepsilon . \end{aligned}$$

We deduce by Lemma 3.2 that the set $E_{T_{h,j}}^h$ is close to a disjoint union of $N_{h,j}$ disks of radius one. Since the measures of $E_{T_{h,j}}^h$ are uniformly bounded, we conclude that there is $N_0$ such that $N_{h,j} \le N_0$. Moreover, we have by Lemma 3.2 that

$$\begin{aligned} \big | P(E_{T_{h,j}}^h) - 2 \pi N_{h,j}\big | + \big | |E_{T_{h,j}}^h| - \pi N_{h,j}\big | \le C \varepsilon . \end{aligned}$$

(4.1)

This implies the following estimate for the energy ${\mathcal {E}}(E_{T_{h,j}}^h) = P(E_{T_{h,j}}^h) - |E_{T_{h,j}}^h|$,

$$\begin{aligned} \big | {\mathcal {E}}_{T_{h,j}}(E_{T_{h,j}}^h) - \pi N_{h,j} \big | \le C \varepsilon . \end{aligned}$$

(4.2)

In other words, at $T_{h,j}$ the energy has almost the value $\pi N_{h,j}$. Since the energy ${\mathcal {E}}_{T_{h,j}}(E_{T_{h,j}}^h)$ is asymptotically almost decreasing by Remark 2.5, we deduce that the sequence of numbers $N_{h,j}$ is decreasing for j large, i.e.,

$$\begin{aligned} N_{h,j} \ge N_{h,j+1} \qquad \text {for every }\, j_\varepsilon \le j \le \sqrt{T}. \end{aligned}$$

By letting $h \rightarrow 0$ we conclude by Proposition 2.3 (iv) and by standard diagonal argument that, by extracting another subsequence if needed, there is sequence of times $T_j$, with $j \ge j_\varepsilon$, such that $(j-1)^2 \le T_j\le j^2$ and the set $E_{T_j}$ is close to $N_{j}$ many disjoint disks of radius one and that $N_j \ge N_{j+1}$ for every $j \ge j_\varepsilon$. This implies that, there is $j_0 \ge j_\varepsilon$ and N such that

$$\begin{aligned} N_{j} = N \qquad \text {for all } \, j \ge j_0. \end{aligned}$$

This means that every $E_{T_{j}}$, for $j\ge j_0$, is close in $L^1$-sense to disjoint union of exactly N many disks of radius one. By the locally uniform $L^1$-convergence $(E_t^h)_t \rightarrow (E_t)$ for every $T>j_0^2$ we have

$$\begin{aligned} N_{h,j} = N \qquad \text {for }~{j_0 \le j \le \sqrt{T},} \end{aligned}$$

(4.3)

when h is small. Therefore we conclude from (4.1) and from the dissipation inequality in Proposition 2.4 that for any $\delta >0$ there is $T_\delta$ such that for all $T > T_\delta$ it holds

$$\begin{aligned} \int _{T_\delta }^T \int _{\partial E_t^h} (k_{E_t^h} - 1)^2 \, \, d {\mathcal {H}}^1 dt \le \delta ^3 \end{aligned}$$

(4.4)

when h is small.

Let us fix $T>> T_\delta$ and denote by $J_h \subset (T_\delta ,T)$ the set of times $t \in (T_\delta ,T)$ for which

$$\begin{aligned} \Vert k_{E_t^h} - 1\Vert _{L^2(\partial E_t^h)} \ge \delta . \end{aligned}$$

Then by (4.4) it holds $|J_h| \le \delta$. If $\delta$ is small enough, by Lemma 3.2, from (4.2), (4.3) and (2.10) we deduce that the sets $E_t^h$ satisfy

$$\begin{aligned} \sup _{x \in E_{t}^h \Delta F_{t}^h} d_{\partial F_{t}^h}(x) \le C\delta \qquad \text {for all } \, t \in (T_\delta ,T) \setminus J_h, \end{aligned}$$

(4.5)

where $F_t^h = \cup _{i=1}^N D_1(x_i)$ with $|x_i-x_j| \ge 2$ for $i \ne j$. Note that the points $x_i$ may depend on t and h.

We will show that for all $t \in (T_\delta +2\delta ,T)$ it holds

$$\begin{aligned} \sup _{x \in E_{t}^h \Delta F_{t}^h} d_{\partial F_{t}^h}(x) \le C \delta ^{1/4} \end{aligned}$$

(4.6)

where $F_t^h$ is a union of N disjoint disks as above. Let us fix $t_0\in (T_\delta , T) \setminus J_h$. By (4.5) we have

$$\begin{aligned} \sup _{x \in E_{t_0}^h \Delta F_{t_0}^h}d_{\partial F_{t_0}^h}(x) \le C \delta . \end{aligned}$$

We use Lemma 3.3 with $E_0 = E_{t_0}^h$ to conclude

$$\begin{aligned} \sup _{x \in E_{t}^h \Delta F_{t_0}^h}d_{\partial F_{t_0}^h}(x) \le C \delta ^{1/4} \qquad \text {for all } \, t \in [t_0, t_0 + \sqrt{\delta }). \end{aligned}$$

This means that if we define

$$\begin{aligned} I = \cup _{t \in (T_\delta ,T) \setminus J_h} [t, t + \sqrt{\delta }) \end{aligned}$$

then (4.6) holds for every $t \in I$. But since $|J_h| \le \delta \le \sqrt{\delta }/2$, it easy to see that $(T_\delta +2\delta ,T) \subset I$. Thus (4.6) holds for every $t \in (T_\delta +2\delta ,T)$.

We have thus proved (4.6). The claim follows by letting $h \rightarrow 0$ and from Proposition 2.3. $\square$

We conclude the paper by proving Theorem 1.4. To this end we recall the Bonnesen symmetrization of a planar set.

Let $E \subset {\mathbb {R}}^2$ be a measurable set. The Bonnesen symmetrization of E with respect to $x_2$-axis is the set $E^*$, with the property that for every $r>0$

$$\begin{aligned} {\mathcal {H}}^1(\partial D_r\cap E^*)={\mathcal {H}}^1(\partial D_r\cap E) \end{aligned}$$

and $\partial D_r \cap E^*$ is the union of two circular arcs $\gamma ^+_r$ and $\gamma ^-_r$ with equal length, symmetric with respect to the $x_2$-axis and such that $\gamma ^-_r$ is obtained by reflecting $\gamma ^+_r$ with respect to the $x_1$-axis.

Clearly this symmetrization leaves the area unchanged. Moreover, if E is a convex set, symmetric with respect to both coordinate axes, then $P(E^*) \le P(E)$, see [6, Page 67] (see also [11]).

Let us prove that the Bonnesen symmetrization decreases the dissipation.

Fig. 3

The point $\sigma (t_2)$ is closer to the arc $\Gamma _\rho$ than $\sigma (t_1)$

Lemma 4.1

Let $G \subset {\mathbb {R}}^2$ be invariant under Bonnesen symmetrization. Then for any measurable set $E \subset {\mathbb {R}}^2$ it holds

$$\begin{aligned} \int _{E^*} {\bar{d}}_{G} \, dx \le \int _E {\bar{d}}_{G} \, dx . \end{aligned}$$

Proof

It is enough to prove that for every $r >0$ it holds

$$\begin{aligned} \int _{\partial D_r \cap E^*} {\bar{d}}_{G} \, d {\mathcal {H}}^1 \le \int _{\partial D_r \cap E} {\bar{d}}_{G} \, d {\mathcal {H}}^1. \end{aligned}$$

(4.7)

Let us fix $r>0$ and without loss of generality we may assume that $r=1$. Let $\sigma :[-\pi ,\pi ] \rightarrow {\mathbb {R}}^2$,

$$\begin{aligned} \sigma (t) = \begin{bmatrix} \cos (t) \\ \sin (t) \end{bmatrix}. \end{aligned}$$

Since G is symmetric with respect to both coordinate axes, the function $t \mapsto {\bar{d}}_{G}(\sigma (t))$ is even and for every $t \in (0,\pi /2)$ it holds ${\bar{d}}_{G}(\sigma (\pi - t)) = {\bar{d}}_{G}(\sigma (t))$. We observe that (4.7) follows once we show that

$$\begin{aligned} t \mapsto {\bar{d}}_{G}(\sigma (t)) \qquad \text {is decreasing on }\, t \in (0,\pi /2). \end{aligned}$$

To this aim we fix $0< t_1< t_2 < \pi /2$. Let us assume that $\sigma (t_1) \in {\mathbb {R}}^2 \setminus G$, the case $\sigma (t_1) \in G$ being similar. If $\sigma (t_2) \in G$ then trivially ${\bar{d}}_{G}(\sigma (t_2)) \le 0 \le {\bar{d}}_{G}(\sigma (t_1))$. Let us thus assume that $\sigma (t_2) \in {\mathbb {R}}^2 \setminus G$. Let $z_1 \in \partial G$ be such that ${\bar{d}}_{G}(\sigma (t_1)) = |\sigma (t_1) -z_1|$ and let $\rho >0$ and $\theta _1 \in (0, \pi /2)$ be such that $z_1 = \rho \sigma (\theta _1)$. We denote by $\Gamma _\rho \subset \partial D_\rho$ the arc with endpoints $\rho e_2$ and $z_1$, i.e.,

$$\begin{aligned} \Gamma _\rho = \{ \rho \sigma (t) : t \in (\theta _1, \pi /2)\}. \end{aligned}$$

Since G is invariant under Bonnesen symmetrization we have $\Gamma _\rho \subset G$. But now since $t_1< t_2 < \pi /2$ it clearly holds (see Fig. 3)

$$\begin{aligned} \text {dist}(\sigma (t_2), \Gamma _\rho ) \le \text {dist}(\sigma (t_1), \Gamma _\rho ) = |\sigma (t_1) - z_1| = {\bar{d}}_{G}(\sigma (t_1)) . \end{aligned}$$

Since $\Gamma _\rho \subset G$ we have

$$\begin{aligned} {\bar{d}}_{G}(\sigma (t_2)) \le \text {dist}(\sigma (t_2), \Gamma _\rho ) \end{aligned}$$

and the claim follows.

$\square$

Proof of Theorem 1.4

Let G be the ellipse

$$\begin{aligned} G = \{ (x_1,x_2) \in {\mathbb {R}}^2 : \, a^2 x_1^2 + x_2^2 < 1 \} \qquad \text {with } \, a>1 \end{aligned}$$

as in the assumption and let $(G_t)_t$ be the classical solution of the volume preserving mean curvature flow

$$\begin{aligned} V_t = - k_{G_t} + {\bar{k}}_{G_t} \end{aligned}$$

(4.8)

starting from G. By [18], $(G_t)_t$ is well defined for all times, remains smooth and uniformly convex and converges exponentially fast to the disk $D_\rho$, where $\rho = \frac{1}{\sqrt{a}}$. Moreover $G_t\not = D_\rho$ for all $t>0$. Let us define $f(t) := {\bar{k}}_{G_t}$ which is therefore a smooth function and converges exponentially fast to $1/\rho$. Note that then f satisfies (1.4) for $c_0 = 1/\rho$.

By the regularity of $E_0$ the flat flow $(E_t)_t$ with the forcing term f starting from $E_0$ coincides with the unique classical solution provided by [18], see [9, Proposition 4.9]. Therefore, by the symmetry of $E_0$ we may conclude that

$$\begin{aligned} E_t = (G_t - \rho e_1) \cup (G_t + \rho e_1) \end{aligned}$$

(4.9)

as long as the components $(G_t - \rho e_1)$ and $(G_t + \rho e_1)$ do not intersect each other. By the convexity of $G_t$, the components $G_t - \rho e_1$ and $G_t + \rho e_1$ do not intersect each other if the first one stays in the half-space $\{ x_1 < 0\}$ and the latter in $\{ x_1 >0 \}$. This is the same as to say that the flow $G_t$ does not exit the strip $\{ -\rho< x_1 < \rho \}$. Let us show this.

Assume that for $h>0$ the family of sets $(G_t^h)_t$ is an approximate flow obtained via (2.1) with the forcing term f and starting from G. We now show that each $G^h_t$ is symmetric with respect to the coordinate axes and convex. Recall that the set $G^{h,1}$ is chosen as a minimizer of the functional

$$\begin{aligned} {\mathcal {F}}(E; G) = P(E) + \frac{1}{h} \int _E {\bar{d}}_{G} \, dx - {{\bar{f}}}(h) |E|. \end{aligned}$$

It is well known that in any dimension the functional above admits a minimal and a maximal minimizer which are convex and, by uniqueness, symmetric with respect to both coordinate axes, see [3, Theorem 2]. However, in our two dimensional setting we can provide a simple self contained proof of this fact.

Given E, we set $E_+ = \{x \in E : x_1>0\}$ and $E_- = \{x \in E: x_1 <0\}$. By reflecting $E_+$ and $E_-$ with respect to the $x_2$-axis we obtain sets $E_1$ and $E_2$, which are symmetric with respect to the $x_2$-axis and satisfy

$$\begin{aligned} {\mathcal {F}}(E_1; G)+ {\mathcal {F}}(E_2; G) \le 2 {\mathcal {F}}(E; G). \end{aligned}$$

Then there exists $i=1,2$ such that ${\mathcal {F}}(E_i; G)\le {\mathcal {F}}(E; G)$. By repeating the same argument with respect to the $x_1$-direction we conclude that we may choose $G^{h,1}$ symmetric with respect to both axes.

Let us show that $G^{h,1}$ is convex. By the Euler–Lagrange equation (2.3) it holds

$$\begin{aligned} \frac{{\bar{d}}_{G}}{h} = -k_{G^{h,1}} + {\bar{f}}(h) \qquad \text {on } \, \partial G^{h,1} \end{aligned}$$

We claim that $\frac{{\bar{d}}_{G}}{h} (x) \le {{\bar{f}}}(h)$ for all $x \in \partial G^{h,1}$. Indeed, suppose $x_0 \in \partial G^{h,1}$ is the maximum of ${\bar{d}}_{G}$ on $\partial G^{h,1}$. If ${\bar{d}}_{G}(x_0) \le 0$, then trivially $\frac{{\bar{d}}_{G}}{h} (x_0) \le {{\bar{f}}}(h)$ as $f \ge 0$. If ${\bar{d}}_{G}(x_0) > 0$ then $x_0\not \in G$ and since it is the furthest point from G and G is convex, it is easy to check that $k_{G^{h,1}}(x_0) \ge 0$. Then by the Euler–Lagrange equation

$$\begin{aligned} \frac{{\bar{d}}_{G}(x_0)}{h} = -k_{G^{h,1}}(x_0) + {\bar{f}}(h) \le {\bar{f}}(h) . \end{aligned}$$

Therefore ${\bar{d}}_{G}/h \le {{\bar{f}}}(h)$ on $\partial G^{h,1}$ and by the Euler–Lagrange equation

$$\begin{aligned} k_{G^{h,1}} = - \frac{{\bar{d}}_{G}}{h} + {\bar{f}}(h) \ge 0 \qquad \text {on } \, \partial G^{h,1}. \end{aligned}$$

Hence, $G^{h,1}$ is convex.

We now apply to $G^{h,1}$ the Bonnesen circular symmetrization with respect to the $x_2$-axis which, we recall, decreases the perimeter, preserves the area and decreases the dissipation term $\int _{G^{h,1}} {\bar{d}}_{G} \, dx$, by Lemma 4.1. Therefore we may assume that $G^{h,1}$ is invariant under the Bonnesen annular symmetrization with respect to the $x_2$-axis. By iterating the argument we deduce that the same holds for $G_t^h$ for all $t>0$. Letting $h \rightarrow 0$ we deduce that the same holds for the flat flow, and by the uniqueness for the classical solution $(G_t)_t$. Therefore for every $t>0$ and $r>0$ the intersection $G_t \cap \partial D_r$ is a union of two circular arcs with equal length which are both symmetric with respect to the $x_2$-axis.

Now if $G_t$ exits the strip $\{ -\rho< x_1 < \rho \}$, say at time $t_0$, then the intersection $G_{t_0} \cap \partial D_\rho$ contains the points $(-\rho ,0)$ and $(\rho ,0)$. Since $G_t \cap \partial D_\rho$ is a union of two circular arcs, which both are symmetric with respect to the $x_2$-axis, we have

$$\begin{aligned} G_{t_0} \cap \partial D_\rho = \partial D_\rho . \end{aligned}$$

By the convexity of $G_{t_0}$ this implies $D_\rho \subset G_{t_0}$. But since the flow (4.8) preserves the area we have $|G_{t_0} | = |D_\rho |$. Then it holds $G_{t_0} = D_\rho$, which is impossible. Therefore the flow $G_t$ does not exit the strip $\{ -\rho< x_1 < \rho \}$, (4.9) holds for all times and the conclusion of the theorem follows.

$\square$