Abstract
In this paper, we consider the curvature flow with driving force on fixed boundary points in the plane. We give a general local existence and uniqueness result of this problem with \(C^2\) initial curve. For a special family of initial curves, we classify the solutions into three categories. Moreover, in each category, the asymptotic behavior is given.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we consider the curvature flow with driving force on fixed boundary points given by
Here V denotes the upward normal velocity(the definition of “upward” is given by Remark 2.2). The sign \(\kappa \) is chosen such that the problem is parabolic. A is a positive constant. P, Q are two different fixed points in \({\mathbb {R}}^2\)
Let \(s\in [0,L(t)]\) be the arc length parameter on \(\Gamma (t)\) and \(F\in C^{2,1}([0,L(t)]\times [0,T)\rightarrow {\mathbb {R}}^2)\) such that \(\Gamma (t)=\{F(s,t)\in {\mathbb {R}}^2\mid 0\le s\le L(t)\}\). Equations (1.1) and (1.2) can be written as
Here \(\Gamma _0=\{F_0(s)\in {\mathbb {R}}^2\mid 0\le s\le L_0\}\); N denotes the unit downward normal vector(the definition of “downward” is given by Remark 2.2) and L(t) denotes the length of \(\Gamma (t)\). And the notation \(\frac{\partial }{\partial t}F(s,t)\) denotes the partial derivative with respect to t by fixing s. Noting the assumption that the sign of \(\kappa \) is chosen such that the problem (1.1) is parabolic, combining Frenet formulas, there holds
The boundary condition 1.3 can be written as follows:
Main results Here we give our main theorems. In the following paper, p is denoted as the arc length parameter on \(\Gamma _0\).
Theorem 1.1
Assume that \(F_0\in C^2([0,L_0]\rightarrow {\mathbb {R}}^2)\) is embedding. Then there exist \(T>0\) and a unique embedding map \({\tilde{F}}\in C^{2,1}([0,L_0]\times [0,T_0)\rightarrow {\mathbb {R}}^2)\) such that the following results hold:
-
(1)
\(\frac{\partial }{\partial t}{\tilde{F}}(p,t)=\kappa N-AN\), \(0<p<L_0\), \(0<t<T\);
-
(2)
\({\tilde{F}}(p,0)=F_0(p)\), \(0\le p\le L_0\);
-
(3)
\({\tilde{F}}(0,t)=P\), \({\tilde{F}}(L_0,t)=Q\), \(0\le t<T\). Moreover, the flow
$$\begin{aligned} \Gamma (t)=\{{\tilde{F}}(p,t)\mid p\in [0,L_0]\},\ 0\le t<T \end{aligned}$$
Assume that \(P=(-a,0)\), \(Q=(a,0)\), where \(0<a\le 1/A\). Before giving the three categories result, we introduce two equilibrium solutions of (1.1) with boundary condition (1.6). Denote
and
Here \(B_r\big ((x,y)\big )\) denotes the ball centered at (x, y) with radii r (Fig. 1).
Equilibrium solutions of (1.1)
Obviously, on \(\Gamma _*\) and \(\Gamma ^*\), there hold \(\kappa =A\) and the fixed boundary condition. Here we give the three categories theorem. In the following theorem, we consider a family of initial curves given by
Here \(\varphi \) is even, \(\varphi \in C^2\big ([-a,a]\big )\), \(\varphi (-a)=\varphi (a)=0\), and \(\varphi ^{\prime \prime }(x)\le 0\), \(-a<x<a\). And assume that for all \(\sigma \in {\mathbb {R}}\), \(\Gamma _{\sigma }\) intersects \(\Gamma ^*\) at most fourth(including the boundary points). Denote \(\Gamma _{\sigma }(t)\) being the solution with \(\Gamma _{\sigma }(0)=\Gamma _{\sigma }\).
Theorem 1.2
There exists \(\sigma ^*>0\) such that
-
(1)
For \(\sigma >\sigma ^*\), there exists \(T_{\sigma }^*<T_{\sigma }\) such that \(\Gamma _{\sigma }(t)\succ \Gamma ^*\), \(T_{\sigma }^*<t<T_{\sigma }\);
-
(2)
For \(\sigma =\sigma ^*\), \(T_{\sigma }=\infty \) and \(\Gamma _{\sigma }(t)\rightarrow \Gamma ^*\) in \(C^1\), as \(t\rightarrow \infty \);
-
(3)
For \(\sigma <\sigma ^*\), \(T_{\sigma }=\infty \) and \(\Gamma _{\sigma }(t)\rightarrow \Gamma _*\) in \(C^1\), as \(t\rightarrow \infty \).
Here \(T_{\sigma }\) denotes the maximal existence time of \(\Gamma _{\sigma }(t)\).
The notation “\(\succ \)” can be seen as an order. The precise definition is given in Sect. 2. We will interpret the sense of \(C^1\) convergence in Definition 2.9.
Main method. Theorem 1.1 can be easily proven by transport map. The transport map is first used by [1] to consider the curvature flow under the non-graph condition. For the three categories result, we use the intersection number principle to classify the type of the solutions in Lemma 4.3. Since \(\Gamma _{\sigma }\) intersects \(\Gamma ^*\) at most fourth, the intersection number between \(\Gamma _{\sigma }(t)\) and \(\Gamma ^*\) can only be two or four. In Lemma 4.3, one of the following three conditions can hold:
-
(1)
The curve \(\Gamma _{\sigma }(t)\) intersects \(\Gamma ^*\) twice and \(\Gamma _{\sigma }(t)\succ \Gamma ^*\) eventually;
-
(2)
The curve \(\Gamma _{\sigma }(t)\) intersects \(\Gamma ^*\) fourth for every \(t>0\).
-
(3)
The curve \(\Gamma _{\sigma }(t)\) intersects \(\Gamma ^*\) twice and \(\Gamma ^*\succ \Gamma _{\sigma }(t)\) eventually.
Considering future, under the condition (2) above, \(\Gamma _{\sigma }(t)\rightarrow \Gamma ^*\) in \(C^1\), as \(t\rightarrow \infty \); under the condition (3) above, \(\Gamma _{\sigma }(t)\rightarrow \Gamma _*\) in \(C^1\), as \(t\rightarrow \infty \). In this paper, we prove the asymptotic behavior by using Lyapunov function introduced in Sect. 5.
A short review for mean curvature flow. For the classical mean curvature flow: \(A=0\) in (1.1), there are many results. Concerning this problem, Huisken [9] shows that any solution that starts out as a convex, smooth, compact surface remains so until it shrinks to a ”round point” and its asymptotic shape is a sphere just before it disappears. He proves this result for hypersurfaces of \({\mathbb {R}}^{n+1}\) with \(n\ge 2\), but Gage and Hamilton [4] show that it still holds when \(n=1\), the curves in the plane. Gage and Hamilton also show that embedded curve remains embedded, i.e. the curve will not intersect itself. Grayson [8] proves the remarkable fact that such family must become convex eventually. Thus, any embedded curve in the plane will shrink to ”round point” under curve shortening flow.
For fixed boundary point problem, Forcadel et al. [3] consider a family of half lines evolved by (1.1), and one boundary point is fixed at the origin. Precisely, the family of curves is given by polar coordinates,
for \(0\le \rho <\infty \). Therefore, \(\theta (\rho ,t)\) satisfies
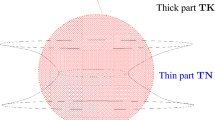
Obviously, this problem is singular near \(\rho =0\). They consider the solution of (1.7) in viscosity sense. Since near the fixed boundary point, curvature flow has singularity by using polar coordinates, there are some papers considering this problem by digging a hole. For example, Giga et al. [5] consider anisotropic curvature flow equation with driving force in the ring domain \(r<\rho <R\). At the boundary, the family of the curves is imposed being perpendicular to the boundary, as seen in Fig. 2.
Research in [5]
Motivation of this research. Ohtsuka et al. first prove the existence and uniqueness of spiral crystal growth for (1.1) by level set method in [6] and [12]. Moreover, they also consider this problem by digging a hole near the fixed points. Recently, [13] simulates the level set of the solution given in [12] by numerical method. In their paper, for \(a>1/A\), the level set evolves as shown in Figs. 3, 4 and 5.
Although, in our paper, we only consider the problem under the condition \(a\le 1/A\), the simulated results in [13] give the hit about this research. We are devoted to considering them in an analytic way.
The rest of this paper is organized as follows. In Sect. 2, we give some preliminary knowledge including the definition of semi-order, comparison principle, and intersection number principle. In Sect. 3, we give the existence and uniqueness result for the fixed boundary points problem. Moreover, in Lemma 3.5, we give a sufficient condition for the solution \(\Gamma _{\sigma }(t)\) remaining regular. In Sect. 4, we give the asymptotic behavior of the solution \(\Gamma _{\sigma }(t)\) when \(\sigma \) is large or small. Lemma 4.3 gives an important result for classifying \(\Gamma _{\sigma }(t)\) by intersection number. In Sect. 5, we prove the asymptotic behavior for the condition (3) in Lemma 4.3 by Lyapunov function. In Sect. 6, we give the proof of Theorem 1.2.
2 Preliminary
Semi-order We want to define a semi-order for curves with the same fixed boundary points.
Definition 2.1
For any points P, \(Q\in {\mathbb {R}}^2\) and \(P\ne Q\), assume that maps \(F_i(s)\in C([0,l_i]\rightarrow {\mathbb {R}}^2)\) are injection and \(F_i\) are differentiable at 0 and \(l_i\).The curves \(\gamma _i\) are given by \(\gamma _i=\{F_i(s)\mid 0\le s\le l_i, F_i(0)=P,F_i(l_i)=Q\}\), where \(l_i\) is the length of \(\gamma _i\), \(i=1,2\). It is easy to see that \(\gamma _i\) have the same boundary points P, Q, \(i=1,2\). We say \(\gamma _1\succ \gamma _2\), if
-
(1)
There exists connect, bounded and open domain \(\Omega \) such that \(\partial \Omega =\gamma _1\cup \gamma _2\);
-
(2)
\(\frac{\mathrm{{d}}}{\mathrm{{ds}}}F_1(0)\cdot \frac{\mathrm{{d}}}{\mathrm{{d}}s}F_2(0)\ne 1\) and \(\frac{\mathrm{{d}}}{\mathrm{{d}}s}F_1(l_1)\cdot \frac{\mathrm{{d}}}{\mathrm{{d}}s}F_2(l_2)\ne 1\);
-
(3)
The domain \(\Omega \) is located in the right hand side of \(\gamma _1\), when someone walks along \(\gamma _1\) from P to Q.
Here “\(\cdot \)” denotes the inner product in \({\mathbb {R}}^2\). We say \(\gamma _1\succeq \gamma _2\), if there exist two sequences of curves \(\{\gamma _{in}\}_{n\ge 1}\), \(i=1,2\) such that
-
(1)
\(\lim \limits _{n\rightarrow \infty }d_H(\gamma _{in},\gamma _i)\rightarrow 0\), \(i=1,2\);
-
(2)
\(\gamma _{1n}\succ \gamma _{2n}\), \(n\ge 1\).
Here \(d_H(A,B)\) denotes the Hausdorff distance for set \(A,B\subset {\mathbb {R}}^2\).
Let \(F(s)\in C^2([0,l]\rightarrow {\mathbb {R}}^2)\) be embedding and \(\gamma =\{F(s)\mid s\in [0,l], F(0)=P, F(l)=Q\}\). Using the definition of semi-order, we can define a shuttle neighborhood of \(\gamma \). Considering the assumption of \(\gamma \), we can extend \(\gamma \) by \(\gamma ^*\) such that \(\gamma ^*\) is \(C^1\) curve and divides \({\mathbb {R}}^2\) into two connect parts denoted by \(\Omega _1\) and \(\Omega _2\). Moreover, \(\Omega _1\) is located in the left hand side when someone walks along \(\gamma ^*\) from P to Q (Fig. 6).
Definition 2.1
Remark 2.2
We say the normal vector of \(\gamma \) is upward(downward), if the normal vector points to the domain \(\Omega _1\)(\(\Omega _2\)).
Definition 2.3
(Shuttle neighborhood) We say V is a shuttle neighborhood of \(\gamma \), if there exist two embedded curves \(\gamma _1\) and \(\gamma _2\) such that
-
(1)
\(\gamma _i\subset \Omega _i\), \(i=1,2\);
-
(2)
\(\gamma _1\succ \gamma \succ \gamma _2\);
-
(3)
\(\partial V=\gamma _1\cup \gamma _2\).
Comparison principle and intersection number principle Here we introduce the comparison principle and intersection number principle. The intersection number principle can help us classify the solutions.
For giving comparison principle, we must define sub,super-solution of (1.4).
Definition 2.4
We say a continuous family of continuous curves \(\{\gamma (t)\}\) is a sub(super)-solution of (1.4) and (1.6), if
-
(1)
\(\gamma (t)\) are continuous curves and have the same boundary points P, Q;
-
(2)
Let \(\{S(t)\}\) be a smooth flow with boundary points P, Q. For some point \(P^*\) and some time \(t_0>0\) satisfying \(P^*\in \gamma (t_0)\) with \(P^*\ne P,\ Q\). If near the point \(P^*\) and time \(t_0\), \(\{S(t)\}\) only intersects \(\{\gamma (t)\}\) at \(P^*\) and time \(t_0\) from above(below). Let \(V_{S(t)}\) denote the upward normal velocity of S(t) and \(\kappa _{S(t)}(P)\) denote the curvature at \(P\in S(t)\). Then
Theorem 2.5
(Comparison principle) For two families of curves \(\{\gamma _1(t)\}_{0\le t\le T}\) and \(\{\gamma _2(t)\}_{0\le t\le T}\), assume \(\{\gamma _1(t)\}_{0\le t\le T}\) is a super-solution of (1.4) and (1.6), \(\{\gamma _2(t)\}_{0\le t\le T}\) is a subsolution of (1.4) and (1.6). If \(\gamma _1(0)\succeq \gamma _2(0)\), then \(\gamma _1(t)\succeq \gamma _2(t)\), \(0\le t\le T\). Moreover, If \(\gamma _1(0)\succeq \gamma _2(0)\) and \(\gamma _1(0)\ne \gamma _2(0)\), then \(\gamma _1(t)\succ \gamma _2(t)\). \(0\le t\le T\).
We can prove this theorem by contradiction. Using local coordinate representation, by maximum principle and Hopf lemma, the conclusion can be got easily. Here we omit the detail.
In this paper, besides intersection number \(Z[\cdot ,\cdot ]\), we introduce a related notion \(SGN[\cdot ,\cdot ]\)(first used by [2]), which turns out to be exceedingly useful in classifying the types of the solutions.
Definition 2.6
For two curves \(\gamma _1\) and \(\gamma _2\) satisfying the same conditions in Definition 2.1, we define
-
(1)
\(Z[\gamma _1,\gamma _2]\) is the number of the intersections between curves \(\gamma _1\) and \(\gamma _2\). Noting that \(\gamma _1\) and \(\gamma _2\) have the same boundary points, then \(Z[\gamma _1,\gamma _2]\ge 2\);
-
(2)
\(SGN[\gamma _1,\gamma _2]\) is defined when \(Z[\gamma _1,\gamma _2]<\infty \). Denoting \(n+1:=Z[\gamma _1,\gamma _2]<\infty \), let \(P=P_0\), \(P_1\), \(\cdots \), \(P_{n-1}\), \(P_n=Q\) be the intersections. Here we assume
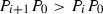 and
and  , \(i=1,\cdots ,n\), where
, \(i=1,\cdots ,n\), where  denotes the arc length of \(\gamma _1\) between \(P_i\) and \(P_j\); \(\widetilde{P_iP_j}\) denotes the arc length of \(\gamma _2\) between \(P_i\) and \(P_j\). If
denotes the arc length of \(\gamma _1\) between \(P_i\) and \(P_j\); \(\widetilde{P_iP_j}\) denotes the arc length of \(\gamma _2\) between \(P_i\) and \(P_j\). If  , we say the sign between \(P_i\) and \(P_{i-1}\) is “\(+\)”; Respectively,
, we say the sign between \(P_i\) and \(P_{i-1}\) is “\(+\)”; Respectively,  , we say the sign between \(P_i\) and \(P_{i-1}\) is “−”, \(i=1,\cdots ,n\). Where
, we say the sign between \(P_i\) and \(P_{i-1}\) is “−”, \(i=1,\cdots ,n\). Where 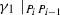 and \(\gamma _2\mid _{\widetilde{P_iP_{i-1}}}\) denote the restriction between \(P_{i-1}\) and \(P_{i}\).
and \(\gamma _2\mid _{\widetilde{P_iP_{i-1}}}\) denote the restriction between \(P_{i-1}\) and \(P_{i}\).
\(SGN[\gamma _1,\gamma _2]\) called ordered word set consists the sign between \(P_i\) and \(P_{i-1}\), \(i=1,\cdots ,n\).
For explaining Definition 2.6, we give an example. Considering Fig. 7, \(Z[\gamma _1,\gamma _2]=6\) and
Let A and B be two ordered word sets, we write \(A\triangleright B\), if B is a sub ordered word set of A. For example,
Remark 2.7
For the curve shortening flow (\(A=0\)), we can deduce that for all \(t_1<t_2\),
However, for the curve shortening flow with driving force (\(A>0\)), even if \(\gamma _1(t)\) and \(\gamma _2(t)\) satisfy (1.4) and (1.6), we can not guarantee that for all \(t_1<t_2\),
For giving the intersection number principle, we need assume \(\gamma _1(t)\) and \(\gamma _2(t)\) are homeomorphism to a curve.
Theorem 2.8
(Intersection number principle) Let M be \(C^1\) embedded curve with boundary points P, Q, V be a shuttle neighborhood of M and flow \(\phi :M\times (-\delta ,\delta )\rightarrow V\) satisfy that for every \(z\in V\), there exist unique \(z^*\in M\) and unique \(\alpha _0\in (-\delta ,\delta )\) such that
Assume that two families of curves \(\{\gamma _i(t)\}_{0\le t\le T}\subset V\) satisfy (1.4) and (1.6) and there exist
such that
for \(i=1,2\). Then one of the following conditions holds
(1)
for all \(0\le t\le T\);
(2) \(Z[\gamma _1(t),\gamma _2(t)]< \infty \) for all \(0<t\le T\). Moreover,
for all \(0< t_1<t_2\le T\).
Proof
If \(\gamma _1(t)\ne \gamma _2(t)\), by the basic parabolic theory, the intersections are discrete. Therefore, \(Z[\gamma _1(t),\gamma _2(t)]< \infty \) for all \(0<t\le T\). It is necessary to prove that for any \(t_0\), there exists \(\epsilon _0\) such that
for all \(t_0-\epsilon _0\le t_1<t_2\le t_0+\epsilon _0\).
We can use the local coordinate to represent the two curves near the intersections and time \(t_0\). Using the classical intersection number principle, for example, considering [2], we can prove this results easily. We omit the detail safely. \(\square \)
Definition 2.9
For a \(C^1\) curve \(\gamma \) and a sequence of \(C^1\) curves \(\gamma _n\) with boundary points P, Q, we say \(\gamma _n\rightarrow \gamma \) in \(C^1\), if
(1) There exist a \(C^1\) curve M with boundary points P, Q and maps
such that
(2)
as \(n\rightarrow \infty \).
3 Time local existence and uniqueness of solution
In this section, we introduce the the transport map first used by [1] and prove Theorem 1.1.
Lemma 3.1
For \(\Gamma _0\) satisfying the assumption in Theorem 1.1, there exist a shuttle neighborhood V of \(\Gamma _0\) and a vector field \(X\in C^1({\overline{V}}\rightarrow {\mathbb {R}}^2)\) such that
and in V, there holds
where N denotes the unit downward normal vector of \(\Gamma _0\).
Proof
We extend \(\Gamma _0\) by \(\Gamma _0^*\) such that \(\Gamma _0^*\) is a \(C^2\) curve and divide \({\mathbb {R}}^2\) into two connect parts \(\Omega _1\) and \(\Omega _2\). Assume \(\Omega _1\)(\(\Omega _2\)) locates in the left(right) side of \(\Gamma _0^*\)(“left side” and “right side” are defined as in Sect. 2).
Let d(x) be the signed distance function defined as follows:
Since \(\Gamma _0^*\) is \(C^2\), as we know, there exists a tubular neighborhood U of \(\Gamma _0^*\) such that d is \(C^2\) in U. Moreover, there exists a projection map P such that for all \(z\in U\), there exists a unique point \(z^*\in \Gamma _0^*\) such that
and \(\nabla d(z)=\nabla d(z^*)=-N(z^*)\). We choose two curves \(\Gamma _1,\Gamma _2\subset U\) and \(\Gamma _i\subset \Omega _i\), \(i=1,2\), such that \(\Gamma _1\succ \Gamma _0\succ \Gamma _2\). Let V be the domain satisfying \(\Gamma _0\subset V\), \(\partial V=\Gamma _1\cup \Gamma _2\), and \(X(z)=\nabla d(z)\). Obviously
and
\(\square \)
Transport map Let \(\phi :\Gamma _0\times (-\delta ,\delta )\rightarrow V\) be the map generated by vector field X, precisely,
Recalling \(\Gamma _0=\{F_0(p)\mid 0\le s\le L_0\}\) and \(F_0\in C^2([0,L_0]\rightarrow {\mathbb {R}}^2)\), let
Considering the assumption of \(F_0\) and X, \(\psi _p\), \(\psi _{\alpha }\), \(\psi _{pp}\), \(\psi _{p\alpha }\), \(\psi _{\alpha \alpha }\) are all continuous vectors for \(0\le p\le L_0\), \(-\delta<\alpha <\delta \).
If \(\Gamma (t)\subset V\) is \(C^1\) close to \(\Gamma _0\) and satisfies (1.4), (1.6), \(0<t<T\) with initial data \(\Gamma (0)=\Gamma _0\), then there exists a function \(u(\cdot ,t):[0,L_0]\rightarrow {\mathbb {R}}\) such that
Moreover, u satisfies
where \(\det (\cdot ,\cdot )\) denotes the determinant. Indeed, the upward normal velocity and the curvature are given by
and
For the computation, we can see, for example, [11].
Following Proposition 3.2 implies Theorem 1.1.
Proposition 3.2
There exist \(T_0>0\) and a unique \(u\in C([0,L_0]\times [0,T_0))\cap C^{2+\alpha ,1+\alpha /2}([0,L_0]\times (0,T_0))\) such that u satisfies (3.1) for \(T=T_0\).
Proof
Since \(\psi _{p}(p,0)\cdot \psi _{\alpha }(p,0)=0\), \(0\le p\le L_0\), then
There exist \(\delta _1>0\) and \(\alpha _0\) such that for all \(-\alpha _0<\alpha <\alpha _0\) and \(0\le p\le L_0\),
By the quasilinear parabolic theory in [10], we can deduce that there exist \(T_0\) and \(u\in C([0,L_0]\times [0,T_0))\cap C^{2+\alpha ,1+\alpha /2}([0,L_0]\times (0,T_0))\) such that u satisfies (3.1) and \(|u|\le \alpha _0\), \(0\le t<T_0\). For the uniqueness, since \(\psi _p\), \(\psi _{\alpha }\), \(\psi _{pp}\), \(\psi _{p\alpha }\), \(\psi _{\alpha \alpha }\) are all continuous vectors for \(0\le p\le L_0\), \(-\alpha _0<\alpha <\alpha _0\), the uniqueness can be obtained easily. \(\square \)
Proof of Theorem 1.1
Let \(T_0\) and u be given by Proposition 3.2. Obviously, \({\tilde{F}}(p,t)=\psi (p,u(p,t))\) is the unique solution.
Let \(\Gamma (t)=\{{\tilde{F}}(p,t)\mid 0\le p\le L_0\}\), \(0\le t<T_0\) and s be the arc length parameter on \(\Gamma (t)\). Then \(F(s,t)={\tilde{F}}(p,t)\) satisfies (1.4), (1.5), (1.6). \(\square \)
Remark 3.3
The assumption for initial curve can be weakened. In this paper, we assume \(F_0\in C^2([0,L_0]\rightarrow {\mathbb {R}}^2)\). Indeed, the initial curve can be assumed to be Lipschitz continuous. Recently, [11] has considered the curve-shortening flow with Lipschitz initial curve, under the Neumann boundary condition. Since the purpose of this paper is to get the three categories of solutions, we do not introduce this part in detail.
Lemma 3.4
For \(\Gamma (t)\) satisfying (1.4), (1.6), for \(0<t<T\), then the curvature \(\kappa (s,t)\) satisfies
where \(\kappa _t\) denotes the derivative with respect to t by fixing s.
For the proof of the first equation, the calculation can be seen in [7]. Since at the boundary points, \(\Gamma (t)\) does not move, the boundary condition is obvious.
Lemma 3.5
For \(\sigma >0\), \(\Gamma _{\sigma }(t)\) given in Theorem 1.2, let \(F_{\sigma }(s,t)\) satisfy
where \(L_{\sigma }(t)\) is the length of \(\Gamma _{\sigma }(t)\). If \(\frac{\partial }{\partial s} F_{\sigma }(0,t)\cdot (0,1)>0\), for all \(0\le t\le t_0\), then \(t_0<T_{\sigma }\).
This lemma gives a sufficient condition under which \(\Gamma _{\sigma }(t)\) does not become singular. The assumption \(\frac{\partial }{\partial s} F_{\sigma }(0,t)\cdot (0,1)>0\) means that the y-component of the tangential vector \(\frac{\partial }{\partial s} F_{\sigma }(0,t)\) is positive.
Proof
Considering the choice of \(\Gamma _{\sigma }(0)\), then \(\kappa _{\sigma }(s,0)\ge 0\), \(0\le s\le L_{\sigma }(0)\), for \(\sigma >0\). Combining Lemma 3.4 and maximum principle, \(\kappa _{\sigma }(s,t)>0\), \(0<s<L(t)\), \(0<t<T_{\sigma }\).
If \(T_{\sigma }=\infty \), the result is trivial. We assume \(T_{\sigma }<\infty \).
We prove the result by contradiction, assuming \(t_0\ge T_{\sigma }\). We claim that every half-line given by
intersects \(\Gamma _{\sigma }(t)\) only once, \(0<t<T_{\sigma }\).
First, for all \(0<t<T_{\sigma }\), we prove \(x=0\), \(y\ge 0\) intersects \(\Gamma _{\sigma }(t)\) only once. If not, suppose that there exists \(t_1<T_{\sigma }\) such that \(x=0\), \(y\ge 0\) intersects \(\Gamma _{\sigma }(t_1)\) more than once. Since \(\Gamma _{\sigma }(t)\) is symmetric about y-axis, it is easy to see that \(\Gamma _{\sigma }(t)\) becomes singular at \(t_1\). This contradicts to \(t_1<T_{\sigma }\).
Next, by contradiction, assume that there exist \(t_2<T_{\sigma }\) and \(k<0\) such that \(y=kx,\ y\ge 0\) intersects \(\Gamma _{\sigma }(t_2)\) more than once. Combining our assumption \(\frac{\partial }{\partial s} F_{\sigma }(0,t)\cdot (0,1)>0\), we can choose \(k_0\) satisfying \(k_0<k<0\) such that half-line \(y=k_0x,\ y\ge 0\) intersects \(\Gamma _{\sigma }(t_2)\) tangentially at some point \(P^*\), and near \(P^*\), \(\Gamma _{\sigma }(t_2)\) is located under the half-line. It is easy to deduce that the curvature at \(P^*\), \(\kappa _{\sigma }(P^*,t_2)\le 0\). This contradicts to that the curvatures on \(\Gamma _{\sigma }(t)\) are all positive, \(0<t<T_{\sigma }.\) Here we complete the proof of claim (Fig. 8).
Regarding \(\frac{\partial }{\partial s} F_{\sigma }(0,t)\cdot (0,1)>0\) and the claim above, \(\Gamma _{\sigma }(t)\subset \{(x,y)\mid y\ge 0\}\), \(t<T_{\sigma }\). The claim implies that we can express \(\Gamma _{\sigma }(t)\) by polar coordinate. For \((x,y)\in \Gamma _{\sigma }(t)\), let
for \(0\le \theta \le \pi \), \(0\le t<T_{\sigma }\). Consequently, \(\rho _{\sigma }\) satisfies
recalling \(P=(-a,0)\), \(Q=(a,0)\).
Since for \(\sigma >0\), \(\Gamma _{\sigma }(0)\succ \Lambda _0=\{(x,y)\mid y=0,\ -a\le x\le a\}\). It is easy to see that \(\Lambda _0\) is a subsolution of (1.4) and (1.6). By comparison principle, \(\Gamma _{\sigma }(t)\succ \Lambda _0\) for \(0<t<T_{\sigma }\). Let
For all \(t_3>0\), we can choose sufficiently large \(R>1/A\) such that
It is easy to check that \(\Lambda _*\) is a subsolution. Then
This implies that there exists \(\rho _1>0\) such that \(\rho _{\sigma }(\theta ,t)\ge \rho _1\) for \(t_3<t<T_{\sigma }\), \(0\le \theta \le \pi \). On the other hand, since \(T_{\sigma }<\infty \), there exists \(\rho _2>0\) such that \(\rho _{\sigma }(\theta ,t)\le \rho _2\) for \(0<t<T_{\sigma }\), \(0\le \theta \le \pi \). Therefore, the quasilinear theory in [10] shows that for \(\epsilon >0\), there exists \(C_{\epsilon }\) such that
Therefore, the curvature of \(\Gamma _{\sigma }(t)\) is uniformly bounded for t close to \(T_{\sigma }\). This implies that the solution \(\Gamma _{\sigma }(t)\) can be extended over time \(T_{\sigma }\). This contradicts to that \(T_{\sigma }\) is the maximal existence time. \(\square \)
Lemma 3.6
Assume \(\rho \) and \(\rho _n\) are the solutions of (3.3) for \(0\le \theta \le \pi \), \(0<t<T\). If \(\rho \) is bounded from below for some positive constant and
then for all \(0<t<T\),
By our assumption that \(\rho \) is bounded from below for some positive constant, this lemma can be proven by Schauder estimate in [10] directly.
4 Behavior for \(\sigma \) sufficient small or large
Proposition 4.1
There exists \(\sigma _1>0\) such that, for all \(\sigma >\sigma _1\), there exists some time \(T_{\sigma }^*<T_{\sigma }\) such that \(\Gamma _{\sigma }(t)\succ \Gamma ^*\), for \(T_{\sigma }^*<t<T_{\sigma }\)
For proving this proposition, we introduce the Grim reaper for the curve shortening flow. Grim reaper is given by
where \(b>0\) and \(C\in {\mathbb {R}}\). It is easy to see that G(x, t) satisfies
The Grim reaper G(x, t) is a traveling wave moving downward with speed 1 / b.
Lemma 4.2
If \(b<2a/\pi \), the curve
is a subsolution of (1.4) and (1.6) in the sense of Definition 2.4.
Proof
When \(0<t<bC\), let \(x(t)>0\) be a point such that \(G(x(t),t)=0\).
For \(|x|<x(t)\), \(\gamma _G=\{(x,y)\mid y=G(x,t)\}\). Therefore,
For \(x(t)<|x|<a\), \(\gamma _G=\{(x,y)\mid y=0\}\). Obviously, \(y=0\) is a subsolution of
At the point \(x=x(t)\)(\(x=-x(t)\)), it is impossible that for smooth flow S(t), near \(x=x(t)\)(\(x=-x(t)\)), S(t) touches \(\gamma _{G}(t)\) at \(x=x(t)\)(\(x=-x(t)\)) only once from above.
Therefore, \(\gamma _G(t)\) is a subsolution of (1.4) and (1.6), for \(0<t<bC\).
When \(t\ge bC\), \(\gamma _G=\Lambda _0=\{(x,y)\mid y=0,\ |x|\le a\}\)(given in the proof of Lemma 3.5). Obviously, \(\gamma _G\) is a subsolution of (1.4) and (1.6), for \(t\ge bC\). \(\square \)
Following lemma gives the result for the classification of the solution \(\Gamma _{\sigma }(t)\).
Lemma 4.3
For \(\Gamma _{\sigma }(t)\) given by Theorem 1.2, for \(\sigma >0\), \(\Gamma _{\sigma }(t)\) satisfies one of the following four conditions:
-
(1)
\(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-]\) for \(t<T_{\sigma }\). Moreover, \(T_{\sigma }=\infty \);
-
(2)
There exists \(t^*_{\sigma }\) such that \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\) for \(t<t^*_{\sigma }\) and \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-]\) for \(t^*_{\sigma }<t<T_{\sigma }\). Moreover, \(T_{\sigma }=\infty \);
-
(3)
\(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\) for \(t<T_{\sigma }\). Moreover, \(T_{\sigma }=\infty \);
-
(4)
There exists \(T_{\sigma }^*<T_{\sigma }\) such that \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\) for \(t<T_{\sigma }^*\) and \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[+]\), \(T_{\sigma }^*<t<T_{\sigma }\).
Proof
Considering the assumption in Theorem 1.2, there exists \(\sigma _0>0\) such that
-
(a)
\(0<\sigma \le \sigma _0\), \(\Gamma ^*\succeq \Gamma _{\sigma }\);
-
(b)
\(\sigma >\sigma _0\), \(\Gamma _{\sigma }\) intersects \(\Gamma ^*\) fourth.
Step 1 For \(0<\sigma \le \sigma _0\), by comparison principle, \(\Gamma ^*\succ \Gamma _{\sigma }(t)\), for \(0<t<T_{\sigma }\). Noting \(\sigma >0\), \(\Gamma _{\sigma }(t)\succ \Lambda _0\), for \(0<t<T_{\sigma }\). Therefore, \(\frac{\partial }{\partial s}F_{\sigma }(0,t)\cdot (0,1)>0\), \(0<t<T_{\sigma }\). By contradiction and the same method in the proof of Lemma 3.5, we can prove \(T_{\sigma }=\infty \). Therefore, for \(0<\sigma \le \sigma _0\), condition (1) holds.
Step 2 For \(\sigma >\sigma _0\), considering the choice of \(\Gamma _{\sigma }\), \(SGN(\Gamma _{\sigma },\Gamma ^*)=[-\ +\ -]\).
Let \(\tau _0\) depending on \(\sigma \) satisfy
Since \(\frac{\partial }{\partial s}F_{\sigma }(0,0)\cdot (0,1)>0\), we can deduce \(\tau _0>0\). Therefore, Lemma 3.5 implies \(T_{\sigma }>\tau _0\). Moreover, \(\Gamma _{\sigma }(t)\) can be represented by polar coordinate, \(0<t<\tau _0\). This means that \(\Gamma _{\sigma }(t)\) satisfies the assumption of Theorem 2.8 for \(0<t<\tau _0\). Then
Considering the symmetry of \(\Gamma _{\sigma }(t)\), then for \(t<\tau _0\), one of the following three conditions holds
-
(i)
\(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[+]\);
-
(ii)
\(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-]\);
-
(iii)
\(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ -]\).
-
(iv)
\(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\).
Step 3 If for some \(t^*_{\sigma }<\tau _0\) (ii) or (iii) holds, then \(\Gamma ^*\succeq \Gamma _{\sigma }(t^*_{\sigma })\). Then by comparison principle, \(\Gamma ^*\succ \Gamma (t)\succ \Lambda _0\), \(t^*_{\sigma }<t<T_{\sigma }\). Therefore, by the same argument in Step 1, condition (2) holds.
If for some \(T_{\sigma }^*<\tau _0\) (i) holds, this means that \(\Gamma _{\sigma }(T_{\sigma }^*)\succ \Gamma ^*\). By comparison principle, \(\Gamma _{\sigma }(t)\succ \Gamma ^*\), \(T_{\sigma }^*<t<T_{\sigma }\). Therefore, condition (4) holds.
If for every \(t<\tau _0\), there holds \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\). Combining \(\Gamma _{\sigma }(t)\succ \Lambda _0\), \(t<\tau _0\), there exists \(\delta >0\) such that
If \(\tau _0<\infty \), by the definition of \(\tau _0\), \(\frac{\partial }{\partial s}F_{\sigma }(0,\tau _0)\cdot (0,1)=0\). This yields a contradiction. Therefore, \(\tau _0=\infty \). Consequently, \(T_{\sigma }=\infty \). Condition (3) holds.
We complete the proof. \(\square \)
In the following, we consider two circles.
and
where \(R>1/A\). We denote
It is easy to check that \(\partial B_2\) intersects \(\Gamma ^*\) tangentially at \((-a,0)\). Let R(t) be the solution of
with \(R(0)=R\). Since \(R(0)>1/A\), R(t) is increasing and \(\lim \limits _{t\rightarrow \infty }R(t)=\infty \). Noting \(a\le 1/A\) and \((1+R/a)/A>R\), there exists \(t^*\) such that \(R(t^*)=(1+R/a)/A\).
Lemma 4.4
Let point \((0,y_{\sigma }(t))=\Gamma _{\sigma }(t)\cap \{(x,y)\mid x=0\}\), \(t<T_{\sigma }\). There exists \(\sigma _1\)(indeed \(\sigma _1\) in this lemma is the one we want to choose in Proposition 4.1) such that for all \(\sigma >\sigma _1\) there holds that if \(t^*<T_{\sigma }\),
We use the Grim reaper to prove this lemma.
Proof
Considering that Grim reaper given by Lemma 4.2
is a traveling wave with uniform speed 1 / b, then choose C large enough such that \(G(0,t)=C-t/b>C-t^*/b>K\), \(t<t^*\).
We can choose \(\sigma _1\) such that for all \(\sigma >\sigma _1\), \(\Gamma _{\sigma }\succ \gamma _{G}(0)\).
If \(t^*<T_{\sigma }\), Lemma 4.2 implies that \(\Gamma _{\sigma }(t)\succ \gamma _{G}(t)\), for \(t<t^*\). This means that \(y_{\sigma }(t)>K\), \(t<t^*\). \(\square \)
Proof of Proposition 4.1
Choose \(\sigma _1\) as in Lemma 4.4.
Step 1. For \(\sigma >\sigma _1\), if \(T_{\sigma }\le t^*\)(\(t^*\) is given in Lemma 4.4), this means that \(T_{\sigma }<\infty \). By Lemma 4.3, only the condition (4) in Lemma 4.3 can hold. Consequently, the result is true.
Step 2. For \(\sigma >\sigma _1\), if \(t^*<T_{\sigma }\), by Lemma 4.4, \(y_{\sigma }(t)>K\), \(t<t^*\). Here we prove
Let
where R(t) is given by (4.1). It is easy to see that \(\partial B(t)\) evolves by \(V=-\kappa +A\).
Let \(\Sigma (t)=\partial B(t)\cap \{(x,y)\mid x\le 0,y\ge 0\}\). There exists \(\delta \) satisfying \(0<\delta <t^*\) such that
Obviously, \(\partial B(\delta )\) passes through the origin (0, 0). As seen in the Figs. 9 and 10 and noting the choice of \(t^*\), the boundary of \(\Sigma (t)\) does not intersect \(\Gamma _{\sigma }(t)\), \(t<t^*\). By maximum principle, \(\Sigma (t)\) cannot intersect \(\Gamma _{\sigma }(t)\) interior. Therefore, \(\Gamma _{\sigma }(t)\) does not intersect \(\Sigma (t)\), \(t<t^*\). Here we omit the detail.
As seen in the Fig. 11, \(\Sigma (t^*)\) intersects \(\Gamma ^*\) tangentially at \((-a,0)\). Since \(\Gamma _{\sigma }(t)\) does not intersect \(\Sigma (t)\) for \(t<t^*\), then \(\Gamma (t^*)\succ \Gamma ^*\). Therefore, \(\Gamma (t)\succ \Gamma ^*\) for \(t^*<t<T_{\sigma }\). Let \(T_{\sigma }^*=t^*\), we complete the proof.\(\square \)
Proof of Proposition 4.1
Proof of Proposition 4.1
Proof of Proposition 4.1
Proposition 4.5
There exists \(\sigma _2>0\) such that for all \(\sigma <\sigma _2\), \(T_{\sigma }=\infty \) and \(\Gamma _{\sigma }(t)\rightarrow \Gamma _*\) in \(C^1\), as \(t\rightarrow \infty \).
Proof
Step 1. (Upper bound)
There exists \(\sigma _2\) such that for all \(\sigma <\sigma _2\), \(\Gamma _*\succ \Gamma _{\sigma }\). Since \(\Gamma _{\sigma }\) is represented by the graph of \(\sigma \varphi \), then \(\Gamma _{\sigma }(t)\) can time locally be represented by the graph of some function \(u_{\sigma }(x,t)\). Let \(T_{\sigma }^g\) be the maximal time such that
Therefore, \(u_{\sigma }(x,t)\) satisfies
Since for all \(\sigma <\sigma _2\) there holds \(\sigma \varphi (x)\le \sqrt{1/A^2-x^2}-\sqrt{1/A^2-a^2}\), \(-a\le x\le a\), by comparison principle, we have
Step 2. Lower bound and derivative estimate.
If \(0\le \sigma <\sigma _2\), by comparison principle,
Differentiating the first equation in (4.2) by x and combining boundary condition (4.5), by maximum principle, we have
If \(\sigma <0\), let \(k>0\) satisfy \(k:=\sigma \varphi ^{\prime }(a)\). We denote function
Obviously, \({\underline{u}}(x)\le \sigma \varphi \), \(-a\le x\le a\) and \({\underline{u}}\) is a subsolution of (4.2) in viscosity sense.
Therefore, by maximum principle, \(u_{\sigma }(x,t)>{\underline{u}}(x)\), \(-a<x<a\), \(0<t<T_{\sigma }^g\). Combining (4.3), we have
Consequently, (4.6) and (4.7) imply that there exists \(C_{\sigma }\) such that
Step 3. We prove the convergence in this step.
By [10], for \(\epsilon >0\), \((u_{\sigma })_{xx}(x,t)\) is bounded for all \(-a\le x\le a,\ \epsilon \le t<T_{\sigma }^g\). This means that \(T_{\sigma }^g=\infty \). Therefore, by [10] again, \(u_{\sigma }(x,t)\), \((u_{\sigma })_{t}(x,t)\), \((u_{\sigma })_{tt}(x,t)\), \((u_{\sigma })_x(x,t)\), \((u_{\sigma })_{xx}(x,t)\) and \((u_{\sigma })_{xxx}(x,t)\) are all bounded for some constant \(D_{\sigma }>0\), \(-a\le x\le a,\ \epsilon \le t<\infty \). By Ascoli–Arzela Theorem, for any sequence \(t_n\rightarrow \infty \), there exist a subsequence \(t_{n_j}\) and function v(x, t) (v may depend on the choice of the subsequence. In Step 5, we will prove v is independent of the choice of the subsequence) such that
as \(j\rightarrow \infty \).
Step 4. In this step, we introduce the Lyapunov function for (4.2).
Let
If u is a solution of (4.2), we calculate
Therefore, there hold
and
Step 5. Using the Lyapunov function, we complete the proof.
For \(u_{\sigma }\) given above, \(u_{\sigma }(x,t)\) is uniformly bounded for \(-a\le x\le a\), \(0<t<\infty \). Then, the integral
is bounded for \(0<t<\infty \). Consequently, \(J[u_{\sigma }(\cdot ,t)]\) is bounded for \(0<t<\infty \). Therefore, the integral
is bounded. Then for all \(s_0>0\),
as \(j\rightarrow \infty \). Considering \(u_{\sigma }(\cdot ,\cdot +t_{n_j})\rightarrow v\), in \(\ C^{2,1}([-a,a]\times [\epsilon ,\infty ))\), as \(j\rightarrow \infty \), we have
Then \(v_t(x,t)=0\), for all \(-a\le x\le a\), \(s_0\le t\le s_0+1\). Considering that the choice of \(s_0\) is arbitrary,
for all \(-a\le x\le a\), \(0<t<\infty \). Therefore, v is independent on t and is a stationary solution of (4.2). Then
Here we get that for any sequence \(t_n\rightarrow \infty \), there exists a subsequence \(t_{n_j}\) such that
as \(j\rightarrow \infty \). Consequently,
as \(t\rightarrow \infty \).
The proof of this proposition is completed. \(\square \)
5 Asymptotic behavior for the condition (3) in Lemma 4.3
Considering Lemma 3.5 and the proof of Lemma 4.3, under the condition (3) in Lemma 4.3, we can assume there exists \(\rho _{\sigma }\) such that
Moreover \(\rho _{\sigma }\) satisfies (3.3) for \(T_{\sigma }=\infty \).
Lemma 5.1
Let \(L_{\sigma }(t)\) be the length of \(\Gamma _{\sigma }(t)\) and \(S_{\sigma }(t)\) be the area of the domain surrounded by \(\Gamma _{\sigma }(t)\) and \(y=0\). Then,
Remark 5.2
(1) Noting that under the condition (3) in Lemma 4.3, \(\Gamma _{\sigma }(t)\) located in \(\{y\ge 0\}\), the definition of \(S_{\sigma }(t)\) is well defined.
(2) The result of this lemma is a general condition for the Lyapunov function in the proof of Proposition 4.5.
Proof
Considering the calculation in [14],
Recall N being the unit downward normal vector. Therefore,
where F is the point on the curve \(\Gamma _{\sigma }(t)\) and for convenience, we omit the subscript of \(F_{\sigma }(s,t)\). Let
By Green’s formula,
where F is the point on the curve \(\gamma _{\sigma }(t)\) and N is the unit inner normal vector. Since the curve
is independent on t,
Computing as in [14],
Considering the calculation in [14],
where \(T=F_s\) is the unit tangential vector, then
Considering the symmetry of \(\Gamma _{\sigma }(t)\) and \(\kappa (0,t)=\kappa (L_{\sigma }(t),t)=A\), at the boundary,
Integrating I by parts, there holds
Therefore,
In the last second equality, we use integral by parts. Therefore,
Consequently, (5.1) holds. \(\square \)
Lemma 5.3
Under the condition (3) in Lemma 4.3, \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\) for \(t<\infty \), there exist \(\rho _2>\rho _1>0\) such that
for \(0\le \theta \le \pi \), \(0<t<\infty \).
Proof
First, we prove \(\rho _{\sigma }<\rho _2\). We prove this by contradiction, assuming \(\rho _{\sigma }\) is not bounded from above.
If \(\rho _{\sigma }(\pi /2,t)\) is bounded for all t, we can easily prove that there exist some \(0<\theta _0<\pi /2\) and \(t_0\) such that \(\kappa _{\sigma }(\theta _0,t_0)\le 0\). This contradicts to that \(\kappa _{\sigma }(\theta ,t)>0\), for all \(0<\theta <\pi \), \(t<\infty \).
Therefore, \(\rho _{\sigma }(\pi /2,t)\) is not bounded. Assume for some \(t_0\), \(\rho _{\sigma }(\pi /2,t_0)\) is large enough. We can use the Grim reaper argument as in Proposition 4.1 to prove that \(\Gamma _{\sigma }(t)\succ \Gamma ^*\) in finite time. This contradicts to that \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\) for \(t<\infty \). Therefore, there exists \(\rho _2>0\) such that \(\rho _{\sigma }(\theta ,t)<\rho _2\), for all \(0<\theta <\pi \), \(t<\infty \).
On the other hand, we note that \(\Gamma _{\sigma }\succ \Lambda _0=\{(x,y)\mid y=0,\ -a\le x\le a\}\), \(0<t<\infty \). Then there exists \(\rho _1>0\) such that \(\rho _{\sigma }(\theta ,t)>\rho _1\), \(0<\theta <\pi \), \(t<\infty \).
We complete the proof. \(\square \)
Here we give the asymptotic behavior under the condition (3) in Lemma 4.3.
Proposition 5.4
Under the condition (3) in Lemma 4.3, \(SGN(\Gamma _{\sigma }(t),\Gamma ^*)=[-\ +\ -]\) for \(t<\infty \),
as \(t\rightarrow \infty \).
Proof
Since \(\rho _1<\rho _{\sigma }<\rho _2\) and \(\rho _{\sigma }\) satisfies (3.3), then there exists \(\epsilon >0\) such that \(\rho _{\sigma t}\), \(\rho _{\sigma tt}\), \(\rho _{\sigma \theta }\), \(\rho _{\sigma \theta \theta }\) and \(\rho _{\sigma \theta \theta \theta }\) are bounded for \(0\le \theta \le \pi \), \(\epsilon \le t<\infty \). Therefore, for any \(t_n\rightarrow \infty \), there exist a subsequence \(t_{n_j}\) and a function \(r(\theta ,t)\) such that
as \(j\rightarrow \infty \). Let
and the curvature \(\kappa _{\sigma }(\cdot ,t)\) be the curvature on \(\Gamma _{\sigma }(t)\), \(\kappa _{r}(\cdot ,t)\) be the curvature on \(\gamma _{r}(t)\). Therefore, \(\kappa _{\sigma }(\cdot ,\cdot +t_{n_j})\rightarrow \kappa _{r}\) in \(C([0,\pi ]\times [\epsilon ,\infty ))\). Obviously, the length \(L_{\sigma }(t)\) and the area \(S_{\sigma }(t)\) are bounded. Using the same argument in Proposition 4.5 and the Lyapunov function in Lemma 5.1, we can deduce that \(\kappa _{r}\equiv A\). Consequently, \(r_t(\theta ,t)=0\) for all \(0\le \theta \le \pi \) and \(t>0\). Considering the curvature of \(\gamma _{r}\) is a positive constant, \(\gamma _{r}\) can only be a part of circle with radius 1 / A. Considering \(r(0,t)=-a\) and \(r(\pi ,t)=a\), then \(\gamma _{r}=\Gamma ^*\) or \(\gamma _{r}=\Gamma _*\). But for all \(t>0\),
as \(j\rightarrow \infty \). If \(\gamma _{r}=\Gamma _*\), then for t large enough, \(\Gamma ^*\succ \Gamma _{\sigma }(t)\). This yields a contradiction. Therefore, \(\gamma _{r}=\Gamma ^*\). Consequently,
as \(t\rightarrow \infty \).
Here we complete the proof. \(\square \)
6 Proof of Theorem 1.2
Lemma 6.1
The set
is open and connect.
Proof
Proposition 4.5 implies that \((-\infty ,0]\subset B_*\ne \emptyset \). In following argument, let \(\sigma _1>0\) and \(\sigma _1\in B_*\).
(1) (Proof of the property connect) We claim that, for all \(\sigma <\sigma _1\), \(\Gamma _{\sigma }(t)\rightarrow \Gamma _*\ \text {in}\ C^1\), as \(t\rightarrow \infty \).
Since \(\Gamma _{\sigma _1}(t)\rightarrow \Gamma _*\ \text {in}\ C^1\), as \(t\rightarrow \infty \), then there holds \(\Gamma ^*\succ \Gamma _{\sigma _1}(t)\) for t large enough. By comparison principle, \(\Gamma _{\sigma _1}(t)\succ \Gamma _{\sigma }(t)\), \(t<T_{\sigma }\). These imply that the condition (4) in Lemma 4.3 can not hold. Therefore, \(T_{\sigma }=\infty \). By the same argument in Proposition 4.5, we can prove
as \(t\rightarrow \infty \). Here we prove that \(B_*\) is connect.
(2) (Proof of the property open) We are going to prove \(B_*\) is open. We only need prove that there exists \(\epsilon _0>0\), \((\sigma _1,\sigma _1+\epsilon _0)\subset B_*\). We divide this proof into two steps.
Step 1. Let
By comparison principle, we can prove that \(\tau _0(\sigma )\) is non-increasing with respect to \(\sigma \). let \(\tau ^*=\sup \{\tau _0(\sigma )\mid \sigma >\sigma _1\}=\lim \limits _{\sigma \downarrow \sigma ^1}\tau _0(\sigma )\). We claim that \(\tau ^*=\infty \).
For all \(t<\tau ^*\), there exists \(\delta _0\), for \(\sigma \in (\sigma _1,\sigma _1+\delta _0)\), \(\tau _0(\sigma )>t\). Therefore, for \(\sigma \in (\sigma _1,\sigma _1+\delta _0)\), \(\Gamma _{\sigma }(t)\) can be represented by polar coordinate and not become singular. By Lemma 3.6,
as \(\sigma \rightarrow \sigma _1\). Considering that the condition (1) or (2) in Lemma 4.3 hold for \(\Gamma _{\sigma _1}(t)\), we can prove that there exists \(\delta >0\) such that
Consequently,
Therefore, \(\tau ^*=\infty \).
Step 2. We complete the proof.
We choose two curves \(\gamma _1\) and \(\gamma _2\) such that \(\Gamma ^*\succ \gamma _1\succ \Gamma _*\succ \gamma _2\) and the domain V be the shuttle neighborhood of \(\Gamma _*\) satisfying \(\partial V=\gamma _1\cup \gamma _2\).
Since
as \(t\rightarrow \infty \), for \(t_0\) large enough \(\Gamma _{\sigma _1}(t_0)\subset V\). Considering the result in Step 1, for \(\sigma \) close to \(\sigma _1\), \(\Gamma _{\sigma }(t_0)\) can be represented by polar coordinate and not become singular. By Lemma 3.6,
as \(\sigma \rightarrow \sigma _1\). Then there exists \(\epsilon _0\) for \(\sigma \in (\sigma _1,\sigma _1+\epsilon _0)\), \(\Gamma _{\sigma }(t_0)\subset V\). Using the Lyapunov function given by Lemma 5.1 and the same argument in Proposition 5.4, for all \(\sigma \in (\sigma _1,\sigma _1+\epsilon _0)\),
as \(t\rightarrow \infty \).
We complete the proof. \(\square \)
Lemma 6.2
The set
is open and connect.
Proof
Propositions 4.1 and 4.5 show that \(B^*\subset (0,\infty )\) is not empty. In the following argument, let \(\sigma _2>0\) and \(\sigma _2\in B^*\). Then there exists \(T_{\sigma _2}^*>0\) such that
(1) (Proof the property connect) We claim \((\sigma _2,\infty )\subset B^*\).
For \(\sigma >\sigma _2\), if \(T_{\sigma }<\infty \), then only the condition (4) in Lemma 4.3 can hold. The result is true for \(T_{\sigma }<\infty \).
In the following argument, we assume \(T_{\sigma }=\infty \), then by comparison principle,
Here we complete the proof that \(B^*\) is connect.
(2) (Proof of the property open) We prove \(B^*\) is open. We only need to prove that there exists \(\epsilon _0>0\) such that \((\sigma _2-\epsilon _0,\sigma _2)\subset B^*\).
We can choose \(t_0\) such that \(\Gamma _{\sigma _2}(t_0)\succ \Gamma ^*\) and
By Lemma 3.5 and comparison principle, it is easy to see that for all \(0<\sigma <\sigma _2\), \(T_{\sigma }>t_0\). For \(\sigma \) close to \(\sigma _2\), \(\Gamma _{\sigma }(t)\) can be represented by polar coordinate for \(0<t\le t_0\). By Lemma 3.6,
as \(\sigma \rightarrow \sigma _2\). Therefore, there exists \(\epsilon _0>0\) such that for all \(\sigma \in (\sigma _2-\epsilon _0,\sigma _2)\), \(\Gamma _{\sigma }(t_0)\succ \Gamma ^*\). By the comparison principle, we can get the result easily.
We complete the proof. \(\square \)
Corollary 6.3
There exist \(0<\sigma _*\le \sigma ^*\) such that
and
Proof
Let \(\sigma ^*=\inf B^*\) and \(\sigma _*=\inf B_*\). Obviously, \(\sigma _*\le \sigma ^*\).
and
Proposition 4.5 shows that \(\sigma _*>0\). The proof is completed. \(\square \)
Proposition 6.4
If \(\Gamma _{\sigma _0}(t)\rightarrow \Gamma ^*\) in \(C^1\), for some \(\sigma _0\), as \(t\rightarrow \infty \), then \((\sigma _0,\infty )\subset B^*\).
Proof
For \(\sigma >\sigma _0\), if \(T_{\sigma }<\infty \), then the claim holds. In the following proof, we only consider \(T_{\sigma }=\infty \). By comparison principle, \(\Gamma _{\sigma }(t)\succ \Gamma _{\sigma _0}(t)\), \(t>0\).
Since
there exist \(t_0\) and \(\delta >0\) such that for all \(t\ge t_0\), there hold
and
Since \(\Gamma _{\sigma }(t_0)\succ \Gamma _{\sigma _0}(t_0)\), then we can choose a small positive constant c such that
where
We claim that \(\Gamma ^c(t)\) is a subsolution for \(t\ge t_0\). Indeed, the part \(\Gamma ^c(t)\cap \{y> c\}\) is a translation of \(\Gamma _{\sigma _0}(t)\). \(\Gamma ^c(t)\cap \{y> c\}\) satisfies (1.4). Since the part \(\Gamma ^c(t)\cap \{y< c\}\) consists of two straight lines, then the part is a subsolution of (1.4). Next at the points \(\{(-a,c),(a,c)\}=\Gamma ^c(t)\cap \{y=c\}\), considering (6.1), (6.2) for any smooth flow S(t) can not touch \((-a,c)\) or (a, c) above only once. Therefore, \(\Gamma ^c(t)\) is a subsolution of (1.4) and (1.6) in the sense of Definition 2.4 (Fig. 12).
By \(\Gamma _{\sigma }(t_0)\succ \Gamma ^c(t_0)\) and \(\Gamma ^c(t)\) being subsolution for \(t>t_0\),
Note that \(\Gamma ^c(t)\rightarrow \Gamma ^{*c}\) in C, as \(t\rightarrow \infty \), where
If \(\Gamma _{\sigma }(t)\) satisfies the condition (3) in Lemma 4.3, by Proposition 5.4, \(\Gamma _{\sigma }(t)\rightarrow \Gamma ^*\). Combining (6.3), we get \(\Gamma ^*\succeq \Gamma ^{*c}\). It is impossible.
If \(\Gamma _{\sigma }(t)\) satisfies the condition (1) or (2) in Lemma 4.3, by the same argument in Proposition 5.4, we can prove the derivative of \(\Gamma _{\sigma }\) are all bounded. Using Ascoli-Arzela Theorem and Lyapunov function as in Proposition 5.4, we can get \(\Gamma _{\sigma }(t)\rightarrow \Gamma _*\), as \(t\rightarrow \infty \). Combining (6.3), \(\Gamma _*\succeq \Gamma ^{*c}\). But they are also impossible. Therefore, only the condition (4) in Lemma 4.3 holds.
The proof is completed. \(\square \)
Proof of Theorem 1.2
Let \(\sigma _*\) and \(\sigma ^*\) be given by Corollary 6.3.
Considering the definition of \(\sigma _*\), \(\sigma _*\notin B^*\) and \(\sigma _*\notin B_*\). Therefore, \(\Gamma _{\sigma _*}(t)\) only satisfies the condition (3) in Lemma 4.3. The result in Sect. 5 shows that \(\Gamma _{\sigma _*}(t)\rightarrow \Gamma ^*\), as \(t\rightarrow \infty \).
By Proposition 6.4, \((\sigma _*,\infty )=B^*\). Consequently, \(\sigma _*=\sigma ^*\).
The proof of Theorem 1.2 is completed. \(\square \)
References
Angenent, S.B.: Parabolic equaitons for curves on surfaces-partII. Ann. Math. 113, 171–215 (1991)
Ducrot, A., Giletti, T., Matano, H.: Existence and convergence to a propagating terrace in one-dimensional reaction-diffusion equations. Trans. Am. Math. Soc. 366, 5541–5566 (2014)
Forcadel, N., Imbert, C., Monneau, R.: Uniqueness and existence of spirals moving by forced mean curvature motion. Interfaces Free Bound. 14, 365–400 (2012)
Gage, M., Hamilton, R.S.: The heat equation shrinking convex plane curves. J. Diff. Geom. 23, 69–96 (1986)
Giga, Y., Ishimura, N., Kohsaka, Y.: Spiral solutions for a weakly anisotropic curvature flow equation. Adv. Math. Sci. Appl. 12, 393–408 (2002)
Goto, S., Nakagawa, M., Ohtsuka, T.: Uniqueness and existence of generalized motion for spiral crystal growth. Indiana Univ. Math. J. 57, 2571–2599 (2008)
Guo, J.S., Matano, H., Shimojo, M., Wu, C.H.: On a free boundary problem for the curvature flow with driving force. Arch. Ration. Mech. Anal. Volume 219(Issue 3), 1207–1272 (2016)
Grayson, M.: The heat equation shrinks emmbedded plane curves to round points. J. Diff. Geom. 26, 285–314 (1987)
Huisken, G.: Asymptotic behavior for singularities of the mean curvature flow. J. Diff. Geom. 31, 285–299 (1990)
Ladyzhenskaya, O.A., Solonnikov, V., Ural’ceva, N.: Linear and quasilinear equations of parabolic type (Translations of Mathematical Monographs). AMS, Providence (1968)
Mori, R.: A free boundary problem for a curve-shortening flow with Lipschitz initial data (to appear)
Ohtsuka, T.: A level set method for spiral crystal growth. Adv. Math. Sci. Appl. 13, 225–248 (2003)
Ohtsuka, T., Tsai, Y.-H.R., Giga, Y.: A level set approac reflecting sheet structure with single auxiliary function for evolving spirals on crystal surface. J. Sci. Comput. 62, 831–874 (2015)
Zhang, L.J.: Asymptotic behavior for curvature flow with driving force when curvature blowing up. To appear in Adv. Math. Sci. Appl
Acknowledgements
The author is grateful to Professor Matano Hiroshi for his inspiring suggestion about Grim reaper argument. He is also grateful to Professor Giga Yoshikazu for letting me know several related useful papers. The author is grateful to the anonymous referee for valuable suggestions to improve the presentation of this paper. The author is the Research Fellow of Japan Society for the Promotion of Science, Number: 17J05160. This research is supported by Japan Society for the Promotion of Science
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Rights and permissions
About this article
Cite this article
Zhang, L. Curvature flow with driving force on fixed boundary points. J Geom Anal 28, 3491–3521 (2018). https://doi.org/10.1007/s12220-017-9967-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-017-9967-0









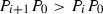 and
and  ,
,  denotes the arc length of
denotes the arc length of  , we say the sign between
, we say the sign between  , we say the sign between
, we say the sign between 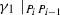 and
and 




