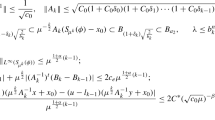Global $W^{1,p}$ estimates for solutions to the linearized Monge–Ampère equations

Abstract

In this paper, we investigate regularity for solutions to the linearized Monge–Ampère equations when the nonhomogeneous term has low integrability. We establish global $W^{1,p}$ estimates for all $p<\frac{nq}{n-q}$ for solutions to the equations with right-hand side in $L^q$ where $n/2<q\le n$. These estimates hold under natural assumptions on the domain, Monge–Ampère measures, and boundary data. Our estimates are affine invariant analogues of the global $W^{1,p}$ estimates of N. Winter for fully nonlinear, uniformly elliptic equations.

1 Introduction and statement of the main result

This paper is a sequel to [20] and is concerned with global $L^p$ estimates for the derivatives of solutions to the linearized Monge–Ampère equations. Let $\Omega \subset {\mathbb R}^n (n\ge 2)$ be a bounded convex domain and $\phi$ be a locally uniform convex function on $\Omega$. The linearized Monge–Ampère equation corresponding to $\phi$ is

$$\begin{aligned} \mathcal {L}_{\phi } u:=- \sum _{i, j=1}^{n} \Phi ^{ij} u_{ij}= f\quad \text{ in }\quad \Omega , \end{aligned}$$

(1.1)

where

$$\begin{aligned} \Phi =\big (\Phi ^{ij}\big )_{1\le i, j\le n} := (\det D^2 \phi )~ (D^2\phi )^{-1} \end{aligned}$$

is the cofactor matrix of the Hessian matrix $\displaystyle D^2\phi = (\phi _{ij})_{1\le i, j\le n}$. The operator $\mathcal {L}_\phi$ appears in several contexts including affine differential geometry [28–31], complex geometry [8], and fluid mechanics [1, 7, 23]. Because $\Phi$ is divergence free, that is, $\displaystyle \sum _{i=1}^n \partial _i \Phi ^{ij}=0$ for all j, we can also write $\mathcal {L}_{\phi }$ as a divergence form operator:

$$\begin{aligned} \mathcal {L}_{\phi } u=- \sum _{i, j=1}^{n} \partial _i \left( \Phi ^{ij} u_{j}\right) . \end{aligned}$$

We note that the Monge–Ampère equation can be viewed as a linearized Monge–Ampère equation because of the identity

$$\begin{aligned} \mathcal {L}_{\phi }\phi = - n\det D^2\phi . \end{aligned}$$

(1.2)

Caffarelli and Gutiérrez initiated the study of the linearized Monge–Ampère equations in the fundamental paper [6]. There they developed an interior Harnack inequality theory for nonnegative solutions of the homogeneous equation $\mathcal {L}_{\phi } u=0$ in terms of the pinching of the Hessian determinant

$$\begin{aligned} \lambda \le \det D^{2} \phi \le \Lambda . \end{aligned}$$

(1.3)

This theory is an affine invariant version of the classical Harnack inequality for linear, uniformly elliptic equations with measurable coefficients.

In applications such as in the contexts mentioned above, one usually encounters the linearized Monge–Ampère equations with the Monge–Ampère measure $\det D^2\phi$ satisfying (1.3). As far as Sobolev estimates for solutions are concerned, as elucidated in [15], one requires the additional assumption that $\det D^2\phi$ is continuous. Let us recall that for this latter case, $D^2\phi$ belongs to $L^p$ for all $p<\infty$ by Caffarelli’s $W^{2,p}$ estimates [4] but $D^2\phi$ is not bounded in view of Wang’s counterexamples [32]. Notice that since $\Phi$ is positive semi-definite, $\mathcal {L}_{\phi }$ is a linear elliptic partial differential operator, possibly both degenerate and singular. Despite these, we still have similar regularity results, both in the interior and at the boundary, as in the classical theory for linear, uniformly elliptic equations such as Harnack inequality, Hölder, $C^{1,\alpha }$ and $W^{2,p}$ estimates; see [6, 14–16, 20–22]. In [20], we established global $W^{2, p}$ estimates for (1.1) when the right-hand side $f\in L^q(\Omega )$ for $q>\max {\{n,p\}}$ and the Monge–Ampère measure $\det D^2\phi$ is continuous. Given this, one might wonder whether similar estimates hold when f is less integrable.

Due to the hidden nonlinear character of the linearized Monge–Ampère equations as revealed in (1.2), when the right-hand side f of (1.1) belongs to $L^q(\Omega )$ where $q<n$, we do not in general expect to get $W^{2,q}$ estimates for the solutions u, by an example of Caffarelli [2] concerning solutions of fully nonlinear, uniformly elliptic equations. However, in [26], Świech obtained surprising $W^{1,p}$-interior estimates, for all $p<\frac{nq}{n-q}$, for a large class of fully nonlinear, uniformly elliptic equations

$$\begin{aligned} F(x, u(x), Du(x), D^2u(x))= f(x) \end{aligned}$$

(1.4)

with $L^q$ right-hand side where $n-\varepsilon _0<q\le n$ and $\varepsilon _0$ depends on the ellipticity constants of the equations. This result is almost sharp in view of the Sobolev embedding $W^{2, q}\hookrightarrow W^{1, \frac{nq}{n-q}}$. It is worth mentioning that Świech’s $W^{1,p}$ estimates in the special case of fully nonlinear, uniformly elliptic equations of the form

$$\begin{aligned} F(D^2 u) =f \end{aligned}$$

(1.5)

follow from Escauriaza’s $W^{2, q}$ estimates [9] for solutions of (1.5) when $f\in L^q$ with $n-\varepsilon _0<q\le n$. Świech’s $W^{1,p}$-interior estimates were later extended up to the boundary by Winter [34].

In view of the aforementioned Hölder, $C^{1,\alpha }$ and $W^{2,p}$ estimates for solutions of (1.1), we might expect $W^{1, p}$ estimates ($p<\frac{nq}{n-q}$) for the linearized Monge–Ampère equation (1.1) and the main purpose of this paper is to confirm this expectation for a large range of q: $n/2<q\le n$. Despite the degeneracy and singularity of (1.1), that is there are no controls on the ellipticity constants, the integrability range allowed for the right-hand side of (1.1) in our main result is remarkably larger than the integrability range allowed for the right-hand side of the nonlinear, uniformly elliptic equations in the above-mentioned papers of Escauriaza’s, Świech’s, and Winter’s.

1.1 The main result

Our main result establishes global $W^{1, p}$ estimates ($p<\frac{nq}{n-q}$) for solutions to equation (1.1) with $L^{q} (n/2<q\le n$) right-hand side and $C^{1,\gamma }$ boundary values under natural assumptions on the domain, boundary data, and the Monge–Ampère measure. Precisely, we obtain:

Theorem 1.1

(Global $W^{1,p}$ estimates) Assume that there exists a small constant $\rho >0$ such that $\Omega \subset B_{1/\rho }(0)$ and for each $y\in \partial \Omega$ there is a ball $B_{\rho }(z)\subset \Omega$ that is tangent to $\partial \Omega$ at y. Let $\phi \in C^{0,1}(\overline{\Omega }) \cap C^2(\Omega )$ be a convex function satisfying

$$\begin{aligned} \det D^2 \phi =g \, \text{ in } \, \Omega \quad \quad \text{ with } \quad \lambda \le g \le \Lambda . \end{aligned}$$

Assume further that on $\partial \Omega , \phi$ separates quadratically from its tangent planes, namely

$$\begin{aligned} \rho \left| x-x_{0}\right| ^2 \le \phi (x)- \phi (x_{0})-D \phi (x_{0}) \cdot (x- x_{0}) \le \rho ^{-1}\left| x-x_{0}\right| ^2, ~\text {for all}~ x, x_{0}\in \partial \Omega .\nonumber \\ \end{aligned}$$

(1.6)

Let $u: \overline{\Omega }\rightarrow {\mathbb R}$ be a continuous function that solves the linearized Monge–Ampère equation

$$\begin{aligned} \left\{ \begin{array}{lll} \Phi ^{ij}u_{ij} ~ &{}&{}= f ~\text {in} ~ \Omega , \\ u &{}&{}= \varphi ~\text {on}~\partial \Omega , \end{array} \right. \end{aligned}$$

where $\varphi$ is a $C^{1,\gamma }$ function defined on $\partial \Omega$ $(0<\gamma \le 1)$ and $f\in L^{q}(\Omega )$ with $n/2<q\le n$. Assume in addition that $g\in C(\overline{\Omega })$. Then for any $1\le p<\frac{nq}{n-q}$, we have the following global $W^{1,p}$ estimates

$$\begin{aligned} \Vert u\Vert _{W^{1, p}(\Omega )} \le K\big ( \Vert \varphi \Vert _{C^{1,\gamma }(\partial \Omega )}+ \Vert f\Vert _{L^q(\Omega )}\big ), \end{aligned}$$

where K is a constant depending only on $n, \rho , \gamma , \lambda , \Lambda , p, q$, and the modulus of continuity of g.

We note from [25, Proposition 3.2] that the quadratic separation (1.6) holds for solutions to the Monge–Ampère equations with the right-hand side bounded away from 0 and $\infty$ on uniformly convex domains and $C^3$ boundary data. Furthermore, Theorem 1.1 complements Savin and the first author’s global $C^{1,\alpha }$ estimates [22] for Eq. (1.1) when the right-hand side f is in $L^q$ $(q>n)$. This result is an affine invariant version of Winter’s global $W^{1,p}$ estimates for fully nonlinear, uniformly elliptic equations [34].

Let us say briefly about the integrability range allowed for the right-hand side of (1.1). Notice that in [26], the exponent q was required to be close to n with the closeness depends on the ellipticity constants. Moreover, the proof of these $W^{1,p}$ estimates for equation (1.4) is rooted in a deep integrability bound of Fabes and Stroock [10] for the Green’s function of linear, uniformly elliptic operators with measurable coefficients. In a recent paper [18], the first author establishes the same global integrability of the Green’s function for the linearized Monge–Ampère operator as the Green’s function of the Laplace operator which corresponds to $\phi (x)=|x|^2/2$ (see also [12, 17, 27] for previous related interior results). Namely, under the pinching condition (1.3) and natural boundary data, the Green’s function of $\mathcal {L}_{\phi }$ is globally $L^p$-integrable for all $p<\frac{n}{n-2}$. Thus, as a degenerate and singular nondivergence form operator, $\mathcal {L}_\phi$ has the Green’s function with global $L^p-$integrability higher than that of a typical uniformly elliptic operator in nondivergence form as established in [10, Corollary 2.4]. This is the reason why we are able to prove Theorem 1.1 for a large range of q: $n/2<q\le n$.

Our strategy to proving $W^{1,p}$ estimates for solutions of (1.1) follows Caffarelli’s perturbation arguments [2, 5] (see also Wang [33]) and local boundedness and maximum principles. Even in the ideal case where $\phi (x)= |x|^2/2$ and (1.1) becomes the Poisson’s equation $\mathcal {L}_{\phi } u= - \Delta u=f$, we do not have local boundedness for solutions when f is not $L^{n/2}$ integrable. Thus the range $n/2<q\le n$ is almost optimal for our approach. However, our method does not give any information for the case $q\le n/2$.

To prove Theorem 1.1, we first establish new pointwise $C^{1,\alpha }$ estimates in the interior and at the boundary for the linearized Monge–Ampère equation (1.1) with $L^{q}(\Omega )$ $(q>n/2)$ right-hand side. These estimates, respectively, extend previous results of Gutiérrez and Nguyen [14] and of Savin and the first author [22] where the cases $q>n$ were treated. Then, we combine these pointwise estimates with the strong-type inequality for the maximal function $\mathcal {M}$ with respect to sections of $\phi$ [19, Theorem 2.7] to get the desired global $W^{1,p}$ estimates. We next indicate some more details on the proof of Theorem 1.1 after introducing several notations.

Throughout, a convex domain $\Omega$ is called normalized if $B_1(0)\subset \Omega \subset B_n(0)$. Also, the section of a convex function $\phi \in C^1(\overline{\Omega })$ at $x\in \overline{\Omega }$ with height h is defined by

$$\begin{aligned} S_\phi (x,h) = \big \{y\in \overline{\Omega }: \, \phi (y)< \phi (x) + D \phi (x)\cdot (y-x) + h\big \}. \end{aligned}$$

For fixed $\alpha \in (0, 1)$ and $r_0>0$, we denote for $z\in \overline{\Omega }$ the following quantities $N_{\phi , f, q, r}(z)$ and $N_{\phi , f, q}(z)$:

$$\begin{aligned} N_{\phi , f, q, r}(z) := r^{\frac{1-\alpha }{2}}\left( \frac{1}{|S_\phi (z, r)|}\int _{S_\phi (z, r)}{|f|^q ~\mathrm{d}x}\right) ^{\frac{1}{q}} ~\text {for}~r>0, \end{aligned}$$

(1.7)

and

$$\begin{aligned} N_{\phi , f, q}(z) :=\sup _{ r\le r_0} N_{\phi , f, q, r}(z) = \sup _{ r\le r_0} r^{\frac{1-\alpha }{2}}\left( \frac{1}{|S_\phi (z, r)|}\int _{S_\phi (z, r)}{|f|^q ~\mathrm{d}x}\right) ^{\frac{1}{q}} . \end{aligned}$$

(1.8)

We will use the letters $c, c_1, C, C_1, C', C^{*}, \theta _{*}, \bar{\theta }, ...$, etc., to denote generic constants depending only on the structural constants $n, q, \rho , \gamma , \lambda , \Lambda$ that may change from line to line. They are called universal constants.

We can assume that all functions $\phi , u$ in this paper are smooth. However, our estimates do not depend on the assumed smoothness but only on the given structural constants.

The main points of the proof of Theorem 1.1 are as follows. By the global maximum principle using the optimal integrability of the Green’s function of the operator $\mathcal {L}_{\phi }$, we have

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )} \le C \left( \Vert \varphi \Vert _{L^{\infty }(\Omega )} +\Vert f\Vert _{L^{q}(\Omega )} \right) . \end{aligned}$$

(1.9)

Let $q'\in (n/2, q)$. By applying the foregoing pointwise $C^{1,\alpha }$ estimates in the interior and at the boundary for (1.1), we obtain the following gradient bound:

$$\begin{aligned} |Du(y)|\le C\Big (\Vert u\Vert _{L^{\infty }(\Omega )} + N_{\phi , f, q'}(y)\Big )\quad \forall y\in \Omega . \end{aligned}$$

(1.10)

Note that $N(y) :=N_{\phi , f, q'}(y)$ can be $\infty$. However, using volume estimates for sections of $\phi$, we find that for $p\ge q>q'$

$$\begin{aligned} \Vert N\Vert _{L^p(\Omega )}\le C \sup _{r\le r_0} \Big \{ r^{\frac{1}{2}\big [(1-\alpha ) -\frac{ n}{q} +\frac{n}{p}\big ]} \Big \} \left( \int _{\Omega } \mathcal M(f^{q'})(y)^{\frac{q}{q'}} \mathrm{d}y\right) ^{\frac{1}{p}} \Vert f\Vert _{L^{q}(\Omega )}^{\frac{p-q}{p}}. \end{aligned}$$

We then employ the strong-type $\frac{q}{q'}-\frac{q}{q'}$ inequality for the maximal function $\mathcal M(f^{q'})$ with respect to sections of $\phi$ and, since $p<\frac{nq}{n-q}$, we can choose $0<\alpha < 1-\frac{n}{q}+ \frac{n}{p}$ to conclude that

$$\begin{aligned} \Vert N\Vert _{L^p(\Omega )} \le C \sup _{r\le r_0} \Big \{ r^{\frac{1}{2}\big [(1-\alpha ) -\frac{ n}{q} +\frac{n}{p}\big ]} \Big \} \Vert f\Vert _{L^q(\Omega )}^{\frac{q}{p}} \Vert f\Vert _{L^{q}(\Omega )}^{\frac{p-q}{p}}\le C \Vert f\Vert _{L^q(\Omega )}.\qquad \end{aligned}$$

(1.11)

By combining (1.9)–(1.11), we obtain the global $W^{1,p}$ estimate in Theorem 1.1.

1.2 Key estimates

As mentioned above, the new key estimates in the proof of Theorem 1.1 are pointwise $C^{1,\alpha }$ estimates in the interior and at the boundary for solutions to the linearized Monge–Ampère equation (1.1) with $L^q$ right-hand side where $q>n/2$.

We first state pointwise $C^{1,\alpha }$ estimates in the interior.

Theorem 1.2

(Pointwise $C^{1,\alpha }$ estimates in the interior) Assume that $q>n/2, 0\le \alpha '<\alpha <1$, and $r_0>0$. There exists $\theta =\theta (n,q,\alpha , \alpha ', r_0)>0$ such that if $\Omega$ is a normalized convex domain, $\phi \in C(\overline{\Omega })$ is a convex solution of

$$\begin{aligned} 1-\theta \le \det D^2 \phi \le 1+\theta \text { in } \Omega ,~ \text {and } \phi =0\text { on } \partial \Omega , \end{aligned}$$

then any solution $u\in W^{2,n}_{loc}(\Omega )$ of $\Phi ^{ij} u_{i j} = f$ in $\Omega$ where $f\in L^q(\Omega )$ satisfies the following pointwise $C^{1,\alpha '}$ estimate at the minimum point $\bar{z}$ of $\phi$:

$$\begin{aligned}&r^{-(1 + \alpha ')}\Vert u-l\Vert _{L^\infty (B_r(\bar{z}))} + |l(\bar{z})| +\Vert D l\Vert \le C \Big [ \Vert u\Vert _{L^\infty (\Omega )} + N_{\phi , f, q}(\bar{z})\Big ]\\&\qquad \text { for all } r\le \mu ^*, \end{aligned}$$

for some affine function l, where $C, \mu ^*$ are positive constants depending only on $n, q, \alpha , \alpha ',$ and $r_0$.

Note that, in the above theorem, $\det D^2\phi$ is only required to be close to a positive constant, but no continuity of $\det D^2\phi$ is needed. Theorem 1.2 extends a previous result of Gutiérrez and the second author [14, Theorem 4.5] from the case $q=n$ to all q satisfying $n/2<q\le n$.

The interior $W^{1,p}$ estimates for (1.1) then follow.

Theorem 1.3

(Interior $W^{1,p}$ estimates) Let $\Omega$ be a normalized convex domain and $\phi \in C(\overline{\Omega })$ be a convex solution to $\det D^2\phi =g$ in $\Omega$ and $\phi =0$ on $\partial \Omega$, where $g\in C(\Omega )$ satisfying $\lambda \le g(x)\le \Lambda$ in $\Omega$. Suppose that $u\in W^{2,n}_{loc}(\Omega )$ is a solution of $\Phi ^{ij} u_{i j} = f$ in $\Omega$ with $f\in L^q(\Omega )$ where $n/2<q\le n$. Then for any $\Omega '\Subset \Omega$ and any $p<\frac{nq }{n-q}$, we have

$$\begin{aligned} \Vert Du\Vert _{L^p(\Omega ')} \le C \Big ( \Vert u\Vert _{L^\infty (\Omega )} + \Vert f\Vert _{L^q(\Omega )} \Big ), \end{aligned}$$

(1.12)

where $C>0$ depends only on $n, p, q, \lambda , \Lambda , \text {dist}(\Omega ', \partial \Omega )$ and the modulus of continuity of g.

We next state pointwise $C^{1,\alpha }$ estimates at the boundary for solutions of (1.1) with $L^{q}$ right-hand side where $q>n/2$ and $C^{1,\gamma }$ boundary data under the local assumptions (1.13)–(1.16) introduced below. These estimates generalize previous results of Savin and the first author in [21, 22] where the cases $q=\infty$ and $q>n$, respectively, were treated.

Let $\Omega \subset {\mathbb R}^{n}$ be a bounded convex set with

$$\begin{aligned} B_\rho (\rho e_n) \subset \, \Omega \, \subset \{x_n \ge 0\} \cap B_{\frac{1}{\rho }} (0), \end{aligned}$$

(1.13)

for some small $\rho >0$ where we denote $e_n:= (0,\dots , 0, 1)\in {\mathbb R}^n$. Assume that

$$\begin{aligned} \text {for each } y\in \partial \Omega \cap B_\rho (0), ~\text {there is a ball } B_{\rho }(z)\subset \Omega \text { that is tangent to } \partial \Omega \text { at } y. \nonumber \\ \end{aligned}$$

(1.14)

Let $\phi \in C^{0,1}(\overline{\Omega }) \cap C^2(\Omega )$ be a convex function satisfying

$$\begin{aligned} 0 <\lambda \le \det D^2\phi \le \Lambda \quad \text {in }\Omega . \end{aligned}$$

(1.15)

We assume that on $\partial \Omega \cap B_\rho (0), \phi$ separates quadratically from its tangent planes on $\partial \Omega$. Precisely we assume that if $x_0 \in \partial \Omega \cap B_\rho (0)$ then

$$\begin{aligned} \rho \left| x-x_{0}\right| ^2 \le \phi (x)- \phi (x_{0})-D\phi (x_{0}) \cdot (x- x_{0}) \le \rho ^{-1}\left| x-x_{0}\right| ^2\quad \text { for all } x \in \partial \Omega . \nonumber \\ \end{aligned}$$

(1.16)

Theorem 1.4

Assume that $\phi$ and $\Omega$ satisfy assumptions (1.13)–(1.16). Let $u: B_{\rho }(0)\cap \overline{\Omega }\rightarrow {\mathbb R}$ be a continuous solution to

$$\begin{aligned} \left\{ \begin{array}{lll} \Phi ^{ij}u_{ij} ~&{} = f &{}\text {in} ~ B_{\rho }(0)\cap \Omega , \\ u &{}= \varphi &{} \text {on}~\partial \Omega \cap B_{\rho }(0), \end{array} \right. \end{aligned}$$

where $f\in L^{q}(B_{\rho }(0)\cap \Omega )$ for some $q>n/2$ and $\varphi \in C^{1,\gamma }(B_{\rho }(0)\cap \partial \Omega )$. Then there exist $\alpha \in (0, 1)$ and $\theta$ small depending only on $n, q, \rho , \lambda , \Lambda , \gamma$ such that for all $\bar{h}\le \theta ^2$, we can find $b\in {\mathbb R}^n$ satisfying

$$\begin{aligned}&\bar{h}^{-\frac{1+\alpha }{2}}\Vert u- u(0)-bx\Vert _{L^{\infty }(S_{\phi }(0, \bar{h}))} + \Vert b\Vert \\&\quad \le C \Big [\Vert u\Vert _{L^{\infty }(B_{\rho }(0)\cap \Omega )} + \Vert \varphi \Vert _{C^{1,\gamma }(B_{\rho }(0)\cap \partial \Omega )} + \sup _{ \bar{h}\le t\le \theta ^2} N_{\phi , f, q, 2\theta ^{-1} t}(0)\Big ], \end{aligned}$$

where C depends only on $n, q, \rho , \lambda , \Lambda$, and $\gamma$. We can take $\alpha \in (0, \min \{\alpha _0, \gamma \}),$ where $\alpha _0$ is the exponent in the boundary Hölder gradient estimates, Theorem 4.1.

In proving global $W^{1,p}$ estimates for solutions of (1.1), we will use new maximum principles, in the interior and at the boundary, for the linearized Monge–Ampère equation (1.1) with $L^q$ right-hand side where q is only assumed to satisfy $q>n/2$. We state here a global maximum principle and refer to Lemmas 2.1 and 4.2 for the interior and boundary maximum principles used in the paper.

Lemma 1.5

(Global maximum principle) Assume that $\Omega$ and $\phi$ satisfy the hypotheses of Theorem 1.1 up to (1.6). Let $f\in L^q(\Omega )$ for some $q>n/2$ and $u\in W^{2,n}_{loc}(\Omega )\cap C(\overline{\Omega })$ satisfy

$$\begin{aligned} \mathcal {L}_{\phi } u\le f\quad \text{ almost } \text{ everywhere } \text{ in }\quad \Omega . \end{aligned}$$

Then there exists a constant $C>0$ depending only on $n, \lambda , \Lambda , \rho$, and q such that

$$\begin{aligned} \sup _{\Omega }{u} \le \sup _{\partial \Omega }{u^+} + C |\Omega |^{\frac{2}{n} -\frac{1}{q}} \Vert f\Vert _{L^q(\Omega )}. \end{aligned}$$

We will also use the following global strong-type estimates for the maximal function $\mathcal {M}$ with respect to sections of the potential function $\phi$.

Theorem 1.6

(Strong-type p–p estimates, [19, Theorem 2.7]) Assume that $\Omega$ and $\phi$ satisfy the hypotheses of Theorem 1.1 up to (1.6). For $f\in L^1(\Omega )$, define

$$\begin{aligned} \mathcal M (f)(x)=\sup _{t>0} \dfrac{1}{|S_\phi (x,t)|}\int _{S_\phi (x,t)}|f(y)|\, \mathrm{d}y\quad \text { for all } x\in \Omega . \end{aligned}$$

Then, for any $1<p<\infty$, there exists $C_p>0$ depending on $p, \rho , \lambda , \Lambda$, and n such that

$$\begin{aligned} \Vert \mathcal {M}(f)\Vert _{L^{p}(\Omega )}\le C_p\, \Vert f\Vert _{L^{p}(\Omega )}. \end{aligned}$$

Note that our new maximum principles in Lemmas 2.1 and 4.2 allow us to establish global Hölder continuity estimates for solutions to the linearized Monge–Ampère equation (1.1) with $L^q$ right-hand side where q is only assumed to satisfy $q>n/2$. These estimates in turn extend our previous results, [16, Theorem 1.4] and [20, Theorem 4.1], where the cases of $L^n$ right-hand side were treated.

Theorem 1.7

(Global Hölder estimates) Assume $\Omega$ and $\phi$ satisfy (1.13)–(1.16). Let $u \in C\big (B_{\rho }(0)\cap \overline{\Omega }\big ) \cap W^{2,n}_{loc}(B_{\rho }(0)\cap \Omega )$ be a solution to

$$\begin{aligned} \left\{ \begin{array}{lll} \Phi ^{ij}u_{ij} ~&{} = f ~&{}\text { in } ~ B_{\rho }(0)\cap \Omega , \\ u &{}= \varphi ~&{}\text { on }~\partial \Omega \cap B_{\rho }(0), \end{array} \right. \end{aligned}$$

where $\varphi \in C^{\alpha }(\partial \Omega \cap B_{\rho }(0))$ for some $\alpha \in (0,1)$ and $f\in L^q(\Omega \cap B_\rho (0))$. Then for any $q>n/2$, there exist constants $\beta , C >0$ depending only on $\lambda , \Lambda , n, \alpha , q$, and $\rho$ such that

$$\begin{aligned}&|u(x)-u(y)|\le C|x-y|^{\beta }\Big ( \Vert u\Vert _{L^{\infty }(\Omega \cap B_{\rho }(0))} + \Vert \varphi \Vert _{C^\alpha (\partial \Omega \cap B_{\rho }(0))} + \Vert f\Vert _{L^q(\Omega \cap B_{\rho }(0))} \Big )\\&\qquad ~\text {for all }x, y\in \Omega \cap B_{\frac{\rho }{2}}(0). \end{aligned}$$

The rest of the paper is organized as follows. In Sect. 2, we establish an interior maximum principle, an interior Hölder estimate, and a comparison estimate for the linearized Monge–Ampère equations with $L^q$ right-hand side. We prove Theorems 1.2 and 1.3 in Sect. 3. The proofs of Theorem 1.4 and Lemma 1.5 will be given in Sect. 4. In the final Sect. 5, we prove Theorems 1.1 and 1.7.

2 Interior maximum principle and Hölder estimates

In this section, we prove an interior maximum principle (Lemma 2.1), an interior Hölder estimate (Corollary 2.4), and a comparison estimate (Lemma 2.5) for the linearized Monge–Ampère equation with $L^q$ right-hand side where q is only assumed to satisfy $q>n/2$. These results will be used in Sect. 3 to prove interior $W^{1,p}$ estimates.

For convenience, we introduce the following hypothesis:

$(\mathbf{H})$ $\Omega$ is a normalized convex domain and $\phi \in C(\overline{\Omega })$ is a convex function such that

$$\begin{aligned} \lambda \le \text {det} D^2\phi \le \Lambda \text{ in } \Omega \quad \text{ and } \quad \phi =0 \text{ on } \partial \Omega . \end{aligned}$$

Given $0<\alpha < 1$, and $\Omega$ and $\phi$ satisfying (H), we define the sections of $\phi$ at its minimum point $\bar{z}$ to be the sets

$$\begin{aligned} \Omega _{\alpha }\equiv \Omega _{\alpha ,\phi }:=S_\phi \left( \bar{z}, -\alpha \min _{\Omega }\phi \right) =\Big \{x\in \overline{\Omega }:\, \phi (x)<(1-\alpha )\,\min _{\Omega }\phi \Big \}. \end{aligned}$$

We record here how the linearized Monge–Ampère equation (1.1) transforms under rescaling. If $Tx= Ax + z$ is an affine transformation where A is an $n\times n$ invertible matrix and $z\in {\mathbb R}^n$, and

$$\begin{aligned} \tilde{\phi }(x)= \frac{1}{a}\phi (Tx), \quad \quad \tilde{u}(x) = \frac{1}{b}u(Tx), \end{aligned}$$

then from (1.1), we find

$$\begin{aligned} \mathcal {L}_{\tilde{\phi }} \tilde{u}(x) = \frac{1}{a^{n-1}b} (\det A)^{2} f(Tx). \end{aligned}$$

(2.1)

Indeed, we can compute

$$\begin{aligned} D^{2}\tilde{\phi }= \frac{1}{a}A^{t} D^{2} \phi A, \quad D^{2}\tilde{u}= \frac{1}{b}A^{t} D^{2} u A, \end{aligned}$$

and the cofactor matrix $\tilde{\Phi }=(\det D^{2}\tilde{\phi }) ( D^{2}\tilde{\phi })^{-1}$ of $D^2\tilde{\phi }$ is

$$\begin{aligned} \tilde{\Phi } =\frac{1}{a^{n-1}}(\det A)^2 (\det D^{2} \phi ) \, A^{-1} (D^{2} \phi )^{-1} (A^{-1})^{t}=\frac{1}{a^{n-1}}(\det A)^2 A^{-1} \Phi (A^{-1})^{t}. \end{aligned}$$

Thus (2.1) easily follows from

$$\begin{aligned} \mathcal {L}_{\tilde{\phi }} \tilde{u}(x)= & {} -\text {trace} (\tilde{\Phi }D^2 \tilde{u})= -\frac{1}{a^{n-1}b} (\det A)^{2}\text {trace} ( \Phi D^2 u (Tx))\\= & {} \frac{1}{a^{n-1}b} (\det A)^{2} f(Tx). \end{aligned}$$

2.1 Interior estimates

Lemma 2.1

(Interior maximum principle) Assume that $\Omega$ and $\phi$ satisfy (H). Let $V\subset \Omega$ be a subdomain, $f\in L^q(V)$ for some $q>n/2$, and $u\in W^{2,n}_{loc}(V)\cap C(\overline{V})$ satisfy

$$\begin{aligned} \mathcal {L}_{\phi } u\le f\quad \text{ almost } \text{ everywhere } \text{ in }\quad V. \end{aligned}$$

Then for any $\alpha \in (0, 1)$, there exists a constant $C>0$ depending only on $\alpha , n, \lambda , \Lambda$, and q such that

$$\begin{aligned} \sup _{V\cap \Omega _\alpha }{u} \le \sup _{\partial V}{u^+} + C |V|^{\frac{2}{n} -\frac{1}{q}} \Vert f\Vert _{L^q(V)}. \end{aligned}$$

Proof

Let $G_V(x,y)$ be the Green’s function of $\mathcal {L}_{\phi }$ in V with pole $y\in V$, namely $G_V(\cdot , y)$ is a positive solution of

$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {L}_{\phi } G_V( \cdot , y) &{}=\delta _y \qquad \text{ in }\quad V,\\ G_V( \cdot , y) &{}=0\ \ \ \ \ \ \ \text{ on }\quad \partial V \end{array}\right. \end{aligned}$$

with $\delta _y$ denoting the Dirac measure giving unit mass to the point y. Define

$$\begin{aligned} v(x) := \int _{V} G_V(x,y) f(y)\, \mathrm{d}y \quad \text{ for }\quad x\in V. \end{aligned}$$

Then v is a solution of

$$\begin{aligned} \mathcal {L}_{\phi } v =f \text{ in } V,~\text {and}~ v =0 \text{ on } \partial V. \end{aligned}$$

Since $\mathcal {L}_{\phi }(u-v)\le 0$ in V, we obtain from the Aleksandrov–Bakelman–Pucci (ABP) maximum principle (see [11, Theorem 9.1]) that

$$\begin{aligned} u(x) \le \sup _{\partial V}{u^+} + v(x)\quad \text{ in } \quad V. \end{aligned}$$

(2.2)

We next estimate v(x) for the case $n\ge 3$ using [27, Lemma 3.3]. The case $n=2$ is treated similarly, using [17, Theorem 1.1]. Notice that Aleksandrov’s estimate (see [13, Theorem 1.4.2]) implies that $\text {dist}(\Omega _\alpha , \partial \Omega )\ge c(n,\lambda ,\Lambda ) (1-\alpha )^n>0$. It follows from this and the proof of [27, Lemma 3.3] that there exists a constant $K>0$ depending on $\alpha , n, \lambda$, and $\Lambda$ such that for every $y\in V\cap \Omega _\alpha$ we have

$$\begin{aligned} |\{x\in V: ~ G_V(x,y)>t\}|\le K t^{-\frac{n}{n-2}}\quad \text{ for }\quad t>0. \end{aligned}$$

(2.3)

As the operator $\mathcal {L}_\phi$ can be written in the divergence form with symmetric coefficient, we infer from [12, Theorem 1.3] that $G_V(x,y)=G_V(y,x)$ for all $x,y\in V$. This together with (2.3) allows us to deduce that for every $x\in V \cap \Omega _\alpha$, there holds

$$\begin{aligned} |\{y\in V: ~ G_V(x,y)>t\}| =|\{y\in V: ~ G_V(y,x)>t\}| \le K t^{-\frac{n}{n-2}}\quad \text{ for }\quad t>0. \end{aligned}$$

It follows that if $q>\frac{n}{2}$, then $q':= \frac{q}{q-1}<\frac{n}{n-2}$ and from the layer cake representation, we have

$$\begin{aligned} \int _{V}{G_V(x,y)^{q'}~\mathrm{d}y}&= q' \int _0^\infty t^{q' -1}|\{y\in V: ~ G_V(x,y)>t\}| \, \mathrm{d}t\\&\le q' |V| \int _0^\epsilon t^{q' -1} \, \mathrm{d}t + q'K \int _\epsilon ^\infty t^{q' -1-\frac{n}{n-2}} \, \mathrm{d}t\\&= |V| \epsilon ^{q'} + C_1 \epsilon ^{q'- \frac{n}{n-2}} \text { for all} ~\epsilon >0. \end{aligned}$$

By choosing $\epsilon = \big (\frac{C_1}{|V|}\big )^{\frac{n-2}{n}}$ in the above right-hand side, we obtain

$$\begin{aligned} \sup _{x\in V \cap \Omega _\alpha }\int _{V}{G_V(x,y)^{q'}~\mathrm{d}y} \le 2C_1^{\frac{n-2}{n} q'} |V|^{1- \frac{n-2}{n} q'}. \end{aligned}$$

We deduce from the definition of v, Hölder inequality and the above estimate for $G_V$ that

$$\begin{aligned} |v(x)|&\le \Vert G_V(x,\cdot )\Vert _{L^{q'}(V)}\Vert f\Vert _{L^q(V)}\\&\le 2C_1^{\frac{n-2}{n}} |V|^{\frac{1}{q'}- \frac{n-2}{n} } \Vert f\Vert _{L^q(V)}\quad \text {for all } x\in V \cap \Omega _\alpha . \end{aligned}$$

This estimate and (2.2) yield the conclusion of the lemma.

By employing Lemma 2.1 and the interior Harnack inequality established in [6] for nonnegative solutions to the homogeneous linearized Monge–Ampère equations, we get:

Lemma 2.2

(Harnack inequality) Assume that $\Omega$ and $\phi$ satisfy (H). Let $f\in L^q(\Omega )$ for some $q>n/2$ and $u\in W^{2,n}_{loc}(\Omega )$ satisfy $\mathcal {L}_{\phi } u= f$ almost everywhere in $\Omega$. Then if $S_\phi (x, t)\Subset \Omega$ and $u\ge 0$ in $S_\phi (x, t)$, we have

$$\begin{aligned} \sup _{S_\phi \left( x, \frac{t}{2}\right) }{u} \le C\left( \inf _{S_\phi \left( x, \frac{t}{2}\right) }{u} + |S_\phi (x,t)|^{\frac{2}{n} -\frac{1}{q}} \, \Vert f\Vert _{L^q(S_\phi (x, t))}\right) , \end{aligned}$$

(2.4)

where $C>0$ depends only on $n, \lambda , \Lambda$, and q.

Proof

For convenience, let us write $S_h$ for the section $S_\phi (x, h)$. Let $u_0$ be the solution of

$$\begin{aligned} \mathcal {L}_{\phi } u_0 =f~\text { in }S_t,~\text {and}~ u_0 =0~\text { on } \partial S_t. \end{aligned}$$

Then $\mathcal {L}_{\phi } (u-u_0)=0$ in $S_t$ and $u-u_0\ge 0$ on $\partial S_t$. Thus we conclude from the ABP maximum principle that $u-u_0\ge 0$ in $S_t$. Hence, we can apply the interior Harnack inequality established in [6, Theorem 5] to obtain

$$\begin{aligned} \sup _{S_{\frac{t}{2}}} (u- u_0) \le C \inf _{S_{\frac{t}{2}}} (u- u_0), \end{aligned}$$

for some constant C depending only on $n, \lambda ,$ and $\Lambda$, which then implies

$$\begin{aligned} \sup _{S_{\frac{t}{2}}} u \le C'\Big ( \inf _{S_{\frac{t}{2}}} u + \sup _{S_{\frac{t}{2}}} |u_0|\Big ). \end{aligned}$$

By normalizing the section $S_t, \phi , u_0$ and applying Lemma 2.1 for $\alpha =1/2$, we get

$$\begin{aligned} \sup _{S_{\frac{t}{2}}}{|u_0|} \le C |S_t|^{\frac{2}{n} -\frac{1}{q}} \Vert f\Vert _{L^q(S_t)}. \end{aligned}$$

(2.5)

Therefore, estimate (2.4) follows as desired.

For reader’s convenience, we include the details of (2.5). By subtracting a linear function from $\phi$, we can assume that $\phi (x)=0$ and $D\phi (x)=0$. By John’s lemma, there is an affine transformation $Ty= Ay + z$ such that

$$\begin{aligned} B_1(0)\subset \tilde{\Omega }:= T^{-1} S_\phi (x,t) \subset B_n(0), \end{aligned}$$

(2.6)

where A is an $n\times n$ invertible matrix and $z\in {\mathbb R}^n$. Rescale $\phi$ and $u_0$ by

$$\begin{aligned} \tilde{\phi }(y)= \frac{1}{|\det A|^{2/n}} [\phi (Ty)-t],~\tilde{u}_0 (y) = u_0 (Ty),\quad y\in \tilde{\Omega }. \end{aligned}$$

Then $\tilde{\Omega }$ and $\tilde{\phi }$ satisfy (H). Moreover, using (2.1) with $a=|\det A|^{2/n}$ and $b=1$, we find

$$\begin{aligned} \mathcal {L}_{\tilde{\phi }}\tilde{u}_0(y)= |\det A|^{2/n} f(Ty):= \tilde{f}(y)~\text {in}~\tilde{\Omega }~ \text { with } ~\tilde{u}_0=0~ \text {on}~ \partial \tilde{\Omega }. \end{aligned}$$

Therefore, we can apply Lemma 2.1 for $V=\tilde{\Omega }$ and $\alpha =1/2$ to get

$$\begin{aligned} \sup _{y\in \tilde{\Omega }_{\frac{1}{2},\tilde{\phi }}} |\tilde{u}_0(y)| \le C(n,\lambda ,\Lambda , q) |\tilde{\Omega }|^{\frac{2}{n}-\frac{1}{q}} \Vert \tilde{f}\Vert _{L^q(\tilde{\Omega })}. \end{aligned}$$

(2.7)

Since

$$\begin{aligned} \Vert \tilde{f}\Vert _{L^q(\tilde{\Omega })} = |\det A|^{\frac{2}{n}-\frac{1}{q}} \Vert f\Vert _{L^q (S_\phi (x, t))}, \end{aligned}$$

and by (2.6),

$$\begin{aligned} C_1^{-1}(n) |S_\phi (x, t)|\le |\det A|\le C_1(n) |S_\phi (x, t)|, \end{aligned}$$

we find from (2.7) that

$$\begin{aligned} \sup _{ S_\phi (x, t)} |u_0|=\sup _{y\in \tilde{\Omega }_{\frac{1}{2},\tilde{\phi }}} |\tilde{u}_0(y)| \le C(n,\lambda ,\Lambda , q)|S_\phi (x, t)|^{\frac{2}{n}-\frac{1}{q}}\Vert f\Vert _{L^q (S_\phi (x, t))}. \end{aligned}$$

This proves (2.5), completing the proof of the lemma.

As a consequence of Lemma 2.2, we obtain the following oscillation estimate:

Corollary 2.3

Assume that $\Omega$ and $\phi$ satisfy (H). Let $f\in L^q(\Omega )$ for some $q>n/2$ and $u\in W^{2,n}_{loc}(\Omega )$ satisfy $\mathcal {L}_{\phi } u= f$ almost everywhere in $\Omega$. Then for any section $S_\phi (x, h)\Subset \Omega$, we have

$$\begin{aligned} \text {osc}_{S_\phi (x,\rho )}{u} \le C\left( \frac{\rho }{h}\right) ^\alpha \Big [ \text {osc}_{S_\phi (x,h)}{u} + h^{1 -\frac{n}{2 q}} \, \Vert f\Vert _{L^q(S_\phi (x, h))}\Big ]\quad \text{ for } \text{ all }\quad \rho \le h, \end{aligned}$$

where $\displaystyle \text {osc}_E u :=\sup _{E} u -\inf _{E} u$ and the constants $C,\,\alpha >0$ depend only on $n, \lambda , \Lambda$, and q.

Proof

Let us write $S_t$ for the section $S_\phi (x, t)$. Then, by [13, Corollary 3.2.4], there exist constants C and $C'$ depending only on $n,\lambda ,\Lambda$ such that the volume of interior sections of $\phi$ satisfies

$$\begin{aligned} C t^{n/2}\le |S_t|\le C' t^{n/2}~ \text {whenever}~ S_t\Subset \Omega . \end{aligned}$$

Set

$$\begin{aligned} m(t) := \inf _{S_t} u,\quad M(t) :=\sup _{S_t} u,\quad \text{ and } \quad \omega (t) := M(t) -m(t). \end{aligned}$$

Let $\rho \in (0, h]$ be arbitrary. Then since $\tilde{u} := u - m(\rho )$ is a nonnegative solution of $\mathcal {L}_{\phi } \tilde{u}= f$ in $S_\rho$, we can apply Lemma 2.2 for $\tilde{u}$ and the volume growth of interior sections of $\phi$ to obtain

$$\begin{aligned} \frac{1}{C} \sup _{S_{\frac{\rho }{2}}}\tilde{u}\le \inf _{S_{\frac{\rho }{2}}}\tilde{u} +\rho ^{1 -\frac{n}{2 q}} \, \Vert f\Vert _{L^q(S_\rho )}. \end{aligned}$$

It follows that for all $\rho \in (0, h]$, we have

$$\begin{aligned} \omega \left( \frac{\rho }{2}\right)&= \sup _{S_{\frac{\rho }{2}}}\tilde{u}- \inf _{S_{\frac{\rho }{2}}}\tilde{u}\le \big (1- \frac{1}{C}\big )\sup _{S_{\frac{\rho }{2}}}\tilde{u} +\rho ^{1 -\frac{n}{2 q}} \, \Vert f\Vert _{L^q(S_\rho )}\\&\le \big (1- \frac{1}{C}\big )\omega (\rho ) +\rho ^{1 -\frac{n}{2 q}} \, \Vert f\Vert _{L^q(S_h)}. \end{aligned}$$

Thus, by the standard iteration we deduce that

$$\begin{aligned} \omega (\rho ) \le C'\big (\frac{\rho }{h}\big )^\alpha \Big [ \omega (h) +h^{1 -\frac{n}{2 q}} \, \Vert f\Vert _{L^q(S_h)}\Big ], \end{aligned}$$

giving the conclusion of the corollary.

Corollary 2.3 implies Hölder estimate. Indeed, from the arguments in [6, pp. 456-457], we have

$$\begin{aligned}&|u(x)-u(y)| \le C \Vert A\Vert ^\beta |x-y|^\beta \Big [ \Vert u\Vert _{L^\infty (S_\phi (x_0, 2h))} + (2h)^{1-\frac{n}{2 q}}\Vert f\Vert _{L^q(S_\phi (x_0, 2h))}\Big ] \\&\qquad \text {for all } x,y\in S_\phi (x_0, h), \end{aligned}$$

where C is a universal constant and $Tx= A(x-x_0) +y_0$ is the affine transformation normalizing $S_\phi (x_0, 2\theta h)$, i.e., $B_1(0) \subset T\big (S_\phi (x_0, 2\theta h) \big )\subset B_n(0)$ ($\theta =\theta (n,\lambda ,\Lambda )>1$ is the engulfing constant). But when $\Omega$ is normalized, we have from [13, Theorem 3.3.8] the inclusion $B_{c_1 h}( x_0) \subset S_\phi (x_0, h).$ Therefore $A B_{c_1 h}(0) + y_0 \subset B_n(0)$ and hence $\Vert A\Vert \le C h^{-1}$. Consequently,

$$\begin{aligned}&|u(x)-u(y)| \le C^* h^{-\beta } |x-y|^\beta \Big [ \Vert u\Vert _{L^\infty (S_\phi (x_0, 2h))} + (2h)^{1-\frac{n}{2q}}\Vert f\Vert _{L^q(S_\phi (x_0, 2h))}\Big ] \\&\qquad \text {for all } x,y\in S_\phi (x_0, h), \end{aligned}$$

where $C^*$ is a universal constant. From this, we deduce the next result.

Corollary 2.4

(Interior Hölder estimate) Assume that $\Omega$ and $\phi$ satisfy $(\mathbf{H})$. Let $f\in L^q(B_1(0))$ for some $q>n/2$ and $u\in W^{2,n}_{loc}(B_1(0))$ be a solution of $\mathcal {L}_{\phi } u= f$ in $B_1(0)$. Then there exist constants $\beta \in (0,1)$ and $C>0$ depending only on $n, \lambda , \Lambda , q$ such that

$$\begin{aligned} |u(x) - u(y)|\le C |x-y|^\beta \Big ( \Vert u\Vert _{L^\infty (B_1(0))} +\Vert f\Vert _{L^q(B_1(0))}\Big )\quad \text {for all } x,y\in B_{\frac{1}{2}}(0). \end{aligned}$$

2.2 Comparison and stability estimates

The following lemma allows us to compare explicitly two solutions originating from two different linearized Monge–Ampère equations.

Lemma 2.5

Let U be a normalized convex domain. Assume that $\phi , w\in C(\overline{U})$ are convex functions satisfying $\frac{1}{2} \le \det D^2 \phi \le \frac{3}{2}, \det D^2 w =1$ in U and $\phi = w =0$ on $\partial U$. Let $\Phi = (\Phi ^{ij})$ and ${\mathrm W}= (W^{ij})$ be the cofactor matrices of $D^2\phi$ and $D^2w$, respectively. Denote $U_{\alpha }= U_{\alpha , \phi }$ for $0<\alpha <1$. Assume that $u\in W^{2,n}_{loc}(U)\cap C(\overline{U})$ satisfies $\Phi ^{i j} D_{i j}u = f$ in U with $|u|\le 1$ in U and $f\in L^q(U)$ $(q>n/2)$. Assume $0<\alpha _1<1$ and $h\in W^{2,n}_{loc}(U_{\alpha _1})\cap C(\overline{U}_{\alpha _1})$ is a solution of

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathrm W}^{i j} D_{i j}h &{}= 0 \quad \text{ in } \quad U_{\alpha _1}\\ h &{}=u\quad \text{ on } \quad \partial U_{\alpha _1}. \end{array}\right. \end{aligned}$$

(2.8)

Then, there exists $\gamma \in (0,1)$ depending only on n and q such that for any $0<\alpha _2<\alpha _1$ we have

$$\begin{aligned}&\Vert u-h\Vert _{ L^\infty (U_{\alpha _2})} +\Vert f-\text {trace}([\Phi -{\mathrm W}]D^2h)\Vert _{L^q(U_{\alpha _2})} \\&\qquad \le C(\alpha _1,\alpha _2,n,q) \left\{ \Vert \Phi - {\mathrm W}\Vert _{L^q(U_{\alpha _1})}^\gamma + \Vert f\Vert _{L^q(U)} \right\} \end{aligned}$$

provided that $\Vert \Phi - {\mathrm W}\Vert _{L^q(U_{\alpha _1})} \le (\alpha _1 -\alpha _2)^{\frac{2n}{1+ (n-1)\gamma }}$.

Lemma 2.5 is an extension of [15, Lemma 4.1]. Its proof is omitted since it is similar to that of [15, Lemma 4.1]. Instead of using the ABP estimate and interior Hölder estimate for equation (1.1) with $L^n$ right-hand side as in [15], we use Lemma 2.1 and Corollary 2.4 for the linearized Monge–Ampère equation with $L^q$ right-hand side.

We close this section by a result about the stability of cofactor matrices, which is a consequence of [14, Lemma 3.5] and [20, Proposition 3.14].

Lemma 2.6

Let $\Omega$ be a normalized convex domain. Let $\phi , w\in C(\overline{\Omega })$ be convex functions satisfying

$$\begin{aligned} 1-\theta \le \det D^2 \phi \le 1+\theta ~\text {in}~\Omega ,~ \det D^2 w= 1~\text {in}~\Omega ~\text {and }\phi =w=0 \text { on } \partial \Omega . \end{aligned}$$

Then for any $q\ge 1$, there exist $\theta _0>0$ and $C>0$ depending only on q and n such that

$$\begin{aligned} \Vert \Phi - {\mathrm W}\Vert _{L^q(B_\frac{1}{2}(0))} \le C \theta ^{\frac{(n-1)\delta }{n(2nq-\delta )}}\quad \text{ for } \text{ all } \theta \le \theta _0, \end{aligned}$$

where $\delta =\delta (n)>0$, and $\Phi , {\mathrm W}$ are the matrices of cofactors of $D^2\phi$ and $D^2 w$, respectively.

3 Pointwise $C^{1,\alpha }$ estimates in the interior and interior $W^{1,p}$ estimates

In this section, we sketch the proof of Theorem 1.2 and then use it to prove Theorem 1.3.

For the proof of Theorem 1.2, we need the next two lemmas from [14] about geometric properties of sections of solutions to the Monge–Ampère equation. For a strictly convex function $\phi$ defined on $\Omega$ and $t>0$, we denote by $S_t(\phi )$ the section of $\phi$ centered at its minimum point with height t, i.e.,

$$\begin{aligned} S_t(\phi ):= \left\{ x\in \Omega : \phi (x) \le \min _{\Omega } \phi + t\right\} . \end{aligned}$$

We denote by I the identity matrix.

Lemma 3.1

[14, Lemma 3.2] Suppose $B_1(0)\subset \Omega \subset B_n(0)$ is a normalized convex domain. Then there exist universal constants $\mu _0>0, \tau _0>0$ and a positive definite matrix $M= A^t A$ and $p\in {\mathbb R}^n$ satisfying

$$\begin{aligned} \det M=1,\quad 0<c_1I\le M\le c_2I,\quad \text {and}\quad |p|\le c, \end{aligned}$$

such that if $\phi \in C(\overline{\Omega })$ is a strictly convex function in $\Omega$ with

$$\begin{aligned} 1-\varepsilon \le \det D^2 \phi \le 1+\varepsilon ~\text {in}~\Omega ,~\text {and }\phi =0 \text { on } \partial \Omega , \end{aligned}$$

then for $0<\mu \le \mu _0$ and $\varepsilon \le \tau _0 \mu ^2$, we have

$$\begin{aligned} B_{\left( 1-C\left( \mu ^{1/2} + \mu ^{-1}\varepsilon ^{1/2}\right) \right) \sqrt{2}} (0)\subset \mu ^{-1/2}TS_\mu (\phi )\subset B_{\left( 1+C\left( \mu ^{1/2} + \mu ^{-1}\varepsilon ^{1/2}\right) \right) \sqrt{2}} (0), \end{aligned}$$

and

$$\begin{aligned}&\left| \phi (x)- \Big [\phi (x_0) + p\cdot (x-x_0) +\frac{1}{2}\langle M(x-x_0), (x-x_0)\rangle \Big ]\right| \\&\quad \le C(\mu ^{3/2}+\varepsilon )~\text {in}~S_\mu (\phi ), \end{aligned}$$

where $x_0\in \Omega$ is the minimum point of $\phi$ and $Tx:= A(x-x_0)$.

Lemma 3.2

[14, Lemma 3.3] Suppose $B_{(1-\sigma )\sqrt{2}}(0)\subset \Omega \subset B_{(1+\sigma )\sqrt{2}}(0)$ is a convex domain where $0<\sigma \le 1/4$. Then there exist universal constants $\mu _0>0, \tau _0>0$ which are independent of $\sigma$, a positive definite matrix $M= A^t A$, and $p\in {\mathbb R}^n$ with

$$\begin{aligned} \det M=1,\quad (1-C\sigma )I\le M\le (1+ C\sigma )I,\quad \text {and} \quad |p-x_0|\le C\sigma , \end{aligned}$$

such that if $\phi \in C(\overline{\Omega })$ is a strictly convex function in $\Omega$ with

$$\begin{aligned} 1-\varepsilon \le \det D^2 \phi \le 1+\varepsilon ~\text {in}~\Omega ,~\text {and }\phi =0 \text { on } \partial \Omega , \end{aligned}$$

then for $0<\mu \le \mu _0$ and $\varepsilon \le \tau _0 \mu ^2$, we have

$$\begin{aligned} B_{\left( 1-C(\sigma \mu ^{1/2} + \mu ^{-1}\varepsilon ^{1/2})\right) \sqrt{2}} (0)\subset \mu ^{-1/2}TS_\mu (\phi )\subset B_{\left( 1+C(\sigma \mu ^{1/2} + \mu ^{-1}\varepsilon ^{1/2})\right) \sqrt{2}} (0), \end{aligned}$$

and

$$\begin{aligned}&\left| \phi (x)- \Big [\phi (x_0) + p\cdot (x-x_0) +\frac{1}{2}\langle M(x-x_0), (x-x_0)\rangle \Big ]\right| \\&\quad \le C(\sigma \mu ^{3/2}+\varepsilon )~\text {in}~S_\mu (\phi ), \end{aligned}$$

where $x_0\in \Omega$ is the minimum point of $\phi$ and $Tx:= A(x-x_0)$.

We also use the following classical Pogorelov’s estimates [13, formula (4.2.6)], and interior $C^{1,1}$ estimates for linear, uniformly elliptic equations [11, Theorem 6.2]; see also the proof of [14, Lemma 3.2] and [14, Theorem 2.7].

Lemma 3.3

Suppose $B_1(0)\subset \Omega \subset B_n(0)$ is a normalized convex domain. Let w be the convex solution to the equation $\det D^2 w=1$ in $\Omega$ with $w=0$ on $\partial \Omega$.

• (i) Let $x_1\in \Omega$ be the minimum point of w. Then $|w(x_1)|\sim c_n$ for some universal constant $c_n$ and we have the Pogorelov’s estimates

  $$\begin{aligned} \frac{2}{C_2^2} I\le D^2 w(x)\le \frac{2}{C_1^2} I~\text { for all}~x\in \Omega ~\text {with}~ dist(x,\partial \Omega )\ge c_n, \end{aligned}$$

  where $C_1$ and $C_2$ are constants depending only on n.

• (ii) For any solution $h\in C^2 (B_1(0))$ of $\mathcal {L}_w h=0$ in $B_1(0)$, we have the classical interior $C^{1,1}$ estimate

  $$\begin{aligned} \Vert h\Vert _{C^{1,1}\left( B_{\frac{1}{2}}(0)\right) }\le c_e \Vert h\Vert _{L^{\infty }\left( \partial B_{\frac{3}{4}}(0)\right) } \end{aligned}$$

  for some constant $c_e$ depending only on n.

Sketch of the proof of Theorem 1.2

Our proof utilizes results obtained in Sect. 2 together with the arguments in the proof of [14, Theorem 4.5]. We sketch its proof here. Also for convenience, we assume that the minimum point of $\phi$ is $\bar{z} =0$.

By diving our equation by $K := \Vert u\Vert _{L^\infty (\Omega )} +\theta ^{-1}N_{\phi , f, q}(0)$, we can assume that

$$\begin{aligned} \Phi ^{ij} u_{ij}(x)=f(x)\quad \text{ in }\quad \Omega \quad \text{ with } \qquad \Vert u\Vert _{L^\infty (\Omega )}\le 1, \end{aligned}$$

and

$$\begin{aligned} \left( \frac{1}{|S_r(\phi )|}\int _{S_r(\phi )}{|f|^q \mathrm{d}x}\right) ^{\frac{1}{q}}\le \theta r^{\frac{\alpha -1}{2}}\quad \text{ for } \text{ all }\quad S_r( \phi )\Subset \Omega \text{ with } r\le r_0. \end{aligned}$$

We need to prove that there exists an affine function l(x) such that

$$\begin{aligned} \sup _{0<r\le \mu ^*}{\Big ( r^{-(1 + \alpha ')} \Vert u-l\Vert _{L^\infty (B_r(0))}\Big )} + |l(0)| + \Vert D l(0)\Vert \le C \end{aligned}$$

(3.1)

with $\theta , \mu ^*$, and C depending only on $n, q, \alpha , \alpha '$, and $r_0$. As in the proof of [14, Theorem 4.5], (3.1) follows from the following Claim.

Claim There exist $0<\mu <1$ depending only on $n, \alpha$, and $r_0$, a sequence of positive definite matrices $A_k$ with $\det A_k =1$ and a sequence of affine functions $l_k(x) = a_k + b_k \cdot x$ such that for all $k=1,2,3,\dots$

• (1) $\Vert A_{k-1} A_k^{-1} \Vert \le \frac{1}{\sqrt{c_1}}, \quad \Vert A_k\Vert \le \sqrt{c_2 (1 +C \delta _0)(1 +C \delta _1)\cdots (1 +C \delta _{k-1})}$;

• (2) $B_{(1-\delta _k)\sqrt{2}}(0)\subset \mu ^{\frac{-k}{2}}A_k S_{\mu ^k}(\phi )\subset B_{(1+\delta _k)\sqrt{2}}(0)$;

• (3) $\Vert u-l_{k-1}\Vert _{L^\infty (S_{\mu ^k}(\phi ))} \le \mu ^{\frac{k-1}{2} (1 + \alpha )}$;

• (4) $|a_k - a_{k-1}| + \mu ^{\frac{k}{2}}\Vert (A_k^{-1})^t \cdot (b_k - b_{k-1})\Vert \le 2 c_e \mu ^{\frac{k-1}{2} (1 + \alpha )}$,

where

$$\begin{aligned}&A_0 :=I,\quad l_0(x) := 0,\quad \delta _0:=0;\quad \delta _1 := C\left( \mu ^{1/2} + \mu ^{-1} \theta ^{1/2}\right) <1- \frac{6}{5\sqrt{2}}, \quad \text{ and }\\&\delta _k := C\left( \delta _{k-1}\mu ^{1/2} + \mu ^{-1} \theta ^{1/2}\right) \quad \text{ for } k\ge 2. \end{aligned}$$

Also $C, c_e, c_1$, and $c_2$ are universal constants: $c_e$ is the constant in Lemma 3.3; $c_1$ and $c_2$ are given by Lemma 3.1 and C is given by Lemma 3.2.

The proof of the claim is by induction. It is quite similar to the proof of [14, Theorem 4.5]. For reader’s convenience, we indicate the proof for the cases $k=1,\, 2$.

Let $\mu _0>0$ and $\tau _0>0$ be the small universal constants given by Lemma 3.1. Let $0<\mu \le \mu _0$ be fixed such that $\mu \le r_0, C_2 \sqrt{3\mu }\le 1/2$, and $6 c_e C_2^2\mu ^{\frac{1 -\alpha }{2}}\le 1$, where $C_2$ is the universal constant in the Pogorelov’s estimates of Lemma 3.3. The constant $\theta \le \theta _0$ will be determined later depending only on $n, q, \mu , \alpha$, and $\alpha '$, where $\theta _0=\theta _0(q,n)$ is given by Lemma 2.6. In particular by taking $\theta$ even smaller if necessary, we assume that $\delta _1 = C(\mu ^{1/2} + \mu ^{-1} \theta ^{1/2})<1- \frac{6}{5\sqrt{2}}$.

k = 1 Applying Lemma 3.1 we obtain a positive definite matrix $M=A^t A$ with $\det A= \det M =1, c_1 I\le M\le c_2 I$ such that if we take $A_1:=A$ then

$$\begin{aligned} B_{(1-\delta _1)\sqrt{2}}(0)\subset \mu ^{\frac{-1}{2}}A_1 S_{\mu }(\phi )\subset B_{(1+\delta _1)\sqrt{2}}(0),\quad \text{ with }\quad \delta _1 := C\left( \mu ^{1/2} + \mu ^{-1} \theta ^{1/2}\right) . \end{aligned}$$

Then (1) and (2) hold obviously since $\Vert A_1^{-1}\Vert \le 1/\sqrt{c_1}$ and $\Vert A_1\Vert \le \sqrt{c_2}$. Also (3) is satisfied as $l_0\equiv 0$ and $\Vert u\Vert _{L^\infty (\Omega )}\le 1$.

k = 2 We first construct $l_1$ and verify (3) for $k=2$ and (4) for $k=1$. Then we construct $A_2$ and verify (1) and (2) for $k=2$.

$+$ Constructing $l_1(x)$: Recall that $D\phi (0)=0$ since the origin is the minimum point of $\phi$. Hence $S_\mu (\phi ) =\{y\in \Omega :~ \phi (y)-\phi (0)-\mu \le 0 \}$. Let $\Omega _1^*:=\mu ^{\frac{-1}{2}}A_1 S_{\mu }(\phi )$, and

$$\begin{aligned}&\phi ^*(y) := \frac{1}{\mu }\big [\phi \left( \mu ^{\frac{1}{2}}A_1^{-1} y\right) -\phi (0) -\mu \big ], \\&v(y) := (u-l_0)\left( \mu ^{\frac{1}{2}}A_1^{-1} y\right) =u\left( \mu ^{\frac{1}{2}}A_1^{-1} y\right) \end{aligned}$$

for $y\in \Omega _1^*$. Then, as $D^2\phi ^*(y) =(A_1^{-1})^t D^2\phi (\mu ^{\frac{1}{2}}A_1^{-1} y)A_1^{-1}$, we get

Let $\Phi ^*(y) \equiv \left( \Phi ^{*ij}(y)\right) := \det D^2\phi ^*(y) ~ (D^2\phi ^*(y))^{-1}.$ Then, by (2.1), we get

$$\begin{aligned} \Phi ^{*ij} v_{ij}(y) = \mu ~ f\big (\mu ^{\frac{1}{2}}A_1^{-1} y\big ) =: \tilde{f}(y) \qquad \qquad \text{ in } \quad \Omega _1^*. \end{aligned}$$

Notice that, from $\det A_1=1$ and $\Omega _1^*:=\mu ^{\frac{-1}{2}}A_1 S_{\mu }(\phi )$, we have

$$\begin{aligned} \left( \frac{1}{|\Omega _1^*|} \int _{\Omega _1^*}{|\tilde{f}(y)|^q \mathrm{d}y}\right) ^{\frac{1}{q}}&=\mu ~\left( \frac{1}{|S_\mu (\phi )|}\int _{S_\mu (\phi )}{|f(x)|^q \mathrm{d}x}\right) ^{\frac{1}{q}} \le \mu \theta \mu ^{\frac{\alpha -1}{2}} = \theta \mu ^{\frac{1+\alpha }{2}}. \end{aligned}$$

We apply Lemma 2.5 with $\phi \rightsquigarrow \phi ^*, f\rightsquigarrow \tilde{f}, u\rightsquigarrow v$, and $U\rightsquigarrow \Omega _1^*$. Note that by (3) we have $\Vert v\Vert _{L^\infty (\Omega _1^*)}\le 1$. Recall that $\theta \le \theta _0$, where $\theta _0$ is the small constant given by Lemma 2.6. Hence if h is the solution of

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathrm W}^{i j} D_{i j}h&{}= 0 \, \quad \text{ in }\quad S_\frac{1}{2}(\phi ^*)\\ h&{}=v\ \ \ \text{ on }\quad \partial S_\frac{1}{2}(\phi ^*) \end{array}\right. \quad \text{ where }\quad \left\{ \begin{array}{ll} \det D^2 w&{}= 1\ \ \text{ in }\quad \Omega _1^*\\ w&{}=0\ \ \text{ on }\quad \partial \Omega _1^*, \end{array}\right. \end{aligned}$$

then

$$\begin{aligned} \Vert v-h\Vert _{L^\infty \left( S_\frac{1}{4}(\phi ^*)\right) }&\le C(n,q) \Big \{\Vert \Phi ^* - {\mathrm W}\Vert _{L^q\left( S_\frac{1}{2}(\phi ^*)\right) }^\gamma + \Vert \tilde{f}\Vert _{L^q(\Omega _1^*)} \Big \}\\&\le C(n,q) \left\{ C \theta ^{\frac{(n-1)\gamma \delta }{n(2nq-\delta )}} + \theta \mu ^{\frac{1+\alpha }{2}} \right\} \le \frac{1}{2} \mu ^{\frac{1+\alpha }{2}}. \end{aligned}$$

We have $\Vert h\Vert _{L^\infty (B_1)}\le 1$ by the maximum principle. Moreover, it follows from the formulas [14, (3.13) and (3.15)] that, for some $C_3=C_3(n)$,

$$\begin{aligned} S_{2\mu }(\phi ^*) \subset B_{C_2 \sqrt{2\mu + C_3 \theta ^{1/2}}}(0)\subset B_{C_2 \sqrt{3\mu }}(0). \end{aligned}$$

Thus, by letting $\bar{l}(y) := h(0) + D h(0)\cdot y$, applying the interior $C^{1,1}$ estimate for h as in Lemma 3.3 and noting that $C_2\sqrt{3\mu }\le 1/2$, we get

$$\begin{aligned} \Vert h - \bar{l}\Vert _{L^\infty (S_{2\mu }(\phi ^*))} \le \Vert h - \bar{l}\Vert _{L^\infty \left( B_{C_2 \sqrt{3\mu }}(0)\right) } \le 3 c_e C_2^2 \mu . \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert v - \bar{l}\Vert _{L^\infty \left( S_{2\mu }(\phi ^*)\right) }&\le \Vert v - h\Vert _{L^\infty \left( S_{2\mu }(\phi ^*)\right) } + \Vert h - \bar{l}\Vert _{L^\infty \left( S_{2\mu }(\phi ^*)\right) }\nonumber \\&\le \frac{1}{2} \mu ^{\frac{1+\alpha }{2}} + 3 c_e C_2^2 \mu \le \mu ^{\frac{1}{2} (1+\alpha )}. \end{aligned}$$

(3.2)

Define

$$\begin{aligned} l_1(x) := l_0(x) + \bar{l}\left( \mu ^{\frac{-1}{2}}A_1 x\right) . \end{aligned}$$

(3.3)

Then since $S_{\mu }(\phi ^*) = \mu ^{\frac{-1}{2}}A_1 S_{\mu ^2}(\phi )$, we obtain from (3.2) for $x\in S_{\mu ^2}(\phi )$ that

$$\begin{aligned} |u(x)-l_1(x)| = |v\left( \mu ^{\frac{-1}{2}}A_1 x\right) -\bar{l}\left( \mu ^{\frac{-1}{2}}A_1 x\right) | \le \Vert v - \bar{l}\Vert _{L^\infty \left( S_{\mu }(\phi ^*)\right) } \le \mu ^{\frac{1}{2} (1+\alpha )}. \end{aligned}$$

Thus (3) for $k=2$ is verified. Also (4) for $k=1$ holds because it follows from the definition (3.3) and the definition of $\bar{l}$ that $a_1 = a_0 + h(0)$ and $b_1= b_0 + \mu ^{\frac{-1}{2}}A_1^t D h(0)$. Hence using the interior $C^{1,1}$ estimate for h, we get (4) for $k=1$ from

$$\begin{aligned} |a_1 - a_0| + \mu ^{\frac{1}{2}} \Vert \left( A_1^{-1}\right) ^t \cdot ( b_1 - b_0)\Vert = |h(0)| + \Vert D h(0)\Vert \le 2 c_e. \end{aligned}$$

$+$ Constructing $A_2$: Applying Lemma 3.2 for $\phi ^*$ and $\Omega _1^*$ we obtain a positive definite matrix $M=A^t A$ with $\det M =1, (1- C\delta _1) I\le M\le (1+C\delta _1)I$ such that

$$\begin{aligned} B_{(1-\delta _2)\sqrt{2}}(0)\subset \mu ^{\frac{-1}{2}}A S_{\mu }(\phi ^*)\subset B_{(1+\delta _2)\sqrt{2}}(0),\quad \text{ with }\quad \delta _2 := C\left( \delta _1\mu ^{1/2} + \mu ^{-1} \theta ^{1/2}\right) . \end{aligned}$$

Define $A_2:=A A_1$ which implies in particular that $A_2$ is a positive definite matrix with $\det A_2 =1$. Then as $S_{\mu }(\phi ^*) = \mu ^{\frac{-1}{2}}A_1 S_{\mu ^2}(\phi )$ we conclude that

$$\begin{aligned} B_{(1-\delta _2)\sqrt{2}}(0)\subset \mu ^{-1}A_2 S_{\mu ^2}(\phi )\subset B_{(1+\delta _2)\sqrt{2}}(0). \end{aligned}$$

Thus (2) and the first part of (1) for $k=2$ hold obviously since $A_1 A_2^{-1} =A^{-1}$ and $\Vert A^{-1}\Vert \le \frac{1}{\sqrt{1-C\delta _1}}\le \frac{1}{\sqrt{c_1}}$. Next observe from the definition of A that $(1-C\delta _1) |x|^2 \le |A x|^2\le (1+C\delta _1)|x|^2$. Hence

$$\begin{aligned} |A_2 x|^2= |A A_1 x|^2 \le (1+C\delta _1)|A_1 x|^2 \le c_2 (1+C\delta _1)|x|^2 \end{aligned}$$

yielding the second part of (1), i.e., $\Vert A_2\Vert \le \sqrt{c_2 (1+C\delta _1)}$. $\square$

We next prove Theorem 1.3, and in this proof we use the following strong-type inequality for the maximal function with respect to sections:

Theorem 3.4

[15, Theorem 2.2] Assume that $\Omega$ and $\phi$ satisfy (H). Let $\Omega '\Subset \Omega$. Fix $h_0>0$ such that $S_\phi (x, 2h_0)\Subset \Omega$ for all $x\in \Omega '$. Define the maximal function $\mathcal {M}(f)$ by

$$\begin{aligned} \mathcal M (f)(x)=\sup _{t\le h_0} \dfrac{1}{|S_\phi (x,t)|}\int _{S_\phi (x,t)}|f(y)|\, \mathrm{d}y\quad \text {for } x\in \Omega '. \end{aligned}$$

For any $1<p<\infty$, there exists a constant C depending on $p, n, \lambda , \Lambda$, and $\text {dist}(\Omega ', \partial \Omega )$ such that

$$\begin{aligned} \left( \int _{\Omega '}{|\mathcal M (f)(x)|^p ~d\mu (x)} \right) ^{\frac{1}{p}}\le C\, \left( \int _{\Omega }{|f(y)|^p \,d\mu (y)} \right) ^{\frac{1}{p}}. \end{aligned}$$

Proof of Theorem 1.3

Let $\Omega '\Subset \Omega$. Let $0<\alpha <1, q'$ be such that $n/2<q'<q$, and

$$\begin{aligned} N(z) :=\sup _{r\le h_0} r^{\frac{1-\alpha }{2}}\left( \frac{1}{|S_\phi (z,r)|}\int _{S_\phi (z,r)} |f|^{q'}\, \mathrm{d}x\right) ^{\frac{1}{q'}}, \end{aligned}$$

where $h_0$ is to be determined. One of the requirements is that $S_\phi (y, 2 h_0)\Subset \Omega$ for all $y\in \Omega '$. Then we have the following pointwise estimate for the gradient Du:

$$\begin{aligned} |Du(y)| \le C \Big [ \Vert u\Vert _{L^\infty (\Omega )} + N(y)\Big ]\quad \text{ for } \text{ a.e. } y\in \Omega '. \end{aligned}$$

(3.4)

The $L^p$ estimate (1.12) for Du then follows from the volume growth of interior sections of $\phi$ and the strong-type inequality for the maximal function $\mathcal {M}(f)$ in Theorem 3.4. Indeed, by Hölder inequality, it suffices to consider the case $q\le p<\frac{nq}{n-q}$. From (3.4) and by using Hölder inequality, we have for any $p\ge q$ that

$$\begin{aligned}&\Vert Du\Vert _{L^p(\Omega ')}\\&\quad \le C \Vert u\Vert _{L^\infty (\Omega )} + C \Vert N\Vert _{L^p(\Omega ')} \\&\quad \le C \Vert u\Vert _{L^\infty (\Omega )}\\&\qquad +C\left( \int _{\Omega '}\sup _{r\le h_0} \Big \{ r^{\frac{p}{2}(1-\alpha )}\mathcal M\left( f^{q'}\right) (y)^{\frac{q}{q'}} \Big (\frac{1}{|S_\phi (y,r)|} \int _{S_\phi (y,r)}{|f(x)|^{q'} \mathrm{d}x} \Big )^{\frac{p-q}{q'}}\Big \} \mathrm{d}y\right) ^{\frac{1}{p}}\\&\quad \le C \Vert u\Vert _{L^\infty (\Omega )}\\&\qquad +C\left( \int _{\Omega '}\sup _{r\le h_0} \Big \{ r^{\frac{p}{2}(1-\alpha )}\mathcal M\left( f^{q'}\right) (y)^{\frac{q}{q'}} \Big (\frac{1}{|S_\phi (y,r)|} \int _{S_\phi (y,r)}{|f(x)|^q \mathrm{d}x} \Big )^{\frac{p-q}{q}}\Big \} \mathrm{d}y\right) ^{\frac{1}{p}} \\&\quad \le C\Vert u\Vert _{L^\infty (\Omega )} +C \sup _{r\le h_0} \Big \{ r^{\frac{1}{2}\big [(1-\alpha ) -\frac{ n}{q} +\frac{n}{p}\big ]} \Big \} \left( \int _{\Omega '} \mathcal M\left( f^{q'}\right) (y)^{\frac{q}{q'}} \mathrm{d}y\right) ^{\frac{1}{p}} \Vert f\Vert _{L^{q}(\Omega )}^{\frac{p-q}{p}} . \end{aligned}$$

The last inequality above follows from the volume estimates of interior sections of $\phi$. These estimates [13, Corollary 3.2.4] say that there exist constants C and $C'$ depending only on $n,\lambda ,\Lambda$ such that

$$\begin{aligned} Cr^{n/2}\le |S_\phi (y, r)|\le C' r^{n/2}~ \text {for all}~ y\in \Omega ' ~\text {and }~ r\le h_0. \end{aligned}$$

As $q/q'>1$, we can apply Theorem 3.4 to conclude that

$$\begin{aligned} \Vert Du\Vert _{L^p(\Omega ')}\le & {} C \Vert u\Vert _{L^\infty (\Omega )} +C\sup _{r\le h_0} \Big \{ r^{\frac{1}{2}\big [(1-\alpha ) -\frac{ n}{q} +\frac{n}{p}\big ]} \Big \}\Vert f\Vert _{L^q(\Omega )}^{\frac{q}{p}} \Vert f\Vert _{L^{q}(\Omega )}^{\frac{p-q}{p}}\\= & {} C \Vert u\Vert _{L^\infty (\Omega )} + C\sup _{r\le h_0} \Big \{ r^{\frac{1}{2}\big [(1-\alpha ) -\frac{ n}{q} +\frac{n}{p}\big ]} \Big \} \Vert f\Vert _{L^{q}(\Omega )}. \end{aligned}$$

Now, since $q\le p< \frac{nq}{n-q}$, we can choose $\alpha \in (0, 1-\frac{n}{q}+\frac{n}{p})$ to obtain estimate (1.12):

$$\begin{aligned} \Vert Du\Vert _{L^p(\Omega ')} \le C \Big ( \Vert u\Vert _{L^\infty (\Omega )} + \Vert f\Vert _{L^q(\Omega )} \Big ). \end{aligned}$$

It remains to prove (3.4). Given $\epsilon _0>0$, since $g\in C(\Omega$) and by [13, Theorem 3.3.8], there exists $h_0>0$ such that for any $y\in \Omega '$,

$$\begin{aligned} B_{C_1 h_0}(y)\subset S_\phi (y, h_0) \subset B_{C_2 h_0^b}(y) \quad \text{ and }\quad |g(x)- g(y)|\le \varepsilon _0 \quad \text {for all } x\in S_\phi (y, h_0). \end{aligned}$$

Fix $y\in \Omega '$, and let $Tx = A(x-y) + \bar{z}$ be an affine transformation such that

$$\begin{aligned} B_1(0)\subset T S_\phi (y, h_0) \subset B_n (0). \end{aligned}$$

Notice that $C^{-1}\le |\det A|^{\frac{2}{n}} h_0 \le C$ for some constant $C>0$ depending only on $n, \lambda$, and $\Lambda$.

Define $\tilde{\Omega }:= T S_\phi (y, h_0)$ and consider the functions

$$\begin{aligned} \tilde{\phi }(z) := \kappa \big [ \phi (T^{-1} z) - l_{y} (T^{-1} z) - h_0 \big ] \quad \text{ and }\quad \tilde{u}(z) := g(y)\kappa ^{\frac{\alpha - 3}{2}} u(T^{-1} z), \quad \text{ for }\quad z\in \tilde{\Omega }\end{aligned}$$

where $\kappa := g(y)^{\frac{-1}{n}} |\det A|^{\frac{2}{n}}$ and $l_y(x)$ is the supporting function of $\phi$ at y. Then

$$\begin{aligned} 1-\frac{\varepsilon _0}{\lambda } \le \det D^2 \tilde{\phi }(z)\le 1+ \frac{\varepsilon _0}{\lambda } \quad \text{ and }\quad \tilde{\Phi }^{i j} \tilde{u}_{i j}(z) = \kappa ^{\frac{\alpha - 1}{2}} f(T^{-1} z) =:\tilde{f}(z)\quad \text{ in }\quad \tilde{\Omega }. \end{aligned}$$

We have

$$\begin{aligned}&r^{\frac{1-\alpha }{2}} \left( \frac{1}{|S_{\tilde{\phi }}(\bar{z},r )|} \int _{S_{\tilde{\phi }}(\bar{z}, r)}{|\tilde{f}|^{q'} dz}\right) ^{\frac{1}{q'}}\\&\quad =(\kappa ^{-1} r)^{\frac{1-\alpha }{2}} \left( \frac{1}{|S_\phi (y, \kappa ^{-1} r)|}\int _{S_\phi (y, \kappa ^{-1} r)}{|f|^{q'} \mathrm{d}x}\right) ^{\frac{1}{q'}} \end{aligned}$$

for all $r\le \kappa h_0$. Since $\kappa h_0 =g(y)^{\frac{-1}{n}} |\det A|^{\frac{2}{n}} h_0\ge c(n,\lambda , \Lambda ) >0$, it follows by letting $r_0:=c(n,\lambda , \Lambda )$ that $N_{\tilde{\phi }, \tilde{f}, q'}(\bar{z})\le N(y)$. Note that $\bar{z}$ is the minimum point of $\tilde{\phi }$ in $\tilde{\Omega }$ . Therefore if we choose $\varepsilon _0 := \lambda \theta$, where $\theta >0$ is the constant given in Theorem 1.2 corresponding to this $r_0, \alpha '=0$, and $q\rightsquigarrow q'$, then by Theorem 1.2 there exist constants $\mu ^*, C >0$ depending only on $n, q', \alpha , \lambda$, and $\Lambda$, and an affine function $\bar{l}$ such that

$$\begin{aligned} |\tilde{u}(z) - \bar{l}(z)| + |z-\bar{z}| |D \bar{l} | \le C |z-\bar{z}| \Big [ \Vert \tilde{u} \Vert _{L^\infty (\tilde{\Omega })} +N(y) \Big ] \quad \text{ for } \text{ all }\quad z \in B_{\mu ^*}(\bar{z}) \Subset \tilde{\Omega }.\nonumber \\ \end{aligned}$$

(3.5)

Observe that as $B_{C_1 h_0}(y)\subset S_\phi (y, h_0)$, we have $T B_{C_1 h_0}(y)\subset B_n(0)$, i.e., $A B_{C_1 h_0}(0) +\bar{z}\subset B_n(0)$. This yields $\Vert A\Vert \le C h_0^{-1}$. Thus $T B_{C^{-1}\mu ^* h_0}(y) \subset B_{\mu ^*}(\bar{z})$ and we obtain from (3.5) and by rescaling back and by taking $\ell (x) =\ell (x,y) := g(y)^{-1} \kappa ^{\frac{3-\alpha }{2}} \bar{l} (T x)$ that

$$\begin{aligned}&|u(x) - \ell (x)| + |x-y| |D \ell | = g(y)^{-1} \kappa ^{\frac{3-\alpha }{2}} \Big [ |\tilde{u}(T x)- \bar{l}(T x)| +|x-y| | D \bar{l} \cdot A|\Big ]\\&\quad \le C \Vert A\Vert |x- y| g(y)^{-1} \kappa ^{\frac{3-\alpha }{2}} \Big [ \Vert \tilde{u} \Vert _{L^\infty (\tilde{\Omega })} + N(y) \Big ]\\&\quad = C \Vert A\Vert |x- y| \Big [ \Vert u\Vert _{L^\infty (S_\phi (y, h_0))} + g(y)^{-1} \big ( g(y)^{\frac{-1}{n}} |\det A|^{\frac{2}{n}} \big )^{\frac{3-\alpha }{2}} N(y)\Big ]\\&\quad \le C h_0^{-1} h_0^{\frac{\alpha - 3}{2}} |x- y| \Big [ \Vert u\Vert _{L^\infty (S_\phi (y, h_0))} + N(y)\Big ] \qquad \text{ for } \text{ all }\quad x \in B_{C^{-1}\mu ^* h_0}(y). \end{aligned}$$

In other words, we proved that for any $y\in \Omega '$ there exists an affine function $\ell$ such that

$$\begin{aligned}&|u(x)-\ell (x)| + |x-y| | D\ell |\le C h_0^{\frac{\alpha - 5}{2}} |x-y|\Big [ \Vert u\Vert _{L^\infty (\Omega )} + N(y)\Big ] \nonumber \\&\quad \text {for all } x \in B_{C^{-1}\mu ^* h_0}(y). \end{aligned}$$

(3.6)

Now, let $y\in \Omega '$ be such that Du(y) exists. Then using (3.6) we get

$$\begin{aligned} |u(x)-u(y)|&\le |u(x) -\ell (x)| + |\ell (x)- \ell (y)| + |u(y)-\ell (y)|\\&\le C |x-y| \Big [ \Vert u\Vert _{L^\infty (\Omega )} + N(y)\Big ] \qquad \text{ for } \text{ all } \quad x \in B_{C^{-1}\mu ^* h_0}(y), \end{aligned}$$

which yields (3.4). Note that the constant C depends also on $h_0$, and hence it depends on the modulus of continuity of g. $\square$

4 Pointwise $C^{1,\alpha }$ estimates at the boundary

In this section, we prove Lemma 1.5 and Theorem 1.4. The proof of Theorem 1.4 is similar to that of [22, Theorem 1.1] but we include it here for the sake of completeness. It uses the perturbation arguments in the spirit of Caffarelli [2, 5] (see also Wang [33]) and boundary Hölder gradient estimates for the case of bounded right-hand side f and $C^{1,1}$ boundary data by Savin and the first author [21]. We recall these estimates in the following theorem.

Theorem 4.1

[21, Theorem 2.1 and Proposition 6.1] Assume $\phi$ and $\Omega$ satisfy assumptions (1.13)–(1.16). Denote for simplicity $S_t = S_\phi (0, t)$. Let $u: S_r\cap \overline{\Omega }\rightarrow {\mathbb R}$ be a continuous solution to

$$\begin{aligned} \Phi ^{ij}u_{ij} = f ~\text {in} ~ S_r\cap \Omega , ~\text {and}~ u = 0~\text {on}~\partial \Omega \cap S_r \end{aligned}$$

where $f\in L^{\infty }(S_r\cap \Omega )$. Then, for all $s\le r/2$, we have

$$\begin{aligned} |\partial _n u(0)| + s^{-\frac{1+\alpha _0}{2}}\max _{S_s}|u-\partial _n u(0)x_n| \le C_0 \left( \Vert u\Vert _{L^{\infty }(S_r\cap \Omega )} + \Vert f\Vert _{L^{\infty }(S_r\cap \Omega )}\right) , \end{aligned}$$

where $\alpha _0\in (0, 1)$ and $C_0$ are constants depending only on $n, \rho , \lambda , \Lambda$.

Assume $\phi$ and $\Omega$ satisfy (1.13)–(1.16). We can also assume that $\phi (0)=0$ and $D \phi (0)=0.$

By Savin’s Localization Theorem for solutions to the Monge–Ampère equations proved in [24, 25], there exists a small constant k depending only on $n, \rho , \lambda , \Lambda$ such that if $h\le k$ then

$$\begin{aligned} kE_h\cap \overline{\Omega }\subset S_{\phi }(0, h)\subset k^{-1} E_h\cap \overline{\Omega }. \end{aligned}$$

(4.1)

Here $E_h:= h^{1/2}A_h^{-1} B_1(0)$ with $A_h$ being a linear transformation (sliding along the $x_n=0$ plane)

$$\begin{aligned} A_h(x) = x- \tau _h x_n,~ \tau _h\cdot e_n =0, ~\det A_h =1\ \end{aligned}$$

(4.2)

and

$$\begin{aligned} |\tau _h|\le k^{-1}\left| log h\right| . \end{aligned}$$

Let us write $\tau _h =(\nu _h,0)$ with $\nu _h\in {\mathbb R}^{n-1}$. Next, we define the following rescaling of $\phi$

$$\begin{aligned} \phi _h(x):= \frac{\phi (h^{1/2} A^{-1}_h x)}{h} \quad \text{ in } \quad \Omega _h:= h^{-1/2}A_h\Omega . \end{aligned}$$

(4.3)

Then

$$\begin{aligned} \lambda \le \det D^2 \phi _h(x)= \det D^2 \phi (h^{1/2}A_{h}^{-1}x)\le \Lambda \quad \text{ in }\quad \Omega _h \end{aligned}$$

and

$$\begin{aligned} B_{k}(0)\cap \overline{\Omega _h}\subset S_{\phi _h}(0, 1)= h^{-1/2} A_{h}S_\phi (0,h)\subset B_{k^{-1}}(0)\cap \overline{\Omega _h}. \end{aligned}$$

We note that Lemma 4.2 in [21] implies that if $h, r\le c$ small then $\phi _h$ satisfies in $S_{\phi _h}(0, 1)$ the hypotheses of the Localization Theorem [24, 25] at all $x_0\in S_{\phi _h}(0, r)\cap \partial S_{\phi _h}(0, 1).$ In particular, there exists $\tilde{\rho }>0$ small depending only on $n, \rho , \lambda , \Lambda$ such that if $x_0\in S_{\phi _h}(0, r)\cap \partial S_{\phi _h}(0, 1)$ then

$$\begin{aligned}&\tilde{\rho }\left| x-x_{0}\right| ^2 \le \phi _h(x)- \phi _h(x_{0})-D \phi _h(x_{0}) \cdot (x- x_{0}) \le \tilde{\rho }^{-1}\left| x-x_{0}\right| ^2,\nonumber \\&\quad \forall x \in \partial S_{\phi _h}(0, 1). \end{aligned}$$

(4.4)

Moreover, for $h, t\le c$, we have the following volumes estimates

$$\begin{aligned} c_1 h^{\frac{n}{2}}\le |S_\phi (0, h)|\le C_1 h^{\frac{n}{2}}; \quad c_1 t^{\frac{n}{2}}\le |S_{\phi _h}(0, t)|\le C_1 t^{\frac{n}{2}}. \end{aligned}$$

(4.5)

We fix r in what follows. Then, the boundary Hölder gradient estimates in Theorem 4.1 for solutions to the linearized Monge–Ampère equation with bounded right-hand side and $C^{1, 1}$ boundary data hold in $S_{\phi _h}(0, r)$.

We now employ the Green’s function estimate obtained in [18] to derive a boundary version of the generalized maximum principle in Lemma 2.1.

Lemma 4.2

(Boundary maximum principle) Let $h, t\le c$ where $c= c(n,\lambda ,\Lambda , \rho )$ is universally small. Let $f\in L^q(S_{\phi _h}(0, t))$ for some $q>n/2$ and $u\in W^{2,n}_{loc}(S_{\phi _h}(0, t))\cap C(\overline{S_{\phi _h}(0, t)})$ satisfy

$$\begin{aligned} \mathcal {L}_{\phi _h} u\le f\quad \text{ almost } \text{ everywhere } \text{ in }\quad S_{\phi _h}(0, t). \end{aligned}$$

Then there exists a constant $C>0$ depending only on $n, \lambda , \Lambda , \rho$, and q such that

$$\begin{aligned} \sup _{S_{\phi _h}(0, t)}{u} \le \sup _{\partial S_{\phi _h}(0, t)}{u^+} + C |S_{\phi _h}(0, t)|^{\frac{2}{n} -\frac{1}{q}} \Vert f\Vert _{L^q(S_{\phi _h}(0, t))}. \end{aligned}$$

Proof

Let $V=S_{\phi _h}(0, t)$. Let $G_V(\cdot , y)$ be the Green’s function of $\mathcal {L}_{\phi _h}$ in V with pole $y\in V$. As in (2.2), we obtain for all $x\in S_{\phi _h}(0, t)$ the estimate

$$\begin{aligned} u(x) \le \sup _{\partial S_{\phi _h}(0, t)} u^{+} +\int _V G_V(x, y) f(y) \mathrm{d}y. \end{aligned}$$

The conclusion of the lemma follows once we establish that for $q'=\frac{q}{q-1}$, we have

$$\begin{aligned} \Vert G_V(x, \cdot )\Vert _{L^{q'}(V)}\le C|V|^{\frac{2}{n}-\frac{1}{q}}\quad \text {for all~}x\in V. \end{aligned}$$

(4.6)

Thanks to (4.4), one can find a constant $\theta _{*}>1$ depending only on $n,\lambda ,\Lambda$, and $\rho$ such that

$$\begin{aligned} S_{\phi _h}(0, t)\subset S_{\phi _h}(x, \theta _*t) ~\text {for all}~x\in S_{\phi _h}(0, t). \end{aligned}$$

(4.7)

This is a boundary version of the engulfing property of sections of the Monge–Ampère equation (see [19, Lemma 4.1]). By the symmetry of the Green’s function, we have

$$\begin{aligned} \int _V G^{q'}_V(x, y) \mathrm{d}y = \int _{V} G_V^{q'}(y, x) \mathrm{d}y \le \int _{S_{\phi _h}(x, \theta _*t)} G^{q'}_{S_{\phi _h}(x, \theta _*t)} (y, x) \mathrm{d}y. \end{aligned}$$

(4.8)

Due to $q'<\frac{n}{n-2}$, we have from [18, Corollary 2.6] that

$$\begin{aligned} \int _{S_{\phi }(x, \theta _*t)} G^{q'}_{S_{\phi }(x, \theta _*t)} (y, x) \mathrm{d}y \le C(n, \lambda ,\Lambda , \rho , q) |S_{\phi }(x, \theta _*t)|^{1-\frac{n-2}{n}q'}. \end{aligned}$$

(4.9)

By inspecting the proof of [18, Corollary 2.6] (see the discussion below), we see that the above inequality also holds with $\phi _h$ replacing $\phi$:

$$\begin{aligned} \int _{S_{\phi _h}(x, \theta _*t)} G^{q'}_{S_{\phi _h}(x, \theta _*t)} (y, x) \mathrm{d}y \le C(n, \lambda ,\Lambda , \rho , q) |S_{\phi _h}(x, \theta _*t)|^{1-\frac{n-2}{n}q'}.\qquad \end{aligned}$$

(4.10)

The desired estimate (4.6) then follows from (4.8), (4.10), and the volume estimate for sections of $\phi _h$ given in (4.5).

Let us describe the proof of (4.10). The difference between (4.10) and (4.9) is that we only know $\phi _h$ and $S_{\phi _h}(0, 1)$ satisfying the quadratic separation condition (4.4) on a portion $S_{\phi _h}(0, r)\cap \partial S_{\phi _h} (0, 1)$ of the boundary $\partial S_{\phi _h} (0, 1)$ while $\phi$ and $\Omega$ satisfy a global condition. For reader’s convenience, we indicate how to obtain (4.10) in our local setting from the proof of (4.9) in [18, Corollary 2.6]. Three main ingredients need to be verified are:

• (1) The engulfing property of sections: there exists some constant $\bar{\theta }= \bar{\theta }(n,\lambda ,\Lambda , \rho )>1$ such that if $x\in S_{\phi _h}(0, \delta )$ with $\delta$ universally small and $y\in S_{\phi _h}(x, t)$ with $t\le c$, then we have

  $$\begin{aligned} S_{\phi _h}(x, t)\subset S_{\phi _h}(y, \bar{\theta }t). \end{aligned}$$

  (4.11)

• (2) The volume growth of sections: if $x\in S_{\phi _h}(0, c)$ and $t\le c$ then

  $$\begin{aligned} C_1^{-1} t^{\frac{n}{2}}\le |S_{\phi _h}(x, t)|\le C_1 t^{\frac{n}{2}}. \end{aligned}$$

• (3) Boundary Harnack inequality for solutions to the homogeneous linearized Monge–Ampère equation $\mathcal {L}_{\phi _h} v=0$ in $S_{\phi _h}(0, 1)$.

We now address these ingredients.

Concerning (1): Suppose $x\in S_{\phi _h}(0, \delta )$ and $y\in S_{\phi _h}(x, t)$. By (4.7), it suffices to consider $x\in S_{\phi _h}(0,\delta )\cap \Omega _h$. We use the strict convexity result for $\phi _h$ (see [21, Lemma 5.4] and also [18, Lemma 3.8(iv)]) which says that the maximal interior section $S_{\phi _h}(x, \bar{h}(x))$ of $\phi _h$ centered at x where

$$\begin{aligned} \bar{h}(x)= \sup \{t|\,\, S_{\phi _h}(x, t)\subset \Omega _h\} \end{aligned}$$

is tangent to $\partial \Omega _h$ at $z\in \partial \Omega _h\cap S_{\phi _h}(0, r/2)$. Using equation (4.11) in the proof of Proposition 2.3 in [19], we find some $K=K(n,\lambda ,\Lambda , \rho )$ such that

$$\begin{aligned} S_{\phi _h}(x, 2t)\subset S_{\phi _h} (z, Kt)~ \text {for all} ~\bar{h}(x) /2<t\le c. \end{aligned}$$

(4.12)

If $t\le \bar{h}(x)/2$, then $S_{\phi _h}(x, 2t)\subset \Omega _h$ and hence the inclusion (4.11) follows from the engulfing property of interior sections for the Monge–Ampère equation with bounded right-hand side (see the proof of Theorem 3.3.7 in [13]). Consider now $\bar{h}(x)/2<t\le c$. Then we have from (4.12) $y\in S_{\phi _h}(z, Kt)$. By (4.7), we have $S_{\phi _h}(z, Kt)\subset S_{\phi _h}(y, \theta _{*} Kt)$. Recalling (4.12), we find that (4.11) follows with $\bar{\theta }= \theta _{*}K$.

Concerning (2): The proof uses the Localization Theorem and (4.12) as in the proof of [19, Corollary 2.4] so we omit it.

Concerning (3): Given (1) and (2), the proof of the boundary Harnack inequality [18, Theorem 1.1] applies in our local setting without change. $\square$

Proof of Lemma 1.5

The proof of this lemma is similar to that of Lemma 4.2. It uses the symmetry of the Green’s function $G_\Omega (x,y)$ and its global integrability established in [18, Corollary 2.6] which says that for $p\in (1, \frac{n}{n-2})$ in the case $n\ge 3$ and $p\in (1,\infty )$ in the case $n=2$, we have

$$\begin{aligned} \sup _{x\in \Omega }\int _{\Omega }{G_\Omega (x,y)^p~\mathrm{d}y} \le C(n,\lambda ,\Lambda , p,\rho ). \end{aligned}$$

$\square$

Proof of Theorem 1.4

Let $M:=\Vert \varphi \Vert _{C^{1,\gamma }(B_{\rho }(0)\cap \partial \Omega )}$. Since $u =\varphi$ on $\partial \Omega \cap B_{\rho }(0)$, by subtracting a suitable affine function l(x), we can assume that u satisfies $\left| u(x)\right| \le M |x'|^{1+\gamma }$ for $x=(x', x_n)\in \partial \Omega \cap B_{\rho }(0)$. In particular, $u(0)=0$.

Fix $0<\alpha <\min \{\gamma , \alpha _0\}$ where $\alpha _0$ is in Theorem 4.1. Let $\bar{h}\le \theta ^2$ with $\theta$ being some universally small constant that will be chosen later. Then by dividing our equation by

$$\begin{aligned} K:= \theta ^{-\frac{1+\alpha }{2}}\big [\Vert u\Vert _{L^{\infty }(B_{\rho }(0)\cap \Omega )} + \sup _{ \bar{h}\le t\le \theta ^2} N_{\phi , f, q, 2\theta ^{-1} t}(0) + M\big ], \end{aligned}$$

we may assume that

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(B_{\rho }(0)\cap \Omega )} + \sup _{\bar{h}\le t\le \theta ^2}N_{\phi , f, q, 2\theta ^{-1} t}(0) + M\le (\theta ^{1/2})^{1+\alpha }=: \delta , \end{aligned}$$

(4.13)

and we only need to show that there exists $b\in {\mathbb R}^n$ such that

$$\begin{aligned} \bar{h}^{-\frac{1+\alpha }{2}}\Vert u -bx\Vert _{L^{\infty }(S_{\phi }(0, \bar{h}))} + \Vert b\Vert \le C(n,q,\rho ,\alpha ,\gamma ,\lambda , \Lambda ). \end{aligned}$$

(4.14)

As a consequence of (4.13), we have

$$\begin{aligned} \left| u(x)\right| \le \delta |x'|^{1+\gamma }\quad \text{ for }\quad x=(x', x_n)\in \partial \Omega \cap B_{\rho }(0). \end{aligned}$$

(4.15)

Claim There exist $\theta >0$ small and $C_2>1$ depending only on $n, \rho , \lambda , \Lambda , \gamma , q$ such that the following holds. If $\sup _{1\le m\le k}N_{\phi , f, q, 2\theta ^m}(0)\le C_2 \delta$ for some integer number $k\ge 2$, then for every $m=1, 2, \dots ,k$ we can find a linear function $l_m(x):= b_m x_n$ with $b_0= b_1 =0$ such that

• (i) $\Vert u-l_m\Vert _{L^{\infty }(S_{\theta ^m})}\le (\theta ^{m/2})^{1+\alpha };$

• (ii) $|b_m-b_{m-1}|\le C_0 (\theta ^{\frac{m-1}{2}})^{\alpha }.$

The desired estimate (4.14) follows from the above claim. Indeed, since $\bar{h}\le \theta ^2$ we can find a positive integer $k\ge 2$ such that $\theta ^{k+1}<\bar{h}\le \theta ^k$ and the conclusion (4.14) follows by choosing $b= b_k$. To see this, we use the definition of N in (1.7) and $2\theta ^k< 2\theta ^{-1}\bar{h}\le 2\theta ^{k-1}$, together with the volume estimate (4.5) to get

$$\begin{aligned} N_{\phi , f, q, 2\theta ^k}(0) \le C_2 N_{\phi , f, q, 2\theta ^{-1}\bar{h}}(0) \end{aligned}$$

for some universal constant $C_2$. This and (4.13) imply that

$$\begin{aligned} \sup _{1\le m\le k}N_{\phi , f, q, 2\theta ^m}(0) \le C_2 \sup _{\bar{h}\le t\le \theta ^2}N_{\phi , f, q, 2\theta ^{-1}t}(0)\le C_2 \delta . \end{aligned}$$

Hence we deduce from the claim by taking into account the affine function $l_k$ that

$$\begin{aligned} (\theta ^k)^{-\frac{1+\alpha }{2}}\Vert u- b_k x\Vert _{L^{\infty }(S_{\theta ^k})} + \Vert b_k\Vert&\le 1+ \sum _{m=1}^k |b_m - b_{m-1}| \le 1\\&\quad + C_0 \sum _{m=1}^\infty \theta ^{\frac{\alpha }{2}(m-1)}\le C. \end{aligned}$$

Therefore, we obtain (4.14) with $b=b_k$ since

$$\begin{aligned} \bar{h}^{-\frac{1+\alpha }{2}}\Vert u- b x\Vert _{L^{\infty }(S_{\phi }(0,\bar{h}))} + \Vert b\Vert \le (\theta ^{k+1})^{-\frac{1+\alpha }{2}}\Vert u- b_k x\Vert _{L^{\infty }(S_{\theta ^k})} + \Vert b_k\Vert \le C \theta ^{-\frac{1+\alpha }{2}}. \end{aligned}$$

It remains to show the claim and we prove it by induction. Let us fix $k\ge 2$ such that

$$\begin{aligned} \sup _{1\le m\le k}N_{\phi , f, q, 2\theta ^m}(0)\le C_2 \delta . \end{aligned}$$

(4.16)

Thanks to (4.15) and $\alpha <\gamma$, (i) and (ii) clearly hold for $m=1$. Suppose (i) and (ii) hold up to $m\in \{1,\dots , k-1\}$. We prove them for $m+1$. As a consequence of (4.16), we have

$$\begin{aligned} N_{\phi , f, q, 2\theta ^{m+1}}(0)\le C_2 \delta . \end{aligned}$$

Let $h := \theta ^m$. We define the rescaled domain $\Omega _h$ and function $\phi _h$ as in (4.3). For $x\in \Omega _h$, let

$$\begin{aligned} v(x):= \frac{(u-l_m)(h^{1/2} A^{-1}_h x)}{h^{\frac{1+\alpha }{2}}},~f_h(x): = h^{\frac{1-\alpha }{2}}f(h^{1/2} A^{-1}_h x), \end{aligned}$$

and

$$\begin{aligned} \Phi _h(x) = (\Phi _h^{ij}(x))= (\det D^2\phi _h(x))\left( D^2\phi _h(x)\right) ^{-1}. \end{aligned}$$

Then, by (2.1), $\Phi _h^{ij}v_{ij}=f_h~\text {in}~S_{\phi _h}(0,1)$ with $\Vert v\Vert _{L^{\infty }(S_{\phi _h}(0,1))}\le 1$ and

$$\begin{aligned} N_{\phi _h, f_h, q, 2\theta }(0)= N_{\phi , f, q, 2\theta h}(0)=N_{\phi , f, q, 2\theta ^{m+1}}(0)\le C_2 \delta . \end{aligned}$$

(4.17)

The first inequality in (4.17) follows from (4.2)–(4.3) and

$$\begin{aligned} r^{\frac{1-\alpha }{2}}\left( \frac{1}{|S_{\phi _h}(0, r)|}\int _{S_{\phi _h}(0, r)}{|f_h|^q ~\mathrm{d}x}\right) ^{\frac{1}{q}}= & {} (rh)^{\frac{1-\alpha }{2}}\left( \frac{1}{|S_\phi (0, hr)|}\int _{S_\phi (0, hr)}{|f|^q ~\mathrm{d}x}\right) ^{\frac{1}{q}}\\&\text {for all }r>0. \end{aligned}$$

Define $\varphi _h$ as follows: $\varphi _h =0$ on $\partial S_{\phi _h}(0, 2\theta )\cap \partial \Omega _h$ and $\varphi _h= v$ on $\partial S_{\phi _h}(0, 2\theta ) \cap \Omega _h.$ Let w solve

$$\begin{aligned} \left\{ \begin{array}{lll} \Phi _h^{ij}w_{ij} ~&{} = 0 &{}\text {in} ~ S_{\phi _h}(0, 2\theta ), \\ w &{}= \varphi _h&{}\text {on}~\partial S_{\phi _h}(0, 2\theta ). \end{array} \right. \end{aligned}$$

By the maximum principle, we have

$$\begin{aligned} \Vert w\Vert _{L^{\infty }(S_{\phi _h}(0, 2\theta ))}\le \Vert v\Vert _{L^{\infty }(S_{\phi _h}(0, 2\theta ))}\le 1. \end{aligned}$$

Let $\bar{l}(x):= \bar{b}x_n$ where $\bar{b}:=\partial _n w(0).$ Then Theorem 4.1 gives

$$\begin{aligned} \left| \bar{b}\right| \le C_0 \Vert w\Vert _{L^{\infty }(S_{\phi _h}(0, 2\theta ))}\le C_0 \end{aligned}$$

(4.18)

and

$$\begin{aligned} \Vert w-\bar{l}\Vert _{L^{\infty }(S_{\phi _h}(0, \theta ))}\le & {} C_0 \left( \theta ^{\frac{1}{2}}\right) ^{1+\alpha _0}\Vert w\Vert _{L^{\infty }(S_{\phi _h}(0, 2\theta ))}\nonumber \\\le & {} C_0 \left( \theta ^{\frac{1}{2}}\right) ^{1+\alpha _0} \le \frac{1}{2}\left( \theta ^{\frac{1}{2}}\right) ^{1+\alpha }, \end{aligned}$$

(4.19)

provided that $\theta$ is universally small. Given this, by reducing $\theta$ further if necessary, we show that

$$\begin{aligned} \Vert w-v\Vert _{L^{\infty }(S_{\phi _h}(0, 2\theta ))} \le \frac{1}{2}\left( \theta ^{\frac{1}{2}}\right) ^{1+\alpha }. \end{aligned}$$

(4.20)

Combining this with (4.19), we obtain

$$\begin{aligned} \Vert v-\bar{l}\Vert _{L^{\infty }(S_{\phi _h}(0, \theta ))}\le \left( \theta ^{\frac{1}{2}}\right) ^{1+\alpha }. \end{aligned}$$

(4.21)

Now, let

$$\begin{aligned} l_{m+1}(x):= l_m(x) + (h^{1/2})^{1+\alpha } \bar{l}(h^{-1/2}A_h x). \end{aligned}$$

Then, from the definition of v and $\bar{l}$, and (4.21), we find

$$\begin{aligned} \Vert u-l_{m+1}\Vert _{L^{\infty }\left( S_{\theta ^{m+1}}\right) }= & {} \left( h^{1/2}\right) ^{1+\alpha }\Vert v- \bar{l}\Vert _{L^{\infty }\left( S_{\phi _h}(0,\theta )\right) }\le \left( h^{1/2}\right) ^{1+\alpha } \left( \theta ^{1/2}\right) ^{1+\alpha }\\= & {} \left( \theta ^{\frac{m+1}{2}}\right) ^{1+\alpha }, \end{aligned}$$

proving (i). On the other hand, by (4.2), we have

$$\begin{aligned} l_{m+1} (x) = b_{m+1}x_n~\text {with}~b_{m+1}:= b_m + (h^{1/2})^{1+\alpha } h^{-1/2} \bar{b} = b_m + h^{\alpha /2}\bar{b}. \end{aligned}$$

Therefore, the claim is established since (ii) follows from (4.18) and

$$\begin{aligned} \left| b_{m+1}-b_m\right| = h^{\alpha /2}\left| \bar{b}\right| = \theta ^{m\alpha /2} \left| \bar{b}\right| . \end{aligned}$$

It remains to prove (4.20). We will apply Lemma 4.2 to $w-v$ which solves

$$\begin{aligned} \left\{ \begin{array}{lll} \Phi _h^{ij}(w-v)_{ij} ~&{} = -f_h &{}\text {in} ~ S_{\phi _h}(0, 2\theta ), \\ w-v &{}= \varphi _h-v&{}\text {on}~\partial S_{\phi _h}(0, 2\theta ). \end{array} \right. \end{aligned}$$

By this lemma and the way $\varphi _h$ is defined, we have

$$\begin{aligned} \Vert w-v\Vert _{L^{\infty }(S_{\phi _h}(0, 2\theta ))}\le & {} \Vert v\Vert _{L^{\infty }(\partial S_{\phi _h}(0, 2\theta )\cap \partial \Omega _h)} + C_{*}|S_{\phi _h}(0, 2\theta )|^{\frac{2}{n}-\frac{1}{q}} \Vert f_h\Vert _{L^{q}(S_{\phi _h}(0, 2\theta ))}\\=: & {} (\mathrm {I}) + (\mathrm {II}), \end{aligned}$$

where $C_{*}$ depends only on $n,\lambda ,\Lambda ,\rho$, and q.

We estimate $(\mathrm {I})$ as in the proof of [22, Theorem 1.1] and find that if $\theta$ is small then

$$\begin{aligned} (\mathrm {I}) \le \frac{1}{4} \left( \theta ^{1/2}\right) ^{1+\alpha }. \end{aligned}$$

To estimate $(\mathrm {II})$, we recall $N_{\phi _h, f_h, q, 2\theta }(0)\le C_2 \delta = C_2 (\theta ^{1/2})^{1+\alpha }$, and note that

$$\begin{aligned} \Vert f_h\Vert _{L^{q}(S_{\phi _h}(0, 2\theta ))}\le N_{\phi _h, f_h, q, 2\theta }(0) (2\theta )^{-\frac{1-\alpha }{2}} |S_{\phi _h}(0, 2\theta )|^{\frac{1}{q}}\le C_2 \delta (2\theta )^{-\frac{1-\alpha }{2}} |S_{\phi _h}(0, 2\theta )|^{\frac{1}{q}}. \end{aligned}$$

We therefore obtain from the volume estimates (4.5)

$$\begin{aligned} (\mathrm {II})= & {} C_{*}|S_{\phi _h}(0, 2\theta )|^{\frac{2}{n}-\frac{1}{q}} \Vert f_h\Vert _{L^{q}(S_{\phi _h}(0, 2\theta ))}\le C_{*} C_2|S_{\phi _h}(0, 2\theta )|^{\frac{2}{n}}(2\theta )^{-\frac{1-\alpha }{2}}\delta \\\le & {} C_*C_2 C_1^{2/n} (2\theta )^{\frac{1+\alpha }{2}}\delta \le \frac{1}{4} \left( \theta ^{1/2}\right) ^{1+\alpha } \end{aligned}$$

if $\theta$ is small. It follows that

$$\begin{aligned} \Vert w-v\Vert _{L^{\infty }\left( S_{\phi _h}(0, 2\theta )\right) } \le (\mathrm {I}) + (\mathrm {II})\le \frac{1}{2}\left( \theta ^{\frac{1}{2}}\right) ^{1+\alpha }, \end{aligned}$$

proving (4.20). The proof of Theorem 1.4 is complete. $\square$

5 Proof of the global $W^{1,p}$ and Hölder estimates

In this section, we prove the main result of the paper (Theorem 1.1) regarding global $W^{1,p}$ estimates for solutions to (1.1). We also prove the global Hölder estimates in Theorem 1.7.

5.1 Global $W^{1,p}$ estimates

Before giving the proof of Theorem 1.1, we indicate its overall structure. First, we bound the solution using the global maximum principle in Lemma 1.5. Then, using a consequence of the boundary Localization Theorem for the Monge–Ampère equations [24, 25], we combine the pointwise $C^{1,\alpha }$ estimates in the interior and at the boundary in Theorems 1.2 and 1.4 to bound the gradient by the function N defined in (1.8). The rest of the proof of Theorem 1.1 is similar to that of Theorem 1.3. Here, we use the global strong-type estimate for the maximal function $\mathcal {M}$ in Theorem 1.6 and the volume growth of sections of $\phi$. Notice that by [19, Corollary 2.4], there exist constants $c_{*}, C_{1}, C_{2}$ depending only on $\rho , \lambda , \Lambda$, and n such that for any section $S_{\phi }(x, t)$ with $x\in \overline{\Omega }$ and $t\le c_{*}$, we have

$$\begin{aligned} C_{1} t^{n/2}\le |S_{\phi }(x, t)|\le C_{2} t^{n/2}. \end{aligned}$$

(5.1)

Proof of Theorem 1.1

We extend $\varphi$ to a $C^{1,\gamma }(\overline{\Omega })$ function in $\overline{\Omega }$. By multiplying u by a suitable constant, we can assume that

$$\begin{aligned} \Vert f\Vert _{L^{q}(\Omega )} + \Vert \varphi \Vert _{C^{1,\gamma }(\overline{\Omega })}\le 1. \end{aligned}$$

By the global maximum principle in Lemma 1.5, we have

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega )} \le C \left( \Vert f\Vert _{L^{q}(\Omega )} + \Vert \varphi \Vert _{L^{\infty }(\Omega )}\right) \le C \end{aligned}$$

(5.2)

for some C depending on $n, q, \rho , \lambda$, and $\Lambda$. It remains to show that for all $p<\frac{nq}{n-q}$, we have

$$\begin{aligned} \Vert Du\Vert _{L^{p}(\Omega )} \le C(n, p, q, \gamma ,\rho , \lambda ,\Lambda ). \end{aligned}$$

(5.3)

Using Theorem 1.3 and restricting our estimates in small balls of definite size around $\partial \Omega$, we can assume throughout that $1-\theta \le g\le 1+ \theta$ where $\theta$ is the smallest of the two $\theta$’s in Theorems 1.2 and 1.4.

Let $y\in \Omega$ with $r:=\text {dist}(y,\partial \Omega ) \le c,$ for c universal ($c\ll \theta$). Since $\phi$ is $C^{1, 1}$ on the boundary $\partial \Omega$, by Caffarelli’s strict convexity theorem [3], $\phi$ is strictly convex in $\Omega$. This implies the existence of the maximal interior section $S_{\phi }(y, h)$ of $\phi$ centered at y with $h:=\sup \{t\,| S_{\phi }(y,t)\subset \Omega \}>0.$ By [21, Proposition 3.2] applied at the point $x_0\in \partial S_{\phi }(y,h) \cap \partial \Omega ,$ we have

$$\begin{aligned} h^{1/2} \sim r, \end{aligned}$$

(5.4)

and $S_{\phi }(y,h)$ is equivalent to an ellipsoid E, that is, $cE \subset S_{\phi }(y,h)-y \subset CE,$ where

$$\begin{aligned} E :=h^{1/2}A_{h}^{-1}B_1(0), \quad \text{ with } \quad \Vert A_{h}\Vert , \Vert A_{ h}^{-1} \Vert \le C |\log h|;\, \, \det A_{h}=1. \end{aligned}$$

(5.5)

Moreover, by [19, Theorem 2.1], we have the engulfing property of sections of $\phi$. That is, there exists $\theta _{*}>0$ depending only on $\rho , \lambda , \Lambda$, and n such that if $y\in S_\phi (x, t)$ with $x\in \overline{\Omega }$ and $t>0$, then $S_\phi (x, t)\subset S_\phi (y, \theta _{*}t).$ Hence, for any $z\in S_\phi (y, h)$ the following inclusions hold:

$$\begin{aligned} z\in S_{\phi }(y, h)\subset S_\phi (x_0,\theta _*h) \subset S_\phi (x_0,2\theta ^{-1} t) \subset S_\phi (z,2\theta _*\theta ^{-1}t)\quad \text {for all }t\ge \theta _{*}h. \nonumber \\ \end{aligned}$$

(5.6)

Let $q'$ be such that $\frac{n}{2}<q'<q$. By Theorem 1.4 applied to the original function u in $S_\phi (x_0,\theta _*h)$, we can find $b\in {\mathbb R}^n$ and a universal constant C such that

$$\begin{aligned}&(\theta _*h)^{-\frac{1+\alpha }{2}}\Vert u(x)- u(x_0)- b(x-x_0)\Vert _{L^{\infty }(S_\phi (x_0,\theta _*h))} +\Vert b\Vert \nonumber \\&\quad \le C\Big [\Vert u\Vert _{L^{\infty }(\Omega )} +\Vert \varphi \Vert _{C^{1,\gamma }(\overline{\Omega })} +\sup _{\theta _*h \le t \le \theta ^2} N_{\phi , f, q', 2\theta ^{-1}t}(x_0) \Big ], \end{aligned}$$

(5.7)

where in the definition of $N_{\phi , f, q', 2\theta ^{-1}t}(x_0)$ in (1.7), $\alpha \in (0,1)$ is the exponent in Theorem 1.4.

We now use (5.5) to rescale our equation. The rescaling $\tilde{\phi }$ of $\phi$

$$\begin{aligned} \tilde{\phi }(\tilde{x}):=\frac{1}{ h} \left[ \phi (y+ h^{1/2}A_{h}^{-1}\tilde{x})-\phi (y) -D \phi (y) (h^{1/2}A_{h}^{-1}\tilde{x})\right] \end{aligned}$$

satisfies

$$\begin{aligned} \det D^2\tilde{\phi }(\tilde{x})=\tilde{g}(\tilde{x}):=g(y+ h^{1/2}A_{h}^{-1}\tilde{x})\in [1-\theta ,1+\theta ], \end{aligned}$$

and

$$\begin{aligned} B_{c}(0) \subset S_{\tilde{\phi }}(0, 1) \subset B_{C}(0), \quad \quad S_{\tilde{\phi }}(0, 1)= h^{-1/2} A_{ h}\big (S_\phi (y, h)- y\big ), \end{aligned}$$

(5.8)

where we recall that $S_{\tilde{\phi }}(0, 1)$ represents the section of $\tilde{\phi }$ at the origin with height 1. We denote $\tilde{S}_{t}= S_{\tilde{\phi }}(0, t).$ We define also the rescaling $\tilde{u}$ for u

$$\begin{aligned} \tilde{u}(\tilde{x}):= h^{-1/2}\big [u(x)- u(x_{0})-b(x-x_0)\big ],\quad \tilde{x}\in \tilde{S}_{1}, \quad x=T\tilde{x}:=y+ h^{1/2}A_{h}^{-1}\tilde{x}. \end{aligned}$$

Let $\tilde{\Phi }= (\tilde{\Phi }^{ij})_{1\le i, j\le n}$ be the cofactor matrix of $D^2\tilde{\phi }$. Then, by (2.1), $\tilde{u}$ solves

$$\begin{aligned} \tilde{\Phi }^{ij} \tilde{u}_{ij} = \tilde{f}(\tilde{x}):= h^{1/2} f(T\tilde{x}). \end{aligned}$$

From (5.7), (5.2), and (5.4), we have

$$\begin{aligned} \Vert \tilde{u}\Vert _{L^{\infty }(\tilde{S}_{1})}\le & {} C h^{-1/2} (\theta _*h)^{\frac{1+ \alpha }{2}} \Big [\Vert u\Vert _{L^{\infty }(\Omega )} +\Vert \varphi \Vert _{C^{1,\gamma }(\overline{\Omega })} + \sup _{\theta _*h \le t \le \theta ^2} N_{\phi , f, q', 2\theta ^{-1}t}(x_0) \Big ]\nonumber \\\le & {} Cr^{\alpha } \Big [1+ \sup _{\theta _*h \le t \le \theta ^2} N_{\phi , f, q', 2\theta ^{-1}t}(x_0) \Big ]. \end{aligned}$$

(5.9)

Now, in the definition of N in (1.8), we let $\alpha \in (0,1)$ be the exponent in Theorem 1.4 and $r_0=2\theta _*\theta$. Apply Theorem 1.2 to $\tilde{u}$ and arguing as in (3.4), we obtain

$$\begin{aligned} \left| D\tilde{u} (\tilde{z})\right| \le C\Big [\Vert \tilde{u} \Vert _{L^{\infty }(\tilde{S}_{1})} + N_{\tilde{\phi }, \tilde{f}, q'}(\tilde{z})\Big ]\quad \text {for a.e. } \tilde{z} \in \tilde{S}_{1/2}. \end{aligned}$$

Note that, by (5.5) and (5.4),

$$\begin{aligned} N_{\tilde{\phi }, \tilde{f}, q'}(\tilde{z})\le h^{\frac{\alpha }{2}} N_{\phi , f, q'}(z) \le C r^{\alpha } N_{\phi , f, q'}(z)\quad \text{ with } \, z=T\tilde{z}. \end{aligned}$$

(5.10)

It is easy to see from the definitions of $N_{\phi , f, q', 2\theta ^{-1} t}(x_0)$ and $N_{\phi , f, q'}(z)$, (5.6) and the volume estimates in (5.1) that

$$\begin{aligned} N_{\phi , f, q', 2\theta ^{-1}t}(x_0)\le CN_{\phi , f, q', 2\theta _{*} \theta ^{-1}t}(z) \le CN_{\phi , f, q'}(z) \quad \text {for all }t\in [ \theta _*h , \theta ^2]. \end{aligned}$$

(5.11)

Hence, using (5.9) and (5.10), we get

$$\begin{aligned} \left| D\tilde{u} (\tilde{z})\right| \le C r^{\alpha }\Big [1 + N_{\phi , f, q'}(z) + \sup _{\theta _*h \le t \le \theta ^2} N_{\phi , f, q', 2\theta ^{-1}t}(x_0)\Big ] \le C r^{\alpha }\big [1 + N_{\phi , f, q'}(z) \big ] \end{aligned}$$

for a.e. $\tilde{z}=T^{-1} z\in \tilde{S}_{1/2}$. Rescaling back, using

$$\begin{aligned} \tilde{z}= h^{-1/2}A_{ h}(z-y),\quad D\tilde{u} (\tilde{z})= (A_h^{-1})^t(Du(z)-b)\, \text { and }\, h^{1/2}\sim r, \end{aligned}$$

together with (5.7) and (5.11), we find for all $z \in S_{\phi }(y,h/2)$ that

$$\begin{aligned} |Du(z)|= & {} |A_{h}^tD\tilde{u} (\tilde{z}) + b| \le C\left| \log h\right| r^{\alpha } \big [1 + N_{\phi , f, q'}(z) \big ] + C \big [1 + N_{\phi , f, q'}(z) \big ]\\\le & {} C\big [ 1 + N_{\phi , f, q'}(z) \big ]. \end{aligned}$$

In particular, we obtain the following gradient estimate for a.e. $y\in \Omega$ with $dist(y,\partial \Omega )=r\le c,$

$$\begin{aligned} |Du(y)| \le C\big [ 1 + N_{\phi , f, q'}(y) \big ]. \end{aligned}$$

This is a global version of (3.4). Now, we argue as in the proof of Theorem 1.3 and using a global version of strong-type estimate for the maximal function in Theorem 1.6 and the volume growth of sections in (5.1) to conclude the proof of Theorem 1.1. $\square$

5.2 Global Hölder estimates

Proof of Theorem 1.7

The proof of the global Hölder estimates in this theorem is similar to the proofs of [16, Theorem 1.4] and [20, Theorem 4.1]. It combines the boundary Hölder estimates in Proposition 5.1 and the interior Hölder continuity estimates in Corollary 2.4 using Savin’s Localization Theorem [24, 25]. Thus we omit the details and only present the proof of Proposition 5.1 below. $\square$

Proposition 5.1

Let $\phi$ and u be as in Theorem 1.7. Then, there exist $\delta , C$ depending only on $\lambda , \Lambda , n, \alpha , \rho$, and q such that, for any $x_{0}\in \partial \Omega \cap B_{\rho /2}(0)$, we have

$$\begin{aligned}&|u(x)-u(x_{0})|\nonumber \\&\quad \le C|x-x_{0}|^{\frac{\alpha _0}{\alpha _0 +3n}} \Big ( \Vert u\Vert _{L^{\infty }(\Omega \cap B_{\rho }(0))} + \Vert \varphi \Vert _{C^\alpha (\partial \Omega \cap B_{\rho }(0))} + \Vert f\Vert _{L^{q}(\Omega \cap B_{\rho }(0))} \Big )\\&\quad \text {for all } x\in \Omega \cap B_{\delta }(x_{0}), \end{aligned}$$

where

$$\begin{aligned} \alpha _0 :=\min \big \{\alpha , \frac{3}{8}(2-\frac{n}{q})\big \}. \end{aligned}$$

The proof of Proposition 5.1 relies on an extension of Lemma 4.2 and a construction of suitable barriers.

In what follows, we assume $\phi$ and $\Omega$ satisfy the assumptions in the proposition. We also assume for simplicity that $\phi (0)=0\, \text{ and } \, \nabla \phi (0)=0.$ Furthermore, we abbreviate $B_r(0)$ by $B_r$ for $r>0$.

We now recall the following construction of supersolution in [20].

Lemma 5.2

[20, Lemma 4.4] Given $\delta$ universally small ($\delta \le \rho$), define

$$\begin{aligned} \tilde{\delta }:= \frac{\delta ^3}{2}\quad \text{ and } \quad M_{\delta }:= \frac{2^{n-1} \Lambda ^n}{\lambda ^{n-1}}\frac{1}{\delta ^{3n-3}} \equiv \frac{\Lambda ^{n}}{(\lambda \tilde{\delta })^{n-1}}. \end{aligned}$$

Then the function

$$\begin{aligned} w_{\delta }(x', x_n):= M_{\delta } x_{n} + \phi - \tilde{\delta }|x'|^2 - \frac{\Lambda ^n}{( \lambda \tilde{\delta })^{n-1}} x_{n}^2\quad \text{ for }\quad (x', x_n)\in \overline{\Omega } \end{aligned}$$

satisfies

$$\begin{aligned} \Phi ^{ij}(w_{\delta })_{ij} \le - n\Lambda \quad \text{ in }\quad \Omega , \end{aligned}$$

and

$$\begin{aligned} w_{\delta } \ge 0 ~\text { on }~ \partial (\Omega \cap B_\delta ), \quad w_{\delta } \ge \frac{\delta ^3}{2} ~\text { on }~ \Omega \cap \partial B_{\delta }. \end{aligned}$$

The next result is an extension of Lemma 4.2 where sections are now replaced by balls.

Lemma 5.3

Let $A= \Omega \cap B_\delta (0)$ where $\delta \le c$ with $c= c(n,\lambda ,\Lambda , \rho )$ being universally small. Assume that $f\in L^q(A)$ for some $q>n/2$ and $u\in W^{2,n}_{loc}(A)\cap C(\overline{A})$ satisfies

$$\begin{aligned} \mathcal {L}_{\phi } u\le f\quad \text{ almost } \text{ everywhere } \text{ in }\quad A. \end{aligned}$$

Then there exists a constant $C>0$ depending only on $n, \lambda , \Lambda , \rho$, and q such that

$$\begin{aligned} \sup _{A}{u} \le \sup _{\partial A}{u^+} + C |A|^{\frac{3}{4}\left( \frac{2}{n} -\frac{1}{q}\right) } \Vert f\Vert _{L^q(A)}. \end{aligned}$$

Proof

Let $G_A(\cdot , y)$ be the Green’s function of $\mathcal {L}_{\phi }$ in A with pole $y\in A$. As in the proof of Lemma 4.2, it suffices to prove that

$$\begin{aligned} \Vert G_A(x, \cdot )\Vert _{L^{q'}(A)}\le C|A|^{\frac{3}{4}\left( \frac{2}{n}-\frac{1}{q}\right) }\quad \text {for all~}x\in A. \end{aligned}$$

(5.12)

Note that from (4.1) and (4.2) we have for $h\le c$

$$\begin{aligned} \overline{\Omega }\cap B^{+}_{ch^{1/2}/\left| \log h\right| }\subset S_{\phi }(0, h) \subset \overline{\Omega } \cap B^{+}_{C h^{1/2} \left| \log h\right| }. \end{aligned}$$

Hence for $|x|\le \delta \le c$, we deduce from the first inclusion that

$$\begin{aligned} A=\Omega \cap B_\delta (0)\subset S_\phi \left( 0, \delta ^{3/2}\right) :=V. \end{aligned}$$

(5.13)

Arguing as in (4.8), (4.10), we find that

$$\begin{aligned} \Vert G_V(x, \cdot )\Vert _{L^{q'}(V)}\le C|V|^{\frac{2}{n}-\frac{1}{q}}\quad \text {for all~}x\in V. \end{aligned}$$

(5.14)

Using the volume estimate for sections in (4.5), we find that

$$\begin{aligned} |V|\le C \delta ^{\frac{3n}{4}}\le C|A|^{\frac{3}{4}}. \end{aligned}$$

This together with (5.14) and (5.13) implies (5.12).

Proof of Proposition 5.1

Our proof follows closely the proof of Proposition 2.1 in [16]. We include here the details for reader’s convenience. Since

$$\begin{aligned} \Vert \varphi \Vert _{C^{\alpha _0}(\partial \Omega \cap B_{\rho })} \le C(\alpha _0, \alpha ,\rho ) \Vert \varphi \Vert _{C^\alpha (\partial \Omega \cap B_{\rho })}, \end{aligned}$$

it suffices to show that

$$\begin{aligned}&|u(x)-u(x_{0})|\le C|x-x_{0}|^{\frac{\alpha _0}{\alpha _0 +3n}} \Big ( \Vert u\Vert _{L^{\infty }(\Omega \cap B_{\rho })} + \Vert \varphi \Vert _{C^{\alpha _0}(\partial \Omega \cap B_{\rho })} + \Vert f\Vert _{L^{q}(\Omega \cap B_{\rho })} \Big )\\&\text {for all }x\in \Omega \cap B_{\delta }(x_{0}). \end{aligned}$$

We can suppose that $K:= \Vert u\Vert _{L^{\infty }(\Omega \cap B_{\rho })} + \Vert \varphi \Vert _{C^{\alpha _0}(\partial \Omega \cap B_{\rho })} + \Vert f\Vert _{L^{q}(\Omega \cap B_{\rho })}$ is finite. By working with the function $v:= u/K$ instead of u, we can assume in addition that

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(\Omega \cap B_{\rho })} + \Vert \varphi \Vert _{C^{\alpha _0}(\partial \Omega \cap B_{\rho })} + \Vert f\Vert _{L^{q}(\Omega \cap B_{\rho })}\le 1 \end{aligned}$$

and need to show that the inequality

$$\begin{aligned} |u(x)-u(x_{0})|\le C|x-x_{0}|^{\frac{\alpha _0}{\alpha _0 +3n}}\quad \text {for all }x\in \Omega \cap B_{\delta }(x_{0}) \end{aligned}$$

(5.15)

holds for all $x_0\in \Omega \cap B_{\rho /2}$, where $\delta$ and C depend only on $\lambda , \Lambda , n, \alpha , \rho$, and q.

We prove (5.15) for $x_{0} =0$. However, our arguments apply to all points $x_0\in \Omega \cap B_{\rho /2}$ with obvious modifications. For any $\varepsilon \in (0,1)$, we consider the functions

$$\begin{aligned} h_{\pm }(x) := u(x)- u(0)\pm \varepsilon \pm \frac{6}{\delta _2^3} w_{\delta _2} \end{aligned}$$

in the region

$$\begin{aligned} A:= \Omega \cap B_{\delta _{2}}(0), \end{aligned}$$

where $\delta _{2}$ is small to be chosen later and the function $w_{\delta _2}$ is as in Lemma 5.2. We remark that $w_{\delta _2}\ge 0$ in A by the maximum principle. Observe that if $x\in \partial \Omega$ with $|x|\le \delta _{1}(\varepsilon ):= \varepsilon ^{1/\alpha _0}$ then,

$$\begin{aligned} |u(x)-u(0)| =|\varphi (x)-\varphi (0)| \le |x|^{\alpha _0} \le \varepsilon . \end{aligned}$$

(5.16)

On the other hand, if $x\in \Omega \cap \partial B_{\delta _2}$ then from Lemma 5.2, we obtain $\frac{6}{\delta _2^3} w_{\delta _2}(x)\ge 3.$ It follows that, if we choose $\delta _{2}\le \delta _{1}$ then from (5.16) and $|u(x)-u(0)\pm \varepsilon |\le 3$, we get

$$\begin{aligned} h_{-}\le 0, \, h_{+}\ge 0~\text { on }~\partial A. \end{aligned}$$

Also from Lemma 5.2, we have

$$\begin{aligned} -\mathcal {L}_{\phi } h_{+}\le f, \, -\mathcal {L}_{\phi } h_{-}\ge f~\text { in }~A. \end{aligned}$$

Here we recall that $\mathcal {L}_{\phi }=-\Phi ^{ij} \partial _{ij}.$ Hence Lemma 5.3 applied in A gives the following estimates

$$\begin{aligned} h_{-}\le C_1 |A|^{\frac{3}{4}\left( \frac{2}{n}-\frac{1}{q}\right) } \Vert f\Vert _{L^{q}(A)}\le C_{1}\delta _{2}^{\frac{3}{4}\left( 2-\frac{n}{q}\right) }~\text { in }~ A \end{aligned}$$

(5.17)

and

$$\begin{aligned} h_{+}\ge - C_{1}|A|^{\frac{3}{4}\left( \frac{2}{n}-\frac{1}{q}\right) } \Vert f\Vert _{L^{q}(A)}\ge -C_1 \delta _{2}^{\frac{3}{4}\left( 2-\frac{n}{q}\right) }~\text { in }~ A \end{aligned}$$

(5.18)

where $C_1>1$ depends only on $n,\lambda ,\Lambda , \rho$, and q. By restricting $\varepsilon \le C_{1}^{-1}(\le 1)$, we can assume that

$$\begin{aligned} \delta _{1}^{\frac{3}{4}\left( 2-\frac{n}{q}\right) } = \varepsilon ^{\left( 2-\frac{n}{q}\right) \frac{3}{ 4\alpha _0}}\le \varepsilon ^2\le \frac{\varepsilon }{C_{1}}. \end{aligned}$$

Then, for $\delta _{2}\le \delta _{1}$, we have $C_{1}\delta _{2}^{\frac{3}{4}(2-\frac{n}{q})}\le \varepsilon$ and thus, for all $x\in A$, we obtain from (5.17) and (5.18) that

$$\begin{aligned} |u(x)-u(0)|\le 2\varepsilon + \frac{6}{\delta _2^3} w_{\delta _2}(x). \end{aligned}$$

Note that, by construction and the boundary estimate for the function $\phi$, we have in A

$$\begin{aligned} w_{\delta _2}(x)\le M_{\delta _2} x_n + \phi (x)\le M_{\delta _2}\left| x\right| + C\left| x\right| ^2\left| \log \left| x\right| \right| ^2\le 2M_{\delta _2}\left| x\right| . \end{aligned}$$

Therefore, choosing $\delta _{2}= \delta _{1}$ and recalling the choice of $M_{\delta _2}$, we get

$$\begin{aligned} |u(x)-u(0)|\le 2\varepsilon + \frac{12 M_{\delta _2}}{\delta _2^3}\left| x\right| = 2\varepsilon + \frac{C_{2}(n,\lambda , \Lambda )}{\delta _{2}^{3n}}|x| = 2\varepsilon + C_{2} \varepsilon ^{-\frac{3n}{\alpha _0}}|x|\nonumber \\ \end{aligned}$$

(5.19)

for all $x,\varepsilon$ satisfying the following conditions

$$\begin{aligned} |x|\le \delta _{1}(\varepsilon ):= \varepsilon ^{1/\alpha _0},\quad \varepsilon \le C_{1}^{-1}. \end{aligned}$$

Finally, let us choose $\varepsilon = |x|^{\frac{\alpha _0}{\alpha _0 + 3n}}.$ It satisfies the above conditions if $|x|\le C_{1}^{-\frac{\alpha _0 +3n}{\alpha _0}}=: \delta .$ Then, by (5.19), we have $|u(x)-u(0)| \le (2 + C_2) |x|^{\frac{\alpha _0}{\alpha _0 + 3n}}\,$ for all $\, x\in \Omega \cap B_{\delta }(0)$. $\square$