Introduction

Microfluidic devices find an application in the study of various chemical engineering, physical, and biological processes (Tian and Finehout 2009). Simultaneously, continuous-flow microreactors (Tian and Finehout 2009; Nguyen 2011; Reschetilowski 2013; Nimafar 2013) have become a decisive breakthrough in the development of chemical engineering since the pharmaceutical industry needs flexible production rather than a large amount of product yield. Microreactors created in the interests of low-tonnage chemical production usually represent an extensive network of converging and diverging channels (Reschetilowski 2013; Levenspiel 1999). The reason is that the products of fine organic synthesis are the final part of multi-component and multistage reactions that proceed under different conditions and have different rates. For more than 50 years of history (Levich et al. 1967; Brodskii and Levich 1967), the evolution of continuous-flow reactors has led to their sharp decrease in size. Although microfluidic devices and microreactors in flow chemistry are similar in many aspects, they operate in slightly different, albeit overlapping, spatial ranges. If the former ones have a typical channel width ranging from 1 to 1000 \(\mu\)m, then the width of the latter ones starts from 500 \(\mu\)m and can go up to centimeters.

Fig. 1
figure 1

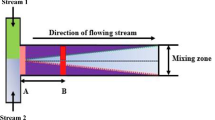
(up) Schematic representation of a Y-shaped microreactor with two inputs and one output. The characteristic sizes of the outlet channel are determined by its height d and the length of the output tube L. (bottom) Photograph of the general view of the laboratory setup: 1 – microreactor with Y-type mixer, 2 – injection syringes connected with inlet tubes, 3 – syringe pump, 4 – laser sheet, 5 – CCD camera

Full size image

In continuous-flow microreactors, the reactants enter the reaction zone through separate channels, where they mix and react, forming the reaction product at the outlet. High productivity, uniform, and stable conditions, simple control in consumption of reagents and energy, and a possibility to increase the output by elements’ replication are the main but not exhaustive advantages concerning the traditional batch-reactors. Influenced by the needs of the pharmaceutical industry in flexible and reconfigurable flow systems with low product yield, miniature systems with a reactor zone size in the millimeter and submillimeter ranges have become widespread in the last decade (Newman and Jensen 2013; Filipponi et al. 2014; Baumann and Baxendale 2015; Pellegatti and Sedelmeier 2015; Martin et al. 2015; Wegner et al. 2011). The transition to the micro-scale led to the problem of reagents mixing. Due to the small transverse dimension of the reaction zone, the laminar flows dominate, and the transverse mixing of the reactants becomes possible solely due to diffusion. Because of the low diffusion rate, one needs a rather extended tube to provide complete mixing, which results in a significant increase in the time required to complete the reaction.

To reduce the reaction time, one proposed various mixing systems. There are two main types of mixing control: active and passive (Hessel et al. 2005; Cai et al. 2017). The first way requires the supply of energy from the outside by mechanical impact (Gershuni and Lyubimov 1998; Bratsun et al. 2017, 2018b), heat (Singer and Bau 1991; Tsai and Lin 2002; Bratsun et al. 2005; Bratsun and De Wit 2008), or electromagnetic fields (Bau et al. 2001). This type of mixing system is usually limited in microreactors due to the small size of the reaction zone or the immunity of the reacting substances to electromagnetic influences (although some new technical solutions have appeared here as well, see for example papers of Boyko et al. (2015, 2016) and Siraev et al. (2021)). Passive mixing systems use the internal energy of the flow. In addition to the diffusion mechanism, convection is an effective way to mix the reagents. Most of the technological solutions to this problem presented in the literature are focused on complicating the channel topology, which leads to forced convection of solutions under the influence of a pressure difference (Nimafar et al. 2012a, b; Ohkawa et al. 2008; Viktorov et al. 2015; Noro et al. 2008; Nguyen et al. 2008). This approach initiates a vortex motion of the liquid, which provides good mixing and a higher reaction rate. The disadvantage of this type of mixing system is significant pressure has to be applied to pump the liquid through geometrically complex zones, involving higher energy costs (Nieves-Remacha et al. 2012).

In the case of a complex reaction sequence developing in several stages, a continuous-flow chemical microreactor can be assembled in the form of a network that consists of standard designer parts. In recent years, these standard parts of the kit have been intensively studied separately for various applications and include T-junction (Minakov et al. 2010; Arias and Montlaur 2018; Han and Chen 2019; Tian et al. 2019; Arias and Montlaur 2020; Hao et al. 2022), Y-junction (Minakov et al. 2010; Cai et al. 2017; Huang et al. 2020), and X-junction (Bratsun et al. 2018b; Bratsun and Siraev 2020b; Raja et al. 2021) of channels.

Previously, we have proposed several designs of mixers that used natural or forced convection. For example, a recent study (Bratsun et al. 2018a) showed the possibility to apply the solutal Marangoni convection to mix solutes in an X-shaped continuous-flow microreactor. We have demonstrated that the gravity-dependent convective mechanisms also can be used for efficient mixing in a Hele-Shaw microreactor (Bratsun and Siraev 2020a, b).

In this work, we demonstrate in a series of experiments that diffusive instabilities initially studied in Refs.  (Stern 1960; Stern and Turner 1969; Turner 1974) could be an efficient instrument to mix two solutions in a Y-shaped long narrow channel. We applied several optical methods to visualize convective flows and the distribution of solutes to estimate how the mixing rate changes along the channel tube. We compare this mixing method with the cases of pure diffusion and the Rayleigh-Taylor convection. In addition, we numerically investigate the efficiency of the above mechanisms of natural convection and compare the obtained numerical results with the experimental data.

Experimental Setup

The experimental setup is presented in Fig. 1. The mixing substances come into the reaction zone through a Y-type mixer (indicated by 1 in Fig. 1), forming a two-layer system at the beginning of the zone. The reaction zone has a form of long narrow channel of \(d=0.25\) cm height, \(h=0.02\) cm width, and \(l=7\) cm length. Both inlets are connected by transparent tubes with injection syringes (2). The volume flow rate q through the each inlet is carefully controlled through a syringe pump SPLab 02, UNIX Instruments (3). The pump fills the channel with aqueous solutions of two different inorganic substances A and B with equal volume flow rates q, that vary in our experiments in the range of \(q=(0.002-0.015)\) ml/min. This range corresponds to the range of volume flow rates inside the channel (for our geometry) \(Q=2 q=(0.004-0.030)\) ml/min.

It is known that we can get different types of diffusion instability by manipulating the initial arrangement of solutions in the upper and lower incoming tubes of the Y-shaped channel. Depending on the inlet tube, which supplies the reaction zone with a solute with a higher diffusion coefficient, we can distinguish two types of diffusive instability. If the faster component enters the mixing zone through the lower inlet tube, then double diffusion (DD) instability develops there. Otherwise, one observes the double-layer convection (DLC). A necessary condition for the development of diffusion instability is a statically stable stratification of a two-layer system, which arises behind the junction of the incoming channels. If this condition is not met, then the system becomes unstable to Rayleigh-Taylor perturbations. In case when none of the above events occurs, convective instability does not develop, and the flow remains laminar throughout the entire outflow channel. Table 1 shows the configurations of the solutions that were used in this work. As one can see from the table, we used various inorganic salts that are chemically inert with respect to each other.

Table 1 Pairs of aqueous solutions with initial concentrations \(A_0\) (the upper inlet channel) and \(B_0\) (the lower inlet channel), which were considered experimentally and numerically in the present work. The table provides dimensional values of physical coefficients characterizing properties of solutions, which include the initial densities of solutions \(\rho _{a}\), \(\rho _{b}\) and their diffusion coefficients \(D_a\), \(D_b\). Also, the values of key dimensionless parameters such as the ratio of the initial concentrations of species \(\gamma =B_0/A_0\), the diffusion coefficient ratio \(\delta =D_b/D_a\), and the buoyancy ratio \(\varphi\) are calculated for all pairs under consideration. The last column indicates the type of convective motion (DD, DLC, and RT) that is excited when the input conditions are met. Laminar flow with the pure diffusive mixing is realized in the case no. 5
Full size table

Experimental Study

For example, to create conditions for the development of the DD instability, we injected through the upper and lower inlet tubes of Y-micromixer a less dense solution of copper sulfate CuSO\(_4\) and a more dense solution of potassium chloride KCl, respectively (see the cases no. 1 and 2 listed in Table 1). If we redirected the same solutions respectively into the lower and upper inlet tubes, then conditions arise for the excitation of the DLC instability (see the case no. 3 listed in Table 1). The RT instability was reproduced using an aqueous solution of KCl and pure water, which were directed, respectively, into the upper and lower channels (see the case no. 4 in Table 1). The salt solution is always denser in relation to pure water, which creates a statically unstable configuration in the mixing zone. If we swap the fluids in places, then we get, on the contrary, an absolutely stable system, in which only the mechanism of diffusion works (see the case no. 5 in Table 1).

To differentiate two streams coming from the upper and lower inlet tubes and visualize the mixing process, we dissolved the fluorescent dye Rhodamine B in the KCl solution. The mass concentration of Rhodamine in KCl solution was \(5\times 10^{-5}\)%. Such a concentration is so low that it does not influence the physical properties of the KCl solution. As an illumination source of the channel, we used the laser sheet (indicated by 4 in Fig. 1) with wavelength \(\lambda =532\) nm. It allowed us to see the concentration distribution of the Rhodamine that in the light of the green spectrum fluoresces in the red one. The quantitative analysis of mixing was carried out based on the intensity field of the dye, which is equivalent to its concentration field.

The experiments were carried out for several volume flow rates Q as shown in Table 2. The corresponding flow velocities and Reynolds numbers are also listed in Table 2. The Reynolds number \(Re={Q{{D}_{H}}}/{\nu S}\;\) is defined in terms of a volume flow rate (\({D}_{H}\) and S are the hydraulic diameter and cross-section of the channel, respectively) and calculated for the properties of solvent (water). The assumption \(Re\ll 1\) ensures that the flow is always laminar in the experiments.

Fig. 2
figure 2

Time evolution of concentration field of Rhodamine at \(Q = 0\) ml/min (no fluid is pumped through the Y-channel). Two aqueous solutions of copper sulfate CuSO\(_4\) and potassium chloride KCl are fed through the upper and lower inlet tubes, respectively. The concentration of the solutions corresponds to case no. 1 in Table 1. Figure presents raw images that have not yet been processed

Full size image

The observed region of the channel was fixed to 3 cm (or 12d in terms of the channel’s height) and includes an initial segment of the output tube (the distance is measured from a point where the two streams converge). During the one test, three consecutive images of the mixing zone with an interval of 1 minute were captured by a high-speed color camera Nikon 5200 (indicated by 5 in Fig. 1). We repeated this procedure for all volume rates. The first image was taken after 30 minutes since the pump started that guaranteeing the steady-state of fluids flow. To minimize the post-processing error, we produced the average image and converted it into greyscale. This procedure is described below in more detail. In some experiments, we applied the shear interferometry method (Wyant 1975) to visualize the structure of convective flows. All experiments we performed at room temperature (24±1)\(^\circ\)C.

Table 2 Parameters of experiments with continuous-flow mixing
Full size table

During the one test, we captured three-color images of the channel at each value of the volume flow rate. Then we converted all images into greyscale monochromatic images following the procedure described in Refs. (Nguyen 2011; Nimafar et al. 2012b). To get the photograph with a higher signal-to-noise ratio, we averaged them to one. Then the background correction was employed. Before each experiment, we took a snapshot of the empty channel illuminated by the laser sheet. In what followed, this snapshot served as the benchmark. We always subtracted it (in greyscale) to correct the inhomogeneity of the light sheet intensity. Then we obtained a ready-to-process matrix of gray values. Lambert-Beer’s law states that the light intensity linearly depends on the concentration change. It implies that we can convert the luminance grey level of the pixel into normalized depth-averaged dye concentration for this pixel. Thus, the two-dimensional matrix of grey values characterizes the two-dimensional distribution of the Rhodamine concentration. However, to estimate the mixing extent of layers with and without dye, it is not necessary to get the values of the dye concentration. The degree of mixing at a chosen area 1 pixel width and 500 pixels height across the channel length can be evaluated by calculation of the mixing parameter M defined in Refs. (Nimafar 2013; Stroock et al. 2002) as

$$\begin{aligned} M = \left( 1 - \frac{\sigma ^2}{\sigma _\mathrm{{max}}^2} \right) ^{1/2} , \end{aligned}$$
(1)

where \(\sigma\) stands for the standard deviation of the grey luminance, \(\sigma _\mathrm{{max}}\) is the maximum standard deviation over the channel. The value of M varies from 0 to 1, with 1 (100%) indicating complete mixing and values tending to 0 indicating the state of spatially separated layers. We can calculate the standard deviation using the following definition:

$$\begin{aligned} \sigma = \left( \frac{1}{N}\sum _{i=1}^N (I_i - {\hat{I}})^2\right) ^{1/2} , \end{aligned}$$
(2)

where N is the number of pixels in the chosen area, \(I_i\) is the intensity at pixel i, and \(\hat{I}\) is the mean intensity of the chosen area. Prior to using the Eq. (2) the value of \(\sigma\) was always normalized by 0.5.

Fig. 3
figure 3

Concentration field of Rhodamine shown for different values of the volume flow rate. The mixture parameters are the same as in Fig. 2. Figure presents raw images that have not yet been processed

Full size image

Experimental Results

Generally, when the solutes in a two-layer system diffuse at different rates, one can observe the development of diffusive instability. If the faster component is dissolved in the upper layer, then the DLC instability arises. In the opposite case, when the lower species diffuse faster, the DD instability develops. Let us focus on the case of the DD instability in more detail. Figure 2 shows the time evolution of the structure of the DD convection without pumping, i.e. at \(Q = 0\) ml/min. The photographs show the distribution of Rhodamine concentration at successive times. At the beginning of evolution (\(t=5\) s), the snapshot has a high contrast level. The lower layer has a color close to white, the upper one – to black. It implies that Rhodamine, at the moment, is only in the lower layer. So, the initial layers are completely separated. Further, we can see the development of the DD convection in the form of finger structure symmetrically propagating up and down from the initial contact surface. Upward and downward convective currents redistribute Rhodamine so that its concentration in the lower layer decreases and, simultaneously, increases in the upper layer.

Fig. 4
figure 4

Visualization of the convective structure (a) and the concentration field of Rhodamine (b) at \(Q=0.020\) ml/min. The mixture parameters are the same as in Fig. 2. The fragment (a) shows the areas of the mixing zone that were selected for processing the photograph (see explanations in the text). Figure presents raw images that have not yet been processed

Full size image

The process of the Rhodamine redistribution in a two-layer system manifests itself by a change in the brightness of its luminescence, which makes it possible to analyze the mixing process. Since no fluid is pumped in this experiment, the degree of mixing does not change along the channel and depends only on time.

When we switch on the pumping of the liquid, the structure of flow changes. Figure 3 shows the snapshots of the channel obtained for several values of flow rates when the flow is at the steady state. We can see that, as a flow rate increases, the length of the area where layers are separated becomes longer. It means that the mixing length also increases with the flow rate. Due to constant pumping, this visualization method does not allow us to see the finger structure. For this purpose, we used a shearing interferometry technique.

Figure 4a and b show the snapshot of the mixing zone for \(Q=0.020\) ml/min, obtained by the shear interferometer and the dye, respectively. The shear interferometer makes it possible to visualize the distribution of the refractive index derivative. In our experiments, the refractive index non-uniformity is affected by variations of solutes concentration. Therefore the interferogram patterns reflect mainly a spatial distribution of the derivative of solutes concentration. Since the characteristic diffusive time is three orders of magnitude larger than the viscous time (the Schmidt number generally is about \(Sc~O(10^3)\)), the moving liquid carries solutes that do not have time to diffuse. It means the interference fringes move together with the liquid medium. Thus, the study of the interference patterns along the channel allows us to visualize the structure of the convective motion.

The interferogram shows how the finger structure changes when we switch on the pumping. Analysis of the shape of the interference fringes allows us to distinguish three distinctive areas along the channel indicated by 1, 2, and 3 in Fig. 4. The first area is at the beginning of the mixing zone. Here, two fluid layers are separated by a narrow diffusion zone, which is visible in the interferogram in the form of many horizontal and not curved bands. The straightness of lines indicates the absence of convection, and, therefore, the diffusion mechanism prevails in this zone. The number of bands characterizes the magnitude of the density gradient between the layers. Since all bands concentrate in a very narrow area, it is impossible to count them and evaluate the value of the density gradient. The second area indicated by 2 corresponds to the onset of the convection. The shape of bands has become more complex. Near the solid boundaries of the tube, we observe a chaotic vortex structure, which indicates the presence of intense convection. Thus, in this region, convection is the leading mass transfer mechanism. Therefore, the process of homogenization of the initially separated layers starts here. On the snapshot showing the dye concentration (Fig. 4b), at the very beginning of the area, we see striking differences in the concentration distribution along the vertical axis. At the end of the region 2, the layers already look well-mixed, and an intermediate color between black and white appears.

In the area indicated by 3, the flow structure again changes suddenly. On the interferogram, we see one wide horizontal band, on the background of which a weak convective motion is visible as periodic sloping stripes. Here, we can conclude that the dominant mass transfer mechanism switched from convection to pure diffusion. At the very beginning of this area, the homogenization proceeds very slow, as it is evidenced by minor changes in the interference pattern and weak changes of grey luminance (Fig. 4). Thus, we analyzed the photographs obtained with the help of Rhodamine and an interferometer. It made it possible to recover the flow structure and formally distinguish the areas with the domination of either the convective or diffusive mechanism of the mass transfer.

We estimated the total length of the mixing zone using the following method. First, we obtained a matrix of gray values from a snapshot of the dye distribution. Then we calculated the M values using the Eq. (1). Figure 5a presents the dependence of the integral M on the distance measured in terms of the height d in a semi-logarithmic scale. Dependencies with different colors correspond to the results for different Reynolds numbers (different volume flow rates). The dependencies obtained fluctuate greatly, which complicates the analysis. To reduce noise of the data we constructed a moving average with a smoothing window of 200 pixels that corresponds to 0.2 in dimensionless units of length (x/d). The resulting dependencies are indicated in the figure by the circle symbols. One can see that the maximum mixing efficiency is achieved at the lowest Reynolds number (\(Q=0.004\) ml/min). In this case, the DD instability results in the convective structure localized at the entrance to the Y-channel. The vortex motion existing in this area mixes the initially separated liquids rather quickly, as evidenced by a sharp increase in the value of the parameter M. Moving along the channel, one can see that the convective mechanism switches to the diffusion one since the value of the parameter M changes more slowly. The length of the zone dominated by the convective mechanism changes due to an increase in the flow velocity. It also affects the mixing length. Figure 5b shows a dependence characterizing the change in the mixing distance L required to achieve mixing of at least 20% (\(M=0.2\)), 50% (\(M=0.5\)), 70% (\(M=0.7\)). We see that the value of L for a fixed pair of liquids increases with the growth of the Reynolds number.

Fig. 5
figure 5

The dependence of a the mixing extent on the channel length for different volume flow rates and b the mixing length required to achieve 20, 50 and 70% mixing, on the volume flow rates. Data obtained for the case no. 1

Full size image

To understand how strongly convection intensifies the mixing process, we also studied a pair of liquids mixing due to diffusion. In this case, the two-layer system consisted of an aqueous solution of KCl supplied from the bottom inlet pipe and pure water incoming from the upper inlet pipe (case no. 5 in Table 1). Under image processing, it turned out that in the case of purely diffusive mixing, the change in the brightness of the dye is comparable to the magnitude of the noise. It leads to a relatively large data scatter in the values of M. Nevertheless, we can still carry out a qualitative analysis of the results in this case, which shows that the diffusion mixing mechanism in the considered geometry is almost an order of magnitude weaker than the convective one.

Comparison of Mixing Efficiency

Let us discuss the efficiency of different mixing techniques using mechanisms of diffusive and convective mass transfer listed in Table 1. Figure 6 shows the images of the mixing zone of a Y-shaped microreactor obtained with the shear interferometer. Figure 6a corresponds to the mixing due to the diffusion mechanism. In this case, the two-layer system is statically stable (heavier liquid in the lower layer), and the dissolved component exists in only one of the layers. One can see that mixing proceeds slowly, and the significant concentration gradient is still evident in the system at a distance of 15d from the place of the first contact of the layers. The total mixing length, in this case, exceeds the downstream distance equal to 50d.

Fig. 6
figure 6

Experimental interferograms showing the process of mixing two solutions, which are pumped through a Y-shaped microfluidic device in the case of a only diffusion processes (water versus aqueous solution of KCl, case no. 5); b double-diffusive instability (aqueous solution of CuSO4 versus aqueous solution of KCl, case no. 2); c diffusive layer convection (aqueous solution of KCl versus aqueous solution of CuSO4, case no. 3); d Rayleigh-Taylor instability (aqueous solution of KCl versus water, case no. 4). The gravity is directed from top to bottom. For ease of perception, black-and-white photographs have been inverted. In all cases, the fluid flow rate is equal to \(Q=0.020\) ml/min

Full size image

If the fast component dissolves in the lower layer, then the DD instability develops as fingers, which propagate vertically in two opposite directions (Fig. 6b). In this case, we found that an almost homogeneous medium appears at a distance of 15d from the junction point. In the opposite case, when the fast component dissolves in the upper layer, the DLC instability develops on both sides of the diffusive layer. The latter is statically stable and separates the channel into two domains of different fluid flows. The diffusion of both solutes leads to the formation of symmetric convective motion in two unstable layers above and below the stable diffusive layer (Fig. 6c). One can see that a stable diffusive zone with significant concentration gradients exists up to the channel end, manifesting the low efficiency of this type of convective flow for the mixing process. Finally, Fig. 6d shows an interferogram of a two-layer system, which is unstable from the very beginning of evolution. Here heavier liquid comes from the upper tube of the Y-shaped microreactor. In this case, the Rayleigh-Taylor instability develops. One can see that this type of convective flow demonstrates the highest mixing efficiency: the total mixing length does not exceed 3d. We should note that the Rayleigh-Taylor instability is sensitive to the channel’s depth. If the channel’s height is comparable to its depth, then the ascending flow of a light fluid prefers to diverge from the descending flow of a heavy liquid in the third dimension. In this case, the actual mixing does not occur because liquids change places.

Theoretical Study

Mathematical Formulation

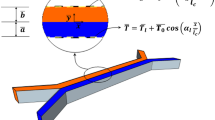
We can use the differences in the physical properties of miscible media to develop one of the convective instabilities. In this work, we consider natural convection defined as a type of flow, in which some parts of the fluid being heavier than the surrounding fluid cause the fluid motion. The driving force for natural convection is gravity \(\mathbf {g}\). We consider an open cavity in the form of three rectilinear tubes converging at one point (see the upper part of Fig. 1). In the literature, this design is commonly referred to as a Y-shaped channel. It is the simplest element of a ramified network of converging and diverging channels designed to maintain a complex multi-step chemical reaction in the flow. To be specific, we assume that the two tubes that come to the branching point on the left serve to supply two different but homogeneously mixed solutions. Then the fluids enter the joint tube, the mixing chamber, at the rate \(v_0\) where they mix, and the result is output further to the right. As in the experiment, we assume that the mixing chamber has a rectangular cross-section 0.25 cm high and 0.02 cm thick (200 \(\mu\)m). Let us set the length of the outlet channel to 7 cm, which is sufficient to complete the mixing process between solutions for the characteristic values of the liquid flow rate (Fig. 1).

Then we assume that both solutions are aqueous and that the solutes are heavier than pure water with a density \(\rho _0\). Let the variables A and B denote the solute concentrations in the upper and lower channels to the left of the bifurcation point. So, these solutions appear above and below the initial contact surface \(y=0\) separating the liquids after the bifurcation point (see the upper part of Fig. 1). We assume that the diffusion coefficients \(D_a\) and \(D_b\) of solutes are constant and independent of their concentrations. The substances dissolved in water are chemically inert, and the entire system, as a whole, is in isothermal conditions.

The Boussinesq approximation is commonly applied in the convection theory for describing buoyancy-driven flows. To complete the work, one needs to expand the density of the medium \(\rho _m\) as a power series of concentrations retaining only linear terms:

$$\begin{aligned} \rho _m = \rho _0 (1 +\alpha A + \beta B) , \end{aligned}$$
(3)

where \(\alpha\) and \(\beta\) are the solutal expansion coefficients for solutes A and B, respectively. In (3), we take into account the fact that all the dissolved substances are heavier than water. The Boussinesq approximation for the convection problems assumes that the variation of density (3) should be taken into account only in terms, which depend on the volumetric force. In our case, this is the only term with a gravity force. The Boussinesq approach is justified for the problems in which “weak” convection exists in the cavity on the laboratory scale, and the density variations caused by thermal or concentration expansion are relatively small.

We choose the following quantities as the units of measurement for length, time, velocity, pressure, and concentrations A, B:

$$\begin{aligned} d,\quad \frac{d^2}{D_a},\quad \frac{D_a}{d},\quad \frac{\rho _0 \nu D_a}{d^2},\quad A_0,\quad B_0, \end{aligned}$$
(4)

respectively. Here, \(\nu\) stands for the dynamic viscosity coefficient of water; \(A_0\) and \(B_0\) are initial concentrations of solutions in the inlet channels.

Thus, the set of governing equations of convection of an incompressible fluid for the problem under consideration includes a three-dimensional Navier-Stokes Eq. (6), coupled with a continuity Eq. (5) and pair of the transport equations for species (7, 8):

$$\begin{aligned} \nabla \cdot {\mathbf {v}} = 0 , \end{aligned}$$
(5)
$$\begin{aligned} \frac{1}{Sc}\left( \frac{\partial {\mathbf {v}}}{\partial t} + {\mathbf {v}}\cdot \nabla {\mathbf {v}}\right) = - \nabla p + \nabla ^2 {\mathbf {v}} - R\rho (A,B) {\mathbf {k}} , \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial A}{\partial t} + {\mathbf {v}}\cdot \nabla A = \nabla ^2 A , \end{aligned}$$
(7)
$$\begin{aligned} \frac{\partial B}{\partial t} + {\mathbf {v}}\cdot \nabla B = \delta \ \nabla ^2 B , \end{aligned}$$
(8)
$$\begin{aligned} \rho (A,B) = A + \varphi \gamma B , \end{aligned}$$
(9)

where \({\mathbf {v}}=(v_x,v_y,v_z)\) is the fluid velocity, p is the pressure, \(\rho\) is the additive to the density of the solvent due to the dissolved substances, and \({\mathbf {k}}\) is a unit vector in the direction of the y-axis.

The transport equations for solutes (7) and (8) are written in a form that ignores the possible effects of both cross-diffusion and concentration-dependent diffusion (the CDD effect). We discussed influence of both phenomena on the system stability in our recent paper (Bratsun et al. 2022), in detail. In short, we use substances that exhibit weak cross-diffusion effect (diffusion of A depends on gradient of B and vice versa), but a fairly strong CDD effect (diffusion coefficients of A and B depend on their concentrations). The properties of aqueous solution LiCl – NaNO\(_3\) used in (Bratsun et al. 2022) and KCl – CuSO\(_4\) (the present study) are similar. In both cases, there are an alkali metal ion (Li\(^{+}\) vs. K\(^{+}\)), a chlorine ion (Cl\(^{-}\)), and a strong acid residue (NO\(_3^{-}\) vs. SO\(_4^{-}\)). Thus, in both cases, cross-diffusion can be neglected, but one could anticipate a strong CDD effect. As we have previously shown (Mizev et al. 2021), the CDD effect manifests itself most clearly near the isopycnal curve, close to that the densities of the solutions are almost equal. In this work, we use solutions with quite divergent density values (see Table 1). Therefore, the CDD effect can also be neglected.

In Eqs. (5)–(9), we obtain several dimensionless parameters that determine the evolution of the system:

$$\begin{aligned} Sc=\frac{\nu }{D_a},\quad R=\frac{g\alpha A_0 d^3}{D_a\nu },\quad Pe=\frac{v_0 d}{D_a},\end{aligned}$$
(10)
$$\begin{aligned} \delta =\frac{D_b}{D_a},\quad \varphi =\frac{\beta }{\alpha },\quad \gamma =\frac{B_0}{A_0}, \end{aligned}$$
(11)

which are, respectively, the Schmidt number, the solutal Rayleigh number, the Péclet number, the diffusion coefficient ratio, the buoyancy ratio, and the ratio of the initial concentrations of species. In experiments, the initial velocity \(v_0\) of solutions in the inlet channels is varied from 0.013 to 0.1 cm/s (see Table 2 for details). Since we are considering a microchannel, the Reynolds numbers for flows developing in this channel are not large \(Re\approx 0.1\). Let us estimate the Peclet number. For example, the corresponding Péclet number Pe for the cases no. 1 and 2 (here, copper sulfate CuSO\(_4\) stands for the substance A) is varied from \(0.71\times 10^3\) to \(5.43\times 10^3\). It is worthy to note that the Péclet number is the ratio of the rate of advection of a solute by the flow to the rate of diffusion of the same solute driven by an appropriate gradient. In our case, the solute gradient is set naturally in the direction of gravity. As can be seen from the estimates, advection significantly exceeds diffusion forcing to construct a longer channel for mixing solutions. Reducing the flow rate through the mixing chamber is often not a good idea because many important applications require a certain amount of product yield (for example, fine chemical synthesis in the continuous-flow microreactors). In this work, we want to find out whether it is possible to at least partially compensate for the length of the channel using the mechanisms of natural convection.

At the entrance and exit of the channels, we set the following boundary conditions for the fluid velocity:

$$\begin{aligned} v|_{x=0} = Pe ,\quad v|_{x=l/d} = Pe . \end{aligned}$$
(12)

The flow direction corresponds to the laminar flow, and the modulus is determined by the Péclet number:

For simplicity, we consider processes only in the pipe, where the solutions are mixed (see mixing chamber zone in Fig. 1). It means that we set the running of the two channels that supply homogeneous solutions with special boundary conditions for the inlet concentrations:

$$\begin{aligned} A|_{x=0, 0\leqslant y< \frac{1}{2}} = 1,\quad A|_{x=0, -\frac{1}{2}< y <0} = 0 ,\end{aligned}$$
(13)
$$\begin{aligned} B|_{x=0, 0\leqslant y< \frac{1}{2}} = 0,\quad B|_{x=0, -\frac{1}{2}< y <0} = 1 , \end{aligned}$$
(14)

At all solid boundaries \(\Gamma\) of the Y-shaped device, we apply the no-slip condition for the velocity and the no-flux condition for the solutes:

$$\begin{aligned} {\mathbf {v}}\bigg |_{\Gamma } = 0 ,\quad \frac{\partial A}{\partial {\mathbf {n}}}\bigg |_{\Gamma } = 0 , \quad \frac{\partial B}{\partial {\mathbf {n}}}\bigg |_{\Gamma } = 0 , \end{aligned}$$
(15)

where \({\mathbf {n}}\) is a unit vector normal to the boundary \(\Gamma\).

In what follows, for convenience of comparison with experiment, we use the dimensional quantities.

Numerical Method

The three-dimensional problem governed by Eqs. (5)–(9), (12, 15) and supplemented by the boundary conditions discussed above has been solved using fluid simulation software, ANSYS CFX (the license no. 1062978 issued to Perm National Research Polytechnical University). Three-dimensional flows have been simulated using the pressure-based numerical scheme. Using this method, ANSYS solves the governing integral equations for the conservation of mass, momentum, and solutes in the dimensional form. A control-volume-based technique consists of the following steps: (a) division of the domain into discrete control volumes using a computational grid, (b) integration of the governing equations on the individual control volumes to construct algebraic equations for the discrete dependent variables such as velocities, pressure, and concentrations, and (c) linearization of the discretized equations and solution of the resulting linear equation system to yield updated values of the dependent variables.

Figure 7 provides details of the construction of the computational mesh we used in 3D simulations. We model the operation of two input channels by setting special boundary conditions for mixture concentrations (11). It is worthy to notice that the concentrations of mixtures near the entrance to the main channel change very quickly, which means high concentration gradients in this area. We accounted for these features of the concentration fields when constructing the grid. One can see from the figure that the grid was denser near the contact surface of two solutions \(y=0\). The smallest size of the mesh elements in the direction of the y-axis was \(5\times 10^{-3}\) mm, while the largest was 0.125 mm. The size of the mesh elements in the direction of the x-axis was constant and fixed to 0.125 mm. The mesh size in the direction of z-axis was significantly smaller: \(2.5\times 10^{-2}\) mm. In total, the computational grid contained 237300 nodes and 206080 elements.

Fig. 7
figure 7

The ANSYS meshing in 3D numerical simulations of the channel flow taking into account possibly large gradients of solutes in the central part of the mixing chamber

Full size image

Verification of the code was carried out on the example of a flow with DD-convection. We gradually reduced the size of the grid elements in different directions. We found that the change in the flow characteristics describing the mixing in the channel was not significant.

Integral quantities play a key role in the analysis of system dynamics. They are constructed based on fields obtained as part of the computational process, and their evolution is tracked throughout the entire simulation.

To compare the numerical results with the experimental data, we introduced the following quantity to characterize the mixing efficiency:

$$\begin{aligned} M_A (x)= & {} \left( 1-\frac{\sigma ^2_A (x)}{\sigma ^2_{Amax}}\right) ^{1/2} , \end{aligned}$$
(16)

where

$$\begin{aligned} \sigma _A (x)= & {} \frac{1}{S(x)}\int \limits _{S(x)}\sqrt{(A-<A>)^2}dydz . \end{aligned}$$
(17)

Here, \(<A>\) is the average value of the concentration in the channel after complete mixing; S(x) stands for a cross-section of the mixing chamber at a distance of x from the channel entry point; \(\sigma _A (x)\) is the standard deviation of the concentration of substance A coming from the upper inlet defined by (17). The maximum deviation \(\sigma _{Amax}\) is given by

$$\begin{aligned} \sigma _{Amax}= & {} \frac{1}{S(0)}\int \limits _{S(0)}\sqrt{(A-<A>)^2}dydz . \end{aligned}$$
(18)

It follows from (18) that the value of the mixing parameter \(M_A (x)\) at the entrance to the channel \(x=0\) is always 0 and then it gradually increases when we move along the x-axis as the solutions are mixed. For fully mixed solutions, we have \(M_A (x^*) = 1\). The latter value means that the solute A is uniformly distributed over the channel cross-section at \(x^*\). It corresponds to the case of ideal mixing, which is practically unattainable in a real experiment. Therefore, we set the value \(M_A (L)=0.8\), which we conventionally define as a sufficient degree of mixing. In other words, it means that the inhomogeneities of the concentration field, on average, are no more than 20% percent of the concentration of a homogeneous system with the same mass of the solute. Then let the distance \(x = L\) is the critical mixing distance if the following condition

$$\begin{aligned} M_A (L)=0.8 \end{aligned}$$
(19)

is satisfied.

The integral value \(M_A (x)\) is designed as close as possible to the experimental mixing parameter M defined by Eq. (1). The main difference is that deviation \(\sigma\) in (2) is determined from the intensity of gray color, while the deviation \(\sigma _A\) in (17) is calculated on the base of the concentration of solute A. Theoretical expression (16) is more accurate than (1), since it takes into account fluctuations of the concentration field along z-axis (in depth channel).

Numerical Results

The densities of aqueous solutions of salts are linearly dependent on their concentration (9). It implies that we can control the onset of various types of convective instability by setting some definite values of the initial concentrations \(A_0\) and \(B_0\) at the entrances to the channels or by changing the location of solutions either in the upper and lower tubes. Combining these conditions at the start, we can generate, at our choice, the onset of DD, DLC, and RT instabilities. We can also specify a laminar flow without convection, in which mixing is carried out only by diffusion. Table 1 presents data for different aqueous solutions considered in 3D numerical simulations.

Double Diffusive Instability

If the solutes in a two-layer system have different diffusion coefficients, this can lead to the excitation of the diffusive instability. Depending on the layer containing a solute with a higher diffusion coefficient, two types of instability can occur. If the faster component is dissolved in the lower layer, then DD instability may occur. This case is represented by the pair of aqueous solutions of CuSO\(_4\) and KCl (see cases no. 1 and 2 in Table 1).

It is known (Stern and Turner 1969) that the DD convection is a form of convection driven by two different density gradients, which have different rates of diffusion. A classic example of DD convection is in oceanography, where heat and salt concentrations exist with different gradients and diffuse at differing rates (Ingel’ 2010). In our case, the instability is caused by two scalar fields of solutes whose diffusion obeys Fick’s law. Finally, the DD convection is driven by density variations under the gravity field.

Figure 8 shows the temporal development of DD instability in the absence of liquid flow \(Q=0\) (\(Pe=0\)) through the mixing chamber (case no.1). One can see the concentration field of CuSO\(_4\) shown at successive times 5, 11, 17, 35, and 50 s. The instability develops as fingers propagating vertically in two opposite directions. These fingers of rising and sinking liquid develop symmetrically concerning the initial contact surface of solutions \(y=0\). One can see that the instability does not develop immediately over the entire contact surface but in the form of separate islands (Fig. 2, \(t=11\) s). Numerical simulation shows that after about a minute, one can observe the appearance of spots of mixed liquid. In Fig. 8, these spots are highlighted in gray compared to the neighboring environment, which looks more contrasting. Complete mixing occurs approximately one and a half minutes after the beginning of the mixing process.

Fig. 8
figure 8

Transient dynamics of the concentration of the solute A shown in the vertical longitudinal cross-section \(z=0\) of the mixing chamber for the case of the DD instability. The frames from up to down correspond to five consecutive times of flow development. The pumping rate is set to zero \(Q=0\). To obtain the numerical results, we used the data for the solution pair no. 1 given in Table 1. The figure shows only part of the mixing chamber \(0\leqslant x/d\leqslant 14\), which is adjacent to the input channels on the left

Full size image

We can compare the results of numerical simulations with the experimental observations shown in Fig. 2. The experiment also records the formation of a system of wave trains of diffusion instability (see Fig. 2, \(t=11\) s). The perturbation development rates obtained in theory and experiment are also close. Also, the instability wavelength obtained numerically is in good agreement with the experimental data: the numerical value \(\lambda _{teor}\approx 0.57\) mm versus experimental value \(\lambda _{exp}\approx 0.53\) mm. One can compare Fig. 2 (\(t=35\) s) and Fig. 8 (\(t=35\) s) where already developed DD convection is shown. It is worthy to notice that the wavelength of DD instability obtained in this work is in good agreement with the known wavelength of these disturbances reported in the classic papers by Stern and Turner (1969) and Turner (1974).

When a longitudinal fluid flow appears in the channel, the convective instability is substantially carried downstream. At a sufficiently high flow rate, convection may not have time to develop at all. Figure 9a demonstrates the development of the DD instability for four gradually increasing values of flow rate pumping solutions through the mixing chamber. The figure shows the final steady-state of the flow, which is established after all transient processes have been completed. One can see that the area characterized by a large concentration gradient gradually expands with an increase in the rate Q of liquid pumping through the channel. We can describe this process more precisely. Figure 10a shows the variation of the integral \(M_A\) with the dimensional distance x/d from the inlet to the mixing chamber. Despite the evident fact that the perturbations are carried away by the flow in the channel, we must admit that the DD instability acts very effectively, completely mixing the solutions for all pumping rates at a distance of approximately \(x/d\approx 25\).

Fig. 9
figure 9

The steady-state concentration field of the solute A (or B where it’s applicable) shown in the vertical longitudinal cross-section \(z=0\) of the mixing chamber of a Y-shaped microchannel in the case of the DD instability (a), the DLC convection (b), the RT instability (c), and the pure diffusion (d). Figures present the final states of the development of flows in the channel when all transient processes have been already completed. For each case, the concentration field is shown for four flow rates pumping liquids through the mixing chamber: \(Q=0.004, 0.01, 0.02, 0.03\) ml/min. To obtain the numerical results shown in (a)–(d), we used the data for the solution pairs no. 1, 3, 4, and 5 given in Table 1, respectively. In the case of convective instabilities (a)–(c), the concentration of solute A incoming from the upper inlet channel is shown. The case of pure diffusion (d) is presented by the concentration field of solute B incoming from the bottom inlet channel

Full size image
Fig. 10
figure 10

Variation of the mixing degree \(M_A\) defined by Eq. (16) with the dimensionless distance x/d from the beginning of the mixing chamber of a Y-shaped microchannel in the case of the DD instability (a), the DLC convection (b), the RT instability (c), and the pure diffusion (d). For each case, the integral \(M_A\) is calculated for four flow rates pumping liquids through the mixing chamber: \(Q=0.004, 0.01, 0.02, 0.03\) ml/min. To obtain the numerical results shown in (a)–(d), we used the data for the solution pairs no. 1, 3, 4, and 5 given in Table 1, respectively

Full size image

Diffusive Layer Convection

If the fast component dissolves in the upper layer, one may observe the DLC instability. This case is represented by the same pair of aqueous solutions of CuSO\(_4\) and KCl, which swap places in the inlet tubes. Now the potassium chloride solution, which diffuses about four times faster than copper sulfate, enters the mixing chamber through the top inlet (see case no. 3 in Table 1). In this case, the instability develops on both sides of the diffusive layer, which is statically stable and separates domains of convective flows. The diffusion of both solutes leads to the formation of symmetric convective motion in two unstable layers above and below the diffusive layer. It results in significant vertical gradients of concentration. This circumstance already implies that the efficiency of DLC instability during the mixing of solutions should be worse than in the case of DD instability. The results of the numerical simulation confirm our preliminary conclusion.

Figure 9b demonstrates the development of the DLC instability for four gradually increasing values of flow rate pumping solutions through the mixing chamber. As above, the figure shows the final steady-state, which is established after all transient processes are finished. It is worth noting the wavy relief of the stationary concentration field of KCl. This fact indicates that the convective cells developing due to the DLC instability are more regular than the DD fingers. Rather, the liquid flow redistributes the solutes instead of mixing them. So, we can conclude that the DLC convection cannot completely mix the solutions since convective disturbances cannot penetrate the diffusive layer occurring at \(y=0\). Thus, only the pure diffusion mechanism remains, which organizes mass transfer through a stable horizontal layer of immobile liquid in the center of the tube. Figure 10b shows that complete mixing, in this case, does not occur at any pumping rate.

Rayleigh-Taylor Convection

If the fluid coming from the upper inlet channel is heavier than the fluid from the lower tube, then conditions for the onset of the RT instability are satisfied in the gravity field. We considered this case using the aqueous solution of KCl and pure water (see case no. 4 in Table 1).

Figures 9c and 10c tell us two interesting facts. On the one hand, the Rayleigh-Taylor instability shows high efficiency at low pumping rates. The mixing chamber we have designed is specifically done to be highly compressed in the direction of z-axis. It prevents the heavy liquid at the top and the light liquid at the bottom from simply swapping places without mixing using the depth of the chamber. In our case, the thickness of the chamber is 200 \(\mu\). It means that the solutions are forced to seep through each other during the development of the RT instability. It results in high mixing efficiency. For example, at a flow rate of \(Q=0.004\) ml/min, complete mixing occurs already at a distance of \(x/d\approx 2\) (Fig. 10c), which should be recognized as an excellent result. On the other hand, the efficiency of the Rayleigh-Taylor mechanism falls off rapidly with an increase in the pumping rate Q. This effect can be explained by the fact that RT disturbances grow much more slowly in the case of an increase in the flow velocity in the channel. In other words, the decrease in the growth rate of disturbances occurs faster than the flow velocity increases.

Finally, mixing due to the pure diffusion mechanism was studied using the same pair as in the case of RT instability. To stabilize the flow, one needs to swap the solutions in places: pure water above and the aqueous solution of KCl in the bottom. So, the system, as a whole, becomes statically stable at any point in its subsequent evolution (see case no. 5 in Table 1). Figures 9d and 10d presents the numerical results obtained for the diffusion mechanism of mixing.

Comparison of Mixing Mechanisms

Figures 9,  10, and Table 3 provide enough data to compare the efficiency of various mechanisms of natural convection and pure diffusion to mix two aqueous solutions incoming in the mixing chamber. Table 3 presents the values of the critical mixing distance \(L/L_{DD}\) measures in terms of the same quantity calculated for the DD instability. We can see that the situation is not unambiguous. The conclusion about efficiency essentially depends on the rate of pumping solutions through the mixing chamber. For small values of Q, the RT convection has no competitors. For example, at \(Q=0.004\) ml/min, this mechanism completely mixes solutions even at about \(L/L_{DD}\approx 0.25\). It is four times more efficient than the DD instability and 16 times more efficient than diffusion. For large values of Q, the situation changes. At \(Q=0.03\) ml/min, the critical mixing length for the RT instability is equal to \(L/L_{DD}\approx 3.2\), which is more than three times smaller than that for the DD instability.

Table 3 Comparison of the numerically obtained critical mixing distance \(L/L_{DD}\) measured in terms of the value \(L_{DD}\) for different flow rates
Full size table
Table 4 Comparison of the dimensionless critical mixing distance L experimentally measured and obtained numerically within 3D simulations
Full size table

Finally, let us compare the obtained numerical results with experimental observations (see Table 4). On the whole, we can state a satisfactory agreement between theory and experiment. When comparing, one must keep in mind that the determination of the critical mixing length L in experiment and theory is based on fundamentally different physical quantities. In experiments, the integral M defined by Eq. (1) demands the information on the standard deviation of the grey luminance, which is produced by the dye (Rhodamine) concentration. This luminescence is scanned in the (x, y)-plane. It does not provide information about the dye distribution in the third dimension (z-axis). It is worthy to note that the methods of experimental observation of dissolved substances with sufficient accuracy are still a complicated problem in fluid mechanics. In the case of the numerical determination of the integral \(M_A\) defined by Eq. (16), we used the concentration field A(x, y, z), which is obtained by solving 3D convection equations. So, the value of the critical mixing length L obtained numerically depends on the degree of mixing, which we take as the state of “complete mixing”. Table 4) presents numerical data for two values of the degree of mixing: \(M_A (L_1) = 0.8\) and \(M_A (L_2) = 1.0\).

Discussion and Conclusions

The mechanisms of natural convection, which most researchers in microfluidics currently underestimate, can be successfully used for mixing flows in microfluidic devices. We have shown that the DD convection can reduce the mixing length by one order of magnitude compared with the case of a pure diffusion mechanism. Efficient mixing becomes possible due to the appearance of a complex convective structure that acts as a local mixing tool. The addition of a fluorescent dye made it possible to quantify the mixing degree. We found that the most mixing efficiency occurs at the lowest volume flow rate. To mix the solutions, the convective disturbances must first develop. With an increase in the rate of pumping liquid, convective disturbances are carried downstream, which requires an increase in the length of the channel.

We have demonstrated, experimentally and numerically, that a Y-shaped microreactor with a characteristic channel’s radius of 1 mm, being in a gravity field, allows efficient mixing by natural convection. It is more than enough for miniature microreactors developed for flow chemistry. However, the dimensions of real microfluidic devices used, for example, in cell research, are three orders of magnitude smaller (about 1 \(\mu\)m). In this connection, we can formulate the following principal question: to what characteristic size of the channel can the mechanisms of natural convection work with a gradual decrease in the dimensions of the system? We can estimate the channel’s height, at which convection still works, using the classical theory of convective stability. For example, for the DD instability to develop, the following condition for the solutal Rayleigh number must be satisfied (Gershuni and Zhukhovitsky 1963)

$$\begin{aligned} \frac{g\beta _C\triangle C d^3}{\nu D_C} > \frac{1}{2}\pi ^4 , \end{aligned}$$
(20)

where \(\nu\) is the kinematic viscosity, \(D_C\) is the diffusion coefficient of solute, \(\beta _C\) is the solutal coefficient of the volume expansion, and \(\triangle C\) stands for the maximum concentration difference across the channel. Then for typical inorganic salts, which we considered in this work, obtain

$$\begin{aligned} d > 100\ \mu \mathrm{m} . \end{aligned}$$

This estimate still leaves a large margin of opportunity to apply natural convection for mixing liquids in microfluidic devices.

As a concluding note, we can state that in this paper, we investigated only the solutions of inorganic substances with constant concentrations. However, by varying the concentration of solutes, one can significantly change the intensity of double-diffusive convection (Mizev et al. 2021; Bratsun et al. 2021) that can enhance even more the effects considered in this work.