Introduction

Double-diffusive convection describes the characteristics of fluid flow that is simultaneously influenced by temperature and concentration gradients Huppert and Turner (1981). It has been the subject of extensive research in recent years due to its wide range of applications in fields such as metal manufacturing, drying processes, oceanography, and so on. Despite the fact that there have been many research dedicated to this topic, the Soret and Dufour effects have been neglected in many cases due to their smaller order of magnitude. However, in industrial domains such as hydrology, chemical reactors, and geosciences, the Soret and Dufour effects play an important role in terms of accuracy. Béghein et al. (1992) numerically investigated double diffusive convection in a square cavity under steady-state conditions. Beckermann and Viskanta (1988) reported experimentally and numerically on thermal and solutal convection during solidification of an ammonium chloride-water solution in a rectangular cavity. Wang et al. (2015) explored thermosolutal natural convection in a cavity with coupling diffusive effects.

Recently, there has been a lot of interest in double diffusive natural convection over porous enclosures with differentially heated walls. Bergman and Ungan (1986) determined the thermal and solutal convection generated by a finite heat source placed at the bottom wall, both experimentally and numerically. Numerical studies on thermosolutal convection from the internal heat generating source in a rectangular cavity has been conducted by Teamah (2008) and Teamah et al. (2012). Beji et al. (1999) performed a numerical simulation of heat and solute induced buoyant convection in a porous annulus. They discovered that the increased curvature effect boosts the average heat and mass transmission rate. Sankar et al. (2012) analyzed the double diffusive convection in a cylindrical porous enclosure in the presence of thermal and solute source and found that the placement of the heat source has a significant influence on the rate of heat and mass transfer. Mallikarjuna et al. (2014) illustrated the combined heat and solute buoyancy forces in an annular region with the effects of Soret and Dufour. They have discussed the thermal, concentration and velocity profiles for various parameters.

In the industrial processes like crystal growth technique, glass manufacturing process and so on, the marangoni effect plays a significant role. Like buoyancy forces, Marangoni convection induced by surface tension forces is likewise impacted by temperature and concentration gradients simultaneously. As a result, a study of the interplay of these two convections with the effects of temperature and concentration is imperative. There has been significant research in the literature on the combined thermal and solutal effects on the buoyancy-capillary flows in rectangle/square cavities Arafune and Hirata (1998); Jue (1998, 1999); Arafune et al. (2001); Alhashash and Saleh (2017). Zhan et al. (2010) examined the thermosolutal capillary convection in the 3-dimensional form and carried out a numerical simulation until the dominance of chaos is achieved. Chen et al. (2017) performed a numerical analysis on the flow pattern and flow behaviour due to double-diffusive buoyancy Marangoni convection in an annular pool and the effect of the capillary ratio has been analyzed significantly.

In recent years, the use of nanofluids in thermal transfer applications has been prompted by the fact that nanofluids outperform pure fluids in terms of thermal performance. Esfahani and Bordbar (2011) studied the rate of heat and solute transfer owing to buoyancy convection in a square cavity filled with nanofluids. They found that the enhanced value of nanoparticle volume fraction diminishes the mass transfer rate and the flow strength. Kefayati (2016) examined the entropy generation associated with thermal and solutal convection in a power-law fluid-filled porous cavity which is inclined. In this work, the Lattice Boltzmann technique was applied. Zhuang and Zhu (2018) analyzed the double-diffusive coupled capillary and natural convection in a heterogeneous porous cubic cavity filled with power-law nanofluids. They discovered that as the power law index falls, the average Nusselt and Sherwood number rises.

Many publications in the literature have focused on the investigation of double diffusive natural or thermocapillary convection in various geometries with or without Soret and Dufour effects. However, there is no noteworthy examination on double diffusive coupled buoyancy and Marangoni convection in a cylindrical enclosure filled with hybrid nanofluid, as well as Soret and Dufour effects. The purpose of this work is to investigate the Marangoni effect on heat and mass transfer in a cylindrical annulus filled with Ag/MgO-water hybrid nanofluid with Soret and Dufour effects.

Mathematical Formulation

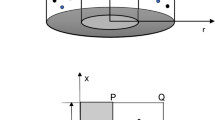
The existing study takes into consideration the fluid flow in the annular region generated by two concentric cylinders. Figure 1 depicts the physical configuration of the current problem. The porous annular zone is filled with a hybrid nanofluid composed of Silver and Magnesium Oxide nanoparticles and water. At the centre of the left inner wall, a discrete heater of finite size is affixed. The top and bottom boundaries and also the unheated portion of the inner wall are supposed to be adiabatic. For the outside wall, a cold temperature is assumed. Local Thermal Equilibrium exists in the isotropic porous media which is under consideration. In the governing equations, the Brinkman extended Darcy model is employed. The nanoparticles are in the state of thermal equilibrium. The thermophysical properties of the nanoparticles are given in Table 1. According to the Boussinesq approximation, the properties of the fluid are constant except for density and it is given as,

$$\begin{aligned} \rho =\rho _{hnf}-(\rho \beta _T)_{hnf}(T-T_{0})-(\rho \beta _C)_{hnf}(C-C_{0}) \end{aligned}$$
Fig. 1
figure 1

Flow Configuration and Coordinate System

Full size image
Table 1 The thermophysical characteristics of nanoparticles and the base fluid Tlili et al. (2020); Benzema et al. (2019)are as follows
Full size table

On the upper boundary, the surface tension parameter is expected to differ linearly with temperature and concentration. It is given as,

$$\begin{aligned} \sigma =\sigma _{0}-\gamma _{T}(T-T_{0})-\gamma _{C}(C-C_{0}) \end{aligned}$$

where, \(\gamma _{T}=-\frac{\partial \sigma }{\partial T}|_{C}\) and \(\gamma _{C}= -\frac{\partial \sigma }{\partial C}|_{T}\).

The system is considered to have an axisymmetric and laminar flow. For the purpose of this investigation, the fluid flow in the rectangular region MNOP is taken into consideration. Taking the aforementioned assumptions into account, the governing equations can be displayed in dimensional form Sankar et al. (2011) as follows:

$$\begin{aligned} \frac{\partial }{\partial r}(ur)+\frac{\partial }{\partial x}(vr)= & {} 0 \end{aligned}$$
(1)
$$\begin{aligned} \frac{1}{\epsilon }\frac{\partial u}{\partial \tau }+\frac{1}{\epsilon ^{2}}\left( u\frac{\partial u}{\partial r}+v\frac{\partial u}{\partial x}\right)= & {} -\frac{1}{\rho _{hnf}}\frac{\partial p}{\partial r}+\nu _{hnf}\left( \bigtriangledown ^{2} u-\frac{u}{r^{2}}\right) -\frac{\nu _{hnf}}{K}u \end{aligned}$$
(2)
$$\begin{aligned} \frac{1}{\epsilon }\frac{\partial v}{\partial \tau }+\frac{1}{\epsilon ^{2}}\left( u\frac{\partial v}{\partial r}+v\frac{\partial v}{\partial x}\right)= & {} -\frac{1}{\rho _{hnf}}\frac{\partial p}{\partial x}+\nu _{hnf}\left( \bigtriangledown ^{2} v\right) -\frac{\nu _{hnf}}{K}v\\& -\frac{(\rho \beta _T)_{hnf}}{\rho _{hnf}}g(T-T_{0})-\frac{(\rho \beta _C)_{hnf}}{\rho _{hnf}}g(C-C_{0}) \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial T}{\partial \tau }+u\frac{\partial T}{\partial r}+v\frac{\partial T}{\partial x}= & {} \alpha _{hnf}\bigtriangledown ^{2} T+K_{TC}\bigtriangledown ^{2}{C} \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial C}{\partial \tau }+u\frac{\partial C}{\partial r}+v\frac{\partial C}{\partial x}= & {} \alpha _{D}\bigtriangledown ^{2} C+K_{CT}\bigtriangledown ^{2}{T} \end{aligned}$$
(5)

where (u, v) signify the velocity vectors in the (r, x) directions. \(K_{TC}\), \(K_{CT}\) are the coefficients meant for Dufour and Soret parameters. The terms \(\epsilon\), K are the porosity and permeability of the porous medium.

The non-dimensional vorticity-stream function form of Eqs. (1)–(5) is given as

$$\begin{aligned} \frac{\partial \theta }{\partial t}+\frac{U}{A}\frac{\partial \theta }{\partial R}+\frac{V}{A}\frac{\partial \theta }{\partial X}= & {} \frac{\alpha _{hnf}}{\alpha _f}\bigtriangledown ^{2}_{1}\theta +D_{f}\bigtriangledown ^{2}_{1}c \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial c}{\partial t}+\frac{U}{A}\frac{\partial c}{\partial R}+\frac{V}{A}\frac{\partial c}{\partial X}= & {} \frac{1}{Le}\bigtriangledown ^{2}_{1}c+\frac{S_{r}}{Le}\bigtriangledown ^{2}_{1}\theta \end{aligned}$$
(7)
$$\begin{aligned} &\frac{1}{\epsilon }\frac{\partial \eta }{\partial t}+\frac{1}{\epsilon ^{2}}\left[ \frac{U}{A}\frac{\partial \eta }{\partial R}+\frac{V}{A}\frac{\partial \eta }{\partial X}-\frac{U}{A}\left( \frac{D}{RD+r_{i}}\right) \eta \right]\\&\quad= \ Pr\frac{\nu _{hnf}}{\nu _{f}}\left[ \bigtriangledown ^{2}_{1} \eta -\left( \frac{D}{RD+r_{i}}\right) ^{2}\right] \eta \\&\qquad -\frac{\nu _{hnf}}{\nu _{f}}\frac{Pr}{Da}\eta +\frac{(\rho \beta _{T})_{hnf}}{\rho _{hnf}(\beta _{T})_{f}}Ra_{T}\left( \frac{\partial \theta }{\partial R}+N\frac{\partial c}{\partial R}\right) \end{aligned}$$
(8)
$$\begin{aligned} \eta =\frac{1}{Pr}\left( \frac{r_{i}}{RD+r_{i}}\right) \left[ \frac{\partial ^{2} \Psi }{\partial R^{2}}-\left( \frac{D}{RD+r_{i}}\right) \frac{\partial \Psi }{\partial R}+\frac{1}{A^{2}}\frac{\partial ^{2} \Psi }{\partial X^{2}}\right] \end{aligned}$$
(9)
$$\begin{aligned} U=\frac{r_{i}}{RD+r_{i}}\frac{\partial \Psi }{\partial X} ; \quad V=-\frac{r_{i}}{RD+r_{i}}\frac{\partial \Psi }{\partial R} \end{aligned}$$
(10)

where

$$\begin{aligned} \eta =\frac{1}{Pr}\left[ \frac{1}{A^{2}}\frac{\partial U}{\partial X}-\frac{\partial V}{\partial R}\right] ; \quad \bigtriangledown ^{2}_{1}=\frac{\partial ^{2} }{\partial R^{2}}+\left( \frac{D}{RD+r_{i}}\right) \frac{\partial }{\partial R}+\frac{1}{A^{2}}\frac{\partial ^{2} }{\partial X^{2}} \end{aligned}$$

The above equations make use of the non-dimensional variables mentioned below.

$$\begin{aligned} U&=\frac{uD}{\alpha _{f}}A \quad V=\frac{vL}{\alpha _{f}A} \quad X=\frac{x}{L} \quad R=\frac{r-r_{i}}{D} \quad \\t&=\frac{\tau \alpha _{f}}{D^{2}} \quad \Psi =\frac{\psi }{r_{i}\alpha _{f}} \eta =\frac{\Omega D^{2}}{{\nu _{f}}} \quad \theta =\frac{(T-T_{0})}{\bigtriangleup T} \quad \\ \bigtriangleup T&=\frac{q_{h}D}{k_{f}} \quad c=\frac{(C-C_{0})}{\bigtriangleup C} \quad \bigtriangleup C=\frac{j_{h}D}{\alpha _{D}} \quad D =r_{0}-r_{i} \end{aligned}$$

The dimensionless form of initial and boundary conditions are

$$\begin{aligned} t&=0: \quad \Psi =\eta =0; \quad \theta =0; \quad c=0; \quad \\U&=V=0; \quad 0\le R\le 1; \quad 0\le X \le 1; \end{aligned}$$

For \(t>0\) :

$$\begin{aligned} \left. \begin{aligned}\Psi = {\frac{\partial \Psi }{\partial R}}=0, {\frac{\partial \theta }{\partial R}}= {\frac{\partial c}{\partial R}}= -1(\mathrm {at \ the \ heater}) \\ {\frac{\partial \theta }{\partial R}}= {\frac{\partial c}{\partial R}}= 0 (\mathrm {elsewhere}) \end{aligned}\right\} R=0 \end{aligned}$$
$$\begin{aligned} \Psi = {\frac{\partial \Psi }{\partial R}}=0, \theta =0; R=1 \end{aligned}$$
$$\begin{aligned} \Psi = {\frac{\partial \Psi }{\partial X}}=0, {\frac{\partial \theta }{\partial X}}=0; X=0 \end{aligned}$$
$$\begin{aligned} \Psi = {\frac{\partial U}{\partial X}}={\frac{\partial ^{2} \Psi }{\partial X^{2}}}=0, \ {\frac{\partial \theta }{\partial X}}=0; \ X=1 \end{aligned}$$

The Taylor series expansion for the stream function is utilized for deriving the boundary condition for the vorticity adjacent to solid walls. At the free surface, the boundary condition for the vorticity is obtained from the relationship between shear stress and the surface tension differences. This aids in the development of thermocapillary flow in the annulus.

$$\begin{aligned} \eta = {\left( \frac{r_{i}}{Pr(RD+r_{i})}\right) \frac{\partial ^{2} \Psi }{\partial R^{2}}}; \ R=0; \ R=1 \ \mathrm{and} \ 0\le X\le 1 \end{aligned}$$
$$\begin{aligned} \eta = {\left( \frac{r_{i}}{A^{2}Pr(RD+r_{i})}\right) \frac{\partial ^{2} \Psi }{\partial X^{2}}}; \ X=0 \ \mathrm{and} \ 0\le R\le 1 \end{aligned}$$
$$\begin{aligned} \eta = {\frac{\partial U}{\partial X}}=AMa_{T}{\left(\frac{\partial \theta }{\partial R}+N_{M}\frac{\partial c}{\partial R}\right)}; \ X=1 \ \mathrm{and} \ 0\le R\le 1 \end{aligned}$$

The dimensionless parameters Le, \(D_{f}\), \(S_{r}\), N, \(N_{M}\), \(Ra_{T}\), \(Ma_{T}\), Da, Pr, \(\lambda\), A are respectively the Lewis number, the Dufour parameter, the Soret parameter, the buoyancy ratio, the capillary ratio, the thermal Rayleigh number, the thermal Marangoni number, the Darcy number, the Prandtl number, the radii ratio and the aspect ratio. These parameters are defined as,

$$\begin{aligned} Le &= {\frac{\alpha _{f}}{\alpha _{D}}}, D_{f}=\frac{K_{TC}\bigtriangleup C}{\alpha _{f}\bigtriangleup T}, S_{r}=\frac{K_{CT}\bigtriangleup T}{\alpha _{D}\bigtriangleup C}, \\N&=\frac{(\beta _{C})_{hnf}\bigtriangleup C}{(\beta _{T})_{hnf}\bigtriangleup T}, N_{M}=\frac{(\gamma _{C})_{hnf}\bigtriangleup C}{(\gamma _{T})_{hnf}\bigtriangleup T}, \end{aligned}$$
$$\begin{aligned} Ra_{T} &= {\frac{g\beta _{f}\bigtriangleup T D^{3}}{\nu _{f}\alpha _{f}}}, Ma_{T} = {-\frac{\partial \sigma _{f}}{\partial T}\frac{\bigtriangleup T D}{\mu _{f} \alpha _{f}}}, \\Da& = {\frac{K}{D^{2}}}, Pr = {\frac{\nu _f}{\alpha _f}}, \lambda = {\frac{r_{0}}{{r_{i}}}}, A = {\frac{L}{D}} \end{aligned}$$

It is worth mentioning here that the governing equations (6)–(10) can be promptly transformed to a rectangular coordinate system by simply substituting D = 0 (\(\lambda\) = 1) in those equations. Also, one can include the values of the radii ratio (\(\lambda\)) in the governing equations and the boundary conditions through the annular gap(D).

As the convective thermal energy loss from the free surface is far lower than the thermal transfer from the heaters at the left wall to the neighbouring fluid, the free surface heat loss can be ignored. As a result, the assumption of an adiabatic state at the free surface is appropriate.

The local thermal and mass transfer along the heater positioned at the left wall is defined as follows:

$$\begin{aligned} Nu_{loc}= & {} -\frac{k_{hnf}}{k_{f}}\frac{1}{\theta (X)} \end{aligned}$$
(11)
$$\begin{aligned} Sh_{loc}= & {} -\frac{1}{c(X)} \end{aligned}$$
(12)

where \(\theta (x)\) and c(X) are the local dimensionless temperature and concentration at the heaters.

The average Nusselt number and Sherwood number along the heater placed at the left wall is given as,

$$\begin{aligned} \overline{Nu}=\frac{1}{\mathcal {L}}\int ^{0.7}_{0.3} Nu_{loc}dX \end{aligned}$$
(13)
$$\begin{aligned} \overline{Sh}=\frac{1}{\mathcal {L}}\int ^{0.7}_{0.3} Sh_{loc}dX \end{aligned}$$
(14)

Here \(\mathcal {L}\) is the length of the heater.

The effective thermal conductivity of the working hybrid nanofluid is given as,

$$\begin{aligned} \frac{k_{hnf}}{k_{f}}=\frac{(k_{eq}+2k_{f})+2(k_{eq}-k_{f})(1+\varsigma )^3\phi }{(k_{eq}+2k_{f})-(k_{eq}-k_{f})(1+\varsigma )^3\phi } \end{aligned}$$
(15)

Adjacent to a solid surface, the molecules of liquid forms a nanolayer which takes the structure of solid is considered in the modified maxwell model. Equation (15) is defined by using this model. In the above equation, \(\varsigma\) is defined as \(\varsigma =\frac{h_{nl}}{r_{p}}\), where \(h_{nl}\) stands for the nanolayer thickness and the actual nanoparticle radius is represented as \(r_{p}\). Here \(h_{nl}\) and \(r_{p}\) take the values 2nm and 3nm respectively.

The nanoparticles equivalent thermal conductivity is given as

$$\begin{aligned} \frac{k_{eq}}{k_{p}}=\vartheta \frac{2(1-\vartheta )+(1+\varsigma )^3(1+2\vartheta )}{-(1-\vartheta )+(1+\varsigma )^3(1+2\vartheta )} \end{aligned}$$
(16)

Here \(\vartheta =\frac{k_{nl}}{k_{p}}\), where \(k_{nl}\) is the thermal conductivity of the nanolayer. \(k_{p}\) represents the nanoparticles thermal conductivity. Also \(k_{nl}\) = \(100k_{f}\). Table 2 lists the hybrid nanofluid models that have been used in this study.

Table 2 The applied models of the working hybrid nanofluids Sheikholeslami et al. (2013)
Full size table

Numerical Solution Procedure

The governing equations (6)–(10) together with the conditions on boundary are evaluated using Finite Difference Method (FDM) Wilkes and Churchill (1966). To discretize the temperature, concentration and vorticity-stream function equations, an Alternating Direction Implicit (ADI) approach is applied. Initially, Dealing with the temperature equation horizontally and vertically for the first half of time and then for the remaining time, the tri-diagonal equations are emerged. Thomas algorithm is used to solve those equations. The vorticity equation utilizes the values produced by the temperature equation and then a similar process is used in assessing the vorticity equations. At last, the Successive Over Relaxation (SOR) method and the central differencing scheme is utilized for evaluating the stream function and velocity terms. The underlying convergence criterion must be met in order to obtain a converged solution.

$$\begin{aligned} \frac{\left| \Phi _{m+1}\left( j,k\right) -\Phi _{m}\left( j,k\right) \right| }{\left| \Phi _{m+1}\left( j,k\right) \right| }\le 10^{-5} \end{aligned}$$
(17)

Here m stands for time step and \(\Phi\) is meant for \(\theta\), c, \(\eta\), \(\Psi\)

Grid Sensitivity Analysis and Numerical Validation

The average nusselt number variation in the annulus has been noticed after an examination of grid sensitivity for a variety of grid sizes. Considering the accuracy and processing time, the best grid size chosen for the current problem is \(81\times 81\). Table 3 displays the acquired results.

Table 3 The grid refinement test for the cylindrical annulus for \(Ra_{T}=10^{4}\), \(Ma_{T}=10^{3}\), \(Le=5\), \(N=1\), \(N_{M}=-1\), \(S_{r}=D_{f}=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\) \(\lambda =2\) and \(A=1\)
Full size table

The presently built computational code is verified against benchmark results accessible in the literature before generating simulation results for the current problem. The numerical results for the square cavity is compared with the results shown in De Vahl Davis (1983) (see Table 4). The thermal transport rate in a cylindrical annulus is correlated with the results of Sankar et al. (2011). The above comparison results indicate that there is a great level of agreement (see Fig. 2).

Fig. 2
figure 2

Comparison of average nusselt number with Sankar et al. (2011)

Full size image

Results and Discussions

In the ongoing study, an analysis has been made numerically for the double diffusive combined buoyancy and Marangoni convection in a cylindrical annulus. The annular region is suffused with Ag/MgO-water hybrid nanofluid. The parameters thermal Rayleigh number \((10^{3}\le Ra_T\le 10^{5})\), thermal Marangoni number \((10^{2}\le Ma_T\le 10^{4})\), Lewis number \((1\le Le\le 5)\), buoyancy ratio \((-5\le N\le 5)\), capillary ratio \((-2\le N_{M}\le 1)\), Dufour parameter \((0\le D_{f}\le 2)\), Soret parameter \((0\le S_{r}\le 2)\) and nanoparticle volume fraction \((0.02\le \phi \le 0.08)\) have been numerically simulated. The Prandtl number Pr, Darcy number Da, porosity \(\epsilon\) and the length of the heater are fixed to the values 6.2, \(10^{-2}\), 0.4 and 0.4 respectively and the geometrical parameters like the aspect ratio \(A=1\) and the radii ratio \(\lambda =1,2,5,10\) are considered. The profile of streamlines, isotherms and isoconcentrations is used to investigate the flow behaviour, temperature, and concentration properties. Heat and mass transfer rates are depicted through the portraits of average Nusselt and average Sherwood numbers.

Table 4 The comparison of average nusselt number on closed cavity
Full size table

Figure 3 depicts the variation of Lewis number for the thermal Marangoni numbers \(Ma_{T}=10^{3}\) and \(Ma_{T}=10^{4}\). Since the Lewis number represents the ratio of thermal diffusivity to mass diffusivity, at \(Le=1\), there is an equality in thermal and mass diffusion rates, resulting in nearly identical thermal and concentration profiles. Once the Lewis number \((Le=5)\) is elevated, the strength of thermal Marangoni convection rises, as evidenced by the creation of a recirculating vortex near the free surface. The diffusion owing to concentration decreases as the Lewis number increases, and hence the thickness of the boundary layer shrinks. The higher thermal Marangoni number \(Ma_{T}=10^{4}\) creates a substantial modification in flow behaviour, temperature and solute profiles, as seen in Fig. 3(c) and (d). At \(Ma_{T}=10^{4}\), thermocapillary induced convection is extremely strong with the higher value of Lewis number.

Fig. 3
figure 3

Streamlines, isotherms and isoconcentrations for \(Ma_{T}\) and Le with \(Ra_{T}=10^4\), \(N=1\), \(N_{M}=-1\), \(S_{r}=D_{f}=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

Figure 4 illustrates the impact of buoyancy ratio on flow field, thermal and solutal profiles by fixing \(Ra_{T}=10^{4}\) and \(Ma_{T}=10^{3}\). The discussion has been focused on opposing, thermally dominant, and assisting flows, which correspond to \(N<0\), \(N=0\), and \(N>0\). The thermocapillary force greatly influences the flow field at \(N=-5\), and the plots of isotherm and isoconcentration demonstrate the dominance of solutal flow. In comparison to \(N=-5\), the temperature and concentration fields show a considerable change in flow direction at \(N=0\). In this instance, the buoyancy-driven flow takes up the majority of the annulus. At \(N=5\), the flow becomes more intense as the two forces (thermal and solutal) interact in the same direction. As seen in Fig. 4(c), the buoyancy force almost completely suppresses Marangoni flow. It can also be noticed that the isotherms and isoconcentrations are gathered collectively near the heater.

Fig. 4
figure 4

Streamlines, isotherms and isoconcentrations for the buoyancy ratio N with \(Ra_{T}=10^4\), \(Ma_{T}=10^{3}\), \(Le=5\), \(N_{M}=-1\), \(S_{r}=D_{f}=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

The effect of Dufour parameter on various contours is demonstrated in Fig. 5. Since the Dufour effect corresponds to the heat flux due to concentration gradient, a considerable change in the isotherm plot is noticed with increasing Dufour value. The streamline pattern at \(D_{f}=2\) displays the disturbances observed in cells created by buoyancy forces with the intrusion of thermocapillary driven vortex at the free surface. In the isotherm, an elevated contour layer develops near the top surface.

Fig. 5
figure 5

Streamlines, isotherms and isoconcentrations for the Dufour parameter \(D_{f}\) with \(Ra_{T}=10^4\), \(Ma_{T}=10^{3}\), \(Le=5\), \(N=1\), \(N_{M}=-1\), \(Sr=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

The impact of Soret effect is manifested in Fig. 6. The streamline profile for different Soret values \((S_{r}=0.5,1,2)\) is most likely similar to the corresponding Dufour profiles. However, there is a significant alteration in the isoconcentration plot for \(S_{r}=2\) which confirms the supremacy of mass transfer over thermal transfer in the annular enclosure.

Fig. 6
figure 6

Streamlines, isotherms and isoconcentrations for the Soret parameter \(S_{r}\) with \(Ra_{T}=10^4\), \(Ma_{T}=10^{3}\), \(Le=5\), \(N=1\), \(N_{M}=-1\), \(D_{f}=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

Figure 7 reports the influence of thermocapillary ratio \((N_{M})\) on thermal Marangoni number\((Ma_{T})\) and Lewis number(Le). With the augmentation of capillary ratio, the thermal and mass transfer is suppressed by the lower values of thermal Marangoni number. Heat transfer improves while mass transfer falls with capillary ratio at \(Ma_{T}=10^4\). The reduction in average Nusselt number in Fig. 7(b) implies that the Lewis number is less efficient in transporting heat. On the contrary, it is extremely effective at transferring mass within the enclosure. Except for heat transmission at \(Le=1\), there is only a meager change in average Nusselt and average Sherwood numbers with the improvement in capillary ratio in both cases.

Fig. 7
figure 7

Effect of capillary ratio \(N_{M}\) on (a) \(Ma_{T}\) (b) Le at \(Ra_{T}=10^{4}\), \(N=1\), \(S_{r}=D_{f}=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

Figure 8 depicts the effect of the thermal Marangoni number on the buoyancy ratio and the Lewis number. The buoyancy ratio achieves the maximum value of heat and mass transfer rates at \(N=-5\) for the thermal Marangoni number \(10^4\), as shown in Fig. 8(a). As the buoyancy ratio grows from negative to positive values, the ascending profile of \(\overline{Nu}\) and \(\overline{Sh}\) for raising thermal Marangoni number at \(N=-5\) diminishes. In Fig. 8(b), At \(Le=1\), there is a small improvement in heat and mass transmission with increasing thermal Marangoni number. But, \(Ma_{T}\) is less significant in transporting heat and mass with the increasing Lewis number. With an enhancement in thermal Marangoni number, the average Nusselt profile declines and the \(\overline{Sh}\) rises for the Lewis number.

Fig. 8
figure 8

Effect of the thermal Marangoni number \(Ma_{T}\) on (a) N (b) Le at \(Ra_{T}=10^{4}\), \(N_{M}=-1\) , \(S_{r}=D_{f}=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

The effect of thermal Marangoni number on Dufour and Soret parameters are manifested in Fig. 9. In Fig. 9(a), the profile of the average Nusselt number continuously decreases as the values of \(Ma_{T}\) and \(D_{f}\) increase. The thermal Marangoni number underperforms in mass transfer. Unlike \(Ma_{T}\), the Dufour parameter boosts mass transfer rate. In contrast to the Dufour parameter’s results on thermal and mass transport, the Soret parameter exhibits good thermal performance and low mass transfer rate with\(Ma_{T}\) as seen in Fig. 9(b).

Fig. 9
figure 9

Effect of the thermal Marangoni number \(Ma_{T}\) on (a) \(D_{f}\) (b) \(S_{r}\) at \(Ra_{T}=10^{4}\), \(Le=5\), \(N=1\) \(N_{M}=-1\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

Figure 10 depicts the influence of nanoparticle volume fraction \((\phi )\) on buoyancy ratio and Lewis number. It is observed from Fig. 10(a) that the \(\overline{Nu}\) curve for nanoparticle volume fraction smoothly picks up along with the buoyancy ratio. Nevertheless, at smaller values of N, the \(\overline{Sh}\) curve is erratic and slowly grows with N. Figure 10(b) demonstrates that \(\overline{Nu}\) escalates with \(\phi\) and drops with Lewis number whereas \(\overline{Sh}\) has a meager increment with volume fraction but an appreciable accession with Le.

Fig. 10
figure 10

Effect of the nanoparticle volume fraction \(\phi\) on (a) N (b) Le at \(Ra_{T}=10^{4}\), \(Ma_{T}=10^{3}\), \(N_{M}=-1\), \(S_{r}=D_{f}=0.5\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

The impact of Dufour and Soret effects on thermal Rayleigh number is presented in Fig. 11. In Fig. 11(a), increasing the Dufour parameter causes a loss in heat transfer while boosting the \(D_{f}\) produces an improvement in mass transfer. In the case of \(S_{r}\), when \(Ra_{T}=10^{3}\), heat transfer downs but mass transfer augments. At higher \(Ra_{T}\) values, heat and mass transfers show an inverse pattern.

Fig. 11
figure 11

Effect of the thermal Rayleigh number \(Ra_{T}\) on (a) \(D_{f}\) (b) \(S_{r}\) at \(Ma_{T}=10^{3}\), \(Le=5\), \(N=1\) \(N_{M}=-1\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\), \(\lambda =1\)

Full size image

Figure 12 indicates the alteration of heat and mass transfers with Lewis number for different values of radii ratio \((\lambda )\). The rate of thermal transfer reduces while the rate of mass transfer improves as the Lewis number grows. The \(\overline{Nu}\) and \(\overline{Sh}\), on the other hand, improve when the radii ratio \((\lambda =1,2,5,10)\) raises.

Fig. 12
figure 12

Effect of radii ratio \(\lambda\) on Le at \(Ra_{T}=10^{4}\), \(Ma_{T}=10^{3}\), \(N=1\), \(N_{M}=-1\), \(S_{r}=D_{f}=0.5\), \(\phi =0.02\), \(Da=10^{-2}\), \(\epsilon =0.4\)

Full size image

Conclusion

In the present research, the double diffusive buoyancy and Marangoni convection in a porous cylindrical annulus filled with Ag/MgO-water hybrid nanofluid with Soret and Dufour effects are numerically studied. This study yielded the following results.

  • With the enhancement in thermal Marangoni number, the average Nusselt and Sherwood numbers improve only for lower values of buoyancy ratio and for lower values of Lewis number at \(Ma_{T}=10^{4}\). In the remaining cases, the \(\overline{Nu}\) and \(\overline{Sh}\) drops.

  • Except for \(Ma_{T}=10^{4}\), the augmentation in buoyancy ratio achieves an efficient rate of thermal and concentration transmission, but the capillary ratio only obtains a better rate of heat transfer at \(Ma_{T}=10^{4}\).

  • The Lewis number and the Dufour parameter are more effective in transferring mass than heat. However, the Soret parameter and the nanoparticle volume fraction are more effective in heat transfer than mass transfer.

  • Enhanced radii ratio \((\lambda )\) results in higher heat and mass transport rates. As a result, the annular enclosure \((\lambda =2,5,10)\) is more appropriate for heat and mass transfer than the rectangular cavity \((\lambda =1)\).