1 Introduction

Thermal gradients along the free surface cause a fluctuation in surface tension. It is commonly understood that buoyant convection happens as a consequence of density variations caused by temperature differences. An examination of the interaction between these two forces is more essential, because thermocapillary flow has important applications in areas such as liquid melting, soap film stabilisation, droplet vaporisation, and so on, whereas buoyancy convection is important in areas such as energy storage, solar collector technology, and so on. A numerical study on the coupled buoyancy and thermocapillary convection in a three-dimensional cubical cavity was made by Behnia et al. [1]. They discovered that for positive Marangoni numbers, the flow structure consists of a core vortex, whereas for negative Marangoni numbers, the flow pattern is more intriguing and complicated. Naimi et al. [2] investigated both analytically and numerically a steady-state mixed buoyancy–thermocapillary convection in a shallow cavity filled with non-newtonian fluid. Raisa Akhtaruzzaman et al. [3] explored the magnetic effects on Marangoni and buoyancy convection in an inclined bottom heated open enclosure and reported that the inclination angle causes an extreme shift in flow field with the Marangoni effect.

Researchers and experimentalists determined that the insertion of baffle in the thermally active walls of the cavity suppressed the thermal transfer rate by modifying the flow pattern. Tasnim and Collins [4] analysed the thermal transport rate in a cavity with a baffle positioned at the hot wall and revealed that anchoring thin baffles at thermally active walls improved the amount of thermal transfer, and that the length of the baffle had a greater impact on heat transfer. Buoyancy convection in a square cavity with horizontally and vertically positioned heated thin baffle was numerically investigated by Oztop et al. [5]. Natural convective heat transfer in a cavity filled with micropolar fluids was studied by Muthtamilselvan et al. [6] with the effect of uniform and non-uniform heated thin fin. Pushpa et al. [7] calculated double diffusive convection in a cylindrical annular region with a circular thin baffle attached to the inner cylinder. The natural convective flow and thermal dissipation in a cylindrical annulus with a circular baffle attached to the inner cylinder has been studied by Pushpa et al. [8, 9]. The above-mentioned works mainly analyse the effect of baffle on natural convective flow in various geometries.

Natural convective flow in various geometries with the influence of viscous dissipation has been examined by many researchers [10, 11]. Taking the viscous dissipation and radiation into account, Ghalambaz et al. [12] made a numerical examination on the free convection in a porous cavity filled with nanofluid and their results reveal that the viscous dissipation effect enhances the value of Nusselt number at the cold wall, whereas it reduces the Nusselt number value at the hot wall. Numerous studies have been made on the influence of viscous dissipation and thermal radiation on the flow over a stretching sheet with Soret and Dufour effects [13,14,15]. Girish et al. [16] obtained numerical and analytical results for mixed convective flow in a double channel annulus created by three concentric cylinders with viscous dissipation. The papers discussed above focus only on the natural or mixed convective flows in enclosures with viscous dissipation, but not on the Marangoni flow in an annular enclosure with viscous dissipation effects.

Nowadays, research in the field of nanofluids has grown rapidly because of its enhanced rate of thermal performance and its wide range of applications in areas such as chemical industry, tribology, pharmaceutical, surfactant, process extraction, and medical industries. Mansour et al. [17] studied the formation of entropy in a nanofluid-filled porous cavity in the presence of a magnetic field and viscous dissipation. The impact of viscous dissipation in a natural convective flow in a porous cavity saturated with nanofluid with the magnetic effects was examined by numerous researchers including Haritha et al. [18] and Chandrashekar et al. [19]. Sankar et al. [20] investigated the conjugate buoyant thermal transport in an enclosed concentric annular region filled with nanoliquids. Their results reveal that Cu–water nanofluids are more effecient in thermal transfer than other nanofluids. Dogonchi et al. [21] tested the influence of viscous dissipation and internal heat generation on free convection in a circular porous enclosure filled with Cu–water nanofluid. They reported that the average Nusselt number ascended with viscous dissipation parameter. In addition to the research on nanofluids, researchers are now focusing on hybrid nanofluids. Hybrid nanofluids exhibit a greater thermal conductivity and stability rate in comparison with nanofluids. Gorla et al. [22] examined the heat source and sink effects in an enclosure filled with hybrid nanofluid in the presence of a magnetic field. Gokulavani et al. [23] conducted a numerical analysis of a copper–titania–water hybrid nanofluid-filled ventilated cavity with the influence of injection/suction. Reddy et al. [24] examined the natural convective flow in a cylindrical geometry filled with different hybrid nanofluids with varying temperature along vertical walls. The above-mentioned investigations mainly analyse the flow inside a cavity or annulus filled with nanoliquids or hybrid nanofluids without baffle.

A comprehensive review of the literature on buoyancy and thermocapillary convection with and without the inclusion of a baffle in the enclosure was conducted. The studies were restricted to the role of baffle only on buoyant convective flow in various geometries, but no such research could be identified in the literature considering the effects of the baffle and viscous dissipation on thermocapillary flow in a hybrid nanofluid-saturated cylindrical porous annular enclosure. The physical configuration considered here has a relevant application in heat exchangers. In general, heat exchangers are used to control the resistance to fluid flow, and in the heat exchangers, the baffles are positioned to diminish the thermal transfer rate. Comprehending this vital application, the current work mainly focuses on the influence of baffle size and position on the coupled mechanism of buoyancy and Marangoni convection in a hybrid nanofluid-filled cylindrical annulus with the effect of viscous dissipation. The main objective of the current article is to study the impact of the viscous dissipation, baffle size and location on the Marangoni convection and nanoparticle volume fraction in a cylindrical annulus filled with Ag/MgO–water hybrid nanofluid.

2 Mathematical formulation

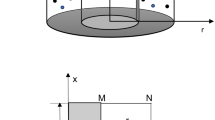
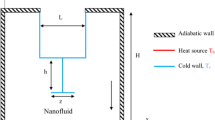
Figure 1 depicts the physical setup under consideration in this investigation. The flow zone is the annular region generated by the two concentric cylinders, and the part PQRS is assumed here for analysis. The flow in the system is presumed to be axisymmetric and laminar. The porous annulus is infiltrated by a hybrid nanofluid which is composed of silver and magnesium oxide nanoparticles with water as a base fluid. A thin circular baffle of size l is positioned at the inner cylinder. The thermal condition of the baffle is the same as that of the inner wall of the annulus, which is taken as hot, while the outer wall is believed to be cold. The top boundary is a free surface. The upper and lower bounds are both adiabatic. The Boussinesq approximation is valid. The Brinkman extended Darcy model is applied. The nanoparticles hold the property of thermal equilibrium. Table 1 summarises the thermophysical characteristics of nanoparticles. The dimensional form of governing equations [25] is constructed by taking into consideration the aforesaid assumptions. It is given as follows:

Fig. 1
figure 1

Flow configuration and coordinate system

Full size image
$$\begin{aligned}&\frac{\partial }{\partial r}(ur)+\frac{\partial }{\partial x}(vr)=0 \end{aligned}$$
(1)
$$\begin{aligned}&\frac{1}{\delta }\frac{\partial u}{\partial \tau }+\frac{1}{\delta ^{2}}\left( u\frac{\partial u}{\partial r}+v\frac{\partial u}{\partial x}\right) =-\frac{1}{\rho _{hnf}}\frac{\partial p}{\partial r}\nonumber \\&\quad + \nu _{hnf}\left( \bigtriangledown ^{2} u-\frac{u}{r^{2}}\right) -\frac{\nu _{hnf}}{K}u \end{aligned}$$
(2)
$$\begin{aligned}&\frac{1}{\delta }\frac{\partial v}{\partial \tau }+\frac{1}{\delta ^{2}}\left( u\frac{\partial v}{\partial r}+v\frac{\partial v}{\partial x}\right) =-\frac{1}{\rho _{hnf}}\frac{\partial p}{\partial x}+\nu _{hnf}\left( \bigtriangledown ^{2} v\right) \nonumber \\&\quad -\frac{\nu _{hnf}}{K}v -\frac{(\rho \beta )_{hnf}}{\rho _{hnf}}g(T-T_{c}) \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial T}{\partial \tau }+u\frac{\partial T}{\partial r}+v\frac{\partial T}{\partial x}=\alpha _{hnf}\bigtriangledown ^{2} {T}+\frac{\mu _{hnf}}{K(\rho c_{p})_{hnf}}(u^{2}+v^{2})\nonumber \\ \end{aligned}$$
(4)

The velocity components along r and x directions are indicated by u and v,  respectively. The porous medium’s permeability and porosity are expressed by K and \(\delta \).

Table 1 The thermophysical characteristics of nanoparticles and the base fluid [26, 27]are as follows
Full size table

By removing the pressure term from Eqs. (2) and (3), the dimensionless equations are framed as follows.

$$\begin{aligned}&\frac{\partial \theta }{\partial t}+\frac{U}{A}\frac{\partial \theta }{\partial R}+\frac{V}{A}\frac{\partial \theta }{\partial X} =\frac{\alpha _{hnf}}{\alpha _f}\bigtriangledown ^{2}_{1}\theta \nonumber \\&\quad +\epsilon _{v}\frac{\mu _{hnf}}{\mu _{f}}\frac{(\rho c_{p})_{f}}{(\rho c_{p})_{hnf}}\left( \frac{r_{i}}{RD+r_{i}}\right) ^{2} \left[ \frac{1}{A^{2}}\left( \frac{\partial \Psi }{\partial X}\right) ^{2}-\left( \frac{\partial \Psi }{\partial R}\right) ^{2}\right] \nonumber \\\end{aligned}$$
(5)
$$\begin{aligned}&\frac{1}{\delta }\frac{\partial \eta }{\partial t}+\frac{1}{\delta ^{2}}\left[ \frac{U}{A}\frac{\partial \eta }{\partial R}+\frac{V}{A}\frac{\partial \eta }{\partial X}-\frac{U}{A}\left( \frac{D}{RD+r_{i}}\right) \eta \right] \nonumber \\&\quad = Pr\frac{\nu _{hnf}}{\nu _{f}}\left[ \bigtriangledown ^{2}_{1} \eta -\left( \frac{D}{RD+r_{i}}\right) ^{2}\right] \eta \nonumber \\&\qquad -\frac{\nu _{hnf}}{\nu _{f}}\frac{Pr}{Da}\eta +\frac{(\rho \beta )_{hnf}}{\rho _{hnf}\beta _{f}}Ra\frac{\partial \theta }{\partial R} \end{aligned}$$
(6)
$$\begin{aligned}&\eta =\frac{1}{Pr}\left( \frac{r_{i}}{RD+r_{i}}\right) \left[ \frac{\partial ^{2} \Psi }{\partial R^{2}}-\left( \frac{D}{RD+r_{i}}\right) \frac{\partial \Psi }{\partial R}+\frac{1}{A^{2}}\frac{\partial ^{2} \Psi }{\partial X^{2}}\right] \nonumber \\ \end{aligned}$$
(7)
$$\begin{aligned}&U=\frac{r_{i}}{RD+r_{i}}\frac{\partial \Psi }{\partial X} ; V=-\frac{r_{i}}{RD+r_{i}}\frac{\partial \Psi }{\partial R}, \end{aligned}$$
(8)

where

$$\begin{aligned}&\eta =\frac{1}{Pr}\left[ \frac{1}{A^{2}}\frac{\partial U}{\partial X}-\frac{\partial V}{\partial R}\right] ; \\&\quad \bigtriangledown ^{2}_{1}=\frac{\partial ^{2} }{\partial R^{2}}+\left( \frac{D}{RD+r_{i}}\right) \frac{\partial }{\partial R}+\frac{1}{A^{2}}\frac{\partial ^{2} }{\partial X^{2}}. \end{aligned}$$

The non-dimensional variables listed below are used in the preceding equations.

$$\begin{aligned}&R=\frac{r-r_{i}}{D}, X=\frac{x}{L}, U=\frac{uD}{\alpha _{f}}A, V=\frac{vL}{\alpha _{f}A}, t=\frac{\tau \alpha _{f}}{D^{2}},\\&\quad \eta =\frac{\Omega D^{2}}{{\nu _{f}}}, \Psi =\frac{\psi }{r_{i}\alpha _{f}} ,\\&\quad \theta =\frac{(T-T_{c})}{\bigtriangleup T}, \bigtriangleup T=T_{h}-T_{c}, D=r_{0}-r_{i}. \end{aligned}$$

The initial and boundary conditions are expressed in dimensionless form as follows.

\(t=0\) : \(\Psi =\eta =0\); \(\theta =0\), \(U=V=0\), \(0\le R\le 1\), \(0\le X \le 1.\) For \(t>0\):

\(\Psi \)= \(\frac{\partial \Psi }{\partial R}\) = 0, \(\theta =1\); \(R=0.\)

\(\Psi \)= \(\frac{\partial \Psi }{\partial R}\) = 0, \(\theta =0\); \(R=1.\)

\(\Psi \)= \(\frac{\partial \Psi }{\partial X}\) = 0, \(\frac{\partial \theta }{\partial X}\) = 0; \(X=0.\)

\(\Psi \)= \(\frac{\partial U}{\partial X}\) = \(\frac{\partial ^{2} \Psi }{\partial X^{2}}\) = 0, \(\frac{\partial \theta }{\partial X}\) = 0; \(X=1\)

\(\Psi \)= \(\frac{\partial \Psi }{\partial X}\) = 0, \(\theta =1\), along the baffle.

Table 2 The applied models of the working hybrid nanofluids [28]
Full size table

The association between shear stress and surface tension differences is used to establish the vorticity boundary condition at the free surface.This promotes the formation of thermocapillary flow in the annulus. The boundary condition for vorticity near the solid walls is calculated using the Taylor series expansion for the stream function.

\(\eta \) = \(\left( \frac{r_{i}}{Pr(RD+r_{i})}\right) \frac{\partial ^{2} \Psi }{\partial R^{2}}\); \(R=0\); \(R=1\) and \(0\le X\le 1,\)

\(\eta \) = \(\left( \frac{r_{i}}{A^{2}Pr(RD+r_{i})}\right) \frac{\partial ^{2} \Psi }{\partial X^{2}}\); \(X~=~0\) and \(0\le R\le 1,\)

\(\eta \)  =  \(\frac{\partial U}{\partial X}\) = MaA \(\frac{\partial T}{\partial R}\); \(X~=~1\) and \(0\le R\le 1.\)

The dimensionless parameters \(\epsilon _{v}\), Ra, Pr, Da, Ma, \(\lambda \), A, L, \(\epsilon \) are, respectively, the viscous dissipation, Rayleigh number, Prandtl number, Darcy number, Marangoni number, radii ratio, aspect ratio, location of the baffle and size of the baffle. These parameters are described as:

\(\epsilon _{v}\) = \(\frac{\alpha _{f}\mu _{f}}{K(T_{h}-T_{c})(\rho c_{p})_{f}}\), Ra = \(\frac{g\beta _{f}\bigtriangleup T D^{3}}{\nu _{f}\alpha _{f}}\), Pr = \(\frac{\nu _f}{\alpha _f}\),

Da = \(\frac{K}{D^{2}}\),

Ma = \(-\frac{\partial \sigma _{f}}{\partial T}\frac{\bigtriangleup T D}{\mu _{f} \alpha _{f}}\), \(\lambda \) = \(\frac{r_{0}}{{r_{i}}}\), A = \(\frac{H}{D}\), L = \(\frac{h}{H}\), \(\epsilon \) = \(\frac{l}{D}.\)

It is important to note that the governing equations (5)–(8) can be quickly changed to a rectangular coordinate system by replacing D = 0 (\(\lambda \) = 1) in those equations. Furthermore, the radii ratio (\(\lambda \)) values can be included in the governing equations and the boundary conditions via the annular gap (D).

Along the annulus, the local thermal transfer rate is given as:

$$\begin{aligned} Nu_{Loc}= & {} -\frac{k_{hnf}}{k_{f}}\frac{\partial \theta }{\partial R}. \end{aligned}$$
(9)

The average Nusselt number is defined as follows:

$$\begin{aligned} \overline{Nu}=\frac{1}{A}\int ^{A}_{0} Nu_{Loc}dX. \end{aligned}$$
(10)

The modified Maxwell model is considered here to define the effective thermal conductivity of the working hybrid nanofluid and it is defined as

$$\begin{aligned} \frac{k_{hnf}}{k_{f}}=\frac{(k_{eq}+2k_{f})+2(k_{eq}-k_{f})(1+\varsigma )^3\phi }{(k_{eq}+2k_{f})-(k_{eq}-k_{f})(1+\varsigma )^3\phi }. \end{aligned}$$
(11)

From the above equation, \(\varsigma =\frac{h_{nl}}{r_{p}}\). Here, the nanolayer thickness \(h_{nl}\) takes the value 2nm and the actual nanoparticle radius \(r_{p}\) takes the value 3nm,  respectively.

The nanoparticle equivalent thermal conductivity is denoted as

$$\begin{aligned} \frac{k_{eq}}{k_{p}}=\vartheta \frac{2(1-\vartheta )+(1+\varsigma )^3(1+2\vartheta )}{-(1-\vartheta )+(1+\varsigma )^3(1+2\vartheta )}. \end{aligned}$$
(12)

Here, \(\vartheta =\frac{k_{nl}}{k_{p}}\), in which \(k_{nl}\) is the thermal conductivity of the nanolayer. \(k_{p}\) represents the nanoparticles’ thermal conductivity. Also, \(k_{nl}\)=\(100k_{f}\). The hybrid nanofluid models employed in this work are listed in Table 2.

Table 3 The grid refinement test for the cylindrical annulus for \(Ra=10^{4}\), \(Ma=10^{3}\), \(L=0.5\), \(\epsilon =0.5\), \(\epsilon _{v}=0.01\), \(\phi =0.02\), \(Da=10^{-2}\), \(\delta =0.4\) \(\lambda =2\) and \(A=1\)
Full size table
Table 4 The comparison of average Nusselt number on closed cavity
Full size table
Fig. 2
figure 2

Comparison of average Nusselt number with Sankar et al. [25]

Full size image
Fig. 3
figure 3

Comparison of flow field (a) and thermal contours (b) with Tasnim and Collins [4]

Full size image
Fig. 4
figure 4

Impact of Marangoni number on streamlines and isotherms for \(Ra=10^4\), \(L=0.5\), \(\epsilon =0.25\), \(\phi =0.02\), \(\epsilon _{v}=0.01\) a \(Ma=10^2\) b \(Ma=10^3\) c \(Ma=10^4\)

Full size image
Fig. 5
figure 5

Impact of baffle location on streamlines and isotherms for \(Ra=10^4\), \(Ma=10^3\), \(\epsilon =0.25\), \(\phi =0.02\), \(\epsilon _{v}=0.01\) a \(L=0.25\) b \(L=0.5\) c \(L=0.75\)

Full size image
Fig. 6
figure 6

Impact of baffle size on streamlines and isotherms for \(Ra=10^4\), \(Ma=10^3\), \(L=0.5\), \(\phi =0.02\), \(\epsilon _{v}=0.01\) a \(\epsilon =0.25\) b \(\epsilon =0.5\) c \(\epsilon =0.75\)

Full size image
Fig. 7
figure 7

Impact of Darcy number on streamlines and isotherms for \(Ra=10^4\), \(Ma=10^3\), \(L=0.5\), \(\epsilon =0.25\), \(\phi =0.02\), \(\epsilon _{v}=0.01\) a \(Da=10^{-4}\) b \(Da=10^{-3}\) c \(Da=10^{-2}\)

Full size image
Fig. 8
figure 8

Variation of local Nusselt number along the left wall of the enclosure for Marangoni number \(Ma=10^2\) on the a location of the baffle(L),  b size of the baffle \((\epsilon ),\) and c viscous dissipation \((\epsilon _{v})\)

Full size image
Fig. 9
figure 9

Variation of local Nusselt number along the left wall of the enclosure for Marangoni number \(Ma=10^4\) on a location of the baffle(L) b size of the baffle \((\epsilon )\) and c viscous dissipation \((\epsilon _{v})\)

Full size image
Fig. 10
figure 10

Effect of the Marangoni number Ma on a location of the baffle(L) b size of the baffle \((\epsilon )\) and c viscous dissipation \((\epsilon _{v})\)

Full size image
Fig. 11
figure 11

Effect of the Rayleigh number Ra on a location of the baffle(L) b size of the baffle \((\epsilon )\) and c viscous dissipation \((\epsilon _{v})\)

Full size image
Fig. 12
figure 12

Effect of the nanoparticle volume fraction \(\phi \) on a location of the baffle(L) b size of the baffle \((\epsilon )\) and c viscous dissipation \((\epsilon _{v})\)

Full size image

2.1 Numerical solution procedure

The specified problem has been numerically examined using finite difference method (FDM) [29]. An alternating direction implicit (ADI) method and successive over-relaxation (SOR) methods are used to solve the discretised partial differential equations. The ADI method, in particular, is employed to solve the vorticity and temperature equations, while the SOR methodology is used to evaluate the stream function equation. Finally, the velocity terms are assessed using a central differencing approach.To produce a converged solution, the following convergence requirement must be met.

$$\begin{aligned} \frac{\left| \Phi _{m+1}\left( j,k\right) -\Phi _{m}\left( j,k\right) \right| }{\left| \Phi _{m+1}\left( j,k\right) \right| }\le 10^{-5}, \end{aligned}$$
(13)

Here m stands for time step and \(\Phi \) is meant for \(\theta \), \(\eta \), \(\Psi \).

2.2 Grid sensitivity analysis and numerical validation

The computational time and accuracy are the crucial elements to be considered while determining the grid size for the current problem. As a result, the fluctuation in average Nusselt number is continuously monitored for different grid sizes, and an appropriate grid size for the problem selected. The grid size \(81\times 81\) is estimated to be quite effective in this work as shown in Table 3.

Our findings are compared to existing conventional benchmark projections before developing simulation results for the current investigation. The thermal transmission rate in the square cavity formed by insulated horizontal walls and the vertical walls with varying temperature is compared to the values shown in De Vahl Davis [30] (Table 4). The numerical outcomes from the currently developed code for the cylindrical enclosure formed by two concentric cylinders are in concordance with the results of Sankar et al. [25] which is given in Fig. 2. The comparison of flow and thermal contours predicted from our simulations with those of Tasnim and Collins [4] for the square enclosure with a baffle positioned at the left wall of the cavity is portrayed in Fig. 3. The comparison results show that there is a high level of agreement.

3 Results and discussions

The existing research discusses the combined buoyancy and Marangoni convection in a hybrid nanofluid-filled porous cylindrical annulus with the impact of the baffle placed at various places and sizes along with the effects of viscous dissipation. An equal amount of silver (Ag) and magnesium oxide (MgO) nanoparticles are suspended in the water \((H_{2}O)\). The numerical simulations make use of a wide range of physical and geometrical parameters such as Rayleigh number \((Ra:10^{3}-10^{5})\), Marangoni number which corresponds to the fluid flow near the free surface \((Ma:10^{2}-10^{4})\), location of the baffle at the bottom, middle and top of the annulus \((L=0.25, 0.5, 0.75)\), size of the baffle \(({\epsilon }=0.25,0.5,0.75)\), Darcy number which accounts for the permeability of the porous medium and its cross-sectional area \((Da:10^{-4}-10^{-2})\), viscous dissipation parameter \({(\epsilon _{v}}=0.001,0.005,0.5)\) and the volume fraction of the nanoparticle \((\phi =2\%,4\%,8\%)\). The values for the constraints like porosity of the porous medium \(\delta =0.4\), Prandtl number \(Pr=6.2\) belonging to water, aspect ratio \(A=1\) and radii ratio \(\lambda =2\) corresponding to the square annulus are fixed throughout the study. To examine the flow behaviour and thermal patterns, the streamline and isotherm contours are employed. To analyse the heat transfer rate inside the annulus, the local Nusselt number variation is detected along the hot wall, and the profile of global Nusselt number is presented.

Figure 4 depicts the profile of the streamline and isotherm contours for various Marangoni numbers, with the magnitude of the Rayleigh number set to \(10^{4}\). For \(Ma=10^{2}\), since the Marangoni number is lesser than the Rayleigh number, the buoyancy-driven cell occupies the whole cavity, and thermal transfer is primarily owing to natural convection. As the value of Ma approaches \(10^{3}\), a surface tension-driven cell emerges near the free surface and also it is evident from the isotherm plots, as they are less distorted along the hot wall close to the top free surface. However, at \(Ma=10^{4}\), the flow behaviour radically changes. The top vortices created by thermocapillary convection are extremely strong, suppressing the buoyancy-driven cell. The streamlines and isotherms are particularly dense towards the free surface. Since the baffle is placed in the cavity’s centre, it has no effect on Marangoni flow, but it does cause a little distortion of the buoyancy-driven cell around the baffle.

Figure 5 examines the influence of baffle location on the flow and thermal fields by keeping the baffle length constant at 0.25. Anchoring the baffle near the enclosure’s bottom reduces fluid movement in the area around the baffle and alters the streamline to a greater extent. Below the baffle, a faint counterclockwise rotating cell forms. The baffle in the centre of the annulus is discovered to have a significant impact on the flow field inside the cavity. It is obvious from Fig. 4a and b that positioning the fin near the bottom and in the centre of the annulus has no effect on thermocapillary flow. It predominantly affects the buoyancy-driven cell. The surface tension driven cell is slightly altered when the baffle is placed at the top half of the enclosure, as shown in Fig. 4c. The isotherm pattern does not vary significantly in any of the scenarios.

The impact of the baffle size on streamlines and isotherms are manifested in Fig. 6. The small-sized fin bends the buoyancy-driven cell marginally, but has no effect on the vortices generated by the Marangoni convection. The principal vortex created by natural convection is shifted from the cavity’s centre to the annulus’s right cold wall, as shown in Fig. 6b, while the Marangoni convection strengthens. The larger baffle causes a spectacular modification in the flow field. The baffle clearly separates the buoyancy-driven flow zone, and in this instance, the thermocapillary-driven convective cell becomes even stronger. There is a powerful transformation in the isotherm profile concerning the size of the baffle.

Figure 7 exemplifies the influence of Darcy number on streamlines and isotherms profiles. For the lower value of Darcy number \(Da=10^{-4}\), the fluid flow gets resisted because of the high impedence provided by the porous medium. The nearly parallel isotherm reveals that the thermal transfer happens through conduction mechanism. As the Darcy value improves, the fluid flows deeply into the porous matrix, and also due to viscous effects, the velocity of the fluid increases. The buoyancy-driven cell occupies the entire cavity suppressing the flow caused by the Marangoni effect. A strong thermal gradient is observed from the isotherm profile for the higher value of Darcy number \(Da=10^{-2}\). The porosity of the porous medium is a measure of the void spaces in a material. For larger porosity, the fluid gets more space to flow through the medium and hence the velocity of the fluid augments. Here, the porosity value is kept as 0.4.

Figure 8 illustrates the fluctuation of the local Nusselt number along the left hot wall of the annulus for different locations of the baffle, fin sizes, and viscous dissipation \((\epsilon _{v})\) when \(Ma=10^{2}\) is fixed. From Fig 8a, it is found that there is an acute bounce in \(Nu_{Loc}\) at the location of the baffle. For \(L=0.25\), the local heat transfer rate is nearly flat below the baffle position and abruptly rises above the baffle. For \(L=0.5\), the local thermal transfer rate gradually decreases until it reaches the baffle position and then rises above the baffle. A modest rise and downfall is observed in the \(Nu_{Loc}\) below the baffle and then improves for the baffle located at the top of the annulus \((L=0.75)\). In Fig. 8b, \(Nu_{Loc}\) gradually declines beneath the fin position and slowly picks up above the fin for all fin sizes. It has been discovered that smaller fin size achieves a higher thermal transmission rate. For altering viscous dissipation, a similar trend of \(Nu_{Loc}\) profile is found in Fig. 8c as in Fig. 8a and b. But for all the values of \(\epsilon _{v},\) there is only a meagre difference in the \(Nu_{Loc}\) rate. In all of the aforementioned circumstances, the \(Nu_{Loc}\) is observed to be damped near the top surface. This is owing to the existence of Marangoni force near the top free surface.

By fixing \(Ma=10^{4}\), the fluctuation in local thermal transfer rate along the left wall for various values of L, \(\epsilon \) and \(\epsilon _{v}\) is exemplified in Fig. 9. In this situation, the \(Nu_{Loc}\) profile is almost identical to the \(Nu_{Loc}\) profile for \(Ma=10^{2}\) shown in Fig. 8. However, a massive reduction in \(Nu_{Loc}\) rate is found towards the top free surface. It signifies that the fluid mobility is more restricted towards the free surface. It could be attributed to the existence of a strong Marangoni force \((Ma=10^{4})\) near the free surface.

Figure 10 outlines the impact of the Marangoni number on the location, size of the baffle, and viscous dissipation. In Fig. 10a, the Marangoni number reaches a maximum value at \(Ma=10^{4}\) and a minimum value at \(Ma=10^{3}\) for the baffle positioned at various locations. It is also determined that when the baffle is placed at the bottom of the annulus \((L=0.25)\), there is increased thermal transfer. The smaller baffle \((\epsilon =0.25)\) achieves a higher thermal transfer rate than the larger baffle \((\epsilon =0.75)\), as illustrated in Fig. 10b. According to Fig. 10c, the average heat transfer rate steadily improves with the Marangoni number and becomes less efficient with the improvement in viscous dissipation.

Impact of the Rayleigh number on L, \(\epsilon \) and \(\epsilon _{v}\) is demonstrated in Fig. 11. In Fig. 11a, At \(Ra=10^{3}\), the thermal transport rate is low when the baffle is anchored in the middle \((L=0.5)\) of the cavity; however, the thermal transport rate is greater for all Rayleigh numbers when \(L=0.25\). An augmented profile of average Nusselt number is obtained in Fig. 11b with increased Rayleigh number and reduced baffle size. From Fig. 11c, it is observed that the global heat transfer rate is roughly the same at \(Ra=10^{3}\) for different values of \((\epsilon _{v})\). The \(\overline{Nu}\) curve grows smoothly with an increase in Ra value and falls with \((\epsilon _{v})\).

Figure 12 reports the effect of nanoparticle volume fraction on fin position, size, and viscous dissipation. As per Fig. 12a, the curve of \(\overline{Nu}\) consistently grows with an elevation in nanoparticle volume fraction and \(\overline{Nu}\) drops with a rise in baffle location. The \(\overline{Nu}\) profile for the fin size in relation to the nanoparticle volume fraction is similar to that seen in Fig. 12a. It is confirmed from Fig. 12c that the average Nusselt number hikes with \(\phi \) and downs with \({\epsilon _{v}}\).

4 Conclusions

A numerical analysis was carried out to demonstrate the effect of baffle length and position on combined buoyancy Marangoni flow in a hybrid nanofluid-filled porous annulus with viscous dissipation effects. The numerical simulation results yielded the following outcomes.

  • The average Nusselt number drops for lower values of Marangoni number and improves significantly for the higher value \(Ma=10^4\) with respect to the viscous dissipation, length, and location of the baffle.

  • When viscous dissipation improves, the rate of heat transfer drops for Ma and \(\phi \).

  • \(\overline{Nu}\) grows as the volume fraction of nanoparticle increases for L, \(\epsilon ,\) and \(\epsilon _{v}\).

  • In all circumstances, anchoring the baffle towards the top free surface reduces thermal transfer rate. This is owing to the presence of Marangoni flow at the free surface.