Comparison Between the FLUIDICS Experiment and Direct Numerical Simulations of Fluid Sloshing in Spherical Tanks Under Microgravity Conditions

Abstract

The fluids behaviour within a spherical tank under microgravity conditions is investigated through a comparison between the original data from the FLUIDICS experiment carried out in the ISS and Direct Numerical Simulations for two-phase flows. The study case consists in the rotation of a spherical tank around a fixed axis. The tank is filled with a liquid with physical properties similar to those of liquid propellants and gases used in the space industry. Two tanks with different filling ratios have been tested in space. Cameras and sensors allow extracting the fluids dynamics and the temporal evolution of the force and torque exerted by the fluids on the tank wall. Several manoeuvres corresponding to different angular velocities and angular accelerations are submitted on both tanks. The velocity profile is divided into four phases: from zero, the angular velocity around the vertical axis increases linearly until it reaches the required constant value for which the fluids stabilise in the second phase, then the angular velocity decreases until it recovers zero. Numerical simulations are computed with the home-made code DIVA which is based on the Level Set method coupled with the Ghost Fluid Method. The force in the radial direction gives the value of the centrifugal force during the constant angular velocity phase. The average centrifugal force is well predicted by the simulations, the comparison with the experimental data exhibits errors lower than 3% for the half-filled tank. Considering the vertical torque, the effect of the Euler acceleration is clearly visible through the important peaks of opposite sign observed during the acceleration and the deceleration phases. Moreover, the oscillations of the gas bubble during the second phase can be observed from the torque evolution. Their magnitude decreases throughout time until the steady state is reached. The measured and predicted temporal evolutions match together until the magnitude of the oscillations reaches the noise level of the data. The bubble oscillations are much more damped for the tank containing a larger amount of liquid (75%). The frequency of these oscillations are investigated applying the Fourier transform of the torque signals and by looking at the videos taken during the experiment. Similar oscillation frequencies are observed with the experimental setup and the numerical simulations, even for the manoeuvre with the lower Bond numbers. We verify that the oscillation frequency increases with the angular velocity. Finally, the comparison exhibits that the numerical simulations provide an accurate prediction of the fluids behaviours in microgravity conditions for this range of Bond numbers.

Introduction

The sloshing of fluids inside tanks is one of the most important disruptions of satellite stability in microgravity conditions (Lepilliez 2015). A satellite tank is filled with liquid propellant and gas to maintain a sufficient pressure during the lifetime of the satellite. During a manoeuvre, the motion of the satellite leads to the motion of the fluids within the tanks. The centre of mass of the fluids evolves and this generates forces and torques on the satellite structure which can deteriorate the pointing performances. For satellites requiring important accuracy on the attitude, the sloshing phenomenon have to be anticipated and technical solutions to limit its effects must be considered. Several studies have been conducted on the prediction of sloshing in microgravity conditions. Analytical models, based on a 1D mass spring system or a pendulum system have been introduced by Abramson (1967) and taken over by Dodge (2000). The parameters of the simplified systems are deduced from the tank geometry, the fluids properties and the accelerations exerted on the tank. Finally, the model allows to compute the sloshing frequencies, damping ratios and forces exerted on the tank wall for a given manoeuvre. However, these analytical models cannot be considered within the framework of low Bond numbers manoeuvres for which the non linear effects of the surface tension cannot be neglected. Very few experimental data exist because of the complexity to maintain microgravity conditions for a long period of time. Parabolic flights and drop towers enable to create several seconds of microgravity environment (Fernandez et al. 2017; Li et al. 2018) but low Bond numbers manoeuvres require several minutes for the fluids to stabilise. Finally, Direct Numerical Simulation is a promising candidate to investigate the fluids behaviour during station-keeping manoeuvres. The capillary effects and the microgravity conditions can be integrated in the numerical models without additional complexity compared to Earth gravity conditions. Numerical studies on the liquid sloshing in tanks have been performed in different configurations (Ebrahimian et al. 2015; Liu and Lin 2008; Tang and Yue 2017; Tang et al. 2018; Veldman et al. 2007; Yue 2008). Nevertheless, experimental data are still needed to validate the numerical results. To provide experimental data on this topic, the French national space agency (CNES) sent an experiment to the International Space Station (ISS) to quantify the sloshing phenomenon in microgravity conditions (Dalmon et al. 2018; Mignot et al. 2017). Our objective in this paper is to carry out comparisons between numerical simulations and data collected in space to validate accurately the numerical methods predicting fluid sloshing. In the “Tank Modelling” section, the description of the study case will be presented and the dominating effects will be highlighted by using the dimensionless Navier-Stokes equations. We will consider the motion of the fluids inside a tank rotating around a staggered axis in microgravity conditions. Because satellite tanks are usually not aligned with the inertial axis of the satellite, this study aims at modelling the fluids behaviour during a typical rotational manoeuvre. Then, the experimental setup will be described in the “The FLUIDICS Experiment” section with the different measuring devices. The “3” section details the numerical methods implemented to predict the fluids behaviour inside the spherical tank. Finally, the “Comparisons” section focuses on the comparisons between the experimental data and the numerical simulations. The temporal evolution of the force and torque exerted by the fluids on the tank wall will be investigated for different angular velocity profiles.

Tank Modelling

Dimensionless Navier-Stokes Equations

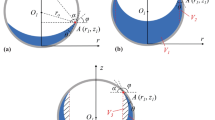
In this study, we consider the rotation of a spherical tank around the z-axis in microgravity conditions. Figure 1 presents a schematic of the study case. The tank is a sphere of diameter D_t, the centre of which is labelled C. The fluid domain inside the tank is denoted by Ω_f and is displayed in blue in Fig. 1. The tank is linked to the rotation axis (located at point O) by a lever arm of length L. The direction of the lever arm defines the radial axis called e_y in the tank referential. The rotation happens around the z-axis and is characterised by its angular velocity Ω and angular acceleration $\dot {\Omega }$.

Fig. 1

Schematic of the study case

To quantify the main effects of the manoeuvre on the fluids, we write the Navier-Stokes equations in the fluid domain

$$ \nabla \cdot \mathbf{u} = 0, $$

(1)

$$ \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \left( \mathbf{u}\cdot \nabla\right)\mathbf{u}\right) = - \nabla p + \nabla \cdot \left( 2 \mu \bar{\bar{\mathbf{D}}} \right) + \mathbf{F_{ext}}, $$

(2)

where t is the time, ρ the fluid density, μ the fluid viscosity, u = (u,v,w) the velocity field, p the pressure, F_ext the volume forces induced by the motion of the satellite and $\bar {\bar {\mathbf {D}}}$ is the rate-of-deformation tensor defined as

$$ \bar{\bar{\mathbf{D}}} = \frac{ \nabla \mathbf{u} + \nabla \mathbf{u}^{T}}{2}. $$

(3)

The referential of the tank is non-Galilean. The inertial and Coriolis accelerations must be taken into account through the external volume force. The Coriolis acceleration corresponds to a₁ = 2Ω ×u and the inertial acceleration is the sum of the Euler acceleration $\mathbf {a_{2}}=\dot {\boldsymbol {\Omega }} \times \mathbf {OM}$, the centrifugal acceleration a₃ = Ω × (Ω ×OM) and the relative acceleration a_R between the tank and the rotating referential at point O. Here, the relative acceleration is zero and the position vector of the fluid particle with respect to the rotation axis is defined as

$$ \mathbf{O}\mathbf{M}=\mathbf{O}\mathbf{C} + \mathbf{C}\mathbf{M} =x \mathbf{e}_{\mathbf{x}} + (L+y)\mathbf{e}_{\mathbf{y}} + z \mathbf{e}_{\mathbf{z}}, $$

(4)

with CM = (x,y,z) the coordinates of a fluid particle in the referential of the tank. The total volume force in the tank reference F_ext is expressed as follows,

$$ \mathbf{F}_{\mathbf{ext}}= -\rho \sum\limits_{i} \mathbf{a}_{\mathbf{i}} = \rho \left( \begin{array}{c} 2 {\Omega} v + (L+y) \dot {\Omega} + x {\Omega}^{2} \\ -2 {\Omega} u - x \dot {\Omega} + (L+y) {\Omega}^{2} \\ 0\end{array}\right). $$

(5)

The fluid domain Ω_f is now divided in two parts: Ω_l the liquid propellant region and Ω_g the gas region. The filling ratio τ_fill represents the volume of liquid divided by the total volume of the tank,

$$ \tau_{fill} = {V_{l} \over V_{f}}. $$

(6)

The physical properties of each fluid are respectively denoted by the subscript l or g. We call Γ the interface between the fluids regions (coloured in blue in Fig. 2) and n its outward normal. From now on, the jump of the physical properties and the effect of surface tension σ are considered at the interface. Moreover, the liquid propellants used in the space industry are perfectly wetting fluids. This forces the liquid to stay in contact with the tank wall. Therefore we consider that the gas initially takes the form of a spherical bubble of diameter D₀ centred in the tank. In Fig. 2, the interface Γ between the fluids is represented in blue, the gas occupies the centre of the tank and the liquid is in contact with the tank wall.

Fig. 2

Inside view of the tank at the initial time

Some dimensionless variables are used to extract characteristic numbers from the Navier-Stokes equations,

$$\begin{array}{@{}rcl@{}} \rho^{*} &=& \frac{\rho}{\rho_{l}}, \quad \mu^{*} = \frac{\mu}{\mu_{l}}, \quad \nabla^{*} = D_{0} \nabla, \quad t^{*} = t \sqrt{\frac{\sigma}{\rho_{l} {D_{0}^{3}}}}, \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} \mathbf{u}^{*} &=& \mathbf{u}\sqrt{\frac{\rho_{l} D_{0}}{\sigma}}, \quad p^{*} = \frac{pD_{0}}{\sigma}, \quad \mathbf{a}_{\mathbf{i}}^{*} = \frac{\mathbf{a_{i}}}{\gamma}, \end{array} $$

(8)

with γ a characteristic acceleration.

Considering the Coriolis and the centrifugal accelerations, the characteristic acceleration is based on the angular velocity and is equal to Ω²L. For the Euler acceleration, the characteristic acceleration is based on the angular acceleration, the value of which is $\dot {\Omega } L$. Finally, the dimensionless Navier-Stokes equations can be written as,

$$ \nabla^{*} \cdot \mathbf{u}^{*} = 0, $$

(9)

$$\begin{array}{@{}rcl@{}} \rho^{*}\left( \frac {\partial \mathbf{u}^{*}}{\partial t^{*}} + \left( \mathbf{u}^{*}\cdot\nabla^{*}\right)\mathbf{u}^{*}\right) &=& - \nabla^{*} p^{*} + Oh \nabla^{*} \cdot\left( 2\mu^{*} \bar{\bar{\mathbf{D}}}^{*}\right) \\ &&{}-{}Bo_{i} \rho^{*} \mathbf{a_{2}^{*}} - Bo_{c} \rho^{*}({}\mathbf{a_{1}^{*}}{}+{}\mathbf{a_{3}^{*}}),\\ \end{array} $$

(10)

with Oh the Ohnesorge number and two Bond numbers defined as,

$$ Oh = \sqrt{\frac{{\mu_{l}^{2}}}{\rho_{l} \sigma D_{0}}}, ~ Bo_{c} = \frac{\rho_{l} {\Omega}^{2} L {D_{0}^{2}}}{\sigma}, ~ Bo_{i} = \frac{\rho_{l} \dot {\Omega} L {D_{0}^{2}}}{\sigma}. $$

(11)

The Ohnesorge number compares the viscosity to the surface tension effects and the Bond numbers compare the inertial effects induced by the manoeuvre to the surface tension effects. Bo_c is the Bond number that focuses on the inertial effects related to the angular velocity and Bo_i is the Bond number that depends on the angular acceleration.

Configuration of the Manoeuvres

The manoeuvre we consider is the typical rotation manoeuvre of satellites in orbit. As defined previously, the rotation of the tank happens around the z-axis and the angular acceleration and velocity are defined as $\dot {\boldsymbol {\Omega }} = \dot {\Omega } \vec {e_{z}}$ and $\boldsymbol {\Omega } = {\Omega } \vec {e_{z}}$. The typical angular velocity profiles we consider are shown in Fig. 3 with the corresponding Bond numbers. They consist in a first phase with a constant angular acceleration $\dot {\Omega }$ until the angular velocity reaches its required value Ω. From then on, the angular acceleration is set to zero and the velocity stays at its constant value. Finally, the opposite angular acceleration is enforced until the angular velocity comes back to zero and the tank remains fixed.

Fig. 3

Angular velocity profile of the manoeuvre

In this study, two different filling ratios are considered: 50% and 75%. Several constant angular velocities are enforced on the tanks. They are defined with respect to the angular velocity of the first manoeuvre, denoted by Ω¹, and are summarised in Table 1. The angular accelerations applied during the first and third phases with opposite signs are characterised by the duration of these phases denoted by t_acc with respect to the time of the first manoeuvre $t^{1}_{acc}$. The corresponding Bond numbers, defined in the “Dimensionless Navier-Stokes Equations” section, are computed for the 6 manoeuvres of this study and are listed in Table 1.

Table 1 Study parameters of the manoeuvres considered

The FLUIDICS Experiment

The FLUIDICS (FLUId DynamICs in Space) experiment was a part of the Proxima mission of the CNES, the French space agency, lead by the astronaut of the ESA (European Space Agency) Thomas Pesquet in the International Space Station (ISS). The FLUIDICS experiment, represented in Fig. 4, is basically a slow rate centrifuge able to reproduce the fluids motion inside a satellite tank in orbit. It consists of a spherical tank containing a safe substitute of propellant and air, connected by an arm to a motor.

Fig. 4

View of the inside of the FLUIDICS experiment

Two spherical tanks with the same diameter D_t have been used in microgravity conditions. They are made of two polycarbonate half spheres glued together. These tanks are respectively filled with 50% and 75% of 3M Novec 2704 liquid. Figure 5 is a photograph taken on earth of the tank half filled with orange Novec liquid. The liquid is an electronic card coating which has the same range of physical properties (viscosity μ_l and density ρ_l) as propellants used in the space industry and complies with the ISS safety guidelines. The perfectly wetting property of these propellants is still respected with the Novec fluid. This will enable us to consider a zero contact angle condition in the simulations presented hereafter. The other fluid contained in these tanks is air, the physical properties of which are denoted by μ_g and ρ_g. The surface tension between the liquid and the gas is symbolised by σ.

Fig. 5

Tank half filled with Novec liquid on earth

Each tank can be plugged at the end of the rotating arm through an interface linked to a force sensor. This sensor gives the forces and torques exerted by the tank on the rotating arm in the three directions. The sensor is located at a distance L_se from the centre of the tank towards the rotating arm. The sensor location is depicted in Fig. 1 at point S. The rotating arm is linked to the motor located at the centre of the experiment. The lever arm L is the distance between the rotation axis and the centre of the tank. Beside the tank, the rotating arm supports two high resolution monochromatic cameras pointing at the tank location and, at the other end, the electronics needed to record data. Finally, the experiment is enclosed in a protection box to comply with safety rules and is fixed to the ISS seat tracks as shown in Fig. 6. A ventilation system cools down the inside of the protection box because of the heat released by the electronics. More details about the experiment are given in Mignot et al. (2017).

Fig. 6

The FLUIDICS experiment fixed to the ISS structure

The 6 manoeuvres described in Table 1 have been executed in the ISS in 2017. The manoeuvres with the half-filled tank have been done twice to ensure repeatability. The data have been post-processed to be correlated with numerical simulations. The data from the force and torque sensor have been filtered and the solid contribution of the empty tank in the measured data has been removed to quantify only the effect of the fluids on the tank wall.

Description of the Numerical Tool

Numerical Methods

In this section, the numerical solver considered in this study is presented. The home-made code DIVA (Dynamics of Interface for Vaporization and Atomization) is based on several numerical methods dedicated to the computation of two-phase flows.

The computational domain can be divided in two regions: a fluid region Ω_f corresponding to the inside of the tank and a solid region Ω_s which consists of the rest of the cubic computational domain. The interface between these regions is denoted by Γ_s and represents the tank wall. As seen in the “Dimensionless Navier-Stokes Equations” section, the fluid region is divided in two phases as well: the liquid region Ω_l and the gas region Ω_g separated by the interface denoted by Γ.

The level-set method of Osher and Sethian (1988) and Sussman et al. (1994) is used to follow the interface motion of Γ through time and to define the static position of Γ_s. Two level-set functions are defined and represent first, the signed distance function from the liquid gas interface ϕ and second, the signed distance from the solid fluid interface ϕ_s. The motion of the liquid-gas interface is captured by solving the following transport equation

$$ \frac{\partial \phi}{\partial t} + \mathbf{u}\cdot \nabla \phi = 0, $$

(12)

coupled with the reinitialization algorithm of Sussman et al. (1994) to maintain the distance property of the level-set function through time. Based on the work of Fedkiw et al. (1999) and Aslam (2004), the following boundary condition on the level-set function ϕ must be considered within the solid domain to enforce the contact angle 𝜃_s if a triple line exists

$$ \mathbf{n}_{\mathbf{s}} \cdot \nabla \phi |_{\Gamma} = - \cos\theta_{s}, $$

(13)

with n_s the outward normal vector of the fluid-solid interface. As previously stated, the simulations involved in this paper will still consider a zero contact angle condition since the spherical tanks are filled with a perfectly wetting fluid. This means that there is always some liquid against the tank wall in our simulations. The zero contact angle hypothesis will be further justified by comparing the numerical results with the experimental data, especially the torque signal which depends on the interface position.

The incompressible Navier-Stokes equations for Newtonian two-phase flows are solved using the Ghost Fluid Conservative viscous Method with an Implicit scheme (GFCMI) of Lepilliez et al. (2016). This method is based on the projection method of Chorin (1967) first introduced by Sussman et al. (2007). It consists in three steps: first, considering the velocity field uⁿ at time tⁿ = nΔt, an intermediate velocity u^∗ is computed without considering the pressure term by solving the following linear system,

$$\begin{array}{@{}rcl@{}} \rho^{n + 1}\mathbf{u}^{\mathbf{*}} &-& {\Delta} t \nabla \cdot \left( 2\mu^{n + 1} \bar{\bar{\mathbf{D}}}^{*}\right) \\ &&= \rho^{n + 1} \left( \mathbf{u}^{n} - {\Delta} t \left( \left( \mathbf{u}^{n}\cdot \nabla\right)\mathbf{u}^{n} - \frac{\mathbf{F}_{\mathbf{ext}}}{\rho^{n + 1}} \right) \right). \end{array} $$

(14)

The rate-of-deformation tensor is solved implicitly to remove the time-step restriction due to the viscosity. The linear system which couples the three components of the velocity is solved using a Gauss-Seidel algorithm.

Then, the pressure field p^n+ 1 is regarded as the scalar potential function of the Hodge decomposition and satisfies the Poisson equation with Neumann boundary conditions

$$ \nabla\cdot \left( \frac{\nabla p^{n + 1}}{\rho^{n + 1}}\right)= \frac {\nabla\cdot \mathbf{u}^{*} }{{\Delta} t} + \nabla \cdot \left( \frac{\sigma \kappa \mathbf{n} \delta_{\Gamma}}{\rho^{n + 1}}\right), $$

(15)

with κ the local curvature of the liquid-gas interface and n the outward normal vector of the interface and δ_Γ a multidimensional Dirac distribution at the interface. The density jump and the pressure jump due to the surface tension term are taken into account with the sharp representation of the interface from Liu et al. (2000). The resolution of the linear system is performed using the Black Box MultiGrid method, see Dendy (1982) and MacLachlan et al. (2008) for more details.

Finally, the velocity at the next time step u^n+ 1 is computed as the projection of the intermediate velocity onto the divergence-free space

$$ \mathbf{u}^{n + 1} = \mathbf{u}^{*} - \frac{{\Delta} t}{\rho^{n + 1}}(\nabla p^{n + 1} - \sigma \kappa \mathbf{n} \delta_{\Gamma}). $$

(16)

The no-slip boundary condition is considered at the tank wall within the computational domain. A subcell Dirichlet boundary condition on the velocity (zero velocity at the tank wall) and a Neumann boundary condition on the pressure (zero normal pressure gradient) are enforced using the methodology of Gibou et al. (2002), Ng et al. (2009), and Lepilliez et al. (2016).

Following the general guidelines of the Ghost Fluid Method, our home-made code DIVA can also consider phase change simulations, by imposing additional jump conditions to maintain mass conservation (Nguyen et al. 2001), energy conservation (Gibou et al. 2007; Tanguy et al. 2014) and chemical species conservation (Papac et al. 2010; Tanguy et al. 2007; Rueda Villegas et al. 2016), and compressible flows (Huber et al. 2015). This solver has been extensively validated with other experimental data both for isothermal two-phase flows (Lalanne et al. 2015; Tanguy and Berlemont 2005) and for two-phase flows with phase change for impacting droplets in the Leidenfrost regime (Rueda Villegas et al. 2017) and for nucleate pool boiling (Huber et al. 2017; Urbano et al. 2018).

Mesh Convergence

To ensure the numerical simulations are well defined, a mesh convergence study on a specific manoeuvre is presented. We consider manoeuvre n^∘1 (see Table 1) which corresponds to the highest values of the Bond numbers: Bo_c = 76 and Bo_i = 23 with the half-filled tank. The maximum angular velocity is maintained during the second phase and the filling ratio of 50% ensures an important motion of the gas bubble within the tank. The simulations have been done on three different meshes with 64, 128 and 256 cells in each direction. The force F and the torque at the sensor location T exerted by the fluids on the tank wall are computed in the simulations as

$$\begin{array}{@{}rcl@{}} \mathbf{F} &=& {\int}_{{\Omega}_{f}} (\nabla p - \sigma \kappa \mathbf{n} \delta_{\Gamma}) dV, \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} \mathbf{T} &=& {\int}_{{\Omega}_{f}} \mathbf{SM} \times (\nabla p - \sigma \kappa \mathbf{n} \delta_{\Gamma}) dV. \end{array} $$

(18)

with SM the vector between the sensor and a fluid particle as SM = xe_x + (L_se + y)e_y + ze_z. As the Reynolds number based on the velocity Ω²L,

$$ Re = \frac{\rho_{l} {\Omega}^{2} L D_{t}}{\mu_{l}}, $$

(19)

varies between 12500 and 37500 for manoeuvres n^∘1 to n^∘4, only the pressure component of the force and the torque exerted on the tank wall has been considered. Indeed, for these high values, the viscous component of the force can be neglected with respect to the pressure component.

Figures 7 and 8 respectively show the evolution of the dimensionless force in the y-direction and the dimensionless torque in the z-direction until t^∗ = 3 for the three meshes. The physics corresponding to the temporal evolution of the force and the torque will be described in the “Comparisons”, this section only takes interest in the grid sensitivity.

Fig. 7

Computed force in the y-direction throughout time for manoeuvre n^∘1 and for three different meshes: 64³, 128³ and 256³

Fig. 8

Computed torque in the z-direction throughout time for manoeuvre n^∘1 and for three different meshes: 64³, 128³ and 256³

The temporal evolutions of the force and the torque are similar for the three meshes. At the beginning, the increase of the force toward the same peak is predicted by all the meshes. The same oscillatory behaviour is obtained with similar frequencies and magnitudes. The mean value of the force after t^∗ = 0.5 varies a little but stays close for the two finest grids. Similarly, the frequency and the magnitude of the torque oscillations for the three meshes are really close to each other.

The meshes containing 128 and 258 cells in each directions are in good agreement and prove the spatial convergence. We will then consider the intermediate mesh 128³ for all the simulations of this paper.

Comparisons

This section aims at comparing the data from the FLUIDICS experiment with the numerical results for the manoeuvres listed in Table 1. The comparison deals with the y-direction force and the z-direction torque. Indeed, because the system is symmetrical to the plane {z = 0}, no external acceleration happens in the z direction leading to no force nor motion of the centre of mass toward e_z. Thus, the relation between the force and the torque at the sensor location becomes

$$ \mathbf{T} = \mathbf{SG} \times \mathbf{F} = \left( x_{g} F_{y} - (L_{se} + y_{g}) F_{x} \right) \mathbf{e}_{\mathbf{z}}, $$

(20)

with SG = SC + CG and CG = (x_g,y_g,z_g ≈ 0) the coordinates of the centre of mass in the tank referential. Because L_se is higher than the maximum coordinates of the centre of mass, the torque in the z-direction has the same temporal evolution than the x-component of the force. To avoid redundant comparisons and because the sensor has a greater sensitivity to the torque than to the force, the x-direction force is not investigated at the expense of the z-direction torque.

Force in the Y-Direction

The force in the y-direction corresponds to the highest component of the forces exerted by the fluids on the tank wall. During the constant angular velocity phase, the centrifugal acceleration is the only external force that remains after the fluids stabilisation. Its asymptotic value is thus a relevant criterion to compare the experimental data with the simulations. Figure 9 shows the dimensionless force evolution measured in the ISS (in solid black) and computed by the code (in dashed blue) for manoeuvre n^∘1.

Fig. 9

Comparison of the measured and computed forces in the y-direction throughout time for manoeuvre n^∘1

First, the dimensionless force increases considerably during the acceleration phase. Once the first phase is over, the angular velocity remains constant and the angular acceleration is set to zero. The volume force is then dominated by the centrifugal force and becomes

$$ \mathbf{F}_{\mathbf{ext}} = \rho \left( \begin{array}{c} 2 {\Omega} v + x {\Omega}^{2} \\ -2 {\Omega} u + (L+y) {\Omega}^{2} \\ 0\end{array}\right). $$

(21)

Consequently, in the second phase, the liquid moves to the direction + e_y because of the centrifugal force and the gas bubble spreads against the tank wall in the opposite direction. At the beginning of the second phase, the fluids are not stabilised and the gas bubble oscillates around the x-axis {x = 0}. This is due to the sign of the x-component of the centrifugal force which changes every time the centre of mass crosses the axis {x = 0}. Four pictures of an oscillation of the gas bubble predicted by the numerical code are shown in Fig. 10. These oscillations are damped with time until the bubble reaches its equilibrium position. At the steady state, the Coriolis contribution of Eq. 21 disappears and only the centrifugal force remains.

Fig. 10

Oscillation of a gas bubble (in blue) in the spherical tank predicted with τ_fill = 50%

Similarly, we observe in Fig. 9 that after t_acc, the force oscillates around a constant value. The magnitude of the oscillations decreases throughout time until they disappear in the simulations (in dashed blue), and until the magnitude of the oscillations reaches the noise level in the experimental data (in solid black).

Figure 11 depicts the gas bubble (in dark blue) inside the spherical tank at the equilibrium state according to the simulations. The gas bubble is spread against the tank wall in the direction −e_y because of the centrifugal force. It is stabilised and symmetrical to the axis {x = 0}, leading to no force in the x-direction nor torque in the z-direction and the x-coordinate of the centre of mass equals zero. Because of the perfectly wetting condition, a thin film of liquid is trapped between the bubble and the tank wall, as can be observed in Fig. 11.

Fig. 11

Gas bubble at the steady state of the second phase of the first manoeuvre and zoom on the film of liquid at the tank wall

Finally, the angular velocity decreases during the deceleration phase, leading to the drop of the y-direction force until it reaches zero when no more external accelerations are enforced.

The two curves in Fig. 9 exhibit the same temporal evolution of the y-direction force. The mean values of the measured and computed forces during the second phase are close to each other. The measured mean value is 34.84 and the computed mean value is 34.16 leading to a difference lower than 2%. This manoeuvre has been enforced a second time in the ISS and the resulting mean value is 34.69 which gives a difference still lower than 2% between the numerical simulations and the experimental data. We observe as well that the first oscillations are well predicted by the simulations. The computed force coincides with the data for the three first oscillations. Over time, the magnitude of the oscillations decreases and the variation of the measured force reaches the level of noise. In the numerical simulations, the oscillations carry on until the end of the second phase with an extremely low magnitude. The more detailed study of the oscillations is presented in the next subsection through the torque evolution.

Figure 12 shows the evolution of the measured and computed dimensionless force in the y-direction throughout time for manoeuvre n^∘2. It consists in the same velocity profile as the first manoeuvre with the tank containing 75% of liquid. The force evolution corresponds to the same behaviour but the force value during the second phase is more important. The filling ratio is higher, which means that more liquid is inside the tank and leads to a higher centrifugal acceleration. The computation of the mean forces shows a slightly larger difference between the data and the simulations compared to the previous manoeuvre. The mean value of the measured force is 51.29 and the mean value of the computed force is 49.31 which leads to an error of 3.85%.

Fig. 12

Comparison of the measured and computed forces in the y-direction throughout time for manoeuvre n^∘2

The damping of the oscillations is stronger than in the previous case. They disappear in the numerical simulation after t^∗ = 4. This phenomenon is a consequence of the high filling ratio. The gas bubble is smaller and spreads with a higher magnitude on the tank wall. Because of the tank geometry, the gas bubble is highly deformed and its motion is more constrained. The low variation of the force at the beginning of the second phase prevents us from extracting more information about the oscillations.

Considering a lower angular velocity, the force evolution measured and predicted for manoeuvre n^∘3 is plotted in Fig. 13. The average values of the force during the second phase stay close for the two experimental runs between 11.35 and 11.72. The comparison with the computed value of 11.37 shows a difference lower than 3% for the two runs of manoeuvre n^∘3 carried out in the ISS. However, the oscillations of the bubble cannot be extracted from the experimental data because the noise level is too important with respect to the centrifugal force. With the simulation, the bubble oscillations are visible but their magnitudes do not exceed the experimental noise level. Whereas the fluid stabilisation may be questionable in Fig. 13, studying the videos helped us to conclude that a steady state has been reached at the end of the constant velocity phase. As a result, the fluctuations of the signals are only due to measuring uncertainties. One can notice that the noise amplitude remains approximately constant whatever the considered manoeuvre, even if it seems more important for lower Bond numbers.

Fig. 13

Comparison of the measured and computed forces in the y-direction throughout time for manoeuvre n^∘3

The same velocity profile enforced on the 75%-filled tank gives the same observations. Figure 14 shows that the bubble oscillations are more damped because of the additional mass of liquid and their magnitudes are still lower than the noise level. The average value of the force increases from values around 11.5 to 16 between the two tanks. Finally, the comparison of the mean values of the force shows a relative difference of 6.08%, which is the highest error we observe in the manoeuvres.

Fig. 14

Comparison of the measured and computed forces in the y-direction throughout time for manoeuvre n^∘4

Table 2 gathers all the average values of the measured and computed dimensionless forces for manoeuvres n^∘1 to 4. Manoeuvres n^∘1 and 3 have been executed twice in the ISS and are respectively denoted with the subscripts ‘a’ and ‘b’. The angular velocities of manoeuvres n^∘5 and 6 are too low to extract reliable data from the force and torque sensor and are not considered in this section.

Table 2 Comparison of the mean force in the y-direction

In brief, the level of force increases with the Bond number Bo_c and the filling ratio. This is explained by the centrifugal force which depends directly on the square of the angular velocity and on the volume of liquid inside the tank. For the highest Bond numbers manoeuvres, the temporal evolution of the force is well predicted by the simulations: the mean force in the second phase and the oscillations are in good agreement with the experimental data. For all the manoeuvres, the numerical simulations predict mean values of forces with a maximum difference of 6%, providing a strong validation of the proposed numerical approach.

Torque in the Z-Direction

The torque in the z direction allows us to extract other contributions of the fluids on the tank wall. In addition to the y-direction force, the z-component of the torque exhibits the effects of the angular acceleration on the fluids and emphasises the oscillations of the bubble around its equilibrium position. Considering manoeuvre n^∘1, the dimensionless torque obtained by the FLUIDICS experiment in a microgravity environment and predicted by the simulations are plotted in Fig. 15 in solid black and dashed blue, respectively.

Fig. 15

Comparison of the measured and computed torques in the z-direction throughout time for manoeuvre n^∘1

During the acceleration phase, we observe an important negative peak of the torque. This is due to the Euler acceleration which dominates the flow at the beginning of the manoeuvre. At early flow time, the angular velocity is low but the angular acceleration is already enforced on the tank. By neglecting the angular velocity with respect to the angular acceleration, the volume force becomes

$$ \mathbf{F}_{\mathbf{ext}} = \rho \dot {\Omega} \left( \begin{array}{c} L+y \\ - x \\ 0\end{array}\right). $$

(22)

Because the lever arm L is higher than the maximal centre of mass coordinates, the volume force is dominated by the contribution of the Euler acceleration in the x-direction. This contribution is recovered in the z-direction torque following Eq. 20 and explains the negative peak we have measured. The same phenomenon appears during the deceleration phase with a positive peak of the z-direction torque (visible at t^∗ = 8.2 in Fig. 15) because the angular acceleration is the opposite. During the constant angular velocity phase, the oscillations due to the bubble motion are clearly visible. The torque oscillates around zero and its magnitude decreases with time until the bubble reaches its equilibrium position, centred at the axis {x = 0}. Indeed, at the steady state, the x-coordinate of the centre of mass is zero and the volume force is only directed toward the y-direction (see Eq. 21).

The comparison between the two curves of Fig. 15 shows a very good agreement on the temporal evolution of the torque measured in microgravity conditions and predicted by numerical simulations. The peaks corresponding to the acceleration and deceleration phases have the same magnitude in both cases and the sharp increase and decrease of the torque is well respected. The oscillations of the computed torque concur with the experimental data until the magnitude of the latter reaches the noise level. Both the magnitude and the frequency of the measured and predicted torque are in good agreement. The frequency of the oscillations is the aim of the next subsection.

Figure 16 represents the time evolution of the dimensionless torque for manoeuvre n^∘2. The same angular acceleration and velocity as for manoeuvre n^∘1 are enforced on the tank with τ_fill = 75%. Similarly, two peaks of opposite signs are observed during the first and third phases. Their magnitudes are increased with the filling ratio. During the constant angular velocity phase, the observed oscillations are more damped than for the half-filled tank. However, the first predicted oscillations have the same magnitude and frequency as the measured torque but the important damping and the data noise prevent us from going further.

Fig. 16

Comparison of the measured and computed torques in the z-direction throughout time for manoeuvre n^∘2

The temporal evolutions of the torque for manoeuvres n^∘3 and n^∘4 are depicted in Figs. 17 and 18, respectively. The magnitude of the torques decreases because of the lower angular velocity. The peaks corresponding to the contribution of the Euler acceleration are still visible and well predicted by the simulations but the angular acceleration being lower, the magnitudes of the peaks decrease. As the magnitude of the torque oscillations also decreases, the noise from the experimental setup becomes too large, preventing a possible comparison of the amplitude and the frequencies of the torque oscillations during the second phase.

Fig. 17

Comparison of the measured and computed torques in the z-direction throughout time for manoeuvre n^∘3

Fig. 18

Comparison of the measured and computed torques in the z-direction throughout time for manoeuvre n^∘4

These comparisons between the numerical and experimental torque signals provide also an indirect validation of the zero contact angle hypothesis. Indeed, as the torque depends both on the force and on the interface position, the good agreement reported previously confirms the relevance of this assumption, since the interface position depends strongly on the contact angle value.

Sloshing Frequency

As previously stated, the oscillations observed at the beginning of the second phase are due to the motion of the gas bubble inside the tank before reaching its equilibrium shape and position depicted in Fig. 11. We consider the oscillations of the torque in the z-direction and apply a discrete Fourier transform to obtain the amplitude spectra of the signals. The transform is applied on the same time range Δt^∗ = 7.5 for all the manoeuvres. The objective of this section is to extract the frequencies of the oscillations for each manoeuvre and to compare the predicted value to the data from FLUIDICS.

Figure 19 depicts the amplitude spectra of the z-direction torque for manoeuvre n^∘1. In dashed blue, the amplitude spectrum of the torque from the simulation exhibits a main peak at f^∗ = 2.67. No other characteristic frequency appears in the simulation. In solid black, the amplitude spectrum from the experimental data is more complex. The same peak appears for the same frequency f^∗ = 2.67. These experimental and numerical frequencies match well within the frequency resolution Δf^∗ = 0.133. For this first manoeuvre, the simulation provides an accurate prediction of the sloshing frequency. A second important peak appears for a lower frequency in the experimental data. It corresponds to the rotation frequency denoted by f_Ω = Ω/2π. Knowing that D_t/L = 0.57, the dimensionless rotation frequency can be expressed as

$$ f^{*}_{\Omega} = f_{\Omega}\sqrt{\rho_{l} {D_{t}^{3}} \over \sigma} = {1 \over 2\pi} \sqrt{D_{t} Bo_{c} \over L (1-\tau_{fill})^{2/3}}. $$

(23)

Fig. 19

Comparison of the measured and computed amplitude spectra of the z-direction torque for manoeuvre n^∘1

For manoeuvres n^∘1 and 2, the dimensionless rotation frequency equals $f^{*}_{\Omega } = 1.322$ and corresponds to the lower frequency peak observed in Fig. 19. This parasitic frequency is likely due to an unbalance of the experiment and explains partly the spurious oscillations observed in the signal torque in Figs. 15 and 16. Other minor peaks appear for higher frequencies and can be attributed to the other kind of perturbations such as the electronic devices, the fans, the structural vibrations... The magnitude of the peaks allows us to compare the effects of the different sources of the oscillations averaged over the constant angular velocity phase.

Figure 20 depicts the amplitude spectra of the vertical torque for manoeuvre n^∘2. In dashed blue, the spectrum of the simulation shows a main frequency around f^∗ = 2.93. In solid black, the range of frequencies [2.64;2.94] have important magnitudes. We assume that this interval contains the sloshing frequency and some disturbing frequencies. The peak corresponding to the same rotation frequency as for the previous manoeuvre is the most important in Fig. 20. In this case, the sloshing oscillation is much more damped compared to manoeuvre n^∘1 and then, the rotation frequency becomes dominant during a longer time period. This explains why the peaks corresponding to the rotation frequency exceed the sloshing oscillation frequencies. Finally, the same minor frequencies as in Fig. 19 appear around f^∗ = 4 and f^∗ = 5.33. As seen in Fig. 16, the torque oscillations are much more damped with the filling ratio of 75%. The interval of time for which the bubble oscillations are noticeable is reduced and the noise due to the unbalance has a greater importance in the amplitude spectrum. This explains why the only frequency for which the amplitude spectrum decreases between the first and second manoeuvres is the sloshing frequency.

Fig. 20

Comparison of the measured and computed amplitude spectra of the z-direction torque for manoeuvre n^∘2

Figure 21 illustrates the amplitude spectra for the third manoeuvre. The oscillation frequency is clearly visible at f^∗ = 1.47 in the numerical results. In the experimental data, several peaks appear, represented in solid black. The lower frequency corresponds to the rotation frequency, which can be computed with Eq. 23 as $f_{\Omega }^{*}= 0.765$. The value of the predicted oscillation frequency is approached by a amplitude peak at f^∗ = 1.6. Then, several higher frequencies appear and correspond to the noise observed in Fig. 17. Finally, considering the most filled tank, the same amplitude spectrum as in manoeuvre n^∘3 is obtained with a decrease of the amplitude corresponding to the sloshing frequency. Despite the high level of noise involved in the signal in Fig. 18, the amplitude spectrum allows recovering the sloshing frequency even for this manoeuvre for which the highest perturbations are observed.

Fig. 21

Comparison of the measured and computed amplitude spectra of the z-direction torque for manoeuvre n^∘3

We observe that in the four amplitude spectra of Figs. 19 to 22, the same frequency f^∗ = 5.33 appears in the experimental data. The angular velocities and the filling ratios being different for each one of these cases, this disturbance frequency is independent from the manoeuvre enforced. This may come from electronic noises, the ventilation system of the experiment or the ISS environment.

Fig. 22

Comparison of the measured and computed amplitude spectra of the z-direction torque for manoeuvre n^∘4

Considering the first manoeuvre, the frequencies corresponding to the rotation frequency and the constant frequency f^∗ = 5.33 have been filtered in the frequency domain. The sources of the other frequencies observed in the amplitude spectra are not clearly identified and thus have not been filtered. After applying the inverse Fourier transform, the resulting torque signal is compared to the numerical results and presented in Fig. 23. We observe that, at early flow time, the filtered signal is quite similar to the signal in Fig. 15 with an improved agreement with the numerical results until t^∗ = 3.

Fig. 23

Comparison of the filtered torque and the computed torque in the z-direction throughout time for manoeuvre n^∘1

Table 3 summarises the oscillation frequency extracted from the amplitude spectra. The predicted and measured frequencies are in close agreement for manoeuvres n^∘1 to 4. Moreover, the oscillation frequencies measured for the two runs of manoeuvres 1 and 3 are identical and listed in Table 3. This demonstrates the repeatability of the experiment and provides a validation of the simulations for the bubble sloshing frequency observed in the second phase of the manoeuvre.

Table 3 Comparison of the computed and measured frequencies of the oscillations with the amplitude spectra

For the lower Bond numbers manoeuvres (n^∘5 and 6), the noise in the experimental data prevents us from extracting the force and torque temporal evolution. Nevertheless, the videos of the tank allow to observe the bubble motion throughout time. Considering the half-filled tank, the bubble oscillations are clearly visible during the constant velocity phase, even for Bo_c around 6. For these ranges of Bond numbers, several oscillations (between 3 for manoeuvre n^∘6 to 11 for manoeuvre n^∘1) are visible during the constant velocity phase and allow to extract the characteristic time of an oscillation. For the tank with τ_fill = 75%, the oscillations are quickly damped and we cannot extract the frequency from the video.

Figure 24 represents six snapshots of an oscillation of the gas bubble inside the half-filled tank. The spherical tank is centred in the pictures and the ring corresponding to the region where the two half-sphere of the tank are glued together is recognisable. The gas bubble is located towards the lever arm direction at the bottom of the pictures such as in Fig. 11. We observe that during the oscillation, the bubble approaches the tank wall in the camera direction and so, rises in the picture until it reaches its maximum (a to d). Then, the bubble goes to the opposite direction and the interface goes down until it reaches its minimum location (e and f).

Fig. 24

Snapshots of a bubble oscillation with τ_fill = 50%

Table 4 summarises the oscillation frequencies measured with the videos for all the Bond numbers exerted on the half-filled tank. They are compared with the values obtained with the Fast Fourier transform of the numerical simulations.

Table 4 Comparison of computed and measured frequencies of the oscillations with the videos

First, considering manoeuvres n^∘1 and 3, the frequencies measured with the videos are close to these from the torque signals (see Table 3). Then, the frequencies of the simulations present a good agreement with the measured ones even for the lower Bond numbers Bo_c of 6 and 13. The frequency resolution with the simulations is still equal to Δf = 0.133 and the accuracy when measuring the time period with the video depends on the manoeuvre. They are summarised in Table 3. Despite the margin of error, the predicted frequencies are close to the measured ones in all cases with the half-filled tank. This extends the use of the numerical code for low Bond numbers manoeuvres.

Figure 25 summarises all the oscillation frequencies obtained with the half-filled tank. As we can assume that Bo_i influences weakly the oscillation phase, we take interest only in the centrifugal Bond number. For these four manoeuvres, we observe clearly that the oscillation frequency increases with Bo_c.

Fig. 25

Computed and mesured frequencies with the sensor and the video for different Bond numbers and τ_fill = 50%

Conclusion

This paper presented the comparison between experimental data and numerical simulations of the fluids behaviour inside a spherical tank rotating around a fixed axis in microgravity conditions. The FLUIDICS experiment in the ISS allowed to measure the force and torque exerted by the fluids on the tank wall for different manoeuvres. These data have been compared to the numerical results from our home-made code DIVA. Preliminarily, the numerical simulations have been validated through a mesh convergence study on the manoeuvre with the highest Bond numbers. Then, results on six different manoeuvres corresponding to different angular velocities and filling ratio are presented both from numerical simulations and experimental data carried out in the ISS.

The comparison of the y-direction force shows a good agreement between the measured and predicted forces. The average value of the centrifugal force is well predicted with an error lower than 6% for all the manoeuvres. This error decreases to 3% for the manoeuvres exerted on the half-filled tank. Moreover, the variations of the force at the beginning of the constant angular velocity phase are similar while their magnitudes are higher than the noise level. Considering the torque evolution, the peaks corresponding to the Euler acceleration contribution are clearly visible and their magnitudes are well predicted by the simulations. The oscillations of the gas bubble during the second phase of the manoeuvre have different magnitudes and damping ratios depending on the angular velocity and filling ratio. For the first two manoeuvres, the oscillations exceed the noise level and the measured and predicted temporal evolutions are in close agreement. By applying the discrete Fourier transform on the second phase of the torque signal, it has been possible to extract their main frequencies. The numerical simulations exhibit only one frequency corresponding to the bubble oscillation frequency. For the experimental data, further disturbing frequencies appear, such as the rotation frequency, which bring out some unbalance of the experimental setup. Higher frequencies may also come from vibrations of the structure, the electronic noises, the cooling system of the experiment or the ISS environment. However, the bubble oscillation frequencies are well predicted by the simulations within the frequency resolution of the data. In the case of the half-filled tank, the videos from the FLUIDICS experiment allowed us to extract the oscillation frequency even for the lower value of the Bond number manoeuvres for which the force and torque signals were too noisy to be used. Similarly, the comparisons with the predicted frequencies show a good agreement within a range of 4%.

The evolution of the force and torque with respect to the Bond numbers and filling ratios present a coherent set of data whether numerical or experimental results are considered. Increasing the angular velocity and the amount of liquid within the tank raises the centrifugal force exerted on the tank wall. Similarly, the damping of the bubble oscillations increases with the filling ratio, which is visible in both the force and torque evolutions. The magnitude of the torque peaks corresponding to the acceleration and deceleration phases depends on the angular acceleration and thus, on Bo_i. The frequency of the bubble oscillations increases with the angular velocity.

In conclusion, the FLUIDICS experiment provided original data on the fluid sloshing in spherical tanks submitted to rotation in micro-gravity conditions. The comparison with the numerical results validates the use of two-phase flows Direct Numerical Simulation to predict the fluids behaviour at low Bond numbers manoeuvres in microgravity conditions.