Introduction

Storage tank is one of the basic components for spacecraft, in which the behavior of liquid is mostly responsible for the safety, stability, fuel supply, and so on. Correspondingly, researchers pay close attentions to the shape of free surface (Kulev and Dreyer 2010; Park et al. 2015; Zhou et al. 2016; Zwicke et al. 2017), the pressure control inside tank (Lopez et al. 2008; Barsi and Kassemi 2013; Chen and Liang 2013; Kassemi and Kartuzova 2016), the liquid sloshing (Zhou and Huang 2015; Deng and Yue 2017), and the measurement of the residual liquid. Among these aspects, the dynamic evolution of the free surface of the liquid inside tank is the key topic, which is principally determined by the surface tension force in microgravity environment.

Table 1 Comparison of the characteristic parameters of present experiments with Kulev and Dreyer (2010)
Full size table

Benefited by the computational fluid dynamics (CFD), especially the volume of fluids (VOF) and level-set methods, the dynamic evolution of interface in a tank can clearly be investigated. Stange et al. (2003) investigated dynamics of capillary-driven flow of perfectly wetting liquids into circular cylindrical tubes under microgravity condition experimentally and numerically. Ho and Rahman (2005) promoted the numerical simulation of tank into three dimensions and compared the difference between two (axis-symmetric) and three-dimensional results. Fries and Dreyer (2008) presented an analytic solution to the momentum balance of a liquid and investigated the initial moments of capillary rise of liquids in a capillary tube. Li et al. (2017) numerically investigated capillary flow in fan-shaped asymmetric interior corner under microgravity taking the effect of contact angle into account. The perspectives of researchers transferred from the properties of fluids, such as SF 0.65, SF 1.00, FC-77 (Stange et al. 2003), LH2 (Kumar et al. 2007), to the outer geometry structure (with empty internal structure) of the tank (Lopez et al. 2007). However, the mainly point is still on the latter, especially the capsule tank was mostly used (Kassemi and Kartuzova 2016).

Importantly, what intimately associated with the free surface in a tank is sloshing, which is a common motivation in space fluid management. A good number of works have been covered with the sloshing behavior both experimentally and numerically. Park et al. (2015) presented an image preprocessing method for particle image velocimetry (PIV) measurements of flow around an arbitrarily moving free surface. They demonstrated that the velocity and oscillation of free surface changed with the increase of forcing frequencies. Chiba and Magata (2017) investigated the influence of sloshing motion on the motions of the main body and flexible appendages of the spacecraft, indicating that the vibration characteristics of the coupled system were dependent on the static contact angle of the liquid, irrespective of whether the angle was larger or smaller than 90∘. Sun et al. (2015) examined the two-dimensional fluid structure interaction with free surface using modified Moving Particle Semi-implicit (MPS) method which showed good agreement with experiment for the free surface profiles. Monaghan and Meriaux (2018) numerically studied the two-dimensional turbulence near free surface based on smoothed particle hydrodynamics (SPH). Deng and Yue (2017) focused on attitude tracking control of a spacecraft with partially filled tank. They found that the improved moving pulsating ball model (MPBM) was useful for an approximate estimates of the liquid’s location. Despite its fundamental importance, our understanding of the sloshing in a tank remains limited, in part due to the working environment of tank. Specifically, research on the behavior of liquid in a tank with capsule geometrical structure under microgravity condition was not sufficient.

In the present study, the behavior of liquid in partially filled capsule storage tank in microgravity was studied both numerically and experimentally. Two sealed and inverted test tubes filled with water were used to simulate the liquid behavior inside a capsule tank after an abrupt drop of gravity by utilizing the Drop Tower Beijing. Experimental data on the oscillation of the free surface obtained during the short-term microgravity (\(\sim \) 3.6 s of duration) were also used to verify the numerical model. The volume of fluids (VOF) method was used to build the numerical model and to reveal detailed liquid behaviors, particularly the oscillation frequency of the free surface. The influences of the air fraction and the tank diameter on the oscillation of the free surface are also discussed.

Experiment

Experimental Apparatus and Procedure

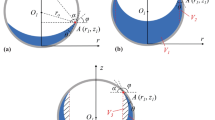
Two characteristic time scales were introduced in present study. \(t_{1}=\sqrt {\rho R^{3}/\sigma } \) is the characteristic response time for settling phenomena, \(t_{2} =R^{3}/\nu \) is viscous time scale (Strange et al. 2003), where \(\rho \) is the density, \(\sigma \) the surface tension, \(\nu \) the kinematic viscosity and R the radius of tank. The Bond number Bo = (ρl − ρg)g0R2/σ presents the relative importance of buoyancy force to capillary force with g0 = 9.807 m/s2. In consideration of the characteristic times \(t_{1}\) and \(t_{2}\) (see Table 1) and the effective duration of microgravity (\(\sim \)3.6 s) of the Drop Tower Beijing, two scale-down test tubes with inner diameters of 21.8 mm (DL) and 12.5 mm (DS) were used in the experiment. As shown in Fig. 1a, the tubes were inverted and sealed to simulate the half capsule storage tank.

Fig. 1
figure 1

Experimental apparatus. a the cylindrical tube used in experiment. b the overall test apparatus

Full size image

The dynamic behavior of free surface of liquid during the free falling process of test tube was recorded by a WAT-660D CCD camera (25 fps, 290k pixels) linked to a video capture card with a resolution of 352×288 pixels. Homogeneous backlight of LED was used on the opposite position of the camera as source light. Sign lamp was installed to indicate the starting point of the free falling process of test tube. All of the experimental components were assembled in a test bench constructed with Aluminum alloy, as shown in Fig. 1b.

The experiment was carried out in single capsule mode utilizing the Drop Tower Beijing which can provide 3.6 s experiment duration and microgravity level of \(\sim 10^{\mathrm {-3}}\ g_{0}\). Before the release of the capsule, it was kept standing for about 15 minutes to make sure the free surface in test tube reach the steady state. Then the drop capsule was released and recovered after 3.6 s.

Data Processing

The recorded video was firstly converted to images by frames. The time interval is 0.04 s determined by CCD camera recording rate. When investigating the dynamic behavior of liquid in the tube, the captured images were amplified 10 times considering the insufficiency of effective pixels and the sharp fluctuation of free surface. In the process of image amplification, the smooth technology (linear interpolation method) was adopted to avoid extra errors. The external diameter of tube and the scale on the wall of tube were selected as reference standard to calibrate the distance on the images. In order to avoiding the error from light and image blurring, the curve fitting method was used to acquire the optimum outline of the tube. In actual operation, the outline of the tube was extracted using 20 points near the outline of the hemisphere selected manually. Then regression analysis of these points were conducted to get the equation of outline of the hemisphere (as a circle). The center point of the hemisphere was selected as the origin of the coordinate o. The position of inner wall of the tube is shown in Fig. 2c.

Fig. 2
figure 2

Schematic geometry of experimental tube. b Original image of the tube. c Data processing procedure of the original tube

Full size image

Binary images were obtained by using the optimal threshold value method in MATLAB. The position of center point of the free surface in test tube was then determined with the position uncertainty of \(\pm 0.3\) mm and the time uncertainty of \(\pm 0.04\) s.

Numerical Model

Governing Equations

The volume of fluids (VOF) method (Hirt and Nichols 1981; Gueyffier et al. 1999) was used in the process of simulating the dynamic behavior of liquid in tube. The momentum equation of VOF method is as follows Gueyffier et al. (1999):

$$ \partial_{t} (\rho \boldsymbol{u})+\nabla \cdot (\rho \boldsymbol{uu})=-\nabla p+\nabla \cdot (2\mu \boldsymbol{D})+\rho{\boldsymbol{g}}+\sigma k\hat{\boldsymbol{n}}\delta_{s} $$
(1)

Where u is the velocity vector, \(\rho \)the density, \(\mu \) the dynamic viscosity, g the acceleration of gravity, D the rate of deformation tensor defined as \(\textit {{\textbf {D}}}=(\nabla \textit {\textbf {u}}+\nabla \textit {\textbf {u}}^{T})/2\). The last term in Eq. 1 stands for the surface tension force where in the \(\sigma \) is the surface tension, k the curvature, \(\hat {\boldsymbol {n}}\) the unit normal to the interface and the \(\delta _{s} \) the surface Dirac delta function.

Considering water and air as incompressible fluids, the continuous equation can be written as:

$$ \nabla \cdot \textit{\textbf{u}}= 0 $$
(2)

The governing differential equation of the volume of fluids is

$$ \frac{\partial C}{\partial t}+\nabla \cdot (\textit{\textbf{u}}C)= 0 $$
(3)

where C is the volume function of fluids. The continuum surface force (CSF) model was adopted (Brackbill et al. 1992), and the piecewise-linear method was used for the reconstruction of the interface (Youngs 1982). Classical SIMPLE solver was adopted for numerical simulation.

Geometry, Initial and Boundary Conditions

The transient axisymmetric model was adopted for numerical simulation of the dynamic behavior of liquid in tube, as shown in Fig. 2a. The inner diameter of large and small tube in simulation model was 23 mm and 13 mm, respectively. The height of the straight cylindrical part of the tube \(H \) was selected as two times of the diameter in the computation domain. Further increase of H exhibited no influence on the dynamic behavior of liquid.

No-slip condition was used on the wall of the tube except the three-phase contact point. A constant contact angle 60∘ was used in the simulation. The tube model was initially patched with water in agreement with the volume fraction of water in experiments. The equilibrium position of free surface in normal gravity was calculated based on the initiallized flat free surface and taken as the initial condition for the successive calculation in microgravity.

In the numerical simulation, the quadrilateral mesh was adopted and the independence of mesh was checked. The final optimal mesh number of the large tube model was 63404 and the small tube model 20327 in the following study. The range of time interval was 0.00005 s \(\sim \) 0.0001 s. The convergence criterion of relative residual error was 10− 6 for every parameter.

Results and Discussion

Experimental Results

In the present study, the air fraction \(k_{v} \) was defined as \(k_{v}= 2V_{a} /V_{0} \), where \(V_{a} \textit {and}V_{0} \) are the volume of air and sphere, respectively, and the \(V_{0} \text {=}\frac {4}{3}\pi R^{3}\). Figure 3 shows the image sequence of the free surface dynamic behaviors in the tubes of \(D_{L} =\) 21.8 mm (kv = 1.20) and \(D_{S} =\) 12.5 mm (kv = 1.84) after the abrupt drop of gravity. Only the image sequences before the steady state in microgravity are shown there. The corresponding evolutions of the center points of the free surface are shown in Fig. 4. The evolution of gravity level in the experiment is added as reference, and an acceleration of nearly 10 \(g_{0}\) emerges after the end of the experiment due to the recovery process. The free surface deflects simultaneously at the start of the abrupt drop of gravity. The motions of contact line and center point of the free surface are coupled after the abrupt drop of gravity in the experiment. In the tube of \(D_{L} \), the evolution of the center point exhibits a damping oscillation with decreasing frequency after the initial maximum deflection (zc = –3.62 mm at \(t_{\mathrm {c } }=\) 0.12 s). The free surface undergoes several oscillation periods and evolves into the equilibrium position in microgravity.

Fig. 3
figure 3

Experimental (DTE) and numerical (NUM) results of the free surface deflection evolutions in the tubes of DL = 21.8 mm (kv = 1.20) and DS = 12.5 mm (kv = 1.84) after the abrupt drop of gravity

Full size image
Fig. 4
figure 4

Experimental results of the evolutions of the center point of the free surface in the tubes with DL = 21.8 mm (kv = 1.20) and DS = 12.5 mm (kv = 1.84) after the abrupt drop of gravity

Full size image

The dynamic behaviors of the free surface in the tube of \(D_{S} \) agree qualitatively. However, in the tube of \(D_{S} \) the surface tension plays more important role in normal gravity according to the small Bond number (see Table 1). At the start of the abrupt drop of gravity, the deviation of the free surface from the equilibrium position in normal gravity is small. Therefore, the initial maximum deflection (zc = -4.90 mm at \(t_{\mathrm {c } }=\) 0.08 s) of the free surface is relatively weak after the abrupt drop of gravity. Moreover, due to the shorter characteristic response time for settling phenomena (Strange et al. 2003) (see Table 1) in the microgravity, the free surface deflection evolution reveals faster damping oscillation and transition into the equilibrium position in microgravity after the initial maximum deflection.

On the other hand, the oscillatory evolution of the center point of the free surface in the tube of \(D_{S} \) qualitatively agrees with the experimental results in Kulev and Dreyer (2010), in which capillary driven surface oscillations of liquid argon (LAr) in cylinder under quasi isothermal boundary condition were investigated in the Drop Tower Bremen. Both the cases show an oscillatory motion with three half-periods. However, due to the large diameter of the cylindrical part and small viscosity of LAr, i.e. much large characteristic response time for settling phenomena \(t_{1}\) (see Table 1) in Kulev and Dreyer (2010). The oscillatory evolution of the center point of the free surface exhibits the oscillation of low frequency and weak damping effects. Therefore, the free surface deflection evolution still can be observed at the end of the microgravity duration time (about 4.7 s) compared to the fast damping transition in the present study.

Numerical Results

Figure 3 also shows the image sequence of dynamic behaviors of the free surface in the tubes of \(D_{L} =\) 23.0 mm (kv = 1.20) and \(D_{S}=\) 13.0 mm (kv = 1.88) after the abrupt drop of gravity. The dynamic behaviors of the free surface deflection qualitatively agree with the experimental results. As shown in Fig. 5, evolutions of the contact line and the center point of the free surface oscillate synchronously with a phase shift \(\pi \) after a step reduction of gravity. The evolutions undergo damping oscillation into respective equilibrium position in the microgravity, and the oscillations are approximately symmetric to the final equilibrium position. In the tube of \(D_{S} \), the free surface deflection evolution reveals smaller oscillation amplitude and faster transition into the equilibrium position in microgravity. It qualitatively agrees that of the experimental results.

Fig. 5
figure 5

Numerical results of the evolutions of the contact line (zw) and the center point (zc) of the free surface in the tubes of DL = 21.8 mm (kv = 1.20) and DS = 12.5 mm (kv = 1.84) after the step reduction of gravity

Full size image

A comaprison of the numerical and experimental resuts of evolutions of center point of the free surface in the tubes of \(D_{L} \) and \(D_{S} \) is presented in Fig. 6 after the abrupt drop of gravity. The evoltuions of the center point of the free surface qualitatively agree. After the abrupt drop of gravity, the evolution of the center point exhibits a damping oscillation and evolves into the equilibrium position in the microgravity. In the tube of \(D_{L} \), the experimental results and numerical results reveal the approximately same averaged oscillation frequency. In the tube of \(D_{S} \), the difference of the averaged oscillation frequencies may attribute to the fact that the time resolution is 0.04 s in the experiment compared to the much higher time resolution in numerical simulation.

Fig. 6
figure 6

Comparison of the experimental and numerical results of the evolutions of center point of the free surface in the tubes of a DL and b DS after the abrupt drop of gravity

Full size image

On the other hand, the gravity level exhibits a step reduction to zero in numerical simulation compared to the gradual reduction in experiment, which results in a longer delay of the first extrema of oscillation of the free surface. The evolutions of the experimental results exhibit significant damping effects of the maximum deflections and faster transition into the equilibrium position in microgravity after the initial maximum deflection compared to the numerical results. To account for the discrepancy, effect of dynamic contact angle, which exerts extra viscous drag force to damp the deflection of the free surface, should be taken into consideration in the future numerical simulations.

Note that there is a shift of 0.17 mm of the initial central point positions in the experimental and numerical results in the tube of \(D_{S} \). It may result from the space uncertainty of 0.3 mm in the image processing and small deviations of tube diameter and \(k_{v} \) in the experiment and numerical simulation. Moreover, in both the tubes of \(D_{L} \) and \(D_{S} \), the equilibrium positions in the microgravity are different between the experimental and numerical results. In addition to the factors mentioned above, the major reason is the deviation between the contact angle of 55.6∘ (see Fig. 7) obtained in experiment and 60∘ used in numerical simulation. The extraction method of the shape and position of meniscus is same with what was used for extracting the outline of the test tube. The contact angle \(\gamma \) was calculated by \(\gamma =\arccos (R/R_{\mathrm {m}} )\), Where R is the inner radius of test tube and \(R_{\mathrm {m}}\) the radius of meniscus. Figure 7 shows the result of extraction of meniscus.

Fig. 7
figure 7

Contact angle in the test tube

Full size image

Dependency of the free surface dynamic behaviors on air fraction \(k_{v} \) was numerically studied in the range of \(k_{v} =\) 0.80 to 1.88 in the tubes of \(D_{L} =\) 21.8 mm and \(D_{S} =\) 12.5 mm, and the results can be divided into three representative states as shown in Fig. 8. S1 is for small \(k_{v} \), e.g. 0.80, the contact line oscillation keeps over the horizontal plane of \(z = 0\). S2 is for intermediate \(k_{v} \), the contact line alternatively oscillates over and below the horizontal plane of \(z = 0\). S3 is for large \(k_{v} \), e.g. 1.88, the contact line oscillation keeps below the horizontal plane of \(z = 0\). Figure 9 depicted the comparison of the corresponding evolutions of the contact line and the center point of the free surface in the tube of \(D_{L} =\) 21.8 mm with \(k_{v} =\) 0.80, 1.20 and 1.88. For all the cases, after the abrupt drop of gravity the evolutions of the contact line and center point of the free surface reveal synchronous damped oscillations into the respective equilibrium position in the microgravity. The oscillations are approximately symmetric to the equilibrium position. However, the time required for the transition to the steady state in the reduced gravity decreases with the increasing \(k_{v} \).

Fig. 8
figure 8

Three representative states of the oscillations of contact line

Full size image
Fig. 9
figure 9

Numerical results of the evolutions of the contact line (zW) and center point (zC) of the free surface in the tubes of DL = 21.8 mm with different kv after the abrupt drop of gravity

Full size image

Figure 10 shows the dependency of the averaged oscillation frequency of the free surface deflection evolution on \(k_{v}\). For both tubes of \(D_{L}= 21.8\) mm and \(D_{S}= 12.5\) mm, the oscillation frequency increases rapidly with the increasing \(k_{v}\) in the transition from state S1 to S2. The increasing tendency becomes mild in the further transition from state S2 to S3. In state S3, the oscillation frequency nearly remains constant with the increasing \(k_{v}\). The tendency becomes more significant with the decreasing tube diameter. Moreover, the oscillation frequency in the tube of \(D_{S}= 12.5\) mm is much higher than that in the tube of \(D_{L}= 21.8\) mm at the same \(k_{v}\), and the deviation increases with the increasing \(k_{v}\). The change if period over the inner diameter of tube is coherent with \(t_{1}\).

Fig. 10
figure 10

Comparison of oscillation frequencies with different kv in the tubes of DL = 21.8 mm and DS = 12.5 mm

Full size image

Conclusions

The behavior of liquid in partially filled capsule storage tank in microgravity was investigated both numerically and experimentally. Two scale-down inverted test tubes filled with water were used to simulate the liquid behavior inside a capsule tank after an abrupt drop of gravity by utilizing the Drop Tower Beijing. Experimental data on the oscillation of the free surface obtained during the short-term microgravity (\(\sim \)3.6 s of duration) were also used to verify the numerical model. The volume of fluids (VOF) method was adopted to build the numerical model, and to reveal more details of the liquid behaviors, particularly the oscillation frequency of the free surface. The results show that the deflections of the free surface in the tubes reveal damping oscillations from its equilibrium position in normal gravity to its equilibrium position in microgravity after the abrupt drop of gravity. The required transition time and oscillation amplitude increases with the increasing tube diameter while the corresponding oscillation frequency decreasing. The numerical predictions qualitatively agree with the experimental results. The quantity discrepancy is mainly in the number and amplitude of the maximum deflection extrema and their occurrence times. To account for the discrepancy, dynamic contact angle should be taken into consideration. On the other hand, the numerical predictions can capture the characteristic oscillation frequency in the experiments. The oscillation frequency increases with the increasing \(k_{v} \) while remains nearly constant at large air fraction \(k_{v} \). For the same \(k_{v} \), the oscillation frequency significantly increases with the decreasing tank diameter.