Shape of Diffusive Interface Under Periodic Excitations at Different Gravity Levels

Abstract

This work discusses the role of gravity on the shape of interfacial waves between miscible liquids under horizontal vibrations. A big difference in the shape of an interfacial pattern has recently been observed in low-gravity experiments when compared to earth-based one. The evolution of an interfacial pattern from zero to normal gravity is discussed in the context of non-linear simulations in a confined system. The development of vibration-induced frozen waves with gravity is characterized by three distinct regimes that are associated with the wave height and the angle at the vertices of saw-tooth shape of the interface.

Introduction

The stability of the system under periodic vibrations perpendicular to the direction of gravity has attracted large research interest in different problems studied under microgravity (Mialdun et al. 2008; Gaponenko and Shevtsova 2008; 2010; Melnikov et al. 2008; Mazzoni et al. 2010; Shevtsova et al. 2010; Shevtsova et al. 2015a; Beysens 2014; Lyubimova et al. 2014; Gandikota et al. 2014a) and normal gravity conditons (Wolf 1969; Ivanova et al. 2001; Jalikop and Juel 2009; Lappa 2014; 2015; Shevtsova et al. 2015b). Liquid-liquid interfaces may become unstable if a shear stress is applied and a well-known example is the Kelvin-Helmholtz instability. Horizontal vibration of the flat liquid-liquid interface produces an instability in the form of frozen waves caused by a shear-driven mechanism similar to the Kelvin-Helmholtz instability (Talib et al. 2007; Yoshikawa and Wesfreid 2011; Gaponenko et al. 2015a). The distinction is that, as a result of a harmonic change in the flow direction, the wave remains on average in the same place, as its profile is frozen in the reference frame of a vibrating container.

In the present study we are interested in miscible fluids, when surface tension vanishes. The idea that the miscible interface should be endowed with a dynamic surface tension was first raised by Korteweg and continues to develop (Pojman et al. 2009; Vorobev 2014). However, the surface tension in miscible liquids is transient and its measurement is complicated (Pojman et al. 2006; Lacaze et al. 2010). Recently, it was demonstrated by Gaponenko et al. (2015a) that the surface tension σ can be determined from the vibrational experiment by measuring the wavelength at the threshold of frozen waves. Particularly, the surface tension between two mixtures of water-isopropanol of different concentrations, which are discussed in the present study, was determined as σ ≈ (5.84±1.05)⋅10⁻⁶N/m. The advantage of this approach with respect to other techniques is that the measurements are made shortly after the initial contact of the miscible liquids. The time delay for the interfacial instability to emerge is only a few seconds and the transient interfacial tension at this point is undiminished.

Instability in miscible systems caused by horizontal vibrations is noticeably different from immiscible ones because of its transient nature. One of the features that highlights the difference between immiscible and miscible fluids is the shape of frozen waves. For immiscible fluids, the shape of frozen waves is sinusoidal (Jalikop and Juel 2009; Ivanova et al. 2001; Yoshikawa and Wesfreid 2011). The curvatures of the crests and troughs of the wave are equal at onset, but as the wave grows, the trough curvature increases more steeply than the crest (Jalikop and Juel 2009) or vice versa (Ivanova et al. 2001) depending on the properties of liquids. The sinusoidal shape of the interface evolves to resemble a trochoid. This qualitative change in the wave shape starts when the vibrational forcing exceeds some critical value of the modified Froude number (Jalikop and Juel 2009).

Modification of the wave shape was observed at a liquid–vapour interface in the experiments with near–critical hydrogen subjected to horizontal vibrations (Gandikota et al. 2014a). These experiments at varying gravity were conducted using a magnetic levitation device, thus both gravity and surface tension were reduced when approaching the critical point. The authors reported a sharp triangle shape far from the critical point and a somewhat rounded shape closer to the critical point. To describe the triangle shape of the liquid-vapor interface Gandikota et al. (2014b) suggested using the phenomenon of dynamic equilibrium. Following Wolf (1969) and considering the interface from a mechanical point of view, it was proposed that an initially horizontal fluid interface attains a dynamic equilibrium at angle α between the vertical and interface positions

$$ \vspace{2mm} sin \, \alpha=\frac{2gL}{\pi A^{2} \omega^{2}}\frac{\rho_{l}+\rho_{v}}{\rho_{l}-\rho_{v}}, $$

(1)

here L is the greater lateral width in the case of a rectangular container, ρ is the density of a liquid (l) or vapor (v). According to assumptions, this relation is valid for so strong vibrational forcing when the role of surface tension is not important. It is worth noting that the angle α depends on a container length. The authors (Gandikota et al. 2014b) attempted to apply Eq. (1) not to the entire interface, but for one side of the triangle and found reasonable agreement with the experiments for small values of α at a certain level of microgravity, g = 0.05g ₀.

Our recent experiments (Gaponenko et al. 2015a; Shevtsova et al. 2015b) demonstrated that an interfacial instability may occur between two miscible liquids of similar (but non-identical) viscosities and densities under horizontal periodic excitations. In a gravity field, a spatially periodic saw-tooth frozen structure is generated on the interface under horizontal vibrations somewhat similar to immiscible liquids. Under the low gravity conditions of a parabolic flight, the crests widen and the final and long-lived pattern consists of a series of vertical columns of alternating liquids (Gaponenko et al. 2015b).

So far, the experimental studies in miscible liquids are limited by normal or reduced gravity of parabolic flights. The present numerical simulations are performed in order to examine the evolution of the interfacial wave shape for parameter ranges that are out of reach experimentally, i.e., when gravity changes within the range from zero up to the Earth’s gravity.

The present paper is organized as follows. The problem description and mathematical model for a miscible multiphase system are presented in Section “Problem Description”. The relevant experimental results of recent studies are compared with numerical findings in Sections “Interfacial Pattern in Normal Gravity” and “Interfacial Pattern in Microgravity”. The effect of gravity on the amplitude and shape of the waves is discussed in Section “Modification of Interfacial Pattern with Gravity”.

Problem Description

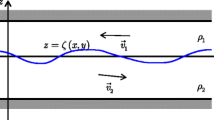
We consider two superposed layers of incompressible and miscible liquids placed in a rectangular container, see geometry in Fig. 1. The denser liquid is placed in the lower layer, so that the configuration is gravitationally stable. The lower liquid is less viscous than the upper one, corresponding to the physical properties listed in Table 1. Both layers have the same thickness H = 3.75 mm and the length of the cavity is L = 15mm. Our previous calculations in normal and reduced gravity have shown that the phenomena is essentially two-dimensional (Gaponenko et al. 2015a). The liquids are solutions of alcohol (isopropanol or IPA) in water of different concentrations, 0.90 water (liquid 1) and 0.50 water (liquid 2) in mass fraction, and they are miscible in all proportions.

Fig. 1

Geometry of problem. The dimensions used in the computer simulations correspond to the experiments discussed in papers by (Gaponenko et al. 2015a, b): L = 15 mm, 2H = 7.5 mm, W = 5 mm

Table 1 The physical properties of the mixtures 90%water-10% IPA and 50 % water-50% IPA (mass fraction) at 25 ^oC: density ρ, kinematic viscosity ν, diffusion coefficient D and the Schmidt number S c = ν/D

Let us consider the mass fraction of the heavier liquid, water, as an independent variable ($\tilde c$), then the initial concentration of liquid 1 is $\tilde {c^{o}_{1}}$=0.90 and liquid 2 is $\tilde {c^{o}_{2}}$=0.50 and ${\Delta } \tilde c=(\tilde {c^{o}_{1}}-\tilde {c^{o}_{2}})$. Furthermore, let us introduce the relative concentration of water to describe both layers with single independent concentration C

$$ C=(\tilde c - \tilde {c^{o}_{2}})/{\Delta} \tilde c, \quad 0\le C \le 1. $$

(2)

Then the initial concentrations of the liquids are: C ^o=1 in the lower layer and C ^o=0 in the upper layer. Due to large concentration gradients at interfaces, density dependence on concentration cannot be disregarded. The dependence of the liquid density $\tilde \rho$ on the concentration c is defined by a simple linearized relation valid for almost all liquid/liquid interfaces due to a small density contrast (i.e. ρ₂/ρ₁=0.92).

$$ \rho=\rho_{2}\,\bigl(1-\beta_{c} \, C \bigr), \quad \beta_{c}= {(\rho_{2} - \rho_{1})}/{\rho_{2}}= -\,0.087 $$

(3)

The mixture viscosity is a function of concentration with a maximum at $\tilde c^{o}$=0.5. In the region of interest, $0.5 \le \tilde c \le 0.9,$ the viscosity can be approximated by a linear dependence.

$$ \mu(c)=\mu_{2}\,\bigl(1- \beta_{\mu}\, C \bigr), \quad \beta_{\mu}= {(\mu_{2}-\mu_{1})}/{\mu_{2}}= 0.538 $$

(4)

The origin of a Cartesian coordinate system is at the bottom left corner of the cell, and the X-axis is parallel to the undeformed fluid interface, and the Z-axis is parallel to the Earth’s gravity, see Fig. 1. In the coordinate system associated with the cell, the acceleration applied to the system is the sum of gravitational and vibrational accelerations:

$${\mathbf g} + A\omega^{2}\cos(\omega t)\, {\mathbf e}, $$

where g is the gravity vector which is the parameter of the problem but its direction coincides with the the Earth’s gravity, so, g = (1,0,0) and e is the unit vector along the axis of vibrations.

It was mentioned in the Introduction that the surface tension for this system is two-three orders of magnitude smaller than that for typical immiscible liquids and we do not take into account interfacial tension in the mathematical model. It allows us to consider a one-layer system with a sharp change in water concentration at Z = H at the initial step.

The system is considered isothermal. The equations of motion and mass transport are written as

$$\begin{array}{@{}rcl@{}} && \partial_{t}\mathbf{V} + (\mathbf{V}\cdot\nabla)\,\mathbf{V} = -\frac{1}{\rho_{2}}\nabla P + \\ && \frac{\mu_{2}}{\rho_{2}} \, \nabla\bigl[(1- \beta_{\mu}\, C) \nabla \mathbf{V} \bigr] - \beta_{C} \,C \bigl({\mathbf g}+A\omega^{2} \cos(\omega t)\,{\mathbf e}\bigr), \\ && \partial_{t} C + \mathbf{V}\cdot\nabla\, C = D \nabla^{2} C, \\ && \nabla \cdot \,\mathbf{V} = 0. \end{array} $$

(5)

Here V is the velocity vector. The cell boundaries are rigid with no–slip condition for velocity and non-permeable for concentration:

$$\begin{array}{@{}rcl@{}} \mathbf{V} = 0; \qquad \quad \partial C/ \partial n=0; \quad \end{array} $$

(6)

The initial condition for velocity: V = 0.

On the interface between liquids the concentration linearly changes within the small zone of the thickness δ = 0.08 H:

$$\begin{array}{@{}rcl@{}} &&C= 2(Z-\delta)/H, \hskip 3mm \text{for} \hskip 3mm H/2-\delta < Z < H/2+\delta \\ &&C=1 \hskip 3mm \text{for} \hskip 3mm 0< Z \le H/2-\delta ; \\ &&C=0 \hskip 3mm \text{for} \hskip 3mm H/2+\delta< Z \le 1. \end{array} $$

(7)

The commercial solver FLUENT v.6.3 was used for solving governing Eqs. (5)-(7) in two space in dimensional variables. The effect of the grid size and the time step were carefully tested for convergence by Gaponenko et al. (2015a). The numerical model is limited to a 2-D study because the previous simulations of 3-D non-linear equations have shown that the problem is essentially 2-D.

Interfacial Pattern in Normal Gravity

The frozen wave instability has a threshold which depends on the frequency and amplitude. The characteristics of the interfacial pattern and its evolution depends critically on the frequency and amplitude of imposed vibrations. Here our focus is on the periodic excitation of high frequencies when non-zero mean flows are formed. It assumes that the period of vibration is much smaller than the reference viscous and diffusion times:

$$ 1/f \ll \min(H^{2}/\nu_{i}, \,H^{2}/D ). $$

(8)

The diffusion time is large, thus the smallest viscous time plays the decisive role, i.e., τ ₂ = H ²/ν ₂=4.15. It was recently shown (Shevtsova et al. 2015a) that for such kind of problems the sign ” ≪” means at least 15-20 times. Consequently, the range of frequencies above 10 Hz will be considered. Another assumption is that the amplitude is smaller than the cell size.

Experiment

We will briefly recall the results of the recent ground experiments (Gaponenko et al. 2015a) with the focus on the wave shape. The typical example of a wave evolution at high frequencies (f = 22.5 Hz) and moderate amplitude forcing (A = 3.7 mm) is shown in Fig. 2 at different times. The flow dynamics in the experiments was monitored from the side by direct shadowgraphy of the interface, and it was adjusted to see the concentration gradient. Correspondingly, the only region where concentration changes can be visible is the region near the contact line between liquids. Here we draw your attention to the shape of the interfacial wave, which has a saw-tooth shape. A tiny interfacial tension is responsible for the very large curvature observed at the peaks and troughs of the triangle waves that develops on the interface.

Fig. 2

(Ground based experiment) The temporal evolution of the interface in the case of high frequency (f = 22.5 Hz) and moderate amplitude (A = 3.7 mm) in normal gravity. The cell height in the pictures is cropped off by 0.5H at the top and bottom. The length of the cell is in scale

The shape of the interface is described by the normal projection of the stress balance between liquids (the normal vector n directed into liquid 1)

$$ [P_{1}-P_{2}] -\left( \textbf{n}\, S_{1} \,\textbf{n}- \textbf{n} \,S_{2}\,\textbf{n} \right) = \sigma K. $$

(9)

Here S = μ(∂ V _i/∂ x _k + ∂ V _k/∂ x _i) is the viscous stress tensor, K is the curvature, P is the pressure. Considering the interface as frozen, the viscous terms can be omitted. Then ΔP∼σ K and in the case of miscible liquids the vanishing interfacial tension σ → 0 should be compensated by a very large curvature, K → ∞, at the crests and troughs. It results in a sawtooth-like wave shape. It has been noticed in different experiments that “frozen ” waves are slightly moving, but these displacements are much smaller than the amplitude of the waves. These small displacements suggest that for a very large viscosity or/and viscosity ratio the viscous terms in Eq. (9) cannot be discarded completely. Correspondingly, it can explain the sinousoidal shape in the experiment with miscible liquids when the viscosities of the liquids differ by 1000 times (Legendre et al. 2003).

Another point to notice is the temporal evolution of the spatial amplitude of the waves. The process begins when capillary waves appear on the free surface, then rearrange, grow in amplitude and reach the maximal height. The time from the initiation of the excitation until the saw-tooth interfacial pattern attains the peak amplitude is about t = 3.0 s and this image is shown in Fig. 2. In the course of time the driving force, that is the density difference across the diffusive interface, diminishes and the wave amplitude slowly decreases as can be seen in Fig. 2 at the time moment t = 7.1 s. Note, that the wavelengths excited in the experiments are comparable to, but smaller than the lateral extent of the cell, so endwall effects can be important (Shevtsova et al. 2015b).

Numerical Modeling

The non-linear numerical simulations of Eqs. (5)-(7) are conducted for the same liquids that were used in ground (Shevtsova et al. 2015b; Gaponenko et al. 2015a) and microgravity experiments (Gaponenko et al. 2015b). To reproduce numerically the experimental results the calculations were performed using a very fine mesh of 800 × 400 points and time step τ = 2.5⋅10⁻⁵ s. Keeping in mind that in the experiments the monitored signal was the concentration gradient, for quantitative comparison of the results the same quantity is displayed in Fig. 3 at the time instant t = 2.85 s. The results of computer simulations nicely reproduce the experimental observations in Fig. 2 in terms of the existence, shape, and temporal development of interfacial patterns. Indeed, the wavelength averaged by three central peaks obtained in calculations is λ _num= 13.9 mm while the experimental value is λ_exp=13.6 ±0.7 mm. The values of the angle α in the triangle waves (see definition in Fig. 9), averaged over four peaks, are also in excellent agreement between the experiment and computations α ≈ 35^∘. This gives us confidence in the correctness of the mathematical model and numerical approach. Visual comparison of wavy structures between Figs. 2 and 3 can be a bit misleading, because the images in Fig. 2 do not have axes and notations on them.

Fig. 3

(Numerical simulations.) The snapshot of the gradient of the concentration field at t = 2.85 s for the parameters similar to those in Fig. 2, f = 22.5 Hz and A = 3.75 mm in normal gravity. Only the central part of the cell is shown in height

Interfacial Pattern in Microgravity

One of the first attempts to study the behavior of a miscible liquid in microgravity under vibrations parallel to the interface was undertaken in 1997 (Duval and Tryggvason). However, due to technical reasons the local mass transport was enhanced and the interface instability was not observed. The recent microgravity experiments were conducted using parabolic flights (Gaponenko et al. 2015b). The parabolic flights provided repeated periods of approximately 20 s of reduced gravity preceded and followed by 20 s of hypergravity (up to 1.8 g ₀), and then normal gravity. The microgravity level during the parabolas was |g _Z/g₀|≤0.05.

Experiment

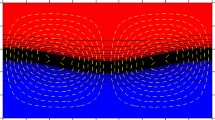
The behavior of miscible liquids becomes totally different when vibrations are applied to the system under reduced gravity. In microgravity, after the formation of waves on the interface, they grow without saturating until the interface reaches the upper and lower walls as shown in Fig. 4. The final enduring flow pattern consists of a series of vertical columns of alternating liquids, which occupy the whole height of the cell. The shape and width of different columns are non-identical when they reach a maximal elongation. Primarily, the selection of patterns depends on vibrationl forcing. However, an additional violation of symmetry between the left and right sides of the cell is imposed by experimental conditions. Due to flight manoeuvers, in the microgravity experiments the interface is tilted between 5 ^∘–7 ^∘ degrees with respect to the X−Z plane. The initial position of the interface and its thickness are outlined by two white lines in Fig. 4. Consequently, the columns on the left side reach faster the top of the cell while the columns on the right side reach faster the bottom of the cell. It is important to note that at a long time scale all the columns reach the top and bottom walls of the cell without touching.

Fig. 4

(Parabolic flight experiment.) The snapshot of the interfacial pattern in reduced gravity when the frequency is f = 22 Hz and amplitude is A = 3.1 mm. The two white lines indicate the inclination and thickness of the interface at t = 0. The cell picture is in scale

Numerical Modeling

In this paragraph, we do not pursue the target to reproduce the experimental pattern because the gravity level is variable during the parabola, it can even change the direction while remaining in the range |g _Z/g ₀|≤0.05. The computer simulations were performed in zero gravity with focus on the evolution of the wave shape and its amplitude. A time sequence of interfacial patterns in a vibrating cell at A = 5 mm, f = 20 Hz is presented in Fig. 5. At the initial stage of excitations, two harmonic waves moving from different sides come into contact and a spatially modulated wavy structure is formed as shown in Fig. 5a at t = 0.7 s. The wavy pattern is spacially symmetric with respect to the cell centre, but it is necessary to compare the profile close to the bottom near the left side with the profile close to the top on the right side. This is associated with two different temporal phases of profiles near the endwalls. On the left side of the figure the waves are passing through a minimum near the endwall, while in the right figure they are passing through a maximum. Such kind of symmetry was also observed at earlier times. The viscosity difference introduces an additional non-symmetry of the pattern with respect to the mid-height, the columns move slightly faster to the bottom (less viscous) part.

Fig. 5

(Numerical results) A time sequence of interfacial patterns in a vibrating cell at A = 5 mm, f = 20 Hz in the absence of gravity, g = 0. The concentration gradient in a two-layered system of miscible liquids is shown at (a) t = 0.7 s; (b) t = 1.1 s; (c) t = 2.0 s

The numerical patterns perfectly support the experimental observations that all the columns reach the cell walls without touching. Importantly, the background wavelength of the pattern (associated with the number of the columns) is predefined at the initial stage and, as can be seen in Fig. 5a, the wavelength is uniform at that time. A finer adjustment of the pattern with changes in the flow at a later time develops defects. In the cases where the spacing would not sustain two new columns, one column grows into a rectangular shape while the other has a defect in the shape; the dynamics of the defect can be traced in the succession of snapshots in Fig. 5. As a result, the third column from the left has a triangular rather than a rectangular profile.

The defect of the interfacial pattern is also seen in the experimental image in Fig. 4 where the initial inclination of the interface only aggravates the situation.

Modification of Interfacial Pattern with Gravity

Transient wave formation between miscible liquids prevents a wave shape from being easily quantified. To highlight the role of gravity the experimental images in Fig. 2b and Fig. 4 are shown at the same time instant for two extreme cases: g = 0 and g = g ₀. These interfacial patterns provide evidence that depending on the gravity level, at least two distinct regimes of instability can be identified: (a) when the wave amplitude reaches saturation and (b) when the wave grows without saturation approaching the cell walls. Yet is still interesting to examine by which law the gravity affects the amplitude and the shape of the waves between these two extremes.

Wave Amplitude

Close examination reveals that depending on the gravity level three regimes of wave formation can be identified based on the type of the long-lived interfacial pattern. The first regime is observed at relatively high gravity levels, g≥0.4g ₀. Fig. 6 presents a sequence of interfacial patterns for the same vibrational forcing as in Fig. 5 but at a moderately reduced gravity, g = 0.75 g ₀. At the initial stage of excitations, instability develops at the diffuse interface in the form of triangle waves with a spatially modulated amplitude. Comparing Fig. 5a and Fig. 6a at early times, e.g., t = 0.7 s, we still find the common features between the patterns in zero and reduced (g = 0.75g ₀) gravity: the waves with the largest amplitude occur near the walls and the amplitude diminishes towards the center. Furthermore, the number of peaks in both cases is somewhat similar. However, this obscure similarity is observed only at a strong excitation, i.e., when vibrational velocity exceeds the critical value $V_{os}= A \omega >V_{os}^{cr}.$ For weaker excitations the gravity damps the instability (Gaponenko et al. 2015b). Particularly in this study we consider the set of parameters corresponding to V _os=0.63 m/s.

Fig. 6

The time sequence of interfacial patterns in a vibrating cell at A = 5 mm, f = 20 Hz at a slightly reduced gravity, g = 0.75 g ₀. The concentration gradient in a two-layered system of miscible liquids is shown at (a) t = 0.7 s; (b) t = 1.1 s; (c) t = 2.0 s. Only the central part of the cell is shown

Later in time, in the snapshot at t = 1.1 s in Fig. 6b, the wavy pattern reveals another structure, when the amplitude of the central peak is the largest. This kind of pattern is similar to that observed in normal gravity (Fig. 2). In line with the experimental findings, at the later stage of excitation the amplitude of all the peaks in Fig. 6c slightly decreases. Thus, the signature of the first regime is that the height of waves varies smoothly as low-high-low and the central peaks have the largest amplitude.

The second regime is associated with non-regular variation of the wave height over the interface and is observed at a lower gravity level, e.g., at 0.15 < g/g ₀ < 0.4. Specifically, the amplitude of the central peak remains smaller than that of the neighbor peaks, while the overall spacial amplitude of the pattern starts to decrease as can be seen in Fig. 7. The third regime of wave dynamics occurs at low gravity 0 < g/g ₀ < 0.15, and is characterized by rapidly growing waves when all the peaks have the same height in the final stage. Moreover, the waves height gets close to the cell height.

Fig. 7

The snapshot of the interfacial pattern typical for the 2nd regime; here g/g ₀=0.25, f = 20 Hz, A = 5.0 mm and t = 1.7 s

The temporal evolution of the wave height a measured as a crest-to-trough length at different gravity levels is shown in Fig. 8. Curves 1-6 correspond to g/g ₀=0, 0.1, 0.25, 0.5, 0.75, 1. At given time the height a was defined as the maximal value among the peaks on the interface. Fig. 8 reveals additional distinct features typical for the first regime (curves 4, 5 and 6): (a) the wave height a does not exceed the height of one layer, a < H; (b) the wave amplitude has a pronounced maximum forming at t ≈ 1.1-1.3 s; (c) the wave amplitude relaxes to its final saturated state which depends on the gravity level. In the second regime (curve 3), which occurs at 0.2 < g/g ₀ < 0.4, the maximum of the time-dependent wave amplitude, even when it exists, is featureless. The third regime (curves 1 and 2) can be characterized by a continuous growth of the wave height until reaching asymptotic value.

Fig. 8

The time-dependence of the wave height (the crest-to-trough length) at different levels of gravity when the cell is horizontally vibrating at A = 5 mm, f = 20 Hz. The curves 1-10 correspond to g/g ₀=0, 0.1, 0.25, 0.5, 0.75, 1

Figure 9 summarizes the above-mentioned waves behavior in different regimes displaying the maximum of the wave height as a function of gravity. Here the distinction between regimes is determined based on a qualitative analysis of waves in terms of the wave height variation with gravity. This figure examines observations from a different perspective and provides additional interpretation of the results in Fig. 8. Although the separation of wave dynamics in three regimes has been made not without some ambiguity, it highlights the role of gravity. In the first regime the amplitude of the waves grows almost linearly when the gravity reduces from the Earth’s value down to g∼0.4g ₀. With further decreasing of gravity (the second regime) the growth rate of the wave height essentially accelerates. The third regime includes a rather narrow range of gravity levels, g < 0.15g ₀, and is associated with wave growth practically without saturation up to the walls of the cell without touching them.

Fig. 9

Maximal height of the interfacial waves as a function of the gravity level for the same parameters as in Fig. 8. The three regimes of the wave amplitude dynamics can be outlined: (I) 0.4 < g/g ₀ < 1, almost linear growth of the amplitude; (II) 0.15 < g/g ₀ < 0.4, strong growth; (III) 0.0 < g/g ₀ < 0.15, waves with the height approaching the cell size

Changes of the Angle of Interfacial Waves with Gravity

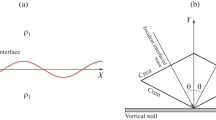
The interfacial waves in miscible liquids have a triangle shape at the onset of the frozen wave instability, and they remain triangle above the threshold for g > 0.15g ₀, this is confirmed experimentally and numerically. To describe the shape of the wave, we have introduced the angle α between the vertical upward position and interface position under vibrations (inclined position) as shown in Fig. 10b. For the cases, shown in Fig. 3 and Fig. 6c, the angle was determined at the time instant when the amplitude attained the maximal value. Although we took the average value over 3-4 central peaks, the scattering was very small. For the set of parameters where the defect of the pattern as in Fig. 5 occurs, the angle was evaluated not without some ambiguity. In this case the angle was averaged by all the peaks.

Fig. 10

Gravity dependence of the shape of the interfacial pattern, i.e., shape of triangle, when frozen wave instability is caused by vibrationl forcing with A = 5 mm, f = 20 Hz. The lower panel presents the definition of the clockwise angle. The filled rhombi show results for the aspect ratio Γ = L/2H = 2 and the open squares correspond to the aspect ratio Γ=4

Dependence of the wave angle on gravity in Fig. 10a displays almost linear behavior but with two distinct slopes: (1) in the wide range of the gravity levels covering I and II regimes in Fig. 9, i.e. 0.15 < g/g ₀≤1.0, the slope is about d s i n(α)/d g = 0.48; (2) the sharp decrease of the angle down to zero in low gravity, i.e. 0.0 < g/g ₀ < 0.15. On the one hand, these results support linear dependence of s i n(α) on gravity which was suggested in Eq. (1); on the other hand, the linear dependence holds only locally.

We have also studied the influence of the length of the cavity L on the angle of a saw-tooth wave. Our results did not reveal any apparent difference in s i n(α) with increasing the cell length by two times; the open squares in Fig. 10a show results obtained at the aspect ratio Γ = L/2H = 4 and they display only a minor difference from those at Γ=2. So, the linear dependence of s i n(α) on the cavity length suggested by Eq. (1) is not confirmed for ordinary miscible liquids.

Conclusions

We have presented a numerical study of the nonlinear evolution of waves at the interface between two miscible liquids subjected to horizontal oscillations at different gravity levels. A detailed comparison between simulations and recent experimental observations in normal and low gravity showed an excellent agreement.

The obtained results delineate parameter space where gravity affects differently interfacial instability. Based on qualitative observation of a large number of snapshot sequences and an extensive quantitative analysis, three distinctive regimes of instability were identified depending on the gravity level.

The first regime (0.4 < g/g ₀ < 1.0) is associated with the typical frozen wave instability similar to that observed at normal gravity. While gravity decreases from the normal level down to g = 0.4 g ₀ only quantitative changes of the pattern occur: the increase of the height of the waves and the decrease of the angle in triangle waves.

The second regime (0.15 < g/g ₀≤0.4) is characterized by a rapid increase in the wave height, but the amplitude sequence in the pattern typical for frozen waves ”low-high-low” is disrupted before it reaches saturation.

In the third regime (0.0 < g/g ₀ < 0.15) waves grow without saturation until they approach the walls and the final enduring flow pattern consists of a series of vertical columns of alternating liquids.

Our study has shown that the angle of the waves decreases linearly with gravity, but the slope abruptly changes on the boundary between the 2nd and 3rd regimes.