Introduction

A drop or bubble, suspending in an immiscible non-isothermal fluid under microgravity, moves toward the hotter region owing to the thermocapillary migration. Thermocapillary migration occurs since the surface tension of the interface is a function of temperature, and thermocapillary migration of drop is of interest in materials processing under microgravity (Uhlmann 1982; Ostrach 1982). The thermocapillary motion of an isolated drop in a bulk fluid with an imposed thermal gradient was investigated firstly by Young et al. (1959), and they proposed the YGB model, in which the convective transport in both momentum and energy equations was ignored. Subsequently, the thermocapillary migration of drop motion was studied extensively by a number of theoretical analyses (Lee and Keh 2013; Subramanian 1981; Balasubramaniam and Subramanian 1996), numerical simulations (Treuner et al. 1996; Yin et al. 2008; Zhao et al. 2010; Ma and Bothe 2011; Yin et al. 2012) and experimental investigations (Hadland et al. 1999; Kang et al. 2008; Hu et al. 2009).

In a quasi-static limit, the thermocapillary migration of two drops along their center line was analyzed by Meyyappan et al. (1983). They revealed that the smaller drop moved faster in the presence of a larger drop than in its absence. Thereafter, Meyyappan and Subramanian (1984) calculated the thermocapillary migration of two drops at arbitrary angle to the applied temperature gradient by using a zeroth-order reflection approximation, and they demonstrated that the equal-sized drops moved with the same velocity of an isolated single drop. Later on, Anderson (1985) developed the reflection method to the first order to simulate two arbitrarily oriented droplets. Sun and Hu (2003) investigated the drops interaction by using the successive reflections method and they presented three typical kinds of drop’s trajectories. Using boundary-integral technique, Zhou and Davis (1996) simulated the thermocapillary interaction of two deformable drops, they revealed that the interaction between two drops resulted in a stronger effect on the smaller drop in terms of both drop’s motion and deformation. Then, Berejnov et al. (2001) developed the boundary-integral method to study the influence of the deformations on the relative motion of equal-sized drops. Based on the front tracking method, Nas and Tryggvason (2003) simulated the interaction of drops at moderate Reynolds and Marangoni numbers, they exhibited that the drops lined up perpendicular to the temperature gradient and were evenly spaced in the horizontal direction. A comprehensive numerical studies on the interaction of two drops under the axisymmetric assumption were conducted by Yin and Li (2015) with the front tracking technique, they revealed the effect of the ratio of the two drop radii, their initial distance apart, etc. on the interaction of two non-merging drops.

Although the thermocapillary migration and interaction of two drops has been investigated numerically in literature. There is little numerical simulation on the process of drop’s coalescence and the effects, i.e., Marangoni number and Capillary numbers, on the drop’s motion and coalescence have not been numerical investigated. In this study, we concentrate on the thermocapillary-driven motion and coalescence of two drops along their center line, which is perpendicular to temperature gradient. The effects of Marangoni number (Ma) and Capillary number (Ca) on the drop’s coalescence were investigated. Thus, an axisymmetric hybrid two-phase model was developed. The flow field was simulated by LBM with the multi-relaxation-time (MRT) collision process. In the meantime, the phase-field equation and energy equation were solved by FDM.

Mathematical Model and Numerical Method

In this section, the three basic parts of our hybrid thermal two-phase model for axisymmetric thermocapillary-driven drop motion are introduced as below.

Axisymmetric MRT LBM for Fluids

In practice, two different axisymmetric lattice Boltzmann methods have been developed. The first axisymmetric LBM model, incorporating the spatial and velocity dependent source terms into the evolution equation to recover Navier-Stokes equations in cylindrical coordinate, was proposed by Halliday et al. (2001). Thereafter, several modified axisymmetric LBM models (Lee et al. 2006; Peng et al. 2003; Reis and Phillips 2007, 2008) were developed and applied to simulate axisymmetric isothermal multiphase flow (Premnath and Abraham 2005; Mukherjee and Abraham 2007). The theoretical differences for these LBM axisymmetric models were discussed by Huang and Lu (2009) and numerical simulations were also carried out to investigate the accuracy of these models. From the continuous Boltzmann equation in cylindrical coordinates, Guo et al. (2009) proposed another axisymmetric kinetic LBM model, in which the source terms contains no gradient parts. Li et al. (2010) presented an improved LBM model with a simplified source term to eliminate velocity gradient for incompressible axisymmetric flows.

A LBM model includes three ingredients. The first ingredient is a discrete phase space defined by a regular lattice together with a set of symmetric discrete velocities (D2Q9 model)

$$ \text{\textbf{e}}_{\alpha} =\left\{\begin{array}{ll} \left( {0,0} \right),&\alpha =0 \\ \left( \cos \left[\left( {\alpha -1} \right)\pi / 2\right],\;\sin \left[\left( {\alpha -1} \right)\pi / 2 \right] \right)c,&\alpha =1-4 \\ \left( \cos \left[\left( {2\alpha -9} \right)\pi / 4\right],\;\sin \left[\left( {2\alpha -9} \right)\pi / 4\right]\right)\sqrt 2 c,&\alpha =5-8, \\ \end{array}\right. $$
(1)

where c = δ x /δ t is the lattice velocity. The second ingredient is the evolution equation:

$$ f_{\alpha} (\textbf{x}+\textbf{e}_{\alpha} \delta_{t} ,t+\delta_{t} )-f_{\alpha} (\textbf{x},t)=-\frac{1}{\tau} [f_{\alpha} (\textbf{x},t)-f_{\alpha}^{eq} (\textbf{x},t)], $$
(2)

where x is x=(r,z), and τ is the single relaxation time and relate to the kinematic viscosity ν.

The third ingredient is an equilibrium distribution function \(\left \{f_{\alpha }^{eq} \left | {\alpha =0,1,...,N} \right . \right \}\), and the equilibrium distribution function \(f_{\alpha }^{eq} \) is adopted as (He et al. 1999; He and Luo 1997)

$$ f_{\alpha}^{eq} =\omega_{\alpha} \left[p+\rho {c_{s}^{2}} \left( \frac{\textbf{e}_{\alpha} \cdot \textbf{u}}{{c_{s}^{2}}} +\frac{\left( {\textbf{e}_{\alpha} \cdot \textbf{u}}\right)^{2}}{2{c_{s}^{4}}} -\frac{\textbf{u}^{2}}{2{c_{s}^{2}}}\right)\right] $$
(3)

where \({c_{s}^{2}} ={\mathrm {c}} \left / 3\right .\), and the weight coef?cients are

$$ \omega_{\alpha} =\left\{\begin{array}{ll} 4 \left/ 9\right.,&\quad\alpha =0\\ 1 \left/ 9\right.,&\quad\alpha =1,2,3,4\\ 1 \left/ 36\right.,&\quad\alpha =5,6,7,8\\ \end{array}\right. $$
(4)

Next, the external force terms are added directly in the right hand side of the evolution (2) as

$$\begin{array}{@{}rcl@{}} &&f_{\alpha} (\textbf{x}+\textbf{e}_{\alpha} \delta_{t} ,t+\delta_{t} )-f_{\alpha} (\textbf{x},t)=-\frac{1}{\tau} [f_{\alpha} (\textbf{x},t)-f_{\alpha}^{eq} (\textbf{x},t)]+\\ &&\left( {1-\frac{1}{\tau} } \right)\left\{\left( \textbf{e}_{\alpha} -\textbf{u}\right)\cdot \left[\nabla \rho {c_{s}^{2}} \left( {\Gamma}_{\alpha} -{\Gamma}_{\alpha} \left( 0 \right) \right)+\left( \textbf{F}_{s} +\textbf{F}_{1,axis}\right){\Gamma}_{\alpha}\right] \right.\\ &&\left.-\omega_{\alpha} F_{0,axis}\vphantom{{c_{s}^{2}}}\right\} \end{array} $$
(5)

where F 0,a x i s is a source term to account for the axisymmetric effect in the continuity equation, and F 1,a x i s is the parts to mimic the axisymmetric contribution for the momentum equation:

$$\begin{array}{@{}rcl@{}} F_{0,axis} &=&{c_{s}^{2}} \frac{\rho u_{r}} {r}\\ \textbf{F}_{1,axis} &=&\left( F_{r,axis} ,\;F_{z,axis}\right)\\ &=&\left( \rho \frac{\nu} {r}\frac{\partial u_{r}} {\partial r}\,+\,\rho \frac{\nu} {r}\frac{\partial u_{r}} {\partial r}\,-\,\rho \frac{u_{r} u_{r}} {r}-2\rho \frac{\nu u_{r}} {r^{2}}, \rho \frac{\nu} {r}\frac{\partial u_{z}} {\partial r}\right.\\ &&\left.\quad+\rho \frac{\nu} {r}\frac{\partial u_{r}} {\partial z}-\rho \frac{u_{r} u_{z}} {r}\right)\\ \end{array} $$
(6)

Γ α is defined as

$$ {\Gamma}_{\alpha} =\omega_{\alpha} \left( 1+\frac{\textbf{e}_{\alpha} \cdot \textbf{u}}{{\mathrm{c}_{\mathrm{s}}^{2}}} +\frac{\left( \textbf{e}_{\alpha} \cdot \textbf{u}\right)^{2}} {2{\mathrm{c}_{\mathrm{s}}^{4}}}-\frac{\textbf{u}^{2}}{2{\mathrm{c}_{\mathrm{s}}^{2}}}\right) $$
(7)

The collision step in the right hand side of the (2) is implemented in velocity space, because of the drawback of the instability at low viscosity values in the single relaxation time LBM model, a MRT collision model, improving the numerical stability, was proposed by d’Humieres (1992). Lallemand and Luo (2000) further developed this model. The collision step in the MRT model is implemented in the moment space

$$ \boldsymbol{\Omega}=-\textbf{M}^{-1}\textbf{S}[\textbf{m}(\textbf{x},t)-\textbf{m}^{eq} (\textbf{x},t)], $$
(8)

where m(x,t) and m eq(x,t) are moments and their corresponding equilibriums. The external force is implemented in the moment space as Guo and Zheng (2008). S is a diagonal matrix

$$ \textbf{S}=diag\left( {s_{0} ,s_{1} ,s_{2} ,s_{3} ,s_{4} ,s_{5} ,s_{6} ,s_{7} ,s_{8}} \right), $$
(9)

whose components represent the inverse of the relaxation time for the transformed distribution function m relaxing to the equilibrium distribution function m eq in moment space. Furthermore, the parameters s 7 and s 8 are related to the collision frequency τ as s 7 = s 8=1/τ with \(\tau = \nu \left /{c_{s}^{2}}+0.5\right .\). The other relaxation parameters are chosen as Lallemand and Luo (2003): s 0 = s 3 = s 5=1.0, s 1=1.64 and s 2 = s 4 = s 6=1.2.

The transformation between the velocity space and moment space is achieved by using the matrix M, which serves as a transformation matrix and maps the distribution functions f(x,t) to their moments as

$$ \begin{array}{l} \textbf{m}=\textbf{Mf}\\ \textbf{f}\;\;=\textbf{M}^{\textbf{-1}}\textbf{m}.\\ \end{array} $$
(10)

The transformation matrix M is constructed via the Gram-Schmidt orthogonalization procedure from some polynomials of the discrete velocity components. The equilibrium moments are obtained from m eq = Mf eq.

The flow field, including the velocity field u and the pressure field p, is obtained from the moments of the distribution function as

$$\begin{array}{@{}rcl@{}} \textbf{u}&=&\frac{1}{\rho} \left( {\frac{1}{{c_{s}^{2}}} \sum\limits_{\alpha} {\text{\textbf{e}}_{\alpha} f_{\alpha} } +\frac{1}{2}\text{\textbf{F}}_{\mathrm{s}} +\frac{1}{2}\textbf{F}_{\text{axis}}} \right),\\ &&p=\sum\limits_{\alpha} {f_{\alpha} +\frac{\delta_{t}} {2}} \left( \textbf{u}\cdot \nabla \rho {c_{s}^{2}}\right). \end{array} $$
(11)

Phase-field Theory

The idea of the phase-field theory is taken the sharp interface as a diffusive one, and therefore, the interface movement and its deformation are simulated in a fixed Eulerian grid (Celani et al. 2009; Zu and He 2013; Yue et al. 2004). In the phase-field method, an order parameter φ is adopted to distinguish the different phases: φ=1 represents the phase one and φ=−1 for the other. A free-energy function (Penrose and Fife 1990) of the system is defined as

$$ \Xi \left( \varphi \right)={\int}_{\Lambda} \left[\Psi \left( \varphi \right)+{\varepsilon^{2}\left| {\nabla \varphi} \right|^{2}} \left/ 2\right.\right]d{\Lambda} , $$
(12)

where Λ is the region of space occupied by the system. The term Ψ(φ) is the bulk energy density and takes the form (Liu et al. 2013) as

$$ \Psi \left( \varphi \right)=\frac{1}{4}\left( {\varphi^{2}-1} \right)^{2}. $$
(13)

The second term ε 2|∇φ|2/2 relates to the surface energy. The chemical potential μ φ is calculated by taking the variation of the free-energy function with respect to the order parameter (Liu et al. 2013; Jacqmin 2000) as

$$ \mu_{\varphi} =\frac{\delta \Xi} {\delta \varphi} =\frac{\partial \Psi} {\partial \varphi} -\varepsilon^{2}\nabla^{2}\varphi =\varphi^{3}-\varphi -\varepsilon^{2}\nabla^{2}\varphi \quad , $$
(14)

where the Laplacian of φ in cylindrical coordinates is

$$ \nabla^{2} \varphi =\frac{\partial^{2}\varphi} {\partial r^{2}}+\frac{1}{r}\frac{\partial \varphi} {\partial r}+\frac{\partial^{2}\varphi} {\partial z^{2}}. $$
(15)

The evolution of interface and order parameter φ is described by the Cahn-Hilliard (Cahn and Hilliard 1958) equation

$$ \frac{\partial \varphi} {\partial t}+\textbf{u}\cdot \nabla \varphi =\nabla M\cdot \nabla \mu_{\varphi} +M\left( \frac{\partial^{2}\mu_{\varphi} } {\partial r^{2}}+\frac{1}{r}\frac{\partial \mu_{\varphi}} {\partial r}+\frac{\partial^{2}\mu_{\varphi} } {\partial z^{2}}\right), $$
(16)

where M is a diffusion parameter named as mobility, and the equation is described in cylindrical coordinates.

In addition, when the equations are solved numerically on the fixed Eulerian grid, the fluid properties on this grid are required. In terms of two-phase flow, each phase is assumed as an incompressible flow, and the fluid properties are taken as constant in each phase. The reconstruction of the fluid properties b(φ,t) at time t in the whole two layers system is achieved through the order parameter

$$ b\left( {\varphi ,t} \right)=b_{2} +\frac{\varphi -\varphi_{2}} {\varphi_{1} -\varphi_{2}} \left( {b_{1} -b_{2}} \right) $$
(17)

where b(φ,t) represents the fluid density ρ, thermal conductivity κ, kinematic viscosity ν and heat capacity c p . φ 1=1 represents the fluid one and φ 2=−1 for fluid two.

Surface Tension

The surface tension is a result of the unbalanced force exerted to the molecules near the interface of the two phases. The continuum surface force model (CSF), which is widely applied in two-phase flows (Brackbill et al. 1992; Zhou and Huang 2010; Liang et al. 2011; Zhou and Huai 2014), is adopted in this work, and the surface tension is reformulated as a volume force in the momentum equation which only acts in the vicinity of the interface. The expression of the unbalanced surface tension F s is

$$ \textbf{F}_{s} =\left( {-\sigma \kappa \textbf{n}+\nabla_{s} \sigma} \right)\delta_{s} , $$
(18)

where the first term is the normal surface tension and the second term expresses the tangential force, which appears because surface tension depends on temperature. ∇ s =(I−nn)⋅∇ is the surface gradient operator and δ s is the Dirac function (Liu et al. 2013). The interface normal vector n and curvature k are calculated from the order parameter φ

$$ \textbf{n}=\frac{\nabla \varphi} {\left| {\nabla \varphi} \right|},\;\;\;\;\;\;\;\;\;\;\;\;k=\nabla \cdot \textbf{n}. $$
(19)

The second term in (18) is rewritten as

$$ \nabla_{s} \sigma =\left( \textbf{I}-\textbf{nn}\right)\cdot \nabla \sigma =\nabla \sigma -\frac{\nabla \varphi} {\left| {\nabla \varphi} \right|^{2}}\left( {\nabla \sigma \cdot \nabla \varphi} \right) $$
(20)

The surface tension σ is taken as

$$ \sigma \left( T \right)=\sigma_{0} +\sigma_{T} \left( {T-T_{0}} \right), $$
(21)

where σ 0 is the surface tension coefficient at a reference temperature T 0, and σ T is a negative constant for most fluids.

Temperature Equation

The governing equation of the temperature field in cylindrical coordinate system is formulated as

$$ \rho c_{p} \left( {\frac{\partial T}{\partial t}+\textbf{u}\cdot \nabla T} \right)=\nabla \kappa \cdot \nabla T+\kappa \left( \frac{\partial^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{\partial^{2}T}{\partial z^{2}}\right), $$
(22)

where κ and c p are coefficients of heat conduction and heat capacity, respectively.

In this hybrid model, the equations (16) and (22) are discretized on the same grid as the evolution (2) by FDM and they are updated at the same time. The two equations is rewritten in a general form as

$$ \frac{\partial \theta} {\partial t}=\mathrm{R}\left( \theta \right)=-\text{\textbf{u}}\cdot \nabla \theta +\frac{1}{\vartheta} \left[ {\nabla \xi \cdot \nabla \theta +\xi \left( {\frac{\partial^{2}\theta} {\partial r^{2}}+\frac{1}{r}\frac{\partial \theta} {\partial r}+\frac{\partial^{2}\theta} {\partial z^{2}}} \right)} \right] $$
(23)

where 𝜃 represents both the order parameter φ and temperature T, 𝜗 equals to ρ c p in the temperature equation, and ξ represents the diffusion parameter. In (23), all the spatial derivative terms are in the right hand side, and the time-derivative term is in the left side, an explicit fourth-order Runge–Kutta scheme is employed as below:

$$ \begin{array}{l} \theta_{1} =\delta_{t} \mathbb{R}\left( {t^{n},\theta^{n}} \right) \\ \theta_{2} =\delta_{t} \mathbb{R}\left( {t^{n}+\frac{1}{2}\delta_{t} ,\theta^{n}+\frac{1}{2}\theta_{1}} \right) \\ \theta_{3} =\delta_{t} \mathbb{R}\left( {t^{n}+\frac{1}{2}\delta_{t} ,\theta^{n}+\frac{1}{2}\theta_{2}} \right) \\ \theta_{4} =\delta_{t} \mathbb{R}\left( {t^{n}+\delta_{t} ,\theta^{n}+\theta_{3}} \right) \\ \theta^{n+1}=\theta^{n}+\frac{1}{6}\left( {\theta_{1} +2\theta_{2} +2\theta_{3} +\theta_{4}} \right). \\ \end{array} $$
(24)

Both the fourth-order and second-order Runge-Kutta schemes are tested, although the two schemes agree well for the monitored quantities (i.e. drop velocity and temperature field), and the second-order scheme takes about 5 % less CPU time than the fourth-order scheme, the fourth-order Runge-Kutta scheme is finally adopted. In addition, the hybrid framework allows a flexible choice on the discretization scheme of the phase-field and temperature equations, for instance, a time-split scheme with a novel semi-implicit discretization, proposed by Badalassi et al. (2003), is also an effective scheme for the phase field equation.

Boundary Conditions

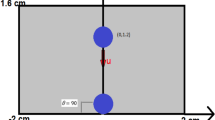
For the D2Q9 LBM model, there are two boundary conditions as illustrated in Fig. 1, the top, bottom and right boundaries are solid walls and the left boundary is the axisymmetric line. The symmetric boundary is taken the radial velocity component and the gradients of any macroscopic variables normal to the boundary as zero

$$ \begin{array}{l} \left. {\textbf{n}\cdot \textbf{u}} \right|_{axis} =0 \\ \left. {\textbf{n}\cdot \nabla \phi} \right|_{axis} =0 \\ \end{array} $$
(25)

where ϕ represents φ, μ φ and temperature T. Specular reflection boundary condition is employed for the distribution functions, of which f 1 = f 3, f 5 = f 6 and f 8 = f 7 are executed after the collision step. The singularity at r=0 is treated following the L’Hôpital’s rule (Reis and Phillips 2007; Premnath and Abraham 2005).

Fig. 1
figure 1

The schematic for thermocapillary migration of two drops in a uniform temperature gradient and the axisymmetric computational domain

Full size image

Numerical Results

In this section, firstly, the thermocapillary migration of single drop is simulated to validate the developed model. Subsequently, two drops motion is simulated and the effects of Ma number and Ca number on drop’s coalescence are investigated.

For the thermocapillary-driven drop motion, the important dimensionless parameters are defined as:

$$ Re=\frac{RV_{r}} {\nu_{2}} ,\;\;\;\;\;\;\;Ma=\frac{\rho_{2} c_{p2} RV_{r}} {\kappa_{2}} ,\;\;\;\;\;\;\;\;Ca=\frac{\rho_{2} \nu_{2} V_{r}} {\sigma_{0}} $$
(26)

where R is the drop radius, and the subscript 2 represents the continuous phase. V r is the reference velocity de?ned by the balance of thermocapillary force and viscosity force on the drop

$$ V_{r} =-\frac{\sigma_{T} R\left| {\nabla T} \right|}{\rho_{2} \nu_{2}} $$
(27)

where |∇T| is temperature gradient imposed on the continuous phase. Furthermore, the so called YGB velocity Young et al. (1959), the velocity of a spherical drop when neglecting the convection is

$$ V_{YGB} =\frac{2\mathrm{V}_{r}} {\left( 2+3{\rho_{1} \nu_{1}} \left/ {\rho_{2} \nu_{2}}\right.\right)\left( 2+{\kappa_{1}} \left/ {\kappa_{2}}\right.\right)}. $$
(28)

The geometrical model with only a single drop is similar as in Fig. 1. The fluid is initially at rest and the temperature linearly increases from the cold bottom wall toward the hot top wall, with T c o l d =0 and T h o t =|∇T|N z (N z is the grids in z direction). In this paper, the results are presented in lattice units.

Migration of Single Drop

To validate the numerical method, the rise of a single drop owing to thermocapillary force was simulated. The dimensionless parameters are chosen as R e=0.1, M a=0.1, C a=0.08. The material properties of the drop are equal to the continuous fluid. In the simulation, the centroid velocity V of the drop in z direction is calculated by

$$ V=\frac{{\int}_{\varphi >0} {rv\left( {r,z} \right)drdz}} {{\int}_{\varphi >0} {rdrdz}} =\frac{\sum\nolimits_{\left. {i,j} \right|\varphi_{i,j} >0} {r_{i,j} v_{i,j}} } {\sum\nolimits_{\left. {i,j} \right|\varphi_{i,j} >0} {r_{i,j}}}. $$
(29)

Initially, the drop center is located at (r,z)=(0,0.5N z ), then, the drop is driven by the thermocapillary force towards the hot side along the symmetric z-axis. The simulated velocity vector and temperature contours are exhibited in Fig. 2a, b, in which (a) is those in the laboratory reference frame and (b) is those in the local reference frame attached to the center of the drop. Quantitatively, the simulated velocity of the drop with three different meshes (i.e. 5R×10R, 8R×16R, 10R×20R, with drop radius R=20 lattice units) versus time are shown in Fig. 3. The velocities are scaled by the YGB velocity as V ∗ = V/V Y G B , and time is dimensionalized as t ∗ = V r t/R. The consistent results are observed between the YGB analytical velocity and the simulated drop velocity with grids 8R×16R and 10R×20R, and there is only negligible effect of the walls on the results when distance of the drop to the walls increases from the grid 8R×16R to 10R×20R. By comparing the simulated result with the corresponding YGB velocity, we found that the accuracy is acceptable when drop size is larger than 16 lattice units.

Fig. 2
figure 2

The velocity vector and temperature contours for thermocapillary migration of the single drop, Ma = Re =0.1, and Ca =0.08. a In the inertial laboratory reference frame; b In the reference frame moving with the drop

Full size image
Fig. 3
figure 3

The evolution of normalized migration velocities with time, and comparison with YGB theory

Full size image

Effect of Ma Number

In this section, the effects of Ma number on the coalescence of two drops (R T =50, R L =20 lattice units) are investigated. The physical properties of the drops are assumed to be equal to the continuous fluid. The computational domain is 8R T ×40R Tlattice units. The different Marangoni numbers (M a=0.5, 50, 250) are achieved by adjusting κ 1 and κ 2 while keeping κ 1 = κ 2. The other governing parameters are: R e=2.5 and C a=0.01. The initial distance between the two drops is taken as R L . The dimensionless parameters are computed according to the parameters of the trailing drop.

Figure 4 shows the transient snapshots for the chasing process of two drops, and finally their coalescence process with M a=0.5,50 and 250. The results reveal that the drop’s coalescence becomes difficult with increasing Ma number. The trailing drop catches up the leading drop and start to coalesce at time t ∗=10.3 for M a=0.5, and at time t ∗=16.3 for M a=50, but no coalescence process is observed for M a=250. This phenomenon can be attributed to the heat transfer around the drops with different M a number as in Fig. 4. When M a is small, the isotherms around the drops are almost straight. With the increase of M a number, the convective transport is enhanced and the isotherms around the drops arch to the hotter region, which resulting the temperature gradient along the drop surface is decreased. The comparison of drops trajectory with different Ma number are plotted in Fig. 5 for clearly observing the process of drops motion and coalescence. It is noted from this figure that the start time of drop’s coalescence is influenced by the M a number apparently.

Fig. 4
figure 4

Snapshots of two drops at different time, exhibiting the drops coalescence process with different Ma number

Full size image
Fig. 5
figure 5

Drop’s trajectory with different Ma number

Full size image

Effect of Ca number

The Capillary number represents the ratio of viscous force to normal surface tension, and it plays an important role in governing the deformation and drop’s coalescence. The different C a numbers (C a=0.01, 0.05, 0.25) are achieved by adjusting σ 0, the Reynolds and Marangoni numbers are R e=2.5 and M a=2.5 respectively, and the other parameters are kept as same as the above case. Figure 6 shows the transient snapshots for the drop’s coalescence. The initiation time of coalescence is t ∗=10.7 for C a=0.01, and t ∗=12.4 for C a=0.05. In addition, the coalescence process takes about 1.5 lattice time for C a=0.01, and about 2.8 lattice time for C a=0.05. In the case of C a=0.25, the deformation of the leading drop is noticeable, and the drop coalescence is not observed. Figure 7 reveals that the deformation of leading drop depends on obviously on the C a number, but the effect of the C a number on the trailing larger drop deformation is relatively weak. A smaller C a number indicates higher magnitude of surface tension predominate viscous force and vice-versa, and the surface tension tends to keep the drop in circle. The comparison of drops trajectory with C a=0.01 and 0.05 is demonstrated in Fig. 8, and the figure also presented that the start time of drop’s coalescence is influenced by the Ca number.

Fig. 6
figure 6

Snapshots of two drops at different time, exhibiting the drops coalescence process with with different Ca number

Full size image
Fig. 7
figure 7

Drop’s profile with Ca =0.01 and 0.25

Full size image
Fig. 8
figure 8

Drop’s trajectory with Ca =0.01 and 0.05

Full size image

Conclusions

A hybrid LBM has been developed to simulate axisymmetric thermocapillary flow, the phase-field theory was applied to capture the drop’s deformation and especially the coalescence process, and the continuum surface force model was adopted to introduce the unbalanced surface tension. The thermocapillary motion and coalescence of two drops have been investigated numerically. The temporal snapshots of drop’s motion and coalescence reveal that the drops tend to coalesce faster and easier with a small Ma. The drop coalescence is not observed for the Ma. The results also indicate that the start time of coalescence is influenced by C a number, and no drop coalescence was observed with large C a number.Nomenclature

f α :

density distribution function

f eq :

equilibrium distribution function

m α :

moment

m eq :

equilibrium moment

e α :

discrete particle speeds

M :

transformation matrix

F :

external forces

s α :

relaxation rates

c p :

heat capacity

u :

velocities

p :

pressure

T :

temperature

n :

interface normal

k :

interface curvature

V :

velocity of the drop

d :

separation distance between the two drops

R T :

radius of the trailing drop

R L :

radius of the leading drop

Re :

Reynolds number

Ma :

Marangoni number

Ca :

Capillary number

Greeks

σ :

surface tension

φ :

order parameter

κ :

thermal conductivity

ν :

kinematic viscosity

ρ :

density

Subscripts/ Superscripts

α :

discrete speed directions (α=0,…,8)

eq :

equilibrium