A conjugate gradient algorithm without Lipchitz continuity and its applications

Abstract

An improved conjugate gradient algorithm is proposed that does not rely on the line search rule and automatically achieves sufficient descent and trust region qualities. It is applicable to solve unconstrained problems and large-scale nonsmooth problems. Furthermore, it demonstrates global convergence properties without the need for Lipschitz continuity conditions. Numerical experiments on nonconvex unconstrained problems and large scale nonsmooth convex optimization problems demonstrate the effectiveness and efficiency of the proposed algorithm compared with the same structural algorithm. Finally, the new algorithm is applied to Muskingum model solving in engineering problems and image restoration, which shows the prospect of the new algorithm.

1 Introduction

Consider optimization problem:

$$\begin{aligned} \min \{q(x)|x\in {\mathbb {R}}^n\}, \end{aligned}$$

(1)

where $q(x):{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, is a convex function that possibly is nonsmooth. With the rapid advancement of information technology, optimization techniques are being applied to various aspects of production and daily life. The need to investigate large-scale nonsmooth convex optimization problems has become increasingly urgent. This paper presents an algorithm for addressing large-scale nonsmooth problems, using the problem of image restoration in image processing as an illustrative example. Image restoration refers to observed images are reconstructed into their original, yet unknown, real forms by establishing image degradation models. In the practical processes of image generation, storage, and transmission, image quality deterioration is an issue that cannot be avoided due to technological constraints and objective factors. To obtain more valuable information and ensure that images meet the high-quality research and application standards, image restoration has become a necessary technique. The following are common image degradation models

$$\begin{aligned} \beta =\varLambda x+\epsilon , \end{aligned}$$

where $\beta \in {\mathbb {R}}^m$ and $x\in {\mathbb {R}}^n$ respectively correspond to the observed and original images, $\varLambda$ is an $m\times n$ matrix responsible for blurring, $\epsilon \in {\mathbb {R}}^m$ is the noise term. To solve $\epsilon$, We first solve problem

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n}\Vert \varLambda x+\beta \Vert ^2+\lambda \Vert Dx\Vert _1, \end{aligned}$$

(2)

where $\lambda$ as regularization parameter, D as linear operator. In this paper, $\Vert \cdot \Vert$ denotes Euclidean norm, $\Vert \cdot \Vert _1$ is $l_1$ norm. Since $l_1$ norm is nonsmooth, (2) described above falls into the category of nonsmooth convex optimization problems, which are typically of large scale.

Compared to unconstrained problems, the objective function of non-smooth problems may include discontinuous components, which pose challenges to problem-solving. Furthermore, in the current conjugate algorithms, the assumption of Lipschitz continuity is required to ensure bounded gradient variations. This condition is a key requirement in the convergence analysis of line search. However, in practice, there are instances where the Lipschitz continuity hypothesis may not hold or cannot be readily verified due to complexity of the objective function or limitations in obtaining accurate gradient information. Some algorithms [1, 2] that do not require Lipschitz continuity have been proposed. To overcome these constraints, we present a novel algorithm in this paper. It tackles unconstrained and nonsmooth issues employing the Moreau-Yosida regularization technique.The new algorithm possesses three characteristics:

• It fulfills the prerequisites of a sufficient descent and trust region properties, eliminates need to specify a step size.

• The algorithm’s performance is improved by incorporating function value and gradient information into the search direction.

• The algorithm integrates Wake-Wolfe-Powell (WWP) linear search(5)(6) and exhibits global convergence for nonLipschitz continuous nonconvex problems and nonsmooth functions.

In Sect. 2, an algorithm is presented which has some good properties for solving unconstrained optimization problems. In Sect. 3, the algorithm is used to solve non-smooth problems. Section 4 states numerical findings of algorithms for unconstrained and nonsmooth problems. Additionally, we show the algorithm’s numerical performance in image restoration problems. The paper ends with a summary in Sect. 5, outlining possible directions for further investigation.

2 Unconstrained optimization

Regarding problem (1), we first discuss the situation under smooth conditions, i.e.

$$\begin{aligned} \min \{f(x)|x\in {\mathbb {R}}^n\}, \end{aligned}$$

(3)

with $f(x):{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is a continuously differentiable nonconvex function. For solving (3), conjugate gradient(CG) algorithm proves to be highly effective, particularly when its dimension n is of a large scale. CG algorithm generates an iterative sequence by the following formula:

$$\begin{aligned} x_{k+1}=x_k+\alpha _kd_k,\quad k=0,1,\ldots \end{aligned}$$

where $\alpha _k>$ 0 is a steplength determined by line search, the search direction $d_k$ is generated by

$$\begin{aligned} d_k=-h_k+\beta _kd_{k-1},\quad d_0=-g_0, \end{aligned}$$

where $h_k$ is the gradient of $f(x_k)$. CG algorithm can be classified according to the choice of parameter $\beta _k$, among them, Polak-Ribière-Polyak(PRP) methods has advantages in dealing with large-scale problems because of its high computational efficiency and small storage capacity. Despite employing strong Wolfe line search, achieving global convergence for PRP methods with general nonlinear functions remains challenging. And its primary applications are currently mostly limited to dealing with smooth problems. The BFGS algorithm constructs an approximate Hessian matrix to expedite the convergence of the objective function, the search direction $d_k$ is generated by

$$\begin{aligned} d_k=-B_k^{-1}h_k, \end{aligned}$$

where $B_k$ is the approximate Hessian matrix. BFGS algorithm has made some progress on global convergence of general functions under WWP line search [3]. But its applicability is challenged in large-scale computations due to storage constraints. An adaptive memoryless BFGS method [4, 5] is proposed that adaptively adjusts Hessian matrix approximation, avoiding the need to store Hessian matrix or its inverse. In an attempt to advance the CG and BFGS techniques, a family of conjugate gradient algorithm is introduced, which $d_k$ can closely aligned with scaled memoryless BFGS method [6]

$$\begin{aligned} d^{\textrm{DK}}_k\left( \gamma _k\right) =-h_k+\left[ \frac{h_k^T y_{k-1}}{d_{k-1}^T y_{k-1}}-\left( \gamma _k+\frac{\left\| y_{k-1}\right\| ^2}{s_{k-1}^T y_{k-1}}-\frac{s_{k-1}^T y_{k-1}}{\left\| s_{k-1}\right\| ^2}\right) \frac{h_k^T s_{k-1}}{d_{k-1}^T y_{k-1}}\right] d_{k-1}, \end{aligned}$$

where $s_{k-1} = x_k-x_{k-1}$, $h_k$ represents gradient of f(x), $\gamma _k$ denotes the self-scaling parameter and the optimal choice for efficiency is

$$\begin{aligned} \gamma _k=\frac{s_{k-1}^Ty_{k-1}}{\left\| s_{k-1}\right\| ^2}. \end{aligned}$$

Li [7, 8] made some modifications based on the Dai-Kou algorithm, resulting in different numerical outcomes. To enhance convergence, we implement a novel technique ensuring that the search direction $d_k$ adheres to trust region property automatically. This plays a crucial role for establishing global convergence.

Besides directly modifying iteration formula for $d_k$ it is also a viable approach to make adjustments to the quasi-Newton equation. Yuan [9] designs a new quasi-Newtonian equation so that $y_k^m$ has information about the gradient of the function, and also about the function itself

$$\begin{aligned} B_{k}s_{k-1}=y_{k-1}^m, \end{aligned}$$

where $y_{k-1}^m=y_{k-1}+\frac{\max \{\varrho _{k-1},0\}}{\Vert s_{k-1}\Vert ^2}s_{k-1}$, $\varrho _{k-1}=(h_k+h_{k-1})^Ts_{k-1}+2(f_{k-1}-f_k)$, denote $f_k=f(x_k)$. Compared with the previous $y_k$, $y_k^m$ enables the new algorithm to obtain satisfactory results in less iterations and shorter operation time, and has better numerical performance and theoretical results.

Drawing inspiration from the previously mentioned techniques, a novel hybrid conjugate gradient algorithm is introduced. $d_k$ is as follows

$$\begin{aligned} d_k=-h_k+\left( \frac{h_k^Ty_{k-1}^m}{\omega _k}-\frac{\Vert y_{k-1}^m\Vert ^2r_k}{\omega _k^2}\right) d_{k-1}+\frac{t_kr_k}{\omega _k}y_{k-1}^m, \quad d_0=-h_0, \end{aligned}$$

(4)

where $\omega _k=c_1\Vert d_{k-1}\Vert \Vert y_{k-1}^m\Vert +c_2\Vert h_k\Vert ^2$, $r_k=h_k^Td_{k-1}$. By choosing the first term of $\omega _k$, $d_k$ is endowed with a trust region property, and the second term sets a lower bound for $\omega _k$, guaranteeing global convergence. Interestingly, $\omega _k$ is never equal to zero, which guarantees that $d_k$ is well-defined.

The algorithm is outlined below

Algorithm 1

BPRP(unconstrained optimization)

Assumption 1

Consider f(x) continuously differentiable, and

$$\begin{aligned} \Psi =\{x|f(x)\le f_0\} \end{aligned}$$

is bounded.

Lemma 1

All $d_k$ follows sufficient descent property

$$\begin{aligned} h_k^Td_k\le -z\Vert h_k\Vert ^2, \end{aligned}$$

(7)

trust region property

$$\begin{aligned} \Vert d_k\Vert \le c\Vert h_k\Vert , \end{aligned}$$

(8)

with $z=1-\frac{(1+\tau )^2}{4}$ and $c=1+\frac{1+\tau }{c_1}+\frac{1}{c_1^2}$.

Proof

Given that $d_0 = -h_0$, we observe that $h_0^Td_0 = -\Vert h_0\Vert ^2$, fulfilling  (7) for $k = 0$. In light of $d_k$’s definition, we can confirm that for all $k>0$,

$$\begin{aligned} \begin{aligned} h_k^Td_k&\le -\Vert h_k\Vert ^2+\frac{\left( 1+t_k\right) ^2}{4}\Vert h_k\Vert ^2+\frac{\Vert y_{k-1}^m\Vert ^2r_k^2}{\omega _k^2} -\frac{\Vert y_{k-1}^m\Vert ^2r_k^2}{\omega _k^2}\\&\le -\left( 1-\frac{\left( 1+\tau \right) ^2}{4}\right) \Vert h_k\Vert ^2, \end{aligned} \end{aligned}$$

which implies that  (7) holds.

When $k = 0$, using $d_0 = -h_0$ as a starting point, we obtain $\Vert d_0\Vert = \Vert h_0\Vert$, implying  (8). For $k>0$, we can use  (7) and Cauchy-Schwarz inequality to establish (8). Assume $y_{k-1}^m \ne 0$, consider

$$\begin{aligned} \omega _k \ge c_1\Vert d_{k-1}\Vert \Vert y_{k-1}^m\Vert . \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned}&\left| \frac{h_k^Ty_{k-1}^m}{\omega _k}-\frac{\Vert y_{k-1}^m\Vert ^2r_k}{\omega _k^2}\right| \le \frac{\Vert h_k\Vert \Vert y_{k-1}^m\Vert }{\omega _k}+\frac{\Vert y_{k-1}^m\Vert ^2\Vert h_k\Vert \Vert d_{k-1}\Vert }{\omega _k^2}\\&\le \frac{\Vert h_k\Vert \Vert y_{k-1}^m\Vert }{c_1\Vert d_{k-1}\Vert \Vert y_{k-1}^m\Vert }+\frac{\Vert y_{k-1}^m\Vert ^2\Vert h_k\Vert \Vert d_{k-1}\Vert }{(c_1\Vert d_{k-1}\Vert \Vert y_{k-1}^m\Vert )^2}=\left( \frac{1}{c_1}+\frac{1}{c_1^2}\right) \frac{\Vert h_k\Vert }{\Vert d_{k-1}\Vert }, \end{aligned} \end{aligned}$$

(9)

and

$$\begin{aligned} \left| t_k\frac{r_k}{\omega _k}\right| \le \tau \frac{\Vert h_k\Vert \Vert d_{k-1}\Vert }{c_1\Vert d_{k-1}\Vert \Vert y_{k-1}^m\Vert }=\tau \frac{\Vert h_k\Vert }{c_1\Vert y_{k-1}^m\Vert }. \end{aligned}$$

(10)

Combining  (9) (10) (4), we yield

$$\begin{aligned} \begin{aligned} \Vert d_k\Vert&\le \Vert h_k\Vert +\left( \frac{1}{c_1}+\frac{1}{c_1^2}\right) \frac{\Vert h_k\Vert }{\Vert d_{k-1}\Vert }\Vert d_{k-1}\Vert +\tau \frac{\Vert h_k\Vert }{c_1\Vert y_{k-1}^m\Vert }\Vert y_{k-1}^m\Vert \\&\le \left( 1+\frac{1+\tau }{c_1}+\frac{1}{c_1^2}\right) \Vert h_k\Vert . \end{aligned} \end{aligned}$$

The proof is completed. $\square$

Theorem 1

Combining Algorithm 2 and Assumption 1, then

$$\begin{aligned} \liminf _{k\rightarrow \infty }\Vert h_k\Vert =0. \end{aligned}$$

(11)

Proof

Proofs by contradiction. If (11) is incorrect, suggests that exist constant $\epsilon > 0$ and have

$$\begin{aligned} \Vert h_k\Vert \ge \epsilon . \end{aligned}$$

(12)

Sequence $\{\alpha _k\}$ is assumed to converge and denote ${\overline{\alpha }}= \limsup _{k\rightarrow \infty }\alpha _k$. We observe that ${\overline{\alpha }} \ge 0$. Accordingly, the discussion follows.

Case (i): ${\overline{\alpha }} > 0$. When $k_i > k$, exists subsequence $\{\alpha _{k_i}\}$ and constant $\xi > 0$ satisfies

$$\begin{aligned} \lim _{i\rightarrow \infty }\alpha _{k_i}>\xi , \end{aligned}$$

By applying (5) and summing up from $k = 0$ to $\infty$ yields

$$\begin{aligned} -\mu \sum _{k=1}^\infty \alpha _kh_k^Td_k<f_0-\lim _{k\rightarrow \infty }f_k<\infty , \end{aligned}$$

then

$$\begin{aligned} \lim _{i\rightarrow \infty }-\alpha _{k_i}g_{k_i}^Td_{k_i}=0. \end{aligned}$$

By  (7) and  (12), thus

$$\begin{aligned} \lim _{i\rightarrow \infty }(1-\frac{(1+\tau )^2}{4})\alpha _{k_i}\Vert \epsilon \Vert ^2\le \lim _{i\rightarrow \infty } (1-\frac{(1+\tau )^2}{4})\alpha _{k_i}\Vert h_{k_i}\Vert ^2\le \lim _{i\rightarrow \infty }-\alpha _{k_i}h_{k_i}^Td_{k_i}=0. \end{aligned}$$

This implies

$$\begin{aligned} \lim _{i\rightarrow \infty }\alpha _{k_i}=0, \end{aligned}$$

which contradicts our assumption. Therefore, the (11) is true.

Case (ii) ${\overline{\alpha }}=0.$ From  (6)

$$\begin{aligned} h(x_{k_l}+\alpha _{k_l}d_{k_l})^Td_{k_l}-\nu h_{k_l}^Td_{k_l}\ge 0. \end{aligned}$$

So we obtain

$$\begin{aligned} \lim _{l\rightarrow \infty }h(x_{k_l}+\alpha _{k_l}d_{k_l})^Td_{k_l}-\nu h(x_{k_l})^Td_{k_l}=(1-\nu )h(x^*)^Td(x^*)\ge 0. \end{aligned}$$

(13)

Combine with (7) and (12), then

$$\begin{aligned} h(x^*)^Td(x^*)\le -z\Vert h(x^*)\Vert ^2\le -z\epsilon <0. \end{aligned}$$

(14)

This is contradictory to (32). $\square$

According to Theorem 1, we assume $\lim _{k\rightarrow \infty }x_k={\hat{x}}$. Then, under the following additional assumptions, we further discuss the convergence rate of BPRP algorithm.

Assumption 2

Assuming f that is uniformly convex and has continuous second derivatives in ${\mathbb {R}}^n$, gradient h satisfies Lipschitz continuity. So f has unique minimal point ${\hat{x}}$ with minimum value ${\hat{f}}$, for all $x\in {\mathbb {R}}^n$ satisfying

$$\begin{aligned} \frac{1}{2} \varphi \left\| x-{\hat{x}}\right\| ^2 \le f(x)-{\hat{f}} \le \frac{1}{2} \phi \left\| x-{\hat{x}}\right\| ^2, \end{aligned}$$

(15)

and

$$\begin{aligned} \varphi \left\| x_k-{\hat{x}}\right\| ^2 \le \left\| h_k\right\| ^2 \le \phi \left\| x_k-{\hat{x}}\right\| ^2, \end{aligned}$$

(16)

where $0<\varphi <\phi$ are constants.

Lemma 2

$\{x_k\}$ is obtained by BPRP algorithm. If the conditions in Assumption 1 and  (15) (16) are satisfied, for all $k\ge 0$ one can derive

$$\begin{aligned} \alpha _k\ge \vartheta , \end{aligned}$$

(17)

where $\vartheta > 0$ a constant.

Proof

Denote

$$\begin{aligned} \Omega _{k-1}=\int _{0}^{1}\nabla ^2f(x_{k-1}+\zeta s_{k-1})d\zeta , \end{aligned}$$

By to mean-value theorem,

$$\begin{aligned} h_k-h_{k-1}=\Omega _{k-1}s_{k-1}=\Omega _{k-1}\alpha _{k-1}d_{k-1}. \end{aligned}$$

From (6), we have

$$\begin{aligned} h\left( x_k+\alpha _kd_k\right) ^Td_k=\left( h_k+\alpha _kd_k\int _{0}^{1}\nabla ^2f\left( x_k+\zeta \alpha _kd_k\right) d\zeta \right) ^Td_k\ge \nu h_k^Td_k, \end{aligned}$$

which implies

$$\begin{aligned} \alpha _kd_k^T\int _{0}^{1}\nabla ^2f\left( x_k+\zeta \alpha _kd_k\right) d\zeta d_k\ge \left( \nu -1\right) h_k^Td_k. \end{aligned}$$

(18)

Based on Assumption 2, then $\varphi \Vert d\Vert ^2\le d^T\nabla ^2f(x)d\le \phi \Vert d\Vert ^2$, combining with (18) have $\phi \alpha _k\Vert d_k\Vert ^2\ge \left( \nu -1\right) h_k^Td_k$. Based on (8), we have

$$\begin{aligned} \begin{aligned} \alpha _k&\ge \frac{\left( \nu -1\right) h_k^Td_k}{\phi \Vert d_k\Vert ^2}\ge \frac{\left( 1 -\nu \right) }{\phi }\frac{\left( 1-\frac{\left( 1+\tau \right) ^2}{4}\right) \Vert h_k\Vert ^2}{\Vert d_k\Vert ^2}\\&\ge \frac{\left( 1-\nu \right) }{\phi }\left( 1-\frac{\left( 1+\tau \right) ^2}{4}\right) \left( 1 +\frac{1+\tau }{c_1}+\frac{1}{c_1^2}\right) ^{-2}\triangleq {\overline{\vartheta }}. \end{aligned} \end{aligned}$$

(17) is obtained by setting $\vartheta = min\{1, {\overline{\vartheta }}\}$. $\square$

Theorem 2

According to Assumption 2, $\{x_k\}$ converges to ${\hat{x}}$, satisfies

$$\begin{aligned} \Vert x_k-{\hat{x}}\Vert \le {\hat{b}}\sigma ^k, \end{aligned}$$

(19)

where ${\hat{b}} > 0$ and $0<\sigma <1$ are constants.

Proof

From (5) in WWP, (7)(15) and (16)

$$\begin{aligned} \begin{aligned} f_{k+1}-{\hat{f}}&\le f_k+\mu \alpha _k h_k^T d_k-{\hat{f}}\\&\le f_k-(1-\frac{(1+\tau )^2}{4})\mu \psi \frac{2 \varphi }{\phi }\left( f_k-{\hat{f}}\right) -{\hat{f}}\\&=\left( 1-\left( 1-\frac{\left( 1+\tau \right) ^2}{4}\right) \mu \psi \frac{2 \varphi }{\phi }\right) \left( f_k-{\hat{f}}\right) . \end{aligned} \end{aligned}$$

Setting $\sigma =\left( 1-(1-\frac{(1+\tau )^2}{4})\mu \psi \frac{2 \varphi }{\phi }\right) ^\frac{1}{2}$, so have

$$\begin{aligned} f_k-{\hat{f}} \le \sigma ^2\left( f_{k-1}-{\hat{f}}\right) \le \cdots \le \sigma ^{2k}\left( f_0-{\hat{f}}\right) . \end{aligned}$$

Combining (15), then

$$\begin{aligned} \left\| x_k-{\hat{x}}\right\| ^2 \le \frac{2}{\varphi }\left( f_k-{\hat{f}}\right) \le \frac{2}{\varphi }\left( f_0-{\hat{f}}\right) \sigma ^{2k}, \end{aligned}$$

which shows that (19) holds, where ${\hat{b}}=\left( \frac{2}{\varphi }\left( f_0-{\hat{f}}\right) \right) ^\frac{1}{2}$. $\square$

3 Nonsmooth problem

Adding regularization term to nonsmooth convex problem (1)

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n}F(x)\triangleq \min _{r\in {\mathbb {R}}^n} \{q(r)+\frac{1}{2\chi }\Vert r-x\Vert ^2\}, \end{aligned}$$

(20)

where $F: {\mathbb {R}}^n\rightarrow {\mathbb {R}}$, $\chi >0$. (20) is considered equivalent to (1). Setting $\Theta (r, x)=q(r)+\frac{1}{2\chi }\Vert r-x\Vert ^2$, and $\ell (x)={\text {argmin}}_r\Theta (r, x)$. For every x, $\Theta (\cdot , x)$ exhibits strong convexity. So F is denoted as

$$\begin{aligned} F(x)=q(\ell (x))+\frac{1}{2\chi }\Vert \ell (x)-x\Vert ^2. \end{aligned}$$

F has the following properties:

• (i) It is Finite-valued and convex. Denote gradient of F as

  $$\begin{aligned} {\hat{h}}(x)=\nabla F(x)=\frac{x-\ell (x)}{\chi }, \end{aligned}$$

  it exists in ${\mathbb {R}}^n$ and continuous

• (ii) When ${\hat{h}}(x)=0$, i.e. $\ell (x)=x$, (1) has unique solution. By minimizing $\Theta (r)$, can get $\ell (x)$, which can expresses F(x) and ${\hat{h}}(x)$. But finding exact minimizer $\Theta (r)$ can be quite challenging or even unfeasible, F(x) and ${\hat{h}}(x)$ are difficult to express explicitly. We can use the finite-valued of F(x). For any $\delta >0$, exists $\ell ^a(x, \delta )$ that satisfies

  $$\begin{aligned} q\left( \ell ^a(x, \delta )\right) +\frac{1}{2 \chi }\left\| \ell ^a(x, \delta )-x\right\| ^2 \le F(x)+\delta . \end{aligned}$$

  (21)

  Therefore, the estimates of F(x) and ${\hat{h}}(x)$ are expressed as

  $$\begin{aligned}{} & {} F^a(x, \delta )=q\left( \ell ^a(x, \delta )\right) +\frac{1}{2 \lambda }\left\| \ell ^a(x, \delta )-x\right\| ^2, \end{aligned}$$

  (22)
  $$\begin{aligned}{} & {} {\hat{h}}(x)^a(x, \delta )=\frac{x-\ell ^a(x, \delta )}{\chi }. \end{aligned}$$

  (23)

  For non-differentiable convex function, some useful algorithms are available to obtain $\ell ^a(x, \delta )$, as introduced in [10].

Proposition 3

Assuming $F^a(x, \delta )$ and ${\hat{h}}(x)^a(x, \delta )$ are obtained from (22)(23), where $\ell ^a(x, \delta )$ satisfies (21), we can deduce [11]

$$\begin{aligned}{} & {} \begin{aligned} F(x) \le F^a(x, \delta )&\le F(x)+\delta , \\ \left\| \ell ^a(x, \delta )-\ell (x)\right\|&\le \sqrt{2 \chi \delta }, \end{aligned}\nonumber \\{} & {} \left\| {\hat{h}}^a(x, \delta )-{\hat{h}}(x)\right\| \le \sqrt{2 \delta /\chi }. \end{aligned}$$

(24)

This means that $F^a(x, \delta )$ and ${\hat{h}}^a(x, \delta )$ can be considered to be close enough approximations of F(x) and ${\hat{h}}(x)$.

Combine above conditions and discussion in Sect. 2, iterative formula for $d_k$ is as follows:

$$\begin{aligned} \begin{aligned} d_k=-{\hat{h}}^a(x_{k},\delta _{k})+\left( \frac{{\hat{h}}^a(x_{k},\delta _{k})^Ty_{k-1}^m}{\varpi _k} -\frac{\Vert y_{k-1}^m\Vert ^2{\tilde{h}}_k}{\varpi _k^2}\right) d_{k-1}+ \frac{t_k{\tilde{h}}_k}{\varpi _k}y_{k-1}^m, \end{aligned} \end{aligned}$$

(25)

where $\varpi _k=c_1\Vert d_{k-1}\Vert \Vert y_{k-1}^m\Vert +c_2\Vert {\hat{h}}_k\Vert ^2$, ${\tilde{r}}_k={\hat{h}}^a(x_{k},\delta _{k})^Td_{k-1}$, with $0\le t_k\le \tau <1$. $d_k$ also exhibits sufficient descent and trust region properties, i.e.

$$\begin{aligned}{} & {} {\hat{h}}^a(x_{k},\delta _{k})^Td_k\le -{\tilde{z}}\Vert {\hat{h}}^a(x_{k},\delta _{k})\Vert ^2,\nonumber \\{} & {} \Vert d_k\Vert \le {\tilde{c}}\Vert {\hat{h}}^a(x_{k},\delta _{k})\Vert , \end{aligned}$$

(26)

where ${\tilde{z}}=1-\frac{\left( 1+\tau \right) ^2}{4}$, ${\tilde{c}}=1+\frac{1+\tau }{c_1}+\frac{1}{c_1^2}$. The steps and properties of the algorithm are as follows.

Algorithm 2

BPRP(Nonsmooth problem)

Theorem 4

$\{x_{k}\}$ and $\{{\hat{h}}_k\}$ are generated by Algorithm 2, we have $\lim _{k\rightarrow \infty }\Vert {\hat{h}}(x_{k})\Vert =0$, and any accumulation point of $x_k$ is an optimal solution of (1).

Proof

The first part. Prove that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert {\hat{h}}^\alpha (x_k,\delta _{k})\Vert =0. \end{aligned}$$

(29)

Assuming (29) is incorrect, thus exist subsequence $\lambda$, constant $\delta _*>0$, and $k_{*}\in {\mathbb {Z}}$ that satisfy

$$\begin{aligned} \Vert {\hat{h}}^a(x_{k},\delta _{k})\Vert \ge \delta _{*},\forall \lambda \ni k>k_{*}. \end{aligned}$$

(30)

For sequence $\{x_k\}$, $x^*$ is one of its limiting points, then have

$$\begin{aligned} \lim _{k\in K,\,k\rightarrow \infty }x_k=x^*. \end{aligned}$$

(31)

Consider two cases for discussion.

Case(I). $\limsup _{k\rightarrow \infty }\alpha _k>0$. Thus, there exists subsequence $\{\alpha _{k_j}\}$ such that $\lim _{j\rightarrow \infty }\alpha _{k_j} > \tau$, $\tau > 0$ is a constant, $k_j > k$. By (27),

$$\begin{aligned} F^{a}(x_{k},\delta _{k}) - F^{a}(x_{k}+\alpha _{k}d_{k},\delta _{k+1})\ge -\mu \alpha _k{\hat{h}}^{a}(x_{k},\delta _{k})^Td_k. \end{aligned}$$

Hence

$$\begin{aligned} -\mu \sum _{k=1}^\infty \alpha _k{\hat{h}}^{a}(x_{k},\delta _{k})^Td_k\le F^{a}(x_{0},\delta _{0}) - \lim _{k\rightarrow \infty }F^{a}(x_{k},\delta _{k}) < \infty . \end{aligned}$$

Then

$$\begin{aligned} \lim _{j\rightarrow \infty }-\alpha _{k_j}{\hat{h}}^{a}(x_{k_j},\delta _{k_j})^Td_{k_j} = 0. \end{aligned}$$

Combining (26), we can derive

$$\begin{aligned} \lim _{j\rightarrow \infty }(1-\frac{(1+\tau )^2}{4})\alpha _{k_j}\Vert \epsilon _*\Vert ^2 \le \lim _{j\rightarrow \infty }-\alpha _{k_j}{\hat{h}}^{a}(x_{k_j},\delta _{k_j})^Td_{k_j} = 0. \end{aligned}$$

It means that

$$\begin{aligned} \lim _{j\rightarrow \infty }\alpha _{k_j} = 0, \end{aligned}$$

which contradicts the assumption of this case.

Case (II). $\limsup _{k\rightarrow \infty }\alpha _k=0$. From (28) and (26),

$$\begin{aligned} {\hat{h}}^{a}(x_{k}+\alpha _{k}d_{k},\delta _{k+1})^Td_k-\nu {\hat{h}}^{a}(x_{k},\delta _{k})^Td_k\ge 0 \nonumber \\ \end{aligned}$$

We can conclude:

$$\begin{aligned} \lim _{j\rightarrow \infty }{\hat{h}}^{a}(x_{k_j}\!+\!\alpha _{k_j}d_{k_j},\delta _{{k_j}\!+\!1})^Td_{k_j} -\nu {\hat{h}}^{a}(x_{k_j},\!\delta _{k_j})^Td_{k_j}\!=\!(1\!-\!\nu ){\hat{h}}(x^*)^Td(x^*)\ge 0.\nonumber \\ \end{aligned}$$

(32)

Combine with (26) and (30), then

$$\begin{aligned} h(x^*)^Td(x^*)\le -{\tilde{z}}\Vert h(x^*)\Vert ^2\le -{\tilde{z}}\delta _{*}<0. \end{aligned}$$

(33)

This is contradictory to (32). So (29) holds, and (24) can see that

$$\begin{aligned} \Vert {\hat{h}}^\alpha (x_k,\delta _k)-{\hat{h}}(x_k)\Vert \le \sqrt{\frac{2\delta _k}{\chi }}. \end{aligned}$$

Combined with $\lim _{k\rightarrow \infty }\delta _k=0$, means

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert {\hat{h}}(x_{k})\Vert =0. \end{aligned}$$

(34)

The second part. Verify $x_k$ that converge to a solution of problem (1). By definition of ${\hat{h}}(x)$, we get ${\hat{h}}(x_k)=\frac{x_k-\ell (x_k)}{\chi }$. Then, by (34) and (31), $x^*=\ell (x^*)$ holds. Therefore, $x^*$ is an optimal solution of (1). $\square$

4 Numerical experiments

Four experiments are used to evaluate the BPRP algorithm’s performance. These results are from a series of experiments, including unconstrained optimization, large-scale nonsmooth problems, Muskingum model in engineering, and Color image restoration. Experimented on Windows 10 computer with 8 GB RAM and 2 GHz CPU.

4.1 Test of unconstrained optimization

Efficacy of BPRP, TTCGPM, TPRP, and HTTCGP algorithms in addressing unconstrained optimization problems becomes evident through the examination of 74 such problem instances. To facilitate a more intuitive comparison regarding the computational efficiency of these algorithms, the analytical tools proposed by Dolan and More [12] are utilized. These tools offer insights into the algorithms’ performance metrics.

This investigation focuses specifically on evaluating the computational performance across three dimensions (3000, 6000, and 9000) for the 74 problems. Throughout the experiment, parameters $c_1$ and $c_2$ are assigned values of 0.001 and 0.01, respectively. Additionally, the calculation of $t_k$ to the formula $t_k = \min \{\tau , \max \{ 0, 1 - \frac{{{y_{k-1}^m}^Ts_{k-1}}}{{\Vert y_{k-1}^m\Vert ^2}} \}\}$ and $\tau = 0.1$.

Fig. 1

Performance of algorithms in terms of number of iterations(NI)

Fig. 2

Performance of algorithms in terms of total of function and gradient evaluations(NFG)

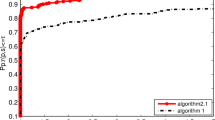
The outcomes are presented in Figs. 1, 2, and 3, where $\tau$ signifies the reciprocal of the algorithm’s performance ratio (NI, NFG, and CPU time) when tackling a specific problem, relative to the optimal performance among all algorithms. The parameter $P_{(p:r(p,s)\le \tau )}$ on the vertical axis succinctly denotes the proportion of problems successfully resolved out of the total problem set when the algorithm’s ratio falls below $\tau$.

By observing the data in Figs. 1, 2, and 3, a trend emerges, the efficacy of the BPRP algorithm in addressing a majority of the examined test problems. Figure 1 shows that the BPRP algorithm has the least number of iterations in $70\%$ problem solving, and can solve $90\%$ of the problems. It can be seen from Fig. 2 that BPRP algorithm calculates function value and gradient value least in $60\%$ of the problems, and adding function value information in the search direction does not cause too much computation burden. Figure 3 shows that the BPRP algorithm can solve $40\%$ of the problems first, and the computational efficiency is relatively high. The performance curve include NI, NFG and CPU time, demonstrates the superior performance of the BPRP algorithm over TTCGPM, TPRP, and HTTCGP algorithms. In summary, BPRP constitutes an efficient and robust approach for addressing unconstrained optimization problems.

Fig. 3

Performance of algorithms in terms of CPU time

Table 1 Problem descriptions for large-scaled testing problems

Table 2 NI, NF(number of function evaluations) and f(x)(eventual iteration) data of BPRP and HTTCGP algorithm

4.2 Nonsmooth problems

Given significant advantages of CG algorithm in handling large-scale problems, we study BPRP algorithm’s efficacy for large-scale non-smooth problems. A comparative analysis is conducted, juxtaposing the BPRP algorithm with the structurally HTTCGP algorithm in [13]. Compared to the BPRP algorithm, the primary distinction of the HTTCGP algorithm is the selection of $\omega _k$ and $y_k$. This is precisely the area where we have made modifications, and we can provide proof of their effectiveness.The test issues listed in Table 1 are taken from [14]. The algorithm stops when $F^{a}(x_{k-1},\delta _{k-1})-F^{a}(x_{k},\delta _{k})<10^{-7}$ is satisfied. The data are listed in Table 2. Parameters were chosen as $c_1=100$, $c_2=100$ and $t_k = \min \{\tau , \max \{ 0, 1 - \frac{{{y_{k-1}^m}^Ts_{k-1}}}{{\Vert y_{k-1}^m\Vert ^2}} \}\}$ where $\tau =0.1$.

Observing data in Table 2, BPRP algorithm has certain competitiveness in the number of iterations and the number of function evaluation, and the final function value is more satisfactory. Additionally, as dimensionality increases, the number of iterations do not exhibit a significant escalation. In summary, it can be conclusively affirmed that the BPRP algorithm proves to be effective in this context.

Fig. 4

The Muskingum model in 1960

Fig. 5

The Muskingum model in 1961

Fig. 6

The Muskingum model in 1964

Fig. 7

25% salt-and-pepper noise

Fig. 8

50% salt-and-pepper noise

Fig. 9

75% salt-and-pepper noise

4.3 The Muskingum model in engineering problems

In solving many practical problems in life, optimization plays a vital role, especially in the field of engineering applications can not be ignored. In order to achieve excellent performance in engineering problems, an excellent optimization algorithm is essential. In the field of hydrologic engineering, Muskingum model is widely used to deal with flood flow problems, and improving the accuracy of model parameters is of great significance for problem solving. Determine Muskingum model’s parameters by applying BPRP modified PRP algorithm, compare the performance of this approach with the HTTCGP, TPRP, and TTCGPM algorithms. The Muskingum model, as defined by Ouyang et al. [15], is as follows

$$\begin{aligned} \begin{aligned} \min f\left( x_{1}, x_{2}, x_{3}\right) =&\sum _{i=1}^{n-1}\left( \left( 1-\frac{\Delta t}{6}\right) x_{1}\left( x_{2} {\tilde{I}}_{i+1}+\left( 1-x_{2}\right) {\tilde{Q}}_{i+1}\right) ^{x_{3}}\right. \\&-\left( 1-\frac{\Delta t}{6}\right) x_{1}\left( x_{2} {\tilde{I}}_{i}+\left( 1-x_{2}\right) {\tilde{Q}}_{i}\right) ^{x_{3}}-\frac{\Delta t}{2}\left( {\tilde{I}}_{i}-{\tilde{Q}}_{i}\right) \\&\left. +\frac{\Delta t}{2}\left( 1-\frac{\Delta t}{3}\right) \left( {\tilde{I}}_{i+1}-{\tilde{Q}}_{i+1}\right) \right) ^{2}. \end{aligned} \end{aligned}$$

where the variable n as total time, $x_1$ as water storage time constant, $x_2$ is weighting coefficient, and $x_3$ is supplementary parameter. $\Delta t$ signifies the length of the calculation period, ${\tilde{I}}_i$ stands for observed inflow flow, ${\tilde{Q}}_i$ represents observed outflow flow. Setting initial point as $x = (0, 1, 1)^T$, calculation period $\Delta t$ is specified as 12 h. The observational data utilized in this experiment are from actual observations of flooding processes along the South Canal of Tianjin Haihe River Basin, spanning the years 1960, 1961, and 1964. Detailed datasets are sourced from [16].

Various algorithms were employed to compute the flows for the years 1960, 1961, and 1964. The calculated results were summarized and juxtaposed with the actual observed flows, as illustrated in Figs. 4, 5, and 6. The analysis indicates that the data obtained through the BPRP method exhibit no discernible deviation from the observed data, shows comparable performance to other methods. The BPRP method demonstrates no lagging behind in its effectiveness when compared to alternative approaches.

4.4 Image restoration problems

The classic application of optimization problem in real life is to restore the damaged image. In this section, the color image damaged by pulse noise is restored using the BPRP method. ColorCheckerTestImage($1542 \times 1024$), llama ($1314 \times 876$), car2 ($3504 \times 2336$) and car1 ($3504 \times 2336$) were selected as test images, and 25$\%$, 50$\%$ and 75$\%$ pulse noise were applied to them. Then the BPRP, TPRP, HTTCGP, and TTCGPM methods were applied to restore the noisy image. The outcomes of this restoration process are showed in Figs. 7, 8, and 9.

To facilitate a more intuitive comparison of the recovery capabilities of various algorithms, the relevant data of the restored images are detailed in Table 3. Peak signal-to-noise ratio (PSNR) is used to evaluate the mean square error between the original image and the restored image, and is one of the commonly used indicators to measure the quality of the restored image. Structural similarity index (SSIM) is a reference index to measure the similarity between images. We consider these two indexes comprehensively to evaluate the image recovery quality. The findings from Table 3 show that: (1) Bprp, TPRP, HTTCGP and TTCGPM methods can all complete image restoration, and the restoration effect is good, SSIM is greater than 0.8, PSNR is similar, and image quality of all four is similar. (2) Among four algorithms, BPRP algorithm has slightly lower CPU time and higher computational efficiency. (3) As the level of noise increases, the quality and efficiency of recovery reduced significantly for all four algorithms, indicating the impact of noise ratio on the overall recovery effectiveness.

Table 3 Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and CPU time data of Bprp, TPRP, HTTCGP and TTCGPM algorithms

5 Discussion

The proposed improved CG algorithm achieve sufficient descent and trust region properties, doesn’t rely on choice of step size. For unconstrained optimization, the algorithm’s global convergence is proven, removing the requirement for Lipschitz continuity conditions. The global convergence of the algorithm is proved for nonsmooth convex problems. The improved algorithm is competitive when compared to other algorithms with comparable structures, according to numerical experiments.