1 Introduction

In this research paper, we treat the following singularly perturbed boundary value problem with nonlocal boundary condition:

$$\begin{aligned}&Lu:=-\varepsilon u^{\prime \prime }(x)+a(x)u(x)=f(x),{ \ }0<x<l, \end{aligned}$$
(1.1)
$$\begin{aligned}&L_{0}u:=-\sqrt{\varepsilon }u^{\prime }\left( 0\right) +\gamma u\left( 0\right) =A, \end{aligned}$$
(1.2)
$$\begin{aligned}&u\left( l\right) -\delta u\left( d\right) =B,\text { }0<d<l, \end{aligned}$$
(1.3)

where \(0<\varepsilon \ll 1\) is a perturbation parameter, A, B, \(\gamma >0\), \(\delta \) and d are given constants, \(a(x)\ge \alpha >0\) and f(x) denote sufficiently smooth real functions of x, so that a unique solution \( u\left( x\right) \) exists for all small \(\varepsilon \) values. This solution has in general boundary layers at \(x=0\) and \(x=l\) as \(\varepsilon \) near 0.

Singularly perturbed differential equations are typically characterized by the presence of a small positive parameter \(\varepsilon \) multiplying some or all of the highest order terms in differential equations. Such types of problems arise frequently in mathematical models of different areas of physics, chemistry, biology, engineering science, economics and even sociology. The well-known examples are heat transfer problem with large Peclet numbers, semiconductor theory, chemical reactor theory, reaction–diffusion process, theory of plates, optimal control, aerodynamics, seismology, oceanography, meteorology, geophysics and so on. Solutions of such equations usually possesses thin boundary or interior layers where the solutions change very rapidly, while away from the layers the solutions behaves regularly and change slowly. More details about these problems can be found in [28, 34, 35, 39] and also the literature cited there.

Due to the presence of these boundary layers, the usual numerical treatment of singularly perturbed problems gives rise to computational difficulties. Standard numerical methods are not appropriate for practical applications when the perturbation parameter \(\varepsilon \) is sufficiently small. Therefore, it is necessary to develop suitable numerical methods that are uniformly convergent with respect to \(\varepsilon \). To solve these problems, there are generally two types approaches, such as fitted operator methods that are reflect the nature of the solution in the boundary layers and fitted mesh methods which use layer-adapted meshes. In resent years, many authors have worked for solving singularly perturbed problems with one or two boundary layers using uniformly convergent numerical methods [20, 22, 27, 30, 31, 33, 37].

Boundary value problems including nonlocal conditions which connect the values of the unknown solution at the boundary with values in the interior are known as nonlocal boundary value problems (so-called multi-point BVP or m-point BVP). The study of this kind of problems was initiated by Il’in and Miseev in [24, 25], motivated by the work of Bitsadze and Samarskii on nonlocal linear elliptic boundary value problems [6]. These problems have been used to represent mathematical models of a large number of phenomena, such as problems of semiconductors in electronics, the vibrations of a guy wire of a uniform cross-section, heat transfer problems, problems of hydromechanics, catalytic processes in chemistry and biology, the diffusion-drift model of semiconducting devices and some other physical phenomena [1, 23, 36]. The existence and uniqueness of the solutions of nonlocal boundary value problems have been studied by many authors [5, 26]. Some approaches for the numerical solution of singularly perturbed nonlocal boundary value problems have been proposed in [2, 7,8,9, 13,14,15, 17, 21, 29, 38]. Uniformly convergent numerical methods of order second and high for solving different singularly perturbed problems have been studied in [4, 10,11,12, 16, 32, 40]. In [18, 19], an accelerated finite difference method for solving singularly perturbed problems with integral boundary condition has been considered. The singularly perturbed nonlocal problem (1.1)–(1.3 ) is different from the singularly perturbed three-point problem considered in [10]. To the best of our knowledge, no work has been done for the second-order uniformly convergent numerical methods for singularly perturbed nonlocal boundary value problems of reaction–diffusion type.

Motivated by paper [2], we give a second-order uniformly convergent numerical method for solving singularly perturbed three-point boundary value problem. The structure of the article is organized as follows: In the next section we demonstrate the asymptotic behavior of the exact solution and its first derivative with respect to \(\varepsilon \). In Sect. 3, we describe the finite difference discretization on a uniform mesh. In Sect. 4, we show that the scheme is \(\varepsilon \)-uniform convergence in discrete maximum norm. In Sect. 5, we present one numerical experiment. Finally, this paper ends with conclusion.

Notation. Throughout the paper we will denote by C a generic positive constant which is independent of \(\varepsilon \) and the mesh parameter. For any continuous function \(g\left( x\right) \) defined on the corresponding interval, we use the maximum norm \(\left\| g\right\| _{\infty }=\underset{x\in \left[ 0,l\right] }{\max }\left| g\left( x\right) \right| \).

2 Continuous problem

Here we establish the asymptotic estimates of the problem (1.1)–(1.3) that are needed in later sections for the analysis appropriate numerical solutions.

Lemma 2.1

Let u(x) be the solution of the problem (1.1)–(1.3) and assume that \(a,f\in C^{1}[0,l]\). Moreover,

$$\begin{aligned} 1-\delta u_{1}\left( d\right) \ne 0, \end{aligned}$$
(2.1)

where \(u_{1}\left( x\right) \) is the solution of the two-point boundary value problem

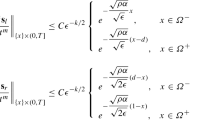
$$\begin{aligned} Lu_{1}= & {} 0,{ \ }0<x<l, \\ L_{0}u_{1}= & {} 0,{ \ }u_{1}\left( l\right) =1. \end{aligned}$$

Then, the estimates

$$\begin{aligned} \left\| u\right\| _{\infty }\le C \end{aligned}$$
(2.2)

and

$$\begin{aligned} \left| u^{\prime }(x)\right| \le C\left\{ 1+\frac{1}{\varepsilon } \left( e^{-\frac{\sqrt{\alpha }x}{\sqrt{\varepsilon }}}+e^{-\frac{\sqrt{ \alpha }(l-x)}{\sqrt{\varepsilon }}}\right) \right\} ,\text { }0\le x\le l, \end{aligned}$$
(2.3)

hold.

Proof

The proof of Lemma 2.1 is similar to that of [2]. \(\square \)

3 Generation of the difference scheme

In what follow, we denote by \(\omega _{h}\) an uniform mesh on \(\left[ 0,l \right] :\)

$$\begin{aligned} \omega _{h}=\{x_{i}=ih,\text { }i=1,2,\ldots ,N-1;h=l/N\},{\ }{\bar{\omega }} _{h}=\omega _{h}\cup \left\{ x_{0}=0, x_{N}=l\right\} . \end{aligned}$$

Assume that \(N_{1}=\frac{dN}{l}\) is an integer. To simplify the notation we set \(g_{i}=g\left( x_{i}\right) \) for any function \(g\left( x\right) \) while \(y_{i}\) denotes an approximation of \(u\left( x\right) \) at \(x_{i}\). For any mesh function \(g\left( x_{i}\right) \) defined on \({\bar{\omega }}_{h}\) we use

$$\begin{aligned} g_{\bar{x},i}=\frac{g_{i}-g_{i-1}}{h},{\ }g_{x,i}=\frac{g_{i+1}-g_{i}}{h },{\ }g_{\overset{0}{x},i}=\frac{g_{x,i}+g_{\bar{x},i}}{2},\text { }g_{ \bar{x}x,i}=\frac{g_{x,i}-g_{\bar{x},i}}{h}. \end{aligned}$$

For (1.1), our discretization will begin with identity

$$\begin{aligned}&\lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{Lu(x)\varphi _{i}(x)dx}=\lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{f}\left( x\right) {\varphi _{i}(x)dx},\nonumber \\&\quad 1\le i\le N-1 \end{aligned}$$
(3.1)

with the basis functions \(\left\{ \varphi _{i}(x)\right\} _{i=1}^{N-1}\) having the form

$$\begin{aligned} \varphi _{i}(x)= & {} \left\{ \begin{array}{c@{\quad }c} \varphi _{i}^{(1)}(x)\equiv \frac{\sinh (\gamma _{i}(x-x_{i-1}))}{\sinh (\gamma _{i}h)}, &{} x_{i-1}<x<x_{i}, \\ \varphi _{i}^{(2)}(x)\equiv \frac{\sinh (\gamma _{i}(x_{i+1}-x))}{\sinh (\gamma _{i}h)}, &{} x_{i}<x<x_{i+1}, \\ 0, &{} x\notin (x_{i-1},x_{i+1}), \end{array} \right. \\ \lambda _{i}= & {} \left[ h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi _{i}(x)dx}\right] ^{-1}=\frac{h\gamma _{i}}{2\tanh (\frac{\gamma _{i}h}{2})}, { \ }\gamma _{i}=\sqrt{\frac{a_{i}}{\varepsilon }}. \end{aligned}$$

We also note that the functions \(\varphi _{i}^{(1)}(x)\) and \(\varphi _{i}^{(2)}(x)\), respectively, are the solutions of the following problems

$$\begin{aligned} -\varepsilon \varphi ^{\prime \prime }+a_{i}\varphi= & {} 0,\text { } x_{i-1}<x<x_{i}, \\ \varphi \left( x_{i-1}\right)= & {} 0,\text { }\varphi \left( x_{i}\right) =1, \end{aligned}$$

and

$$\begin{aligned} -\varepsilon \varphi ^{\prime \prime }+a_{i}\varphi= & {} 0,\text { } x_{i}<x<x_{i+1}, \\ \varphi \left( x_{i}\right)= & {} 1,\text { }\varphi \left( x_{i+1}\right) =0. \end{aligned}$$

Integration by parts and a little rearrangement show that (3.1) may be rewritten as

$$\begin{aligned}&\varepsilon \lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi }_{i}^{\prime }{(x)u}^{\prime }\left( x\right) {dx+}a_{i}\lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi }_{i}{(x)u}\left( x\right) {dx}\nonumber \\&\quad {=f} _{i}+R_{i},\text { }1\le i\le N-1, \end{aligned}$$
(3.2)

where

$$\begin{aligned} R_{i}= & {} \lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}\left[ a_{i}-a\left( x\right) \right] {\varphi }_{i}{(x)u}\left( x\right) {dx} \nonumber \\&+\lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}\left[ f\left( x\right) -{f}_{i} \right] {\varphi }_{i}{(x)}dx. \end{aligned}$$
(3.3)

Applying the formulas (2.1) and (2.2) from [3] to subintervals \(\left( x_{i-1},\text { }x_{i}\right) \) and \(\left( x_{i},\text { }x_{i+1}\right) \) with the weight functions \(\varphi _{i}^{(1)}(x)\) and \(\varphi _{i}^{(2)}(x)\) , we obtain the following precise relation

$$\begin{aligned}&\varepsilon \lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi } _{i}^{\prime }{(x)u}^{\prime }\left( x\right) {dx+}a_{i}\lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi }_{i}{(x)u}\left( x\right) {dx} \nonumber \\&\quad =-\varepsilon \lambda _{i}h^{-1}\left\{ 1+a_{i}\varepsilon \int _{x_{i-1}}^{x_{i}}{\varphi }_{i}^{\left( 1\right) }{(x)(x-x}_{i}{)dx} \right\} (u_{x,i}-u_{\bar{x},i}) \nonumber \\&\qquad +\,a_{i}\lambda _{i}h^{-1}u_{i}\int _{x_{i-1}}^{x_{i}}{\varphi }_{i}^{\left( 1\right) }{(x)dx+}a_{i}\lambda _{i}h^{-1}u_{i}\int _{x_{i}}^{x_{i+1}}{\varphi }_{i}^{\left( 2\right) }{(x)dx} \nonumber \\&\quad = -\varepsilon \theta _{i}u_{\bar{x}x,i}+a_{i}u_{i}, \end{aligned}$$
(3.4)

with

$$\begin{aligned} \theta _{i}=\frac{a_{i}h^{2}}{4\varepsilon \sinh ^{2}(\frac{\sqrt{a_{i}}h}{2 \sqrt{\varepsilon }})}. \end{aligned}$$
(3.5)

Thus, from (3.2) and (3.4) we get

$$\begin{aligned} \ell u_{i}:=-\varepsilon \theta _{i}u_{\bar{x}x,i}+a_{i}u_{i}=f_{i}+R_{i}, { \ \ }1\le i\le N-1. \end{aligned}$$
(3.6)

In order to present an approximation for the boundary condition (1.2), we now begin by identity

$$\begin{aligned} \chi \int _{0}^{x_{1}}{Lu(x)\varphi _{0}(x)dx}=\chi \int _{0}^{x_{1}}{f}\left( x\right) {\varphi _{0}(x)dx,} \end{aligned}$$
(3.7)

where

$$\begin{aligned} \chi= & {} \left\{ \sqrt{\varepsilon }+a_{0}\gamma ^{-1}\int _{0}^{x_{1}}{ \varphi _{0}(x)dx}\right\} ^{-1} \\= & {} \left\{ \sqrt{\varepsilon }+a_{0}\gamma ^{-1}\tanh (\frac{\gamma _{0}h}{2} )\right\} ^{-1}, { \ }\gamma _{0}=\sqrt{\frac{a_{0}}{\varepsilon }}, \varphi _{0}(x)=\left\{ \begin{array}{c@{\quad }c} \frac{\sinh (\gamma _{0}(x_{1}-x))}{\sinh (\gamma _{0}h)}, &{} x_{0}<x<x_{1}, \\ 0, &{} x\notin (x_{0},x_{1}). \end{array} \right. \end{aligned}$$

Note that the basis function \(\varphi _{0}(x)\) is the solution of the problem

$$\begin{aligned} -\varepsilon \varphi ^{\prime \prime }+a_{0}\varphi= & {} 0,\text { } x_{0}<x<x_{1}, \\ \varphi \left( x_{0}\right)= & {} 1,\text { }\varphi \left( x_{1}\right) =0. \end{aligned}$$

Then, using the same method as that in (3.6) for (3.7) we obtain

$$\begin{aligned} \ell _{0}u:=-\sqrt{\varepsilon }\theta _{0}u_{x,0}+\gamma u_{0}-\sqrt{ \varepsilon }\chi A=\kappa _{1}f_{0}+\kappa _{2}f_{x,0}-r, \end{aligned}$$
(3.8)

where

$$\begin{aligned} \theta _{0}= & {} \chi \left[ 1-\varepsilon ^{-1}a_{0}\int _{0}^{x_{1}}x{\varphi _{0}(x)dx}\right] =\frac{\gamma _{0}h}{\sinh (\gamma _{0}h)+2\sqrt{a_{0}} \gamma ^{-1}\sinh ^{2}\left( \frac{\gamma _{0}h}{2}\right) }, \nonumber \\ \end{aligned}$$
(3.9)
$$\begin{aligned} \kappa _{1}= & {} \chi \int _{0}^{x_{1}}{\varphi _{0}(x)dx}=\frac{\tanh \left( \frac{\gamma _{0}h}{2}\right) }{\sqrt{a_{0}}+a_{0}\gamma ^{-1}\tanh \left( \frac{\gamma _{0}h}{2}\right) }, \end{aligned}$$
(3.10)
$$\begin{aligned} \kappa _{2}= & {} \chi \int _{0}^{x_{1}}x{\varphi _{0}(x)dx} \nonumber \\= & {} \left[ \sqrt{\varepsilon }+a_{0}\gamma ^{-1}\tanh \left( \frac{\gamma _{0}h}{2}\right) \right] ^{-1}\left[ \frac{\sqrt{\varepsilon }}{a_{0}}-\frac{h}{\sqrt{a_{0}} \sinh (\gamma _{0}h)}\right] , \end{aligned}$$
(3.11)
$$\begin{aligned} r= & {} \chi \int _{0}^{x_{1}}\left[ a_{0}-a(x)\right] u(x){\varphi _{0}(x)dx}\nonumber \\&{+}\chi \int _{0}^{x_{1}}f^{\prime \prime }(\xi )\left[ \int _{0}^{x_{1}}K_{1}(x,\xi ){\varphi _{0}(x)dx}\right] d\xi , \end{aligned}$$
(3.12)
$$\begin{aligned} K_{1}(x,\xi )= & {} T_{1}(x-\xi )-h^{-1}x(h-\xi ), \nonumber \\ T_{1}(\lambda )= & {} \left\{ \begin{array}{c} 1,{ \ \ }\lambda \ge 0, \\ 0,{ \ \ }\lambda <0. \end{array} \right. \end{aligned}$$
(3.13)

Based on (3.6) and (3.8), we propose the following difference scheme for approximating the problem (1.1)–(1.3)

$$\begin{aligned} \ell y_{i}:= & {} -\varepsilon \theta _{i}y_{\bar{x}x,i}+a_{i}y_{i}=f_{i},\text { } 1\le i\le N-1, \end{aligned}$$
(3.14)
$$\begin{aligned} \ell _{0}y:= & {} -\sqrt{\varepsilon }\theta _{0}y_{x,0}+\gamma y_{0}-\sqrt{ \varepsilon }A\chi =\kappa _{1}f_{0}+\kappa _{2}f_{x,0}, \end{aligned}$$
(3.15)
$$\begin{aligned} y_{N}-\delta y_{N_{1}}= & {} B, \end{aligned}$$
(3.16)

where \(\theta _{i}\), \(\theta _{0}\), \(\kappa _{1}\) and \(\kappa _{2}\) are given by (3.5), (3.9), (3.10) and (3.11), respectively.

We can write the difference scheme (3.14)–(3.16) of the form

$$\begin{aligned} A_{i}y_{i-1}-C_{i}y_{i}+B_{i}y_{i+1}=-F_{i},{ \ \ }i=1,2,\ldots ,N-1, \end{aligned}$$

where

$$\begin{aligned} A_{i}=\varepsilon \theta _{i},{ \ \ \ }B_{i}=\varepsilon \theta _{i}, { \ \ \ }C_{i}=2\varepsilon \theta _{i}+a_{i}h^{2}. \end{aligned}$$

Since \(A_{i}=\varepsilon \theta _{i}>0\), \(B_{i}=\varepsilon \theta _{i}>0\) and \(D_{i}=C_{i}-A_{i}-B_{i}=a_{i}h^{2}\ge 0\), the difference scheme (3.14)–(3.16) is monotone.

4 Convergence results

For the error \(z_{i}=y_{i}-u_{i}\), \(0\le i\le N\) from (3.6), (3.8) and (3.14)–(3.16) we have

$$\begin{aligned}&\ell z_{i}=-R_{i},\text { }1\le i\le N-1, \end{aligned}$$
(4.1)
$$\begin{aligned}&\ell _{0}z_{i}=r, \end{aligned}$$
(4.2)
$$\begin{aligned}&z_{N}-\delta z_{N_{1}}=0, \end{aligned}$$
(4.3)

where the truncation errors \({R}_{i}\) and r are defined by (3.3) and (3.12), respectively.

Lemma 4.1

Assume that \(a,f\in C^{2}\left[ 0,l\right] \) and \(a^{\prime }(0)=a^{\prime }(l)\). Then the truncation errors of the difference scheme (3.6) and (3.8) satisfy

$$\begin{aligned}&\left| R_{i}\right| \le Ch^{2}, { \ }1\le i\le N-1, \end{aligned}$$
(4.4)
$$\begin{aligned}&\left| r\right| \le Ch^{2}. \end{aligned}$$
(4.5)

Proof

We first prove the inequality (4.4). To this end we split \({R}_{i}\) as

$$\begin{aligned} {R}_{i}={R}_{i}^{(1)}+{R}_{i}^{(2)}, \end{aligned}$$
(4.6)

with

$$\begin{aligned} {R}_{i}^{(1)}= & {} \lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}\left[ a(x_{i})-a(x) \right] {\varphi }_{i}{(x){u}(x)dx}, \end{aligned}$$
(4.7)
$$\begin{aligned} {R}_{i}^{(2)}= & {} \lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}\left[ f(x)-f(x_{i}) \right] {\varphi }_{i}{(x)}dx. \end{aligned}$$
(4.8)

Here we first handle with \({R}_{i}^{(2)}\). Using Taylor expansion for the function f(x) in (4.8), we get

$$\begin{aligned}&\left| {R}_{i}^{(2)}\right| \le \lambda _{i}h^{-1}\left| f^{\prime }(x_{i})\right| \left| \int _{x_{i-1}}^{x_{i+1}}\left( x-x_{i}\right) {\varphi }_{i}{(x)}dx\right| \nonumber \\&\quad {+}\frac{\lambda _{i}h^{-1}}{2}\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}\left| f^{\prime \prime }(\xi _{i}(x))\right| {\varphi }_{i}{(x)}dx. \end{aligned}$$

After taking also into account that

$$\begin{aligned} \int _{x_{i-1}}^{x_{i+1}}(x-x_{i}){\varphi }_{i}{(x)}dx=0, \end{aligned}$$
(4.9)

the inequality (4.9) reduces to

$$\begin{aligned} \left| {R}_{i}^{(2)}\right| \le \frac{\lambda _{i}h^{-1}}{2} \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}\left| f^{\prime \prime }(\xi _{i}(x))\right| {\varphi }_{i}{(x)}dx. \end{aligned}$$
(4.10)

Therefore, from the inequality (4.10) we obtain

$$\begin{aligned} \left| {R}_{i}^{(2)}\right|\le & {} \frac{h^{2}}{2} \max _{[x_{i-1},x_{i+1}]}\left| f^{\prime \prime }(x)\right| \lambda _{i}h^{-1}\int _{x_{i-1}}^{x_{i+1}}{\varphi }_{i}{(x)}dx \nonumber \\= & {} \frac{h^{2}}{2}\max _{[x_{i-1},x_{i+1}]}\left| f^{\prime \prime }(x)\right| =O(h^{2}),{ \ }1\le i\le N-1. \end{aligned}$$
(4.11)

Next we handle with \({R}_{i}^{(1)}\) for \(1<i<N-1\). Using the relations

$$\begin{aligned} a(x)-a(x_{i})=(x-x_{i})a^{\prime }(x_{i})+\frac{(x-x_{i})^{2}}{2}a^{\prime \prime }(\xi _{i}),{ \ \ }\xi _{i}\in (x_{i},x) \end{aligned}$$

and

$$\begin{aligned} u(x)=u(x_{i})+(x-x_{i})u^{\prime }(\eta _{i}),{ \ \ }\eta _{i}\in (x_{i},x) \end{aligned}$$

in (4.7), we get

$$\begin{aligned} {R}_{i}^{(1)}= & {} -\lambda _{i}h^{-1}a^{\prime }(x_{i})u_{i}\int _{x_{i-1}}^{x_{i+1}}(x-x_{i}){\varphi }_{i}{(x)dx} \nonumber \\&-\lambda _{i}h^{-1}a^{\prime }(x_{i})\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{ \varphi }_{i}{(x)u^{\prime }(\eta _{i}}\left( x\right) {)dx} \nonumber \\&-\frac{\lambda _{i}h^{-1}}{2}\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}a^{ \prime \prime }(\xi _{i}(x)){\varphi }_{i}{(x)u(x)dx.} \end{aligned}$$
(4.12)

After taking into account (4.9) in (4.12) we have

$$\begin{aligned} \left| {R}_{i}^{(1)}\right|\le & {} \left| \lambda _{i}h^{-1}a^{\prime }(x_{i})\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{\varphi } _{i}{(x)u^{\prime }(\eta _{i}}\left( x\right) {)dx}\right| \nonumber \\&+\left| \frac{\lambda _{i}h^{-1}}{2} \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}a^{\prime \prime }(\xi _{i}(x)){\varphi }_{i}{(x)u(x)dx}\right| {.} \end{aligned}$$
(4.13)

For the second term in right-side of (4.13) we obtain

$$\begin{aligned}&\left| \frac{\lambda _{i}h^{-1}}{2} \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}a^{\prime \prime }(\xi _{i}(x)){\varphi }_{i}{(x)u(x)dx}\right| \nonumber \\&\quad \le \frac{C\lambda _{i}h^{-1}}{2}\max _{[x_{i-1},x_{i+1}]}\left| a^{\prime \prime }(x)\right| \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{ \varphi }_{i}{(x)}dx \nonumber \\&\quad \le \frac{1}{2}C\max _{[x_{i-1},x_{i+1}]}\left| a^{\prime \prime }(x)\right| h^{2}\le {\tilde{C}}h^{2}. \end{aligned}$$
(4.14)

For the first expression in right-side of (4.13), after using (2.3) we get

$$\begin{aligned}&\left| \lambda _{i}h^{-1}a^{\prime }\left( x_{i}\right) \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{\varphi }_{i}{(x)u}^{\prime }{(\eta } _{i}\left( {x}\right) {)dx}\right| \nonumber \\&\quad \le C\lambda _{i}h^{-1}\left| a^{\prime }\left( x_{i}\right) \right| \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{\varphi }_{i}{(x)}\left\{ 1+\frac{1}{\sqrt{\varepsilon }}(e^{-\frac{\sqrt{\alpha }x_{i-1}}{\sqrt{ \varepsilon }}}+e^{-\frac{\sqrt{\alpha }(l-x_{i+1)}}{\sqrt{\varepsilon }} })\right\} {dx} \nonumber \\&\quad \le C\lambda _{i}h^{-1}\left| a^{\prime }\left( x_{i}\right) \right| \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{\varphi }_{i}{(x)dx} \nonumber \\&\qquad +\frac{C\lambda _{i}h^{-1}\left| a^{\prime }\left( x_{i}\right) \right| }{\sqrt{\varepsilon }}\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{ \varphi }_{i}{(x)e^{-\frac{\sqrt{\alpha }x_{i-1}}{\sqrt{\varepsilon }}}dx} \nonumber \\&\qquad +\frac{C\lambda _{i}h^{-1}\left| a^{\prime }\left( x_{i}\right) \right| }{\sqrt{\varepsilon }}\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{ \varphi }_{i}{(x)e^{-\frac{\sqrt{\alpha }(l-x_{i+1)}}{\sqrt{\varepsilon }}}dx } \nonumber \\&\quad \le C\left\{ h^{2}+\frac{\left| a^{\prime }\left( x_{i}\right) \right| \lambda _{i}h^{-1}}{\sqrt{\varepsilon }} \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{\varphi }_{i}{(x)e^{-\frac{\sqrt{ \alpha }x_{i-1}}{\sqrt{\varepsilon }}}dx}\right. \nonumber \\&\qquad \left. +\frac{\left| a^{\prime }\left( x_{i}\right) \right| \lambda _{i}h^{-1}}{\sqrt{\varepsilon }}\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2} {\varphi }_{i}{(x)e^{-\frac{\sqrt{\alpha }(l-x_{i+1)}}{\sqrt{\varepsilon }} }dx}\right\} . \end{aligned}$$
(4.15)

Let us estimate the second and third expressions inside the brackets in (4.15) separately.

For the second term on right-side in (4.15) we have

$$\begin{aligned}&\left| \frac{Ca_{i}^{\prime }\lambda _{i}h^{-1}}{\sqrt{\varepsilon }} \int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{\varphi }_{i}{(x)}e^{-\frac{\sqrt{ \alpha }x_{i-1}}{\sqrt{\varepsilon }}}dx\right| \nonumber \\&\quad \le \frac{C\lambda _{i}h^{-1}}{\sqrt{\varepsilon }}\left| a^{\prime \prime }({\bar{\xi }}_{i})\right| x_{i}e^{-\frac{\sqrt{\alpha }x_{i-1}}{ \sqrt{\varepsilon }}}\int _{x_{i-1}}^{x_{i+1}}(x-x_{i})^{2}{\varphi }_{i}{(x)} dx \nonumber \\&\quad \le \frac{Ch^{2}}{\sqrt{\varepsilon }}x_{i}e^{-\frac{\sqrt{\alpha }x_{i-1} }{\sqrt{\varepsilon }}} \nonumber \\&\quad \le \frac{Ch^{2}}{\sqrt{\alpha }}\frac{x_{i}}{x_{i-1}}\frac{\sqrt{\alpha } x_{i-1}}{\sqrt{\varepsilon }}e^{-\frac{\sqrt{\alpha }x_{i-1}}{\sqrt{ \varepsilon }}} \nonumber \\&\quad \le \frac{Ch^{2}}{\sqrt{\alpha }}\frac{i}{i-1}e^{-\frac{\sqrt{\alpha } x_{i-1}}{2\sqrt{\varepsilon }}}\le Ch^{2}. \end{aligned}$$
(4.16)

We also have used the inequality \(te^{-t}\le e^{-\frac{t}{2}}\) for \(t>0\) and the condition \(a^{\prime }(0)=0\) in (4.16). The same estimate, under the condition \(a^{\prime }(l)=0\), is obtained for the third term on right-side in (4.15). Next, substituting the estimates (4.14) and (4.16) in (4.13) we obtain

$$\begin{aligned} \left| {R}_{i}^{(1)}\right| =O(h^{2}). \end{aligned}$$
(4.17)

Using the estimates (4.11) and (4.17) in (4.6), we get

$$\begin{aligned} \left| {R}_{i}\right| =O(h^{2}), \ \ \text {for }1<i<N-1. \end{aligned}$$

We now prove the inequality (4.4) for \(i=1\) (It is proved for case \( i=N-1\) in a similar way). From (4.6) we rewrite \({R}_{1}\) as

$$\begin{aligned} {R}_{1}= & {} {R}_{1}^{(1)}+{R}_{1}^{(2)} \nonumber \\= & {} \lambda _{1}h^{-1}\int _{x_{0}}^{x_{2}}\left[ a(x_{1})-a(x)\right] { \varphi }_{1}{(x){u}(x)dx} \nonumber \\&{+}\lambda _{1}h^{-1}\int _{x_{0}}^{x_{2}}\left[ f(x)-f(x_{1})\right] { \varphi }_{1}{(x)}dx. \end{aligned}$$
(4.18)

For the second term on right side in (4.18) as before, we can easily obtain

$$\begin{aligned} \left| {R}_{1}^{(2)}\right| \le \lambda _{1}h^{-1}\int _{x_{0}}^{x_{2}}\left| f(x)-f(x_{1}\right| {\varphi } _{1}{(x)}dx=O(h^{2}),\text { for }f\in C^{2}\left[ 0,l\right] . \end{aligned}$$
(4.19)

By using the relations

$$\begin{aligned} a(x)-a(x_{1})=(x-x_{1})a^{\prime }(x_{1})+\frac{(x-x_{1})^{2}}{2}a^{\prime \prime }(\xi _{1}(x)),{ \ \ }\xi _{1}\in (x_{1},x) \end{aligned}$$

and

$$\begin{aligned} u(x)=u(x_{0})+\int _{x_{0}}^{x}u^{\prime }(\xi )d\xi \end{aligned}$$

for the first term on right side in (4.18), we can easily get

$$\begin{aligned} {R}_{1}^{(1)}= & {} \lambda _{1}h^{-1}\int _{x_{0}}^{x_{2}}\left[ a(x_{1})-a(x) \right] {\varphi }_{1}{(x){u}(x)dx} \nonumber \\= & {} -a^{\prime }(x_{1})\lambda _{1}h^{-1}\int _{x_{0}}^{x_{2}}(x-x_{1})\left[ \int _{x_{0}}^{x}u^{\prime }(\xi )d\xi \right] {\varphi }_{1}{(x)dx} \nonumber \\&-\frac{\lambda _{1}h^{-1}}{2}\int _{x_{0}}^{x_{2}}(x-x_{1})^{2}a^{\prime \prime }(\xi _{1}(x)){\varphi }_{1}{(x)u(x)dx.} \end{aligned}$$
(4.20)

It is obvious that the second term on right side in (4.20)is

$$\begin{aligned} \frac{\lambda _{1}h^{-1}}{2}\left| \int _{x_{0}}^{x_{2}}(x-x_{1})^{2}a^{\prime \prime }(\xi _{1}(x)){\varphi } _{1}{(x)u(x)dx}\right| =O(h^{2}). \end{aligned}$$
(4.21)

Using the condition \(a^{\prime }(0)=0\) and the inequality (2.3) for the first term on right side in (4.20), we obtain

$$\begin{aligned}&\left| a^{\prime }(x_{1})\lambda _{1}h^{-1}\int _{x_{0}}^{x_{2}}(x-x_{1})\left[ \int _{x_{0}}^{x}u^{\prime }(\xi )d\xi \right] {\varphi }_{1}{(x)dx}\right| \nonumber \\&\quad \le \left| a^{\prime }(x_{1})\right| h\int _{x_{0}}^{x_{2}}\left| u^{\prime }(x)\right| dx \nonumber \\&\quad \le Cx_{1}h\left| a^{\prime \prime }(\eta _{1})\right| \int _{x_{0}}^{x_{2}}\left[ 1+\frac{1}{\sqrt{\varepsilon }}(e^{-\frac{\sqrt{ \alpha }x}{\sqrt{\varepsilon }}}+e^{-\frac{\sqrt{\alpha }(l-x_{)}}{\sqrt{ \varepsilon }}})\right] \nonumber \\&\quad \le Ch^{2}(h+\frac{1}{\sqrt{\varepsilon }}\int _{x_{0}}^{x_{2}}e^{-\frac{ \sqrt{\alpha }x}{\sqrt{\varepsilon }}}dx) \nonumber \\&\quad \le Ch^{2}\left[ h+\alpha ^{-\frac{1}{2}}(1-e^{-\frac{2\sqrt{\alpha }h}{ \sqrt{\varepsilon }}})\right] =O(h^{2}),\text { }\eta _{1}\in \left( 0,x_{1}\right) . \end{aligned}$$
(4.22)

From (4.21) and (4.22), we have

$$\begin{aligned} \left| {R}_{1}^{(1)}\right| =O(h^{2}). \end{aligned}$$
(4.23)

Hence, from (4.19) and (4.23) we have

$$\begin{aligned} \left| {R}_{1}\right| =O(h^{2}). \end{aligned}$$

This completes the proof of (4.4).

We now estimate the inequality (4.5). We can rewrite (3.12) in the form

$$\begin{aligned} r=r_{1}+r_{2}, \end{aligned}$$
(4.24)

where

$$\begin{aligned} r_{1}= & {} \chi \int _{0}^{x_{1}}\left[ a_{0}-a(x)\right] u(x){\varphi _{0}(x)dx,} \end{aligned}$$
(4.25)
$$\begin{aligned} r_{2}= & {} \chi \int _{0}^{x_{1}}f^{\prime \prime }(\xi )\left[ \int _{0}^{x_{1}}K_{1}(x,\xi ){\varphi _{0}(x)dx}\right] d\xi . \end{aligned}$$
(4.26)

We first estimate the relation (4.25). Using the condition \(a^{\prime }(0)=0\) and Taylor expansion

$$\begin{aligned} a(x)-a(0)=xa^{\prime }(0)+\frac{x^{2}}{2}a^{\prime \prime }(\eta ),{ \ \ }\eta \in \left( 0,x\right) , \end{aligned}$$

in (4.25), we obtain

$$\begin{aligned} \left| r_{1}\right|= & {} \left| \chi \int _{0}^{x_{1}}\frac{x^{2}}{2 }a^{\prime \prime }(\eta \left( x\right) )u(x){\varphi _{0}(x)dx}\right| \nonumber \\\le & {} \frac{Ch^{2}}{2}\max _{[0,x_{1}]}\left| a^{\prime \prime }(x)\right| \int _{0}^{x_{1}}{\varphi _{0}(x)dx} \nonumber \\= & {} \frac{Ch^{2}}{2\gamma _{0}}\max _{[0,x_{1}]}\left| a^{\prime \prime }(x)\right| \tanh \left( \frac{\gamma _{0}h}{2}\right) \nonumber \\= & {} \frac{Ch^{2}}{2\sqrt{a_{0}}}\max _{[0,x_{1}]}\left| a^{\prime \prime }(x)\right| \tanh \left( \frac{\gamma _{0}h}{2}\right) \nonumber \\\le & {} Ch^{2}. \end{aligned}$$
(4.27)

We then estimate the relation (4.26). From (4.26) we obtain

$$\begin{aligned} \left| r_{2}\right|= & {} \left| \chi \int _{0}^{x_{1}}f^{\prime \prime }(\xi )\left[ \int _{0}^{x_{1}}K_{1}(x,\xi ){\varphi _{0}(x)dx}\right] d\xi \right| \nonumber \\\le & {} 2\chi h^{2}\max _{[0,x_{1}]}\left| f^{\prime \prime }(x)\right| \int _{0}^{x_{1}}{\varphi _{0}(x)dx} \nonumber \\= & {} \frac{2\chi h^{2}}{\gamma _{0}}\max _{[0,x_{1}]}\left| f^{\prime \prime }(x)\right| \tanh \left( \frac{\gamma _{0}h}{2}\right) \nonumber \\= & {} \frac{2\chi h^{2}}{\sqrt{a_{0}}}\max _{[0,x_{1}]}\left| f^{\prime \prime }(x)\right| \tanh \left( \frac{\gamma _{0}h}{2}\right) \nonumber \\\le & {} Ch^{2}. \end{aligned}$$
(4.28)

Taking into account (4.27) and (4.28) in (4.24), we arrive at (4.5). Thus, the proof of lemma is completed. \(\square \)

Lemma 4.2

Let \(z_{i}\), \(0\le i\le N\) be the solution of the problem (4.1)–(4.3) and moreover

$$\begin{aligned} 1-\delta z_{N_{1}}^{\left( 1\right) }\ne 0. \end{aligned}$$

Then the following estimate holds

$$\begin{aligned} \left\| z\right\| _{\infty ,{\bar{\omega }}_{h}}\le C\left( \gamma ^{-1}\left| r\right| +\alpha ^{-1}\left\| R\right\| _{\infty ,\omega _{h}}\right) . \end{aligned}$$
(4.29)

Proof

The solution of difference problem (4.1)–(4.3) can be expressed as

$$\begin{aligned} z_{i}(x)=z_{i}^{\left( 0\right) }(x)+\lambda z_{i}^{\left( 1\right) }(x), \end{aligned}$$
(4.30)
Table 1 Point-wise error and rate of convergence for different values of \(\varepsilon \) and N
Full size table
Fig. 1
figure 1

Approximate solutions for different values \(\varepsilon \)

Full size image
Fig. 2
figure 2

Exact solution and approximation solution for different values N and \(\varepsilon =2^{-2}\)

Full size image
Fig. 3
figure 3

The rates of convergence for different values N and \(\varepsilon =2^{-2}\)

Full size image

where the functions \(z_{i}^{\left( 0\right) }(x)\) and \(z_{i}^{\left( 1\right) }\) \(\left( 0\le i\le N\right) \) are the solutions of the following problems, respectively.

$$\begin{aligned} -\varepsilon \theta _{i}z_{\bar{x}x,i}+a_{i}z_{i}= & {} -R_{i},\text { }1\le i\le N-1, \end{aligned}$$
(4.31)
$$\begin{aligned} -\sqrt{\varepsilon }\theta _{0}z_{x,0}+\gamma z_{0}= & {} r, \end{aligned}$$
(4.32)
$$\begin{aligned} z_{N}= & {} 0, \end{aligned}$$
(4.33)
$$\begin{aligned} -\varepsilon \theta _{i}z_{\bar{x}x,i}+a_{i}z_{i}= & {} 0,{ \ }1\le i\le N-1, \end{aligned}$$
(4.34)
$$\begin{aligned} -\sqrt{\varepsilon }\theta _{0}z_{x,0}+\gamma z_{0}= & {} 0, \end{aligned}$$
(4.35)
$$\begin{aligned} z_{N}= & {} 1, \end{aligned}$$
(4.36)

and

$$\begin{aligned} \lambda =\frac{\delta z_{N_{1}}^{\left( 0\right) }}{1-\delta z_{N_{1}}^{\left( 1\right) }},{ \ }(1-\delta z_{N_{1}}^{\left( 1\right) }\ne 0). \end{aligned}$$

From (4.30) we have

$$\begin{aligned} \left\| z\right\| _{\infty ,{\bar{\omega }}_{h}}\le \left\| z^{\left( 0\right) }\right\| _{\infty ,{\bar{\omega }}_{h}}+\left| \lambda \right| \left\| z^{\left( 1\right) }\right\| _{\infty ,{\bar{\omega }} _{h}}. \end{aligned}$$
(4.37)

For difference problem (4.31)–(4.33) according to the maximum principle, we get

$$\begin{aligned} \left\| z^{\left( 0\right) }\right\| _{\infty ,{\bar{\omega }}_{h}}\le \gamma ^{-1}\left| r\right| +\alpha ^{-1}\left\| R\right\| _{\infty ,\omega _{h}}. \end{aligned}$$
(4.38)

For the estimate of the problem (4.34)–(4.36) we have

$$\begin{aligned} \left\| z^{\left( 1\right) }\right\| _{\infty ,{\bar{\omega }}_{h}}\le 1. \end{aligned}$$
(4.39)

Hence, substituting the estimates (4.38), (4.39) and \(\left| \lambda \right| \le Ch^{2}\) into (4.37) we arrive at (4.29). \(\square \)

We now can statement the convergence result of this paper.

Theorem 4.1

Let u be the solution of (1.1)–(1.3) and y the solution of (4.3)–(4.5). Then, under the conditions of Lemmas 4.1 and 4.2, the following \(\varepsilon \)-uniform error estimate holds

$$\begin{aligned} \left\| y-u\right\| _{\infty ,{\bar{\omega }}_{h}}\le Ch^{2}. \end{aligned}$$

Proof

The proof of Theorem 4.1 follows from combining Lemmas 4.1 and 4.2. \(\square \)

5 Numerical results

In this section, we present one numerical example to demonstrate the applicability and the efficiency of the proposed method.

Example 5.1

Consider the following singularly perturbed nonlocal boundary value problem.

$$\begin{aligned}&\varepsilon u^{\prime \prime }(x)-u(x)=\cos ^{2}(\pi x)+2\varepsilon \pi ^{2}\cos (2\pi x),\text { }0<x<1,\\&\quad -\sqrt{\varepsilon }u^{\prime }(0)+u(0)=0, { \ \ }u\left( 1\right) - \frac{1}{2}u(\frac{1}{2})=-1. \end{aligned}$$

The exact solution of the problem is

$$\begin{aligned} u(x)=\frac{e^{\frac{2x-1}{2\sqrt{\varepsilon }}}-e^{\frac{x-1}{\sqrt{ \varepsilon }}}}{4e^{\frac{1}{\sqrt{\varepsilon }}}-2e^{\frac{1}{2\sqrt{ \varepsilon }}}}+\frac{1}{2}e^{-\frac{x}{\sqrt{\varepsilon }}}-\cos ^{2}(\pi x). \end{aligned}$$

We define the maximum point-wise error and the computed \(\varepsilon \)-uniform maximum point-wise error as follows

$$\begin{aligned} e_{\varepsilon }^{N}=\left\| {y-u}\right\| _{\infty ,{\bar{\omega }} _{h}},\ e^{N}=\max _{\varepsilon }e_{\varepsilon }^{N}. \end{aligned}$$

where u is the exact solution and y is the numerical solution obtained for various values of N and \(\varepsilon \). We also define the rate of convergence and compute the \(\varepsilon \)-uniform rate of convergence by the form

$$\begin{aligned} p_{\varepsilon }^{N}=\frac{\ln \left( {e_{\varepsilon }^{N}/e_{\varepsilon }^{2N}}\right) }{\ln 2}, { \ \ \ \ }p^{N}=\frac{\ln \left( {e^{N}/e^{2N}} \right) }{\ln 2}. \end{aligned}$$

We give the maximum point-wise errors and the rates of convergence obtained for the values \(\varepsilon =2^{-i}\), \(i=2,4,\ldots ,20\) and \( N=64,128,256,512,1024\) by our method in Table 1. We observe that \( \varepsilon \)-uniform experimental rate of convergence is close to 2 for sufficiently large N. The numerical results support the theoretical rate estimation given by Theorem 4.1. Furthermore, graphics for Example 5.1 are shown in Figs. 1, 2, 3.

6 Conclusion

In this article, we have presented a second-order \(\varepsilon \)-uniformly convergent numerical method for solving singularly perturbed nonlocal boundary value problems. We have constructed the method on the basis of the method of integral identities with the use of interpolating quadrature rules with the weight and remainder terms in integral form. This approach has the advantage that difference schemes can also be effective in the case where the original problem considered under certain singularities. For the numerical solution of this problem, we have used finite difference schemes on a uniform mesh. We have obtained second-order convergent, in the discrete maximum norm, independently of the singular perturbation parameter \( \varepsilon \). The proposed method is tested on one example and numerical results are shown for various values of \(\varepsilon \) and N in Table 1. We can observe that the numerical results seem to be \(\varepsilon \)-uniform and the rates of convergence are close to 2 for sufficiently large N, independently of the singular perturbation parameter \(\varepsilon \). Hence, it is proved that the method has accuracy of second order.