1 Introduction

It is well known that fractional differential equations are gaining more and more attention in different research areas, such as physics, engineering and control (see [1–11]). In recent years, there are many important quality analysis and control results for various fractional differential equations (see for example, [12–18]).

On the other hand, iterative learning control is a useful control method in terms of basic theory and experimental applications by adjusting the past control experience again and again to improve the current tracking performance. Recently, there are many contribution on P-type and D-type iterative learning control for integer order ordinary differential equations [19–29], linearization theorem of fenner and pinto [30] and varieties of local integrability [31] and few work on iterative learning control of fractional order differential equations [32–36]. In particular, the authors obtain the robust convergence of the tracking errors with respect to initial positioning errors under P-type iterative learning control scheme for fractional order nonlinear differential equations [34] and noninstantaneous impulsive fractional order differential equations [36]. Meanwhile, the authors discuss D-type iterative learning control to fractional order linear time-delay equations [35]. We remark that the above convergence results are valid for fractional order \(\alpha \in (0,1)\).

In this paper, we consider the following linear differential equations of fractional order:

$$\begin{aligned} \left\{ \begin{array}{l} ^c_0 D^\alpha _t x_k(t)=ax_k(t)+bu_k(t),~t\in [0,T],~\alpha \in (1,2),\\ \dot{x}_k(0)=0,\\ y_k(t)=cx_k(t)+d\int _0^t u_k(s)ds, \end{array} \right. \end{aligned}$$
(1)

where k denotes the iterative times, T denotes pre-fixed iteration domain length, and the symbol \(^c_0 D^\alpha _t x_k(t)\) is the Caputo derivative with lower limit zero of order \(\alpha \) to the function \(x_k\) at the point t (see Definition 2.1, [37, p. 91]), \(x_k, y_k, u_k\in \mathbb {R}\) and \(a\in \mathbb {R}^+\), \(b,c,d\in \mathbb {R}\).

Consider the boot time of the machine, \(x_k(t)\) may not change immediately on a very small finite time interval \([0,\delta ]\). Letting \(\delta \rightarrow 0\), we obtain the condition \(\dot{x}_k(0)=0\) in (1). Then the solution of (1) can be formulated by (see [37, p. 140–141, (3.1.32)–(3.1.34)]):

$$\begin{aligned} x_k(t)= & {} {\mathbb {E}}_\alpha (at^\alpha )x_k(0)+ t{\mathbb {E}}_{\alpha ,2}(at^\alpha )\dot{x}_k(0) +\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )bu_k(s)ds\nonumber \\= & {} {\mathbb {E}}_\alpha (at^\alpha )x_k(0)+\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )bu_k(s)ds, \end{aligned}$$
(2)

where the Mittag–Leffler functions \({\mathbb {E}}_{\alpha }(z)\) and \({\mathbb {E}}_{\alpha ,\beta }(z)\) are described as:

$$\begin{aligned} {\mathbb {E}}_{\alpha }(z)=\sum _{i=0}^{\infty }\frac{z^i}{\Gamma (i\alpha +1)},~~ {\mathbb {E}}_{\alpha ,\beta }(z)=\sum _{i=0}^{\infty }\frac{z^i}{\Gamma (i\alpha +\beta )},~~ \end{aligned}$$

\(z\in \mathbb {R}\) and \(\alpha ,~\beta \) are positive real numbers.

Let

$$\begin{aligned} y_d(t)=cx_d(t)+d\int _0^t u_d(s)ds,~t\in [0,T], \end{aligned}$$

be a desired trajectory where \(x_d(t)\), \(u_d(t)\) are the desired state trajectory and the desired control, respectively. As usual, we denote \(e_k(t):=y_d(t)-y_k(t)\) be a tracking error and \(\delta u_k(t):=u_d(t)-u_k(t)\).

The main objective of this paper is to design open-loop and closed-loop iterative learning schemes with zero initial error and random but bounded initial error in the sense of \(\lambda \)-norm. We adopt the PD-type iterative learning law.

The paper is organized as follows. In Sect. 2, we present integral and derivative properties of Mittag–Leffler functions. In Sects. 3 and 4, we give main results, open-loop and closed-loop iterative learning schemes with zero initial error and random but bounded initial error in the sense of \(\lambda \)-norm respectively. Examples are presented in Sect. 5 to demonstrate the validity of the design methods.

2 Preliminaries

Let \(C\left( [0,T],\mathbb {R}\right) \) be the space of \(\mathbb {R}\)-valued continuous functions on [0, T]. We consider three possible norms: \(\lambda \)-norm: \( \Vert x\Vert _\lambda =\max _{t\in [0,T]} e^{-\lambda t}|x(t)|\) and C-norm: \( \Vert x\Vert _C=\max _{t\in [0,T]}|x(t)|\) and \(L^2\)-norm: \( \Vert x\Vert _{L^2}=\left( \int _0^T |x(s)|^2 ds\right) ^{\frac{1}{2}}. \) Obviously, \(\Vert x\Vert _\lambda \le \Vert x\Vert _C\) for any \(x\in C\left( [0,T],\mathbb {R}\right) \).

Definition 2.1

(see [37, p. 91]) The Caputo derivative of order \(\gamma \) for a function \(f:[a,\infty )\rightarrow \mathbb {R}\) can be written as

$$\begin{aligned} ^c_a D^q _tf(t)=~^{RL}_a D^q _t\bigg [ f(t)-\sum ^{n-1}_{k=0}\frac{t^k}{k!} f^{(k)}(a)\bigg ],~t>a, ~q\in (n-1,n), \end{aligned}$$

where

$$\begin{aligned} ^{RL}_a D^q _t f(t)=\frac{1}{\Gamma (n-q)}\frac{d^n}{dt^n}\int _{a}^{t} \frac{f(\tau )}{(t-\tau )^{q+1-n}}d\tau . \end{aligned}$$

The following properties of Mittag–Leffler functions will be used in the sequel.

Lemma 2.2

(see [38, (4.3.1)] ) Let \(\alpha >0\), \(\beta \in \mathbb {R}\),

$$\begin{aligned} \frac{d}{dz}[z^{\beta -1}{\mathbb {E}}_{\alpha ,\beta }(z^\alpha )] =z^{\beta -2}{\mathbb {E}}_{\alpha ,\beta -1}(z^\alpha ). \end{aligned}$$

Lemma 2.3

(see [39, (7.1)] or [38, (4.9.3)]) Let \(\lambda , \alpha , \beta \in \mathbb {R}^+\), and \(|a\lambda ^{-\alpha }|<1\),

$$\begin{aligned} \int _0^\infty e^{-\lambda x}x^{\beta -1}{\mathbb {E}}_{\alpha ,\beta }(\pm ax^\alpha )dx=\frac{\lambda ^{\alpha -\beta }}{\lambda ^\alpha \mp a}. \end{aligned}$$

Lemma 2.4

(see [40, p. 1861]) Let \(z\in \mathbb {R}\), \(\alpha >0\),

$$\begin{aligned} \frac{d}{dz}{\mathbb {E}}_{\alpha }(z)=\frac{1}{\alpha }{\mathbb {E}}_{\alpha ,\alpha }(z). \end{aligned}$$

Lemma 2.5

(see [41]) Let \(\bar{\alpha } \in (0,2)\) and \(\bar{\beta }\in {\mathbb {R}}\) be arbitrary. Then for \(\bar{p}=[\frac{\bar{\beta }}{\bar{\alpha }}]\), the following asymptotic expansion hold:

$$\begin{aligned} E_{\bar{\alpha },\bar{\beta }}(z)=\frac{1}{\bar{\alpha }}z^{\frac{1 -\bar{\beta }}{\bar{\alpha }}} \exp (z^{\frac{1}{\bar{\alpha }}})-\sum _{k=1}^{\bar{p}} \frac{z^{-k}}{\Gamma (\bar{\beta }-\bar{\alpha } k)}+O(z^{-1-\bar{p}})\quad \text {as }z\rightarrow \infty . \end{aligned}$$

By inserting \(\bar{\alpha }=\alpha \), \(\bar{\beta }=\alpha \) and \(z=at^{\alpha }\), we give asymptotic expansions for Mittag–Leffler functions \(E_{\alpha ,\alpha }\).

Lemma 2.6

For any \(a>0\), \(\alpha \in (0,2)\), it holds

$$\begin{aligned} t^{\alpha -1}E_{\alpha ,\alpha }(a t^{\alpha })\sim \frac{\exp (a^{\frac{1}{\alpha }}t)}{\alpha a^{\frac{\alpha -1}{\alpha }}} \quad \text {as } t\rightarrow \infty . \end{aligned}$$

It is clearly that \(t^{\alpha -1}E_{\alpha ,\alpha }(a t^{\alpha })\) is an increasing function for any \(t\in [0,T]\) since \(a>0\).

To end this section, we recall the following convergence theorem.

Lemma 2.7

(see [42, Lemma 3]) Let \(\{a_k\}\), \(k\in \mathbb {N}\) be a real sequence defined as

$$\begin{aligned} a_k\le p a_{k-1}+d_k, \end{aligned}$$

where \(d_k\) is a specified real sequence. If \(p<1\), then

$$\begin{aligned} \limsup _{k\rightarrow \infty }d_k\le d \end{aligned}$$

implies that

$$\begin{aligned} \limsup _{k\rightarrow \infty }a_k\le \frac{d}{1-p}. \end{aligned}$$

3 Convergence analysis of open-loop law

In this section, we investigate (1) with the following PD-type learning control law:

$$\begin{aligned} u_{k+1}(t)=u_k(t)+k_pe_k(t)+k_d\dot{e}_k(t). \end{aligned}$$
(3)

Now we are ready to give the first results for zero initial error.

Theorem 3.1

Assume that the ILC scheme (3) is applied to (1) and the initial condition at each iteration remains the desired, i.e., \(x_k(0)=x_d(0)\), \(k=0,1,2,\ldots .\) If \(|1-k_d d|<1\), then \(\lim _{k\rightarrow \infty }y_k(t)=y_d(t)\) uniformly on \(t\in [0,T]\).

Proof

It follows from (2), we have

$$\begin{aligned} e_k(t)= & {} y_d(t)-y_k(t) \nonumber \\= & {} c\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )b\delta u_k(s)ds +d\int _0^t \delta u_k(s)ds. \end{aligned}$$
(4)

Taking the derivative on both side of (4), we have

$$\begin{aligned} \dot{e}_k(t)= & {} c\frac{d}{dt}\left[ \int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )b\delta u_k(s)ds\right] +d\delta u_k(t)\nonumber \\= & {} c\int _0^t\frac{d}{dt}\left[ (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha } (a(t-s)^\alpha )\right] b\delta u_k(s)ds+d\delta u_k(t)\nonumber \\= & {} c\int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ) b\delta u_k(s)ds+d\delta u_k(t), \end{aligned}$$
(5)

where we set \(z=a^\frac{1}{\alpha }(t-s)\) and use Lemma 2.2 to derive

$$\begin{aligned} \frac{d}{dt}\left[ (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )\right]= & {} \frac{d}{dt}\left[ a^\frac{1-\alpha }{\alpha }z^{\alpha -1}{\mathbb {E}}_{\alpha , \alpha }(z^\alpha )\right] \\= & {} a^\frac{2-\alpha }{\alpha }\frac{d}{dz}\left[ z^{\alpha -1}{\mathbb {E}}_{\alpha , \alpha }(z^\alpha )\right] \\= & {} a^\frac{2-\alpha }{\alpha }\left[ a^\frac{\alpha -2}{\alpha } (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha )\right] \\= & {} (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ). \end{aligned}$$

By using (3), (4) and (5), we have

$$\begin{aligned} \delta u_{k+1}(t)= & {} \delta u_k(t)-k_pe_k(t)-k_d\dot{e}_k(t)\nonumber \\= & {} (1-k_d d)\delta u_{k}(t)-k_pc\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )b\delta u_k(s)ds \nonumber \\&-\,\,k_d c\int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ) b\delta u_k(s)ds+k_p d\int _0^t \delta u_k(s)ds.\nonumber \\ \end{aligned}$$
(6)

Taking the absolute value on both side of (6) and multiplying both side by \(e^{-\lambda t}\), we obtain

$$\begin{aligned} |\delta u_{k+1}(t)|e^{-\lambda t}\le & {} |1-k_d d||\delta u_{k}(t)|e^{-\lambda t}+|k_p d|e^{-\lambda t}\int _0^t |\delta u_k(s)|ds \nonumber \\&+\,|k_pc|e^{-\lambda t}\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )|b\delta u_k(s)|ds \nonumber \\&+\,|k_d c|e^{-\lambda t}\int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ) | b\delta u_k(s)|ds. \end{aligned}$$
(7)

By using Lemma 2.3, we have

$$\begin{aligned}&\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )|\delta u_k(s)|ds\nonumber \\&\quad = \int _0^t e^{-\lambda (t-s)}(t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha } (a(t-s)^\alpha )e^{\lambda (t-s)}|\delta u_k(s)|ds\nonumber \\&\quad \le e^{\lambda t}\Vert \delta u_k\Vert _\lambda \int _0^t e^{-\lambda (t-s)}(t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )ds\nonumber \\&\quad \le e^{\lambda t}\Vert \delta u_k\Vert _\lambda \int _0^\infty e^{-\lambda (t-s)}(t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )ds\nonumber \\&\quad =\frac{ e^{\lambda t}}{\lambda ^\alpha -a}\Vert \delta u_k\Vert _\lambda . \end{aligned}$$
(8)

Repeating the similar computation in (8) and using Lemma 2.3 again, one has

$$\begin{aligned} \int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha )|\delta u_k(s)|ds \le \frac{ \lambda e^{\lambda t}}{\lambda ^\alpha -a}\Vert \delta u_k\Vert _\lambda . \end{aligned}$$
(9)

Substituting (8) and (9) into (7), and taking \(\lambda \)-norm, we obtian

$$\begin{aligned} \Vert \delta u_{k+1}\Vert _\lambda \le \left( |1-k_d d|+\frac{|k_p cb|}{\lambda ^\alpha -a}+\frac{|k_d cb|\lambda }{\lambda ^\alpha -a}+\frac{|k_p d|}{\lambda }\right) \Vert \delta u_{k}\Vert _\lambda , \end{aligned}$$
(10)

where

$$\begin{aligned} e^{-\lambda t}\int _0^t |\delta u_k(s)|ds= & {} \int _0^t |\delta u_k(s)|e^{-\lambda s}e^{-\lambda (t-s)}ds\nonumber \\\le & {} \Vert \delta u_k\Vert _\lambda \int _0^t e^{-\lambda (t-s)}ds\le \frac{1}{\lambda }\Vert \delta u_k\Vert _\lambda . \end{aligned}$$
(11)

Note that the condition \(0\le |1-k_d d|<1\), it is possible to make

$$\begin{aligned} \rho = |1-k_d d|+\frac{|k_p cb|}{\lambda ^\alpha -a}+\frac{|k_d cb|\lambda }{\lambda ^\alpha -a}+\frac{|k_p d|}{\lambda }<1, \end{aligned}$$

for some \(\lambda \) large enough. Thus, (10) derives that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert \delta u_{k}\Vert _\lambda =0. \end{aligned}$$

By using (4), (8) and (11), we have

$$\begin{aligned} \Vert e_k\Vert _\lambda \le \left( \frac{|cb|}{\lambda ^\alpha -a}+\frac{|d|}{\lambda } \right) \Vert \delta u_{k}\Vert _\lambda . \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{k\rightarrow \infty }y_{k}(t)=y_d(t), \end{aligned}$$

uniformly on \(t\in [0,T]\). \(\square \)

In general, the initial condition may be varying with the change of iterative times but in a small range. That is, the initial condition is always in the neighborhood of \(x_d(0)\) at each iteration such that

$$\begin{aligned} |\delta x_k(0)|:=|x_d(0)-x_k(0)|\le \bar{\Delta }, \end{aligned}$$
(12)

The expression (12) implies that the initial output error is also bounded.

Next, we are ready to give the Robustness results for random but bounded initial error.

Theorem 3.2

Assume that the ILC scheme (3) is applied to (1) and the initial condition at each iteration conform to (12). If \(|1-k_dd|<1\), then the error between \(y_d(t)\) and \(y_k(t)\) is bounded and its bound depends on \(\bar{\Delta }\), \(|k_p|\) and \(|k_d|\).

Proof

Similar to the proof of Theorem 3.1, we obtain

$$\begin{aligned} e_k(t)= & {} y_d(t)-y_k(t) \nonumber \\= & {} c{\mathbb {E}}_{\alpha }(at^\alpha )\delta x_k(0)+c\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )b\delta u_k(s)ds\nonumber \\&+\,d\int _0^t \delta u_k(s)ds. \end{aligned}$$
(13)

Taking the derivative on both side of the above equality, we obtain

$$\begin{aligned} \dot{e}_k(t)= & {} c\delta x_k(0)\frac{d}{dt}{\mathbb {E}}_{\alpha }(at^\alpha )+ c\frac{d}{dt}\left[ \int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha } (a(t-s)^\alpha )b\delta u_k(s)ds\right] \\&+\,d\delta u_k(t)\\= & {} cat^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(at^\alpha )\delta x_k(0)+c\int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ) b\delta u_k(s)ds\\&+\,d\delta u_k(t), \end{aligned}$$

where we use Lemma 2.4 to derive

$$\begin{aligned} \frac{d}{dt}{\mathbb {E}}_{\alpha }(at^\alpha )= & {} a\alpha t^{\alpha -1}\frac{d}{a\alpha t^{\alpha -1}dt}{\mathbb {E}}_{\alpha }(at^\alpha )\\= & {} a\alpha t^{\alpha -1}\frac{d}{d(at^\alpha )}{\mathbb {E}}_{\alpha }(at^\alpha )\\= & {} a t^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(at^\alpha ). \end{aligned}$$

By learning law (3), we have

$$\begin{aligned} \delta u_{k+1}(t)= & {} \delta u_k(t)-k_pe_k(t)-k_d\dot{e}_k(t) \\= & {} (1-k_d d)\delta u_{k}(t)-k_pc\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )b\delta u_k(s)ds \\&-\,\,k_d c\int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ) b\delta u_k(s)ds-k_p d\int _0^t \delta u_k(s)ds \\&-\,\,k_p c{\mathbb {E}}_{\alpha }(at^\alpha )\delta x_k(0)-k_d cat^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(at^\alpha )\delta x_k(0). \end{aligned}$$

Taking \(\lambda \)-norm, we have

$$\begin{aligned} \Vert \delta u_{k+1}\Vert _\lambda\le & {} \rho \Vert \delta u_{k}\Vert _\lambda +| k_p c||\delta x_k(0)|\Vert {\mathbb {E}}_{\alpha }(a(\cdot )^\alpha )\Vert _\lambda \nonumber \\&+|k_d ca||\delta x_k(0)|\Vert (\cdot )^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(\cdot )^\alpha )\Vert _\lambda . \end{aligned}$$
(14)

Keeping in mind of \({\mathbb {E}}_{\alpha }(at^\alpha )\) and \(t^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(at^\alpha )\), \(\alpha \in (1,2)\) are increasing functions (see Lemma 2.6) for \(t\ge 0\) and the relationship between \(\lambda \)-norm and C-norm, we have

$$\begin{aligned} \Vert {\mathbb {E}}_{\alpha }(a(\cdot )^\alpha )\Vert _\lambda \le \Vert {\mathbb {E}}_{\alpha }(a(\cdot )^\alpha )\Vert _C\le {\mathbb {E}}_{\alpha }(aT^\alpha ), \end{aligned}$$

and

$$\begin{aligned} \Vert (\cdot )^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(\cdot )^\alpha ) \Vert _\lambda \le \Vert (\cdot )^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(\cdot )^\alpha )\Vert _C\le T^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(aT^\alpha ). \end{aligned}$$

Thus, (14) becomes

$$\begin{aligned} \Vert \delta u_{k+1}\Vert _\lambda \le \rho \Vert \delta u_{k}\Vert _\lambda +| k_p c|\bar{\Delta }{\mathbb {E}}_{\alpha }(aT^\alpha ) +|k_d ca|\bar{\Delta }T^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(aT^\alpha ). \end{aligned}$$

Using Lemma 2.7, we have

$$\begin{aligned} \limsup _{k\rightarrow \infty }\Vert \delta u_{k}\Vert _\lambda \le \frac{1}{1-\rho }\left( | k_p c|{\mathbb {E}}_{\alpha }(aT^\alpha ) +|k_d ca|T^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(aT^\alpha )\right) \bar{\Delta }. \end{aligned}$$

It follows (13) that we have

$$\begin{aligned} \Vert e_k\Vert _\lambda\le & {} \left( \frac{|cb|}{\lambda ^\alpha -a} +\frac{|d|}{\lambda }\right) \Vert \delta u_{k}\Vert _\lambda +|c|\bar{\Delta }\Vert {\mathbb {E}}_{\alpha }(a(\cdot )^\alpha ) \Vert _\lambda \nonumber \\\le & {} \left( \frac{|cb|}{\lambda ^\alpha -a}+\frac{|d|}{\lambda }\right) \Vert \delta u_{k}\Vert _\lambda +|c|\bar{\Delta }{\mathbb {E}}_{\alpha }(aT^\alpha ). \end{aligned}$$
(15)

Let iterative time \(k\rightarrow \infty \), we have

$$\begin{aligned}&\limsup _{k\rightarrow \infty }\Vert e_{k}\Vert _\lambda \nonumber \\&\quad \le \left( \frac{|cb|}{\lambda ^\alpha -a}+\frac{|d|}{\lambda }\right) \limsup _{k\rightarrow \infty }\Vert \delta u_{k}\Vert _\lambda +|c|\bar{\Delta }{\mathbb {E}}_{\alpha }(aT^\alpha )\nonumber \\&\quad \le |c|\bar{\Delta }\left( \left( \frac{|cb|}{\lambda ^\alpha -a} +\frac{|d|}{\lambda }\right) \frac{1}{1-\rho }\left( |k_p|{\mathbb {E}}_{\alpha }(aT^\alpha ) +|k_d||a|T^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(aT^\alpha ) \right) \right. \nonumber \\&\qquad \left. +\,\,{\mathbb {E}}_{\alpha }(aT^\alpha ) \right) . \end{aligned}$$
(16)

The proof is completed. \(\square \)

Remark 3.3

For some pre-fixed iteration domain length T. Linking the formula (16), one can make the tracking error decreasing by applying two possible methods: (i) Adjusting the learning law, i.e., making \(|k_p|\) decrease, (ii) Improving the system initial state tracking accuracy, i.e., making \(\bar{\Delta }\) decreasing. But we can’t see that \(|k_d|\) increase or decrease will effect on the tracking error by (16). In fact, \(\frac{1}{1-\rho }\) would increase if \(|k_d|\) decrease.

Remark 3.4

Suppose that the initial error satisfy \(x_d(0)\ne x_0\) and \(|x_k(0)-x_0|\le \Delta ^*\). Denote \(|x_d(0)- x_0|=\Delta ^{**}\). Then (12) becomes to \(|\delta x_k(0)|\le \Delta ^*+\Delta ^{**}:=\bar{\Delta }\). One can obtain similar results in Theorem 3.2.

4 Convergence analysis of close-loop law

In this section, we investigate the following PD-type learning control law:

$$\begin{aligned} u_{k+1}(t)=u_k(t)+k_pe_{k+1}(t)+k_d\dot{e}_{k+1}(t). \end{aligned}$$
(17)

In this law, proportional closed-loop learning algorithm can provide faster convergence speed. We assume that \(\dot{e}_k(t)=\lim _{\tau \rightarrow t^-}\frac{e_k(\tau )-e_k(t)}{\tau -t}\) without violate the law of causality.

Below is the first result in this section.

Theorem 4.1

Assume that the ILC scheme (17) is applied to (1) and the initial condition at each iteration remains the desired, i.e., \(x_k(0)=x_d(0)\), \(k=0,1,2,\ldots .\) If \(|1+k_d d|>1\), then \(\lim _{k\rightarrow \infty }y_k(t)=y_d(t)\) uniformly on \(t\in [0,T]\).

Proof

By repeating the same argument as Theorem 3.1, it can be proved easily that

$$\begin{aligned}&(1+k_d d)\delta u_{k+1}(t)= \delta u_{k}(t)-k_pc\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )b\delta u_{k+1}(s)ds \\&\quad -\,\,k_d c\int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ) b\delta u_{k+1}(s)ds-k_p d\int _0^t \delta u_{k+1}(s)ds, \end{aligned}$$

and

$$\begin{aligned} |1+k_d d|\Vert \delta u_{k+1}\Vert _\lambda \le \Vert \delta u_{k}\Vert _\lambda +\left( \frac{|k_p cb|}{\lambda ^\alpha -a}+\frac{|k_dcb|\lambda }{\lambda ^\alpha -a}+\frac{|k_p d|}{\lambda }\right) \Vert \delta u_{k+1}\Vert _\lambda . \end{aligned}$$

From above, we obtain

$$\begin{aligned} \Vert \delta u_{k+1}\Vert _\lambda \le \left( |1+k_d d|-\frac{|k_p cb|}{\lambda ^\alpha -a}-\frac{|k_d cb|\lambda }{\lambda ^\alpha -a}-\frac{|k_p d|}{\lambda }\right) ^{-1}\Vert \delta u_{k}\Vert _\lambda . \end{aligned}$$

Owning to \(|1+k_dd|>1\), there exists a sufficiently large \(\lambda \) such that:

$$\begin{aligned} \bar{\rho }=|1+k_dd|-\frac{|k_p cb|}{\lambda ^\alpha -a}-\frac{|k_d cb|\lambda }{\lambda ^\alpha -a}-\frac{|k_p d|}{\lambda }>1. \end{aligned}$$

Now the rest of proof is similar to that of Theorem 3.1, so we omit it here. \(\square \)

We also give the Robustness results for random but bounded initial error.

Theorem 4.2

Assume that the ILC scheme (17) is applied to (1) and the initial condition at each iteration conform to (12). If \(|1+k_dd|>1\), then the error between \(y_d(t)\) and \(y_k(t)\) is bounded and its bound depends on \(\bar{\Delta }\), \(|k_p|\) and \(|k_d|\).

Proof

From the learning law (17) that

$$\begin{aligned} (1+k_dd)\delta u_{k+1}(t)= & {} \delta u_{k}(t)-k_pc\int _0^t (t-s)^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(a(t-s)^\alpha )b\delta u_{k+1}(s)ds \nonumber \\&-\,\,k_d c\int _0^t (t-s)^{\alpha -2}{\mathbb {E}}_{\alpha ,\alpha -1}(a(t-s)^\alpha ) b\delta u_{k+1}(s)ds\nonumber \\&-\,\,k_p d\int _0^t \delta u_{k+1}(s)ds\nonumber \\&-\,\,k_p c{\mathbb {E}}_{\alpha }(at^\alpha )\delta x_k(0)-k_d cat^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(at^\alpha )\delta x_k(0). \end{aligned}$$
(18)

Substituting (8), (9) into (18), we obtain

$$\begin{aligned} \Vert \delta u_{k+1}\Vert _\lambda \le \frac{1}{\bar{\rho }}\Vert \delta u_{k}\Vert _\lambda +\frac{\bar{\Delta }}{\bar{\rho }}\left( |k_p c|{\mathbb {E}}_{\alpha }(aT^\alpha ) +|k_d ca|T^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(aT^\alpha ) \right) . \end{aligned}$$

Since \(|1+k_dd|>1\), it is possible to choose \(\lambda \) sufficiently large that \(\bar{\rho }>1\). By using Lemma 2.7, we have

$$\begin{aligned} \limsup _{k\rightarrow \infty }\Vert \delta u_k\Vert _\lambda \le \frac{\bar{\Delta }\left( |k_p c|{\mathbb {E}}_{\alpha }(aT^\alpha ) +|k_d ca|T^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha }(aT^\alpha ) \right) }{\bar{\rho }-1}. \end{aligned}$$

By using (15), we obtain

$$\begin{aligned}&\limsup _{k\rightarrow \infty }\Vert e_{k}\Vert _\lambda \\&\quad \le |c|\bar{\Delta }\left( \left( \frac{|cb|}{\lambda ^\alpha -a} +\frac{|d|}{\lambda }\right) \frac{1}{\bar{\rho }-1}\left( |k_p|{\mathbb {E}}_{\alpha }(aT^\alpha )+|k_d||a|T^{\alpha -1}{\mathbb {E}}_{\alpha ,\alpha } (aT^\alpha ) \right) \right. \\&\left. \qquad +\,\,{\mathbb {E}}_{\alpha }(aT^\alpha ) \right) . \end{aligned}$$

The proof is completed. \(\square \)

To end this section, we give two remarks as the extension of Sects. 3 and 4.

Remark 4.3

When \(\alpha =1\), the Eq. (1) become an one-order ordinary differential equation as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{ x}_k(t)=ax_k(t)+bu_k(t),~t\in [0,T],\\ y_k(t)=cx_k(t)+d\int _0^t u_k(s)ds. \end{array} \right. \end{aligned}$$
(19)

It is well known that the solution of (19) is given as

$$\begin{aligned} x_k(t)=e^{at}x_k(0)+\int _0^t e^{a(t-s)}bu_k(s)ds. \end{aligned}$$

By repeating some elementary computation, we obtain the error formula:

$$\begin{aligned} e_k(t)=ce^{at}x_k(0)+c\int _0^t e^{a(t-s)}bu_k(s)ds+d\int _0^t \delta u_k(s)ds. \end{aligned}$$

Taking the derivative, we have

$$\begin{aligned} \dot{e}_k(t)=cae^{at}x_k(0)+c\int _0^t ae^{a(t-s)}bu_k(s)ds+d\delta u_k(t). \end{aligned}$$

Similar to the contents of Sects. 3 and 4, one can give the convergence analysis of open-loop and closed-loop law immediately.

Remark 4.4

For learning law (3) and (17), the main results of Sects. 3 and 4 can be extended to the following the fractional relaxation semilinear differential equations

$$\begin{aligned} \left\{ \begin{array}{l} ^c_0 D^\alpha _t x_k(t)=ax_k(t)+f(t,x_k(t),u_k(t)),~t\in [0,T],~\alpha \in (1,2),\\ \dot{x}_k(0)=0,\\ y_k(t)=cx_k(t)+d\int _0^t u_k(s)ds, \end{array} \right. \end{aligned}$$
(20)

when \(f: [0,T]\times \mathbb {R} \times \mathbb {R}\) is a Lipschitz type continuous function with respect to the second and third variables. We will give more details in our forthcoming paper.

5 Simulation examples

In this section, numerical examples are presented to demonstrate the validity of the design methods.

In order to describe the stability of the system which is associated with the increase of iterations, we denote the total energy in kth iteration as \( E_k=\Vert u_k\Vert _{L^2}. \)

Example 5.1

Consider the following fractional order differential system:

$$\begin{aligned} \left\{ \begin{array}{l} ^c_0 D^{1.5} _t x_k(t)=0.5x_k(t)+0.5u_k(t),~t\in [0,1],\\ y_k(t)=0.8x_k(t)+0.5\int _0^t u_k(s)ds. \end{array} \right. \end{aligned}$$
(21)

The learning law in the system is set as (3), where \(k_p=1\), \(k_d=1.2\). The initial state and the 1st control are proposed as \(x_k(0)=0\), \(~k=1.2,\ldots ,\) and \(u_1(t)=1\), \(t\in [0,1]\), respectively.

Next, we set the desired trajectory as \(y_d(t)=12t(1-t)\), \(t\in [0,1]\). Obviously, all the conditions of Theorem 3.1 are satisfied.

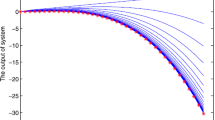
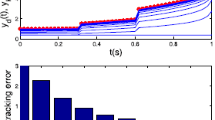
The upper figure of Fig. 1 shows the system (21) output \(y_k\) of the first 25 iterations and the referenced trajectory \(y_d\). The middle figure shows the \(L^2\)-norm of the tracking error in each iteration. The tracking error at the 25th iteration is 0.0378, which is very small. The lower figure shows the total energy in each iteration. We can see the total energy become stable gradually with increase of iterations.

Fig. 1
figure 1

The system output, the \(L^2\)-norm of the tracking errors, and the total energy in each iteration

Full size image

Example 5.2

Consider the following one-order differential system:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_k(t)=0.5x_k(t)+0.5u_k(t),~t\in [0,1],\\ y_k(t)=0.8x_k(t)+0.5\int _0^t u_k(s)ds. \end{array} \right. \end{aligned}$$
(22)

The learning law in the system, the initial state, the 1st control and the desired trajectory are proposed as Example 5.1, respectively.

The upper figure of Fig. 2 shows the system (22) output \(y_k\) of the first 25 iterations and the referenced trajectory \(y_d\). The middle figure shows the \(L^2\)-norm of the tracking error in each iteration. The tracking error at the 25th iteration is 0.0042, which is very small. The lower figure shows the total energy in each iteration. We can see the total energy become stable gradually with increase of iterations.

Fig. 2
figure 2

The system output, the \(L^2\)-norm of the tracking errors, and the total energy in each iteration

Full size image

Between Examples 5.1 and 5.2, we need to more input energy in order to offset the memory of the fractional order system.

Example 5.3

Consider the system, initial control and the desired trajectory in Example 5.1. In this example, the initial errors are assumed to be random but bounded. We set the initial condition \(x_k(0)\) is a random number which is uniformly distributed in \([-0.1,0.1]\).

Next we analysis the tracking error to by the different parameters of learning law. Due to the initial state of random, we take the average tracking error of the 20th to 200th iterations as the evaluation criteria of tracking error (Fig. 3; Table 1).

Fig. 3
figure 3

The tracking error by the different paramenters of learning law

Full size image
Table 1 The corresponding error of different \(k_p\) and \(k_d\)
Full size table

By figures (a), (b) and (c), the \(|k_d|\) decrease will result in \(\Vert e_k\Vert _{L^2}\) increased. By (b) and (d), the \(|k_p|\) decrease will lead to \(\Vert e_k\Vert _{L^2}\) decrease.