Double domination on intuitionistic fuzzy graphs

Abstract

Let $G=(V,E)$ be an intuitionistic fuzzy graph. A subset D of V is a double dominating set of G if for each vertex in $V-D$ is dominated by at least two vertices in D. The double domination number of G is the minimum fuzzy cardinality of all double domination set of G and is denoted by $\gamma _{dd} (G)$. In this paper, some theorems are proved on double domination of intuitionistic fuzzy graph G. An interesting result on $\gamma _{dd} (G)$ using some known parameter of G is obtained. Application of domination in intuitionistic fuzzy graph is also presented.

1 Introduction

In twentyfirst century, the graph theory has been fully exploited by fuzzy theory. Fuzzy set has emerged as a potential area of interdisciplinary research. Zadeh [29] published his seminal work on fuzzy sets in 1965, in which he detailed the mathematics of fuzzy set theory. Kaufmann [4] discussed fuzzy set and fuzzy relations in detail. When introducing fuzzy graph theory in 1975, Rosenfeld [24] obtained fuzzy analogues of several graph theoretic concepts. Bhattacharya [2] introduced some remarks on fuzzy graphs and obtained fuzzy graph theory results concerning center and eccentricity. Bhutani [3] studied automorphism of fuzzy graphs. Mordeson and Nair [6] studied cycles and cocycles of fuzzy graphs. Mordeson and Peng [7] defined complement of a fuzzy graph and derived its properties. Sunitha and Vijayakumar [28] characterized fuzzy trees.

Somasundaram and Somasundaram [27] presented more concepts of independent domination, connected domination in fuzzy graphs. Nagoorgani and Ahamed [12] studied strong and weak domination in fuzzy graphs. Nagoorgani and Chandrasekaran [13] introduced domination in fuzzy graphs using strong edges. They gave the concept of free nodes and busy nodes of a fuzzy graph [14]. Nagoorgani and Hussain [15] defined and studied global domination of a fuzzy graph. Nagoorgani and Malarvizhi [16] studied some properties antipodal fuzzy graphs. Nagoorgani and Radha [17] have obtained regular fuzzy graphs. Nagoorgani et al. [18] gave some interesting properties of fuzzy dominating set, fuzzy minimal dominating set, fuzzy independent dominating set and fuzzy irredundant set. The fundamental field of research interest for Atanassov [1] are fuzzy sets, defined by Zadeh, which he significantly extended by launching the concept of Intuitionistic Fuzzy Sets (IFSs) and investigated their basis properties. He has also initiated the applications of intuitionistic fuzzy sets in expert systems, systems theory, decision making and others. He has studied and defined a lot of operations and relations over intuitionistic fuzzy sets, part of which has analogues in the theory of fuzzy sets. Shannon and Atanassov [26] discussed a new generalization Intuitionistic Fuzzy Graphs (IFGs). Chountas and Alzebdi [19] along with them discussed intuitionistic fuzzy version of the graph—the tree called intuitionistic fuzzy tree. Parvathi and Karunambigai  [20] introduced intuitionistic fuzzy graph as a special case of Atanassov’s intuitionistic fuzzy graph and analysed its components. They have also worked on operations on intuitionistic fuzzy graphs [21]. Parvathi and Tamizhendhi [22] defined domination in intuitionistic fuzzy graphs and discussed some of its properties. In this paper, double dominating set in IFGs and its properties are studied.

2 Preliminaries

In this section, some basic definitions relating to IFGs are given. Also the definition of double dominating set, cardinality of double dominating set, strength of the connectedness, degree of vertex and minimal domination in IFGs are studied.

Definition 2.1

An Intuitionistic Fuzzy Graph (IFG) is of the form $G = (V,E)$, where

• (i) $V=\left\{ v_{1},v_{2}, \ldots , v_n \right\}$ such that $\mu _{1}:V\rightarrow [0,1]$ and $\gamma _{1}:V\rightarrow [0,1]$ denote the degree of membership and non-membership of the element $v_{i} \in V$ respectively and $0\le \mu _{1} (v_{i})+\gamma _{1} (v_{i})\le 1$, for every $v_{i} \in V \left( i=1,2,\ldots , n\right)$.

• (ii) $E \subset V\times V$ where $\mu _{2}:V\times V\rightarrow [0,1]$ and $\gamma _{2}:V\times V\rightarrow \left[ 0,1\right]$ are such that

  $$\begin{aligned} \mu _{2} (v_{i}, v_{j})&\le \min \left[ \mu _{1}\left( v_{i}\right) ,\mu _{1} (v_{j}) \right] \\ \gamma _{2} (v_{i} v_{j})&\le \max \left[ \gamma _{1} \left( v_{i}\right) ,\gamma _{1} (v_{j}) \right] \\ \text{ and } 0&\le \mu _{2} (v_{i}, v_{j})+\gamma _{2} (v_{i}, v_{j})\le 1,\quad \text{ for } \text{ every } \left( v_{i}, v_{j}\right) \in E. \end{aligned}$$

Here the triple $\left( v_{i},\mu _{1i},\gamma _{1i}\right)$ denotes the degree of membership and degree of non-membership of the vertex relation and $\left( e_{ij},\mu _{2ij},\gamma _{2ij}\right)$ denotes the degree of membership and degree of non-membership of the edge relation $e_{ij} =\left( v_{i},v_{j}\right)$ on V.

Note 1: When $\mu _{2ij} =\gamma _{2ij} =0$ for some i and j, then there is no edge between $v_{i}$ and $v_{j}$. Otherwise there exists an edge between $v_{i} and v_{j}$.

Definition 2.2

An IFG $H= \left( V^{\prime }, {E} ^{\prime }\right)$ is said to be an IF-subgraph (IFSG) of $G = (V,E)$ if ${V} ^{\prime } \subseteq V$ and $E^{\prime } \subseteq E$. That is $\mu _{1i} ^{\prime } \le \mu _{1i}$;$\gamma _{1i} ^{\prime } \ge \gamma _{1i}$ and $\mu _{2ij} ^{\prime } \le \mu _{2ij};\gamma _{2ij} ^{\prime } \ge \gamma _{2ij}$ for every $i,j=1,2,3,\ldots ,n$.

Definition 2.3

Let $G = (V,E)$ be an IFG. Then the cardinality of G is defined to be

$$\begin{aligned} \vert G \vert =\left| \sum \limits _{v_{i} \in V} \frac{1+\mu _{1} \left( v_{i}\right) -\gamma _{1} \left( v_{i}\right) }{2} +\sum \limits _{v_{i},v_{j} \in E} \frac{1+\mu _{2} \left( v_{i},v_{j}\right) -\gamma _{2} \left( v_{i},v_{j}\right) }{2} \right| \end{aligned}$$

Definition 2.4

Let $G = (V, E)$ be an IFG. Then the vertex cardinality of V defined by

$$\begin{aligned} \vert V \vert =\sum \limits _{v_{i} \in V} \frac{1+\mu _{1} \left( v_{i}\right) -\gamma _{1} \left( v_{i}\right) }{2}; \quad \hbox { for all }v_{i} \in V. \end{aligned}$$

Definition 2.5

Let $G = (V, E)$ be an IFG. Then the edge cardinality of E defined by

$$\begin{aligned} \vert E \vert =\sum \limits _{v_{i},v_{j} \in E} \frac{1+\mu _{2} \left( v_{i},v_{j}\right) -\gamma _{2} \left( v_{i},v_{j}\right) }{2};\quad \hbox { for all }(v_{i}, v_{j})\in E. \end{aligned}$$

Definition 2.6

The number of vertices is called the order of an IFG and is denoted by O(G). The number of edges is called size of an IFG and is denoted by S(G).

Definition 2.7

The degree of a vertex v in an IFG, $G =(V, E)$ is defined to be sum of the weights of the strong edges incident at v. It is denoted by $d_{G} (v)$.

The minimum degree of G is $\delta (G) =\min \{d_{G}(v)\mid v \in V \}$.

The maximum degree of G is $\Delta (G) =\max \{d_{G}(v)\mid v \in V \}$.

Definition 2.8

Two vertices $v_{i}$ and $v_{j}$ are said to be neighbors in IFG, if either one of the following conditions hold

• (i) $\mu _{2} \left( v_{i}, v_{j}\right) >0$, $\gamma _{2} (v_{i}, v_{j})>0$,

• (ii) $\mu _{2} \left( v_{i}, v_{j}\right) =0$, $\gamma _{2} (v_{i}, v_{j})>0$,

• (iii) ${\mu } _{2} \left( v_{i}, v_{j}\right) >0$, $\gamma _{2} \left( v_{i}, v_{j}\right) =0,\, v_{i}, v_{j} \epsilon V$.

Definition 2.9

A path in an IFG is a sequence of distinct vertices $v_{1} v_{2} {\ldots v} _{n}$ such that either one of the following conditions is satisfied:

• (i) $\mu _{2} \left( v_{i}, v_{j}\right) >0$, $\gamma _{2} (v_{i}, v_{j})>0$, for some i and j,

• (ii) $\mu _{2} \left( v_{i}, v_{j}\right) =0$, $\gamma _{2} \left( v_{i}, v_{j}\right) >0$, for some i and j,

• (iii) $\mu _{2} \left( v_{i}, v_{j}\right) >0$, $\gamma _{2} \left( v_{i}, v_{j}\right) =0$ for some i and j. The length of a path $P = v_{1}, v_{2}, \ldots , v_{n+1}$,  $(n >0)$ is n.

Definition 2.10

Two vertices that are joined by a path is called connected.

Definition 2.11

If $v_{i}, v_{j}$ are vertices in $G=(V, E)$ and if they are connected by means of a path then the strength of that path is defined as $\big (\min \limits _{i,j} \mu _{2ij}, \max \limits _{i,j}\gamma _{2ij} \big )$ where $\min _{i,j}\mu _{2ij}$ is the $\mu$-strength of the weakest arc and $\max \limits _{i,j}\gamma _{2ij}$ is the is the $\gamma$-strength of the strongest arc.

Definition 2.12

If $v_{i}, v_{j} \in V\subseteq G$, then $\mu$-strength of connectedness between $v_{i}$ and $v_{j}$ is ${\mu } _{2} ^{\infty } \left( v_{i},v_{j}\right) =\sup \left\{ \mu _{2} ^{k} \left( v_{i},v_{j}\right) /k=1,2\ldots ,n \right\}$. $\gamma$-strength of connectedness between $v_{i}$ and $v_{j}$ is $\gamma _{2} ^{\infty } \left( v_{i},v_{j}\right) =\inf \left\{ \gamma _{2} ^{k} \left( v_{i},v_{j}\right) /k=1,2\ldots ,n \right\}$.

If u, v are connected by means of paths of length k then $\mu _{2} ^{k} (u,v)$ is defined as

$$\begin{aligned}&\sup \big \{\mu _{2} \left( u,v_{1}\right) \wedge \mu _{2} \left( v_{1},v_{2}\right) \wedge \mu _{2} \left( v_{2},v_{3}\right) \cdots \wedge \mu _{2} \left( v_{k-1},v \right) /\\&\quad \quad \,\, \left( u_{1}, v_{1},v_{2},\ldots ,v_{k-1},\ v\in V \right) \big \} \end{aligned}$$

and ${\gamma } _{2} ^{k} (u,v)$ is defined as

$$\begin{aligned}&\inf \big \{\gamma _{2} \left( u,v_{1}\right) \vee \gamma _{2} \left( v_{1},v_{2}\right) \vee \gamma _{2} \left( v_{2},v_{3}\right) \cdots \vee \gamma _{2} \left( v_{k-1},v \right) /\\&\quad \quad \,\, (u_{1} v_{1},v_{2},\ldots ,\ v_{k-1},v\in V) \big \}. \end{aligned}$$

Definition 2.13

An IFG, $G = (V,E)$ is said to be complete IFG if $\mu _{2ij} =\min \left\{ \mu _{1i},\mu _{1j}\right\}$ and $\gamma _{2ij} =\max \left\{ \gamma _{1i},\gamma _{1j}\right\}$ for every $v_{i}, v_{j} \in V$.

Definition 2.14

The complement of an IFG, $G = (V,E)$ is an IFG, $\bar{G} = (\bar{V} \bar{E})$ where

• (i) $\bar{V} =V$

• (ii) $\bar{\mu }_{1i} =\mu _{1i}$ and $\bar{\gamma }_{1i} =\gamma _{1i}$ for all $i = 1,2,\ldots , n$

• (iii) $\bar{\mu } _{2ij} =\min \left( \mu _{1i}, \mu _{1j}\right) -\mu _{2ij}$ and $\bar{\gamma _{2ij}} =\max \left( \gamma _{1i}, \gamma _{1j}\right) -\gamma _{2ij}$ for all $i = 1,2\ldots ,n$.

Definition 2.15

An IFG, $G = (V,E)$ is said to bipartite if the vertex set V can be partitioned into two non-empty sets $V_{1}$ and $V_{2}$ such that

• (i) $\mu _{2} \left( v_{i},v_{j}\right) =0$ and $\gamma _{2} \left( v_{i},v_{j}\right) =0$ if $v_{i}, v_{j} \in V_{1}$ (or) $v_{i}, v_{j} \in V_{2}$

• (ii) $\mu _{2} \left( v_{i},v_{j}\right) >0$ and $\gamma _{2} \left( v_{i},v_{j}\right) >0$ if $v_{i} \in V_{1}$ and ${v} _{j} \in V_{2}$ for some i and j (or) $\mu _{2} \left( v_{i},v_{j}\right) =0$ and $\gamma _{2} \left( v_{i},v_{j}\right) >0$ if $v_{i} \in V_{1}$ and ${v} _{j} \in V_{2}$ for some i and j (or) $\mu _{2} \left( v_{i},v_{j}\right) >0$ and $\gamma _{2} \left( v_{i},v_{j}\right) =0$ if $v_{i} \in V_{1}$ and ${v} _{j} \in V_{2}$ for some i and j.

Definition 2.16

A bipartite IFG, $G =(V, E)$ is said to be complete if $\mu _{2} \left( v_{i},v_{j}\right) =\min \left( \mu _{1} \left( v_{i}\right) ,\mu _{1} \left( v_{j}\right) \right)$ and $\gamma _{2} \left( v_{i},v_{j}\right) =\max (\gamma _{1} \left( v_{i}\right) ,\gamma _{1} \left( v_{j}\right) )$ for all $v_{i} \in V_{1}$ and ${v} _{j} \in V_{2}$. It is denoted by $K_{v_{1i}, v_{2i}}$.

Definition 2.17

Let u be a vertex in an IFG $G =(V, E)$, then $N(u) =\{v \in V/ (u, v) \hbox { is a strong arc} \}$ is called neighborhood of u.

Definition 2.18

A vertex $u \in V$ of an IFG $G = (V, E)$ is said to be an isolated vertex if $\mu _{2} (u,v)=0$ and $\gamma _{2} (u,v)=0$ for all $v\in V$. That is $N(u) = \varphi$. Thus, an isolated vertex does not dominate any other vertex in G.

Definition 2.19

An arc (u, v) is said to be a strong arc, if $\mu _{2} (u,v)\ge \mu _{2} ^{\infty } (u,v)$ and $\gamma _{2} (u,v)\ge \gamma _{2} ^{\infty } (u,v)$.

Definition 2.20

Let $G =(V, E)$ be an IFG on V. Let u$, v \in V$, we say that u dominates v in G, if there exists a strong arc between them.

Note 2: If ${\mu } _{2} \left( u,v\right) < {\mu } _{2} ^{{\infty }} \left( u,v\right)$ and ${\gamma } _{2} \left( u,v\right) < {\gamma } _{2} ^{{\infty }} {(u,v)}$ for all $u,v\in V$, then the only dominating set of G is V.

Definition 2.21

A subset S of V is called a dominating set in G if for every $v\in V -S$, there exists $u \in S$ such that u dominates v.

Definition 2.22

A dominating set S of an IFG is said to be minimal dominating set if no proper subset of S is a dominating set.

Definition 2.23

Minimum cardinality among all minimal dominating set is called lower-domination number of G, and is denoted by d(G).

Maximum cardinality among all minimal dominating set is called upper-domination number of G, and is denoted by D(G).

Definition 2.24

Two vertices in an IFG, $G = (V,E)$ are said to be independent if there is no strong arc between them.

Definition 2.25

A subset S of V is said to be independent set of G if $\mu _{2} (u,v)<\mu _{2} ^{\infty } (u,v)$ and $\gamma _{2} (u,v)<\gamma _{2} ^{\infty } (u,v)$ for all $u,v\in S$.

Definition 2.26

An independent set S of G in an IFG is said to be maximal independent, if for every vertex $v \in V-S$, the set $S \cup \{v\}$ is not independent.

Definition 2.27

The minimum cardinality among all maximal independent set is called lower independence number of G, and it is denoted by i(G).

Definition 2.28

The maximum cardinality among all maximal independent set is called upper independence number of G, and it is denoted by I(G).

Definition 2.29

Let G be an intuitionistic fuzzy graph. Let D be a minimum dominating set of G. If $V-D$ contains a dominating set $D^{-1}$ of G, then $D^{-1}$ is called an inverse dominating set of G with respect to D. The inverse domination number$\gamma ^{-1} (G)$ of G is the cardinality of a smallest inverse dominating set of G.

Definition 2.30

Let $G=(V,E)$ be a fuzzy graph. A subset D of V is a double dominating set of G, if for each vertex in $V-D$ is dominated by at least two vertices in D. The double domination number of G is the minimum fuzzy cardinality of all double dominating set of G and is denoted by $\gamma _{Dd} (G)$.

Definition 2.31

A vertex $v\in G$ is said to be end-vertex of IFG, if it has at most one strong neighbor in G.

Definition 2.32

An edge $(v_{i}, v_{j})$ is said to be a bridge in IFG G, if either $\mu _{2xy} ^{'\infty } <\mu _{2xy} ^{\infty }$ and $\gamma _{2xy} ^{'\infty } \ge \mu _{2xy} ^{\infty }$ (or) $\mu _{2xy} ^{'\infty } \le \mu _{2xy} ^{\infty }$ and $\gamma _{2xy} ^{'\infty } >\mu _{2xy} ^{\infty }$ for some ${v} _{x}, v_{y} \in V$.

Definition 2.33

A vertex $v_{i}$ is said to be a cut-vertex in IFG G if deleting a vertex $v_{i}$ reduces the strength of the connectedness between some pair of vertices.

3 Double dominating set

Definition 3.1

Let $G=(V,E)$ be an intuitionistic fuzzy graph. A subset D of V is a double dominating set of G, if for each vertex in $V-D$, is dominated by at least two vertices in D. The double domination number of G is the minimum fuzzy cardinality of all double dominating set of G and is denoted by $\gamma _{dd} (G)$

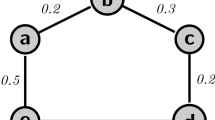
Example 3.2

Consider Fig. 1:

Fig. 1

Graph with double domination number

Here strong arcs are ${e} _{1}, e_{2}, e_{5}$ and $e_{6}$.

Minimum dominating set $D=\left\{ v_{1},v_{2},v_{3},v_{5},v_{6}\right\}$ is a double dominating set. $V-D=\left\{ v_{4}\right\}$. Double domination number is ${\gamma } _{dd} (G)=3.2$.

Theorem 3.3

In Intuitionistic fuzzy graph G, Double dominating set exists only if every vertex in $V-D$ contains at least two strong neighbors.

Proof

Let D be a double dominating set. Suppose a vertex $u\in V-D$ has only one strong neighbor, other vertices in $V-D$ have at least two strong neighbors. Then for every $u\in V-D$, there exists a vertex $v\in D$ such that D is a dominating set, which contradicts the assumption. Hence every vertex in $V-D$ should contain at least two strong neighbors.

Example 3.4

Consider Fig. 2:

Fig. 2

At least two strong neighbours in $V-D$

Here strong arcs are $e_{2}, e_{3}, e_{5}$. $D=\left\{ v_{1},v_{2},v_{4}\right\}$. $V-D=\left\{ v_{3}\right\}$. Therefore, $v_{3}$ has at least two strong neighbors.

Theorem 3.5

If G is an intuitionistic fuzzy graph, then cardinality of any double dominating set is greater than (or) equal to cardinality of $V-D$, i.e., $|D|\ge |V-D|$.

Proof

Let D be a Double dominating set. By definition of Double domination set, each vertex u in $V-D$ need at least two vertices in D. And neighborhood of each u will occur in D. Also if every arc in G is strong, then we get more double dominating sets and adjacent vertices of u will occur in D. This implies the result $|D|\ge |V-D|$. $\square$

Example 3.6

Consider Fig. 3:

Fig. 3

Graph with cardinality

Here all are strong arcs. Let $D=\left\{ v_{1},v_{3},v_{5},v_{6}\right\}$ and $V-D=\left\{ v_{2},v_{4}\right\}$. Therefore $|D|=2.7$ and $|V-D|=1.1$.

Hence $|D|>|V-D|$.

Theorem 3.7

The double dominating set D is minimal if and only if for any two vertices $\left\{ v,w \right\} \in D$, one of the following must hold.

• 1. There exists a vertex $u\in V-D$, such that $N(u)\cap D=\left\{ v,w \right\}$

• 2. $V-D$ is disconnected (or) isolated.

Proof

Let D be a minimal double domination set of an Intuitionistic fuzzy graph. Suppose there exists two vertices $\left\{ v,w \right\} \in D$ such that $\left\{ v,w \right\}$ does not satisfy any one of the conditions. By condition (i), there exist a vertex $u\in V-D$ such that $N(u)\cap D\ne \left\{ v,w \right\}$ and by condition (ii) $V-D$ is connected (or) not isolated.

Let $D^{\prime } =D-\left\{ v,w \right\}$. This implies $D^{\prime }$ is a double domination set which satisfies the above two conditions. Hence $V-D^{\prime }$ is disconnected (or) isolated, which contradicts the condition (ii). Hence the vertices $\left\{ v,w \right\} \in D$. Therefore D is minimal double dominating set which satisfies one of the above conditions.

Conversely, Let D be a double domination set. For each $\left\{ v,w \right\} \in D$ one of the following conditions hold. Let us prove that D is minimal. Suppose D is not minimal double dominating set. Then there exists two vertices $\left\{ v,w \right\} \in D$ such that $D-\left\{ v,w \right\}$ is a double dominating set. Thus $\left\{ v,w \right\}$ are strong neighbors to at least one node in $D-\left\{ v,w \right\}$. This implies $\left\{ v,w \right\}$ are not strong neighbor to any node in D. Hence there is a node $u\in V-D$ such that $N(u)\cap D\ne \left\{ v,w \right\}$ which is a contradiction. Therefore D is minimal double dominating set.

Hence the proof. $\square$

Example 3.8

Consider Fig. 4:

Fig. 4

Minimal double dominating set in G

Here strong arcs are $e_{3}, e_{5}, e_{7} D=\left\{ v_{1},v_{2},v_{3},v_{5} \text{ and } v_{6}\right\}$ and $V-D=\{v_{4}\}$. Also $N_{s} \left( v_{4}\right)$ is $v_{3}$ and $v_{6}$. Clearly $v_{3} \cap D=\left\{ v_{3} \right\}$ and $v_{6} \cap D=\left\{ v_{6}\right\}$. Hence $v_{4}$ is isolated.

Theorem 3.9

For any Intuitionistic fuzzy graph $G = (V,E)$, if D is minimum double dominating set then

• (i) $W(D)\le \delta (G)+2$

• (ii) $W(D)\ge \Delta (G)-1$,

where W(D) is the weight of double dominating set. $\Delta (G)$ and $\delta (G)$ are maximum and minimum degree of G respectively.

Proof

Let D be a minimum double dominating set.

$$\begin{aligned} \mathrm{(i)}\quad W(D)&=\left\{ \sum \min \limits _{1\le i\le n} \left[ d_{\mu } \left( v_{i}\right) \right] , \sum \max \limits _{1\le i\le n} \left[ d_{\gamma } \left( v_{i}\right) \right] \right\} \\&\ge \left\{ \min \left[ \sum \left[ d_{\mu } \left( v_{i}\right) \right] , \min \left[ \sum \left[ d_{\gamma } \left( v_{i}\right) \right] \right] \right] \right\} \\&=\left\{ \delta _{\mu } (G),\delta _{\gamma } (G) \right\} \\&= \delta (G)\\&\le \delta (G)+2.\\ \mathrm{(ii)}\quad W(D)&=\left\{ \sum \min \limits _{1\le i\le n} \left[ d_{\mu } \left( v_{i}\right) \right] , \sum \max \limits _{1\le i\le n} \left[ d_{\gamma } \left( v_{i}\right) \right] \right\} \\&\le \left\{ \max \left[ \sum \left[ d_{\mu } \left( v_{i}\right) \right] \right] , \max \left[ \sum \left[ d_{\gamma } \left( v_{i}\right) \right] \right] \right\} \\&=\left\{ \Delta _{\mu } (G),\Delta _{\gamma } (G) \right\} \\&=\Delta (G)\\&\ge \Delta (G)-1. \end{aligned}$$

$\square$

Theorem 3.10

If G is an Intuitionistic fuzzy graph with only end nodes, then double dominating set D does not exist.

Proof

Let G be an Intuitionistic fuzzy graph with only end nodes. Let D be a subset of V. Since G has only end nodes, for each $u\in V-D$, there exist $v\in D$ such that D is a dominating set.

Also no vertex in $V-D$ is dominated by at least two vertices in D which implies the double dominating set D does not exists. Hence the proof. $\square$

Example 3.11

Consider Fig. 5:

Fig. 5

Graph G with only end nodes

Here strong arcs are $e_{1}$ and $e_{3}$. Double dominating set does not exists, since $v_{2}$ and $v_{4}$ need another strong arc.

Theorem 3.12

For any Intuitionistic fuzzy graph $G, \gamma _{dd} (G)\ge \frac{O(G)}{\Delta _{\gamma } (G)+1}$ where $\Delta _{\gamma } (G)$ is the maximum $\gamma$-degree of G.

Proof

Let D be a double dominating set of IFG G with $\left| D \right| =\gamma _{dd} (G)$. Since every vertex in $V-D$ is adjacent to some vertices in D, we have

$$\begin{aligned} \left| V-D \right|&\le \sum \limits _{i=1} ^n {d\left( v_{i}\right) \le \gamma _{dd} (G).\Delta _{\mu } (G)} \\ \Rightarrow O(G)-\gamma _{dd} (G)&\le \gamma _{dd} (G)\Delta _{\gamma } (G)\\ \Rightarrow O(G)&\le \gamma _{dd} (G)\,+\,{\gamma } _{dd} (G)\Delta _{\gamma } (G)\\ \Rightarrow O(G)&\le \gamma _{dd} (G)\left[ 1+\Delta _{\gamma } (G) \right] \\ \text{ Thus, } \gamma _{dd} (G)&\ge \frac{O(G)}{1+\Delta _{\gamma } (G)} \end{aligned}$$

Hence the result. $\square$

Theorem 3.13

If G is an Intuitionistic fuzzy graph with cut vertices, then at least one cut vertex in G, will occur in double dominating set D.

Proof

Let G be an Intuitionistic fuzzy graph with cut vertices. Suppose there is no cut vertex in double domination set D. Let $u\in V-D$ be a cut vertex, Since most of the cut vertices are end node, u has only one strong neighbor which lies in D. Also u, is not dominated by at least two vertices in D. Hence D is not a double dominating set, which contradicts the assumption. This implies a cut vertex u, should be in double dominating set D. Hence the proof. $\square$

Example 3.14

Consider Fig. 6:

Fig. 6

A double dominating set with at least one cut-vertex in G

Here the strong arcs are $e_{1}, e_{2}, e_{4}$ and $e_{5}$. Let $D=\left\{ v_{1},v_{3},v_{4}\right\}$ and $V-D=\left\{ v_{2}\right\}$. Here $v_{4}$ is a cut vertex which occur in D.

Theorem 3.15

An Intuitionistic fuzzy graph G with effective edge has D as its unique double dominating set if and only if for each $v \in V-D$ there is a vertex u with weight $W(u)=\left\{ \sigma (u,v),\mu (u,v) \right\}$ in N(v).

Proof

If for each $v\in V-D$, v has unique neighbor in D. We know that, if D is a unique double dominating set of G then $\gamma _{dd} (G)\le \vert V \vert$ Hence for every $v\in V-D$ has a unique neighbor. Suppose that there exists $v\in V-D$, which has two neighbors and for all $u\in N(v)$ has at least two neighbors. Then $\left\{ V-D \right\} -v$ is a double dominating set of G with order greater than${\gamma } _{dd} (G)$, which is a contradiction. Hence the theorem. $\square$

Theorem 3.16

For any Intuitionistic fuzzy graph G, ${\gamma } ^{-1} (G)\le \gamma _{dd} (G)\le \vert V \vert$ where $\gamma ^{-1} (G)$ is an inverse domination number.

Proof

Let G be an Intuitionistic fuzzy graph. By definition of Inverse dominating set, $D^{-1}$ is a subset of $V-D$. Also by Theorem 3.5 $|D|\ge |V-D|$. This implies double domination number is greater than inverse domination number. i.e, $\gamma _{dd} (G)\ge \gamma ^{-1} (G)$. Double dominating set does not contain all the vertices of G. This implies at least one vertex u should be in $V-D$. Hence $G-\left\{ u \right\}$ vertices gives the double domination number. Clearly $\gamma _{dd} (G)\le \left| V \right|$. Therefore, ${\gamma } ^{-1} (G)\le \gamma _{dd} (G)\le \vert V \vert$. Hence the theorem. $\square$

Theorem 3.17

Let G be an Intuitionistic fuzzy graph. The double dominating set D in G is independent whereas not in $\bar{G}$.

Proof

Let D be a double dominating set in G which is independent. Let $\bar{G}$ be a complement of Intuitionistic fuzzy graph G. In $\bar{G}, \bar{V} =V,\bar{\mu }_{2ij} =\min \left( \mu _{1i},\mu _{1j}\right) -\mu _{2ij}$ and $\bar{\gamma } _{2ij} =\max \left( \gamma _{1i},\gamma _{1j}\right) -\gamma _{2ij}$. Here, only the values of edges are changed in $\bar{G}$. This implies most of the adjacent vertices in $\bar{G}$ have strong neighbors and also different double dominating set exists in $\bar{G}$. Therefore the same double dominating set D in G is not independent in $\bar{G}$. Hence the theorem. $\square$

Fig. 7

Independence in double dominating set

Consider a graph G (Fig. 7), here strong arcs are $e_{3}$ and $e_{5}$. Let $D=\left\{ v_{3},v_{4}\right\}$ and $V-D=\left\{ v_{2}\right\}$. Here D is independent whereas in $\bar{G}$, D is not independent.

4 Application of domination in intuitionistic fuzzy graphs

A political leader wants to conduct election campaign in a village. But he does not have enough time to meet all the voters in that village. So he wants to minimize the election campaign time, but at the same time without meeting all the voters, all of them must vote in favor of his party.

Now we can solve the problem by using intuitionistic fuzzy dominating set. Let us draw an intuitionistic fuzzy graph as follows. Every voter in the village be a node of the intuitionistic fuzzy graph. One voter may be a friend or may not be a friend of the other. The friendship may vary from person to person. If any two voters may be a very close friend or close friend or just know, then join the two nodes by an arc and give value of the arc corresponding to the friendship between the nodes of the voter. If one voter does not know the other, then there is no arc between the corresponding nodes of the voter.

Using domination in intuitionistic fuzzy graph, we have a minimum dominating set in the intuitionistic fuzzy graph and the political leader, enough only to meet the members in the minimum dominating set, then every member of the dominating set may canvass all the non member of the dominating set. Automatically all the voters in that village will vote in favor of the party without the party leader meet all the voters.

Fig. 8

Minimum dominating set

In Fig. 8, the strong arcs are $e_{1}, e_{4}, e_{6},e_{8}, e_{9}, e_{10}, e_{12}, e_{14}, e_{15}, e_{16}, e_{18}$ and ${e}_{19}$.

Let the nodes $V=\left\{ v_{1},v_{2},v_{3},v_{4},v_{5},v_{6}, v_{7},v_{8},v_{9}, v_{10}\right\}$ be the voters of the village. Let us assume that

• (i) if any two voters are very close friend, then the membership and non-membership value of the arc is (0.1, 0.2).

• (ii) if any two voters are close friend, then the arc is (0.2, 0.2).

• (iii) if any two voters are just know, then the arc is (0.3, 0.3)

Let $D=\left\{ v_{1},v_{4},v_{8}\right\}$, be the minimum dominating set in intuitionistic fuzzy graph G.

Here $V-D=\left\{ v_{2},v_{3},v_{5},v_{6}, v_{7},v_{9} v_{10}\right\}$.

Therefore, it is enough for the political leader to meet the voters $v_{1}, v_{4}$ and $v_{8}$ for his successful election campaign.

5 Conclusion

Fuzzy graph theory is finding an increasing number of applications in modeling real time systems where the level of information inherent in the system varies with different levels of precision. Fuzzy models are becoming useful because of their aim in reducing the differences between the traditional numerical models used in engineering and sciences and the symbolic models used in expert systems. This paper identifies double domination number of intuitionistic fuzzy graph G. We have investigated how this parameter is related with many other parameters such as independent sets, end nodes, cut-vertices and minimal dominating sets. By using above parameters on non-split dominating set, may be explored as a future work.