A Brunn–Minkowski type inequality for extended symplectic capacities of convex domains and length estimate for a class of billiard trajectories

Abstract

In this paper, we firstly generalize the Brunn–Minkowski type inequality for Ekeland–Hofer–Zehnder symplectic capacity of bounded convex domains established by Artstein-Avidan–Ostrover in 2008 to extended symplectic capacities of bounded convex domains constructed by authors based on a class of Hamiltonian non-periodic boundary value problems recently. Then we introduce a class of non-periodic billiards in convex domains, and for them we prove some corresponding results to those for periodic billiards in convex domains obtained by Artstein-Avidan–Ostrover in 2012.

1 Introduction and main results

Throughout this paper, a compact, convex subset of ${\mathbb {R}}^m$ with nonempty interior is called a convex body in ${\mathbb {R}}^m$. The set of all convex bodies in ${\mathbb {R}}^m$ is denoted by $\mathcal {K}({\mathbb {R}}^m)$. As usual, a domain in ${\mathbb {R}}^m$ means a connected open subset of ${\mathbb {R}}^m$. For $r>0$ and $p\in {\mathbb {R}}^m$ let $B^{m}(p, r)$ be the open ball centered at p of radius r in ${\mathbb {R}}^m$, and $B^{m}(r):=B^{m}(0, r)$, $B^{m}:=B^{m}(1)$. We always use J to denote standard complex structure on ${\mathbb {R}}^{2n}$, ${\mathbb {R}}^{2n-2}$ and ${\mathbb {R}}^{2}$ without confusions. With the linear coordinates $(q_1,\ldots ,q_n,p_1,\ldots ,p_n)$ on ${\mathbb {R}}^{2n}$ it is given by the matrix

$$\begin{aligned} J=\left( \begin{array}{cc} 0 &{} -I_n \\ I_n &{} 0 \\ \end{array} \right) \end{aligned}$$

where $I_n$ denotes the identity matrix of order n. We also use ${\textrm{GL}}(n)$ and $\textrm{O}(n)$ to denote the set of invertible real matrix and orthogonal real matrix of order n, respectively.

For a convex body $K\subset {\mathbb {R}}^{2n}$ containing 0 in its interior, let

$$\begin{aligned} j_K:{\mathbb {R}}^{2n}\rightarrow {\mathbb {R}},\quad j_K(z)=\inf \left\{ \lambda >0\;\Big |\; \frac{z}{\lambda }\in K\right\} \end{aligned}$$

(1.1)

be the Minkowski functional of K and let

$$\begin{aligned} h_K:{\mathbb {R}}^{2n}\rightarrow {\mathbb {R}},\quad h_K(z)=\sup \{\langle x,z\rangle \,|\,x\in K\} \end{aligned}$$

be the support function of K. The polar body of K is defined by $K^{\circ }=\{x\in {\mathbb {R}}^{2n}\,|\, \langle x,y\rangle \le 1\;\forall y\in K\}$. Then $h_K=j_{K^{\circ }}$ ([15, Theorem 1.7.6]). For two convex bodies $D, K\subset {\mathbb {R}}^{2n}$ containing 0 in their interiors and a real number $p\ge 1$, there exists a unique convex body $D+_pK\subset {\mathbb {R}}^{2n}$ with support function

$$\begin{aligned} {\mathbb {R}}^{2n}\ni w\mapsto h_{D+_pK}(w)=(h^p_{D}(w)+h_{K}^p(w))^{\frac{1}{p}} \end{aligned}$$

([15, Theorem 1.7.1]). $D+_pK$ is called the p-sum of D and K by Firey (cf. [15, (6.8.2)]).

For any two convex bodies $D, K\subset {\mathbb {R}}^{2n}$ containing 0 in their interiors, Artstein-Avidan and Ostrover [2] proved that their Ekeland–Hofer–Zehnder symplectic capacities satisfy the following Brunn–Minkowski type inequality

$$ \begin{aligned} \left( c_{\textrm{EHZ}}(D+_pK)\right) ^{\frac{p}{2}}\ge \left( c_{\textrm{EHZ}}(D)\right) ^{\frac{p}{2}}+ \left( c_{{\textrm{EHZ}}}(K)\right) ^{\frac{p}{2}}, \quad p\in {\mathbb {R}}\; \& \; p\ge 1. \end{aligned}$$

(1.2)

As applications, Artstein-Avidan and Ostrover [3] used them to derive several very interesting bounds and inequalities for the length of the shortest periodic billiard trajectory in a smooth convex body in ${\mathbb {R}}^n$.

Recently, we established extended versions of Ekeland–Hofer and Hofer–Zehnder symplectic capacities in [13],¹ which are not symplectic capacities in general. For the reader’s convenience, we recall the definition of the extended Hofer–Zehnder symplectic capacities with respect to symplectomorphisms on symplectic manifolds (Definition 2.1) and also some related properties in Sect. 2. In particular, for given $\Psi \in \textrm{Sp}(2n,{\mathbb {R}})$ and $B\subset {\mathbb {R}}^{2n}$ such that $B\cap {\textrm{Fix}}(\Psi )\ne \emptyset$, we constructed the extended versions of Ekeland–Hofer capacity $c_\textrm{EH}(B)$ and Hofer–Zehnder capacity $c_\textrm{HZ}(B)$ relative to $\Psi$, denoted respectively by

$$\begin{aligned} c^{\Psi }_\textrm{EH}{(B)} \quad \hbox {and} \quad c^{\Psi }_{\textrm{HZ}}(B). \end{aligned}$$

If $\Psi =I_{2n}$, then $c^{\Psi }_\textrm{EH}(B)=c_\textrm{EH}(B)$ and $c^{\Psi }_\textrm{HZ}(B)=c_\textrm{HZ}(B)$. As the Ekeland–Hofer and Hofer–Zehnder symplectic capacities, $c^{\Psi }_\textrm{EH}$ and $c^{\Psi }_\textrm{HZ}$ agree on any convex body $D\subset {\mathbb {R}}^{2n}$.

In this case we denote

$$\begin{aligned} c^\Psi _{\textrm{EHZ}}(D):=c^\Psi _\textrm{HZ}(D,\omega _0)(=c^\Psi _\textrm{EH}(D)) \end{aligned}$$

and refer to it as extended Ekeland–Hofer–Zehnder capacity of D. Because of these, it is natural to generalize work by Artstein-Avidan and Ostrover [2, 3]. The precise versions will be stated in the following two subsections, respectively.

1.1 A Brunn–Minkowski type inequality for $c^\Psi _{\textrm{EHZ}}$-capacity of convex bodies

Here is the first main result of this paper.

Theorem 1.1

Let $D, K\subset {\mathbb {R}}^{2n}$ be two convex bodies containing 0 in their interiors. Then for any $\Psi \in \textrm{Sp}(2n,{\mathbb {R}})$ and any real $p\ge 1$ it holds that

$$\begin{aligned} \left( c^{\Psi }_{\textrm{EHZ}}(D+_pK)\right) ^{\frac{p}{2}}\ge \left( c^{\Psi }_{\textrm{EHZ}}(D)\right) ^{\frac{p}{2}}+ \left( c^{\Psi }_{\textrm{EHZ}}(K)\right) ^{\frac{p}{2}}. \end{aligned}$$

(1.3)

Moreover, the equality in (1.3) holds if D and K satisfy the condition:

$$\begin{aligned} \left. \begin{array}{ll} &{}\hbox { There exist }c^\Psi _{\textrm{EHZ}}-\hbox { carriers for }D \hbox { and }K, \gamma _D:[0,T]\rightarrow \partial D \hbox { and }\\ &{} \gamma _K:[0,T]\rightarrow \partial K, \hbox { such that they coincide up to dilation and }\\ &{}\hbox { translation by elements in }{\textrm{Ker}}(\Psi -I_{2n}), i.e., \gamma _D=\alpha \gamma _K+ \textbf{b}\\ &{}\hbox { for some }\alpha \in {\mathbb {R}}\setminus \{0\} \hbox { and }{\textbf{b}}\in {\textrm{Ker}}(\Psi -I_{2n})\subset {\mathbb {R}}^{2n}. \end{array}\right\} \end{aligned}$$

(1.4)

When $p>1$ the condition (1.4) is also necessary for the equality in (1.3) holding.

Readers can refer to Definition 2.7 for the concept of $c^\Psi _{\textrm{EHZ}}$-carriers for a convex body. Theorem 1.1 has some interesting corollaries, see Sect. 3.2.

1.2 Length estimate for a class of non-periodic billiard trajectories in convex domains

Using the inequality (1.2) and its corollaries Artstein-Avidan and Ostrover [3] studied the length estimates of the shortest periodic billiard trajectory in a smooth convex body in ${\mathbb {R}}^n$ and obtained some very interesting results. Since the Ekeland–Hofer capacity of a smooth convex body $D\subset {\mathbb {R}}^{2n}$ is equal to the minimum of absolute values of actions of closed characteristics on the boundary $\partial D$, and we generalized this relation to our extended Ekeland–Hofer–Zehnder capacity $c^\Psi _{\textrm{EHZ}}(D)$ and $\Psi$-characteristics on $\partial D$ in [13], it is natural using Theorem 1.1 or Corollaries 3.5, 3.6 to study corresponding conclusions for some non-periodic billiard trajectory in a smooth convex body in ${\mathbb {R}}^n$, which motivates the following definitions.

Definition 1.2

For a convex body $\Omega \subset {\mathbb {R}}^n$ with boundary $\partial \Omega$ of class $C^2$ and $A\in \textrm{O}(n)$, a nonconstant, continuous, and piecewise $C^\infty$ path $\sigma :[0,T]\rightarrow \overline{\Omega }$ with $\sigma (T)=A\sigma (0)$ is called an A -billiard trajectory in $\Omega$ if there exists a finite set $\mathscr {B}_\sigma \subset (0, T)$ such that $\ddot{\sigma }\equiv 0$ on $(0, T)\setminus \mathscr {B}_\sigma$ and the following conditions are also satisfied:

(ABi):

$\sharp \mathscr {B}_\sigma \ge 1$ and $\sigma (t)\in \partial \Omega \;\forall t\in \mathscr {B}_\sigma$.

(ABii):

For each $t\in \mathscr {B}_\sigma$, $\dot{\sigma }^\pm (t):=\lim _{\tau \rightarrow t\pm }\dot{\sigma }(\tau )$ fulfils the equation

$$\begin{aligned} \dot{\sigma }^+(t)+\dot{\sigma }^-(t)\in T_{\sigma (t)}\partial \Omega ,\quad \dot{\sigma }^+(t)-\dot{\sigma }^-(t)\in (T_{\sigma (t)}\partial \Omega )^\bot \setminus \{0\}. \end{aligned}$$

(1.5)

(So $|\dot{\sigma }^+(t)|^2-|\dot{\sigma }^-(t)|^2=\langle \dot{\sigma }^+(t)+\dot{\sigma }^-(t), \dot{\sigma }^+(t)-\dot{\sigma }^-(t)\rangle _{{\mathbb {R}}^n}=0$ for each $t\in \mathscr {B}_\sigma$, that is, $|\dot{\sigma }|$ is constant on $(0, T)\setminus \mathscr {B}_\sigma$.) Let

$$\begin{aligned} \dot{\sigma }^+(0)=\lim _{t\rightarrow 0+}\dot{\sigma }(t)\quad \hbox {and}\quad \dot{\sigma }^-(T)=\lim _{t\rightarrow T-}\dot{\sigma }(t). \end{aligned}$$

(1.6)

If $\sigma (0)\in \partial \Omega$ (resp. $\sigma (T)\in \partial \Omega$) let $\dot{{\sigma }}^-(0)$ (resp. $\dot{{\sigma }}^+(T)$) be the unique vector satisfying

$$\begin{aligned} \dot{\sigma }^+(0)+\dot{{\sigma }}^-(0)\in T_{\sigma (0)}\partial \Omega ,\quad \dot{\sigma }^+(0)-\dot{{\sigma }}^-(0)\in (T_{\sigma (0)}\partial \Omega )^\bot \end{aligned}$$

(1.7)

(resp.

$$\begin{aligned} \dot{{\sigma }}^+(T)+\dot{\sigma }^-(T)\in T_{\sigma (T)}\partial \Omega ,\quad \dot{{\sigma }}^+(T)-\dot{\sigma }^-(T)\in (T_{\sigma (T)}\partial \Omega )^\bot . ) \end{aligned}$$

(1.8)

(ABiii):

If $\{\sigma (0), \sigma (T)\}\in \textrm{int} \Omega$ then

$$\begin{aligned} A\dot{\sigma }^+(0)=\dot{\sigma }^-(T). \end{aligned}$$

(1.9)

(ABiv):

If $\sigma (0)\in \partial \Omega$ and $\sigma (T)\in \textrm{int}\Omega$, then either (1.9) holds, or

$$\begin{aligned} A\dot{{\sigma }}^-(0)=\dot{\sigma }^-(T). \end{aligned}$$

(1.10)

(ABv):

If $\sigma (0)\in \textrm{int}\Omega$ and $\sigma (T)\in \partial \Omega$, then either (1.9) holds, or

$$\begin{aligned} A\dot{\sigma }^+(0)=\dot{{\sigma }}^+(T). \end{aligned}$$

(1.11)

(ABvi):

If $\{\sigma (0), \sigma (T)\}\in \partial \Omega$, then either (1.9) or (1.10) or (1.11) holds, or

$$\begin{aligned} A\dot{{\sigma }}^-(0)=\dot{{\sigma }}^+(T). \end{aligned}$$

(1.12)

Remark 1.3

(i):

For each $t\in \mathcal {B}_\sigma$, (1.5) is a reflection condition which describes the motion of a billiard when arriving at the boundary of the billiard table.

(ii):

Roughly speaking, A-billiard trajectory requires a billiard trajectory to satisfy boundary conditions for starting position and ending position, as well as for starting velocity and ending velocity. If $A=I_n$, an A-billiard trajectory becomes periodic (or closed). In this case, $\sigma (T)=\sigma (0)$ and (ABiv) and (ABv) do not occur. If (ABiii) holds then all bounce times of this periodic billiard trajectory $\sigma$ consist of elements of $\mathscr {B}_\sigma$. If $\sigma (0)=\sigma (T)\in \partial \Omega$ and either (1.9) or (1.12) holds then the periodic billiard trajectory $\sigma$ is tangent to $\partial \Omega$ at $\sigma (0)$, and so the set of its bounce times is also $\mathscr {B}_\sigma$. When $\sigma (0)=\sigma (T)\in \partial \Omega$ and either (1.10) or (1.11) holds, it follows from (1.7)–(1.8) that

$$\begin{aligned} \dot{\sigma }^+(0)+\dot{{\sigma }}^-(T)\in T_{\sigma (0)}\partial \Omega \quad \hbox {and}\quad \dot{\sigma }^+(0)-\dot{{\sigma }}^-(T)\in (T_{\sigma (0)}\partial \Omega )^\bot . \end{aligned}$$

When $\dot{\sigma }^+(0)-\dot{{\sigma }}^-(T)= 0$, the set of all bounce times of this periodic billiard trajectory $\sigma$ is $\mathscr {B}_\sigma$. When $\dot{\sigma }^+(0)-\dot{{\sigma }}^-(T)= \ne 0$, the set of all bounce times of this periodic billiard trajectory $\sigma$ is $\mathscr {B}_\sigma \cup \{0\}=\mathscr {B}_\sigma \cup \{T\}$ (because 0 and T are identified).

(iii):

If $A\ne I_n$, an A-billiard trajectory in $\Omega$ might not be periodic even if $\sigma (0)=\sigma (T)$ since the starting velocity and ending velocity may not satisfy the condition for periodic billiard trajectory.

The existence of A-billiard trajectories in $\Omega$ will be studied in other places.

Definition 1.2 can be generalized to convex domain with non-smooth boundary. Recall that for a convex body $\Delta \in {\mathbb {R}}^n$ and $q\in \partial \Delta$

$$\begin{aligned} N_{\partial \Delta }(q)=\{y\in {\mathbb {R}}^{2n}\,|\, \langle u-q, y\rangle \le 0\;\forall u\in \Delta \} \end{aligned}$$

is the normal cone to $\Delta$ at $q\in \partial \Delta$. $y\in N_{\partial \Delta }(q)$ is called an outward support vector of $\Delta$ at $q\in \partial \Delta$. It is unique if q is a smooth point of $\partial \Delta$. Corresponding to the generalized periodic billiard trajectory introduced by Ghomi [9], we have the following generalized version of the billiard trajectory in Definition 1.2.

Definition 1.4

For a convex body in $\Delta \subset {\mathbb {R}}^n$ and $A\in \textrm{O}(n)$, a generalized A-billiard trajectory in $\Delta$ is defined to be a finite sequence of points in $\Delta$

$$\begin{aligned} q=q_0,q_1,\ldots ,q_m=Aq \end{aligned}$$

with the following properties:

(AGBi):

$m\ge 2$ and $\{q_1,\ldots ,q_{m-1}\}\subset \partial \Delta$.

(AGBii):

Both $q_0,\ldots ,q_{m-1}$ and $q_1,\ldots ,q_m$ are sequences of distinct points.

(AGBiii):

For every $i=1,\ldots ,m-1$,

$$\begin{aligned} \nu _i:=\frac{q_i-q_{i-1}}{\Vert q_i-q_{i-1}\Vert }+ \frac{q_{i}-q_{i+1}}{\Vert q_{i}-q_{i+1}\Vert } \end{aligned}$$

is an outward support vector of $\Delta$ at $q_i$.

(AGBiv):

If $\{q, Aq\}\subset \textrm{int}(\Delta )$ then

$$\begin{aligned} \frac{A(q_1-q_{0})}{\Vert q_1-q_{0}\Vert }=\frac{q_m-q_{m-1}}{\Vert q_m-q_{m-1}\Vert }. \end{aligned}$$

(1.13)

(AGBv):

If $q\in \partial \Delta$ and $Aq\in \textrm{int}(\Delta )$, then either (1.13) holds or there exists a unit vector $b_0\in {\mathbb {R}}^n$ such that

$$\begin{aligned} \nu _0:=b_0-\frac{q_1-q_{0}}{\Vert q_1-q_{0}\Vert }\in N_{\partial \Delta }(q) \quad {\textrm{and}}\quad Ab_0=\frac{q_m-q_{m-1}}{\Vert q_m-q_{m-1}\Vert }. \end{aligned}$$

(1.14)

(AGBvi):

If $q\in \textrm{int}(\Delta )$ and $Aq\in \partial \Delta$, then either (1.13) holds or there exists a unit vector $b_m\in {\mathbb {R}}^n$ such that

$$\begin{aligned} \nu _m:=\frac{q_m-q_{m-1}}{\Vert q_m-q_{m-1}\Vert }-b_m\in N_{\partial \Delta }(Aq)\quad \textrm{and}\quad \frac{A(q_1-q_{0})}{\Vert q_1-q_{0}\Vert }=b_m. \end{aligned}$$

(1.15)

(AGBvii):

If $\{q,Aq\}\subset \partial \Delta$, then either (1.13) or (1.14) or (1.15) holds, or there exist unit vectors $b'_0, b'_m\in {\mathbb {R}}^n$ such that

$$\begin{aligned} \nu _0:=\!b'_0\!-\!\frac{q_1\!-\!q_{0}}{\Vert q_1\!-\!q_{0}\Vert }\in N_{\partial \Delta }(q),\, \nu _m\!:=\!\frac{q_m-q_{m-1}}{\Vert q_m-q_{m-1}\Vert }-b'_m\in N_{\partial \Delta }(Aq) \,\hbox {and}\, Ab'_0=b'_m. \end{aligned}$$

(1.16)

Remark 1.5

(i):

It is easily checked that a generalized $I_n$-billiard trajectory in $\Delta$ is exactly a generalized periodic billiard trajectory in the sense of [9].

(ii):

For a smooth convex body in $\Delta \subset {\mathbb {R}}^n$ and $A\in \textrm{O}(n)$, a nonconstant, continuous, and piecewise $C^\infty$ path $\sigma :[0,T]\rightarrow \Delta$ with $\sigma (T)=A\sigma (0)$ is an A-billiard trajectory in $\Delta$ with $\mathscr {B}_\sigma =\{t_1<\cdots <t_{m-1}\}$ if and only if the sequence

$$\begin{aligned} q_0=\sigma (0), q_1=\sigma (t_1),\ldots , q_{m-1}=\sigma (t_{m-1}), q_m=\sigma (T) \end{aligned}$$

is a generalized A-billiard trajectory in $\Delta$.

In order to study A-billiard via extended Ekeland–Hofer–Zehnder capacity, we will define $(A, \Delta , \Lambda )$-billiard trajectory for $A\in {\textrm{GL}}(n)$ and convex domians $\Delta \subset {\mathbb {R}}^n_q$ and $\Lambda \subset {\mathbb {R}}^n_p$, following the idea in [3] which defines closed $(\Delta ,\Lambda )$-billiard trajectory.

Suppose that $\Delta \subset {\mathbb {R}}^n_q$ and $\Lambda \subset {\mathbb {R}}^n_p$ are two smooth convex bodies containing the origin in their interiors. Then $\Delta \times \Lambda$ is a smooth manifold with corners $\partial \Delta \times \partial \Lambda$ in the standard symplectic space $({\mathbb {R}}^{2n},\omega _0)=({\mathbb {R}}^n_q\times {\mathbb {R}}^n_p, dq\wedge dp)$. Note that $\partial (\Delta \times \Lambda )=(\partial \Delta \times \partial \Lambda )\cup ({\textrm{Int}}(\Delta )\times \partial \Lambda )\cup (\partial \Delta \times {\textrm{Int}}(\Lambda ))$. Since $j_{\Delta \times \Lambda }(q,p)=\max \{j_\Delta (q), j_\Lambda (p)\}$, we have

$$\begin{aligned} \nabla j_{\Delta \times \Lambda }(q,p)=\left\{ \begin{array}{cc} (0,\nabla j_\Lambda (p)) &{}\forall (q,p)\in {\textrm{Int}}(\Delta )\times \partial \Lambda , \\ (\nabla j_\Delta (q),0) &{}\forall (q,p)\in \partial \Delta \times {\textrm{Int}}(\Lambda ). \end{array} \right. \end{aligned}$$

Moreover, for $(q,p)\in \partial \Delta \times \partial \Lambda$ there holds

$$\begin{aligned} N_{\partial (\Delta \times \Lambda )}(q,p)= & {} \{(y_1,y_2)\;|\;y_1\in N_{\partial \Delta }(q),\; y_2\in N_{\partial \Lambda }(p)\}\\= & {} \{\mu (\nabla j_\Delta (q),0)+\lambda (0,\nabla j_\Lambda (p))\;|\;\lambda \ge 0,\;\mu \ge 0\}. \end{aligned}$$

Define

$$\begin{aligned} \mathfrak {X}(q,p):=J\nabla j_{\Delta \times \Lambda }(q,p)=\left\{ \begin{array}{cc} (-\nabla j_\Lambda (p),0) &{}\forall (q,p)\in {\textrm{Int}}(\Delta )\times \partial \Lambda , \\ (0, \nabla j_\Delta (q)) &{}\forall (q,p)\in \partial \Delta \times {\textrm{Int}}(\Lambda ). \end{array} \right. \end{aligned}$$

It is well-known that every $A\in {\textrm{GL}}(n)$ induces a natural linear symplectomorphism

$$\begin{aligned} \Psi _A:{\mathbb {R}}^n_q\times {\mathbb {R}}^n_p\rightarrow {\mathbb {R}}^n_q\times {\mathbb {R}}^n_p,\;(q, v)\mapsto (Aq, (A^t)^{-1}v), \end{aligned}$$

(1.17)

where $A^t$ is the transpose of A.

Definition 1.6

Let $A\in {\textrm{GL}}(n)$, and let $\Delta \subset {\mathbb {R}}^n_q$ and $\Lambda \subset {\mathbb {R}}^n_p$ be two smooth convex bodies containing the origin in their interiors. A continuous and piecewise smooth map $\gamma :[0, T]\rightarrow \partial (\Delta \times \Lambda )$ with $\gamma (T)=\Psi _A\gamma (0)$ is called an $(A, \Delta , \Lambda )$-billiard trajectory if

(BT1):

for some positive constant $\kappa$ it holds that $\dot{\gamma }(t)=\kappa \mathfrak {X}(\gamma (t))$ on $[0, T]{\setminus }\gamma ^{-1}(\partial \Delta \times \partial \Lambda )$;

(BT2):

$\gamma$ has a right derivative $\dot{\gamma }^+(t)$ at any $t\in \gamma ^{-1}(\partial \Delta \times \partial \Lambda ){\setminus }\{T\}$ and a left derivative $\dot{\gamma }^-(t)$ at any $t\in \gamma ^{-1}(\partial \Delta \times \partial \Lambda ){\setminus }\{0\}$, and $\dot{\gamma }^\pm (t)$ belong to

$$\begin{aligned} \{-\lambda (\nabla j_\Lambda (\gamma _p(t)),0)+\mu (0,\nabla j_\Delta (\gamma _q(t)))\,|\, \lambda \ge 0, \;\mu \ge 0,\;(\lambda ,\mu )\ne (0,0)\} \end{aligned}$$

(1.18)

with $\gamma (t)=(\gamma _q(t),\gamma _p(t))$.

Remark 1.7

(i):

Every $(A, \Delta , \Lambda )$-billiard trajectory is a generalized $\Psi _A$-characteristic on $\partial (\Delta \times \Lambda )$ in the sense of Definition 2.4(ii). In fact, we only need to note that for $(q,p)\in \partial \Delta \times {\textrm{Int}} (\Lambda )\cup (\mathrm Int)\Delta \times \partial \Lambda$ there holds

$$\begin{aligned} \mathfrak {X}(q,p)=J\nabla j_{\Delta \times \Lambda }(q,p) \end{aligned}$$

and for $(q,p)\in \partial \Delta \times \partial \Lambda$ there holds

$$\begin{aligned} JN_{\partial (\Delta \times \Lambda )}=\{-\lambda (\nabla j_\Lambda (\gamma _p(t)),0)+\mu (0,\nabla j_\Delta (\gamma _q(t)))\,|\, \lambda \ge 0, \;\mu \ge 0,\;(\lambda ,\mu )\ne (0,0)\}. \end{aligned}$$

(ii):

For a given $A\in {\textrm{GL}}(n)$, we can generalize Definition 1.6 to smooth convex bodies $\Delta \subset {\mathbb {R}}^n_q$ and $\Lambda \subset {\mathbb {R}}^n_p$ satisfying

$$\begin{aligned} {\textrm{Fix}}(A)\cap {{\textrm{Int}}}(\Delta )\ne \emptyset \quad \hbox {and}\quad {\textrm{Fix}}(A^t)\cap {\textrm{Int}}(\Lambda )\ne \emptyset , \end{aligned}$$

(1.19)

(which not necessarily contain the origin in their interiors). In this case, a continuous and piecewise smooth map $\gamma :[0, T]\rightarrow \partial (\Delta \times \Lambda )$ is said to be an $(A, \Delta , \Lambda )$-billiard trajectory if there exists $\bar{q}\in {\textrm{Fix}}(A)\cap {\textrm{Int}}(\Delta )$ and $\bar{p}\in {\textrm{Fix}}(A^t)\cap {\textrm{Int}}(\Lambda )$ such that $\gamma -(\bar{q},\bar{p})$ is an $(A, \Delta -\bar{q}, \Lambda -\bar{p})$-billiard trajectory in the sense of Definition 1.6. (Here $\gamma -(\bar{q},\bar{p})$ is the composition of $\gamma$ and the affine linear symplectomorphism

$$\begin{aligned} \Phi _{(\bar{q},\bar{p})}:{\mathbb {R}}^n_q\times {\mathbb {R}}^n_p\rightarrow {\mathbb {R}}^n_q\times {\mathbb {R}}^n_p,\;(u, v)\mapsto (u-\bar{q}, v-\bar{p}), \end{aligned}$$

(1.20)

which commutes with $\Psi _A$.) The condition (1.19) insures that

$$\begin{aligned} {\textrm{Int}}(\Delta \times \Lambda )\cap {\textrm{Fix}}(\Psi _A)\ne \emptyset \end{aligned}$$

so that $c^{\Psi _A}_{\textrm{EHZ}}(\Delta \times \Lambda )$ is well defined and we can associate the lengths of $(A, \Delta ,\Lambda )$-billiard trajectories with it.

Corresponding to the classification for closed $(\Delta ,\Lambda )$-trajectories in [3] we introduce:

Definition 1.8

Let A, $\Delta$ and $\Lambda$ satisfy (1.19). An $(A, \Delta , \Lambda )$-billiard trajectory is called proper (resp. gliding) if $\gamma ^{-1}(\partial \Delta \times \partial \Lambda )$ is a finite set (resp. $\gamma ^{-1}(\partial \Delta \times \partial \Lambda )=[0,T]$, i.e., $\gamma ([0,T])\subset \partial \Delta \times \partial \Lambda$ completely).

For $A\in {\textrm{GL}}(n,{\mathbb {R}}^n)$ and convex bodies $\Delta \subset {\mathbb {R}}^n_q$ and $\Lambda \subset {\mathbb {R}}^n_p$ satisfying (1.19), we define

$$\begin{aligned} \xi ^A_\Lambda (\Delta )=c^{\Psi _A}_{\textrm{EHZ}}(\Delta \times \Lambda )\quad \hbox {and}\quad \xi ^A(\Delta )=c^{\Psi _A}_{\textrm{EHZ}}(\Delta \times B^n). \end{aligned}$$

(1.21)

If $A=I_n$ then $\xi ^A(\Delta )$ becomes $\xi (\Delta )$ defined in [3, p. 177]. Clearly, $\xi ^A_{\Lambda _1}(\Delta _1)\le \xi ^A_{\Lambda _2}(\Delta _2)$ if both are well-defined and $\Lambda _1\subset \Lambda _2$ and $\Delta _1\subset \Delta _2$.

In Sect. 4, based on studies on the above several classes of billiard trajectories we show in Proposition 4.4 that $\xi ^A(\Delta )$ provides a positive lower bound for infimum of length of A-billiard trajectories in $\Delta$. Therefore it is important to study properties of $\xi ^A(\Delta )$ and more general $\xi ^A_\Lambda (\Delta )$. As in the proof of [3, Theorem 1.1] using Corollary 3.5 we may derive the following Brunn–Minkowski type inequality for $\xi ^A_\Lambda$, which is the second main result of this paper.

Theorem 1.9

For $A\in {\textrm{GL}}(n)$, suppose that convex bodies $\Delta _1, \Delta _2\subset {\mathbb {R}}^n_q$ and $\Lambda \subset {\mathbb {R}}^n_p$ satisfy ${\textrm{Int}}(\Delta _1)\cap {\textrm{Fix}}(A)\ne \emptyset$, ${\textrm{Int}}(\Delta _2)\cap {\textrm{Fix}}(A)\ne \emptyset$ and ${\textrm{Int}}(\Lambda )\cap {\textrm{Fix}}(A^t)\ne \emptyset$. Then

$$\begin{aligned} \xi ^A_\Lambda (\Delta _1+\Delta _2)\ge \xi ^A_\Lambda (\Delta _1)+ \xi ^A_\Lambda (\Delta _2) \end{aligned}$$

(1.22)

and the equality holds if there exist $c^{\Psi _A}_{\textrm{EHZ}}$-carriers for $\Delta _1\times \Lambda$ and $\Delta _2\times \Lambda$ which coincide up to dilation and translation by elements in $\textrm{Ker}(\Psi _A-I_{2n})$.

When $\Lambda =B^n$ and $A=I_{n}$, this result was first proved in [3], and Irie also gave a new proof in [12].

In order to estimate $\xi ^A(\Delta )$, for a symplectic matrix $\Psi \in \textrm{Sp}(2n,{\mathbb {R}})$ we define

$$\begin{aligned} g^{\Psi }:{\mathbb {R}}\rightarrow {\mathbb {R}}, \,s\mapsto \det (\Psi -e^{sJ}), \end{aligned}$$

(1.23)

where $e^{tJ}=\sum ^\infty _{k=0}\frac{1}{k!}t^k J^k$. The set of zeros of $g^{\Psi }$ in $(0, 2\pi ]$ is a nonempty finite set ([13, Lemma A.1]) and

$$\begin{aligned} \mathfrak {t}(\Psi ):=\min \{t\in (0, 2\pi ]\,|\, g^{\Psi }(t)=0\}=2c^{\Psi }_{\textrm{EHZ}}(B^{2n}) \end{aligned}$$

(1.24)

by [13, (1.28)]. In particular, if $\Psi =I_{2n}$ then $\mathfrak {t}(\Psi )=2\pi$ ([13, Lemma A.1]) and (1.24) becomes $c_{\textrm{EHZ}}(B^{2n})=\pi$. Since $\Psi _A=\textrm{diag}(A, (A^t)^{-1})$ for $A\in GL(n)$, by [13, Lemma A.5], $\mathfrak {t}(\Psi _A)$ is equal to the smallest zero in $(0, 2\pi ]$ of the function

$$\begin{aligned} {\mathbb {R}}\rightarrow {\mathbb {R}},\;\,s\mapsto \det (I_n+ (A^t)^{-1}A-\cos s (A+ (A^t)^{-1})). \end{aligned}$$

(1.25)

(It must exist!) Moreover, if A is an orthogonal matrix similar to one of form [13, (A.2)], i.e.,

$$\begin{aligned} A= \textrm{diag}\left( \left( \begin{array}{cc} \cos \theta _1 &{} \sin \theta _1 \\ -\sin \theta _1 &{} \cos \theta _1\\ \end{array} \right) ,\ldots , \left( \begin{array}{cc} \cos \theta _m &{} \sin \theta _m \\ -\sin \theta _m &{} \cos \theta _m\\ \end{array} \right) , I_k, -I_l\right) , \end{aligned}$$

where $2\,m+k+l=n$ and $0<\theta _1\le \cdots \le \theta _m<\pi$, then

$$\begin{aligned} \mathfrak {t}(\Psi _A)=\left\{ \begin{array}{lll} \theta _1 &{}\hbox {if}\;m>0, \\ \pi &{}\hbox { if }\; m=0\,\,and\,\,l>0,\\ 2\pi &{}\hbox { if }\; m=l=0. \end{array}\right. \end{aligned}$$

(1.26)

The width of a convex body $\Delta \subset {\mathbb {R}}^n_q$ is the thickness of the narrowest slab which contains $\Delta$, i.e., $\textrm{width}(\Delta )=\min \{h_\Delta (u)+ h_\Delta (-u)\,|\, u\in S^n\}$, where $S^n=\{u\in {\mathbb {R}}^n\;|\;\Vert u\Vert =1\}$. Let

$$\begin{aligned}{} & {} S^n_\Delta :=\{u\in S^n\,|\, {\textrm{width}}(\Delta )=h_\Delta (u)+ h_\Delta (-u)\}, \end{aligned}$$

(1.27)

$$\begin{aligned}{} & {} H_u:=\{x\in {\mathbb {R}}^n\,|\,\langle x, u\rangle =(h_\Delta (u)- h_\Delta (-u))/2\},\end{aligned}$$

(1.28)

$$\begin{aligned}{} & {} Z^{2n}_\Delta :=([-\textrm{width}(\Delta )/2, \textrm{width}(\Delta )/2]\times {\mathbb {R}}^{n-1})\times ([-1,1]\times {\mathbb {R}}^{n-1}). \end{aligned}$$

(1.29)

Proposition 1.10

Let $A\in {\textrm{GL}}(n)$ and a convex body $\Delta \subset {\mathbb {R}}^n_q$ satisfy ${\textrm{Fix}}(A)\cap {\textrm{Int}}(\Delta )\ne \emptyset$.

• (i) If $\Delta$ contains a ball $B^{n}(\bar{q},r)$ with $A\bar{q}=\bar{q}$, then

  $$\begin{aligned} \xi ^A(\Delta )\ge rc^{\Psi _A}_{\textrm{EHZ}}(B^n\times B^n,\omega _0)\ge \frac{r \mathfrak {t}(\Psi _A)}{2}. \end{aligned}$$

  (1.30)

• (ii) For any $u\in S^n_\Delta$, $\bar{q}\in H_u$ and any $\textbf{O}\in O(n)$ such that $\textbf{O}u=e_1=(1,0,\ldots ,0)\in {\mathbb {R}}^n$ let

  $$\begin{aligned} \Psi _{\textbf{O}, \bar{q}}:{\mathbb {R}}^n_q\times {\mathbb {R}}^n_p\rightarrow {\mathbb {R}}^n_q\times {\mathbb {R}}^n_p,\;(q, v)\mapsto (\textbf{O}(q-\bar{q}), \textbf{O}v), \end{aligned}$$

  (1.31)

  that is, the composition of translation $(q,v)\mapsto (q-\bar{q},v)$ and $\Psi _\textbf{O}$ defined by (1.17), then

  $$\begin{aligned} \xi ^A(\Delta )\le c_{\textrm{EHZ}}^{\Psi _{\textbf{O}, \bar{q}}\Psi _A\Psi _{\textbf{O}, \bar{q}}^{-1}}(Z^{2n}_\Delta , \omega _0). \end{aligned}$$

  (1.32)

  Moreover, the right-side is equal to $c_{\textrm{EHZ}}^{\Psi _{\textbf{O}}\Psi _A\Psi _{\textbf{O}}^{-1}}(Z^{2n}_\Delta , \omega _0)$ if $A\bar{q}=\bar{q}$, and to $c_{\textrm{EHZ}}^{\Psi _A}(Z^{2n}_\Delta , \omega _0)$ if $A\bar{q}=\bar{q}$ and $A\textbf{O}=\textbf{O}A$.

By Proposition 4.4 and (1.30) we immediately get our third main result.

Theorem 1.11

For $A\in \textrm{O}(n)$ and a smooth convex body $\Delta \subset {\mathbb {R}}^n_q$ with ${\textrm{Fix}}(A)\cap {\textrm{Int}}(\Delta )\ne \emptyset$, if $\Delta$ contains a ball $B^{n}(\bar{q},r)$ with $A\bar{q}=\bar{q}$ then it holds that

$$\begin{aligned} \frac{r \mathfrak {t}(\Psi _A)}{2}\le \inf \{ L(\sigma )\,|\,\sigma \hbox { is an }A\!-\!\hbox {billiard trajectory in }\Delta \}. \end{aligned}$$

(1.33)

Recall that the inradius of a convex body $\Delta \subset {\mathbb {R}}^n_q$ is the radius of the largest ball contained in $\Delta$, i.e., ${\textrm{inradius}}(\Delta )=\sup _{x\in \Delta }{\textrm{dist}}(x,\partial \Delta )$. For any centrally symmetric convex body $\Delta \subset {\mathbb {R}}^n_q$, Artstein-Avidan, Karasev, and Ostrover recently proved in [4, Theorem 1.7]:

$$\begin{aligned} c_{\textrm{HZ}}(\Delta \times \Delta ^\circ ,\omega _0)=4. \end{aligned}$$

(1.34)

As a consequence of this and (1.33) we obtain:

Corollary 1.12

(Ghomi [9]) Every periodic billiard trajectory $\sigma$ in a centrally symmetric convex body $\Delta \subset {\mathbb {R}}^n_q$ has length $L(\sigma )\ge 4\, \textrm{inradius}(\Delta )$.

Proof

Since $c^{\Psi _A}_\textrm{HZ}=c_\textrm{HZ}$ for $A=I_n$, from the first inequality in (1.30) and (1.34) we deduce

$$\begin{aligned} \xi (\Delta ):=\xi ^{I_n}(\Delta )\ge 4\, \textrm{inradius}(\Delta ). \end{aligned}$$

(1.35)

When $\Delta$ is smooth, since $\xi (\Delta )$ is equal to the length of the shortest periodic billiard trajectory in $\Delta$ (see the bottom of [3, p. 177]), we get $L(\sigma )\ge 4\, \textrm{inradius}(\Delta )$. (In this case another new proof of [9, Theorem 1.2] was also given by Irie [12, Theorem 1.9].) For general case we may approximate $\Delta$ by a smooth convex body $\Delta ^*\supseteq \Delta$ such that $\sigma$ is also periodic billiard trajectory $\Delta ^*$. Thus $L(\sigma )\ge \xi (\Delta ^*)\ge \xi (\Delta )\ge 4\, {\textrm{inradius}}(\Delta )$ because of monotonicity of $c_{\textrm{HZ}}$. $\square$

Remark 1.13

• (i) Corollary 1.12 only partially recover [9, Theorem 1.2] by Ghomi. [9, Theorem 1.2] did not require $\Delta$ to be centrally symmetric. It also stated that $L(\sigma )=4\, \textrm{inradius}(\Delta )$ for some $\sigma$ if and only if $\textrm{width}(\Delta )=4\, \textrm{inradius}(\Delta )$.

• (ii) When $A=I_n$ we may take $r=\textrm{inradius}(\Delta )$ in (1.33), and get a weaker result than Corollary 1.12: $L(\sigma )\ge \pi \textrm{inradius}(\Delta )$ for every periodic billiard trajectory $\sigma$ in $\Delta$.

• (iii) In order to get a corresponding result for each A-billiard trajectory in $\Delta$ as in Corollary 1.12, an analogue of (1.35) is needed. Hence we expect that (1.34) has the following generalization:

  $$\begin{aligned} c^{\Psi _A}_{\textrm{EHZ}}(\Delta \times \Delta ^\circ )=\frac{2}{\pi } \mathfrak {t}(\Psi _A). \end{aligned}$$

  (1.36)

For a bounded domain $\Omega \subset {\mathbb {R}}^n$ with smooth boundary, there exist positive constants $C_n$, $C_n'$ only depending on n, C independent of n, and (possibly different) periodic billiard trajectories $\gamma _1$, $\gamma _2$, $\gamma _3$ in $\Omega$ such that their length satistfies

$$\begin{aligned}{} & {} L(\gamma _1)\le C_n{\textrm{Vol}}(\Omega )^{\frac{1}{n}}(\text {Viterbo} [18]), \end{aligned}$$

(1.37)

$$\begin{aligned}{} & {} L(\gamma _2)\le C{\textrm{diam}}(\Omega ) {\text {(Albers and Mazzucchelli}}[1]), \end{aligned}$$

(1.38)

$$\begin{aligned}{} & {} L(\gamma _3)\le C_n'{\textrm{inradius}}(\Omega ) {\text {(Irie} [11])}, \end{aligned}$$

(1.39)

where $\textrm{inradius}(\Omega )$ is the inradius of $\Omega$, i.e., the radius of the largest ball contained in $\Omega$. If $\Omega$ is a smooth convex body $\Delta \subset {\mathbb {R}}^n_q$, Artstein-Avidan and Ostrover [3] recently obtained the following more concrete estimates than (1.39) and (1.37):

$$\begin{aligned}{} & {} \xi (\Delta )\le 2(n+1){\textrm{inradius}}(\Delta ), \end{aligned}$$

(1.40)

$$\begin{aligned}{} & {} \xi (\Delta )\le C'\sqrt{n}{\textrm{Vol}}(\Delta )^{\frac{1}{n}}, \end{aligned}$$

(1.41)

where $C'$ is a positive constant independent of n.

Remark 1.14

Since $c^{\Psi _A}_\textrm{HZ}=c_\textrm{HZ}$ for $A=I_n$, from (1.32) we recover (1.40) as follows

$$\begin{aligned} \xi (\Delta )=\xi ^{I_n}(\Delta )\le c_{\textrm{HZ}}(Z^{2n}_\Delta , \omega _0) =2{\textrm{width}}(\Delta )\le 2(n+1){\textrm{inradius}}(\Delta ) \end{aligned}$$

because ${\textrm{width}}(\Delta )\le (n+1){\textrm{inradius}}(\Delta )$ by [16, (1.2)].

Finally, we have an improvement for (1.38) in the case that $\Omega$ is a smooth convex body.

Theorem 1.15

For a smooth convex body $\Delta \subset {\mathbb {R}}^n_q$, suppose that periodic billiard trajectories in $\Delta$ include projections to $\Delta$ of periodic gliding billiard trajectories in $\Delta \times B^n$. Then

$$\begin{aligned} L(\sigma )\le \pi \textrm{diam}(\Delta ) \end{aligned}$$

for some periodic billiard trajectory $\sigma$ in $\Delta$.

Organization of the paper. Section 3 proves Theorem 1.1 and Corollaries 3.5, 3.6. In Sect. 4 we give the classification of $(A, \Delta , \Lambda )$-billiard trajectories and studied related properties of proper trajectories. Theorems 1.9, 1.15 and Proposition 1.10 will be proved In Sect. 5.

2 The extended Hofer–Zehnder symplectic capacities

For convenience we review the extended Hofer–Zehnder symplectic capacities and related results in [13]. Given a symplectic manifold $(M,\omega )$ and a symplectomorphism $\Psi \in \textrm{Symp}(M,\omega )$, let $O\subset M$ be an open subset such that $O\cap {\textrm{Fix}}(\Psi )\ne \emptyset$. Denote by $\mathcal {H}^\Psi (O,\omega )$ the set of smooth functions $H :O\rightarrow {\mathbb R}$ satisfying

• (i) there exists a nonempty open subset $U\subset O$ (depending on H) such that $U\cap {\textrm{Fix}}(\Psi )\ne \emptyset$ and $H|_U=0$,

• (ii) there exists a compact subset $K\subset O{\setminus }\partial O$ (depending on H) such that $H|_{O{\setminus } K}=m(H):=\max H$,

• (iii) $0\le H\le m(H)$.

Denote by $X_H$ the Hamiltonian vector field defined by $\omega (X_H, \cdot )=-dH$. Note that for $H\in \mathcal {H}^\Psi (O,\omega )$, the condition $U\cap {\textrm{Fix}}(\Psi )\ne \emptyset$ ensures that there exists a constant solution to the Hamiltonian boundary value problem

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}=X_H(x), \\ x(T)=\Psi x(0). \end{array} \right. \end{aligned}$$

(2.1)

We call $H\in \mathcal {H}^\Psi (O,\omega )$ $\Psi$-admissible if all solutions $x:[0, T]\rightarrow O$ to the Hamiltonian boundary value problem (2.1) with $0<T\le 1$ are constant. The set of all such $\Psi$-admissible Hamiltonians is denoted by $\mathcal {H}_{ad}^{\Psi }(O,\omega )$. In [13] we defined the following analogue (or extended version) of the Hofer–Zehnder capacity of $(O, \omega )$.

Definition 2.1

For open subset O in symplectic manifold $(M,\omega )$ and symplectomorphism $\Psi \in \textrm{Symp}(M,\omega )$, define

$$\begin{aligned} \displaystyle {c^\Psi _\textrm{HZ}}(O,\omega )=\sup \{\max H\,|\, H\in {\mathcal {H}}_{ad}^{\Psi }(O,\omega )\}. \end{aligned}$$

Clearly If $\Psi =id_M$ then $c^\Psi _\textrm{HZ}(O,\omega )=c_{\textrm{HZ}}(O,\omega )$ for any open subset $O\subset M$, where $c_{\textrm{HZ}}(O,\omega )$ is the Hofer–Zehnder capacity defined in [10].

The following proposition lists some basic properties of the extended Hofer–Zehnder capacity. In this paper, the standard symplectic structure on ${\mathbb {R}}^{2n}$ is given by $\omega _0=\sum _{i=1}^{n}dq_i\wedge dp_i$ with linear coordinates $(q_1,\ldots ,q_n,p_1,\ldots ,p_n)$. Let $\textrm{Sp}(2n,{\mathbb {R}})$ denote the set of symplectic matrix of order 2n. Each symplectic matrix $\Psi \in \textrm{Sp}(2n,{\mathbb {R}})$ is identified with the linear symplectomorphism on $({\mathbb {R}}^{2n},\omega _0)$ which has the representing matrix $\Psi$ under the standard symplectic basis of $({\mathbb {R}}^{2n},\omega _0)$, $(e_1,\ldots ,e_n,f_1,\ldots ,f_n)$, where the i-th(resp. $i+n$-th) coordinate of $e_i$ (resp. $f_{n+i}$) is 1 and other coordinates are zero.

Proposition 2.2

[13, Proposition 1.2]

• (i) (Conformality.) $c^\Psi _{\textrm{HZ}}(M,\alpha \omega )=\alpha c^\Psi _{\textrm{HZ}}(M,\omega )$ for any $\alpha \in {\mathbb {R}}_{>0}$, and $c^{\Psi ^{-1}}_\textrm{HZ}(M,\alpha \omega )=-\alpha c^\Psi _\textrm{HZ}(M,\omega )$ for any $\alpha \in {\mathbb {R}}_{<0}$.

• (ii) (Monotonicity.) Suppose that $\Psi _i\in {\textrm{Symp}}(M_i,\omega _i)$ $(i=1, 2)$. If there exists a symplectic embedding $\phi :(M_1,\omega _1)\rightarrow (M_2,\omega _2)$ of codimension zero such that $\phi \circ \Psi _1=\Psi _2\circ \phi$, then for open subsets $O_i\subset M_i$ with $O_i\cap {\textrm{Fix}}(\Psi _i)\ne \emptyset$ $(i=1, 2)$ and $\phi (O_1)\subset O_2$, it holds that $c^{\Psi _1}_{\textrm{HZ}}(O_1,\omega _1)\le c^{\Psi _2}_{\textrm{HZ}}(O_2,\omega _2)$.

• (iii) (Inner regularity.) For any precompact open subset $O\subset M$ with $O\cap {\textrm{Fix}}(\Psi )\ne \emptyset$, we have

  $$\begin{aligned} c^\Psi _\textrm{HZ}(O,\omega )=\sup \{c^\Psi _{\textrm{HZ}}(K,\omega )\,|\, K\;\hbox {open},\;K\cap {\textrm{Fix}}(\Psi ) \ne \emptyset ,\; \overline{K}\subset O\}. \end{aligned}$$

• (iv) (Continuity.) For a bounded convex domain $A\subset {\mathbb {R}}^{2n}$, suppose that $\Psi \in \textrm{Sp}(2n, {\mathbb {R}})$ satisfies $A\cap {\textrm{Fix}}(\Psi )\ne \emptyset$. Then for every $\varepsilon >0$ there exists some $\delta >0$ such that for all bounded convex domain $O\subset {\mathbb {R}}^{2n}$ intersecting with ${\textrm{Fix}}(\Psi )$, it holds that

  $$\begin{aligned} |c^\Psi _\textrm{HZ}(O,\omega _0)-c^\Psi _\textrm{HZ}(A,\omega _0)|\le \varepsilon \end{aligned}$$

  provided that A and O have the Hausdorff distance $d_\textrm{H}(A,O)<\delta$.

Remark 2.3

• (i) The two symplectomorphisms $\Psi _i\in \textrm{Symp}(M_i,\omega _1)$ ($i=1, 2$) involved in the above monotonicity property are different in general.

• (ii) By the above mononicity property, for any $\Psi , \phi \in \textrm{Symp}(M,\omega )$ and any open subset $O\subset M$ with $O\cap {\textrm{Fix}}(\Psi )\ne \emptyset$, there holds

  $$\begin{aligned} c^\Psi _{\textrm{HZ}}(O,\omega )=c_{\textrm{HZ}}^{\phi \circ \Psi \circ \phi ^{-1}}(\phi (O),\omega ). \end{aligned}$$

  (2.2)

  In particular, denote $\textrm{Symp}_{\Psi }(M,\omega ):=\{\phi \in \textrm{Symp}(M,\omega )\,|\,\phi \circ \Psi =\Psi \circ \phi \}$, i.e., the set of stabilizers at $\Psi$ for the adjoint action on $\textrm{Symp}(M,\omega )$. Then for any $\phi \in \textrm{Symp}_{\Psi }(M,\omega )$ there holds

  $$\begin{aligned} c^\Psi _\textrm{HZ}(O,\omega )=c_\textrm{HZ}^{\Psi }(\phi (O),\omega ). \end{aligned}$$

  That is to say, unlike the Hofer–Zehnder capacity which is invariant under the action of $\textrm{Symp}(M,\omega )$, the extended Hofer–Zehnder capacity $c^\Psi _\textrm{HZ}(O,\omega )$ is only invariant under the action of a subgroup of $\textrm{Symp}(M,\omega )$ related to $\Psi$.

• (iii) For $\Psi \in \textrm{Sp}(2n, {\mathbb {R}})$ and any open set $O\ni 0$ in $({\mathbb {R}}^{2n},\omega _0)$, (i)–(ii) of Proposition 2.2 implies

  $$\begin{aligned} c^\Psi _{\textrm{HZ}}(\alpha O,\omega _0)=\alpha ^2 c_{\textrm{HZ}}^{\Psi }(O,\omega _0),\quad \forall \alpha \ge 0. \end{aligned}$$

  (2.3)

In [2], a key for the proof of the inequality (1.2) is the representation theorem for Ekeland–Hofer and Hofer–Zehnder capacity of convex bodies [7, 8, 10, 17]. To present such a representation theorem for $\displaystyle c^\Psi _{\textrm{EHZ}}(D)$ given in [13], which is crucial for the proof of Theorem 1.1, we recall the concept of characteristic on hypersurfaces in symplectic manifolds.

Definition 2.4

[13, Definition 1.1] (i) For a smooth hypersurface ${\mathcal {S}}$ in a symplectic manifold $(M, \omega )$ and $\Psi \in \textrm{Symp}(M, \omega )$, a $C^1$ embedding z from [0, T] (for some $T>0$) into ${\mathcal {S}}$ is called a $\Psi$-characteristic on ${\mathcal {S}}$ if

$$\begin{aligned} z(T)=\Psi z(0)\; {\textrm{and}} \;\dot{z}(t)\in ({\mathcal {L}}_{{\mathcal {S}}})_{z(t)}\;\forall t\in [0,T], \end{aligned}$$

where ${\mathcal {L}}_{\mathcal {S}}$ is the characteristic line bundle given by

$$\begin{aligned} {\mathcal {L}}_{\mathcal {S}}={\Big \{}(x,\xi )\in T{\mathcal {S}}\ {\Big |}\ {\omega }_x(\xi ,\eta )=0\;\hbox {for all}\; \eta \in T_{x}{\mathcal {S}}{\Big \}}. \end{aligned}$$

Clearly, $z(T-\cdot )$ is a $\Psi ^{-1}$-characteristic, and for any $\tau >0$ the embedding $[0, \tau T]\rightarrow {\mathcal {S}},\;t\mapsto z(t/\tau )$ is also a $\Psi$-characteristic.

(ii) If ${\mathcal {S}}$ is the boundary of a convex body D in $({\mathbb {R}}^{2n},\omega _0)$, corresponding to the definition of closed characteristics on ${\mathcal {S}}$ in Definition 1 of [6, Chap.V,§1] we say a nonconstant absolutely continuous curve $z:[0,T]\rightarrow {\mathcal {S}}$ (for some $T>0$) to be a generalized characteristic on ${\mathcal {S}}$ if

$$\begin{aligned} \dot{z}(t)\in JN_{\mathcal {S}}(z(t))\;\hbox {a.e.}, \end{aligned}$$

where

$$\begin{aligned} N_{\mathcal {S}}(x)=\{y\in {\mathbb {R}}^{2n}\,|\, \langle u-x, y\rangle \le 0\;\forall u\in D\} \end{aligned}$$

is the normal cone to D at $x\in {\mathcal {S}}$. If z satisfies $z(T)=\Psi z(0)$ for $\Psi \in \textrm{Sp}(2n,{\mathbb {R}})$ in addition, then we call z a generalized $\Psi$-characteristic on ${\mathcal {S}}$. For a generalized characteristic $z:[0,T]\rightarrow {\mathcal {S}}$, define its action by

$$\begin{aligned} A(x)=\frac{1}{2}\int _0^T\langle -J\dot{x},x\rangle dt, \end{aligned}$$

(2.4)

where $\langle \cdot ,\cdot \rangle =\omega _0(\cdot ,J\cdot )$ is the standard inner product on ${\mathbb {R}}^{2n}$.

Remark 2.5

If ${\mathcal {S}}$ in (ii) is also $C^{1,1}$ then generalized $\Psi$-characteristics on ${\mathcal {S}}$ are $\Psi$-characteristics up to reparameterization.

As a generalization of the representation theorem for Ekeland–Hofer and Hofer–Zehnder capacity of convex bodies [7, 8, 10, 17], we have:

Theorem 2.6

[13, Theorem 1.8] Let $\Psi \in \textrm{Sp}(2n,{\mathbb {R}})$ and let $D\subset {\mathbb {R}}^{2n}$ be a convex bounded domain with boundary ${\mathcal {S}}=\partial D$ and contain a fixed point p of $\Psi$. Then there is a generalized $\Psi$-characteristic $x^{*}$ on ${\mathcal {S}}$ such that

$$\begin{aligned} A(x^{*})= & {} \min \{A(x)>0\,|\,x\;\text {is a generalized}\;\Psi \hbox {-characteristic on}\;{\mathcal {S}}\} \end{aligned}$$

(2.5)

$$\begin{aligned}= & {} c^\Psi _{\textrm{EHZ}}(D,\omega _0). \end{aligned}$$

(2.6)

If ${\mathcal {S}}$ is of class $C^{1,1}$, (2.5) and (2.6) become

$$\begin{aligned} c^\Psi _{\textrm{EHZ}}(D,\omega _0)=A(x^{*})=\inf \{A(x)>0\,|\,x\;\text {is a}\;\Psi \hbox {-characteristic on}\;{\mathcal {S}}\}. \end{aligned}$$

Definition 2.7

A generalized $\Psi$-characteristic $x^{*}$ on ${\mathcal {S}}$ satisfying (2.5)–(2.6) is called a $\displaystyle c^\Psi _{\textrm{EHZ}}$ -carrier for D.

3 Proofs of Theorem 1.1 and Corollaries

3.1 Proof of Theorem 1.1

The basic proof ideas are similar to those of [2]. For $\Psi \in {\textrm{Sp}}(2n)$, let $E_1\subset {\mathbb {R}}^{2n}$ be the eigenvector space which belongs to eigenvalue  1 of  $\Psi$ and $E_1^{\bot }$ be the orthogonal complement of $E_1$ with respect to the standard Euclidean inner product in ${\mathbb {R}}^{2n}$. For $p>1$, let

$$ \begin{aligned} {\mathcal {F}}_p=\{x\in W^{1,p}([0,1],{\mathbb {R}}^{2n})\,|\,x(1)=\Psi x(0)\; \& \; x(0)\in E_1^{\bot }\}, \end{aligned}$$

which is a subspace of $W^{1,p}([0,1],{\mathbb {R}}^{2n})$. Since the functional

$$\begin{aligned} {\mathcal {F}}_p\ni x\mapsto A(x)=\frac{1}{2}\int _0^1\langle -J\dot{x}(t),x(t)\rangle dt \end{aligned}$$

is $C^1$ and $dA(x)[x]=2$ for any $x\in {\mathcal {F}}_p$ with $A(x)=1$, we deduce that

$$\begin{aligned} {\mathcal {A}}_p:=\{x\in {\mathcal {F}}_p\,|\,A(x)=1 \} \end{aligned}$$

is a regular $C^1$ submanifold.

Recall that for convex body $D\subset {\mathbb {R}}^{2n}$, $h_D$ is the support function (see the beginning in Sect. 1.1). If D contains 0 in its interior, then $j_D$ is the associated Minkowski function. $H_D^*$ is the Legendre transform of $H_D:=(j_D)^2$.

Remark 3.1

• (i) By the homogeneity of $H_D$ and $H_D^*$, there exist constants $R_1, R_2\ge 1$ such that

  $$\begin{aligned} \frac{|z|^2}{R_1}\le H_D(z)\le R_1|z|^2, \quad \frac{|z|^2}{R_2}\le H^{*}_D(z)\le R_2|z|^2, \quad \forall z\in {\mathbb {R}}^{2n}. \end{aligned}$$

  (3.1)

• (ii) For $p>1$, let $q=p/p-1$, denote by $\left( j_D^p/p\right) ^{*}$ the Legendre transform of $j_D^p/p$. Then there holds

  $$\begin{aligned} \left( \frac{1}{p}j_D^p\right) ^{*}(w)=\frac{1}{q}(h_D(w))^q. \end{aligned}$$

  (3.2)

  In particular, we obtain that $H_D^{*}$ and the support function $h_D$ have the following relation:

  $$\begin{aligned} H_D^{*}(w)=\frac{h_D(w)^2}{4}. \end{aligned}$$

  (3.3)

  In fact, we can compute directly as follows:

  $$\begin{aligned} \left( \frac{1}{p}j_D^p\right) ^{*}(w)= & {} \sup _{\xi \in {\mathbb {R}}^{2n}}\bigl (\langle \xi ,w\rangle - \frac{1}{p}(j_D^p(\xi ))\bigr )\\= & {} \sup _{t\ge 0,\zeta \in \partial D}(\langle t\zeta ,w\rangle - \frac{t^p}{p}(j_D^p(\zeta ))\bigr )\\= & {} \sup _{\zeta \in \partial D,\langle \zeta ,w\rangle \ge 0}\max _{t\ge 0}\bigl (\langle t\zeta ,w\rangle -\frac{t^p}{p}\bigr )\\= & {} \sup _{\zeta \in \partial D,\langle \zeta ,w\rangle \ge 0}\frac{\langle \zeta ,w\rangle ^q}{q}\\= & {} \sup _{\zeta \in D,\langle \zeta ,w\rangle \ge 0}\frac{\langle \zeta ,w\rangle ^q}{q}\\= & {} \frac{1}{q}(h_D(w))^q. \end{aligned}$$

To prove Theorem 1.1, we need the following representation for $(c^{\Psi }_{\textrm{EHZ}}(D))^{\frac{p}{2}}$ for convex body $D\subset {\mathbb {R}}^{2n}$ and $p\ge 1$, which is a generalization of [2, Proposition 2.1].

Proposition 3.2

For $p_1>1$ and $p_2\ge 1$, there holds

$$\begin{aligned} (c^{\Psi }_{\textrm{EHZ}}(D))^{\frac{p_2}{2}}=\min _{x\in \mathcal {A}_{p_1}} \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p_2}{2}}dt=\min _{x\in {\mathcal {A}}_{p_1}}\frac{1}{2^{p_2}}\int _0^1 (h_{D}(-J\dot{x}))^{p_2}dt. \end{aligned}$$

Proposition 3.2 is derived based on the following Lemma. For the case $\Psi =I_{2n}$, it is proved in [2, Proposition 2.2].

Lemma 3.3

For $p>1$, there holds

$$\begin{aligned} (c^{\Psi }_{\textrm{EHZ}}(D))^{\frac{p}{2}}=\min _{x\in \mathcal {A}_p} \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p}{2}}dt. \end{aligned}$$

(3.4)

We firstly give the proof of Lemma 3.3 and Proposition 3.2. The proof of Theorem 1.1 is given in the final part of this section.

Proof of Lemma 3.3

Define

$$\begin{aligned} I_p:{\mathcal {F}}_p\rightarrow {\mathbb {R}},\;x\mapsto \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p}{2}}dt. \end{aligned}$$

Then $I_p$ is convex. If D is strictly convex with $C^1$-smooth boundary then $I_p$ is a $C^{1}$ functional with derivative given by

$$\begin{aligned} dI_p(x)[y]=\int _0^1\langle \nabla (H_D^{*})^{\frac{p}{2}}(-J\dot{x}(t)),-J\dot{y}\rangle dt,\quad \forall x,y\in {\mathcal {F}}_p. \end{aligned}$$

By Theorem 2.6, in order to prove (3.4) we only need to show that

$$\begin{aligned} \min \{A(x)>0\,|\,x\;\text {is a generalized}\;\Psi \hbox {-characteristic on}\;\partial D\}=(\min _{x\in \mathcal {A}_p}I_p)^{\frac{2}{p}}. \end{aligned}$$

(3.5)

We will prove this in four steps.

Step 1.    $\mu _p:=\inf _{x\in \mathcal {A}_p}I_p(x)$ is positive. It is easy to prove that

$$\begin{aligned} \Vert x\Vert _{L^\infty }\le \widetilde{C}_1\Vert \dot{x}\Vert _{L^p}\quad \forall x\in {\mathcal {F}}_{p} \end{aligned}$$

(3.6)

for some constant $\widetilde{C}_1=\widetilde{C}_1(p)>0$. So for any $x\in \mathcal {A}_p$ we have

$$\begin{aligned} 2=2A_p(x)\le \Vert x\Vert _{L^q}\Vert \dot{x}\Vert _{L^p}\le \Vert x\Vert _{L^\infty }\Vert \dot{x}\Vert _{L^p}\le {\widetilde{C}}_1\Vert \dot{x}\Vert _{L^p}^2, \end{aligned}$$

and thus $\Vert \dot{x}\Vert _{L^p}\ge \sqrt{2/\widetilde{C}_1 }$, where $1/p+1/q=1$. Let $R_2$ be as in (3.1). These lead to

$$\begin{aligned} I_p(x)\ge \left( \frac{1}{R_2}\right) ^{p/2}\Vert \dot{x}\Vert _{L^p}^p\ge \widetilde{C}_2, \quad \hbox {where}\quad \widetilde{C}_2= \left( \frac{2}{R_2\widetilde{C}_1}\right) ^{\frac{p}{2}}>0. \end{aligned}$$

Step 2. There exists $u\in \mathcal {A}_p$ such that $I_p(u)=\mu _p$, i.e. the infimum of $I_p$ on $\mathcal {A}_p$ can be attained by some $u\in \mathcal {A}_p$. Let $(x_n)\subset \mathcal {A}_p$ be a sequence satisfying $\lim _{n\rightarrow +\infty }I_p(x_n)=\mu _p$. Then there exists a constant $\widetilde{C}_3>0$ such that

$$\begin{aligned} \left( \frac{1}{R_2}\right) ^{p/2}\Vert \dot{x}_n\Vert _{L^p}^p\le I_p(x_n)\le \widetilde{C}_3,\quad \forall n\in {\mathbb {N}}. \end{aligned}$$

By (3.6) and the fact that $\Vert x\Vert _{L^p}\le \Vert x\Vert _{L^\infty }$, we deduce that $(x_n)$ is bounded in $W^{1,p}([0,1],{\mathbb {R}}^{2n})$. Note that $W^{1,p}([0,1])$ is reflexive for $p>1$. $(x_n)$ has a subsequence, also denoted by $(x_n)$, which converges weakly to some $u\in W^{1,p}([0,1],{\mathbb {R}}^{2n})$. By Arzelá-Ascoli theorem, there also exists $\hat{u}\in C^{0}([0,1],{\mathbb {R}}^{2n})$ such that

$$\begin{aligned} \lim _{n\rightarrow +\infty }\sup _{t\in [0,1]}|x_n(t)-\hat{u}(t)|=0. \end{aligned}$$

A standard argument yields $u(t)=\hat{u}(t)$ almost everywhere. We may consider that $x_n$ converges uniformly to u. Hence $u(1)=\Psi u(0)$ and $u(0)\in E_1^{\bot }$. As in Step 2 of [13, Section 4.1], we also have $A_p(u)=1$, and so $u\in {\mathcal {A}}_p$. Standard argument in convex analysis shows that there exists $\omega \in L^q([0,1],{\mathbb {R}}^{2n})$ such that $\omega (t)\in \partial (H_D^{*})^{\frac{p}{2}}(-J\dot{u}(t))$ almost everywhere. These lead to

$$\begin{aligned} I_p(u)-I_p(x_n)\le \int _0^1\langle \omega (t),-J(\dot{u}(t)-\dot{x}_n(t))\rangle dt\rightarrow 0 \quad \hbox {as}\quad n\rightarrow \infty , \end{aligned}$$

since $x_n$ converges weakly to u. Hence $\mu _p\le I_p(u)\le \lim _{n\rightarrow \infty }I_p(x_n)= \mu _p$.

Step 3.   There exists a generalized $\Psi$-characteristic on $\partial D$, ${x}^*:[0, 1]\rightarrow \partial D$, such that $A({x}^*)=(\mu _p)^{\frac{2}{p}}$. Since u is the minimizer of $I_p|_{\mathcal {A}_p}$, applying Lagrangian multiplier theorem (cf. [5, Theorem 6.1.1]) we get some $\lambda _p\in {\mathbb {R}}$ such that $0\in \partial (I_p+\lambda _p A)(u)=\partial I_p(u)+\lambda _p A'(u)$. This means that there exists some $\rho \in L^q([0,1],{\mathbb {R}}^{2n})$ satisfying

$$\begin{aligned} \rho (t)\in \partial (H_D^{*})^{\frac{p}{2}}(-J\dot{u}(t))\quad \hbox {a.e.} \end{aligned}$$

(3.7)

and

$$\begin{aligned} \int _0^1\langle \rho (t),-J\dot{\zeta }(t)\rangle +\lambda _p\int _0^1\langle u(t),-J\dot{\zeta }(t)\rangle =0\quad \forall \zeta \in \mathcal {F}_p. \end{aligned}$$

From the latter we derive that for some $\textbf{a}_0\in \textrm{Ker}(\Psi -I)$,

$$\begin{aligned} \rho (t)+\lambda _p u(t)=\textbf{a}_0,\quad \hbox {a.e..}\quad \end{aligned}$$

(3.8)

Computing as in the case of $p=2$ (cf. Step 3 of [13, Section 4.1]), we get that

$$\begin{aligned} \lambda _p=-\frac{p}{2}\mu _p. \end{aligned}$$

Since $p>1$, $q=p/(p-1)>1$. From (3.2) we may derive that $(H_D^{*})^{\frac{p}{2}}=(\frac{h_D}{2})^p$ has the Legendre transformation given by

$$\begin{aligned} \left( \frac{h_D^p}{2^p}\right) ^{*}(x) =\left( \frac{h_D^p}{p}\right) ^{*}\left( \frac{2}{p^{\frac{1}{p}}}x\right) =\frac{1}{q}j_D^q\left( \frac{2}{p^{\frac{1}{p}}}x\right) =\frac{2^q}{qp^{\frac{q}{p}}}j_D^q(x) =\frac{2^q}{qp^{q-1}}j_D^q(x). \end{aligned}$$

Using this and (3.7)–(3.8), we get that

$$\begin{aligned} -J\dot{u}(t)\in \frac{2^q}{qp^{q-1}}\partial j_D^q(-\lambda _p u(t)+\textbf{a}_0),\quad \hbox {a.e.}. \end{aligned}$$

Let $v(t):=-\lambda _p u(t)+\textbf{a}_0$. Then

$$\begin{aligned} -J\dot{v}(t)\in -\lambda _p\frac{2^q}{qp^{q-1}}\partial j_D^q(v(t)) \quad \hbox {and}\quad v(1)=\Psi v(0). \end{aligned}$$

This implies that $j_D^q(v(t))$ is a constant by [14, Theorem 2], and

$$\begin{aligned} \frac{-2^{q-1}\lambda _p}{p^{q-1}}j_D^q(v(t))=\int ^1_0\frac{-2^{q-1}\lambda _p}{p^{q-1}}j_D^q(v(t))dt =\frac{1}{2}\int ^1_0\langle -J\dot{v}(t), v(t)\rangle dt=\lambda _p^2=\left( \frac{p\mu _p}{2}\right) ^2 \end{aligned}$$

by the Euler formula [19, Theorem 3.1]. Therefore $j_D^q(v(t))=\left( \frac{p}{2}\right) ^q\mu _p$ and

$$\begin{aligned} A(v)=\frac{1}{2}\int ^1_0\langle -J\dot{v}(t), v(t)\rangle dt=\lambda _p^2=\left( \frac{p\mu _p}{2}\right) ^2. \end{aligned}$$

Let $x^{*}(t)=\frac{v(t)}{j_D(v(t))}$. Then $x^{*}$ is a generalized $\Psi$-characteristic on $\partial D$ with action

$$\begin{aligned} A(x^{*})=\frac{1}{j_D^2(v(t))}A(v)=\mu _p^{\frac{2}{p}}. \end{aligned}$$

Step 4. For any generalized $\Psi$-characteristic on $\partial D$ with positive action, $y:[0,T]\rightarrow \partial D$, there holds $A(y)\ge \mu _p^{\frac{2}{p}}$. Since [5, Theorem 2.3.9] implies $\partial j_D^q(x)=q(j_D(x))^{q-1}\partial j_D(x)$, by [13, Lemma 4.2], after reparameterization we may assume that $y\in W^{1,\infty }([0,T],{\mathbb {R}}^{2n})$ and satisfies

$$\begin{aligned} j_D(y(t))\equiv 1\quad \hbox {and}\quad -J\dot{y}(t)\in \partial j_D^q(y(t))\quad \hbox {a.e. on}\;[0, T]. \end{aligned}$$

It follows that

$$\begin{aligned} A(y)=\frac{qT}{2}. \end{aligned}$$

(3.9)

Similar to the case $p=2$, define $y^{*}:[0,1]\rightarrow {\mathbb {R}}^{2n}$, $t\mapsto y^{*}(t)=a y(tT)+ \textbf{b}$, where $a>0$ and $\textbf{b}\in E_1$ are chosen so that $y^{*}\in \mathcal {A}_p$. Then (3.9) leads to

$$\begin{aligned} 1=A(y^{*})=a^2A(y)=\frac{a^2qT}{2}. \end{aligned}$$

(3.10)

Moreover, it is clear that

$$\begin{aligned} -J\dot{y}^{*}(t)\in \frac{2^q}{qp^{q-1}}\partial (j_D^q)\left( (aT)^{\frac{1}{q-1}} \frac{q^{\frac{1}{q-1}}p}{2^p}y(tT)\right) . \end{aligned}$$

We use this, (3.2) and the Legendre reciprocity formula (cf. [6, Proposition II.1.15]) to derive

$$\begin{aligned}{} & {} \frac{2^q}{qp^{q-1}}j_D^q \left( (aT)^{\frac{1}{q-1}} \frac{q^{\frac{1}{q-1}}p}{2^p}y(tT)\right) + \left( \frac{h_D^p}{2^p}\right) ^{*}(-J\dot{y}^{*}(t))\\{} & {} \quad =\left\langle -J\dot{y}^{*}(t),(aT)^{\frac{1}{q-1}} \frac{q^{\frac{1}{q-1}}p}{2^p}y(tT)\right\rangle \end{aligned}$$

and hence

$$\begin{aligned} (H_D^{*}(-J\dot{y}^{*}(t)))^{\frac{p}{2}}= & {} \left( \frac{h_D^p}{2^p}\right) ^{*}(-J\dot{y}^{*}(t))\\= & {} (aT)^p\frac{q^pp}{2^p}-(aT)^p\frac{q^{p-1}p}{2^p}\\= & {} (aT)^p\frac{q^{p-1}p(q-1)}{2^p}\\= & {} (aT)^p\frac{q^{p}}{2^p}\ge \mu _p. \end{aligned}$$

By Step 1 we get $I_p(y^*)\ge \mu _p$ and so $(aT)^p\frac{q^{p}}{2^p}\ge \mu _p$. This, (3.9) and (3.10) lead to $A(y)\ge \mu _p^{\frac{2}{p}}$.

Summarizing the four steps we get (3.5) and hence (3.4) is proved. $\square$

Remark 3.4

• (i) Checking Step 3, it is easily seen that for a minimizer u of $I_p|_{\mathcal {A}_p}$ there exists $\textbf{a}_0\in \textrm{Ker}(\Psi -I)$ such that

  $$\begin{aligned} x^*(t)=\left( c^\Psi _{\textrm{EHZ}}(D)\right) ^{1/2}u(t)+ \frac{2}{p}\left( c^\Psi _{\textrm{EHZ}}(D)\right) ^{(1-p)/2}{} \textbf{a}_0 \end{aligned}$$

  gives a generalized $\Psi$-characteristic on $\partial D$ with action $A(x^{*})=c^\Psi _{\textrm{EHZ}}(D)$, namely, $x^*$ is a $c^\Psi _{\textrm{EHZ}}$-carrier for $\partial D$.

• (ii) For a generalized $\Psi$-characteristic on $\partial D$ with action $A(x^{*})=c^\Psi _{\textrm{EHZ}}(D)$, computation in Step 4 implies that

  $$\begin{aligned} u(t)=\frac{x^*(tT)}{\sqrt{c_{\textrm{EHZ}}^\Psi (D)}}+b=\frac{x^*(tT)}{\sqrt{A(x^*)}}+b,\quad \hbox {for some}\quad b\in E_1 \end{aligned}$$

  is a minimizer of $I_p|_{\mathcal {A}_p}$.

Proof of Proposition 3.2

Firstly, suppose $p_1\ge p_2>1$. Then $\mathcal {A}_{p_1}\subset \mathcal {A}_{p_2}$ and the first two steps in the proof of Proposition 3.3 implies that $I_{p_1}|_{\mathcal {A}_{p_1}}$ has a minimizer $u\in \mathcal {A}_{p_1}$. It follows that

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D)= & {} \left( \int _0^1(H_D^{*}(-J\dot{u}(t)))^{\frac{p_1}{2}}dt\right) ^ {\frac{2}{p_1}}\\\ge & {} \left( \int _0^1(H_D^{*}(-J\dot{u}(t)))^{\frac{p_2}{2}}dt\right) ^ {\frac{2}{p_2}}\\\ge & {} \inf _{x\in \mathcal {A}_{p_1}}\left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p_2}{2}}dt\right) ^ {\frac{2}{p_2}}\\\ge & {} \inf _{x\in \mathcal {A}_{p_2}}\left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p_2}{2}}dt\right) ^ {\frac{2}{p_2}}\\= & {} c^{\Psi }_{\textrm{EHZ}}(D), \end{aligned}$$

where two equalities come from Lemma 3.3 and the first inequality is because of Hölder’s inequality. Hence the functional $\int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p_2}{2}}dt$ attains its minimum at u on $\mathcal {A}_{p_1}$ and

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D)=\min _{x\in \mathcal {A}_{p_1}} \left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p_2}{2}}dt\right) ^{\frac{2}{p_2}}. \end{aligned}$$

(3.11)

Next, if $p_2\ge p_1>1$, then $\mathcal {A}_{p_2}\subset \mathcal {A}_{p_1}$ and we have $u\in \mathcal {A}_{p_2}$ minimizing $I_{p_2}|_{\mathcal {A}_{p_2}}$ such that

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D)= & {} \left( \int _0^1(H_D^{*}(-J\dot{u}(t)))^{\frac{p_2}{2}}dt\right) ^ {\frac{2}{p_2}}\\\ge & {} \inf _{x\in \mathcal {A}_{p_1}}\left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p_2}{2}}dt\right) ^ {\frac{2}{p_2}}\\\ge & {} \inf _{x\in \mathcal {A}_{p_1}}\left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p_1}{2}}dt\right) ^ {\frac{2}{p_1}}\\= & {} c^{\Psi }_{\textrm{EHZ}}(D). \end{aligned}$$

This yields (3.11) again.

Finally, for $p_2=1$ and $p_1>1$ let $u\in \mathcal {A}_{p_1}$ minimize $I_{p_1}|_{\mathcal {A}_{p_1}}$. It is clear that

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D)= & {} \left( \int _0^1(H_D^{*}(-J\dot{u}(t)))^{\frac{p_1}{2}}dt\right) ^ {\frac{2}{p_1}}\nonumber \\\ge & {} \left( \int _0^1(H_D^{*}(-J\dot{u}(t)))^{\frac{1}{2}}dt\right) ^{2}\nonumber \\\ge & {} \inf _{x\in \mathcal {A}_{p_1}}\left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{1}{2}}dt \right) ^{2} \end{aligned}$$

(3.12)

Let $R_2$ be as in (3.1). Then

$$\begin{aligned} (H_D^{*}(-J\dot{x}(t)))^{\frac{p}{2}}\le (R_2|\dot{x}(t)|^2)^{\frac{p}{2}}\le (R_2+1)^{\frac{p_1}{2}} |\dot{x}(t)|^{p_1} \end{aligned}$$

for any $1\le p\le p_1$. By (3.11)

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D)=\min _{x\in \mathcal {A}_{p_1}} \left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{p}{2}}dt\right) ^{\frac{2}{p}},\quad 1<p\le p_1. \end{aligned}$$

Letting $p\downarrow 1$ and using Lebesgue dominated convergence theorem we get

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D)\le \inf _{x\in \mathcal {A}_{p_1}}\left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{1}{2}}dt\right) ^ {2}. \end{aligned}$$

This and (3.12) show that the functional $\mathcal {A}_{p_1}\ni x\mapsto \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{1}{2}}dt$ attains its minimum at u and

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D)=\min _{x\in \mathcal {A}_{p_1}} \left( \int _0^1(H_D^{*}(-J\dot{x}(t)))^{\frac{1}{2}}dt\right) ^{2}. \end{aligned}$$

Proposition 3.2 is proved. $\square$

Proof of Theorem 1.1

Choose a real $p_1>1$. Then for $p\ge 1$ Proposition 3.2 implies

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D+_pK)^{\frac{p}{2}}= & {} \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{D+_pK}(-J\dot{x}))^{p}dt \end{aligned}$$

(3.13)

$$\begin{aligned}= & {} \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 ((h_{D}(-J\dot{x}))^{p}+(h_{K}(-J\dot{x}))^{p})dt\nonumber \\\ge & {} \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{D}(-J\dot{x}))^{p}+\min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{K}(-J\dot{x}))^{p}dt\nonumber \\= & {} c^{\Psi }_{\textrm{EHZ}}(D)^{\frac{p}{2}}+c^{\Psi }_{\textrm{EHZ}}(K)^{\frac{p}{2}}. \end{aligned}$$

(3.14)

Now suppose that $p\ge 1$ and there exist $c^\Psi _{\textrm{EHZ}}$ carriers $\gamma _D:[0, T]\rightarrow \partial D$ and $\gamma _K:[0, T]\rightarrow \partial K$ satisfying $\gamma _D=\alpha \gamma _K+\textbf{b}$ for some $\alpha \in {\mathbb {R}}\setminus \{0\}$ and some $\textbf{b}\in \textrm{Ker}(\Psi -I_{2n})$. We will prove the equality in (1.3) holds. (2.4) implies $A(\gamma _D)=\alpha ^2 A(\gamma _K)$. Moreover by Remark 3.4(ii) for suitable vectors $\textbf{b}_D, \textbf{b}_K\in \textrm{Ker}(\Psi -I_{2n})$

$$\begin{aligned} z_D(t)=\frac{1}{\sqrt{A(\gamma _D)}}\gamma _D(Tt)+\textbf{b}_D\quad \hbox {and}\quad z_K(t)=\frac{1}{\sqrt{A(\gamma _K)}}\gamma _K(Tt)+\textbf{b}_K \end{aligned}$$

in $\mathcal {A}_{p_1}$ satisfy

$$\begin{aligned}{} & {} c^{\Psi }_{\textrm{EHZ}}(D)^{\frac{p}{2}}=\min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{D}(-J\dot{x}))^{p}dt=\frac{1}{2^p}\int _0^1 (h_{D}(-J\dot{z}_D))^{p}dt, \end{aligned}$$

(3.15)

$$\begin{aligned}{} & {} c^{\Psi }_{\textrm{EHZ}}(K)^{\frac{p}{2}}= \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{K}(-J\dot{x}))^{p}dt=\frac{1}{2^p}\int _0^1 (h_{K}(-J\dot{z}_K))^{p}dt. \end{aligned}$$

(3.16)

It follows that $\dot{z}_D(t)=\alpha \left( \frac{A(\gamma _K)}{A(\gamma _D)}\right) ^{1/2}\dot{z}_K=\dot{z}_K$ because $A(\gamma _D)=\alpha ^2 A(\gamma _K)$. Then (3.15) and (3.16) lead to

$$\begin{aligned}{} & {} c^{\Psi }_{\textrm{EHZ}}(D)^{\frac{p}{2}}+c^{\Psi }_{\textrm{EHZ}}(K)^{\frac{p}{2}}\\{} & {} \quad =\frac{1}{2^p}\int _0^1((h_{D}(-J\dot{z}_D))^{p}+(h_{K}(-J\dot{z}_D))^{p})dt\\{} & {} \quad =\frac{1}{2^p}\int _0^1h_{D+_pK}(-J\dot{z}_D)^pdt\\{} & {} \quad \ge \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{D+_pK}(-J\dot{x}))^{p}dt\\{} & {} \quad = c^{\Psi }_{\textrm{EHZ}}(D+_pK)^{\frac{p}{2}}. \end{aligned}$$

Combined with (3.13) we get

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D+_pK)^{\frac{p}{2}} =c^{\Psi }_{\textrm{EHZ}}(D)^{\frac{p}{2}}+c^{\Psi }_{\textrm{EHZ}}(K)^{\frac{p}{2}}. \end{aligned}$$

Now suppose that $p>1$ and the equality in (1.3) holds. We may require that the above $p_1$ satisfies $1<p_1<p$. By Proposition 3.2 there exists $u\in \mathcal {A}_{p_1}$ such that

$$\begin{aligned} c^{\Psi }_{\textrm{EHZ}}(D+_pK)^{\frac{p}{2}}=\frac{1}{2^p}\int _0^1 \left( (h_{D+_pK}(-J\dot{u}))\right) ^{p}dt. \end{aligned}$$

The equality in (1.3) yields

$$\begin{aligned}{} & {} \frac{1}{2^p}\int _0^1 ((h_{D}(-J\dot{u}))^{p}+(h_{K}(-J\dot{u}))^{p})dt\\{} & {} \quad = \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{D}(-J\dot{x}))^{p}dt+\min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{K}(-J\dot{x}))^{p}dt \end{aligned}$$

and thus

$$\begin{aligned}{} & {} c^\Psi _{\textrm{EHZ}}(D)^{\frac{p}{2}}=\min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{D}(-J\dot{x}))^{p}dt=\frac{1}{2^p}\int _0^1 (h_{D}(-J\dot{u}))^{p}dt\quad \hbox {and}\\{} & {} c^\Psi _{\textrm{EHZ}}(K)^{\frac{p}{2}}=\min _{x\in \mathcal {A}_{p_1}}\frac{1}{2^p}\int _0^1 (h_{K}(-J\dot{x}))^{p}dt=\frac{1}{2^p}\int _0^1 (h_{K}(-J\dot{u}))^{p}dt. \end{aligned}$$

These and Propositions 3.3, 3.2 and Hölder’s inequality lead to

$$\begin{aligned} \min _{x\in \mathcal {A}_{p_1}}\left( \int _0^1 (h_{D}(-J\dot{x}))^{p_1}dt\right) ^{\frac{1}{p_1}}= & {} 2(c^{\Psi }_{\textrm{EHZ}}(D))^{\frac{1}{2}} \\= & {} \min _{x\in \mathcal {A}_{p_1}}\left( \int _0^1 (h_{D}(-J\dot{x}))^{p}dt\right) ^{\frac{1}{p}}\\= & {} \left( \int _0^1(h_{D}(-J\dot{u}))^{p}dt\right) ^{\frac{1}{p}}\ge \left( \int _0^1 (h_{D}(-J\dot{u}))^{p_1}dt\right) ^{\frac{1}{p_1}},\\ \min _{x\in \mathcal {A}_{p_1}}\left( \int _0^1 (h_{K}(-J\dot{x}))^{p_1}dt\right) ^{\frac{1}{p_1}}= & {} 2(c^{\Psi }_{\textrm{EHZ}}(K))^{\frac{1}{2}} \\= & {} \min _{x\in \mathcal {A}_{p_1}}\left( \int _0^1 (h_{K}(-J\dot{x}))^{p}dt\right) ^{\frac{1}{p}}\\= & {} \left( \int _0^1(h_{K}(-J\dot{u}))^{p}dt\right) ^{\frac{1}{p}}\ge \left( \int _0^1 (h_{K}(-J\dot{u}))^{p_1}dt\right) ^{\frac{1}{p_1}}. \end{aligned}$$

It follows that

$$\begin{aligned} 2(c^\Psi _{\textrm{EHZ}}(D))^{\frac{1}{2}}= & {} \left( \int _0^1(h_{D}(-J\dot{u}))^{p}dt\right) ^{\frac{1}{p}}= \left( \int _0^1(h_{D}(-J\dot{u}))^{p_1}dt\right) ^{\frac{1}{p_1}},\\ 2(c^\Psi _{\textrm{EHZ}}(K))^{\frac{1}{2}}= & {} \left( \int _0^1(h_{K}(-J\dot{u}))^{p}dt\right) ^{\frac{1}{p}} =\left( \int _0^1(h_{K}(-J\dot{u}))^{p_1}dt\right) ^{\frac{1}{p_1}}. \end{aligned}$$

By Remark 3.4(i) there are $\textbf{a}_D, \textbf{a}_K\in \textrm{Ker}(\Psi -I_{2n})$ such that

$$\begin{aligned}{} & {} \gamma _D(t)=\left( c^\Psi _{\textrm{EHZ}}(D)\right) ^{1/2}u(t)+ \frac{2}{p_1}\left( c^\Psi _{\textrm{EHZ}}(D)\right) ^{(1-p_1)/2}\textbf{a}_D,\\{} & {} \gamma _K(t)=\left( c^\Psi _{\textrm{EHZ}}(K)\right) ^{1/2}u(t)+ \frac{2}{p_1}\left( c^\Psi _{\textrm{EHZ}}(K)\right) ^{(1-p_1)/2}{} \textbf{a}_K \end{aligned}$$

are $c^\Psi _{\textrm{EHZ}}$ carriers for $\partial D$ and $\partial K$, respectively. Clearly, they coincide up to dilation and translation in $\textrm{Ker}(\Psi -I_{2n})$. Theorem 1.1 is proved. $\square$

3.2 Some interesting consequences of Theorem 1.1

Since $D+_1K=D+K=\{x+y\,|\, x\in D\;\textrm{and}\;y\in K\}$ we have:

Corollary 3.5

Let $\Psi \in \textrm{Sp}(2n,{\mathbb {R}})$, and let $D, K\subset {\mathbb {R}}^{2n}$ be two convex bodies containing fixed points of $\Psi$ in their interiors. Then

• (i)
  $$\begin{aligned} \left( c^{\Psi }_{\textrm{EHZ}}(D+K)\right) ^{\frac{1}{2}}\ge \left( c^{\Psi }_{\textrm{EHZ}}(D)\right) ^{\frac{1}{2}}+ \left( c^{\Psi }_{\textrm{EHZ}}(K)\right) ^{\frac{1}{2}}, \end{aligned}$$

  (3.17)

  and the equality holds if there exist $c^\Psi _{\textrm{EHZ}}$-carriers for D and K which coincide up to dilation and translation by elements in $\textrm{Ker}(\Psi -I_{2n})$.

• (ii) For $x,y\in {\textrm{Fix}}(\Psi )$, if both ${\textrm{Int}}(D)\cap {\textrm{Fix}}(\Psi )-x$ and ${\textrm{Int}}(D)\cap {\textrm{Fix}}(\Psi )-y$ are intersecting with ${\textrm{Int}}(K)$, then

  $$\begin{aligned}{} & {} \lambda \left( c^\Psi _{\textrm{EHZ}}(D\cap (x+K))\right) ^{1/2}+ (1-\lambda )\left( c^\Psi _{\textrm{EHZ}}(D\cap (y+K))\right) ^{1/2}\nonumber \\{} & {} \quad \le \left( c^\Psi _{\textrm{EHZ}}(D\cap (\lambda x+(1-\lambda )y+K))\right) ^{1/2},\quad \forall \, 0\le \lambda \le 1. \end{aligned}$$

  (3.18)

  In particular, if D and K are centrally symmetric, i.e., $-D=D$ and $-K=K$, then

  $$\begin{aligned} c^\Psi _{\textrm{EHZ}}(D\cap (x+K))\le c^\Psi _{\textrm{EHZ}}(D\cap K),\quad \forall x\in {\textrm{Fix}}(\Psi ). \end{aligned}$$

  (3.19)

Proof

(i) Indeed, let $p\in {\textrm{Fix}}(\Psi )\cap {\textrm{Int}}(D)$ and $q\in {\textrm{Fix}}(\Psi )\cap {\textrm{Int}}(K)$. Then (1.3) implies

$$\begin{aligned} \left( c^{\Psi }_{\textrm{EHZ}}(D+K-p-q)\right) ^{\frac{1}{2}}= & {} \left( c^{\Psi }_{\textrm{EHZ}}((D-p)+(K-q))\right) ^{\frac{1}{2}}\\\ge & {} \left( c^{\Psi }_{\textrm{EHZ}}(D-p)\right) ^{\frac{1}{2}}+ \left( c^{\Psi }_{\textrm{EHZ}}(K-q)\right) ^{\frac{1}{2}}. \end{aligned}$$

For $z\in {\mathbb {R}}^{2n}$, consider the symplectomorphism $\phi _z:({\mathbb {R}}^{2n},\omega _0)\rightarrow ({\mathbb {R}}^{2n},\omega _0),\;x\mapsto x-z$. Since p, q and $p+q$ are all fixed points of $\Psi$, and $\phi _p$, $\phi _q$ and $\phi _{p+q}$ commute with $\Psi$, by Proposition 2.2 it is clear that

$$\begin{aligned}{} & {} c^{\Psi }_{\textrm{EHZ}}(D+K-p-q)=c^{\Psi }_{\textrm{EHZ}}(\phi _{p+q}(D+K))=c^{\Psi }_{\textrm{EHZ}}(D+K),\\{} & {} c^{\Psi }_{\textrm{EHZ}}(D-p)=c^{\Psi }_{\textrm{EHZ}}(\phi _{p}(D))=c^{\Psi }_{\textrm{EHZ}}(D),\\{} & {} c^{\Psi }_{\textrm{EHZ}}(K-q)=c^{\Psi }_{\textrm{EHZ}}(\phi _{q}(K))=c^{\Psi }_{\textrm{EHZ}}(K). \end{aligned}$$

Other claims easily follow from the arguments therein.

(ii) Since $x,y\in {\textrm{Fix}}(\Psi )$, both ${\textrm{Int}}(D)\cap {\textrm{Fix}}(\Psi )-x$ and ${\textrm{Int}}(D)\cap {\textrm{Fix}}(\Psi )-y$ are intersecting with ${\textrm{Int}}(K)$, we deduce that for any $0\le \lambda \le 1$ interiors of $\lambda (D\cap (x+K))$ and $(1-\lambda )(D\cap (y+K))$ contain fixed points of $\Psi$. (3.18) follows from Proposition 2.2 and (i) directly.

Suppose further that D and K are centrally symmetric, i.e., $-D=D$ and $-K=K$. Then $D\cap (-x+K)=-(D\cap (x+K))$ and $c^\Psi _{\textrm{EHZ}}(-(D\cap (x+K)))=c^\Psi _{\textrm{EHZ}}(D\cap (x+K))$ since the symplectomorphism ${\mathbb {R}}^{2n}\rightarrow {\mathbb {R}}^{2n},\,z\mapsto -z$ commutes with $\Psi$. Thus taking $y=-x$ and $\lambda =1/2$ in (3.18) leads to $c^\Psi _{\textrm{EHZ}}(D\cap (x+K))\le c^\Psi _{\textrm{EHZ}}(D\cap K)$. $\square$

Let D, K and $\Psi$ be as in Corollary 3.5. As in [2, 3] we may derive from Corollary 3.5 that the limit

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0+}\frac{c^\Psi _{\textrm{EHZ}}(D+\varepsilon K)-c^\Psi _{\textrm{EHZ}}(D)}{\varepsilon } \end{aligned}$$

(3.20)

exists, denoted by $d^\Psi _K(D)$. In fact, by the assumptions we can choose $p\in {\textrm{Fix}}(\Psi )\cap {\textrm{Int}}(D)$ and $q\in {\textrm{Fix}}(\Psi )\cap {\textrm{Int}}(K)$. Then $(K-q)\subset R(D-p)$ for some $R>0$ (since $0\in \textrm{int}(D-q)$). Note that $p+\varepsilon q\in {\textrm{Fix}}(\Psi )\cap {\textrm{Int}}(D+\varepsilon K)$. By the proof of Corollary 3.5(i) and Proposition 2.2(ii) we get

$$\begin{aligned} c^\Psi _{\textrm{EHZ}}(D+\varepsilon K)-c^\Psi _{\textrm{EHZ}}(D)= & {} c^\Psi _{\textrm{EHZ}}((D-p)+\varepsilon (K-q))-c^\Psi _{\textrm{EHZ}}(D-p)\\\le & {} c^\Psi _{\textrm{EHZ}}((D-p)+\varepsilon R(D-p))-c^\Psi _{\textrm{EHZ}}(D-p)\\\le & {} (1+\varepsilon R)c^\Psi _{\textrm{EHZ}}(D-p)-c^\Psi _{\textrm{EHZ}}(D-p)\\= & {} \varepsilon Rc^\Psi _{\textrm{EHZ}}(D) \end{aligned}$$

and therefore that the function of $\varepsilon >0$ in (3.20) is bounded. This function is also decreasing by Corollary 3.5(i) (see reasoning [2, pp. 21–22]). Hence the limit in (3.20) exists.

The number $d^\Psi _K(D)$ may be viewed as the rate of change of the function $D\mapsto c^\Psi _{\textrm{EHZ}}(D)$ in the “direction" K. From Corollary 3.5 we can estimate it as follows.

Corollary 3.6

Let D, K and $\Psi$ be as in Corollary 3.5. Then it holds that

$$\begin{aligned} 2(c^\Psi _{\textrm{EHZ}}(D))^{1/2}(c^\Psi _{\textrm{EHZ}}(K))^{1/2}\le d^\Psi _K(D)\le \inf _{z_D}\int _0^1h_K(-J\dot{z}_D(t))dt, \end{aligned}$$

(3.21)

where $z_D:[0,1]\rightarrow \partial D$ takes over all $c^\Psi _{\textrm{EHZ}}$-carriers for D.

In [2, 3] ${\textrm{length}}_{JK^\circ }(z_D)=\int _0^1j_{JK^\circ }(\dot{z}_D(t))dt$ is called the length of $z_D$ with respect to the convex body $JK^\circ$. In the case $0\in \textrm{int}(K)$, since $h_K(-Jv)=j_{JK^\circ }(v)$, (3.21) implies

$$\begin{aligned} d^\Psi _K(D)\le \inf _{z_D}\int _0^1j_{JK^\circ }(\dot{z}_D(t))dt\quad \hbox {and hence}\quad c^\Psi _{\textrm{EHZ}}(D)c^\Psi _{\textrm{EHZ}}(K)\le \frac{1}{4}\inf _{z_D}(\textrm{length}_{JK^\circ }(z_D))^2. \end{aligned}$$

It is not hard to see that (3.19) may not hold if one of D and K is not convex. Therefore the symplectic capacities only show good behavior in the convex category.

Proof of Corollary 3.6

The first inequality in (3.21) easily follows from Corollary 3.5(i). In order to prove the second one let us fix a real $p_1>1$. By Proposition 3.2 we have $u\in \mathcal {A}_{p_1}$ such that

$$\begin{aligned} (c^{\Psi }_{\textrm{EHZ}}(D))^{\frac{1}{2}}=(c^{\Psi }_{\textrm{EHZ}}(D-p))^{\frac{1}{2}}= & {} \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2}\int _0^1 h_{D-p}(-J\dot{x}))\nonumber \\= & {} \frac{1}{2}\int _0^1h_{D-p}(-J\dot{u})) \end{aligned}$$

(3.22)

and that for some $\textbf{a}_0\in \textrm{Ker}(\Psi -I_{2n})$

$$\begin{aligned} x^*(t)=\left( c^\Psi _{\textrm{EHZ}}(D)\right) ^{1/2}u(t)+ \frac{2}{p_1}\left( c^\Psi _{\textrm{EHZ}}(D)\right) ^{(1-p_1)/2}{} \textbf{a}_0 \end{aligned}$$

(3.23)

is a $c^\Psi _{\textrm{EHZ}}$ carrier for $\partial (D-p)$ by Remark 3.4. Proposition 3.2 also leads to

$$\begin{aligned} (c^{\Psi }_{\textrm{EHZ}}(D+ \varepsilon K))^{\frac{1}{2}}= & {} (c^{\Psi }_{\textrm{EHZ}}((D-p)+ \varepsilon (K-q)))^{\frac{1}{2}}\end{aligned}$$

(3.24)

$$\begin{aligned}= & {} \min _{x\in \mathcal {A}_{p_1}}\frac{1}{2}\int _0^1 (h_{D-p}(-J\dot{x})+ \varepsilon h_{K-q}(-J\dot{x}))\nonumber \\\le & {} \frac{1}{2}\int _0^1 h_{D-p}(-J\dot{u})+\frac{\varepsilon }{2}\int _0^1 h_{K-q}(-J\dot{u})\nonumber \\= & {} (c^{\Psi }_{\textrm{EHZ}}(D,\omega _0))^{\frac{1}{2}}+\frac{\varepsilon }{2}\int _0^1 h_{K-q}(-J\dot{u}) \end{aligned}$$

(3.25)

because of (3.22). Let $z_D(t)=x^*(t)+p$ for $0\le t\le 1$. Since q and $\textbf{a}_0$ are fixed points of $\Psi$ it is easily checked that $z_D$ is a $c^\Psi _{\textrm{EHZ}}$ carrier for $\partial D$. From (3.24) it follows that

$$\begin{aligned} \frac{(c^\Psi _{\textrm{EHZ}}(D+\varepsilon K))^{\frac{1}{2}}-(c^\Psi _{\textrm{EHZ}}(D))^{\frac{1}{2}}}{\varepsilon }\le \frac{1}{2}\left( c^\Psi _{\textrm{EHZ}}(D)\right) ^{-\frac{1}{2}} \int _0^1h_{K-q}(-J\dot{z}_D). \end{aligned}$$

(3.26)

Since $h_{K-q}(-J\dot{z}_D)=h_{K}(-J\dot{z}_D)+\langle q, J\dot{z}_D\rangle$ (see page 37 and Theorem 1.7.5 in [15]) and

$$\begin{aligned} \int _0^1\langle q, J\dot{z}_D\rangle =\langle q, J(z_D(1)-z_D(0))\rangle =-\langle Jq, \Psi z_D(0)\rangle +\langle Jq, z_D(0)\rangle =0 \end{aligned}$$

(by the fact $\Psi ^tJ=J\Psi ^{-1}$), letting $\varepsilon \rightarrow 0+$ in (3.26) we arrive at the second inequality in (3.21). $\square$

4 Classification of $(A, \Delta , \Lambda )$-billiard trajectories and related properties of proper trajectories

In this section, we give the classification of $(A, \Delta , \Lambda )$-billiard trajectories, related properties of proper trajectories, the relation between A-billiard trajectories in $\Delta$ and $(A,\Delta ,B^n)$-billiard trajectories. Moreover, on the base of the latter we prove that $\xi ^A(\Delta )$ provides a lower bound of lengths of A-billiard trajectory in $\Delta$.

Proposition 4.1

Let A, $\Delta$ and $\Lambda$ be as in (1.19).

• (i) If both $\Delta$ and $\Lambda$ are also strictly convex (i.e., they have strictly positive Gauss curvatures at every point of their boundaries), then every $(A, \Delta , \Lambda )$-billiard trajectory is either proper or gliding.

• (ii) Every proper $(A, \Delta , \Lambda )$-billiard trajectory $\gamma :[0, T]\rightarrow \partial (\Delta \times \Lambda )$ cannot be contained in $\Delta \times \partial \Lambda$ or $\partial \Delta \times \Lambda$. Consequently, $\gamma ^{-1}(\partial \Delta \times \partial \Lambda )$ contains at least a point in (0, T).

Remark 4.2

If the condition “proper” in (ii) in the above claim is dropped, then “$\Delta \times \partial \Lambda$ or $\partial \Delta \times \Lambda$” should changed into “${\textrm{Int}}(\Delta )\times \partial \Lambda$ or $\partial \Delta \times {\textrm{Int}}(\Lambda )$”.

Proof of Proposition 4.1

(i) can be obtained form Proposition 2.12 in [3]. Let us prove (ii). By the definition we may assume that $\Delta \subset {\mathbb {R}}^n_q$ and $\Lambda \subset {\mathbb {R}}^n_p$ contain the origin in their interiors. We only need to prove that every proper $(A, \Delta , B^n)$-billiard trajectory cannot be contained in $\Delta \times \partial \Lambda$. (Another case may be proved with the same arguments.) Otherwise, let $\gamma =(\gamma _q,\gamma _p):[0, T]\rightarrow \partial (\Delta \times \Lambda )$ be such a trajectory, that is, $\gamma ([0,T])\subset \Delta \times \partial \Lambda$. Then $\gamma ^{-1}(\partial \Delta \times \partial \Lambda )$ is finite (including empty) and there holds

$$\begin{aligned} \dot{\gamma }(t)=(\dot{\gamma }_q(t), \dot{\gamma }_p(t))=(\kappa \nabla j_{\Lambda }({\gamma }_p(t)),0) \quad \forall t\in [0, T]\setminus \gamma ^{-1}(\partial \Delta \times \partial \Lambda ) \end{aligned}$$

for some positive constant $\kappa$. It follows that $\gamma _p$ is constant on each component of $[0, T]{\setminus }\gamma ^{-1}(\partial \Delta \times \partial \Lambda )$, and so constant on $[0, T]{\setminus }\gamma ^{-1}(\partial \Delta \times \partial \Lambda )$ by continuity of $\gamma$. Hence $\gamma _p\equiv p_0\in \partial \Lambda$, and so $\gamma _q(t)=q_0+\kappa t\nabla j_{\Lambda }(p_0)$ on [0, T], where $q_0=\gamma _q(0)$. Now

$$\begin{aligned} (q_0+\kappa T\nabla j_{\Lambda }(p_0), p_0)=\gamma (T)=\Psi _A\gamma (0)=(A\gamma _q(0), (A^t)^{-1}\gamma _p(0))= (Aq_0, (A^t)^{-1}p_0). \end{aligned}$$

This implies that $A^tp_0=p_0$ and $q_0-Aq_0=-\kappa T\nabla j_{\Lambda }(p_0)$. The former equality leads to $\langle p_0, v-Av\rangle =0\;\forall v\in {\mathbb {R}}^n$. Combing this with the latter equality we obtain $\langle p_0, \nabla j_{\Lambda }(p_0)\rangle =0$. This implies $j_{\Lambda }(p_0)=0$ and so $p_0=0$, which contradicts $p_0\in \partial \Lambda$ since $0\in \textrm{int}(\Lambda )$. $\square$

Recall that the action of an $(A, \Delta ,\Lambda )$-billiard trajectory $\gamma$ is given by (2.4). The length of an A-billiard trajectory $\sigma :[0,T]\rightarrow \Delta$ is given by

$$\begin{aligned} L(\sigma ):=\sum _{i=0}^n\Vert q_{j+1}-q_j\Vert , \end{aligned}$$

with

$$\begin{aligned} q_0=\sigma (0),\; q_1=\sigma (t_i),\; \ldots ,\; q_{m-1}=\sigma (t_{m-1}), \;q_m=\sigma (T), \end{aligned}$$

where

$$\begin{aligned} \{t_1,\ldots ,t_{m-1}\}:=\mathcal {B}_{\sigma } \end{aligned}$$

is the finite set in Definition 1.2. Here $\Vert \cdot \Vert$ is the Euclid norm in ${\mathbb {R}}^n$.

The following proposition gives the relation between A-billiard trajectories in $\Delta$ and $(A,\Delta ,B^n)$-billiard trajectories.

Proposition 4.3

For a smooth convex body in $\Delta \subset {\mathbb {R}}^n$ and $A\in \textrm{O}(n)$ satisfying ${\textrm{Fix}}(A)\cap {\textrm{Int}}(\Delta )\ne \emptyset$, every A-billiard trajectory in $\Delta$, $\sigma :[0,T]\rightarrow \Delta$, is the projection to $\Delta$ of a proper $(A, \Delta , B^n)$-billiard trajectory whose action is equal to the length of $\sigma$.

Proof

By the definitions we only need to consider the case that $0\in {\textrm{Int}}(\Delta )$. Let $\sigma :[0,T]\rightarrow \Delta$ be a A-billiard trajectory in $\Delta$ with $\mathscr {B}_\sigma =\{t_1<\cdots <t_k\}\subset (0, T)$ as in Definition 1.4. Then $|\dot{\sigma }(t)|$ is equal to a positive constant $\kappa$ in $(0,T)\setminus \mathscr {B}_\sigma$.

Suppose that (ABiii) occurs. Define

$$\begin{aligned}{} & {} \alpha _1(t)=(\sigma (t), -\frac{1}{\kappa }\dot{\sigma }^+(0)),\quad 0\le t\le t_1,\\{} & {} \beta _1(t)=(\sigma (t_1), -\frac{1}{\kappa }\dot{\sigma }^+(0)+ \frac{t}{\kappa }(\dot{\sigma }^-(t_1)-\dot{\sigma }^+(t_1)),\quad 0\le t\le 1. \end{aligned}$$

Since the second equality in (1.5) implies that $\dot{\sigma }^-(t_i)-\dot{\sigma }^+(t_i)$ is an outer normal vector to $\partial \Delta$ at $\sigma (t_i)$ for each $t_i\in \mathscr {B}_\sigma$, it is easily checked that both are generalized characteristics on $\partial (\Delta \times \Lambda )$ and $\alpha _1(t_1)=\beta _1(0)$. Similarly, define

$$\begin{aligned}{} & {} \alpha _2(t)=(\sigma (t), -\frac{1}{\kappa }\dot{\sigma }^+(t_1)),\quad t_1\le t\le t_2,\\{} & {} \beta _2(t)=(\sigma (t_1), -\frac{1}{\kappa }\dot{\sigma }^+(t_1)+ \frac{t}{\kappa }(\dot{\sigma }^-(t_2)-\dot{\sigma }^+(t_2)),\quad 0\le t\le 1,\\{} & {} \vdots \\{} & {} \alpha _k(t)=(\sigma (t), -\frac{1}{\kappa }\dot{\sigma }^+(t_{k-1})),\quad t_{k-1}\le t\le t_k,\\{} & {} \beta _k(t)=(\sigma (t_{k-1}), -\frac{1}{\kappa }\dot{\sigma }^+(t_{k-1})+ \frac{t}{\kappa }(\dot{\sigma }^-(t_k)-\dot{\sigma }^+(t_k)),\quad 0\le t\le 1,\\{} & {} \alpha _{k+1}(t)=(\sigma (t), -\frac{1}{\kappa }\dot{\sigma }^+(t_{k}))= (\sigma (t), -\frac{1}{\kappa }\dot{\sigma }^-(T)),\quad t_{k}\le t\le T. \end{aligned}$$

Then $\beta _1(1)=\alpha _2(t_1)$, $\alpha _2(t_2)=\beta _2(0)$, $\ldots$, $\beta _k(1)=\alpha _{k+1}(t_k)$, that is, $\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1}$ is a path. Note also that

$$\begin{aligned} \alpha _{k+1}(T)=(\sigma (T), -\frac{1}{\kappa }\dot{\sigma }^-(T))=(A\sigma (0), -\frac{1}{\kappa }A\dot{\sigma }^+(0))= \Psi _A\alpha _1(0) \end{aligned}$$

by (1.9). Hence $\gamma :=\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1}$ is a generalized $\Psi _A$-characteristic on $\partial (\Delta \times \Lambda )$. Clearly, $\beta _1,\ldots ,\beta _k$ all have zero actions. So

$$\begin{aligned} A(\gamma )=\sum _{i=0}^{k+1}\int _{t_i}^{t_{i+1}}\langle -\dot{\sigma }(t),-\frac{1}{\kappa }\dot{\sigma }^+(t_{i})\rangle _{{\mathbb {R}}^n}dt =\kappa T=L(\sigma ). \end{aligned}$$

Suppose that (ABiv) occurs. Let $\alpha _i$ and $\beta _j$ be defined as above for $i=1,\ldots ,k+1$ and $j=1,\ldots ,k$. If (1.9) holds, we also define $\gamma$ as above, and get a generalized $\Psi _A$-characteristic on $\partial (\Delta \times \Lambda )$.

If (1.10) occurs, we also need to define

$$\begin{aligned} \beta _0(t)=(\sigma (0), -\frac{1}{\kappa }\dot{\sigma }^-(0)+ \frac{t}{\kappa }(\dot{\sigma }^-(0)-\dot{\sigma }^+(0)),\quad 0\le t\le 1. \end{aligned}$$

By (1.8), $\dot{\sigma }^-(0)-\dot{\sigma }^+(0)$ is an outer normal vector to $\partial \Delta$ at $\sigma (0)$. It is easy to see that $\beta _0$ is a generalized characteristic on $\partial (\Delta \times \Lambda )$ satisfying $\beta _0(1)=\alpha _1(0)$. Moreover

$$\begin{aligned} \Psi _A\beta _0(0)=\Psi _A(\sigma (0), -\frac{1}{\kappa }\dot{\sigma }^-(0))\!=\! (A\sigma (0), -\frac{1}{\kappa }A\dot{\sigma }^-(0))\!=\!(\sigma (T), \!-\!\frac{1}{\kappa }\dot{\sigma }^-(T))\!=\!\alpha _{k+1}(T) \end{aligned}$$

by (1.10). Thus $\gamma :=\beta _0\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1}$ is a generalized $\Psi _A$-characteristic on $\partial (\Delta \times \Lambda )$.

Suppose that (ABv) occurs. If (1.9) holds, we define $\gamma$ as in the case of (ABv). When (1.11) occurs, we need to define

$$\begin{aligned} \beta _{k+1}(t)\!=\!(\sigma (T), -\!\frac{1}{\kappa }\dot{\sigma }^-(T)\!+\! \frac{t}{\kappa }(\dot{\sigma }^-(T)\!-\!\dot{\sigma }^+(T)),\, 0\le t\le 1. \end{aligned}$$

Then $\gamma :=\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1}\beta _{k+1}$ is a generalized $\Psi _A$-characteristic on $\partial (\Delta \times \Lambda )$.

Suppose that (ABvi) occurs. If (1.9) or (1.10) or (1.11) holds, we define

$$\begin{aligned} \gamma \!:=\!\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1},\,\hbox {or}\, \gamma \!:=\!\beta _0\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1},\,\hbox {or}\, \gamma \!:=\!\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1}\beta _{k+1}. \end{aligned}$$

Finally, if (1.12) holds, we define $\gamma :=\beta _0\alpha _1\beta _1\cdots \alpha _k\beta _k\alpha _{k+1}\beta _{k+1}$. $\square$

However, under the assumptions of Proposition 4.3 we cannot affirm that the projection to $\Delta$ of a proper $(A, \Delta , B^n)$-billiard trajectory is an A-billiard trajectory in $\Delta$.

Proposition 4.4

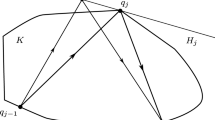
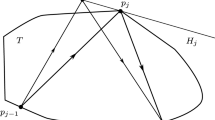
Let $\Delta \subset {\mathbb {R}}^n$ be a smooth convex body and $A\in {\textrm{O}}(n)$ satisfy ${\textrm{Fix}}(A)\cap {\textrm{Int}}(\Delta )\ne \emptyset$. Then it holds that

$$\begin{aligned} \xi ^A(\Delta )\le \inf \{L(\sigma )\,|\,\sigma \hbox { is an } A\!-\!\hbox {billiard trajectory in }\Delta \}. \end{aligned}$$

Proof

This may directly follow from Proposition 4.3, Remark1.7(i) and Theorem 2.6. $\square$

The statement about relation between the action of a proper $(A, \Delta ,B^n)$-billiard trajectory and the length of its projection to $\Delta$ in Proposition 4.3 is a special case of the following proposition. When $A=I_n$ it was showed in [3, (7)].

Proposition 4.5

Let A, $\Delta$ and $\Lambda$ satisfy (1.19). If $\gamma :[0, T]\rightarrow \partial (\Delta \times \Lambda )$ is a proper $(A, \Delta , \Lambda )$-billiard trajectory with $\gamma ^{-1}(\partial \Delta \times \partial \Lambda )\cap (0,T)=\{t_1<\cdots <t_m\}$, then the action of $\gamma$ is given by

$$\begin{aligned} A(\gamma )=\sum ^{m}_{j=0}h_\Lambda (q_j-q_{j+1}) \end{aligned}$$

(4.1)

with $q_j=\pi _q(\gamma (t_j))$, $j=0,\ldots ,m+1$, where $t_0=0$, $t_{m+1}=T$ and $q_{m+1}=Aq_0$. In particular, if $\Lambda =B^n(\tau )$ for $\tau >0$ and $L(\pi _q(\gamma ))$ denotes the length of the projection of $\gamma$ in $\Delta$ then

$$\begin{aligned} A(\gamma )=\tau \sum ^{m}_{j=0}\Vert q_{j+1}-q_j\Vert =\tau L(\pi _q(\gamma )) \end{aligned}$$

(4.2)

since $\Lambda ^\circ =\frac{1}{\tau }B^n$ and thus $h_\Lambda =j_{\Lambda ^\circ }=\tau \Vert \cdot \Vert$. Moreover, if $\Delta$ is strictly convex, then the action of any gliding $(A,\Delta , B^n)$-billiard trajectory $\gamma :[0, T]\rightarrow \partial (\Delta \times B^n)$ is also equal to the length of the projection $\pi _q(\gamma )$ in $\Delta$.

Proof

Firstly, we prove (4.1) in the case that $0\in {\textrm{Int}}(\Delta )$ and $0\in {\textrm{Int}}(\Lambda )$. By a direct computation we have

$$\begin{aligned} A(\gamma )= & {} \frac{1}{2}\int ^T_0\langle -J\dot{\gamma }(t),\gamma (t)\rangle dt\\= & {} \frac{1}{2}\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}\langle -J\dot{\gamma }(t),\gamma (t)\rangle dt\\= & {} \frac{1}{2}\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}\left[ (\dot{p}(t), q(t))_{{\mathbb {R}}^n}-(\dot{q}(t),p(t))_{{\mathbb {R}}^n}\right] dt\\= & {} -\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}(\dot{q}(t),{p}(t))_{{\mathbb {R}}^n}dt+ \frac{1}{2}\sum ^{m}_{j=0}\left[ (q(t_{j+1}),p(t_{j+1}))_{{\mathbb {R}}^n}-(q(t_j), p(t_j))_{{\mathbb {R}}^n}\right] \\= & {} -\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}(\dot{q}(t), {p}(t))_{{\mathbb {R}}^n}dt+ \frac{1}{2}\left[ (q(t_{m+1}),p(t_{m+1}))_{{\mathbb {R}}^n}-(q(t_0),p(t_0))_{{\mathbb {R}}^n}\right] \\= & {} -\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}(\dot{q}(t), p(t))_{{\mathbb {R}}^n}dt \end{aligned}$$

since $(q(t_{m+1}),p(t_{m+1}))_{{\mathbb {R}}^n}=(Aq(t_0), (A^t)^{-1}p(t_0))_{{\mathbb {R}}^n}= (q(t_0),p(t_0))_{{\mathbb {R}}^n}$. By (BT1) we have

$$\begin{aligned} -\int ^{t_{i+1}}_{t_i}(\dot{q}(t),p(t))_{{\mathbb {R}}^n}dt= -(q(t_{i+1})-q(t_i), p(t_i))_{{\mathbb {R}}^n}=-(q_{i+1}-q_i, p_i)_{{\mathbb {R}}^n}, \end{aligned}$$

where $j_\Lambda (p_i)=1$ and $q_{i+1}-q_i=-\kappa (t_{i+1}-t_i)\nabla j_\Lambda (p_i)$. The last two equalities mean that $-(q_{i+1}-q_i, p_i)_{{\mathbb {R}}^n}$ is either the maximum or the minimum of the function $p\mapsto -(q_{i+1}-q_i, p)_{{\mathbb {R}}^n}$ on $j^{-1}_\Lambda (1)$. Note that

$$\begin{aligned} -\int ^{t_{i+1}}_{t_i}(\dot{q}(t),p(t))_{{\mathbb {R}}^n}dt= \int ^{t_{i+1}}_{t_i}(\kappa \nabla j_\Lambda (p(t_i)), p(t_i))_{{\mathbb {R}}^n}dt= \kappa (t_{i+1}-t_i)>0. \end{aligned}$$

So $-(q_{i+1}-q_i, p_i)_{{\mathbb {R}}^n}$ must be the maximum of the function $p\mapsto -(q_{i+1}-q_i, p)_{{\mathbb {R}}^n}$ on $j^{-1}_\Lambda (1)$, which by definition equals $h_\Lambda (q_i-q_{i+1})$. In this case (4.1) follows immediately.

Next, we deal with the general case. Now we have $\bar{q}\in {\textrm{Int}}(\Delta )$ and $\bar{p}\in {\textrm{Int}}(\Lambda )$ such that the above result can be applied to $\gamma -(\bar{q},\bar{p})$ yielding

$$\begin{aligned} A(\gamma -(\bar{q},\bar{p}))= & {} \sum ^{m}_{j=0}h_{\Lambda -\bar{p}}((q_j-\bar{q})-(q_{j+1}-\bar{q}))= \sum ^{m}_{j=0}h_{\Lambda -\bar{p}}(q_j-q_{j+1})\\= & {} \sum ^{m}_{j=0}h_{\Lambda }(q_j-q_{j+1})-\sum ^{m}_{j=0}(\bar{p}, q_j-q_{j+1})_{{\mathbb {R}}^n} \end{aligned}$$

because $h_{\Lambda -\bar{p}}(u)=h_{\Lambda }(u)-(\bar{p}, u)_{{\mathbb {R}}^n}$, where $q_j=\pi _q(\gamma (t_i))$, $i=0,\ldots ,m+1$, where $t_0=0$, $t_{m+1}=T$ and $q_{m+1}=Aq_0$. Moreover, as above we may compute

$$\begin{aligned} A(\gamma )= & {} -\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}(\dot{q}(t), p(t))_{{\mathbb {R}}^n}dt,\\ A(\gamma -(\bar{q},\bar{p}))= & {} -\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}(\dot{q}(t), p(t)-\bar{p})_{{\mathbb {R}}^n}dt\\= & {} -\sum ^{m}_{j=0}\int ^{t_{j+1}}_{t_j}(\dot{q}(t), p(t))_{{\mathbb {R}}^n}dt-\sum ^{m}_{j=0}(\bar{p}, q_j-q_{j+1})_{{\mathbb {R}}^n} \end{aligned}$$

These lead to the desired (4.1) directly.

Thirdly, we prove the final claim. Now $\bar{p}=0$, The above expressions show that $A(\gamma )=A(\gamma -(\bar{q},0)$. Since $\pi _q(\gamma )-\bar{q}$ and $\pi _q(\gamma )$ have the same length, we only need to prove the case $\bar{q}=0$.

Since $\gamma$ is gliding, by Proposition 4.1(i) we have

$$\begin{aligned} \dot{\gamma }(t)=(\dot{\gamma }_q(t), \dot{\gamma }_p(t))=(-\alpha (t)\gamma _p(t)/|\gamma _p(t)|, \beta (t)\nabla g_\Delta (\gamma _q(t))), \end{aligned}$$

where $\alpha$ and $\beta$ are two smooth positive functions satisfying a condition as in [3, (8)]. Hence $\gamma _q=\pi _q(\gamma )$ has length

$$\begin{aligned} L(\gamma _q)=\int ^T_0|\dot{\gamma }_q(t)|dt=\int ^T_0\alpha (t)dt. \end{aligned}$$

On the other hand, as above we have

$$\begin{aligned} A(\gamma )= & {} \frac{1}{2}\int ^T_0\langle -J\dot{\gamma }(t),\gamma (t)\rangle dt\\= & {} \frac{1}{2}\int ^T_0\bigl ((\dot{\gamma }_p(t),\gamma _q(t))_{{\mathbb {R}}^n}- (\dot{\gamma }_q(t)\gamma _p(t)))_{{\mathbb {R}}^n}\bigr )dt\\= & {} -\int ^T_0(\gamma _p(t),\dot{\gamma }_q(t)))_{{\mathbb {R}}^n}dt=\int ^T_0\alpha (t)dt. \end{aligned}$$

$\square$

5 Proofs of Theorems 1.9, 1.15 and Proposition 1.10

Proof of Theorem 1.9

Let $\lambda \in (0,1)$. Since ${\textrm{Int}}(\Delta _1)\cap {\textrm{Fix}}(A)\ne \emptyset$, ${\textrm{Int}}(\Delta _2)\cap {\textrm{Fix}}(A)\ne \emptyset$ and ${\textrm{Int}}(\Lambda )\cap {\textrm{Fix}}(A^t)\ne \emptyset$, ${\textrm{Fix}}(\Psi _A)$ is intersecting with both ${\textrm{Int}}(\Delta _1\times \Lambda )$ and ${\textrm{Int}}(\Delta _2\times \Lambda )$. Note that

$$\begin{aligned}{} & {} \bigl (\lambda \Delta _1\bigr )\times \bigl (\lambda \Lambda \bigr )+ \bigl ((1-\lambda )\Delta _2\bigr )\times \bigl ((1-\lambda )\Lambda \bigr )\\{} & {} \quad =\bigl (\lambda \Delta _1+(1-\lambda )\Delta _2\bigr )\times \bigl (\lambda \Lambda + (1-\lambda )\Lambda \bigr )\\{} & {} \quad =\bigl (\lambda \Delta _1+(1-\lambda )\Delta _2\bigr )\times \Lambda . \end{aligned}$$

It follows from Corollary 3.5 that

$$\begin{aligned}{} & {} \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\lambda \Delta _1\times \lambda \Lambda \bigr )\bigr )^{\frac{1}{2}}+ \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl ((1-\lambda )\Delta _2\times (1-\lambda )\Lambda \bigr )\bigr )^{\frac{1}{2}}\nonumber \\{} & {} \quad \le \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\bigl (\lambda \Delta _1+(1-\lambda )\Delta _2\bigr )\times \Lambda \bigr )\bigr )^{\frac{1}{2}}, \end{aligned}$$

(5.1)

which is equivalent to

$$\begin{aligned}{} & {} \lambda \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _1\times \Lambda \bigr )\bigr )^{\frac{1}{2}}+ (1-\lambda )\bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _2\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\nonumber \\{} & {} \quad \le \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\bigl (\lambda \Delta _1+(1-\lambda )\Delta _2\bigr )\times \Lambda \bigr )^{\frac{1}{2}}. \end{aligned}$$

(5.2)

By this and the weighted arithmetic–geometric mean inequality

$$\begin{aligned}{} & {} \lambda \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _1\times \Lambda \bigr )\bigr )^{\frac{1}{2}}+ (1-\lambda )\bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _2\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\\{} & {} \quad \ge \left( \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _1\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\right) ^\lambda \left( \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _2\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\right) ^{(1-\lambda )}, \end{aligned}$$

we get

$$\begin{aligned}{} & {} \left( \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _1\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\right) ^\lambda \left( \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _2\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\right) ^{(1-\lambda )} \nonumber \\{} & {} \quad \le \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\bigl (\lambda \Delta _1+(1-\lambda )\Delta _2\bigr )\times \Lambda \bigr )^{\frac{1}{2}}. \end{aligned}$$

(5.3)

Replacing $\Delta _1$ and $\Delta _2$ by $\Delta _1':=\lambda ^{-1}\Delta _1$ and $\Delta _2':=(1-\lambda )^{-1}\Delta _2$, respectively, we arrive at

$$\begin{aligned} \left( \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_1\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\right) ^\lambda \left( \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_2\times \Lambda \bigr )\bigr )^{\frac{1}{2}}\right) ^{(1-\lambda )} \le \bigl (c^{\Psi _A}_{\textrm{EHZ}}\bigl (\bigl (\Delta _1+\Delta _2\bigr )\times \Lambda \bigr )^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$

(5.4)

For any $\mu >0$, since

$$\begin{aligned} \phi :(\Delta _1\times \Lambda , \mu \omega _0)\rightarrow ((\mu \Delta _1)\times \Lambda , \omega _0),\;(x,y)\mapsto (\mu x,y) \end{aligned}$$

is a symplectomorphism which commutes with $\Psi _A$, we have

$$\begin{aligned} c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_1\times \Lambda \bigr )=\lambda ^{-1}c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _1\times \Lambda \bigr ), \qquad c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_2\times \Lambda \bigr )=(1-\lambda )^{-1}c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _2\times \Lambda \bigr ). \end{aligned}$$

Let us choose $\lambda \in (0,1)$ such that $\Upsilon :=c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_1\times \Lambda \bigr )=c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_2\times \Lambda \bigr )$, i.e.,

$$\begin{aligned} \lambda =\frac{c^{\Psi _A}_{\textrm{EHZ}}(\Delta _1\times \Lambda )}{ c^{\Psi _A}_{\textrm{EHZ}}(\Delta _1\times \Lambda )+ c^{\Psi _A}_{\textrm{EHZ}}(\Delta _2\times \Lambda )}. \end{aligned}$$

(5.5)

Then

$$\begin{aligned} \xi ^A_\Lambda (\Delta _1+\Delta _2)= & {} c^{\Psi _A}_{\textrm{EHZ}}\bigl (\bigl (\Delta _1+\Delta _2\bigr )\times \Lambda \bigr )\nonumber \\\ge & {} \left( c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_1\times \Lambda \bigr )\right) ^\lambda \left( c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_2\times \Lambda \bigr )\right) ^{(1-\lambda )}\nonumber \\= & {} \Upsilon =\lambda \Upsilon +(1-\lambda )\Upsilon \nonumber \\= & {} \lambda c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_1\times \Lambda \bigr )+(1-\lambda )c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta '_2\times \Lambda \bigr ) \nonumber \\= & {} c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _1\times \Lambda \bigr )+c^{\Psi _A}_{\textrm{EHZ}}\bigl (\Delta _2\times \Lambda \bigr )\nonumber \\= & {} \xi ^A_\Lambda (\Delta _1)+ \xi ^A_\Lambda (\Delta _2) \end{aligned}$$

(5.6)

and hence (1.22) holds.

Final claim follows from Corollary 3.5. Theorem 1.9 is proved. $\square$

Proof of Proposition 1.10

(i) By the definition of $\xi ^A$ and Proposition 2.2(i)–(ii) we have

$$\begin{aligned} \xi ^A(\Delta )= & {} c^{\Psi _A}_{\textrm{EHZ}}(\Delta \times B^n)\nonumber \\\ge & {} c^{\Psi _A}_{\textrm{EHZ}}(B^{n}(\bar{q},r)\times B^n)\nonumber \\= & {} c^{\Psi _A}_{\textrm{EHZ}}(B^{n}(0,r)\times B^n) \end{aligned}$$

(5.7)

since $(\bar{q},0)$ is a fixed point of $\Psi _A$. Note that

$$\begin{aligned} B^n(0,r)\times B^n\rightarrow B^n(0,\sqrt{r})\times B^n(0,\sqrt{r}),\;(q,p)\mapsto (q/\sqrt{r}, \sqrt{r}p) \end{aligned}$$

(5.8)

is a symplectomorphism which commutes with $\Psi _A$. Using Proposition 2.2(i)–(ii) we deduce

$$\begin{aligned} c^{\Psi _A}_{\textrm{EHZ}}(B^{n}(0,r)\times B^n)= & {} c^{\Psi _A}_{\textrm{EHZ}}(B^n(0,\sqrt{r})\times B^n(0,\sqrt{r}))\\= & {} rc^{\Psi _A}_{\textrm{EHZ}}(B^n\times B^n)\\\ge & {} rc^{\Psi _A}_{\textrm{EHZ}}(B^{2n})=\frac{r \mathfrak {t}(\Psi _A)}{2} \end{aligned}$$

because of (1.24). Then (1.30) follows from (5.7).

(ii) For any $u\in S^n_\Delta$, $\Delta$ sits between support planes $H(\Delta ,u)$ and $H(\Delta ,-u)$, and the hyperplane $H_u$ is between $H(\Delta ,u)$ and $H(\Delta ,-u)$ and has distance $\textrm{width}(\Delta )/2$ to $H(\Delta ,u)$ and $H(\Delta ,-u)$ respectively. Obverse that $\Psi _{\textbf{O}, \bar{q}}(\Delta \times B^n)=(\textbf{O}(\Delta -\bar{q}))\times B^n$ is contained in $Z^{2n}_\Delta$. From this and (2.2) it follows that

$$\begin{aligned} \xi ^A(\Delta )=c^{\Psi _A}_{\textrm{EHZ}}(\Delta \times B^n) =c_{\textrm{EHZ}}^{\Psi _{\textbf{O}, \bar{q}}\Psi _A\Psi _{\textbf{O}, \bar{q}}^{-1}}( \Psi _{\textbf{O}, \bar{q}}(\Delta \times B^n)) \le c_{\textrm{EHZ}}^{\Psi _{\textbf{O}, \bar{q}}\Psi _A\Psi _{\textbf{O}, \bar{q}}^{-1}}(Z^{2n}_\Delta ). \end{aligned}$$

Hence (1.32) is proved. $\square$

In order to prove Theorem 1.15 we need:

Lemma 5.1

For $A\in {\textrm{GL}}(n)$ and a convex body $\Delta \subset {\mathbb {R}}^n_q$ with ${\textrm{Fix}}(A)\cap {\textrm{Int}}(\Delta )\ne \emptyset$, if $\Delta$ is contained in the closure of the ball $B^{n}(\bar{q},R)$ with $A\bar{q}=\bar{q}\in {\textrm{Int}}(\Delta )$, then

$$\begin{aligned} \xi ^A(\Delta )\le \mathfrak {t}(\Psi _A)R. \end{aligned}$$

(5.9)

Proof

As in the proof of Proposition 1.10(i) we deduce

$$\begin{aligned} \xi ^A(\Delta )= & {} c^{\Psi _A}_{\textrm{EHZ}}(\Delta \times B^n)\\\le & {} c^{\Psi _A}_{\textrm{EHZ}}(B^{n}(\bar{q},R)\times B^n)\nonumber \\= & {} c^{\Psi _A}_{\textrm{EHZ}}(B^{n}(0,R)\times B^n)\\= & {} c^{\Psi _A}_{\textrm{EHZ}}(B^{n}(0,\sqrt{R})\times B^n(0,\sqrt{R}))\\= & {} Rc^{\Psi _A}_{\textrm{EHZ}}(B^{n}\times B^n)\\\le & {} Rc^{\Psi _A}_{\textrm{EHZ}}(B^{2n}(0,\sqrt{2}))\le \mathfrak {t}(\Psi _A)R \end{aligned}$$

by (1.24). This and Theorem 2.6 yield the desired claims. $\square$

Proof of Theorem 1.15

Under the assumptions of Theorem 1.15 it was stated in the bottom of [3, p. 177] that $\xi (\Delta )=L(\sigma )$ for some periodic billiard trajectory $\sigma$ in $\Delta$. It follows from Lemma 5.1 that $\xi (\Delta )=\xi ^{I_n}(\Delta )\le \pi \textrm{diam}(\Delta )$, and so $L(\sigma )\le \pi \textrm{diam}(\Delta )$. $\square$