Algebraic realization for projective special linear actions

Abstract

Suppose $q=p^r$, where p is a prime congruent to 3 or 5 modulo 8 and r is odd or $q = 2^r$ for any r. Then every closed smooth ${\text {PSL}}(2,q)$ manifold has a strongly algebraic model.

1 Introduction

Seifert [21, Satz 3] showed that an oriented closed smooth manifold $M^m \subset {\mathbb {R}}^{m+\epsilon }$ with $\epsilon = 1,2$ can be deformed through an arbitrary small isotopy into the real branch of an algebraic manifold. Nash [19] generalized Seifert’s result and also asked whether every closed smooth manifold can be isotoped to a nonsingular real algebraic variety. This was confirmed by Tognoli [23]. The approach quickly evolved [1, 18] into showing that the manifold together with a classifying map of its tangent bundle can be deformed into a nonsingular variety and an entire rational map. Then Benedetti and Tognoli [2] showed that a closed smooth manifold is diffeomorphic to a nonsingular real algebraic variety X, so that all vector bundles over X are classified by entire rational maps.

Let G be a compact Lie group. If a closed smooth G manifold $M$ is equivariantly diffeomorphic to a nonsingular real algebraic G variety X then we say that $M$ is algebraically realized and that X is an algebraic model of $M$. If all G vector bundles over X are classified, up to equivariant homotopy, by entire rational maps, then we call X a strongly algebraic model. For more detailed definitions see Sect. 2. Existing results motivate

Conjecture 1.1

[12, p. 32] Let G be a compact Lie group. Then every closed smooth G manifold has a strongly algebraic model.

In support of the conjecture we show:

Theorem 1.2

Let $q = p^r$, where p is a prime congruent to $\pm 3 \mod 8$ and r is odd or $q=2^r$ for any r. Then every closed smooth ${\text {PSL}}(2,q)$ manifold has a strongly algebraic model.

Equivariant history: Basic techniques in real algebraic transformation groups were developed in [10, 12]. In Sect. 6 we collect the algebraic realization results that are used in this paper. Closed smooth G manifolds have strongly algebraic models if G is cyclic [9, 13, 14], or if the Sylow 2 subgroup of G is cyclic [8], or if the group is a product of an elementary abelian 2 group and an odd order group [12]. In this paper we are discussing an infinite family of groups whose Sylow 2 subgroup is ${\mathbb {Z}}_2 \times {\mathbb {Z}}_2$. We also have results for compact Lie groups of positive dimension, see Theorem 6.3 and Proposition 6.4. In [11] we also showed the existence and uniqueness of an equivariant real algebraic structure on a homogeneous space. For a more extensive history see [8].

Organization: In Sect. 2 we provide careful definitions of the terms we use and the canonical real algebraic structure on a Grassmannian. In Sect. 3 we summarize everything that we need about ${\text {PSL}}(2,q)$. In Sect. 4 we set up the strategy for, and in Sect. 5 carry out the proof of Theorem 1.2. The proof makes use of topological tools that are collected and proved in Sect. 6. In Sect. 7 we analyze the blow–up process in detail and carefully work out how it removes fixed point sets. In Sect. 8, as an example, we sketch the partial order of the isomorphism classes of subgroups of ${\text {PSL}}(2,p^{2k+1})$ in case p is congruent to 5 modulo 8.

Thanks: The authors would like to thank R. Freese and R. Solomon for help with the group theory. They also thank the referee, whose insightful suggestions helped to improve the paper.

2 Definitions, conventions, and background material

2.1 G manifolds

We allow G manifolds to have components of different dimension. Under this convention, if G acts smoothly on a manifold $M$, the fixed point set $M^G$ is going to be a smooth submanifold of $M$.

2.2 Real algebraic varieties and entire rational maps

Let G be a compact Lie group and $\Omega$ an orthogonal representation of G.

Definition 2.1

A real algebraic G variety is a G invariant, common set of zeros of a finite set of polynomials $p_1$,..., $p_m:\Omega \rightarrow {\mathbb {R}}$:

$$\begin{aligned} V = \{ x \in \Omega \mid p_1(x) = \cdots = p_m(x) = 0 \}. \end{aligned}$$

We do not require varieties to be irreducible. Unless stated otherwise, we use the Euclidean topology on varieties. The action of G on V is the restriction of the action on $\Omega$.

Definition 2.2

[25, 3, p. 59] The variety $V \subset {\mathbb {R}}^n$ is said to be nonsingular at $x\in V$ if there are polynomials $q_1, \dots , q_s:{\mathbb {R}}^n \rightarrow {\mathbb {R}}$ which vanish on V and a Zariski open neighborhood U of x in ${\mathbb {R}}^n$ such that

• (1) $V \cap U = U \cap q_1^{-1}(0) \cap \cdots \cap q_s^{-1}(0)$, and

• (2) the gradients $(\nabla q_i)_x$ are linearly independent for $i = 1, \dots , s$.

We say that V is nonsingular if V is nonsingular at each point $x\in V$ and all connected components of V have the same dimension.

Let $V \subseteq {\mathbb {R}}^n$ and $W \subseteq {\mathbb {R}}^m$ be real algebraic varieties. A map $f:V \rightarrow W$ is said to be regular if it extends to a map $F: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ such that each of its coordinates $F_i$ is a polynomial. We say that f is entire rational if there are regular maps $p:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ and $q:{\mathbb {R}}^n \rightarrow {\mathbb {R}}$, such that $f=p/q$ on V and q does not vanish anywhere on V.

The ideas of regular and entire rational functions generalize naturally to the equivariant setting.

2.3 Canonical algebraic structure on the Grassmannians

Let $\Xi$ be an orthogonal representation of G. Then ${\text {End}}_{{\mathbb {R}}}(\Xi )$ is a real representation of G with the action given by

$$\begin{aligned} G \times {\text {End}}_{{\mathbb {R}}}(\Xi ) \rightarrow {\text {End}}_{{\mathbb {R}}}(\Xi ) \quad \text{ with } \quad (g,L) \mapsto g L g^{-1}. \end{aligned}$$

Let d be a natural number. We set

$$\begin{aligned} G_{{\mathbb {R}}}(\Xi ,d)= & {} \{L \in {\text {End}}_{{\mathbb {R}}}(\Xi ) \mid L^2 = L, \ L^* = L, {\text {trace}}L = d\} \end{aligned}$$

(2.1)

$$\begin{aligned} E_{{\mathbb {R}}}(\Xi ,d)= & {} \{(L,u) \in {\text {End}}_{{\mathbb {R}}}(\Xi ) \times \Xi \mid L \in G_{{\mathbb {R}}}(\Xi ,d),\ Lu = u\} \end{aligned}$$

(2.2)

$$\begin{aligned} \gamma _{{\mathbb {R}}}(\Xi ,d)= & {} \left( p:E_{{\mathbb {R}}}(\Xi ,d) \rightarrow G_{{\mathbb {R}}}(\Xi ,d)\right) \end{aligned}$$

(2.3)

Here $L^*$ denotes the adjoint of L. If $\Xi$ is of dimension n and one chooses an orthonormal basis of $\Xi$, then ${\text {End}}_{{\mathbb {R}}}(\Xi )$ is canonically identified with the set of $n \times n$ matrices, and $L^*=L^t$. This description specifies $G_{{\mathbb {R}}}(\Xi ,d)$ and $E_{{\mathbb {R}}}(\Xi ,d)$ as real algebraic G varieties. These varieties are nonsingular. The map in (2.3) is projection on the first factor, and $\gamma _{{\mathbb {R}}}(\Xi ,d)$ is an equivariant vector bundle.

Proposition 2.3

The variety $G_{{\mathbb {R}}}(\Xi ,d)$ is the Grassmannian consisting of real subspaces of $\Xi$ of dimension d.

Proof

A proof is given in [3, §3.4]. There is a bijection between subspaces of $\Xi$ and orthogonal projections. To a projection one associates its image. $\square$

2.4 Strongly algebraic vector bundles

In our setting the preferred concept of a vector bundle is the one of a strongly algebraic vector bundle.

Definition 2.4

A strongly algebraic G vector bundle over a real algebraic G variety is a bundle whose classifying map to $G_{{\mathbb {R}}}(\Xi ,d)$ is equivariantly homotopic to an entire rational map.

Expressed differently, a vector bundle over a variety X is strongly algebraic if it is isomorphic to the pullback of the universal algebraic bundle $\gamma _{\mathbb {R}}(\Xi ,d)$ in (2.3) under an entire rational map.

2.5 Algebraic models

Because nonsingular varieties have a specific dimension, we have to adjust our definition of algebraic model from the introduction for manifold that have components of different dimension. If $M$ is a closed smooth manifold and $M_{(d)}$ is the union of all components of dimension d, then $M$ is the disjoint union of the $M_{(d)}$. An algebraic model of $M$ is a variety X that is the union of nonsingular varieties $X_{(d)}$, so that each $M_{(d)}$ is diffeomorphic to $X_{(d)}$. We say that X is a strongly algebraic model of $M$ if all vector bundles over X are strongly algebraic. The ideas generalize naturally to the equivariant setting.

3 Group theory

Suppose $q=p^r$ and p is a prime. Recall that ${\text {SL}}(2,q)$ is the group of $2 \times 2$ matrices of determinant 1, with coefficients in the finite field with q elements. This group has order $(q-1)q(q+1)$. Its center, the subgroup generated by $-{\text {Id}}$, has order 2, except of course in characteristic 2, where is has order 1. The projective special linear group ${\text {PSL}}(2,q)$ is the quotient of ${\text {SL}}(2,q)$ by its center, and so has half the order of ${\text {SL}}(2,q)$ if q is odd. Accordingly we set $d=2$ if p is odd and $d=1$ if $p=2$.

L. E. Dickson [6] classified the maximal proper subgroups of ${\text {PSL}}(2,q)$. Actually, he credits older sources. As a comprehensive source for our needs we quote Dickson’s theorem from [15, Theorem 6.5.1], see also [17, II.8.27]. We write $C_m$ for the cyclic group of order $M$ and $D_{2m}$ for the dihedral group of order 2$M$.

Theorem 3.1

Suppose $q=p^r$ where p is an odd prime, $p \equiv \pm 3 \mod 8$ and r odd, or $q=2^r$ for any r. Let d be as above and $q>5$. Then the order of ${\text {PSL}}(2,q)$ is $(q^3-q)/d$ and any proper subgroup of ${\text {PSL}}(2,q)$ is isomorphic to a subgroup of one of the following groups:

• (1) Dihedral groups of order $2(q-1)/d$ and $2(q+1)/d$.

• (2) Borel subgroups B of ${\text {PSL}}(2,q)$ of order $q(q-1)/d$. More explicitly, any Sylow p subgroup of ${\text {PSL}}(2,q)$ is of the form $(C_p)^r$, and B is a semi–direct product of $(C_p)^r$ and a cyclic group of order $(q-1)/2$.

• (3) The alternating group $A_5$, if 5 divides the order of ${\text {PSL}}(2,q)$.

• (4) The alternating group $A_4$.

• (5) The groups ${\text {PSL}}(2,p^s)$ where s is a proper divisor of r.

The groups listed in (1)–(5) are their own normalizers in ${\text {PSL}}(2,q)$ and any Sylow 2 subgroup of ${\text {PSL}}(2,q)$ is elementary abelian.

If $p=2$, then the very last assertion repeats (2). If p is odd, then any Sylow 2 subgroup is of order 4. A result of Frobenius implies that a cyclic Sylow 2 subgroup would have a normal 2 complementary subgroup. That is a contradiction as ${\text {PSL}}(2,q)$ for $q\ge 5$ is simple. We assume that $q>5$ to avoid some exceptional cases. This does no harm because we have proved our main result already in case $q\le 5$.

4 Preparation and strategy

Let G be a group. Unless otherwise stated, we assume from now on that G is finite. The set of subgroups of G is partially ordered by inclusion, with G as the unique maximal element and the trivial group as the unique minimal element. If H is a subgroup of G then we denote by [H] the class of all subgroups of G isomorphic to H, and by (H) the class of all subgroups of G conjugate to H. The partial order on the set of subgroups of G induces a partial order on the set of isomorphism classes. This requires G to be finite.

Suppose $M$ is a closed smooth G manifold. Given x in $M$, its isotropy group is $G_x = \{ g\in G \mid gx=x \}$. Then $G_{gx} = g G_x g^{-1}$. For $H \subseteq G$ we set

$$\begin{aligned} \begin{aligned} M^H&= \{ x\in M \mid G_x \supseteq H\} \\ M^{[H]}&= \{x \in M \mid G_x \supseteq H' \in [H] \} = \bigcup _{H'\in [H]} M^{H'} \end{aligned} \end{aligned}$$

(4.1)

A point $x\in M$ belongs to $M^H$ if x is left fixed by all $h \in H$, and x belongs to $M^{[H]}$ if x is left fixed by all $h \in H'$ for some $H'\in [H]$. The H fixed point set $M^H$ is an $N_GH$ manifold. The set $M^{[H]}$ is G invariant.

Notation 4.1

Let $M$ be a closed smooth G manifold.

• (1) If A is a G invariant submanifold, then B($M$, A) denotes the blow–up of $M$ along A. For details of the construction, see Sect. 7.

• (2) Suppose H a subgroup of G. Denote by $R^H$ the union of all components of $M^H$ that are of codimension zero in $M$, and by $R^{[H]}$ the union of all components of $M^{H'}$ that are of codimension zero in $M$, where $H'$ ranges over all $H' \in [H]$. The components of $R^H$ are also components of $M$.

• (3) With H understood, we set ${\overline{M}} = M \setminus R^{[H]}$.

Definition 4.2

Let Y be a closed smooth G manifold and H a nontrivial subgroup of G. We say that we can successfully remove the H fixed point set if

• (1) The blow–up ${\widehat{Y}} = B\left( {\overline{Y}}, {\overline{Y}}^{[H]} \right)$ exists.

• (2) ${\widehat{Y}}^H = \emptyset$ and [$Y^L = \emptyset \implies {\widehat{Y}}^L = \emptyset$] for all subgroups L of G.

• (3) ${\widehat{Y}}$ having a strongly algebraic model implies that Y has a strongly algebraic model.

It goes without saying that when we remove the H fixed point set we also remove the fixed point set for groups isomorphic to H. In addition, if H is not a maximal isotropy group of the action, then removing the H fixed point set may remove, as a bonus, the K fixed point set for some $K \supset H$ at the same time. There is no need to repeat the word successful.

The point of Definition 4.2 is that a successful blow–up reduces the strongly algebraic realization problem for Y to the one of ${\widehat{Y}}$, and the latter problem may be easier to answer because ${\widehat{Y}}^L$ is nonempty for fewer subgroups of G than for Y. In Sect. 7 we will show

Proposition 4.3

Let Y be a closed smooth G manifold and H a nontrivial subgroup of G. We can successfully remove the H fixed point set if the following conditions are met:

• (1) $Y^{H'} \cap Y^{H''} = \emptyset$ whenever $H'\ne H'' \in [H]$.

• (2) H does not have an index 2 subgroup.

• (3) The $N_G H$ manifolds $R^H$ and ${\overline{Y}}^H$ have strongly algebraic models.

We want to find a finite sequence $H_0$, $H_1$, ..., $H_{k-1}$ of subgroups of G that, for any given G manifold $M$, provides us with a sequence of G manifolds

$$\begin{aligned} M_0=M,\ M_1 = B\left( {\overline{M}}_0, {\overline{M}}_0^{[H_0]}\right) , \dots ,\ M_k = B\left( {\overline{M}}_{k-1}, {\overline{M}}_{k-1}^{[H_{k-1}]}\right) . \end{aligned}$$

(4.2)

We will make sure that in each step the $H_j$ fixed point set is removed successfully. This implies that whenever $M_k$ has a strongly algebraic model, then so does the manifold $M=M_0$ that we started out with. If we can remove the fixed point set for all groups that are not 2 groups, then our next result tells us that $M_k$, and with this $M$, has a strongly algebraic model.

Proposition 4.4

Suppose $G = {\text {PSL}}(2,q)$ is as in Theorem 1.2. If $M$ is a closed smooth ${\text {PSL}}(2,q)$ manifold, all of whose isotropy groups are 2 groups, then $M$ has a strongly algebraic model.

Proof

The assertion follows from Proposition 6.7 and Proposition 6.8 using that any Sylow 2 subgroup of ${\text {PSL}}(2,q)$ is a 2 torus, see Theorem 3.1. $\square$

5 Proof of Theorem 1.2

Let $G={\text {PSL}}(2,q)$ be as in Theorem 1.2 and $M$ a closed smooth G manifold. Assume that $q>5$. We may do so because the theorem has been proven already for ${\text {PSL}}(2,2) = S_3$, ${\text {PSL}}(2,3) = A_4$ and ${\text {PSL}}(2,4) = {\text {PSL}}(2,5) = A_5$, see [7, 8].

We will find a sequence $H_0$, ..., $H_{k-1}$ of subgroups of ${\text {PSL}}(2,q)$ that leads to a blow–up sequence as in (4.2), so that the isotropy groups for the final manifold $M_k$ are all 2 groups. Then Proposition 4.4 tells us that this final manifold $M_k$ has a strongly algebraic model. This will be done in three multi–step phases. At each step we make sure that $M_{j+1}$ having a strongly algebraic model implies that $M_j$ has a strongly algebraic model as well. Hence $M = M_0$ itself has a strongly algebraic model and the theorem is proved.

In Sect. 8 we sketch the partially ordered set of isomorphism classes of subgroups of ${\text {PSL}}(2,q)$ when $p \equiv 5 \mod 8$. This may help some readers.

Phase 1: At this time we will eliminate as isotropy group all subgroups of G of the form ${\text {PSL}}(2,p^s)$ as well as $A_5$ (if present) and $A_4$.

Compatibly with the partial order we can order the groups, and with it their isomorphism types, linearly:

$$\begin{aligned} {\text {PSL}}(2,p^r)> \cdots> {\text {PSL}}(2,p^j)> \cdots> {\text {PSL}}(2,p) \ge A_5 > A_4, \end{aligned}$$

(5.1)

where j ranges over the divisors of r.

Let H be any of the groups in (5.1) and Y a closed smooth $G = {\text {PSL}}(2,p^r)$ manifold with $Y^L = \emptyset$ for all $[L]>[H]$. Then H is a maximal isotropy group of the action of ${\text {PSL}}(2,p^r)$ on Y. Any $x\in Y^{H'} \cap Y^{H''}$ for $H' \ne H'' \in [H]$ would have an isotropy group that contains $H'$ and $H''$, contradicting the maximality assumption of H as an isotropy group. No such x can exist, and we verified (1) in Proposition 4.3. Condition (2) in the proposition holds because none of the groups in (5.1) has an index 2 subgroup.

Each of the groups is (5.1) is its own normalizer (see Theorem 4.3) and the action of $N_GH$ on ${\overline{Y}}^H$ and $R^H$ is trivial. Proposition 6.4 tells us that the $N_GH$ manifolds ${\overline{Y}}^H$ and $R^H$ have strongly algebraic models. We verified (3) in Proposition 4.3.

Having verified all assumption of Proposition 4.3, we deduce that we can successfully remove the H fixed point set.

Applying above process repeatedly we find a sequence $M_0$, ..., $M_i$ as in (4.2) so that $M_i^H = \emptyset$ for all H as in (5.1). If $M_i$ has a strongly algebraic model, then so does $M = M_0$.

Phase 2: Suppose p is odd. We state a proposition that allows us to stepwise and successfully remove the fixed point set for all subgroups of ${\text {PSL}}(2,p^r)$ whose order is divisible by p. Its proof is given in Sect. 6.3. This step is not needed when $p=2$.

Proposition 5.1

Let Y be a closed smooth $G = {\text {PSL}}(2,q)$ manifold, where $q = p^r > 5$ and p is a prime congruent to 3 or 5 modulo 8. Assume that $Y^\Gamma = \emptyset$ for all $\Gamma$ as in Theorem 3.1 (3)–(5). Suppose $H \subset G$ is a nontrivial p group, and there is no $\Gamma$ whose order is divisible by a higher power of p than the order of H with $Y^\Gamma \ne \emptyset$. Then we can successfully remove the H fixed point set from Y.

We linearly order the isomorphism classes of the nontrivial p subgroups of ${\text {PSL}}(2,q)$

$$\begin{aligned}{}[H_i]> [H_{i+1}]> \cdots > [H_{i+k}]. \end{aligned}$$

(5.2)

Proposition 5.1 says that if the $H_j$ fixed point set of Y is empty up to a certain point, then we can successfully remove the fixed point set for the groups in $[H_{j+1}]$, the next class. Note that at the same time we remove the fixed point sets for groups that contain groups isomorphic to $H_{j+1}$ that are not p groups.

We do it repeatedly. This extends the sequence of manifolds from the first phase to $M_0, \dots M_i, M_{i+1} \dots , M_{i+k}$, where $M_{i+k}^\Gamma = \emptyset$ for all groups $\Gamma$ as in Theorem 3.1 (3)–(5) and any $\Gamma$ of an order divisible by p. Furthermore, if $M_{i+k}$ has a strongly algebraic model, then so does $M = M_0$.

Phase 3: Finally we remove the remaining fixed point sets for groups that are not 2 groups. We apply the following proposition repeatedly. For its proof see Sect. 6.3.

Proposition 5.2

Let q be as in Theorem 3.1 and Y a closed smooth $G = {\text {PSL}}(2,q)$ manifold. Assume that $Y^\Gamma = \emptyset$ for all $\Gamma$ as in Theorem 3.1 (3)–(5) and, if p is odd, all $\Gamma$ whose order is divisible by p. Suppose $H \subset G$ is a nontrivial odd order cyclic subgroup of $D_{2(q-1)/d}$ or of $D_{2(q+1)/d}$ (see Theorem 3.1 (1)) and there is no strictly larger order odd order cyclic subgroup $\Gamma$ of $D_{2(q-1)/d}$ or of $D_{2(q+1)/d}$ so that $Y^\Gamma \ne \emptyset$. Then we can successfully remove the H fixed point set from Y.

Linearly order the isomorphism classes of the nontrivial odd order cyclic subgroups of $C_{(q-1)/2}$ and $C_{(q+1)/2}$.

$$\begin{aligned}{}[C_{\alpha (1)}]> \cdots > [C_{\alpha (s)}] \end{aligned}$$

(5.3)

Proposition 5.2 says that if the $C_{\alpha (j)}$ fixed point set of Y is empty up to a certain point, then we can successfully remove the fixed point set for the next group. This extends the sequence of manifolds from the first two phases to

$$\begin{aligned} M_0, \dots M_i, M_{i+1}, \dots , M_{i+k}, M_{i+k+1}, \dots , M_{i+k+s}. \end{aligned}$$

The only isotropy groups of $M_{i+k+s}$ are 2 groups and if $M_{i+k}$ has a strongly algebraic model, then so does $M = M_0$.

As explained at the outset of the proof, our last observation completes the proof of Theorem 1.2.

6 Topological tools

6.1 Propagation and induction

Our next two propositions explain how strongly algebraic realization interacts with the operations of disjoint union and blow–up.

Proposition 6.1

[12, Proposition 2.7] Let $M$, $M_1$ and $M_2$ be closed smooth G manifolds and $M = M_1 \sqcup M_2$. Then any of the manifolds has a strongly algebraic model if the other two do.

Proposition 6.2

[14, Proposition 3.1] Suppose $M$ is a closed smooth G manifold and A a closed G invariant submanifold. If A and B($M$, A), the blow–up of $M$ along A, have strongly algebraic models, then so does $M$.

We review induction. Suppose N is a closed subgroup of G and X is a smooth N manifold then

$$\begin{aligned} {\text {Ind}}_N^G X = G \times _N X. \end{aligned}$$

(6.1)

The balanced product $G \times _N X$ consists of equivalence classes [g, x] of pairs $(g,x)\in G\times X$, where $(g,x) \sim (gh^{-1},hx)$ whenever $h\in N$.

If X is a smooth N manifold, then ${\text {Ind}}_N^G X$ is a smooth G manifold [5, Chapter VI]. In the real algebraic setting we have:

Theorem 6.3

[12, Proposition 2.8] Suppose G is a compact Lie group and N a closed subgroup. If X is a strongly algebraic model of an N manifold $M$, then ${\text {Ind}}_N^G X$ is a strongly algebraic model of the G manifold ${\text {Ind}}_N^G M$.

See also [10, Section 3], [20, Corollary 1.4], [11, Corollary 7.3], and [24].

6.2 Strongly algebraic realization results

Under certain assumptions we know that a closed smooth G manifold has a strongly algebraic model. We list cases that we make use of.

Proposition 6.4

[12, Theorem A] Let G be a compact Lie group and $M$ a closed smooth G manifold. If the action is semifree (the only isotropy groups of the action are the trivial group $\{1\}$ and the group G itself), then $M$ has a strongly algebraic model.

The proposition covers actions that are either free or trivial.

Proposition 6.5

[8, Theorem 1.3] Suppose G has a cyclic Sylow 2 subgroup. Then every closed smooth G manifold has a strongly algebraic model.

Proposition 6.6

[7, Theorem 1.2] Suppose $G = D_{2q}$ is a dihedral group of order 2q, and q is not divisible by 4. Then every closed smooth G manifold has a strongly algebraic model.

A classical result of Stong [22, Lemma 13.3] implies:

Proposition 6.7

[8, Proposition 2.2] Suppose G is a finite group and $G_2$ a Sylow 2 subgroup. Closed smooth G manifolds, all of whose isotropy groups are 2 groups, have strongly algebraic models if all closed smooth $G_2$ manifolds have strongly algebraic models.

Proposition 6.8

[12, Theorem B] Suppose G is the product of a 2 torus and an odd order group. Then every closed smooth G manifold has a strongly algebraic model.

The last two propositions were used in the proof of Proposition 4.4.

6.3 Proof of Proposition 5.1 and 5.2

We catch up with the proofs of two propositions that we employed earlier.

Proof of Proposition 5.1

We verify the assumptions of Proposition 4.3 for the p group $H \subset G$, which will then imply our assertion. We assume that $Y^H \ne \emptyset$ because otherwise the assertion is vacuous.

Working towards a contradiction, we suppose that $\Gamma = G_x$ is the isotropy group of some $x \in Y^{H'} \cap Y^{H''}$ where $H' \ne H'' \in [H]$. This group $\Gamma$ must be contained in a proper subgroup of ${\text {PSL}}(2,q)$, it is an isotropy group, and its order is divisible by p. By assumption it is not one of the groups in Theorem 3.1 (3)–(5). We conclude that $\Gamma \subset B$, where B is as in Theorem 3.1 (2). Normality of any Sylow p subgroup $(C_p)^r$ of ${\text {PSL}}(2,q)$ in B implies that both $H'$ and $H''$ are subgroups of $(C_p)^r$. This would mean that the order of $G_x$ is divisible by too high a power of p. Thus, as anticipated, $Y^{H'} \cap Y^{H''} = \emptyset$. We verified (1) in Proposition 4.3. The group H is of odd order, so that (2) in Proposition 4.3 holds trivially.

Finally we verify that the $N_GH$ manifolds $Y^H$ and $R^H$ have strongly algebraic models. We know that H is a subset of some isotropy group, and because the groups in Theorem 3.1 (3)–(5) have been excluded, H and $N_GH$ are subgroups of a Borel subgroup B as in Theorem 3.1 (2). We know that 4 does not divide the order of B, and neither does it divide the order of $N_GH$. The Sylow 2 subgroup of $N_GH$ is $C_2$ or trivial. It follows from Proposition 6.5 that, as $N_GH$ manifolds, ${\overline{Y}}^H$ and $R^H$ have strongly algebraic models. With this we verified (3) in Proposition 4.3, and the proof of Proposition 5.1 is complete. $\square$

Proof of Proposition 5.2

Suppose H is a nontrivial odd order cyclic subgroup of $C_{(q \pm 1)/d} \subset D_{2(q\pm 1)/d}$, see Theorem 3.1 (1). We verify the assumptions of Proposition 4.3.

Anticipating a contradiction, we suppose that $\Gamma = G_x$ is the isotropy group of some $x \in Y^{H'} \cap Y^{H''}$ where $H' \ne H'' \in [H]$. By assumption, $\Gamma$ is not one of the groups in Theorem 3.1 (3)–(5), and, in case p is odd, the order of $\Gamma$ is not divisible by p. Then $H', H'' \subset \Gamma \subseteq D_{2(q\pm 1)/d}$. The two odd order cyclic subgroups $H'$ and $H''$ of $C_{(q\pm 1)/d}$ must be the same. This contradicts our assumption and verifies (1) in Proposition 4.3. Assumption (2) in Proposition 4.3 holds trivially because H is of odd order.

We verify the third assumption in Proposition 4.3. Because $H \subseteq D_{2(q \pm 1)/d}$ and $D_{2(q \pm 1)/d}$ is a maximal proper subgroup of ${\text {PSL}}(2,q)$ we deduce that $N_GH \subseteq D_{2(q\pm 1)/d}$. The order of $N_GH$ will not be divisible by 8. It follows from Proposition 6.5 if $N_GH$ is cyclic and from Proposition 6.6 if $N_GH$ is dihedral that the $N_GH$ manifolds ${\overline{Y}}^H$ and $R^H$ have strongly algebraic models.

We completed the verification of the assumptions of Proposition 4.3 and conclude that we can successfully remove the H fixed point set from Y. $\square$

7 Blow-ups

Suppose Y is a closed smooth G manifold and A a G invariant closed smooth submanifold. We describe the construction of the blow–up B(Y, A) of Y along A, see [16, pp. 175–176] and [22, p.41]. Let $\nu = \nu (A,Y)$ be the normal bundle of A in Y and $\underline{{\mathbb {R}}}$ the product bundle with fibre ${\mathbb {R}}$ over a space understood from context. Taking fibrewise projective spaces gives us the (total space of the) projective bundle ${\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}})$. The lines $0 \oplus {\mathbb {R}}$ in each fibre define a canonical section in ${\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}})$ that we denote by A. By construction $\nu (A, {\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}})) \cong \nu (A,Y)$. The identification, restricted to the disk bundles, provides us with a diffeomorphism of tubular neighborhoods $U_Y$ and $U_P$ of A in Y and ${\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}})$. Removing the interiors of the tubular neighborhoods and identifying the spaces along the boundary is the blow–up of Y along A:

$$\begin{aligned} B(Y,A) = \left( Y \setminus \overset{\circ }{U}_Y \right) \cup _{S(\nu )} \left( {\mathbb {R}} P(\nu \oplus \underline{{\mathbb {R}}}) \setminus \overset{\circ }{U}_P\right) . \end{aligned}$$

(7.1)

Alternatively, we can construct

$$\begin{aligned} W = \Big ( (Y \sqcup {\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}})) \times [0,1]\Big ) \cup _{\varphi } \Big ( D(\nu ) \times [0,1]\Big ), \end{aligned}$$

(7.2)

where the attaching map $\varphi : D(\nu ) \times \{0,1\} \rightarrow \big ( Y \sqcup {\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}})\big ) \times \{1 \}$ identifies the top and bottom edge of $D(\nu ) \times [0,1]$ with closed tubular neighborhoods of A in $Y \times \{ 1 \}$ and A in ${\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}}) \times \{ 1 \}$. The smooth G manifold W (after rounding corners) provides a bordism between $Y \sqcup {\mathbb {R}}{ {P}}(\nu \oplus \underline{{\mathbb {R}}})$ and B(Y, A).

Throughout we will blow up fixed point sets of a subgroup H of G, and its translates. Our next two observations follow immediately from the definition of the blow–up.

Proposition 7.1

Let Y be a closed smooth G manifold and H a subgroup of G. The blow–up $B\left( Y,Y^{[H]}\right)$ exists if $Y^{[H]}$ is a submanifold of Y.

Proposition 7.2

If Y is a closed smooth G manifold and A a G invariant submanifold of codimension 0, then $Y = B(Y,A)$.

The last proposition is the reason for setting aside $R^{[H]}$ in the blow–up and for treating it separately in Proposition 4.3 (3).

We denote the conjugacy class of $H \subseteq G$ by (H). In analogy to (4.1) we set $Y^{(H)} = \{ x\in Y \mid G_x \supseteq H' \in (H)\}$. The obvious question raised by Proposition 7.1 is answered by :

Proposition 7.3

Suppose Y is a closed smooth G manifold and H is a subgroup of G. If $Y^{H'} \cap Y^{H''} = \emptyset$ whenever $H' \ne H'' \in (H)$, then $Y^{(H)}$ is a submanifold of Y. In particular:

$$\begin{aligned} Y^{(H)} \approx G \times _{N_GH} Y^H. \end{aligned}$$

The balanced product notation was introduced in (6.1). Our argument will be a modification of one given in [5, 5.9 Theorem]. The ideas go back to [4, Chapter XII]. We do not need to assume that G is finite.

Proof

Note that $Y^H$ is a submanifold of Y, see [5]. By definition $Y^{(H)}$ is the union of the submanifolds $Y^{H'}$, where $H'$ varies over $H' \in (H)$. We assumed that the $Y^{H'}$ are disjoint for different conjugates. Hence the union of the $Y^{H'}$ is a submanifold of Y.

We show that the map $\varphi : G\times _{N_GH} Y^H \rightarrow Y^{(H)}$, defined by setting $\varphi [g,y] = gy$, is an equivariant homeomorphism. The map is clearly continuous, equivariant, and surjective. Its restriction $\varphi _|$:

$$\begin{aligned} G \times _{N_GH} Y^H \supseteq N_GH \times _{N_GH} Y^H \approx Y^H \overset{\varphi _|}{\longrightarrow } Y^H \subset Y^{(H)} \end{aligned}$$

is bijective.

To show injectivity it suffices to show, if $g \not \in N_GH$ and $y \in Y^H$, then $\varphi [g,y] = gy \not \in Y^H$. Assume to the contrary, that $gy \in Y^H$. Then $G_y \supseteq H$ and $G_{gy} = g G_y g^{-1} \supseteq H$. The latter implies that $G_y \supseteq g^{-1} Hg$ and $y \in Y^H \cap Y^{g^{-1}Hg} = \emptyset$, which is a contradiction. Hence $\varphi$ is injective and the proof is complete. $\square$

Example 7.4

Let us give an example. It explains the need to distinguish between subgroups with nonempty fixed point set and isotropy groups. Set $G = C_6$. Let $X = S^2 \subset {\mathbb {R}}^3$. Let a generator of G act on X as a rotation by $2\pi / 6 = \pi /3$ around the z axis. Then $X^G = X^{C_3}$ consists of the north and south pole of the sphere. The set of isotropy groups of X is ${\text {Iso}}(X) = \{ \{1\}, G\}$.

Set ${\widehat{X}} = B(X,X^{C_3})$. That means that at each pole of X we are taking a connected sum with ${\mathbb {P}} = {\mathbb {R}}{P}(\Omega \oplus {\mathbb {R}})$. Here $\Omega \cong {\mathbb {R}}^2$ denotes the tangent representation at either pole. One may check that ${\mathbb {P}}^G = {\mathbb {P}}^{C_3}$ consists of a single point. Forming the connected sum removes the G and $C_3$ fixed point set. On the other hand, ${\mathbb {P}}^{C_2}$ consists of a point and a circle. The points cancel out in the blow–up, and instead we inherit two circles as $C_2$ fixed point set of ${\widehat{X}}$. We see that ${\text {Iso}}({\widehat{X}}) = \{ \{1\}, C_2\}$. We may say that the blow–up removed the $C_3$ fixed point set. It also removed $C_6$ as an isotropy group. No more supergroup to $C_3$ is an isotropy group. In return, we have a new isotropy group, $C_2$.

Proof of Proposition 4.3

We need to verify the conditions for the successful removal of the H fixed point set as formulated in Definition 4.2.

For the blow–up ${\widehat{Y}} = B\left( {\overline{Y}}, {\overline{Y}}^{[H]} \right)$ to exist, we need to see that ${\overline{Y}}^{[H]}$ is a submanifold of ${\overline{Y}}$. This follows from Proposition 7.3 for ${\overline{Y}}^{(H)}$. The isomorphism class [H] of H is a disjoint union of various conjugacy classes $(H')$ with $H'\in [H]$, and ${\overline{Y}}^{[H]}$ is a disjoint union of the ${\overline{Y}}^{(H')}$ for these $H'$. This makes ${\overline{Y}}^{[H]}$ into a submanifold of ${\overline{Y}}$, so that (1) in Definition 4.2 is satisfied.

Let is show: ${\widehat{Y}}^L \ne \emptyset \implies {\overline{Y}}^L \ne \emptyset$. As in (7.1) we write

$$\begin{aligned} {\widehat{Y}} = Y_1 \cup Y_2 \quad \text{ where } \quad Y_1 = {\overline{Y}} \setminus \overset{\circ }{U}_{{\overline{Y}}} \quad \text{ and } \quad Y_2 = {\mathbb {R}} P(\nu \oplus \underline{{\mathbb {R}}}) \setminus \overset{\circ }{U}_P. \end{aligned}$$

Because $Y_1$ is ${\overline{Y}}$ with a tube around the H fixed point set removed, it follows that $Y_1^H = \emptyset$ and if $Y^L = \emptyset$, then $Y_1^L = \emptyset$. For the latter we write $Y_1^L \ne \emptyset \implies Y^L \ne \emptyset$.

Now look at $Y_2$. Consider $y \in Y_2$ in the fibre ${\mathbb {R}} P(\nu _x \oplus {\mathbb {R}})$ of ${\mathbb {R}} P(\nu \oplus \underline{{\mathbb {R}}})$ above $x \in {\overline{Y}}^H$. Expressed in homogeneous coordinates we have $y = [v,t]$. By construction $v \ne 0$ and corresponds to a point $v' \in {\overline{Y}}$ near x. If $t \ne 0$, then the isotropy group of y, v, and $v'$ are the same. Given such a point $y \in {\widehat{Y}}^L$ for some group L we have $v' \in {\overline{Y}}^L$.

If $t=0$ then the isotropy group $G_y$ of y is the group that leaves the line through v invariant, and it it necessarily a subgroup of $G_x$, the group that leave the fibre invariant. Given any L and a point $y = [v,0] \in Y_2^L$ we have that $x \in {\overline{Y}}^L$. Formally, $Y_2^L \ne \emptyset \implies Y^L \ne \emptyset$.

Combining the above: ${\widehat{Y}}^L \ne \emptyset \implies Y_1^L \ne \emptyset \vee Y_2^L \ne \emptyset \implies {\overline{Y}}^L \ne \emptyset$, which is the second part of (2).

We show the first part of (2), that ${\widehat{Y}}^H = \emptyset$. By construction, as we mentioned before, $Y_1^H = \emptyset$. Let us look at $Y_2$. Note that $\nu _x$, the fibre of $\nu (Y^H,Y)$ over x, is a representation of $\Gamma = G_x$. Let $y = [z,t] \in Y_2$. We expressed y in homogeneous coordinates. There are three types of points in $Y_2$, z or t can be zero, but not both.

The first kind, points with $z=0$, have been removed in the blow–up process.

Secondly, if z and t are both nonzero, then $G_y = \Gamma _z$. Under the identification of the normal bundle $\nu$ with the normal tube $U_Y$, z corresponds to a point ${\widehat{z}}$ in ${\overline{Y}}$ near (but not equal to) x. In particular $G_{{\widehat{z}}} \subsetneqq H$, and y will not be a point in $Y_2^H$.

Finally, consider points of the form $y = [z,0]$. We construct a contradiction to the assumption that $y \in Y_2^H$. We know that $\Gamma _z \ne H$ because $z \ne 0$ is in the normal slice to the H fixed point set. Thus H has to leave the line y invariant without fixing it. The kernel of such a linear action on a real line is an index 2 subgroup, which H does not have. Any such point $y = [z,0] \notin Y_2^H$

Combining these three cases we see, as asserted, that ${\widehat{Y}}^H = \emptyset$.

To verify condition (3) in Definition 4.2 we need to show that ${\overline{Y}}^{[H]}$ and $R^{[H]}$ have strongly algebraic models. We assumed that $R^H$ and ${\overline{Y}}^H$ have strongly algebraic models. Denote the conjugacy class of $H \subseteq G$ by (H), and set

$$\begin{aligned} {\overline{Y}}^{(H)}:= & {} \{ y \in {\overline{Y}} \mid G_y \supseteq H' \in (H) \} \approx G \times _{N_GH} {\overline{Y}}^H \\ R^{(H)}:= & {} \bigsqcup _{H'\in (H)} R^{H'} \approx G \times _{N_GH} R^H \end{aligned}$$

The assumption that $Y^{H'} \cap Y^{H''} = \emptyset$ for $H' \ne H'' \in (H)$ implies the diffeomorphisms $\approx$ in the above, see Proposition 7.3. According to Theorem 6.3, ${\overline{Y}}^{(H)}$ and $R^{(H)}$ have strongly algebraic models. We get ${\overline{Y}}^{[H]}$ and $R^{[H]}$ from ${\overline{Y}}^{(H)}$ and $R^{(H)}$ by varying the conjugacy classes (H) within the isomorphism class [H] and taking the disjoint union of the spaces. Proposition 6.1 tells us that ${\overline{Y}}^{[H]}$ and $R^{[H]}$ have strongly algebraic models. This completes the verification of the third and final assertion in Definition 4.2.

In retrospect one may draw attention to the trivial special case when $Y^{[H]} = R^{[H]}$ and ${\overline{Y}}^{[H]} = \emptyset$. Then the H fixed point set is removed by setting it aside. It is removed from Y, see Notation 4.1 (3). $\square$

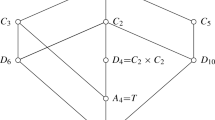
8 Partially ordered isomorphism class of subgroups of ${\text {PSL}}(2,q)$

For $q=p^{2n+1}$ and $p \equiv 5 \mod 8$ we sketch the partially ordered set of isomorphism classes of subgroups of ${\text {PSL}}(2,q)$. We omit square brackets that indicate isomorphism classes.

Here are some remarks for understanding the diagram:

• (1) In case p is 3 modulo 8, the Borel subgroup B in ${\text {PSL}}(2,q)$ will be of odd order, and $C_2$ is not a subgroup of B. The roles of $C_\beta$ and $C_\epsilon$ are interchanged.

• (2) The names of the groups are as earlier in this section. The subscripts indicate the order of the groups, and $\alpha (j) = p^j(p^j-1)/2$, $\beta (j) = (p^j-1)/2$, $\gamma (j) = (p^j-1)$, $\delta (j) = (p^j+1)$, and $\epsilon (j) = (p^j+1)/2$.

• (3) Solid lines indicate a subgroup relation, dashed ones that there is a family of similar groups in between the end points of the line.

• (4) The group $A_5$ occurs only if 5 divides the order of ${\text {PSL}}(2,p^k)$. Then $A_5 \subseteq {\text {PSL}}(2,p)$. If $p = 5$ then $A_5$ should be identified with ${\text {PSL}}(2,5)$.

• (5) There are lines missing from $A_4$ to a $C_3$, which will be either a subgroup of $C_{\beta (1)}$ or $C_{\epsilon (1)}$, depending on the value of p. For the same reason, lines from $A_5$, if present, are missing.

• (6) Along the line from ${\text {PSL}}(2,p)$ to ${\text {PSL}}(2,p^k)$ there is one group for every divisor of k. Along the line from $C_{\beta (1)}$ to $C_{\beta (k)}$ there is a partially ordered set of subgroups of $C_{\beta (k)}$, and $C_{\beta (1)}$ may not even be the smallest group. A corresponding remark applies to $C_\epsilon$.