Fuzzy differential equations: conceptual interpretations

Abstract

This paper aims to shed light on some of the conceptual interpretations that might be extracted from either the information conveyed by fuzzy differential equations (FDEs) or a fusion of such information with other data sources. Although no explicit effort has been conducted on the topic, there are two significant imperatives for such interpretations. First, conceptual interpretations are necessary when FDEs are employed in modelling, prediction, control theory, and suchlike subjects. Simply put, FDEs fail to be applicable if their corresponding interpretations have not been recognized conceptually. Second, when FDEs are supposed to be analyzed. In other words, in the lack of such interpretations of FDEs, any analysis on this type of differential equations is conceptually devoid of meaning. The interpretations are associated with the concept of possibility distribution and differential equations which might be called imprecise differential equations (IDEs) that are in effect the mother of differential equations. The concept of IDE makes a convenient point of departure for the development of the interpretations in question in terms of the concepts such as machine-oriented meaning precisiation, modal solutions, precisiations compatibility, and some new facets of sureness. Specifically, interpretations associated with the compatibility of precisiations and the notion of human-machine-based sureness demonstrate the role played by information resident in an FDE fused with perception-based meaning precisiation, that stems from the knowledge of an expert. Some illustrations and examples are presented to clarify the basic concepts and the applications of interpretations.

1 Introduction

Differential equations, as a mathematical tool, have long played a pivotal role in the description of a wide range of dynamical systems. Such a role might also be well played by fuzzy differential equations (FDEs) when there is uncertainty that relates to classes whose boundaries are defined unsharply. An FDE presents a description of a dynamical system in the form of a differential equation such that the uncertainties in question are emerged in some of the coefficients and/or parameters and/or boundary conditions of the differential equation, and they are regarded as a class of fuzzy sets. The class of fuzzy sets is mainly regarded as the class of fuzzy numbers, denoted by E, consisting of sets that are normal, fuzzy convex, upper semi-continuous, and compactly supported fuzzy subsets of the real numbers ${\mathbb {R}}$.

Since 1978 when the term fuzzy differential equations emerged in the literature, prevailing research effort has been dedicated not only to the development of the concepts concerning the topic, but also to its potential applications. So far, the extensive research works carried out on fuzzy differential equations have been mainly dealt with proving the existence and uniqueness of an FDE solution, proposing methods for solving FDEs, introducing various types of fuzzy derivatives, and an analysis of the behavior of FDEs, for an insightful review on FDEs see [1]. Nevertheless, what has not been addressed in the literature is an answer to these queries: What information is conveyed by an FDE? and how can such information be exploited? This paper is devoted to providing some answers to the queries. The answers underlie some conceptual interpretations of information resident in FDEs. Thus, as the title of this paper suggests, various and yet new conceptual interpretations, mainly in terms of possibility distribution and the notion of precisiations are presented in this work.

There are two major imperatives for the conceptual interpretations. First, conceptual interpretations are necessary when FDEs are employed in modelling, prediction, control theory, and suchlike subjects. Simply put, FDEs fail to be applicable if their corresponding interpretations have not been recognized conceptually. As an instance, there is a great deal of effort to suggest the applications of FDEs, e.g. see Sect. 4 in [1]. However, none of them has explained either the reasons for the importance of utilizing or any interpretations of FDEs in the suggested applications. Thus, if someone looks for the reasons, they may only encounter such familiar and unconvincing comments expressing that, due to the existence of uncertainty, the fuzzy differential equations are used, or FDEs are useful when there is uncertainty. Nevertheless, the advantages of FDEs and their significance in the applications have remained unclear. For example, suppose that the mathematical model of a phenomenon has been proposed in the form of an FDE. If those who have put forward this model are asked to explain why they have considered the FDE as a mathematical model of the phenomenon, they highly likely fail to give convincing answers, apart from the above common comment.

Second, when FDEs are supposed to be analyzed. In other words, in the lack of such interpretations of FDEs, any analysis on this type of differential equations is conceptually devoid of meaning. As a case in point, there are numerous research works, e.g. see Sect. 3 in [1], which are intended to find or prove a solution for FDEs. Nevertheless, none of them has provided a convincing and straightforward answer to such a question: Why does finding the solutions of fuzzy differential equations matter? To put that simply, there are a number of approaches by which solutions of FDEs are obtained. Yet it is almost unknown what the importance of such solutions is. In other words, suppose that someone solves an FDE by one of the proposed approaches and raises such queries: What can I do with this solution? What is the importance of this solution? What does this solution mean? So far, no explicit answer has been given to such queries. As a matter of fact, a common thread which runs through these examples - and indeed all research works carried out on FDEs since 1978 till now - relates to the lack of conceptual interpretations coming with FDEs. However, this paper, for the first time in the literature, presents conceptual interpretations concerning with FDEs through which explicit and convincing answers to the mentioned questions can be found.

The conceptual interpretations presented here provide a way for describing the behavior of a dynamical system imprecisely by the use of words or sentences in a natural language. For example, assume that the aim is to describe the behavior of pressure in a dynamical system S. The interpretation of information conveyed by an FDE presenting a type of mathematical model of S, may lead to following statements:

• It is not possible that the pressure reaches 240(mmH2O) before 2 hours,

• The possibility degree that the pressure is 190(mmH2O) at $t=1$ is 0.7,

• We should be $63\%$ sure that the pressure is high at $t=2$,

• That the pressure of system will be low (mmH2O) at $t=1$ is $75\%$ compatible with our opinion.

• It can be stated we are $70\%$ sure that the pressure of S will be very high at $t=3$ and it is $75\%$ compatible with our opinion. In addition, the pressure reaches 250(mmH2O) with $90\%$ possibility.

Since some of the major interpretations associated with FDEs bear a close relation to differential equations that may be called imprecise differential equations (IDEs), the concept of an IDE with its solution and some properties are introduced briefly. As a matter of fact, the concept of an IDE makes a convenient point of departure for presenting the interpretations in question in terms of other concepts such as precisiation, compatibility, and sureness. In addition, a principle, compatibility of precisiations principle (CoP), is introduced, which makes it possible to investigate the interpretation associated with compatibility. Furthermore, some facets of sureness are presented, among which machine-based sureness and human-machine-based sureness are shed light in accord with the role that FDEs may play.

In this paper, it has been presumed in prior that readers are well familiar with some concepts and subjects such as possibility theory, fuzzy calculus, fuzzy information granulation, generalized theory of uncertainty, computing with words, generalized constraint language, precisiation, probability theory, random differential equations, and preliminaries of fuzzy sets theory.

It should also be noted that - in their closed form, FDEs, just as any other types of differential equations, present some information about the relationship between variables involved in the equation and their effects, or interactions, on each other. Nonetheless, this paper is intended to focus on information that might be exploited from an FDE by the aid of concepts pertaining to fuzzy set theory, in a broad sense, rather than the investigation of the relationship between variables or their interactions. Indeed, such an investigation may also be carried out based on the approach presented here. In addition, it is stressed that the current paper is a brief exposition of several important conceptual interpretations of FDEs rather than a full exposition of all interpretations.

The information resident in an FDE also comes with the FDE solution and, even more, it might manifest itself more clearly in the solution. Thus, the conceptual interpretations of FDEs solutions serve as a convenient point of departure for the explicitation of the information contained in FDEs. Besides, they pave the way for the exploitation of such information. For the sake of simplicity, we shall concern our attention with FDEs in which fuzzy number-valued functions are involved. In addition, for the illustration and to have an impression of the interpretations, the following simple FDE presenting a mathematical model of cerebrospinal fluid (CSF) pressure [2] - that is a medical disorder - with an uncertain initial condition is considered in whole this paper.

$$\begin{aligned} \dot{{\tilde{x}}}(t)=\frac{-k}{r}{\tilde{x}}^2(t)+k\left( I_f(t)+\frac{{\tilde{x}}_d}{r}\right) {\tilde{x}}(t), \ \ \ \ {\tilde{x}}(t_0)\in E \end{aligned}$$

(1)

In (1), ${\tilde{x}}(t)$ denotes the CSF pressure in mmH2O, and ${\tilde{x}}(t_0)$ does the initial condition assumed to be a triangular fuzzy number¹. Fig. 1 illustrates approximately the solution of (1), denoted by ${\tilde{x}}^*$, for $t\in [0, 8]$, ${\tilde{x}}(0)=(110,115,120)$, $k=\frac{1}{0.5}, r=600, I_f(t)=0.15,$ and ${\tilde{x}}_d={\tilde{x}}(0)$. It should be noted that this paper has nothing to do with approaches based on which a solution to an FDE may be obtained. In other words, the conceptual interpretations that will be introduced in the sequel are independent of approaches by which FDEs are dealt with².

Fig. 1

The solution of the fuzzy differential equation associated with the model of CSF pressure system

2 The interpretation associated with the possibility distribution concept

The simplest and yet important interpretation of information conveyed by an FDE is related to the concept of possibility distribution. Let ${\tilde{x}}^*(t)$ satisfy an FDE, e.g. $\dot{{\tilde{x}}}(t)=f(t,{\tilde{x}}(t))$, over $t\in (a,b)\subseteq {\mathbb {R}}$. The value of ${\tilde{x}}^*(t)$ at any $t=t'$ is a fuzzy set which might be regarded as an elastic constraint on the values that may be assigned to ${\tilde{x}}^*(t')$. Such an elastic constraint induces a possibility distribution with the possibility distribution function, $\pi _{{\tilde{x}}^*(t')}$, equated to $\mu _{{\tilde{x}}^*(t')}$ that is the membership function of ${\tilde{x}}^*(t')$. Thus, $\pi _{{\tilde{x}}^*(t')}=\mu _{{\tilde{x}}^*(t')}$. Such an equation serves as a means of interpreting the solution of an FDE as a possibilistic process. Thus, at any $t=t'$, the fuzzy set ${\tilde{x}}^*(t')$ characterized by $\pi _{{\tilde{x}}^*(t')}$ includes information about the degree of possibility or feasibility of a value $u \in {\mathbb {R}}$ which may be assigned to ${\tilde{x}}^*(t')$. Such an interpretation makes it possible providing some answers to queries concerning dynamical systems modeled by FDEs exemplified by:

• Is it feasible that the pressure is equal to 120(Pa) ?

• How much is the possibility that the temperature is equal to $37 ({}^{o}C)$?

• Does it happen that the speed of DC motor reaches 235(Rpm)?

• Is it hard that the voltage of the resistor in the RLC circuit assumes 15(V)?

Therefore, an FDE includes information about all possible behaviors of a dynamical system and its solution associates a possibilistic process with the dynamical system output. As a way of illustration, consider the model of CSF pressure system. On the basis of the presented interpretation, Fig. 1 illustrates the possibilistic process corresponding to the CSF pressure model based on which the following queries are answered.

• Is it possible that the pressure of the patient’s CSF reaches 190? Yes, it is. It happens for $t\in [2.8, 4.12]$ with the most possibility at $t=3.36$. The possibility is increased by the passage of time from $t=2.8$ to $t=3.36$ and then it is decreased to its lowest amount at $t=4.12$.

• How much is it easy that the pressure of the patient’s CSF is equal to 200 at $t=7$? The degree of ease is 0.3.

• Is it feasible that the pressure of the patient’s CSF reaches less than 200 after $t=5$? Yes, it is.

• Is it possible that the pressure of the patient’s CSF is 205 before $t=6$? Yes, it is, and the most degree of possibility is 0.5.

Thus, a fuzzy differential equation may also be termed as a possibilistic differential equation whose solution illustrates a possibilistic process - similar to, but not the same as, a random process corresponding to a random differential equation. In other words, a fuzzy differential equation conveys information describing possible behaviors of a dynamical system with different degrees of feasibility in the form of a possibilistic differential equation.

What follows presents interpretations of FDEs that bear a close relation to the concept of a type of differential equations which may be called imprecise differential equations (IDEs). Thus, we shall first introduce a brief exposition of IDEs.

3 Imprecise differential equations

In the theory of generalized uncertainty [3] information is equated to a generalized constraint. A generalized constraint (GC) is a constraint of the form $X \ \ \text {is}r \ \ R$ where X is the constrained variable, R is a constraining relation and r defines the modality of the constraint or the mode of precisiation [4, 5]. There are some modes of precisiation³ among which more important are possibility distribution, $r=\textit{blank}$, probability distribution, $r=p$, and fuzzy graph, $r=fg$. The generalized constraint is used to precisiate a precisiend , p. A precisiend, p, may be a proposition, or a set of propositions, sentences, or a combination of words expressed in a natural language which is precisiable and includes imprecise information that is precisiated under a mode of precisiation resulting in a precisiand, $p^*$. In fact, information conveyed by a precisiend, p, can be precisiated, i.e. $p^*$, in the form of a generalized constraint. Thus, the precisiand $p^*: X \ \ \text {is}r \ \ R$ may be called the GC form of the precisiend p and written as $GC(p)=p^*$. As a way of illustration consider the following precisiends

$p_1$:

: “The temperature of room is high”,

$p_2$:

: “The speed of car is approximately 80(km/h)”

whose precisiands may be, respectively, as follows

$p^*_1$:

: “ $T(\text {room})$ is ${\tilde{T}}=(35,40,45)$”,

$p^*_2$:

: “ $S(\text {car})$ is ${\tilde{v}}=(70, 80, 85)$”

where $T(\text {room})$ and $S(\text {car})$ are respected focal variables in $p_1$ and $p_2$. The mode of precisiation applied in the above propositions is that of possibility distribution.

A mathematical model of the system S conveys information about the system behavior. Such information is utilized to analyze or predict the behavior of S. In most cases, the mathematical model of S is in the form of a differential equation, or a system of differential equations, whose boundary conditions, coefficients, and the other constituents might be imprecise and expressed in the form of precisiends stemming from the knowledge of an expert. Such a differential equation that deals with precisiends might be called imprecise differential equation (IDE). As simple examples related to the context of this paper, let us consider the IDEs ${\dot{x}}(t)=f(x(t))$ and ${\dot{x}}(t)=kx(t)$ for which the subjective precisiends may be respectively as follows:

p:

: “the initial condition of the equation ${\dot{x}}(t)=f(x(t))$ is near 25”,

p:

: “the value of the parameter, k, in the equation ${\dot{x}}(t)=kx(t)$ is more than 8”

In fact, an IDE is a result of a combination of our knowledge from physics laws⁴ and perception-based, or generally imprecise, information from the system S. Since perception-based information is intrinsically imprecise [5], an IDE also represents an imprecise description of S in an abstracted form. In this perspective, an IDE is an imprecisely mathematical precisiation (im-precisiation) or machine-oriented precisiation (m-precisiation)⁵ of S⁶. Specifically, if $x^*(t)$ is the solution of an IDE associated with the system S, then it is a set of precisiends which, in effect, gives some perception-based information about S. Therefore, S might be precisiated by a disjunction of Cartesian product of t and $x^*(t)$ written as

$$\begin{aligned} S^*: X \ \ \text {isx} \ \ \int t \times x^*(t) \end{aligned}$$

(2)

or equivalently as

$$\begin{aligned} S^*:\int p_t \end{aligned}$$

(3)

where X is the focal variable in S, $\int$ denotes a disjunction operator⁷, $p_{t}: X \ \ \text {isx} \ \ x^*(t)$. Symbolically we may write $GC(S)=S^*$. In GC form of S a new value denoted by x has been considered for the indexing variable r which will be introduced in the sequel. The definition of x as a value of r in GC form of a system comes from two major differences between precisiation of a system and a precisiend. In precisiation of a precisiend, p, perception-based information conveyed by p is precisiated that results in a precisiand, $p^*$. Thus, the precisiand of p is not imprecise and the mode of precisiation is known. Nevertheless, in precisiation of a system S⁸, the result of precisiation is perception-based information that plays the role of a precisiand of S playing the role of a precisiend. Thus, the precisiand of S is itself imprecise in nature and the mode of precisiation is unknown. Due to these reasons a new value x - meaning unknown or imprecise - along with other values of indexing variable r has been defined here. Therefore, hereafter,

$$\begin{aligned} X \ \ \text {isx} \ \ R(t) \end{aligned}$$

(4)

or equivalently

$$\begin{aligned} \int p_t \end{aligned}$$

(5)

in which $p_{t}: X \ \ \text {isx} \ \ x^*(t)$, signifies that X is the focal variable of a system being precisiated, x means that the precisiation is in the mode of imprecision, and $R(t)\triangleq \int t \times x^*(t)$⁹ is a set of perception-based information about X expressed in a natural language, $t \times x^*(t)$ is the Cartesian product of precisiend $x^*(t)$ and t, and $\int$ denotes a disjunction operator which is replaced by $\sum$ for a finite number or countable samples of t, see Fig. 2.

Fig. 2

The role of imprecise differential equation in the precisiation of a dynamical system S

What follows explains how the interpretation of information resident in an FDE on the basis of precisiation concept bears a close relation to the GC form of a mathematical model of a system.

3.1 The interpretation associated with the concept of mm-precisiation

Although imprecise precisiation of a system may be given by the aid of an IDE, i.e. machine-oriented precisiation, no direct approach for obtaining the solution of an IDE exists, at this juncture. Nonetheless, an IDE can be precisiated and the solution of the result of the precisiation of the IDE is obtained. The precisiation of an imprecise differential equation is defined as the precisiation of precisiends associated with the IDE. The precisiation of an IDE results in an uncertain differential equation (UDE) that may be viewed as a GC form of the IDE expressed symbolically as

$$\begin{aligned} GC(\text {IDE})=\text {UDE} \end{aligned}$$

(6)

The mode of precisiation determines the role that is played by the UDE. Specifically, the GC form of an IDE results in an uncertain differential equation which is called fuzzy differential equation if the precisiation of the IDE is in the mode of a possibility distribution, i.e. $r=\textit{blank}$ in the generalized constraint. The UDE plays the role of a random differential equation (RDE) if $r=p$ in the generalized constraint, i.e. the precisiation of the IDE is in the mode of a probability distribution. Crisp differential equations , interval-valued differential equations, Z-differential equations are also considered as the result of precisiation of IDE when the mode of precisiation is the respected singleton, interval, and possibility-probability distribution. Thus, in symbols we may write:

$$\begin{aligned} \begin{array}{l} GC\left( \text {IDE}\right) \big \vert _{r=\textit{blank}}=\text {FDE} \\ \\ GC\left( \text {IDE}\right) \big \vert _{r=\textit{p}}=\text {RDE} \end{array} \end{aligned}$$

(7)

Fig. 3

The derivation of some types of differential equations from imprecise differential equations

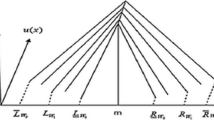
Moreover, new types of differential equations that have not been introduced or recognized yet might be derived as the result of precisiation of IDE with possibly various combinations of precisiation modes. In this perspective, IDEs may be viewed as the mother of differential equations from which all other types of differential equations can be derived, see Fig. 3. As a way of illustration, the precisiation of IDEs ${\dot{x}}(t)=f(x(t))$ and ${\dot{x}}(t)=kx(t)$, with their corresponding precisiends, in the mode of a possibility distribution may lead to FDEs $\dot{{\tilde{x}}}(t)=f({\tilde{x}}(t))$ and $\dot{{\tilde{x}}}(t)={k}{\tilde{x}}(t)$ with respected precisiands

$p^*$:

: “the initial condition of the equation $\dot{{\tilde{x}}}(t)=f({\tilde{x}}(t))$ is ${\tilde{x}}(t_0)=(22,25,27)$”,

$p^*$:

: “the value of the parameter, k , in the equation $\dot{{\tilde{x}}}(t)={k}{\tilde{x}}(t)$ is ${\tilde{k}}=(8,8,15)$”.

Therefore, FDE (1) might be regarded as the result of the precisiation of an IDE in the same structure of (1) with the initial condition in the form of a precisiend such as

p:

: “the initial pressure of the patient’s CSF is approximately 115”.

Such a precisiend is, in effect, perception-based information that has been come from the knowledge of an expert.

As a result, if ${\tilde{x}}^*(t)$ satisfies an FDE, e.g. $\dot{{\tilde{x}}}(t)=f(t,{\tilde{x}}(t))$, which represents a type of mathematical model of a system, S, then it may be employed to precisiate x(t) which satisfies the imprecise differential equation ${\dot{x}}(t)=f(t,x(t))$ containing precisiends that imprecisely precisiate S. In other words, ${\tilde{x}}^*(t)$ may be viewed as the GC form of x(t) , i.e. symbolically $GC(x^*(t))={\tilde{x}}^*(t)$¹⁰. Thus, an FDE plays the role of a mathematically precisiated model of S. Such a role is also played by other UDEs and emerges in nested precisiations of S, see Fig. 4.

Fig. 4

The precisiation of an imprecise differential equation and nested generalized constraint of a dynamical system S

As a way of illustration, let us consider the CSF pressure system whose mathematical precisiated model has been given by FDE (1) that is satisfied by ${\tilde{x}}^*(t)$ shown in Fig. 1. In this case, the following simple subjective precisiends may be stated as an imprecise description of the behavior of patient’s CSF pressure status at $t=0, 1, 2, 3, 7$:

$p_0$:

: “The initial pressure of patient’s CSF is approximately 115”,

$p_1$:

: “The pressure of patient’s CSF will be low at $t=1$”,

$p_2$:

: “The patient’s CSF pressure will be medium, 2 minutes later”,

$p_3$:

: “The pressure will be high, at $t=3$”,

$p_7$:

: “The CSF pressure will be high, 7 minutes later”,

whose precisiation might be considered as follows:

$p^*_0$:

: “The initial pressure of patient’s CSF is ${\tilde{x}}^*(0)=(110,115,120)$”,

$p^*_1$:

: “The pressure of patient’s CSF will be ${\tilde{x}}^*(1)=(140.8,147,153)$ at $t=1$”,

$p^*_2$:

: “The patient’s CSF pressure will be ${\tilde{x}}^*(2)=(164.5,171,177)$, 2 minutes later”,

$p^*_3$:

: “The pressure will be ${\tilde{x}}^*(3)=(180,186,192)$, at $t=3$”,

$p^*_7$:

: “The CSF pressure will be ${\tilde{x}}^*(7)=(198.4,203.6,208.8)$, 7 minutes later”.

In fact, just as the precisiands $p^*_0$ to $p^*_7$ may be viewed as a model of $p_0$ to $p_7$; so may FDE (1) be viewed as a model of the IDE

$$\begin{aligned} {\dot{x}}(t)=\frac{-k}{r} {x}^2(t)+k\left( I_f(t)+\frac{x_d}{r}\right) {x}(t) \end{aligned}$$

(8)

containing the following perception-based information: the initial pressure of patient’s CSF, i.e. x(0) , is approximately 115, ${x_d}={x}(0)$, $k=\frac{1}{0.6}, r=700, I_f(t)=0.1$. As such, ${\tilde{x}}^*(t)$ that satisfies FDE (1) may be regarded as a model of x(t) satisfying IDE (8).

More concretely, based on information given by an expert and the rules governing the operations, an FDE with its structure serves as a machine for the modification of information in order to precisiate the meaning of m-precisiation of a dynamical system S.

Thus, an FDE may be viewed as an active machine-oriented meaning precisiation¹¹, active mm-precisiation, whose solution, as a whole, is active mm-precisiand of S; and precisiates a perception-oriented description of S. In other words, a fuzzy differential equation contains information about precisiands which may be used as the result of the precisiation of precisiends describing imprecisely the behavior of the dynamical system S for which the FDE plays the role of a mathematical precisiated model.

What should be underscored is that two modes of precisiation may be associated with an FDE. First, when an FDE, e.g. $\dot{{\tilde{x}}}(t)=f(t,{\tilde{x}}(t))$, for all $t\in (a,b)\subseteq {\mathbb {R}}$ is regarded as a machine-oriented representation of S, then the precisiation may be viewed in the mode of a fuzzy graph. As such, S may be precisiated, in the form of nested generalized constraints, as

$$\begin{aligned} GC\left( GC(S): X \ \ \text {isx} \ \ R(t)\right) : X \ \ \text {isfg} \ \ R^*(t) \end{aligned}$$

(9)

where $R(t)\triangleq \int t \times x(t)$, $R^*(t)\triangleq \int t \times {\tilde{x}}^*(t)$, x(t) comes from the solution of an IDE associated with S and ${\tilde{x}}^*(t)$ is the solution of the FDE associated with the IDE.

Second, the precisiation in the mode of a possibility distribution is associated with the FDE if ${\tilde{x}}^*(t)$ or $\dot{{\tilde{x}}}^*(t)$ at the specified instant $t=t'$ is employed for the precisiation of a precisiend concerning S. Specifically, if $p_{t'}$ is a proposition with $x(t')$ being the imprecise value of its focal variable; and describes the behavior of S at $t=t'$, then its precisiation, in the form of a generalized constraint, results in $p_{t'}^*: X$ is ${\tilde{x}}^*(t')$. The precisiands $p^*_0$ to $p^*_7$ may be viewed as cases of the precisiation of $p_0$ to $p_7$ in the mode of a possibility distribution which have been determined based on FDE (1).

Another point that should be stressed is the dual role played by an IDE concerning the system S and an FDE. When an IDE is employed as a machine-oriented precisiation of a system, its solution characterizes precisiands of S denoted by $p_{t}: X \ \ \text {isx} \ \ x(t)$, at each $t\in (a,b)\subseteq {\mathbb {R}}$. Thus, the GC form of S may be written symbolically as a collection of propositions $p_t$ by $\int p_t$ (or by $\sum p_t$ for countable samples), i.e. $GC(S): \int p_t$. For example, in the case of CSF pressure system, the m-precisiation of the system may be stated as $GC(S): \sum p_t= p_0+p_1+p_2+p_3+p_7$ with the understanding that “$+$” denotes the disjunction operator rather than the arithmetic sum.

Fig. 5

The modal solution of an IDE obtained by the aid of FDE.

Since propositions $p_t$ are imprecise in nature, an FDE may be employed as a machine-oriented meaning precisiation of $p_t$ resulting in precisiands $p^*_t: X \ \ \text {is} \ \ {\tilde{x}}^*(t)$ where ${\tilde{x}}^*(t)$ is the solution of the FDE. More concretely, the precisiands characterized by an IDE are regarded as precisiends by an FDE. Therefore, precisiation of a system in the form of nested generalized constraints shown in (9) may be equivalently written as

$$\begin{aligned} GC\left( GC(S): \int p_t \right) : \int p^*_t \end{aligned}$$

(10)

For more illustration see Fig. 4.

It should be noted that by considering the precisiation in the mode of a possibility distribution, a relation between the present interpretation with the preceding one is made. The interpretation presented here might be also employed in combination with other interpretations. Such combinations will be demonstrated in the sequel.

3.2 The interpretation associated with a modal solution of an IDE

An imprecise differential equation conveys information in the form of precisiends which serve as a means of a precisiation of a system S. The solution of the IDE places these precisiends in evidence. However, there is no direct approach, at this juncture, for obtaining the solution of an IDE. In spite of this fact, it may be possible to determine approximately the IDE solution on the basis of a mode of the precisiation of the IDE. Such an approximate solution is called the modal solution that is denoted by ${x}_r^*(t)$ in which r indicates the mode of mm-precisiation.

One the modal solutions may be obtained through an FDE. Specifically, an FDE, e.g. $\dot{{\tilde{x}}}(t)=f(t,{\tilde{x}}(t))$, is the result of the precisiation of an IDE, e.g. $\dot{{x}}(t)=f(t,{x}(t))$, in the mode of a possibility distribution. Let ${\tilde{x}}^*(t)$ be the solution of the FDE associated with the result of the precisiation of the IDE whose solution is denoted by ${x}^*(t)$. The aim is to characterize the imprecise precisiend ${x}_r^*(t)$ as an approximation of ${x}^*(t)$ by the use of ${\tilde{x}}^*(t)$. It should be noted that, ${x}^*(t)$ includes imprecise information about the focal variable X of the system, and has been precisiated in the mode of a possibility distribution. Thus, some information about X granulated by fuzzy sets is to be provided by the knowledge of an expert or a data set. Such information granulation (IG)¹² may be presented in the form of a perception-based data set or the plane of precisiends of X. Suppose that the pair $(x_i, \pi _{x_i})$, $i=1,...,m$, indicates the ith precisiend associated with IG of X, denoted by $x_i$, with $\pi _{x_i}$ being the possibility distribution function of the precisiand of $x_i$, and m is the number of fuzzy granules. Then, a modal solution of the IDE may be determined as

$$\begin{aligned} {x}_r^*(t)=x_i \leftrightarrow {\mathcal {D}}_r(\pi _{{\tilde{x}}^*(t)}, \pi _{x_i})\le \epsilon \end{aligned}$$

(11)

where $r=$ possibility distribution, ${\mathcal {D}}_r$ is a metric serving as a similarity measure of precisiands¹³, and $\epsilon \ge 0$ is a small real number, see Fig. 5. In the figure, assignment module refers to (11).

Therefore, the precisiands included in an FDE may be utilized for the characterization of precisiends resulting in a modal solution of an IDE which precisiates the system S. Further to aforementioned explanations, there are a few comments in need.

First, another modal solution of an IDE may be also determined, in a similar fashion explained above, based on another mode of precisiation of the IDE in a combination with IG. Specifically, in the mode of a probability distribution, a modal solution of the IDE may be characterized by an RDE solution in a combination with IG. Thus, a modal solution of an IDE, in a general setting, may be determined by

$$\begin{aligned} {x}_r^*(t)=x_i \leftrightarrow {\mathcal {D}}_r({x}_{\small {UDE}}^*(t), {x^*_i})\le \epsilon \end{aligned}$$

(12)

where r indicates the mode of mm-precisiation, ${x}_{UDE}^*(t)$ is the solution of the UDE resulted from the mm-precisiation of IDE in the mode of r; ${x^*_i}$ and ${x_i}$ are the ith precisiand and precisiend of $IG_r$ that is the IG associated with the knowledge of an expert or a data set in the mode of r, see Fig. 6 as an illustration. In the figure, assignment module refers to (12).

Fig. 6

The modal solution of an IDE obtained by the aid of UDE

Second, depending on the mode of precisiation of the IDE, different modal solutions may be obtained. The difference in question comes from the differences between the type of modes, the employed IG and the metric, ${\mathcal {D}}$, that is used for the similarity measure of precisiands.

Third, a modal solution is a reflection of the solution of an IDE hitting a mode of precisiation, see Fig.  7. In this perspective, the solution of an IDE is defined as follows:

Definition 1

If ${x}^*(t)$ is the solution of an IDE, then it is the modal solution of the IDE independent of the mode of precisiation.

Fig. 7

The relation between a modal solution of an IDE and the solution of the IDE

In other words, if the reflection of the solution of an IDE hitting any mode of precisiation is the same, then the modal solution is the IDE solution, see Fig. 8 for the illustration. The IDE solution as the m-precisiation of S might differ from human-oriented precisiation (h-precisiation) of S. In what follows, we shall discuss briefly about this matter which leads to the other interpretation of information conveyed by FDEs.

Fig. 8

The solution of an IDE

3.3 The interpretation associated with the compatibility of precisiations

The other interpretation of information resident in an FDE, that is presented here, bears a close relation to the concepts of compatibility of precisiations. As was stated already, a system S may be precisiated imprecisely as

$$\begin{aligned} GC(S): X \ \ \text {isx} \ \ R(t) \end{aligned}$$

(13)

or equivalently as

$$\begin{aligned} GC(S): \sum p_t \end{aligned}$$

(14)

Such a precisiation has been called machine-oriented precisiation if R(t) , or $p_t$, is characterized by an IDE. The precisiation may be called human-oriented precisiation (h-precisiation) if S is precisiated imprecisely based on the knowledge of an expert. The GC form of S associated with h-precisiation is written as

$$\begin{aligned} GC(S): X \ \ \text {isx} \ \ {\hat{R}}(t) \end{aligned}$$

(15)

or equivalently as

$$\begin{aligned} GC(S): \sum {\hat{p}}_t \end{aligned}$$

(16)

where ${\hat{R}}(t)\triangleq \sum t \times {\hat{x}}(t)$, ${\hat{p}}_{t}: X \ \ \text {isx} \ \ {\hat{x}}(t)$, and ${\hat{x}}(t)$ is the precisiend coming from the perception of the expert about the system; and might be postulated as if it is the perception-based solution of the IDE whose solution has been assumed to be x(t) . It should be noted that due to the bounded ability of the human mind and sensory organs to resolve detail and store information¹⁴, in h-precisiation a finite number of propositions is employed. Thus, in (15) and (16) $\sum$ has replaced $\int$. The meaning precisiation of the result of the h-precisiation of system S is called perception-based meaning precisiation (pm-precisiation) or expert-oriented meaning precisiation (em-precisiation). Although em-precisiation and pm-precisiation are almost interchangeable, there is a slight difference between them. The pm-precisiation stems purely from the expert perception, however, em-precisiation comes from either expert cognition or analysis of a data set. Both meaning precisiations result in precisiands ${\hat{p}}^*_t: X \ \ \text {isr} \ \ {\hat{x}}^*(t)$. Correspondingly, in symbols we may write

$$\begin{aligned} GC\left( GC(S): \sum {\hat{p}}_t \right) : \sum {\hat{p}}^*_t \end{aligned}$$

(17)

A point that is worthy of note is that the mode of pm-precisiation in (17) is known and determined by the expert. However, the mode of precisiation in h-precisiation, analogous to m-precisiation, is imprecise.

Therefore, the system S may be precisiated by either m-precisiation or h-precisiation. These precisiations coincide each other or are said to be equal if the expert cognition, including em-precisiation, about S does not change by replacing precisiends associated with h-precisiation, i.e. ${\hat{p}}_t$, with those that are associated with m-precisiation, i.e. ${p}_t$. If h-precisiation coincides m-precisiation, that may be written symbolically as $\sum {\hat{p}}_t=\sum {p}_t$, then their meaning precisiation in the same mode also do, i.e. $\sum {\hat{p}}^*_t=\sum {p}^*_t$¹⁵. However, in most cases machine-oriented precisiation ceases to coincide with human-oriented precisiation. As an example, let us assume that an expert is asked to answer a set of queries¹⁶, $q_i$, pertaining to the CSF pressure system. The first query is:

$q_1$:

: “How much is the the initial pressure of the patient’s CSF?”

with the answer being

${\hat{p}}_0$:

: “The initial pressure of the patient’s CSF is approximately 115”

The precisiand of ${\hat{p}}_0$ can be also determined if the expert is asked to precisiate the proposition, ${\hat{p}}_0$, by the model that they may have got in their mind. Suppose that ${\hat{p}}_0$ is precisiated as

${\hat{p}}^*_0$:

: “The initial pressure of the patient’s CSF is ${\hat{x}}^*(0)=(110,115,120)$”

Since in FDE (1), ${\tilde{x}}^*(0)={\hat{x}}^*(0)$, thus the precisiation of ${\hat{p}}_0$ on the basis of the FDE results in a precisiand, ${p}^*_0$, that is readily the same as ${\hat{p}}^*_0$. In other words, at $t=0$, the precisiation of ${\hat{p}}_0$ based on the FDE coincides that is based on the perception of the expert. On the basis of given initial information and the rules governing the operations, the information is processed in FDE (1) and exposed in the solution for $t\ge 0$. Now, the expert is asked to answer the second query

$q_2$:

: “How much will be the pressure of the patient’s CSF 7 minutes later than the initial time based on your perception?”

The answer is assumed to be the following proposition

${\hat{p}}_7$:

: “The patient’s CSF pressure will be high 7 minutes later”

whose pm-precisiation according to the knowledge of the expert may result in

${\hat{p}}^*_7$:

: “The patient’s CSF pressure will be ${\hat{x}}^*_7={\hat{G}}_7$, 7 minutes later”,

where ${\tilde{G}}_7$ is a possibility distribution characterized by a Gaussian possibility distribution function. Nevertheless, based on Fig. 1, FDE (1) suggests the precisiand

${p}^*_7$:

: “The patient’s CSF pressure will be ${\tilde{x}}^*(7)=(198.4,203.6,208.8)$, 7 minutes later”

which differs from the model of precisiend expressed by the expert in ${\hat{p}}^*_7$. The difference may be also explicitly in terms of precisiends. For example, the expert may answer to the second query by

${\hat{p}}_7$:

: “The patient’s CSF pressure will be very high 7 minutes later”

However, m-precisiation, on the basis of IDE solution, may state that

${p}_7$:

: “The patient’s CSF pressure will be medium 7 minutes later”.

In other words, the information extracted from an FDE, or IDE, may not be completely in accord with that extracted from the knowledge of an expert for the precisiation of a precisiend, or a system. Such a phenomenon, that happens in most cases, may be called precisiations incompatibility. In other words, precisiations incompatibility, in a sense, is referred to as a gap between machine-oriented precisiation and human-oriented precisiation. The source of such a gap may come from the incompatibility of the structure of, and rules governing the operations involving in the precisiations; and the imprecision that is intrinsic in the perception-based meaning precisiation. Precisiations incompatibility suggests to determine the compatibility degree of the precisiations in question which underlies the following principle.

3.3.1 Compatibility of precisiations principle (CoP principle)

The compatibility degree of precisiations with each other is equivalent to that of their corresponding meaning precisiation.

Therefore, underlined CoP principle, the compatibility degree of a machine-oriented precisiation with a human-oriented precisiation is equivalent to that of mm-precisiation with pm-precisiation. The CoP principle may derive from the fact that the causes and effects might reflect some information, implicitly or explicitly, about the causation. Simple instances of this fact may be found in dynamical systems theory, mathematics, sociology, psychology and the other fields. As a simple illustration, let us consider the dynamical system $S_1$ whose structure and constituents are unknown, however, a set of input-output data of the system carrying some information about $S_1$ are known¹⁷. Now, assume there is also another dynamical system $S_2$, and the aim is to compare it with $S_1$. Such a comparison is made, mainly, based on a set of specified inputs given to both systems and comparing the obtained outputs, see Fig. 9.

Fig. 9

The comparison of dynamical systems $S_1$ and $S_2$ based on a set of input-output data

Fig. 10

Compatibility of precisiations principle

Analogously, the structure, constituents, operators and the rules governing the operators in h-precisiation and m-precisiation are unknown or partially known, however, a compatibility degree between these precisiations might be obtained by the aid of pm-precisiation and mm-precisiation, see Fig.  10 as an illustration. The figure signifies the fact that the more compatible the precisiands, the more compatible the precisiations. What follows is intended to introduce the definition of the concept of compatibility of m-precisiation with h-precisiation.

3.3.2 Precisiations compatibility degree

Suppose that $\sum {\hat{p}}_t$, is a set of propositions pertaining to h-precisiation of a dynamical system, S, with precisiands ${\hat{p}}_t^*$ resulting from perception-based meaning precisiation of ${\hat{p}}_t$. The pm-precisiation is supposed to be in the mode of a possibility distribution with $\pi _{{\hat{x}}^*_t}$ denoting the distribution function induced by ${\hat{p}}_t$.

Moreover, let $\sum {p}_t$ be the m-precisiation of S with machine-oriented meaning precisiation associating the precisiand ${p}_t^*$ with ${\tilde{x}}^*(t)$ that satisfies a fuzzy differential equation which represents a mathematical precisiated model of S. Then, the compatibility degree of m-precisiation with h-precisiation denoted by c is defined as

$$\begin{aligned} c \triangleq \bigwedge _{t} \left( \frac{\int _{u\in D_m}\pi _{{\tilde{x}}^*(t)}(u)\bigwedge \pi _{{\hat{x}}^*_t}(u)du}{\int _{u\in D_m} \pi _{{\tilde{x}}^*(t)}(u)du}\right) \end{aligned}$$

(18)

where $c\in [0, 1]$, $\bigwedge \triangleq min$¹⁸, $\pi _{{\tilde{x}}^*(t)}$ is the possibility distribution function of ${\tilde{x}}^*(t)$, and $\int _{u\in D_m}$ is the conventional integral over ${D_m}$ denoting the support of ${\tilde{x}}^*(t)$.

It should be noted that according to Definition 1, if the solution of an IDE is determined then it is equal to any modal solution. Thus, the compatibility degree of propositions associated with the modal solution, characterized through an FDE, with h-precisiends implies the compatibility degree of propositions related to the solution of IDE with h-precisiends. Therefore, the compatibility degree of ${p}_{t}: X \ \ \text {isx} \ \ {x}(t)$ with ${\hat{p}}_{t}: X \ \ \text {isx} \ \ {\hat{x}}(t)$ where x(t) and ${\hat{x}}(t)$ are respectively the IDE modal solution and h-precisiend is defined as

$$\begin{aligned} c_{t}= \frac{\int _{u\in D_m}\pi _{{\tilde{x}}^*(t)}(u)\bigwedge \pi _{{\hat{x}}^*_t}(u)du}{\int _{u\in D_m} \pi _{{\tilde{x}}^*(t)}(u)du} \end{aligned}$$

(19)

in which ${\tilde{x}}^*(t)$ is the solution of the FDE by which - according to relation (11) - a modal solution of the IDE is obtained. As such, the compatibility degree of $\sum {p}_t$, i.e. m-precisiation, with $\sum {\hat{p}}_t$, i.e. h-precisiation, may be rewritten abstractly as

$$\begin{aligned} c \triangleq \bigwedge _{t} c_{t} \end{aligned}$$

(20)

A point that is worthy of note is that if, at the instant $t=t'$, $c_{t'}=1$, then ${p}_{t'}$ semantically entails ${\hat{p}}_{t'}$. Therefore, ${\hat{x}}(t')$ is a modal solution of the IDE at $t=t'$. Moreover, $c_{t'}=\pi _{{\hat{x}}^*_{t'}}(u)$ providing that the support of ${\tilde{x}}^*(t)$ at $t=t'$ is only the point u, i.e. ${\tilde{x}}^*(t')$ is a fuzzy singleton. As a result, for any t at which the solution of FDE is a fuzzy singleton such that it coincides the core of ${{\hat{x}}^*_t}$, it can be concluded that ${\hat{x}}(t)$ is a modal solution of IDE.

Let us assume that the compatibility degree of precisiations is $c=0.4$. Then it may be stated that:

• The compatibility of machine-oriented precisiation with the human-oriented precisiation is $40\%$,

• The machine-oriented meaning precisiation is $40\%$ compatible with the perception-based meaning precisiation,

• The compatibility of information conveyed by the FDE concerning S with the expert’s opinion about S is $40\%$.

As a way of illustration, let us consider the CSF pressure system for which some of the precisiends of h-precisiation are assumed to be as follows

${\hat{p}}_1$:

: “The pressure of patient’s CSF will be low at t=1”,

${\hat{p}}_2$:

: “Patient’s CSF pressure will be medium, 2 minutes later”,

${\hat{p}}_3$:

: “The pressure will be high, 3 minutes later”,

${\hat{p}}_7$:

: “Patient’s CSF pressure will be high, 7 minutes later”

whose pm-precisiation may be respectively as

${\hat{p}}^*_1$:

: “The pressure of patient’s CSF will be ${{\hat{x}}^*(1)}=(110,110,140,160)$ at t=1”,

${\hat{p}}^*_2$:

: “Patient’s CSF pressure will be ${{\hat{x}}^*(2)}=(140,160,190)$, 2 minutes later”,

${\hat{p}}^*_3$:

: “The pressure will be ${{\hat{x}}^*(3)}=(160,190,230,230)$, 3 minutes later”,

${\hat{p}}^*_7$:

: “Patient’s CSF pressure will be ${{\hat{x}}^*(7)}=(160,190,230,230)$, 7 minutes later”.

According to the solution of FDE (1), the mm-precisiation of the system in question, in the mode of a possibility distribution, is

${p}^*_1$:

: “The pressure of patient’s CSF will be ${\tilde{x}}^*(1)=(140.8,147,153)$ at t=1”,

${p}^*_2$:

: “Patient’s CSF pressure will be ${\tilde{x}}^*(2)=(164.5,171,177)$, 2 minutes later”,

${p}^*_3$:

: “The pressure will be ${\tilde{x}}^*(3)=(180,186,192)$, 3 minutes later”,

${p}^*_7$:

: “Patient’s CSF pressure will be ${\tilde{x}}^*(7)=(198.4,203.6,208.8)$, 7 minutes later”.

In virtue of (19) we have $c_1= 0.87, c_2=0.86, c_3=0.98$, and $c_7=1$. Thus, it may be stated that m-precisiation is up to $86\%$ compatible with the expert cognition of the system.

As a result, information conveyed by an FDE serves as a means of filling in the gap between machine-oriented precisiation and human-oriented precisiation of dynamical systems behavior.

3.4 The interpretation associated with sureness level of m-precisiation

The preceding interpretation dealt with a combination of m-precisiation and h-precisiation under this assumption that they cease to coincide each other. The assessment of the compatibility of m-precisiation with h-precisiation was one of the results of such a particular combination. In the following discussion, a combination of meaning precisiations for the assessment of the sureness of m-precisiation is investigated.

As was stated already, a system S may be precisiated in the mode of imprecision by an IDE, i.e. m-precisiation. There are a variety of modes by which the IDE in its own right may be also precisiated, mm-precisiation. Specifically, an FDE is the result of mm-precisiation of the IDE in the mode of a possibility distribution. However, the IDE may be also precisiated in the mode of a probability distribution which results in a random differential equation representing a mathematical precisiated model of S. Therefore, the precisiation of S in a form of nested generalized constraint may also be written as

$$\begin{aligned} GC\left( GC(S): \int p_t \right) : \int {\bar{p}}^*_t \end{aligned}$$

(21)

where ${\bar{p}}^*_t: X \ \ \text {isp} \ \ {\bar{x}}^*(t)$ with ${\bar{x}}^*(t)$ being the solution of the RDE.

A question that arises here is: Which mode of mm-precisiation should be employed for the precisiation of an IDE? The answer to this question depends on the knowledge of an expert about the system and the type of information that is desired to be exploited. Specifically, mm-precisiation in the mode of a possibility distribution makes a convenient way for exploiting some information about the feasible behavior of the system, determining a modal solution of an IDE, and the compatibility degree of m-precisiation with h-precisiation. If some information about the probable behavior of the system is going to be exploited, then mm-precisiation should be in the mode of a probability distribution. Nevertheless, one of important information, that in most cases is desirable, concerns with the level of reliability or sureness of either a precisiation of S or propositions associated with the precisiation of S. In the sequel, the sureness level of machine-oriented precisiation is assessed¹⁹. As we shall see, some information about the level of sureness is exploited by a fusion of information resident in the results of mm-precisiation of m-precisiation in two different modes. As a way of illustration, let us assume that some precisiends drawn from an m-precisiation of patient’s CSF pressure system at $t=1, 2, 3, 7$ are as:

${p}_1$:

: “The pressure of patient’s CSF will be low at t=1”,

${p}_2$:

: “Patient’s CSF pressure will be medium, 2 minutes later”,

${p}_3$:

: “The pressure will be high, 3 minutes later”,

${p}_7$:

: “Patient’s CSF pressure will be high, 7 minutes later”

whose meaning precisiation in the mode of a possibility distribution, according to the solution of the FDE, is as follows:

${p}^*_1$:

: “The pressure of patient’s CSF will be ${\tilde{x}}^*(1)=(140.8,147,153)$ at t=1”,

${p}^*_2$:

: “Patient’s CSF pressure will be ${\tilde{x}}^*(2)=(164.5,171,177)$, 2 minutes later”,

${p}^*_3$:

: “The pressure will be ${\tilde{x}}^*(3)=(180,186,192)$, 3 minutes later”,

${p}^*_7$:

: “Patient’s CSF pressure will be ${\tilde{x}}^*(7)=(198.4,203.6,208.8)$, 7 minutes later”.

In addition, the meaning precisiation in the mode of a probability distribution, according to the solution of an RDE, is supposed to be as:

${\bar{p}}^*_1$:

: “The pressure of patient’s CSF will be $G_1=(145,4)$ at t=1”,

${\bar{p}}^*_2$:

: “Patient’s CSF pressure will be $G_2=(170,3)$, 2 minutes later”,

${\bar{p}}^*_3$:

: ”The pressure will be $G_3=(185,2.5)$, 3 minutes later”,

${\bar{p}}^*_7$:

: ”Patient’s CSF pressure will be $G_7=(202,2)$, 7 minutes later”.

where $G_{t'}=(m,\sigma ^2)$ is a normal probability density function whose respected mean value and variance have been denoted by m and $\sigma ^2$. The probability density function $G_{t'}$ comes from the solution of the RDE at $t=t'$. Now, the question is: How much the m-precisiation of patient’s CSF pressure system is reliable? What follows presents a definition of the sureness (or reliability) level of m-precisiation²⁰.

Definition 2

Suppose that $\int {p}_t$, is a set of propositions pertaining to machine-oriented precisiation of a dynamical system, S. Let $\int {p}_t^*$ and $\int {\bar{p}}_t^*$ be the results of two machine-oriented meaning precisiations of $\int {p}_t$ in the modes of possibility and probability distributions, respectively. In addition, suppose that ${p}_t^*$ and ${\bar{p}}_t^*$ are associated with ${\tilde{x}}^*(t)$ and ${\bar{x}}^*(t)$ which satisfy respectively a fuzzy differential equation and a random differential equation representing mathematical precisiated models of S. Then, the sureness level of the m-precisiation of S is defined as

$$\begin{aligned} s_m \triangleq \bigwedge _{t}\int _{u\in D_m} {\mathcal {P}}_{{\bar{x}}^*(t)}(u)\pi _{{\tilde{x}}^*(t)}(u) du \end{aligned}$$

(22)

where ${\mathcal {P}}_{{\bar{x}}^*(t)}$ is the probability density function of ${\bar{x}}^*$ at the instant t, $\pi _{{\tilde{x}}^*(t)}$ is the possibility distribution function of ${\tilde{x}}^*(t)$ at the instant t, and $D_m$ is the support of ${\tilde{x}}^*(t)$.

Relation (22) can be also written as $s_m \triangleq \displaystyle \bigwedge _{t} s_t$ in which $s_t$, equating the integral term, signifies the sureness level of the proposition $p_t$ in $\int {p}_t$. As a way of illustration let us consider precisiends $p_1, p_2, p_3$ and $p_7$ drawn from the m-precisiation of patient’s CSF pressure system with their corresponding mm-precisiation already given in the modes of possibility and probability distributions. Thus, the sureness level of precisiends are determined as $s_1=0.63 , s_2=0.75 , s_3=0.75$ and $s_7=0.66$. On the basis of the captured information it can be concluded that the sureness level of m-precisiation is not more than $63\%$.

A point that is worthy of note is that a Z-differential equation (ZDE) [2, 8] bears a close relation to the concept of sureness defined in Definition 2. Specifically, according to the notion of the conceptual unity presented in [2], a ZDE may be viewed as a bimodal meaning precisiation of an IDE in the modes of probability and possibility distributions. In other words, a ZDE is an mm-precisiation of m-precisiation with a combination of probability and possibility distribution modes, symbolically

$$ \begin{aligned} GC\left( \text {IDE}\right) \big \vert _{r=\{\textit{blank} \ \& \ p\}}=\text {ZDE} \end{aligned}$$

(23)

As an illustration, Fig. 11 shows the sureness levels $s_t$ for $t\in [0,25]$. This result has been adopted from the solution of ZDE, as a mathematical precisiated model of CSF pressure system, presented in [2]. As the result shows, the sureness level of m-precisiation of CSF pressure system is $s_m=64\%$.

Fig. 11

The machine-based sureness levels

The concept of sureness has some facets. What may be called machine-based sureness (m-sureness) is the concept which has been already explained. More concretely, m-sureness is referred to as the sureness level of an m-precisiation that is obtained from a combination of mm-precisiations. The m-sureness, denoted by $s_m$, is obtained according to relation (22). The sureness measure of m-precisiation may be called human-machine-based sureness (hm-sureness) if it is determined in terms of pm-precisiation and mm-precisiation. There are also two more facets of sureness that are related to the sureness of h-precisiation, which may be called human-based and machine-human-based sureness, h-sureness and mh-sureness for short. The former is defined based on a combination of pm-precisiations, and the latter is defined on the basis of mm-precisiation, in the mode of a probability distribution, and pm-precisiation, in the mode of a possibility distribution. Fig. 12 illustrates some facets of sureness. In the sequel, a brief exposition of hm-sureness is presented.

Fig. 12

Various new facets of sureness

The hm-sureness level of m-precisiation of a system is defined based a combination of meaning precisiation of h-precisiation and m-precisiation in the modes of probability and possibility distributions respectively. Suppose that $GC(S):\sum {\hat{p}}_t$ is the h-precisiation of system S with $GC(GC(S):\sum {\hat{p}}_t): \sum {\hat{p}}^*_t$ being the em-precisiation of h-precisiation in the mode of a probability distribution, i.e. ${\hat{p}}^*_t: X \ \ \text {isp} \ \ {\hat{x}}^*(t)$. Then, the hm-sureness level of the m-precisiation of S is defined as

$$\begin{aligned} s_{hm} \triangleq \bigwedge _{t}\int _{u\in D_m} {\mathcal {P}}_{{\hat{x}}^*(t)}(u)\pi _{{\tilde{x}}^*(t)}(u) du \end{aligned}$$

(24)

where ${\mathcal {P}}_{{\hat{x}}^*(t)}$ is the probability density function of ${\hat{x}}^*$ at the instant t, $\pi _{{\tilde{x}}^*(t)}$ is the possibility distribution function of ${\tilde{x}}^*(t)$ at the instant t and associated with mm-precisiation of m-precisiation, and $D_m$ is the support of ${\tilde{x}}^*(t)$ .

As a result of this section, it may be stated that a fusion of information resident in an FDE with that conveyed by expert-oriented meaning precisiation leads to assessing the reliability or sureness level of m-precisiation.

,

4 Conclusions

Presenting various interpretations of a subject often makes the imperatives of the subject more clear. This is also the case for FDEs. In fact, conceptual interpretations outlined in this paper may serve as a means of a manifestation of the importance of FDEs in the description of the behavior of dynamical systems. It has been shown that there is a relationship between FDEs and our perceptions of the behavior of a phenomenon. However, among various interpretations presented for information conveyed by an FDE, the most important may be stated by the equation

Fuzzy differential equations=machine-oriented meaning precisiation

It should be well realized that such interpretations can also be applied for fuzzy integro-differential equations, fuzzy fractional differential equations, intuitionistic fuzzy differential equations, and suchlike. To sum up, the introduced conceptual interpretations suggest that we have a comprehensively new outlook to the results that have been already obtained and enlarge the territory of FDEs applications.

Appendix A Abbreviations

Table 1 shows the descriptions of abbreviations used in this article.

Table 1 Abbreviations