Comparisons of metaheuristic algorithms for unrelated parallel machine weighted earliness/tardiness scheduling problems

Abstract

This paper investigates unrelated parallel machine scheduling problems where the objectives are to minimize total weighted sum of earliness/tardiness costs. Three different metaheuristic algorithms are compared with others to determine what kind (swarm intelligence based, evolutionary or single solution) of metaheuristics is effective to solve these problems. In this study, artificial bee colony (ABC), genetic algorithm and simulated annealing algorithm are chosen as swarm intelligence based algorithm, evolutionary algorithm and single solution algorithm. All proposed algorithms are created without modification in order to determine effectiveness of these metaheuristics. Experimental results show that ABC outperforms its opponents in view of solution quality as swarm intelligence based metaheuristic algorithm.

1 Introduction

Weighted earliness/tardiness scheduling problems with common due date are significant for just-in-time (JIT) philosophy. Each company that accepts JIT philosophy wants to complete jobs on their due dates. This is significant for profitability of the company because each early or tardy job has a cost. If a job is completed before its due date, then this job is an early job and there are some costs for the company. For instance, the company has to stock this job until its due date, then the company will pay for stocking cost and/or insurance cost. If a job is completed after its due date then this job is a tardy job and there are some costs because of tardiness. For instance, the company will have to delay the shipment or the company will have to lose some of its earnings because of the contract signed with the costumer. Common due dates are used in order to determine a shipment date for the jobs that will be transshipped simultaneously in a common transportation vehicle (cargo, air-cargo, truck etc.). Most of costumers of the company are from different countries and orders of a costumer must be completed until shipment date of transportation vehicle (cargo, air-cargo, truck etc.). If some of orders in a shipment are completed before shipment date, the company has to stock these ones until the shipment date and there will be a holding, stocking or assuring costs for these stocks. On the contrary, if some of orders in a shipment completed after the shipment date, this situation leads a penalty cost such as loss of reputation, reshipment of tardy jobs and perhaps loss of costumer. Due dates or common due date can be determined by internal or external costumers. The internal costumer may want to have all jobs on a certain date, for instance the packaging department may want to package all jobs in a specific order on a their predetermined date. Furthermore, an external costumer may want to have all jobs simultaneously. In that sense, the external costumer sends its transportation vehicle to the company to pick up all of their order. Therefore the optimal schedule is important for decreasing total earliness/tardiness cost. Although finding the optimal schedule is critical for earliness/tardiness problems in JIT company, the problem is in the class of NP hard.

The common due date consideration in parallel machine problems has been investigated by researchers since 1990. While some of researchers have considered the common due date as a predetermined value, others have considered it as a decision variable. Adamopoulos and Pappis [1] considered common due date as a decision variable in parallel machine scheduling problems and they proposed a heuristic procedure that is to minimize total cost of weighted common due date, earliness and tardiness cost. Their proposed heuristic’s complexity is O(n³) so their proposed heuristic is a polynomial time heuristic for a NP-Hard problem. Even if the complexity of their proposed heuristic is polynomial, they only used small test instances to check the performance of the proposed algorithm. Bank and Werner [2] proposed some heuristic methods for parallel machine scheduling problem with pre-determined common due date and release dates where the objective is to minimize total cost of earliness and tardiness. Bank and Werner [2] presented two different type algorithms. The first type of algorithms was constructive algorithms and the other was iterative algorithms. They stated that the performance of constructive algorithms depends on some parameters settings and the performance of iterative algorithms depends on shifting jobs from one machine to another. They compared their proposed algorithms with some metaheuristics and they concluded that none of the tested variants is clearly superior to the remaining ones in general. Yang et al. [3] introduced an evolutionary strategy method for parallel machine earliness/tardiness scheduling problem with common due date. They stated that computational results of different scale problems show that the method can effectively solve the parallel machine scheduling problem with relatively large scale. Xiao and Li [4] considered the problem of assigning a common due date to a set of jobs and scheduling the jobs on a set of parallel machines so that the weighted sum of the due date, total earliness, and total tardiness is minimized. They developed a heuristic is to solve the problem. Mönch and Unbehaun [5] proposed three decomposition heuristics for the parallel machine batch scheduling with pre-determined common due date where the objective is to minimize total earliness/tardiness cost. Their first heuristic is to apply and exact algorithm for non-batching problem and then it uses some job sequencing rules and dynamic programming in order to form batches for the early and tardy job sets and sequence them optimally. Their second algorithm uses genetic algorithm in order to assign jobs to each machine and then, it uses again sequencing rules and dynamic programming techniques to the early and tardy jobs sets on each single machine in order to form batches. Their third algorithm firstly separated equally jobs as early and tardy and then uses again genetic algorithm and applies again dynamic programming and sequencing rules. They reported their computational experiments and stated that the property-based heuristic beats the genetic algorithm-based heuristics with respect to solution quality in case of a large number of jobs. Toksarı and Güner [6,7,8,9] investigated parallel machine scheduling problem under effects of learning and deterioration with common due date where the objective is to minimize total earliness/tardiness cost. Srirangacharyulu and Srinivasan [10] considered the problem of scheduling n jobs on two identical parallel machines in order to minimize the mean squared deviation of job completion times about a given common due date. They proposed a heuristic to provide quick solutions for problems of larger size. Drobouchevitch and Sidney [11] considered a problem of scheduling n identical nonpreemptive jobs with a common due date on m uniform parallel machines where the objective is to determine an optimal value of the due date and an optimal allocation of jobs onto machines so as to minimize a total cost of earliness, tardiness and due date values. They proposed a two-phase algorithm to solve the problem. Kim et al. [12] presented a mathematical programming model and two types of heuristics for parallel machine earliness/tardiness scheduling problem where the common due date is a decision variable and the objective is to minimize the sum of due-date assignment, earliness and tardiness penalties. Their two types of heuristics were: (a) a fast two-stage heuristic with obtaining an initial solution and improvement; and (b) two meta-heuristics, tabu search and simulated annealing, with new neighbourhood generation methods. They stated that each of the heuristic types outperforms the existing one. Beyranvand et al. [13] considered the quadratic programming formulation of the unrelated parallel machine scheduling problem with restrictive common due date. Awasthi et al. [14] investigated single and parallel machine earliness/tardiness scheduling problems with common due date. They presented an exact polynomial algorithms for optimizing a given job sequence for single and parallel machines with the run-time complexities of O(n log n) and O(mn2log n) respectively. Lin et al. [15] investigated the problem of minimizing total weighted earliness and tardiness penalties on identical parallel machines against a restrictive common due date. They proposed a fast ruin-and-recreate (FR&R) algorithm is proposed to obtain high-quality solutions to this complex problem. They stated that computational results provide evidence of the efficiency of FR&R, which consistently outperform existing algorithms when applied to benchmark instances.

Although earliness/tardiness parallel machine scheduling problem is a well-known and classical problem in the literature, the problem is in NP hard class. For combinatorial optimization problem such as scheduling problems in NP hard class, metaheuristics promise to find near optimal solution for these problems within a reasonable time. Metaheuristic algorithms are classified into swam intelligence based algorithms, evolutionary algorithms and single solution algorithms. All of these algorithms are adaptable for different types of combinatorial problems (see [16,17,18,19]). In fact, a hybrid method including any two different algorithms can be used in order to solve and to find near-optimal or optimal solutions for these problems. For unrelated parallel machine weighted earliness/tardiness scheduling problem, in order to find what kind of algorithms are more efficient than others, this study investigates the performance of ABC, GA and SA algorithms that are well-known examples of swam intelligence based algorithms, evolutionary algorithms and single solution algorithms. The difference of the paper from the literature for the problem and its variants is to make a comparison among different types of well-known metaheuristic algorithms and to suggest one of alternatives for the readers.

2 Mathematical model for unrelated parallel machine weighted earliness/tardiness scheduling problems

In this section, a position-dependent mixed integer programming model for unrelated parallel machine weighted earliness/tardiness scheduling problems with common due-date is introduced. If a job is completed after its due date then that job is a tardy job and tardiness of that job can be calculated as follows:

$$T_{i} = \hbox{max} (C_{i} - D,0) \;\;\forall i$$

(1)

where $T_{i}$ is tardiness of the $i$th job, $C_{i}$ is completion time of the $i$th job and $D$ is the common due-date for all jobs. If a job is completed before its due date then that job is an early job and earliness of that job can be calculated as follows:

$$E_{i} = \hbox{max} (D - C_{i} ,0) \;\;\forall i$$

(2)

where $E_{i}$ is tardiness of the $i$th job. In a JIT company, jobs are wanted to be completed on its due-dates. Earliness and tardiness are not desired because each early/tardy job has some costs such as insurance, holding, stocking, additional cargo, etc., for the company. The company may define costs of earliness and tardiness amounts of jobs and then the total cost of earliness and tardiness can be calculated as follows:

$$f = \alpha \mathop \sum \limits_{i = 1}^{n} E_{i} + \beta \mathop \sum \limits_{i = 1}^{n} T_{i}$$

(3)

where $\alpha$ is the cost for one time-unit earliness and $\beta$ is the cost for one time-unit tardiness. A position-dependent mixed integer linear programming model for unrelated parallel machine weighted earliness/tardiness scheduling problems with common due-date is as follows:

Indexes

$i$::

index for jobs,

$j$::

index for machines,

$r$::

Index for position numbers on machines,

Parameters

$P_{ij}$::

processing time of job $i$ for machine $j$,

$D$::

common due date for all jobs,

$\alpha$::

weight for early jobs,

$\beta$::

weight for tardy jobs,

n::

number of jobs

m::

number of machines

Decision variables

$P_{[r],j}$::

processing time of the job at position r of machine j,

$C_{[r],j}$::

completion time of the job at position r of machine j,

$C_{i}$::

completion time of job i,

$X_{i,r,j}$::

if job $i$ is assigned at position $r$ of machine $j$, then it is equal to 1, else 0

$E_{i}$::

earliness time of job $i$

$T_{i}$::

tardiness time of job $i$

Objective function

$$\hbox{min} \,z :\; \alpha \mathop \sum \limits_{i = 1}^{n} E_{i} + \beta \mathop \sum \limits_{i = 1}^{n} T_{i}$$

(4)

Constraints

$$P_{[r],j} = \mathop \sum \limits_{i}^{n} X_{i,r,j} P_{ij} \;\;\forall r,j$$

(5)

$$C_{[r],j} = P_{[r],j} + C_{[r - 1],j} \;\;\forall r,j$$

(6)

$$C_{[0],j} = 0 \;\; \forall j$$

(7)

$$C_{i} = \mathop \sum \limits_{r}^{n} \mathop \sum \limits_{j}^{m} X_{i,r,j} C_{[r],j} \;\;\forall i$$

(8)

$$E_{i} \ge D - C_{i} \;\;\forall i$$

(9)

$$T_{i} \ge C_{i} - D\;\;\forall i$$

(10)

$$\mathop \sum \limits_{i}^{n} x_{i,r,j} \le 1\;\;\forall r,j$$

(11)

$$\mathop \sum \limits_{r}^{n} \mathop \sum \limits_{j}^{m} x_{i,r,j} = 1 \;\;\forall i$$

(12)

$$x_{i,r,j} + \mathop \sum \limits_{I = 1}^{n} x_{I,r + 1,j} \le 2 \;\;\;(I \ne i),\; (r = 1,2, \ldots ,n - 1)\;\forall i,j$$

(13)

$$x_{i,r + 1,j} \le x_{I,r,j} \;\;(I \ne i), \;(r = 1,2, \ldots ,n - 1)\;\forall i,j$$

(14)

$$P_{[r],j} , C_{[r],j} \ge 0 \;\;\forall r,j$$

(15)

$$C_{i} , E_{i} ,T_{i} \ge 0\; \forall i$$

(16)

$$X_{i,r,j} \in \{ 0,1\}$$

(17)

The objective function (4) is to minimize the sum of total weighted earliness/tardiness costs for all jobs. Constraint (5) shows the calculation for actual processing times of jobs assigned at position $r$ of machine $j$. Constraint (6) ensures that completion time of the job at position $r$ of machine $j$ is equal to sum the of the actual time of same job and previous job’s completion time in same machine. Constraint (7) shows that each machine is ready to process jobs at the beginning. Constraint (8) is to determine completion time of job $i$ by transforming machine and position indexes. Constraint (9) assures that earliness of a job must be equal to time interval between common due date and early job’s completion time. Constraint (10) assures that tardiness of a job must be equal to time interval between common due date and tardy job’s completion time. Constraint (11) ensures that a job can be assigned at a position of a machine at most once. Constraint (12) shows that each job must be assigned on a position of a machine. Constraint (13) assures that each job must come after another job and no position number is idle between two jobs. Constraint (14) shows that if a job assigned on previous position, then the current position may be used for another job or not. For Constraints (13–14), $I$ index is an alias of $i$ index and it is also index for jobs. Constraints (15–17) show that $X_{i,r,j }$ are binary decision variables and other decision variables are non-negative.

3 Solution approaches

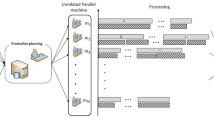
In this section, three different metaheuristics are introduced for unrelated parallel machine weighted earliness/tardiness scheduling problems with common due-date. These are artificial bee colony (ABC), genetic algorithm (GA) and simulated annealing (SA) algorithm. These metaheuristics are well known samples of swarm intelligence based algorithms, evolutionary algorithms and single solution algorithms. The solution (encoding) representation of each proposed algorithm is directly encoding by using numbers of positions and machines i.e., if there are 4 jobs and 3 machines then there are 12 genes in a chromosome (solution). Figure 1 illustrates an example for encoding in a solution for this study.

Fig. 1

Encoding strategy for a solution for all proposed metaheuristics in this study

The encoding strategy illustrated in Fig. 1 is common for all proposed metaheuristics to make a fair comparison.

3.1 Artificial bee colony algorithm

The artificial bee colony (ABC) algorithm is a swarm based meta-heuristic algorithm that was introduced by Karaboga [20] for optimizing numerical problems. It was inspired by the intelligent foraging behavior of honey bees as seen in Fig. 2. As a well-known optimization approach, ABC algorithm provides robust and near-optimal solutions. In basic structure of ABC, there is a population including individuals called food positions and the individuals are evaluated with artificial bees in order to discover the best food resource or the area of good food resources. Artificial bees are classified in three groups as employed bees, onlooker bees and scout bees. As an assumption in ABC, the number of food resources is equal to the number of employed bees. In initialization phase, scout bees fly randomly to food resources and discover these resources’ nectar amounts. Then, employed bees exploit the food resources by using the knowledge gained from scout bees. Then feedbacks of employed bees are used for selection of effective food resources and onlooker bees fly to neighbors of effective food resources. If an employed bee whose food source has been exhausted, then that bee becomes a scout bee. This process goes on until a stopping condition has been occurred. The general schema of ABC algorithm is given in Fig. 3. ABC algorithm is a swarm based algorithm that combines benefits of local and global searches and it also has a feedback structure that disables to investigate bad solutions that have been previously investigated.

Fig. 2

The behaviour of honey bee foraging for nectar [20]

Fig. 3

Artificial bee colony algorithm for optimization problems [20]

Karaboga proposed ABC algorithm for continuous optimization problems where the objective is to maximize or minimize a $f\left( {\overrightarrow {{x_{m} }} } \right)$ function and each member $x_{mi}$ of $\overrightarrow {{x_{m} }}$ vector is bounded with a lower bound $l_{i}$ and an upper bound $u_{i}$. In this study, solutions in proposed ABC are represented as in Fig. 1. Let us assume $\vec{\beta }$ is vector for genes in a solution and there are $nm$ ($n$ is number of jobs and $m$ is number of machines) genes $\vec{\beta } = \left( {\beta_{1} ,\beta_{2} ,\beta_{3} , \ldots ,\beta_{nm} } \right)$. There is a $f\left( {\vec{\beta }} \right)$ function as follows:

$$f\left( {\vec{\beta }} \right) = \alpha \mathop \sum \limits_{i = 1}^{n} E_{i} \left( {\vec{\beta }} \right) + \beta \mathop \sum \limits_{i = 1}^{n} T_{i} \left( {\vec{\beta }} \right)$$

(18)

where $E_{i} \left( {\vec{\beta }} \right)$ is the earliness of $i$th job for $\vec{\beta }$ solution and $T_{i} \left( {\vec{\beta }} \right)$ is the tardiness of $i$th job for $\vec{\beta }$ solution. $E_{i} \left( {\vec{\beta }} \right)$ and $T_{i} \left( {\vec{\beta }} \right)$ are calculated by using Eqs. (1–2) and completion times $C_{i} \left( {\vec{\beta }} \right)$ of jobs in $\vec{\beta }$ solution.

If we set number of employed bees (number of food researches or individual in the population) in proposed ABC as $SN$ (solution number) then there are $SN$ different $\vec{\beta }$ vectors such as $\vec{\beta }_{l}$ where $l = 1,2, \ldots ,SN$. So the purpose of the forecasting is to find best forecasted values close to the observed values then there is a best $\vec{\beta }^{*}$ vector that have optimum or near optimum as follows:

$$f\left( {\vec{\beta }^{*} } \right) = \hbox{min} \left( {f\left( {\vec{\beta }_{1} } \right),f\left( {\vec{\beta }_{2} } \right), \ldots ,f\left( {\vec{\beta }_{SN} } \right)} \right)$$

(19)

In initialization phase of ABC, all the vectors $\vec{\beta }_{l}$$(l = 1,2, \ldots ,SN)$ are initialized by scout bees. Since each food source $\vec{\beta }_{l}$, is a set of genes in solution representation in Fig. 1, each $\vec{\beta }_{l}$ vector holds $nm$ variables, ($\beta_{lt}$, $t = 1,2,3, \ldots ,nm$), which are to be optimized so as to find minimum $f\left( {\vec{\beta }^{*} } \right)$. For initialization of all $\vec{\beta }_{l} \; (l = 1,2,3, \ldots SN)$, a procedure illustrated in Fig. 4 is used.

Fig. 4

Pseudo code for generating initial population

The procedure illustrated in Fig. 4 is also used in proposed GA in this study. Employed bees search for a new set of genes or a new solution ($\vec{\upsilon }_{l}$) that have more suitable to be the best candidate. The searching procedure for a neighboring solution by using existing $\vec{\beta }_{l}$ is simply swapping two random genes’ positions in $\vec{\beta }_{l}$ for proposed ABC algorithm. After searching procedure taking place, a repair operation regulates the solution as in the proposed GA in this study, if necessary.

Employed bees find a new $\vec{\upsilon }_{l}$ and they evaluate its profitability (fitness). After producing a new set of genes $\vec{\upsilon }_{l}$, its fitness is calculated and a greedy selection is applied between $\vec{\upsilon }_{l}$ and $\vec{\beta }_{l}$. The fitness value of $\vec{\beta }_{l}$ is illustrated with $fitness_{l} \left( {\vec{\beta }_{l} } \right)$ notation and it is calculated as follows:

$$fitness_{l} \left( {\vec{\beta }_{l} } \right) = 1/\left( {1 + f\left( {\vec{\beta }_{l} } \right)} \right)$$

(20)

In ABC algorithm, employed bees give information about their own sets of genes to onlooker bees. Then, onlooker bees start selecting probabilistically their sets by using the feedback from employed bees. This selection phase is done with a fitness based selecting technique and the probability $p_{l}$ of the set $\vec{\beta }_{l}$ can be determined as follows:

$$p_{l} = \frac{{fitness_{l} \left( {\vec{\beta }_{l} } \right)}}{{\mathop \sum \nolimits_{l = 1}^{SN} fitness_{l} \left( {\vec{\beta }_{l} } \right)}} \;\forall l$$

(21)

After a set $\vec{\beta }_{l}$ for an onlooker bee is probabilistically chosen, a neighbourhood set $\vec{\upsilon }_{l}$ is determined by swapping operation, and its fitness value is computed by using Eq. (20). As in the employed bees phase, a greedy selection is applied between $\vec{\upsilon }_{l}$ and $\vec{\beta }_{l}$ . Thus, the number of onlooker bees recruiting better solution spaces is increased. In this phase, to disable to inefficient set, a counter $failure_{l} \left( {\vec{\beta }_{l} } \right)$ for each $\vec{\beta }_{l}$ takes places. If $fitness_{l} \left( {\vec{\beta }_{l} } \right)$ is better than $fitness_{l} \left( {\vec{\upsilon }_{l} } \right)$, then $failure_{l} \left( {\vec{\beta }_{l} } \right)$ increases one. If $fitness_{l} \left( {\vec{\beta }_{l} } \right)$ is not better than $fitness_{l} \left( {\vec{\upsilon }_{l} } \right)$, then $failure_{l} \left( {\vec{\beta }_{l} } \right)$ is set as zero. If $failure_{l} \left( {\vec{\beta }_{l} } \right)$ reaches a pre-determined $limit$, then the employee bee dealing with $\vec{\beta }_{l}$ becomes a scout bee that abandons $\vec{\beta }_{l}$ and finds a random set of genes. The number of scout bees is generally limited for preventing ABC becoming a random search algorithm. The algorithm runs until a pre-determined stopping condition occurrence.

3.2 Genetic algorithm

Genetic algorithm (GA) is a metaheuristic search method for optimization problems and it is well-known example of evolutionary algorithms. GA uses stochastic random search methods to generate new alternative solutions from initially generated solution population. Each solution in the initial population is evaluated by comparing with others in order to determine how much proper (fitness value) this candidate to be the best solution. Then, these candidates are transmitted into matching pool for crossover process in order to randomly generate new solutions from good solutions in the current population. After some population generations, crossover process drives solutions in the population to be similar to each other. Thus, a mutation process randomly takes place to protect the diversity of the population. After these processes, solutions in the new population are evaluated again. If the stopping criterion occurs, then GA stops and displays the best solution. Otherwise, GA continues to search for better solutions until stopping criteria occurs.

The general schema of GA in this study is illustrated with a pseudo code in Fig. 5. Encoding strategy of GA in this study illustrates the indexes of jobs assigned on any position number of machines. This strategy makes computationally easy to execute GA operations. This encoding strategy is common for all methods investigated in this paper and can be seen in Fig. 1. Evaluation and selection steps in this GA do not let the worse solution in the current population to transmit to matching pool. After crossover and mutation steps, if the feasibility of solutions is going wrong, then a repair operation takes place to fix infeasible solutions. Thus, GA only searches for the fitness of objective function instead of the fitness of constraints of the model. These are the advantages of proposed GA.

Fig. 5

Pseudo code for genetic algorithm

Generating initial population In order to generate an initial solution for the problem, the pseudocode in Fig. 4 is proposed in this study. After generating randomly an initial population, feasibilities of candidate solutions in the population must be controlled. The pseudo code in Fig. 4 checks the feasibility and fixes solutions in the population if it is required.

Evaluating The evaluation step in GA depends on fitness values of solutions in the population. Let $k\,(k = 1, \ldots ,P)$ is the index for population and $P$ is the size of population. The fitness value $f_{k}$ of solution $k$ in the current population is calculated as follows:

$$f_{k} = { \hbox{max} }\left\{ {\left( {\alpha \mathop \sum \limits_{i = 1}^{n} E_{i}^{1} + \beta \mathop \sum \limits_{i = 1}^{n} T_{i}^{1} } \right), \ldots ,\left( {\alpha \mathop \sum \limits_{i = 1}^{n} E_{i}^{P} + \beta \mathop \sum \limits_{i = 1}^{n} T_{i}^{P} } \right)} \right\} - \left( {\alpha \mathop \sum \limits_{i = 1}^{n} E_{i}^{k} + \beta \mathop \sum \limits_{i = 1}^{n} T_{i}^{k} } \right)$$

(22)

where $E_{i}^{k}$ is earliness of job $i$ and $T_{i}^{k}$ is tardiness of job $i$ in solution $k$ in the current population.

Selection The selection step in this GA is roulette wheel selection. Selection probability values of solutions are used to determine which solutions will be transmitted into the matching pool. The selection probability values are calculated as follows:

$$P_{k} = \frac{{f_{k} }}{{\sum f_{k} }},$$

(23)

where $P_{k}$ is the selection probability for solution $k$ by comparing its fitness value with sum of all fitness values.

Crossover Crossover step in GA takes place after the selection step. This step is required to generate new alternative solutions by using a selected solution pair from the matching pool. Crossover is a random step with a probability $p_{c}$. In this study, two points crossover method is preferred. Once crossover step occurs for a selected pair of solutions, a repair operation may be required in order to fix infeasible solutions. Figure 6 illustrates an example for crossover and repair steps.

Fig. 6

Crossover and repair steps

Mutation Mutation is another random step with a probability $p_{m}$ in GA in order to protect solution diversity in the population because crossover step in GA makes solutions in the population get similar to each other after some generations. In this study, randomly selected two genes are replaced with each other. Then, if it is required, a repair step may take place to fix infeasibility. Figure 7 illustrates an example for mutation and repair steps.

Fig. 7

Mutation and repair steps

Repair The chromosome in Figs. 6 and 7 represents a solution for 4 jobs and 3 machines. There are 12 (4 * 3) genes in each chromosome. The first four-gene in the chromosome belongs to the first machine’s jobs and the second four-gene belongs to the second machine’s jobs. When crossover or mutation operation takes place as seen in Fig. 6, a repair operation regulates sequence of genes to disable idle genes get in between two genes having jobs. Furthermore, if there is an idle gene before a gene having job, then idle gene and that gene are replaced as illustrated in Figs. 6 and 7.

3.3 Simulated annealing algorithm

Simulated annealing (SA) is another metaheuristic method in order to deal with optimization problems. SA is inspired from the annealing process in metal work. SA’s best advantage by comparing it with other search methods is avoiding from a local optimum by using stochastic search. SA starts with an initial system temperature and this temperature is decreased at each iteration. At each system temperature, SA looks for neighboring solutions in order to improve its current best solution. While temperature is decreasing at each iteration, number of searching for neighboring solutions at each iteration is being increased by SA. Furthermore, if SA sticks around a local optimum, then a stochastic movement for new search point takes place to release SA from the local optimum. This process ends when the system temperature reaches the stopping temperature. Figure 8 shows the pseudo code for SA in this study. In this proposed SA, searching procedure for neighboring solutions is simply swapping two random genes’ positions as in ABC algorithm. Encoding strategy of SA in this study illustrates the indexes of jobs assigned on any position number of machines. This strategy makes computationally easy to execute SA operations. This encoding strategy is common for all methods investigated in this paper and can be seen in Fig. 1.

Fig. 8

Pseudo code for SA

4 Experimental results

In this section, some test instances are generated to determine which proposed metaheuristic is better than others. 16 test instances group and 10 instances in each group are generated. Numbers of jobs in instances are 100, 200, 300 and 400. Numbers of machines in instances are 5, 10, 15 and 20. The processing times are uniformly generated $P_{ij} = U[1,20]$ for 160 instances. As earliness and tardiness weights ($\alpha ,\beta$), two sets are used {(2, 3); (3, 2)} for all test instances. The common due date $D$ for each instances are determined with the way proposed by Bank and Werner [2] as follows:

$$D = \left\lfloor {\frac{1}{3}\frac{n}{m}\bar{P}} \right\rfloor$$

(24)

where

$$\bar{P} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \mathop \sum \nolimits_{j = 1}^{m} P_{ij} }}{nm}$$

(25)

Each proposed metaheuristic was coded with C# programming language and MS Access database by using a standard desktop having i5 CPU and 8 GB RAM. The parameter settings of metaheuristic are determined by considering general parameter settings in the literature. For proposed GA, crossover and mutation probabilities are set as 0.85 and 0.15. The initial temperature and temperature decrease rate of proposed SA are set as 10⁶ and 0.8. The numbers of employee bees, onlooker bees and scout bees are set as 30, 30 and 1 for proposed ABC. The limit value for failures of proposed ABC is equal to 15 times of the product of number of machines and number of jobs for each instance. Each proposed metaheuristic is executed 10 times until pre-determined solution time limits for each test instances. Average solution values of each test instance group for earliness and tardiness weights ($\alpha = 2,\beta = 3$) are given in Table 1. Average solution values of each test instance group for earliness and tardiness weights ($\alpha = 3,\beta = 2$) are given in Table 2.

Table 1 Average solutions of each test instance group for earliness and tardiness weights ($\alpha = 2,\beta = 3$)

Table 2 Average solutions of each test instance group for earliness and tardiness weights ($\alpha = 3,\beta = 2$)

As seen from Table 1, ABC algorithm gives better results than its opponents in average. All results obtained from all proposed metaheuristics for $\alpha = 2$ and $\beta = 3$ are analyzed with ANOVA for objective function values. The ANOVA results for total weighted earliness/tardiness values obtaining by different methods give us a p value as zero. Therefore, we can say that methods are significantly different considering solution quality. Furthermore, the interval plot in Fig. 9 show us ABC gives better solution in a more narrow interval.

Fig. 9

Interval plots f results obtained proposed algorithms ($\alpha = 2$ and $\beta = 3$)

As seen from Table 2, ABC algorithm gives better results than its opponents in average. All results obtained from all proposed metaheuristics for $\alpha = 3$ and $\beta = 2$ are analyzed with ANOVA for objective function values. The ANOVA results for total weighted earliness/tardiness values obtaining by different methods give us a p value as 0.001. Therefore, we can say that methods are significantly different considering solution quality. Furthermore, the interval plot in Fig. 10 show us ABC gives better solution in a more narrow interval.

Fig. 10

Interval plots f results obtained proposed algorithms ($\alpha = 3$ and $\beta = 2$)

As a conclusion of above analyses for the problem, we can say that ABC algorithm as swarm intelligence based metaheuristic outperforms well-known samples of evolutionary and single solution metaheuristics. Each type of metaheuristic has own its advantages. For a fair comparison, the encoding strategies of all methods are the same and this strategy is illustrated in Fig. 1. For instance, evolutionary algorithms have a population based structure to help searching multiple solutions, a selection mechanism that helps to focus on better candidate solutions, and an escape mechanism from local optima. Single point or solution methods such as SA are relatively easy to code and to apply arbitrary problems and cost functions. Swarm intelligence based algorithms such as ABC imitate intelligent swarms’ self organizing and information sharing models among individuals in the swarm so positive or negative feedbacks of individuals in the swarms help to improve the quality of the solution. Furthermore, each metaheuristic can be hybrid with other heuristics or metaheuristic considering advantages and disadvantages of alternative methods.

5 Conclusion

In this study, we investigated metaheuristic algorithm alternatives among well-known samples of swarm intelligence based, evolutionary and single solution algorithms for unrelated parallel machine earliness/tardiness scheduling problems with common due date. ABC, GA and SA were chosen for comparison in view of solution quality in a pre-determined time limitation. All proposed algorithms are created without modification in order to determine solution qualities of these metaheuristics. Furthermore, the encoding strategies of all methods are the same for a fair comparison. Experimental results show that ABC outperforms its opponents in view of solution quality as swarm intelligence based metaheuristic algorithm. Future researchers may use a hybrid algorithm having main structure and advantages of ABC for unrelated parallel machine earliness/tardiness scheduling problems with common due date. Furthermore, ABC algorithm can be used for the same problem with other constrains such as release dates, setup times and.