Design of a fuzzy robust-adaptive control law for active suspension systems

Abstract

This paper outlines a new approach in control of active vibration systems to make the system robust to parametric uncertainties, unmodeled dynamic effects and external disturbances. Namely, it is aimed to ensure robustness of the system towards all kind of disturbances such as road surface inputs and unexpected system parameter changes. So, a new robust-adaptive controller is designed as a vibration isolator and then applied on a full car active suspension system to improve the ride comfort of a vehicle in the presence of structured parameter uncertainties and unstructured unknown parameters or unmodeled dynamics. For this purpose, new parametric uncertainty upper bound adaptation algorithm is developed to isolate any platform from vibrations. Using adaptive laws, the controller can operate properly under changing conditions. The robustness of controller is also ensured by robust control law. This new approach represents a groundbreaking solution to eliminate any disturbance on a vehicle. Stability of the system is guaranteed by using Lyapunov theory, thus uniform boundedness error convergence is achieved. Afterwards, fuzzy logic controller is used to achieve the optimum values of controller gains. Also, comparative numerical solution using a fuzzy logic controlled suspension is performed on the same full-car model, both in time and frequency domain since classical FLC is an effective control method for active suspensions. At the end, it has been verified that the designed fuzzy robust-adaptive controller improves ride comfort more successfully than fuzzy logic one.

1 Introduction

In the presence of model parametric uncertainty, adaptive and robust controllers have drawn great attention. Slotine et al [1], Sciavicco et al [2] and Spong [3] defined adaptive and robust control laws and applied these controllers to robotic manipulators. They proved that the proposed controllers worked properly. Since vehicles are systems with parameter uncertainties, adaptive and robust control methods are used for vehicle suspension control widely. Therefore, there have been many studies on this subject.

Chen et al [4] designed an adaptive sliding mode controller for non-autonomous suspension systems. Initially, they modeled a quarter car based on the nominal parameters of system. A function approximation technique was utilized for the system uncertainties and nonlinearities. Then, they guaranteed the stability of system by a control rule and an estimation law. They applied this control method to a quarter car model and explained that the results were satisfactory. Boada et al [5] developed fuzzy logical yaw moment control for vehicle ride comfort. Fuzzy logic controller was used in the study since it could control nonlinear systems properly. The proposed controller produces the yaw moment obtained from the difference in braking forces between the two front wheels. The eight-degrees-of-freedom vehicle model including nonlinearities was used to show the effectiveness of controller. Huang and Chen [6] developed functional approximation based adaptive sliding controller with fuzzy compensation and applied this controller to a quarter car active suspension system. Lyapunov theory was utilized to ensure the stability of system. It was understood experimentally that the developed controller improved vehicle ride comfort. Hajjaji et al [7], introduced robust fuzzy control law for four wheels steering vehicle. The system was subjected to road uncertainties and variable road conditions. They developed Takagi-Sugeno model. Stability analysis of the controller was ensured by using Linear Matrix Inequality (LMI) technique. When both controlled and uncontrolled simulations were performed, it was understood that the fuzzy logic control was more beneficial on the vehicle lateral dynamics. Chen and Huang [8] developed adaptive sliding mode controller with fuzzy compensation and applied this new controller to a quarter car suspension system. The stability of system was ensured by Lyapunov theory. The aim of study was to improve the ride comfort of a vehicle. Numerical simulation and experimental results showed that the proposed controller seemed to be effective. Kaleemullah et al [9] designed robust H∞, fuzzy and LQR for an active suspension system. They combined the best features of all 3 controllers (robust, LQR and fuzzy) and developed a hybrid controller. Then, in line with the comparison between active and passive suspension systems, it was observed that robust controller had better settling time, LQR controller had better performance in body acceleration and it was seen that the fuzzy controller required less control force. Yagiz et al [10] introduced fuzzy sliding mode control law for the ride comfort of a vehicle. They presented a sliding mode controller, then they improved this controller with single input-single output fuzzy logic controller. They applied this controller to a nonlinear half car model and guaranteed the robustness of controller for different vehicle parameters. The results indicated that the performance of developed controller was significant. Pang et al [11] designed an improved linear quadratic and Gaussian distributed (LQG) controller for active suspension systems under the unknown road disturbances. They aimed to optimize vehicle parameters and to better control the system by using the LQG controller and Genetic Algorithm (GA). In order to demonstrate the performance of controller, they compared the proposed method with that of traditional one and showed that the developed controller increased vehicle ride comfort. Pang et al [12] designed fuzzy-sliding mode controller for semi-active suspension systems. They tried to reduce the chattering problem by using the fuzzy-logic controller. In addition to this, they used ideal skyhook damping which has very common usage on semi-active suspension systems. In order to show effectiveness of the controller, they carried out simulations under the random and bump road surface inputs. Li et al [13] designed reliable fuzzy H∞ controller for active suspension systems. The controller was designed considering the spring and unsprung mass variations, actuator delay, fault and suspension performance. This proposed controller was applied to a quarter vehicle suspension system with uncertainties. Simulation results showed that the effectiveness of controller was remarkable. Sun et al [14] developed a new adaptive robust control (ARC) for nonlinear active suspension systems with saturated inputs. The novelty of study is to add an anti-windup compensator in order to increase the controller performance. For that reason, a half vehicle model was used to demonstrate the capability of controller. Lian [15] suggested a self-organizing fuzzy controller (SOFC). Then, he proposed an enhanced adaptive self-organizing fuzzy sliding mode controller (EASFSC) for active suspension systems. A sliding surface and its rate were selected as the input parameters of fuzzy controller. The stability of system was guaranteed by using the Lyapunov theory. The experimental results proved that the developed controller (EASFSC) was more successful than the (SOFC) controller. Guo et al [16] dealt with the problem of lateral dynamics in vehicles. They developed an adaptive fuzzy sliding mode controller for vision-based automated vehicles. The control strategy consists of nonlinearities, parametric uncertainties and external disturbances. They enhanced the stability of the suggested control law by using Lyapunov Theory. Wu et al [17] designed robust fuzzy disturbance observer-based control (DOBC) for a hypersonic vehicle. First, a Takagi-Sugeno fuzzy control law was presented for nonlinear dynamics of vehicle then, a new fuzzy disturbance observer was introduced to estimate the disturbances. Finally, a robust L∞ fuzzy DOBC design with adaptive bounding was developed. Numerical analysis showed that the performance of proposed controller was significant. Wang and Er [18], presented a self-constructing adaptive robust fuzzy neural control (SARFNC) strategy for tracking surface vehicles and proposed a self-constructing fuzzy neural network (SCFNN) strategy to estimate the disturbances and system uncertainties. Both controllers were applied to a CyberShip II model and the results were compared. It was observed from simulation results that the self-constructing adaptive robust fuzzy neural control was more effective in trajectory tracking. Wang et al [19] proposed an adaptive robust online constructive fuzzy control (AR-OCFC) scheme. They developed an online constructive fuzzy approximator (OCFA) to ensure the tracking problem of surface vehicles including uncertainties and unknown disturbances. Pan et al [20] dealt with the problem of trajectory tracking of suspension systems with external disturbances. They presented a disturbance compensator with finite-time convergence instead of compensating unknown disturbances. In other words, they aimed to improve the ride comfort of an active suspension system via finite-time disturbance compensation. Experimental results confirmed that the proposed control method worked with low energy costs and increased the ride comfort. Wen et al [21], developed a hybrid control law that consisted of fuzzy logic and sliding mode controllers. Sliding mode strategy was proposed for the control of nonlinear active suspension system. A T-S fuzzy logic method was used to achieve the control target. Simulation results verified that the proposed control method worked well. Pang et al [22] studied variable universe fuzzy logic controller for semi-active suspension systems with MR damper. They presented non-parametric MR damper system. The data was collected from a quarter car test rig. Then, they developed fuzzy logic controller to achieve the effective control of input current for MR damper. It was seen from simulation results that the control effort was effective.

A disturbance estimation law for a ground vehicle in the presence of structured and unstructured unknown parameters or unmodeled dynamics was introduced in [23]. Then, a robust control law for estimation of upper bound model uncertainties for railway suspension systems was introduced in [24]. Pan and Sun [25], proposed a novel disturbance estimator with finite-time convergence to protect passengers from road disturbances. This approach has two separately designed parts; one is the homogeneous nominal control part and the other one is disturbance compensator. First, the homogeneous nominal control part determines the suspension performance without any disturbance. Then, the disturbance compensator deals with any uncertainties on the system and unknown external disturbances. An experimental study was carried out and RMS values showed that the vehicle ride comfort was significantly improved in the presence of unknown external disturbance.

In addition, actuator faults have drawn attention in literature. Pan et al [26], introduced an adaptive fault-tolerant compensator for an active suspension system so as to guarantee closed-loop system stability in the presence of nonlinear actuators with random failures. They studied three actuator failures; partial and complete actuator failures as well as stuck at a certain value. Each of these failures were described by a Markovian type function. A quarter-car suspension system which subjected to sinusoidal road disturbance was used to perform simulations. A comparison was performed between passive, backstepping and proposed controller with three predetermined times. The results indicated that the closed-loop system stability was guaranteed by proposed controller in the presence of actuator failures and nonlinearities.

Corless and Leitmann [27] approach based on Lyapunov theory is used for robust controller design. Some robust control laws developed based on the approaches by Corless and Leitmann [27] are given in [3], [28], [29] and [30]. In this study, a new robust adaptive control law is designed based on Lyapunov theory and by using Corless and Leitmann [27] approach for vehicle suspension systems that is robust to both model parametric uncertainty and unknown unstructured system parameters or dynamics, external disturbances, suspension dry friction, etc.

This paper is organized as follows: the second section gives a detailed analysis of a new fuzzy robust-adaptive control law that is developed for full car active suspension systems. By using Lyapunov Stability Theory, it is ensured that the system is robust against external disturbances and non-parameterized model uncertainties such as unestimated body mass, dry friction in damper, degenerated suspension spring or damper, unknown body mass center position. Initially, a robust-adaptive control law is proposed, then fuzzy logic controller is used to determine some controller gains. Afterwards, the third section interprets the numerical results on a full car active suspension model with the given limited ramp road surface input. Our conclusions on both time and frequency responses so as to see the effects of proposed controller are analyzed in the final section.

2 Design of fuzzy robust-adaptive controller

2.1 Robust-adaptive control scheme

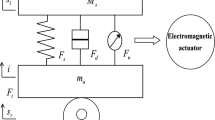
Considering the previous studies [31], [32] and [33] equations of motion for an n-degrees-of-freedom active vibration system¹ which subject to any type of disturbance can be given as:

$$ M\ddot{x} + C(\dot{x} - \dot{x}_{0} ) + K(x - x_{0} ) + d = Bu $$

(1)

where M, C and K stand for nxn matrices of mass, damping and stiffness, respectively. B is nxr (r≥n) matrix for linear control input, d is the nx1 vector for unstructured parameters, such as the frictions and disturbances, u is the nx1 vector for controller input. Notice that friction force matrix given in [31] is modeled as Coulomb friction. However, in this study, d includes all kinds of unstructured parameters such as all kind of friction forces and all kind of external disturbances, and these are assumed to be unknown as would be in [28]. Then, Eq. (1) can be rearranged as:

$$ \begin{aligned} M\ddot{x} + C(\dot{x} - \dot{x}_{0} ) + K(x - x_{0} ) + d & = Bu \\ \, Y(\ddot{x},\dot{x},x)a + d & = Bu \\ \end{aligned} $$

(2)

where, $a^{T} = [K,\;C,\;M]$ is the column vector composed of system parameters matrices and $Y = [x - x_{0} , \, \dot{x} - \dot{x}_{0} , { }\ddot{x}]$ is the matrix of measurable states. Considering the previous studies [3] and [29] a nominal control is defined as follows:

$$ \begin{aligned} u_{0} & = B^{ - 1} [M_{0} \ddot{x}_{r} + C_{0} (\dot{x} - \dot{x}_{0} ) + K_{0} (x - x_{0} ) + K_{D} \sigma ] \\ u_{0} & = B^{ - 1} [Y_{r} a_{0} + K_{D} \sigma ] \\ \end{aligned} $$

(3)

Then, a₀ and Y_r are defined as:

$$ a_{0} = [K_{0} \;C_{0} \;M_{0} ]^{T} \quad {\text{and}}\quad Y_{r} = [x - x_{0} ,\;\dot{x} - \dot{x}_{0} ,\;\ddot{x}_{r} ] $$

(4)

where $a_{0}$ identifies nominal control for parameters, the controller input based on parametric uncertainties upper bound adaptation algorithm. The nominal control parameters K₀, C₀, M₀, namely, $a_{0}$ is fixed during the control action. Considering the previous studies [2], [3], [28] and [29], the following control law is designed so as to estimate upper bound of uncertainties on model parameters and to eliminate effects of any disturbances on the system or effects of unmodeled dynamics:

$$ u = B^{ - 1} [Y_{r} (a_{0} + p(t)) + u_{d} + K_{D} \sigma ] $$

(5)

where u_d is a control input to ensure robustness of the system to any type of disturbances including suspension frictions, unmodeled dynamics, etc. and the term$K_{D} \sigma$ has PD effect on the error. The equations defined in Eq. (6) and Eq. (7) give error and reference input based on desired motion [2]:

$$ \tilde{x} = x_{d} - x;\;\dot{\tilde{x}} = \dot{x}_{d} - \dot{x};\;\dot{x}_{r} = \dot{x}_{d} + \lambda \tilde{x};\;\ddot{x}_{r} = \ddot{x}_{d} + \lambda \dot{\tilde{x}} $$

(6)

$$ \sigma = \dot{x}_{r} - \dot{x} = \dot{\tilde{x}} + \lambda \tilde{x} $$

(7)

where x_d and x denote desired input and actual output, respectively, $\tilde{x}$ denotes tracking error, K_D and $\lambda$ are positive definite diagonal matrix and $\sigma$ stands for error dynamics. Combining Eqs. (1), (2) and (5), the following equation is obtained:

$$ M\dot{\sigma } = Y_{r} (\tilde{a} + p(t)) + u_{d} - K_{D} \sigma + d $$

(8)

where $\tilde{a}$ denotes estimation error of model parameters. In this equation $\tilde{a}, \rho ,$ are defined as follows similar to robust control law [3], [29]:

$$ \tilde{a} = a - a_{0} ;\quad \parallel \tilde{a}\parallel = \parallel a - a_{0} \parallel \; \le \rho \,;\quad \tilde{\rho } = \rho - \hat{\rho } $$

(9)

It is well-known that non-parameterized model uncertainties and any type of external disturbances on a system are not constant and are bounded as:

$$ \left\| d \right\| \le \rho_{d} $$

(10)

where $\rho_{d1}$∈R and is assumed to be unknown. Herein, the term $\rho_{d1}$ is considered to be determined through an estimation law. Then, related estimation error $\tilde{\rho }_{d1}$ is defined in accordance with [28] and [29] as follows:

$$ {\tilde{\rho }}_{\text{d}} =\uprho_{\text{d}} - {\hat{\rho }}_{\text{d}} $$

(11)

Considering the control input (5), the following theorem is presented to guarantee the stability of system.

Theorem

Let $\varepsilon_{p}$ > 0 and $\varepsilon_{d}$ > 0. $u_{d}$ in Eq. (5) is defined in the following way:

$$ u_{d} = \left\{ {\begin{array}{*{20}l} {\frac{\sigma }{\left\| \sigma \right\|}\hat{\rho }_{d} } \hfill & {if\quad \left\| \sigma \right\| > \varepsilon_{d} } \hfill \\ {\frac{\sigma }{{\varepsilon_{d} }}\hat{\rho }_{d} } \hfill & {if\quad \, \left\| \sigma \right\| \le \varepsilon_{d} } \hfill \\ \end{array} } \right. $$

(12)

Then,$\hat{\rho }_{d1}$, $\hat{\rho }_{d2}$and $\hat{\rho }_{d}$ are defined as follows:

$$ \dot{\hat{\rho }}_{d1} = B_{1} \left\| \sigma \right\|;\quad \hat{\rho }_{d2} = \frac{{\psi^{2} }}{\gamma }({\text{e}}^{{ - \gamma \int {\left\| \sigma \right\|} dt}} - {\text{e}}^{{ - 2\gamma \int {\left\| \sigma \right\|} dt}} );\quad \hat{\rho }_{d} = \hat{\rho }_{d1} + \hat{\rho }_{d2} $$

(13)

where B₁ЄR+ and ψ, γ ЄR are adaptation gains. Parameter uncertainty upper bound adaptation algorithm $\hat{\rho }$ is defined as follows:

$$ \dot{\hat{\rho }} = \left\{ {\begin{array}{*{20}c} {\alpha_{1} \parallel Y^{T}_r \sigma \parallel } \\ 0 \\ \end{array} } \right.\quad \quad \begin{array}{*{20}c} {\parallel Y^{T}_r \sigma \parallel {\kern 1pt} \; > \;\varepsilon_{p} } \\ {\parallel Y^{T}_r \sigma \parallel \;{\kern 1pt} \le \;\varepsilon_{p} } \\ \end{array} \; $$

(14)

Here, α₁ is a positive constant and is an adaptive control gain. The control input $p\left( t \right)$ given in Eq. (5) is defined as:

$$ p(t) = \left\{ {\begin{array}{*{20}c} {\frac{{Y^{T}_r \sigma }}{{\parallel Y^{T}_r \sigma \parallel }}\hat{\rho }} \\ {\frac{{Y^{T}_r \sigma }}{{\varepsilon_{p} }}\hat{\rho }} \\ \end{array} } \right.\quad \quad \quad \begin{array}{*{20}c} {\parallel Y^{T}_r \sigma \parallel {\kern 1pt} \; > \;\varepsilon_{p} } \\ {} \\ {\parallel Y^{T}_r \sigma \parallel \;{\kern 1pt} \le \;\varepsilon_{p} } \\ \end{array} $$

(15)

If the control input defined in Eqs. (12) and (15) are replaced by the control rule given in Eq. (5), then, the uniform ultimate boundedness of σ will be achieved.

Proof

In order to prove the above-mentioned theorems, a Lyapunov candidate function is given as follows:

$$ V = \frac{1}{2}\sigma^{T} M\sigma + \frac{1}{2\alpha }\tilde{\rho }^{2} (t) + \frac{1}{{2B_{1} }}\tilde{\rho }_{d1}^{2} + \frac{1}{2}\varphi^{2} \hat{\rho }_{d2}^{2} $$

(16)

where φ denotes a time-dependent matrix. The time derivative of Lyapunov function is:

$$ \begin{aligned} \dot{V} &= \sigma^{T} M\dot{\sigma } + \frac{1}{\alpha }\tilde{\rho }\dot{\hat{\rho }} + \frac{1}{{B_{1} }}\tilde{\rho }_{d1} \,\dot{\hat{\rho }}_{d1} \hfill \\ & \quad + \hat{\rho }_{d2}^{2} \varphi \dot{\varphi } + \hat{\rho }_{d2} \dot{\hat{\rho }}_{d2} \varphi^{2} \hfill \\ & = \sigma^{T} M\dot{\sigma } - \frac{1}{{\alpha_{1} }}(\rho - \hat{\rho })\dot{\hat{\rho }} \hfill \\ & \quad -\frac{1}{{B_{1} }}(\rho_{d1} - \hat{\rho }_{d1} )\,\dot{\hat{\rho }}_{d1} + \hat{\rho }_{d2}^{2} \varphi \dot{\varphi } + \hat{\rho }_{d2} \dot{\hat{\rho }}_{d2} \varphi^{2} \hfill \\ \end{aligned} $$

(17)

Note that $\tilde{\rho } = \rho - \hat{\rho }$ and $\tilde{\rho }_{d} = \rho_{d} - \hat{\rho }_{d}$. By substituting the Eqs. (13), (14) and (15) into Eq. (17), Eq. (17) takes the following form:

$$ \begin{aligned} \dot{V} & = \sigma^{T} M\dot{\sigma } - \rho \parallel Y^{T}_r \sigma \parallel + \hat{\rho }\parallel Y^{T}_r \sigma \parallel - \rho_{d1} \left\| \sigma \right\| \\ & \quad + \hat{\rho }_{d1} \left\| \sigma \right\| + \hat{\rho }_{d2}^{2} \varphi \dot{\varphi } + \hat{\rho }_{d2} \dot{\hat{\rho }}_{d2} \varphi^{2} \\ \end{aligned} $$

(18)

If Eq. (8) is written in Eq. (18), the following equation is obtained:

$$ \begin{aligned} \dot{V} & = \sigma^{T} Y_r\tilde{a} - \rho \parallel Y^{T}_r \sigma \parallel - \sigma^{T} Y_rp(t) + \hat{\rho }\parallel Y^{T}_r \sigma \parallel \\ & \quad - \sigma^{T} K_{D} \sigma - \sigma^{T} u_{d} + \sigma^{T} d - \rho_{d1} \left\| \sigma \right\| \\ & \quad + \hat{\rho }_{d1} \left\| \sigma \right\| + \hat{\rho }_{d2}^{2} \varphi \dot{\varphi } + \hat{\rho }_{d2} \dot{\hat{\rho }}_{d2} \varphi^{2} \\ \end{aligned} $$

(19)

2.1a

Dynamic compensators for unknown unstructured friction forces and disturbances

Below defined a time-dependent function of φ is used to reject the effects of unknown friction forces and disturbances on a vehicle suspension system [28]:

$$ \phi = \frac{{{\text{e}}^{{\gamma \int {\left\|\upsigma \right\|} {\text{dt}}}} }}{\psi } $$

(20)

It is crucial to note that there is no any certain rule for control input $u_{d}$ that yields $\dot{V} \le 0$. To prove the theorem and to define an appropriate φ function, system state parameters and mathematical point of view are used. Using Eq. (13), $\dot{\hat{\rho }}_{d2}$ is written as:

$$ \dot{\hat{\rho }}_{d2} = \frac{{\psi^{2} }}{\gamma }( - {\text{e}}^{{ - \gamma \int {\left\|\upsigma \right\|} {\text{dt}}}} + 2{\text{e}}^{{ - 2\gamma \int {\left\|\upsigma \right\|} {\text{dt}}}} )(\gamma \left\| \sigma \right\|) $$

(21)

By substituting the terms $\hat{\rho }_{d2}$,$\dot{\hat{\rho }}_{d2}$, $\phi$ and $\dot{\phi }$ in Eq. (19), $\hat{\rho }_{d2}^{2} \phi \dot{\phi } + \hat{\rho }_{d2} \dot{\hat{\rho }}_{d2} \phi^{2}$ takes the following form:

$$ \hat{\rho }_{d2}^{2} \phi \dot{\phi } + \hat{\rho }_{d2} \dot{\hat{\rho }}_{d2} \phi^{2} = \frac{{\psi^{2} }}{\gamma }({\text{e}}^{{ - \gamma \int {\left\| {\,\sigma \,} \right\|} \;d{\kern 1pt} t}} - {\text{e}}^{{ - 2\gamma \int {\left\| {\,\sigma \,} \right\|} \;d{\kern 1pt} t}} )\left\| \sigma \right\| $$

(22)

Then, Eq. (19) becomes:

$$ \begin{aligned} \dot{V} &= Y^{T}_r \sigma \tilde{a} - \rho \parallel Y^{T}_r \sigma \parallel - Y^{T}_r \sigma p(t) + \hat{\rho }\parallel Y^{T}_r \sigma \parallel \hfill \\ & \quad - \sigma^{T} K_{D} \sigma - \sigma^{T} u_{d} + \sigma^{T} d - \rho_{d1} \left\| \sigma \right\| + \hat{\rho }_{d1} \left\| \sigma \right\| \hfill \\ & \quad + \frac{{\psi^{2} }}{\gamma }({\text{e}}^{{ - \gamma \int {\left\| {\,\sigma \,} \right\|} \;d{\kern 1pt} t}} - {\text{e}}^{{ - 2\gamma \int {\left\| {\,\sigma \,} \right\|} \;d{\kern 1pt} t}} )\left\| \sigma \right\| \hfill \\ \end{aligned} $$

(23)

where $\hat{\rho }_{d2} = \frac{{\psi^{2} }}{\gamma }({\text{e}}^{{ - \gamma \int {\left\| \sigma \right\|} dt}} - {\text{e}}^{{ - 2\gamma \int {\left\| \sigma \right\|} dt}} )$ and $\hat{\rho }{}_{d} = \hat{\rho }_{d1} + \hat{\rho }_{d2}$. Then, Eq. (23) can be written as:

$$ \begin{aligned} \dot{V} &= - \sigma^{T} K_{D} \sigma + \sigma^{T} Y_r\tilde{a} - \rho \parallel Y^{T}_r \sigma \parallel - \sigma^{T} Y_rp(t) \hfill \\ & \quad + \hat{\rho }\parallel Y^{T}_r \sigma \parallel - \sigma^{T} u_{d} + \sigma^{T} d - \rho_{d1} \left\| \sigma \right\| + \hat{\rho }_{d} \left\| \sigma \right\| \hfill \\ \end{aligned} $$

(24)

For stability analysis, 4 different cases are considered similar to studies in [30].

Case 1:

If $\left\| {Y^{T}_r \sigma } \right\| \ge \varepsilon_{p}$ and $\left\| \sigma \right\| \ge \varepsilon_{d}$. For the first case, control inputs are defined as $u_{d} = \frac{\sigma }{\left\| \sigma \right\|}\hat{\rho }_{d}$ and $(u_{p} ) = \frac{{Y^{T}_r \sigma }}{{\left\| {Y^{T}_r \sigma } \right\|}}\hat{\rho }$.

Then, Eq. (23) is obtained as:

$$ \begin{aligned} {\dot{\text{V}}} & \le - \sigma^{T} K_{D} \sigma + \sigma^{\text{T}} Y_r\tilde{a} - \rho \parallel Y^{T}_r \sigma \parallel - (Y^{T}_r \sigma )^{T} \frac{{Y^{T}_r \sigma }}{{\left\| {Y^{T}_r \sigma } \right\|}}\hat{\rho } \\ & \quad + \hat{\rho }\parallel Y^{T}_r \sigma \parallel + \left\| \sigma \right\|\hat{\rho }_{d} - \frac{{\sigma^{T} \sigma }}{\left\| \sigma \right\|}\hat{\rho }_{d} + \left\| \sigma \right\|( - \rho_{d} + \left\| d \right\|) \\ & \le - \sigma^{T} K_{D} \sigma + \left\| {Y^{T}_r \sigma } \right\|(\hat{\rho } - \hat{\rho }) + \left\| \sigma \right\|(\hat{\rho }_{d} - \hat{\rho }_{d} ) \le 0 \\ \end{aligned} $$

(25)

Since K_D is a positive definite matrix, the derivative of Lyapunov function will be $\dot{V} \le 0$. As a result, the system will be stable. Eq. (15) shows that V is a positive continuous function and V tends to a constant as $t \to \infty$ and therefore V remains bounded. Thus $\dot{\tilde{x}}$ and $\tilde{x}$ are bounded, that is, $\dot{\tilde{x}}$ and $\tilde{x}$ converge to zero and this implies that σ is bounded and converges to zero.

Case 2:

If $\left\| {Y^{T}_r \sigma } \right\| \ge \varepsilon_{p}$ and $\left\| \sigma \right\| \le \varepsilon_{d}$. For the second case, the control inputs are defined as $(u_{p} ) = \frac{{Y^{T}_r \sigma }}{{\left\| {Y^{T}_r \sigma } \right\|}}\hat{\rho }$ and $u_{d} = \frac{\sigma }{{\varepsilon_{d} }}\hat{\rho }_{d}$. Then, Eq. (23) is obtained as:

$$ \begin{aligned} \dot{V} & \le - \sigma^{T} K_{D} \sigma + \sigma^{\text{T}} Y_r\tilde{a} - \rho \parallel Y^{T}_r \sigma \parallel \\ & \quad - (Y^{T}_r \sigma )^{T} \frac{{Y^{T}_r \sigma }}{{\left\| {Y^{T}_r \sigma } \right\|}}\hat{\rho } + \hat{\rho }\parallel Y^{T}_r \sigma \parallel \\ & \quad + \left\| \sigma \right\|( - \rho_{d} + \left\| d \right\|) + \left\| \sigma \right\|\hat{\rho }_{d} - \sigma^{T} \frac{\sigma }{{\varepsilon_{d} }}\hat{\rho }_{d} \le 0 \\ & \le - \sigma^{T} K_{D} \sigma + \left\| \sigma \right\|(\hat{\rho }_{d} - \frac{\left\| \sigma \right\|}{{\varepsilon_{d} }}\hat{\rho }_{d} ) \le 0 \\ \end{aligned} $$

(26)

Note that the last term $\varepsilon \frac{{\hat{\rho }_{d} }}{4}$ reaches its maximum value when ||σ||=ε/2. Then, the following equation is defined:

$$ \dot{V} \le { - }\sigma^{\text{T}} K_{D} \sigma + \varepsilon \frac{{\hat{\rho }_{d} }}{4} $$

(27)

$$ \dot{V} \le 0 $$

if:

$$ \sigma^{T} K_{D} \sigma \ge \varepsilon_{d} \frac{{\hat{\rho }_{d} }}{4} $$

(28)

It is shown that $\dot{V} \le 0$ for ||σ|| where:

$$ \left\| \sigma \right\| \ge \sqrt {\frac{{\varepsilon \hat{\rho }_{d} }}{{4\delta_{\hbox{min} } (K_{D} )}}} $$

(29)

Case 3:

If $\left\| {Y^{T}_r \sigma } \right\| \le \varepsilon_{p}$ and $\left\| \sigma \right\| \ge \varepsilon_{d}$. The time derivative of the Lyapunov function is:

$$ \begin{aligned} \dot{V} & \le - \sigma^{T} K_{D} \sigma + \sigma^{\text{T}} Y_r\tilde{\pi } - (\sigma^{T} Y_r)\frac{{Y^{T}_r \sigma }}{{\varepsilon_{p} }}\hat{\rho } + \left\| \sigma \right\|\hat{\rho }_{d} - \frac{{\sigma^{T} \sigma }}{\left\| \sigma \right\|}\hat{\rho }_{d} \le 0 \\ & \le - \sigma^{T} K_{D} \sigma + \left\| {Y^{T}_r \sigma } \right\|(\hat{\rho } - \frac{{Y^{T}_r \sigma }}{{\varepsilon_{p} }}\hat{\rho }) \le 0 \\ \end{aligned} $$

(30)

The maximum term of the last Eq. (23) will be $\varepsilon_{p} \frac{{\hat{\rho }}}{4}$:

$$ \dot{V} \le - \sigma^{\text{T}} K_{D} \sigma + \varepsilon_{p} \frac{{\hat{\rho }}}{4} $$

(31)

The rest of the proof is the same as would be case 2.

Case 4:

If $\left\| {Y^{T}_r \sigma } \right\| \le \varepsilon_{p}$ and $\left\| \sigma \right\| \le \varepsilon_{d}$. For the fourth case, the Eq. (23) will be:

$$ \begin{aligned} \dot{V} & = - \sigma^{T} K_{D} \sigma + \sigma^{\text{T}} Y_r\hat{\rho } - (Y^{T}_r \sigma )^{T} \frac{{Y^{T}_r \sigma }}{{\varepsilon_{p} }}\hat{\rho } \\ & \quad - (Y^{T}_r \sigma )^{T} \frac{{\left\| {Y^{T}_r \sigma } \right\|}}{{\varepsilon_{p} }}\hat{\rho } + \left\| \sigma \right\|\hat{\rho }_{d} - \frac{{\sigma^{T} \sigma }}{{\varepsilon_{d} }}\hat{\rho }_{d} \le 0 \\ & \le - \sigma^{T} K_{D} \sigma + \left\| {Y^{T}_r \sigma } \right\|(\hat{\rho } - \frac{{\left\| {Y^{T}_r \sigma } \right\|}}{{\varepsilon_{p} }}\hat{\rho }) \\ & \quad + \left\| \sigma \right\|(\hat{\rho }_{d} - \frac{\left\| \sigma \right\|}{{\varepsilon_{d} }}\hat{\rho }_{d} ) \le 0 \\ \end{aligned} $$

(32)

The values $\left\| {Y^{T}_r \sigma } \right\|(\hat{\rho } - \frac{{\left\| {Y^{T}_r \sigma } \right\|}}{{\varepsilon_{p} }}\hat{\rho })$ and $\left\| \sigma \right\|(\hat{\rho }_{d} - \frac{\left\| \sigma \right\|}{{\varepsilon_{d} }}\hat{\rho }_{d} )$ are bounded by $\varepsilon_{p} \frac{{\hat{\rho }}}{4}$ and $\varepsilon_{d} \frac{{\hat{\rho }_{d} }}{4}$ respectively. Thus:

$$ \dot{V} \le { - }\sigma^{T} {\text{K}}_{D} \sigma + \varepsilon_{p} \frac{{\hat{\rho }}}{4} + \varepsilon_{d} \frac{{\hat{\rho }_{d} }}{4} \le 0 $$

(33)

Similar to the second and third cases, it is shown that $\dot{V} \le 0$ for ||σ|| where:

$$ \left\| \sigma \right\| \ge \sqrt {\frac{{\varepsilon_{p} \hat{\rho }}}{{4\delta_{\hbox{min} } K_{D} }} + \frac{{\varepsilon_{d} \hat{\rho }_{d} }}{{4\delta_{\hbox{min} } K_{D} }}} $$

(34)

2.2 FAM (Fuzzy Associative Memory) for determination of controller parameters

In 1965, [34] presented a study under the name of fuzzy logic theory. In this study, unlike the classical control methods, the control methods should have intermediate results besides absolute results. Then, Mamdani and Assilian [35] developed this controller and applied this law to small model steam engine. By means of fuzzy logic, intermediate values are expressed by membership functions. Membership functions can be expressed in geometric shapes such as triangles, bells and trapezes.

MAMDANI-type fuzzy inference and triangular membership functions are among the most commonly investigated types of fuzzy inference system. So, a Fuzzy Associative Memory (FAM) is developed within the framework of this technique. Fuzzy logic controller has following stages; fuzzification, rules and defuzzification. First, crisp input variables are converted into fuzzy values during fuzzification stage. Then, a relationship is specified based on membership functions using linguistic parameters and fuzzy inference system determines a rule between the input and output variables in rule evaluation stage. Finally, obtained fuzzy values are converted into crisp values in

defuzzification stage. In this study, $- \dot{e}/e$ is used as input and K_D, λ are used as output variables as can be seen from the block diagram of proposed controller presented in figure 1. Here, the acronym SF₁ stands for Scale Factor of input, SF_2λ and SF_2KD stand for Scale Factors of output variables. Earlier studies underline how controller parameters, e.g., slope constants, are found through the fuzzy logic controller [10], [36]. Membership functions for the fuzzy-logic input and output variables are given in figures 2 and 3, respectively.

Figure 1

Block diagram of proposed fuzzy-logic coefficient decision.

Figure 2

Membership functions for the fuzzy input variable.

Figure 3

Membership functions of K_D and λ.

Table 1 demonstrates the FAM (Fuzzy Associative Memory) in order to identify proper values of K_D and λ. Keep in mind that N denotes Negative, Z denotes Zero and P denotes Positive. Additionally, S denotes Small, M denotes Medium, B denotes Big, VS denotes Very Small and VB denotes Very Big for the fuzzy output variables. These membership functions can be read as, for instance; if $- \dot{e}/e$ is NB, then λ is M, K_D is M.

Table 1 FAM (Fuzzy Associative Memory) table

As a result, it will be verified whether the proposed control method satisfies all control measures. These measures are performance, applicability to non-linear systems, stability and the advantage of minimum system knowledge. Besides this controller improves the ride comfort without any negative effect on road holding and without causing any suspension working space degeneration. On the other hand, it must be noted that the success of the proposed controller is insensitive to system parameter changes and road surface disturbances.

3 Results and discussion

Application of Model-Reaching Adaptive Controller on a multi-degrees-of-freedom isolation platform and a half-car suspension system is given in [33]. Initially, some sensors are placed on the connecting points of each suspensions to the main platform (also known as upper ends). Then, one sensor measures the vertical velocity of suspension connecting point or upper end $\dot{x}$ while another sensor measures suspension gap or relative displacement $(x - x_{0} )$ to provide information for Eq. (1). This controller takes these two measurements as inputs and then generates controller force for actuators. Thus, angular motions are controlled, as well.

To sum up, vertical and all angular vibrations of a vehicle can be easily attenuated by using local suspension control [33].

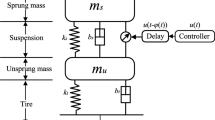
In this study, the active suspension system is controlled by the proposed new fuzzy adaptive controller on a seven-degrees-of-freedom vehicle making it robust to parametric uncertainties, unknown frictions and external disturbances. The seven-degrees-of-freedom full car model with active suspensions is shown in figure 4. The results are compared with that of the passive suspension system.

Figure 4

Full-car active suspension system.

It is crucial to note that each four suspensions are controlled within themselves independently as would be in model reaching adaptive control law [33]. A limited ramp road surface input is chosen since it gives a broad knowledge in understanding of suspension gap loss problem (see figure 5). In addition to this, it is worthwhile noting that the actuator is limited between ± 4000 N because of physical limitations [10].

Figure 5

Road surface input.

The parameters of full car model are given as follows. M: sprung mass, I_Ө: mass moment inertia of sprung mass for pitch motion, I_α: mass moment inertia of sprung mass for roll motion, m_i: unsprung mass, c_i: suspension damping coefficient, k_i: suspension stiffness coefficient, k_ti: tire stiffness coefficients, y: body bounce, Ө: pitch motion of vehicle body, α: roll motion of vehicle body, y_i: vertical displacement of unsprung mass, z_i: road surface input, u_i: controller force.

Note that i = 1, 2, 3, 4 front left, front right, rear left, rear right, respectively. Herein, x_1, x_2, x_3, x₄ denote front left, front right, rear left, rear right suspension upper ends motion, respectively and are given in Appendix A.

On the other hand, road surface input for front tires is given in figure 5. Note that road surface input for rear tires has the same height and slope as that of the front tires but has a time delay of Δt:

$$ \Delta t = \frac{{\left( {\text{a} + \text{b}} \right)}}{v} $$

(35)

where v denotes the vehicle velocity while a and b refer to distance from front and rear suspensions to the center of gravity of vehicle, respectively. One possible way to avoid suspension gap loss, a following reference signal is recommended [10]:

$$ x_{i,ref} = y_{i} .\frac{1}{\tau .s + 1} $$

(36)

where $\tau$ denotes a time constant, $x_{i, ref}$ denotes produced reference signal (i=1, 2, 3, 4). By following a smoothened unsprung mass displacement, suspension gap degeneration problem reaches a solution.

The suggested fuzzy robust-adaptive controller is applied on a full-car active suspension system. The controller gains are listed in Appendix B. Furthermore, numerical parameters of vehicle used in this study is presented in Appendix C.

In order to carry out simulations, a limited ramp road surface input is given in figure 5.

To better assess the effect of proposed controller on vehicle ride comfort, the results are compared with that of passive system and Multi-Input Single-Output (MISO) fuzzy logic controller (FLC) with well-known MAMDANI type inference. The error and the derivative of error are considered as the input variables of classical FLC and controller force as the output variable.

The FAM (Fuzzy Associative Memory) table used for FLC in order to determine the controller force is given in Appendix D and equations of motion for a full-car active suspension are given in Appendix E. The results are presented in figures 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15.

Figure 6

Body bounce and acceleration of sprung mass.

Figure 7

Pitch motion and acceleration of sprung mass.

Figure 8

Roll motion and acceleration of sprung mass.

Figure 9

Suspension displacements; (a) front left, (b) front right, (c) rear left, (d) rear right.

Figure 10

Controller force for actuators; (a) front left, (b) front right, (c) rear left, (d) rear right.

Figure 11

Frequency response of body bounce (a) and its acceleration (b).

Figure 12

Frequency response of pitch acceleration (a) and roll acceleration (b).

Figure 13

Frequency response of dynamic tire loads; (a) front left, (b) front right, (c) rear left and (d) rear right.

Figure 14

Comparative results with existing control methods; frequency response of body bounce (a) and its acceleration (b).

Figure 15

Frequency response of body bounce (a) and its acceleration (b) for different vehicle body masses.

The main objective of this study is to improve vehicle ride comfort by reducing the amplitudes of vibrations and their accelerations in the presence of model uncertainties and external disturbances.

For this purpose, body bounce, pitch and roll motions and related accelerations are given in figures 6, 7 and 8, respectively.

As can be seen from figures that amplitudes of displacements and accelerations are more significantly attenuated by proposed controller than that of passive system and FLC. It is important to note that the settling time for vibrations in actively controlled system are also remarkably reduced. Given the fact that the accelerations cause undesired forces on passengers, our technique shows a clear advantage on vibration insulation. Besides there happens no uncomfortable resonance around 5 Hz. The roll acceleration of the vehicle is remarkably decreased by proposed controller than the one of FLC.

The time histories for suspension displacements are given in figure 9. As illustrated in figure 9, suspensions do not lose their working spaces, namely they go to zero and keep their initial positions at the end of vibration. This implies that any lock on suspensions does not occurred. It is crucial to indicate that suspension lock problem has negative effects on passengers. In addition, it needs additional time to reach original working space dimensions for FLC. Thus, one can easily say that the proposed controller is more successful to keep suspension working space since it is considered in this study to evaluate controller performance on suspension gap degeneration problem.

Due to sharp changes on the controller force values also known as chattering phenomenon, the controller forces produced by actuators with regard to time should be taken into consideration. It is observed that no chattering happens which is harmful for mechanical components in figure 10.

In Automotive Engineering, final decision is reached by using frequency responses. Therefore, frequency responses will be checked now. In active suspension applications, the main aim is to suppress resonance frequency of vehicle main body which is at around 1 Hz without any deterioration in resonance frequency due to unsprung masses at around 10 Hz. Thus, it is said that the vehicle ride comfort is improved without any deterioration in road holding characteristics. For this purpose, frequency responses of body bounce, its acceleration, pitch and roll angular accelerations are given in figures 11 and 12. It is apparent from the figures that the resonance frequencies at around 1 Hz are significantly reduced by proposed controller.

Additionally, there are no significant deterioration observed in resonance frequencies at around 10 Hz. This implies that vehicle ride comfort is improved and we have obtained satisfactory results in terms of vehicle ride comfort. However, it is observed that FLC causes undesired resonance frequencies at higher levels which means uncomfortable ride for passengers even than the ride with conventional ordinary uncontrolled suspensions. A key problem with FLC on frequency responses is that it fails to fully suppress the resonance frequency of sprung mass. All observations indicate that the proposed method represents a valuable alternative to classical methods on fully suppression of undesired resonances at higher frequencies.

Since improving ride comfort and road holding are two conflicting criteria in vehicles, frequency responses of dynamic tire loads are evaluated as a main indicator for road holding character of a vehicle (see figure 13). The most remarkable result emerging from the figures is that vehicle ride comfort is increased by proposed controller without deterioration in road holding. As witnessed, uncomfortable resonances are shown up in the figures and our results show that these resonances do not vanish with FLC. This underlines just how successful proposed control method is.

Frequency responses of body bounce and vertical acceleration for an additional comparative results with existing classical control methods FLC and PID are given in figure 14. It is obvious from the figure that the proposed controller remarkably reduces the first resonance frequency which belongs to sprung mass on which passengers ride and at around 1 Hz. However, the undesired resonance frequencies are shown up at higher values by classical PID and Fuzzy controllers. During the simulations, it has been observed that the classical methods generate these undesired resonance frequencies at higher levels for different controller parameters. From this point of view, it is crucial to note that the proposed controller has significant role on reducing the resonance frequency of sprung mass without causing additional resonance frequencies at higher frequency levels when compared with classical ones. Thus, one can easily say that the improved vehicle ride comfort is guaranteed by proposed controller. Furthermore, the proposed controller can be applied on non-linear systems and it ensures the stability.

The mass of the vehicle may change or cannot be exactly known. These changes practically result in fuel consumption, additional payload or number of passengers, etc. Any parametric uncertainty on a system must not affect the controller performance. For that reason, the almost robust behavior of proposed controller for different values of sprung mass is presented in figure 15. As can be seen from figure that the proposed controller works well under the unexpected system parameter changes. The most remarkable result to emerge from this is that the success of proposed controller is insensitive to parameter changes.

4 Conclusions

The proposed controller consists of four control inputs. These are nominal control law, robust control law for bounded disturbances on model parameters, control input for external disturbances or suspension frictions and finally feedforward control law which has PD action on error. We have designed a new control law that estimates upper bound of parametric uncertainty whereas systems parameters themselves are estimated in the previous studies. Our research corroborates that uniform boundedness of the error is achieved by using Lyapunov Stability Theorem and Corless-Leitman approach.

The proposed approach was applied on a seven-degrees-of-freedom full-car active suspension system. It is worth to note that each suspensions or upper ends were controlled within themselves independently. Thus, vertical, pitch and roll vibrations of the vehicle can be remarkably reduced. A comparative study was carried out with FLC. It is clear from the figures that the vibration amplitudes of body bounce, pitch motion, roll motion and related accelerations are drastically attenuated by designed fuzzy robust-adaptive controller. As the research has demonstrated that vehicle ride comfort is improved by proposed control approach. Here, a limited ramp road surface input is used so as to see whether the proposed approach gives rise to suspension working space loss or not. The results of this study show that no suspension gap loss problem has been encountered. Finally, the time history of controller force values showed that the required actuator forces are held within reasonable ranges as in the literature and no chattering occurred. Thus, it is concluded that the suggested robust control approach can be applied successfully on vehicle active suspension systems which can highly improve the ride comfort without any degeneration in suspension working space and without losing the road holding character of the vehicle.

Appendices

Appendix A

Position definition of suspension upper ends.

x1 = y + a.sinӨ − c.sinα x2 = y + a.sinӨ + d.sinα x3 = y - b.sinӨ − c.sinα x1 = y - b.sinӨ + d.sinα

Appendix B

Controller parameters.

Parameters	Values
SF1	100
SF2KD	1
SF2λ	0.05
τ0	0.3
εd, εp	0.012
α1	0.975
γ	1
ψ	1
B1	10

Appendix C

Numerical parameters of full-car model.

Parameters	Values	Unit
M	1000	kg
IӨ	1600	kg.m2
Iα	1400	kg.m2
m1,m2,m3,m4	60	kg
c1,c2	1200	N/m/s
c3,c4	2000	N/m/s
k1,k2	16000	N/m
k3,k4	20000	N/m
kt1,kt2	150000	N/m
kt3,kt4	170000	N/m
v	20	m/s
a	1	m
b	1.2	m
c	0.7	m
d	0.8	m

Appendix D

FAM (Fuzzy Associative Memory) table for FLC.

e	${\dot{\text{e}}}$
	NB	NS	ZE	PS	PB
NB	NB	NB	NM	NS	ZE
NS	NB	NM	NS	ZE	PS
ZE	NM	NS	ZE	PS	PM
PS	NS	ZE	PS	PM	PB
PB	ZE	PS	PM	PB	PB

Appendix E

Equation of motion for full-car model:

$$ \left[ M \right]\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\ddot{x}} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f} \left( {x,\dot{x}} \right) + \left[ A \right]\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} = \left[ B \right]\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u} $$

where

$$ [M] = \left[ {\left. {\begin{array}{*{20}c} M & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {I_{\theta } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {I_{\alpha } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {m_{1} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {m_{2} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {m_{3} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {m_{4} } \\ \end{array} } \right]} \right.,\quad [A] = \left[ {\left. {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ { - k_{t1} } & 0 & 0 & 0 \\ 0 & { - k_{t2} } & 0 & 0 \\ 0 & 0 & { - k_{t3} } & 0 \\ 0 & 0 & 0 & { - k_{t4} } \\ \end{array} } \right]} \right.,\quad [B] = \left[ {\left. {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ \text{a} & \text{a} & { - \text{b}} & { - \text{b}} \\ { - \text{c}} & \text{d} & { - \text{c}} & \text{d} \\ { - 1} & 0 & 0 & 0 \\ 0 & { - 1} & 0 & 0 \\ 0 & 0 & { - 1} & 0 \\ 0 & 0 & 0 & { - 1} \\ \end{array} } \right]} \right. $$

$$ x = \left[ {\begin{array}{*{20}c} y & \theta & \alpha & {y_{1} } & {y_{2} } & {y_{3} } & {y_{4} } \\ \end{array} } \right]^{T} ,\quad u = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & {u_{3} } & {u_{4} } \\ \end{array} } \right]^{T} ,\quad z = \left[ {\begin{array}{*{20}c} {z_{1} } & {z_{2} } & {z_{3} } & {z_{4} } \\ \end{array} } \right]^{T} $$

$$ \begin{aligned} f(x,\dot{x}) = \left[ {\begin{array}{*{20}c} { + k_{1} \left( {y + \text{a}\sin {\kern 1pt} {\kern 1pt} \theta - \text{c}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{1} } \right){\kern 1pt} + k_{2} \left( {y + \text{a}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{2} } \right) + k_{3} \left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta - \text{c}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{3} } \right) + k_{4} \left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{4} } \right) \cdots } \\ { + \text{a}\cos \theta k_{1} \left( {y + \text{a}\sin \theta - \text{c}\sin \alpha - y_{1} } \right){\kern 1pt} + \text{a}\cos \theta k_{2} \left( {y + \text{a}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin \alpha - y_{2} } \right) - \text{b}\cos \theta k_{3} \left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta - \text{c}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{3} } \right) - \text{b}\cos \theta k_{4} \left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{4} } \right) \cdots } \\ { - \text{c}\cos \alpha k_{1} \left( {y + \text{a}\sin {\kern 1pt} {\kern 1pt} \theta - \text{c}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{1} } \right){\kern 1pt} \,{\kern 1pt} \, + \text{d}\cos \alpha k_{2} \left( {y + \text{a}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{2} } \right) - \text{c}\cos \alpha k_{3} \left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta - \text{c}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{3} } \right) + \text{d}\cos \alpha k_{4} \left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{4} } \right) \cdots } \\ { - k_{1} \left( {y + \text{a}\sin {\kern 1pt} {\kern 1pt} \theta - \text{c}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{1} } \right) + k_{t1} y_{1} - \text{c}_{1} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos \,{\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{1} } \right)} \\ { - k_{2} \,\left( {y + \text{a}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{2} } \right) + k_{t2} y_{2} - \text{c}_{2} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{2} } \right)} \\ { - k_{3} \,\left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta - \text{c}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{3} } \right) + k_{t3} y_{3} - \text{c}_{3} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{3} } \right)} \\ { - k_{4} \left( {y - \text{b}\sin {\kern 1pt} {\kern 1pt} \theta + \text{d}\sin {\kern 1pt} {\kern 1pt} \alpha - y_{4} } \right) + k_{t4} y_{4} - \text{c}_{4} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{4} } \right)} \\ \end{array} } \right. \hfill \\ \left. {\quad \begin{array}{*{20}c} { \cdots + \text{c}_{1} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos \,{\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{1} } \right) + \text{c}_{2} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{2} } \right) + \text{c}_{3} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{3} } \right) + \text{c}_{4} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{4} } \right)} \\ { \cdots + \text{a}\cos \theta \text{c}_{1} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos \,{\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{1} } \right) + \text{a}\cos \theta \text{c}_{2} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{2} } \right) - \text{b}\cos \theta \text{c}_{3} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{3} } \right) - \text{b}\cos \theta \text{c}_{4} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{4} } \right)} \\ { \cdots - \text{c}\cos \alpha \text{c}_{1} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos \,{\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{1} } \right) + \text{d}\cos \alpha \text{c}_{2} \left( {\dot{y} + \text{a}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{2} } \right) - \text{c}\cos \alpha \text{c}_{3} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } - \text{c}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{3} } \right) + \text{d}\cos \alpha \text{c}_{4} \left( {\dot{y} - \text{b}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \dot{\theta } + \text{d}\cos {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \dot{\alpha } - \dot{y}_{4} } \right)} \\ \end{array} } \right] \hfill \\ \end{aligned} $$