1 Introduction

As an essential part of the automotive chassis, the suspension systems are required to satisfy the significant demands of driving safety, handling stability and ride comfort. Generally speaking, suspension systems can be classified into passive suspensions, semi-active suspensions, and active suspensions [1,2,3]. It is worth mentioning that the active suspension has great advantages in terms of improving vehicle ride comfort and handling stability, because it can forwardly generate and adjust the required control force according to different driving conditions.

It should be pointed out that the vehicle system parameters constantly vary along with the change of the driving environment in practical applications. This inevitably causes the parameter uncertainties of the active suspension systems (ASSs) [4]. To effectively address the inherent uncertainties in ASSs, the interval type-2 (IT-2) fuzzy method has been proven as an excellent tool, owing to its prominent ability of capturing system uncertainties [5, 6]. An active levitation control system based on an interval IT-2 model-based fuzzy logic controller was investigated in [7]. Meanwhile, the suspension system is nonlinear due to the varying configuration. To deal with nonlinear systems, the Takagi–Sugeno (T–S) fuzzy model has been confirmed as a well-grounded method. For instance, the authors in [8] applied the T–S fuzzy method to explain the electrohydraulic ASSs with consideration of uncertain sprung mass and the control input. However, it is still challenging to handle the nonlinearity and uncertainties of the ASSs by an IT-2 T–S fuzzy model.

Apart from the construction of the ASSs model, the design of control strategy is also significant to refine the performance of the active suspension. Therefore, in recent ten years, researchers have proposed many feasible active suspension control strategies, such as sliding model control [9,10,11,12], adaptive control [13,14,15], and \(H_{\infty }\) control [16, 17]. The \(H_{\infty }\) control has been widely investigated by researchers due to its good robustness and anti-interference ability. In general, the \(H_{\infty }\) control can be divided into state feedback \(H_{\infty }\) control and the output feedback \(H_{\infty }\) control. Given that not all state vectors can be measured online, the state feedback controller is not feasible in actual suspension system. Compared with the state feedback controller , the structure of output feedback controller is simpler and easier to implement [18]. Furthermore, the traditional \(H_{\infty }\) control is based on the premise that the controller can be realized accurately. However, it should be noted that the controller will be affected by many uncertain factors in practice, such as the delay of the actuator and the aging of the corresponding equipment [19,20,21]. These uncertainties could cause fragility of the controller and further lead to the degradation of the closed-loop system performance. Hence, much effort was devoted to deal with the controller fragility issue for suspension control systems, such as safety assessment method [22], fault-tolerant [23] method, and non-fragile method [24]. Among them, the non-fragile methods that can resist interference have attracted scholars’ attention.

With the wide application of network communication technology in the field of vehicles, unlike the traditional point-to-point connection, the signal transmission delay may be an inevitable phenomenon due to the shared and band-limited channels of vehicle-mounted network [25]. The delay may lead to system oscillation and divergence in the operation of the active suspension system [26, 27]. Nevertheless, previous studies regard this time delay as a fixed value [28], or only confine the upper and lower limits of the time delay and set the lower limit as zero [29]. However, in fact, this network-induced delay is usually a random phenomenon. Since the data transmission in the process of network control always exists, its lower limit cannot be zero. Therefore, it is necessary to design a more practical representation method of the network-induced time delay.

Based on the above motivations, this paper proposes an IT-2 fuzzy \(H_{\infty }\) controller for the uncertain ASSs with stochastic network-induced delay. The major contributions of this research are listed as follows:

  1. (1)

    An IT-2 T–S fuzzy method is developed to construct the model of the suspension system with parameter uncertainties.

  2. (2)

    A variable substitution approach is employed to calculate the output feedback control gains to reduce the computational burden and ensure satisfactory system response.

  3. (3)

    A more generalized lumped delay form is adopted to present the stochasticity of the network-induced delay to improve system stability and control effectiveness.

The rest of this work is organized as follows: Sect. 2 establishes the uncertain active suspension model and formulates the control objective. Section 3 presents the non-fragile output feedback controller design method. Simulation and experimental results are illustrated in Sects. 4 and 5, respectively. Finally, Sect. 6 concludes this research.

Notation With regard to a matrix X, \(X^{-1}\) and \(X^T\) denote its inverse and transpose, respectively. \([X]_{\textrm{s}}\) denotes \(X+X^T\). The n-dimensional Euclidean space is denoted by \(R_n\). \(diag{\left\{ \cdot \right\} }\) denotes a block diagonal matrix.

Fig. 1
figure 1

Quarter-car automotive active suspension model

Full size image
Table 1 Symbol definitions of vehicle model
Full size table

2 Modeling and problem formulation

2.1 Quarter-car ASS model

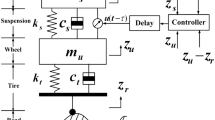
Figure 1 shows a common quarter-car active suspension model, and all symbol definitions of vehicle parameters are listed in Table 1. On the basis of the Newton’s second law, the vertical motion equations of suspension are acquired as:

$$\begin{aligned} \left\{ \begin{aligned}&m_{\textrm{s}} \ddot{z}_{\textrm{s}}(t)=-b_{\textrm{s}}\left( {\dot{z}}_{\textrm{s}}(t) \right. \\ {}&\left. -{\dot{z}}_{\textrm{u}}(t)\right) -k_{\textrm{s}}\left( z_{\textrm{s}}(t)-z_{\textrm{u}}(t)\right) +u(t) \\&m_{\textrm{u}} \ddot{z}_{\textrm{u}}(t)=-b_{\textrm{t}}\left( {\dot{z}}_{\textrm{u}}(t)-{\dot{z}}_{\textrm{r}}(t)\right) \\ {}&\quad -k_{\textrm{t}}\left( z_{\textrm{u}}(t)-z_{\textrm{r}}(t)\right) \\&\quad +b_{\textrm{s}}\left( {\dot{z}}_{\textrm{s}}(t)-{\dot{z}}_{\textrm{u}}(t)\right) +k_{\textrm{s}}\left( z_{\textrm{s}}(t)-z_{\textrm{u}}(t)\right) -u(t) \end{aligned}\right. \nonumber \\ \end{aligned}$$
(1)

Define \(x_{1}=z_{\textrm{s}}(t)-z_{\textrm{u}}(t)\), \(x_{2}={\dot{z}}_{\textrm{s}}(t)\), \(x_{3}=z_{\textrm{u}}(t)-z_{\textrm{r}}(t)\), \(x_{4}={\dot{z}}_{\textrm{u}}(t)\).

The equations of vehicle suspension system in (1) can be presented as:

$$\begin{aligned} {\dot{x}}(t)=A(t) x(t)+B_{\omega }(t) \omega (t)+B_{\textrm{u}}(t) u(t) \end{aligned}$$
(2)

where

$$\begin{aligned} \begin{aligned}&x(t)=\left[ \begin{array}{lllc} x_{1}&\quad x_{2}&\quad x_{3}&\quad x_{4} \end{array}\right] ^{T},\;\omega (t)={\dot{z}}_{\textrm{r}}(t), \\&A(t)=\left[ \begin{array}{cccc} 0 &{} \quad 1 &{} \quad 0 &{} \quad -1 \\ -\frac{k_{\textrm{s}}}{m_{\textrm{s}}(t)} &{} \quad -\frac{b_{\textrm{s}}}{m_{\textrm{s}}(t)} &{} \quad 0 &{} \quad \frac{b_{\textrm{s}}}{m_{\textrm{s}}(t)} \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 1 \\ \frac{k_{\textrm{s}}}{m_{\textrm{u}}(t)} &{} \quad \frac{b_{\textrm{s}}}{m_{\textrm{u}}(t)} &{} \quad -\frac{k_{\textrm{t}}}{m_{\textrm{u}}(t)} &{} \quad -\frac{b_{\textrm{s}}+b_{\textrm{t}}}{m_{\textrm{u}}(t)} \end{array}\right] , \\&B_{\omega }(t)=\left[ \begin{array}{c} 0\\ 0 \\ -1 \\ \frac{b_{\textrm{t}}}{m_{\textrm{u}}(t)} \end{array}\right] ,\; B_{\textrm{u}}(t)=\left[ \begin{array}{c} 0 \\ \frac{1}{m_{\textrm{s}}(t)} \\ 0 \\ \frac{-1}{m_{\textrm{u}}(t)} \end{array}\right] . \end{aligned} \end{aligned}$$

Considering that the aim of controller design is to enhance the ride comfort and guarantee the road holding ability, the controlled output can be expressed as:

$$\begin{aligned} \left\{ \begin{aligned}&z_{1}(t)=\ddot{z}_{\textrm{s}}(t) \\&z_{2}(t)=\left[ \frac{z_{\textrm{s}}(t)-z_{\textrm{u}}(t)}{z_{\max }} \frac{k_{\textrm{t}}\left( z_{\textrm{u}}(t)-z_{\textrm{r}}(t)\right) }{\left( m_{\textrm{s}}(t)+m_{\textrm{u}}(t)\right) g}\right] ^{\textrm{T}} \end{aligned}\right. \end{aligned}$$

As a result, (1) can be written as:

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{x}}(t)=A(t)x(t)+B_{\omega }(t) \omega (t)+B_{\textrm{u}}(t) u(t) \\&z_{1}(t)=C_{1}(t) x(t)+D_{1}(t) u(t) \\&z_{2}(t)=C_{2}(t) x(t) \end{aligned}\right. \end{aligned}$$
(3)

where \( \begin{aligned}&C_{1}(t)=\left[ \begin{array}{cccc} \frac{-k_{\textrm{s}}}{m_{\textrm{s}}(t)}&\quad -\frac{b_{\textrm{s}}}{m_{\textrm{s}}(t)}&\quad 0&\quad \frac{b_{\textrm{s}}}{m_{\textrm{s}}(t)} \end{array}\right] , \\ {}&D_{1}(t)=\frac{1}{m_{\textrm{s}}(t)}, \\&C_{2}(t)=\left[ \begin{array}{cccc} \frac{1}{z_{m a x}} &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \frac{k_{\textrm{t}}}{\left( m_{\textrm{s}}(t)+m_{\textrm{u}}(t)\right) g} \end{array}\right] . \end{aligned} \)

2.2 IT2-T–S model

With regard to uncertain variables \(m_{\textrm{s}}\left( t\right) \) and \(m_{\textrm{u}}\left( t\right) \), some assumptions are made as:

$$\begin{aligned} \begin{aligned}&m_{\textrm{s}}(t) \in \left[ m_{s \min }, m_{s \max }\right] ,&m_{\textrm{u}}(t) \in \left[ m_{u \min }, m_{u \max }\right] \end{aligned} \end{aligned}$$

For brevity, the fuzzy membership functions are listed in Table 2, and the following definitions are given as:

Table 2 Fuzzy membership functions
Full size table

These membership functions are plotted in Fig. 2.

Fig. 2
figure 2

Membership functions of the IT-2 fuzzy systems

Full size image

Thereafter, the uncertain nonlinear suspension system is expressed by the following IT-2 T–S fuzzy models.

Model Rule i: If \(\xi _1\left( t\right) \) is \(M_{i1}\left( \xi _1\left( t\right) \right) \), \(\xi _2\left( t\right) \) is \({\ M}_{i2}\left( \xi _2\left( t\right) \right) \), Then

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{x}}(t)=A_{i} x(t)+B_{\omega } \omega (t)+B_{u i} u(t) \\&z_{1}(t)=C_{1 i} x(t)+D_{1 i} u(t) \\&z_{2}(t)=C_{2 i} x(t) \end{aligned}\right. \end{aligned}$$
(4)

The interval set of the ith rule firing strength is as

$$\begin{aligned} {\tilde{g}}_{i}(\xi (t))=\left[ {\underline{g}}_{i}(\xi (t)), {\overline{g}}_{i}(\xi (t))\right] \end{aligned}$$

where \(\mathrm {f =1, 2,} \mathrm {i=1, 2, 3, 4},\;\xi \left( t\right) \) denotes the premise variables, \({{\underline{\mu }}}_{M_{if}}\left( \xi _f\left( t\right) \right) \) and \({{\overline{\mu }}}_{M_{if}}\left( \xi _f\left( t\right) \right) \) denote the lower membership function and upper membership function, \({\underline{g}}_{i}(\xi (t))=\prod _{f=1}^{4}{\underline{\mu }}_{M_{i f}}\left( \xi _{f}(t)\right) \) and \({\overline{g}}_{i}(\xi (t))=\prod _{f=1}^{4} {\overline{\mu }}_{M_{i f}}\) \(\left( \xi _{f}(t)\right) \) denote the lower grade of membership and upper grade of membership, and \(0 \le {\underline{\mu }}_{M_{if}}\left( \xi _{f}(t)\right) \le {\overline{\mu }}_{M_{if }}\left( \xi _{f}(t)\right) \), \({\underline{g}}_{i}(\xi (t)) \le {\overline{g}}_{i}(\xi (t))\). Then, the following definitions are given:

$$\begin{aligned} \begin{aligned}&g_{i}(\xi (t))={\underline{z}}_{i}(\xi (t)){\underline{g}}_{i}(\xi (t))+{\overline{z}}_{i}(\xi (t)) {\overline{g}}_{i}(\xi (t))\\&\underline{z_{i}}(\xi (t))+{\overline{z}}_{i}(\xi (t))=1\\&\sum _{i=1}^{4} g_{i}(\xi (t))=1 \end{aligned} \end{aligned}$$

Thus, the uncertain ASSs can be described as:

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{x}}(t)=\sum _{i=1}^{4} g_{i}(\xi (t))\left( A_{i} x(t)+B_{\omega {i}} \omega (t)+B_{u i} u(t)\right) \\&z_{1}(t)=\sum _{i=1}^{4} g_{i}(\xi (t))\left( C_{1 i} x(t)+D_{1 i} u(t)\right) \\&z_{2}(t)=\sum _{i=1}^{4} g_{i}(\xi (t))\left( C_{2 i} x(t)\right) \end{aligned}\right. \end{aligned}$$
(5)

where \(A_i\), \(B_{ui}\), \(C_{1i}\), \(D_{1i}\), \(C_{2i}\) are obtained by replacing \(\frac{1}{m_{\textrm{s}}\left( t\right) }\) and \(\frac{1}{m_{\textrm{u}}\left( t\right) }\), with (or and (or ) in A, \(B_{\textrm{u}}\), \(C_1\), \(D_1\), \(C_2\).

Then, for simplification, the system in (5) can be written as:

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{x}}(t)=A_{\textrm{s}} x(t)+B_{\omega s} \omega (t)+B_{u s} u(t) \\&z_{1}(t)=C_{1 s} x(t)+D_{1 s} u(t) \\&z_{2}(t)=C_{2 s} x(t) \end{aligned}\right. \end{aligned}$$
(6)

where

\(\begin{aligned}&A_{\textrm{s}}=\sum _{i=1}^{4} g_{i}(\xi (t)) A_{i}, B_{\omega s}=\sum _{i=1}^{4} g_{i}(\xi (t)) B_{\omega i}, \\&B_{u s}=\sum _{i=1}^{4} g_{i}(\xi (t)) B_{u i}, C_{1 s}=\sum _{i=1}^{4} g_{i}(\xi (t)) C_{1 i}, \\&D_{1 s}=\sum _{i=1}^{4} g_{i}(\xi (t)) D_{1 i}, C_{2 s}=\sum _{i=1}^{4} g_{i}(\xi (t)) C_{2 i}. \end{aligned}\)

Remark 1

It is worth noting that different from type-1 fuzzy method, the IT-2 fuzzy actual grades of membership \(g_i\left( \xi \left( t\right) \right) \) in (5) can be reconstructed as a linear combination of \({{\underline{g}}}_i\left( \xi \left( t\right) \right) \) and \({{\overline{g}}}_i\left( \xi \left( t\right) \right) \), characterized by the lower and upper membership functions \({{\underline{\mu }}}_{M_{is}}\left( \xi _{\textrm{s}}\left( t\right) \right) \) and \({{\overline{\mu }}}_{M_{is}}\left( \xi _{\textrm{s}}\left( t\right) \right) \), which are scaled by the nonlinear functions \({{\underline{z}}}_i\left( \xi \left( t\right) \right) \) and \({{\overline{z}}}_i\left( \xi \left( t\right) \right) \), respectively. This also means that IT-2 fuzzy sets consist of countless type 1 fuzzy sets. In other words, by using IT-2 fuzzy method, any membership function with uncertain parameters can be reconstructed by the upper and lower membership functions.

2.3 Non-fragile fuzzy controller with stochastic delay

Fig. 3
figure 3

Schematic diagram of the control-loop for the IT2 T–S fuzzy ASSs with stochastic network-induced delay

Full size image

Design of different membership functions for both the model and the controller is a challenging work without sufficient expert knowledge. However, with consideration of the model simplicity and controller effectiveness, fuzzy rules with the same membership functions are used for both the model and the controller. Figure 3 presents the schematic diagram of the control-loop for the IT2 T–S fuzzy ASSs with stochastic network-induced delay

Subsequently, a fuzzy controller is considered as follows:

Control Rule j: If \(\xi _1\left( t\right) \) is\(\ {M{\textrm{r}}}\left( \xi _1\left( t\right) \right) \), \(\xi _2\left( t\right) \) is\(\ N{\textrm{r}}\left( \xi _2\left( t\right) \right) \), Then

$$\begin{aligned} u(t)=\sum _{j=1}^{4}\left( g_{j}^{L}(\xi (t))+g_{j}^{U}(\xi (t))\right) K_{j} x(t) \end{aligned}$$
(7)

where

$$\begin{aligned} \begin{aligned}&g_{j}^{L}\xi (t)=\frac{g_{j}(\xi (t))}{\sum _{j=1}^{4}\left( {\underline{g}}_{j}(\xi (t))+{\overline{g}}_{j}(\xi (t))\right) }, \\&g_{j}^{U}\xi (t)=\frac{{\overline{g}}_{j}(\xi (t))}{\sum _{j=1}^{4}\left( {\underline{g}}_{j}(\xi (t))+{\overline{g}}_{j}(\xi (t))\right) }. \end{aligned} \end{aligned}$$

The perturbation of controller gain is represented by \(\Delta K(t)\) and it is presumed to be a multiplication form as:

$$\begin{aligned} \Delta K(t)=H F(t) E K \end{aligned}$$
(8)

where \(F\left( t\right) \) is an unknown continuous function with time-varying characteristics; H and E are the preset real constant matrices.

Thus, the fuzzy control input can be rewritten as:

$$\begin{aligned} u(t)=\sum _{j=1}^{4} g_{j}\left( \xi (t) K_{j}(1+H F(t) E) x(t)\right. \end{aligned}$$
(9)

where \(g_{j}(\xi (t))={\underline{g}}_{j}(\xi (t))+{\overline{g}}_{j}(\xi (t))\).

With the wide application of network communication technology in the field of vehicles, the signal transmission delay is a critical challenge. Due to the network-induced delay, the real controller can be depicted as:

$$\begin{aligned} u(t)= & {} \sum _{j=1}^{4} g_{j}(\xi (t)) K_{j}(1+H F(t) E) x\left( t_{k}-\varphi _{k}\right) , \nonumber \\{} & {} 0<t_{k+1}-t_{k}, \triangleq h_{k} \le h \end{aligned}$$
(10)

where \(t_k\le t<t_{k+1}\), \(t_k\) denotes the kth sampling instant, h denotes the sampling period, the local control gain of jth fuzzy controller is expressed by \(K_j\). The network-induced delay encountered at the sampling instant \(t_k\) is denoted as \(\varphi _k=\varphi _{\textrm{s}}+\varphi _c\), where\({\ \varphi }_{\textrm{s}}\) stands for the delay encountered in the sensor-to-controller link and \(\varphi _c\) stands for the delay encountered in the controller-to-actuator link. After defining \(\varphi \left( t\right) =t-t_k-\varphi _k\), the controller in (10) can be depicted as:

$$\begin{aligned} u(t)=\sum _{j=1}^{4} g_{j}(\xi (t)) K_{j}(1+H F(t) E) x\left( t-\varphi _{\textrm{t}}\right) \end{aligned}$$
(11)

In order to present a more generalized delay form, the randomness can be described as:

$$\begin{aligned} \begin{aligned}&{\text {prob}}\left\{ \varphi (t) \in \left[ 0, \varphi _{l}(t)\right] \right\} ={\text {prob}}\{\beta (t)=1\} ={\mathcal {E}}\{\beta (t)\}=\beta \\&{\text {prob}}\left\{ \varphi (t) \in \left[ \varphi _{l}(t)\varphi _{11}(t)\right] \right\} ={\text {prob}}\{\beta (t)=0\} =1-{\mathcal {E}}\{\beta (t)\} \\&\quad =1-\beta \end{aligned} \end{aligned}$$

where \(0<\varphi _l\left( t\right) <\varphi _{\textrm{u}}\left( t\right) \), \(\beta \left( t\right) \) is a stochastic variable satisfying Bernoulli random, and \(\ {\mathcal {E}}\left\{ \beta \left( t\right) \right\} \)denotes the mathematical expectation of\(\ \beta \left( t\right) \). Hence, the controller in (11) can be depicted as:

$$\begin{aligned} u(t)= & {} \sum _{j=1}^{4} g_{j}(\xi (t)) K_{j}(1+H F(t) E)\left( \beta (t) x\left( t-\varphi _{1}(t)\right) \right. \nonumber \\{} & {} +\left. (1-\beta (t)) x\left( t-\varphi _{2}(t)\right) \right) \end{aligned}$$
(12)

where \(\varphi _1(t)\) and \(\varphi _2(t)\) are defined as :

$$\begin{aligned} \begin{aligned}&\varphi _{1}(t)=\left\{ \begin{array}{ll} \varphi (t), &{} \quad \varphi (t) \in \left[ 0, \varphi _{l}\right] \\ 0, &{} \quad \varphi (t) \in \left( \varphi _{l}, \varphi _{\textrm{u}}\right] \end{array}\right. \\&\varphi _{2}(t)=\left\{ \begin{array}{ll} \varphi _{l}, &{} \quad \varphi (t) \in \left[ 0, \varphi _{l}\right] \\ \varphi (t), &{} \quad \varphi (t) \in \left( \varphi _{l}, \varphi _{\textrm{u}}\right] \end{array}\right. \end{aligned} \end{aligned}$$

Finally, by applying the non-fragile fuzzy controller in (15) to the fuzzy ASS in (5), the overall closed-loop system with parameter uncertainties and stochastic network-induced delay can be depicted as:

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{x}}(t)=f(t)+(\beta (t)-\beta ) g(t) \\&z_{1}(t)=C_{1 g} x(t)+\beta D_{1 g} K_{s f} x\left( t-\varphi _{1}(t)\right) \\&\quad +(1-\beta ) D_{1 g} K_{s f} x\left( t-\varphi _{2}(t)\right) \\&\quad +(\beta (t)-\beta )\left( D_{1 g} K_{s f} x\left( t-\varphi _{1}(t)\right) \right) \\&\quad -(\beta (t)-\beta )\left( D_{1 g} K_{s f} x\left( t-\varphi _{2}(t)\right) \right) \\&z_{2}(t)=C_{2 g} x(t) \end{aligned}\right. \end{aligned}$$
(13)

where

$$\begin{aligned} A_{g}= & {} \sum _{i=1}^{4} g_{i} A_{i}, B_{\omega g}=\sum _{i=1}^{4} g_{i} B_{\omega i},B_{u g}\\= & {} \sum _{i=1}^{4} g_{i} \sum _{j=1}^{4} g_{j} B_{u i}, \\ C_{1 g}= & {} \sum _{i=1}^{4} g_{i} C_{1 i}, C_{2 g}=\sum _{i=1}^{4} g_{i} C_{2 i}, D_{1 g}\\= & {} \sum _{i=1}^{4} g_{i} \sum _{j=1}^{4} g_{j} D_{1 i},\\ K_{s f}= & {} \sum _{j=1}^{4} K_{j}(1+H F(t) E),x(t) \\= & {} \phi (t), t \in \left( -2 \varphi _{\textrm{u}}, 0\right) ,\\ f(t)= & {} A_{g} x(t)+B_{\omega g} \omega (t) \\{} & {} +B_{u g} K_{s f}\left( \beta x\left( t-\varphi _{1}(t)\right) \right. \\{} & {} \left. \quad +(1-\beta ) x\left( t-\varphi _{2}(t)\right) \right) , \\ g(t)= & {} B_{u g} K_{s f}\left( x\left( t-\varphi _{1}(t)\right) -x\left( t-\varphi _{2}(t)\right) \right) . \end{aligned}$$

Briefly speaking, the objective of this work is to present a control strategy to compute a non-fragile fuzzy output feedback controller based on (12) for the IT2 T–S fuzzy ASSs. Then, the following conditions are satisfied:

  1. (1)

    The value of sprung mass acceleration needs to be minimal enough to improve ride comfort.

  2. (2)

    The closed-loop system in (13) is exponentially mean-square stable (EMSS) with the following \(\gamma \) attenuation level [30, 31].

  3. (3)

    The mechanical constraints of the T–S fuzzy system in (13) are guaranteed [32]:

$$\begin{aligned}{} & {} \left| \left\{ z_{2}(t)\right\} _{p}\right| \le 1, \quad p=1,2 \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \left| \frac{u(t)}{u_{\max }}\right| \le 1 \end{aligned}$$
(15)

where \(\left\{ z_2\left( t\right) \right\} _p\) represents the pth row vector of \(z_2(t)\), \(u_{\max }\) denotes the maximal actuator force.

After taking parameter uncertainties, controller fragile and stochastic delay into consideration, the closed-loop system in (13) is a stochastic system.

3 Main results

In this section, a novel non-fragile output feedback control algorithm is presented for uncertain ASSs with stochastic network-induced delay. This algorithm is efficient to ensure the stability and the expected performance indexes of the closed-loop system in (13).

3.1 Stability analysis

The following theorem proposed a set of sufficient conditions to guarantee that the closed-loop system in (13) is EMSS with \(\gamma \) attenuation level.

Theorem 1

Considering the closed-loop system in (13), for given scalars \(0<\varphi _l<\varphi _{\textrm{u}}\), \(\varphi _m=\varphi _{\textrm{u}}-\varphi _l\), \(\beta \in \left[ 0,1\right] \), \(\delta ^2=\beta (1-\beta )\) and \(\gamma \), if there exist positive definite matrices Q, \(P_1\), \(P_2\), \(Z_{11}\), \(Z_{12}\), \(Z_{21}\), \(Z_{22}\), and general matrices \(M_1\), \(M_2\), \(M_3\), \(M_4\), so that the following conditions hold, the closed-loop system in (13) is EMSS.

$$\begin{aligned} \Xi _{1}<0, \Xi _{2}<0 \end{aligned}$$
(16)
$$\begin{aligned} \Xi _{3}<0, \Xi _{4}<0 \end{aligned}$$
(17)
$$\begin{aligned} \left[ \begin{array}{cc} -Q &{} \quad \sqrt{\rho }\left\{ C_{2 i}\right\} _{q}^{T} \\ * &{} \quad -I \end{array}\right] <0 \end{aligned}$$
(18)
$$\begin{aligned} \left[ \begin{array}{cc} -I &{} \quad \frac{\sqrt{\rho } K_{s f}}{u \max } \\ * &{} \quad -Q \end{array}\right] <0 \end{aligned}$$
(19)

where

$$\begin{aligned}{} & {} \Xi _{1}=\left[ \begin{array}{lcc} \Phi &{} \quad \sqrt{\varphi _{l}}\left[ M_{1}, M_{1}\right] &{} \quad \sqrt{\varphi _{m}}\left[ M_{3}, M_{3}\right] \\ * &{} \quad -Z_{1} &{} \quad 0 \\ * &{} \quad * &{} \quad -Z_{2} \end{array}\right] , \\{} & {} \Xi _{2}=\left[ \begin{array}{ccc} \Phi &{} \quad \sqrt{\varphi _{l}}\left[ M_{1}, M_{1}\right] &{} \quad \sqrt{\varphi _{m}}\left[ M_{4}, M_{4}\right] \\ * &{} \quad -Z_{1} &{} \quad 0 \\ * &{} \quad * &{} \quad -Z_{2} \end{array}\right] , \\{} & {} \Xi _{3}=\left[ \begin{array}{ccc} \Phi &{} \quad \sqrt{\varphi _{l}}\left[ M_{2}, M_{2}\right] &{} \quad \sqrt{\varphi _{m}}\left[ M_{3}, M_{3}\right] \\ * &{} \quad -Z_{1} &{} \quad 0 \\ * &{} \quad * &{} \quad -Z_{2} \end{array}\right] ,\\{} & {} \Xi _{4}=\left[ \begin{array}{ccc} \Phi &{} \quad \sqrt{\varphi _{l}}\left[ M_{2}, M_{2}\right] &{} \quad \sqrt{\varphi _{m}}\left[ M_{4}, M_{4}\right] \\ * &{} \quad -Z_{1} &{} \quad 0 \\ * &{} \quad * &{} \quad -Z_{2}\\ \end{array}\right] , \end{aligned}$$
$$\begin{aligned} \begin{aligned} \Phi&=\Phi _{1}+\Phi _{2},\\ \Phi _{1}&={\text {diag}}\left( P_{1}+P_{2}, 0,-P_{1}, 0,-P_{2},-\gamma ^{2} I\right) \\&\quad +2\left[ N_{1}^{T} Q Y_{f}+M_{1} N_{2}+M_{2} N_{3}+M_{3} N_{4}+M_{4} N_{5}\right] ,\\ \Phi _{2}&=\left[ \begin{array}{ll} Y_{f}^{T}&\quad \delta Y_{g}^{T} \end{array}\right] \left[ \varphi _{l} Z_{1}+\varphi _{m} Z_{2}\right] \left[ \begin{array}{ll} Y_{f}^{T}&\quad \delta Y_{g}^{T} \end{array}\right] ^{T}\\&\quad +Z_{1 m}^{T} Z_{1 m}+Z_{2 m}^{T} Z_{2 m},\\ N_{1}&=\left[ \begin{array}{llllll} I&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array}\right] , \\ N_{2}&=\left[ \begin{array}{llllll} I&\quad -I&\quad 0&\quad 0&\quad 0&\quad 0 \end{array}\right] ,\\ N_{3}&=\left[ \begin{array}{llllll} 0&\quad I&\quad -I&\quad 0&\quad 0&\quad 0 \end{array}\right] , \\ N_{4}&=\left[ \begin{array}{llllrl} 0&\quad 0&\quad I&\quad -I&\quad 0&\quad 0 \end{array}\right] , \\ N_{5}&=\left[ \begin{array}{lllccc} 0&\quad 0&\quad 0&\quad I&\quad -I&\quad 0 \end{array}\right] , \\ Y_{f}&=\left[ \begin{array}{llllll} A_{g}&\quad B_{u g} K_{s f} \beta&\quad 0&\quad B_{u g} K_{s f}(1-\beta )&\quad 0&\quad B_{\omega g} \end{array}\right] ,\\ Y_{g}&=\left[ \begin{array}{llllll} 0&\quad B_{u g} K_{s f}&\quad 0&\quad -B_{u g} K_{s f}&\quad 0&\quad 0 \end{array}\right] ,\\ Z_{1 m}&=\left[ \begin{array}{llllll} C_{1 g}&\quad \beta D_{1 g} K_{s f}&\quad 0&\quad (1-\beta ) D_{1 g} K_{s f}&\quad 0&\quad 0 \end{array}\right] ,\\ Z_{2 m}&=\left[ \begin{array}{llllll} C_{2 g}&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{array}\right] ,\\ Z_{1}&=\left[ \begin{array}{cc} Z_{11} &{} \quad 0 \\ 0 &{} \quad Z_{12} \end{array}\right] , Z_{2}=\left[ \begin{array}{cc} Z_{21} &{} \quad 0 \\ 0 &{} \quad Z_{22} \end{array}\right] . \end{aligned} \end{aligned}$$

Proof

A Lyapunov function \(V\left( t\right) \) is chosen as follows:

$$\begin{aligned} \begin{aligned} V(t)&= x^{T}(t) Q x(t)+\int _{t-\varphi _{l}}^{t} x^{T}(\alpha ) P_{1} x(\alpha ) d \alpha \\&\quad +\int _{-\varphi _{l}}^{0} \int _{t+a}^{t}\left[ f^{T}(s), \delta g^{T}(s)\right] \\&\quad \times Z_{1}\left[ f^{T}(s), \delta g^{T}(s)\right] ^{T} d s \mathrm {~d} \alpha \\&\quad +\int _{-\varphi _{\textrm{u}}}^{-\varphi _{l}} \int _{t+a}^{t}\left[ f^{T}(s), \delta g^{T}(s)\right] \\&\quad \times Z_{2}\left[ f^{T}(s), \delta g^{T}(s)\right] ^{T} d s \mathrm {~d} \alpha \\&\quad +\int _{t-\varphi _{\textrm{u}}}^{t} x^{T}(\alpha ) P_{2} x(\alpha ) d \alpha \end{aligned} \end{aligned}$$
(20)

Then, the derivative is obtained as follows:

$$\begin{aligned} {\dot{V}}(t)= & {} 2 x^{T}(t) Q f(t)+x^{T}(t) P_{1} x(t)+x^{T}(t) P_{2} x(t) \nonumber \\{} & {} -x^{T}\left( t-\varphi _{l}\right) P_{1} x\left( t-\varphi _{l}\right) \nonumber \\{} & {} -x^{T}\left( t-\varphi _{\textrm{u}}\right) P_{2} x\left( t-\varphi _{\textrm{u}}\right) \nonumber \\{} & {} +\left[ f^{T}(t), \delta g^{T}(t)\right] \varphi _{l} Z_{1}\left[ f^{T}(t), \delta g^{T}(t)\right] ^{T} \nonumber \\{} & {} -\int _{t-\varphi _{l}}^{t}\left[ f^{T}(s), \delta g^{T}(s)\right] Z_{1}\left[ f^{T}(s), \delta g^{T}(s)\right] ^{T} d s \nonumber \\{} & {} +\left[ f^{T}(t), \delta g^{T}(t)\right] \varphi _{m} Z_{2}\left[ f^{T}(t), \delta g^{T}(t)\right] ^{T} \nonumber \\{} & {} -\int _{t-\varphi _{\textrm{u}}}^{t-\varphi _{l}}\left[ f^{T}(s), \delta g^{T}(s)\right] Z_{2}\left[ f^{T}(s), \delta g^{T}(s)\right] ^{T} d s\nonumber \\ \end{aligned}$$
(21)

According to the basic theorem of calculus, the following equalities hold:

$$\begin{aligned}{} & {} \begin{aligned}&x(t)-x\left( t-\varphi _{1}(t)\right) -\int _{t-\varphi _{1}}^{t} f(s) \\ {}&+g(s)(\beta (s)-\beta ) d s=0 \\ \end{aligned} \\{} & {} \begin{aligned}&x\left( t-\varphi _{1}(t)\right) -x\left( t-\varphi _{l}(t)\right) \\&\quad -\int _{t-\varphi _{l}}^{t-\varphi _{1}(t)} f(s)+g(s)(\beta (s)-\beta ) d s=0 \\ \end{aligned} \\{} & {} \begin{aligned}&x\left( t-\varphi _{l}(t)\right) -x\left( t-\varphi _{2}(t)\right) \\&\quad -\int _{t-\varphi _{2}(t)}^{t-\varphi _{l}} f(s)+ g(s)(\beta (s)-\beta ) d s=0 \\ \end{aligned} \\{} & {} \begin{aligned}&x\left( t-\varphi _{2}(t)\right) -x\left( t-\varphi _{\textrm{u}}\right) \\&\quad -\int _{t-\varphi _{\textrm{u}}}^{t-\varphi _{2}(t)} f(s)+g(s) (\beta (s)-\beta ) d s=0 \end{aligned} \end{aligned}$$

If the following equation is defined:

$$\begin{aligned} \begin{aligned} \xi ^{T}(t)=\left[ x^{T}(t), x^{T}\left( t-\varphi _{1}(t)\right) , x^{T}\left( t-\varphi _{l}\right) \right. \\ \left. x^{T}\left( t-\varphi _{2}(t)\right) , x^{T}\left( t-\varphi _{\textrm{u}}\right) , \omega ^{T}(t)\right] \end{aligned} \end{aligned}$$

the following equations can hold:

$$\begin{aligned} \begin{aligned}&2 \xi ^{T}(t) M_{1}\left[ x(t)-x\left( t-\varphi _{1}(t)\right) \right. \\&\quad -\int _{t-\varphi _{1}(t)}^{t} f(s)+g(s)(\beta (s)-\beta ) \left. d s\right] =0 \\&2 \xi ^{T}(t) M_{2}\left[ x\left( t-\varphi _{1}(t)\right) -x\left( t-\varphi _{l}(t)\right) \right. \\&\quad -\int _{t-\varphi _{3}}^{t-\varphi _{1}(t)} f(s)+g(s)(\beta (s)-\beta ) \left. d s\right] =0 \\&2 \xi ^{T}(t) M_{3}\left[ x\left( t-\varphi _{l}(t)\right) -x\left( t-\varphi _{2}(t)\right) \right. \\&\quad -\int _{t-\varphi _{2}(t)}^{t-\varphi _{1}} f(s)+g(s) (\beta (s)-\beta ) \left. d s\right] =0 \\&2 \xi ^{T}(t) M_{4}\left[ x\left( t-\varphi _{2}(t)\right) -x\left( t-\varphi _{11}\right) \right. \\&\quad -\int _{t-\varphi _{3}}^{t-\varphi _{2}(t)} f(s)+g(s) (\beta (s)-\beta ) \left. d s\right] =0 \end{aligned} \end{aligned}$$

Then, the following inequalities are obtained as:

$$\begin{aligned}{} & {} \begin{aligned}&2 \xi ^{T}(t) M_{1}\left[ x(t)-x\left( t-\varphi _{1}(t)\right) \right. \\&\qquad -\int _{t-\varphi _{1}(t)}^{t} f(s)+g(s)(\beta (s)-\beta ) \left. d s\right] \\&\quad \le \varphi _{1}(t) \xi ^{T}(t)\left[ M_{1}, M_{1}\right] Z_{1}^{-1}\left[ M_{1}, M_{1}\right] ^{T} \xi (t) \\ {}&\quad +\int _{t-\varphi _{1}(t)}^{t} \\&\left[ f^{T}(s),(\beta (s)-\beta ) g^{T}(s)\right] \\ {}&\quad \times Z_{1}\left[ f^{T}(s),(\beta (s)-\beta ) g^{T}(s)\right] ^{T} d s \\ \end{aligned}\\{} & {} \begin{aligned}&2 \xi ^{T}(t) M_{2}\left[ x\left( t-\varphi _{1}(t)\right) -x\left( t-\varphi _{l}(t)\right) \right. \\&\qquad -\int _{t-\varphi _{l}}^{t-\varphi _{1}(t)} f(s)+g(s)(\beta (s)-\beta ) \left. d s\right] \\&\quad \le \left( \varphi _{l}-\varphi _{1}(t)\right) \xi ^{T}(t)\left[ M_{2}, M_{2}\right] Z_{1}^{-1}\left[ M_{2}, M_{2}\right] ^{T} \\&\xi (t)+\int _{t-\varphi _{l}}^{t-\varphi _{1}(t)} \left[ f^{T}(s),(\beta (s)-\beta ) g^{T}(s)\right] \\&Z_{1}\left[ f^{T}(s),(\beta (s)-\beta ) \delta g^{T}(s)\right] ^{T} d s \\ \end{aligned} \\{} & {} \begin{aligned}&2 \xi ^{T}(t) M_{3}\left[ x\left( t-\varphi _{l}(t)\right) -x\left( t-\varphi _{2}(t)\right) \right. \\&\qquad -\int _{t-\varphi _{2}(t)}^{t-\varphi _{l}} f(s)+g(s)(\beta (s)-\beta ) \left. d s\right] \\&\quad \le \left( \varphi _{2}(t)-\varphi _{l}\right) \xi ^{T}(t)\left[ M_{3}, M_{3}\right] Z_{2}^{-1}\left[ M_{3}, M_{3}\right] ^{T} \\&\xi (t)+\int _{t-\varphi _{l}(t)}^{t t} \left[ f^{T}(s),(\beta (s)-\beta ) g^{T}(s)\right] \\&Z_{2}\left[ f^{T}(s),(\beta (s)-\beta ) g^{T}(s)\right] ^{T} d s \\ \end{aligned} \\{} & {} \begin{aligned}&2 \xi ^{T}(t) M_{4}\left[ x\left( t-\varphi _{2}(t)\right) -x\left( t-\varphi _{\textrm{u}}\right) \right. \\&\qquad -\int _{t-\varphi _{\textrm{u}}}^{t-\varphi _{2}(t)} f(s)+g(s)(\beta (s)-\beta ) \left. d s\right] \\&\quad \le \left( \varphi _{\textrm{u}}-\varphi _{2}(t)\right) \xi ^{T}(t)\left[ M_{4}, M_{4}\right] Z_{2}^{-1}\left[ M_{4}, M_{4}\right] ^{T} \\&\xi (t)+\int _{t-\varphi _{\textrm{u}}}^{t-\varphi _{2}(t)} \left[ f^{T}(s),(\beta (s)-\beta ) g^{T}(s)\right] \\&Z_{2}\left[ f^{T}(s),(\beta (s)-\beta ) g^{T}(s)\right] ^{T} d s \end{aligned} \end{aligned}$$

By taking the expectation of \({\dot{V}}\left( t\right) \), it gives:

$$\begin{aligned} \begin{aligned} \mathcal {E V}(t)&\le {\mathcal {E}}\left\{ \xi ^ { T } ( t ) \left[ {\hat{\Phi }}+\varphi _{1}(t)\left[ M_{1}, M_{1}\right] Z_{1}^{-1}\left[ M_{1}, M_{1}\right] ^{T}\right. \right. \\&\quad +\left( \varphi _{l}-\varphi _{1}(t)\right) \left[ M_{2}, M_{2}\right] Z_{1}^{-1}\left[ M_{2}, M_{2}\right] ^{T} \\&\quad +\left( \varphi _{2}(t)-\varphi _{l}\right) \left[ M_{3}, M_{3}\right] Z_{2}^{-1}\left[ M_{3}, M_{3}\right] ^{T} \\&\quad +\left. \left. \left( \varphi _{\textrm{u}}-\varphi _{2}(t)\right) \left[ M_{4}, M_{4}\right] Z_{2}^{-1}\left[ M_{4}, M_{4}\right] ^{T}\right] \xi (t)\right\} \end{aligned} \nonumber \\ \end{aligned}$$
(22)

Through applying Schur complement to (30), the following condition is true.

$$\begin{aligned} \varepsilon \left\{ z_{1}^{T}(t) z_{1}(t)-\gamma ^{2} \omega ^{T}(t) \omega (t)+{\dot{V}}(t)\right\} <0 \end{aligned}$$
(23)

According to Lemma 1 in [33], the closed-loop system in (13) is EMSS.

Under zero initial conditions, it can be obtained that \(V(0)=0\),\(V(\infty )\ge 0\), and \(\cdot {\mathcal {E}}\left\{ \left\| z_1(t)\right\| _2\right\} <\gamma {\mathcal {E}}\left\{ \Vert \omega (t)\Vert _2\right\} \) for all nonzero \( \omega (t) \in L 2[0, \infty ]\). Hence, the closed-loop system in (13) satisfies the desired \( H_{\infty }\) robust requirement.

Based on (23), the following inequality is obtained:

$$\begin{aligned} {\dot{V}}(t)-\gamma ^{2} w^{T}(t) w(t)<0 \end{aligned}$$

Integrating two sides of the above inequality from zero to any \(t>0\), it can be acquired as:

$$\begin{aligned} V(t)-V(0)<\gamma ^{2} \int _{0}^{t} w^{T}(\tau ) w(\tau ) \textrm{d} \tau <\gamma ^{2}\Vert w\Vert _{2}^{2} \end{aligned}$$

Thus, the following inequality is obtained:

$$\begin{aligned} x^{T}(t) Q x(t)<\gamma ^{2} \omega _{\max }+V(0) \end{aligned}$$

Defining \(\gamma ^2\omega _{\max }+V\left( 0\right) =\rho \), the following inequality holds as:

$$\begin{aligned} \begin{aligned}&\max _{t>0}\left| \left\{ z_{2}(t)\right\} _{q}\right| ^{2} \le \max _{t>0}\left\| \sum _{i=1}^{4} h_{i} x^{T}(t) Q^{\frac{1}{2}}\right. \\&Q^{\frac{-1}{2}}\left\{ C_{2 i}\right\} _{q}^{T}\left\{ C_{2 i}\right\} _{q} Q^{\frac{1}{2}} Q^{\frac{-1}{2}} \left. x(t)\right\| _{2} \end{aligned} \end{aligned}$$

It leads to that the constraints in (14) are guaranteed, if

$$\begin{aligned} \rho \cdot \sum _{i=1}^{4} h_{i} Q^{-\frac{1}{2}}\left\{ C_{2 i}\right\} _{q}^{T}\left\{ C_{2 i}\right\} _{q} Q^{-\frac{1}{2}}<I \end{aligned}$$
(24)

Through applying Schur complement to (20), the following inequality is obtained as:

$$\begin{aligned} \frac{\rho x(t) K_{s f} K_{s f}^{T} x^{T}(t)}{u_{\max }^{2}}<x(t) Q x^{T}(t)<\rho \end{aligned}$$

which means the constraints in (15) are guaranteed. Thus, the proof is completed.

3.2 The state feedback control design

Taking gain perturbations into account, the following theorem is obtained based on Theorem 1 to calculate the desired state feedback controller gains.

Theorem 2

Considering the closed-loop system in (13), with regard to given scalars \(\gamma \), \(0<\varphi _{l}<\varphi _{\textrm{u}}\), \(\varphi _{m}=\varphi _{\textrm{u}}-\varphi _{l}\), \(\beta \in [0,1]\), \(\delta ^{2}=\beta (1-\beta )\), and \(\Delta Kx(t)<\Delta u_{\max }\), the closed-loop system in (13) is EMSS, if there exist positive definite matrices P, \({\overline{P}}\), \(\breve{P}_{1}\), \(\breve{P}_{2}\), \(\breve{Z}_{1}\), \(\breve{Z}_{2}\), and general matrices \(\breve{M}_{1}\), \(\breve{M}_{2}\), \(\breve{M}_{3}\), \(\breve{M}_{4}\), such that the following conditions apply to i, \(j=1, 2, 3, 4\).

$$\begin{aligned} \left[ \begin{array}{cc} \breve{\Xi }_{1 i j} &{} \quad \Pi \\ * &{} \quad \Lambda \end{array}\right]<0,\left[ \begin{array}{cc} \breve{\Xi }_{2 i j} &{} \quad \Pi \\ * &{} \quad \Lambda \end{array}\right] <0 \end{aligned}$$
(25)
$$\begin{aligned} \left[ \begin{array}{cc} \breve{\Xi }_{3 i j} &{} \quad \Pi \\ * &{} \quad \Lambda \end{array}\right]<0,\left[ \begin{array}{cc} \breve{\Xi }_{4 i j} &{} \quad \Pi \\ * &{} \quad \Lambda \end{array}\right] <0 \end{aligned}$$
(26)
$$\begin{aligned} \left[ \begin{array}{cc} -I &{} \quad \sqrt{\rho }\left\{ C_{2 i}\right\} _{q} P \\ * &{} \quad -P \end{array}\right] <0 \end{aligned}$$
(27)
$$\begin{aligned} \left[ \begin{array}{cc} -I &{} \quad \frac{\sqrt{\rho } V_{j}}{u_{\max }-\Delta u_{\max }} \\ * &{} \quad -{\bar{P}} \end{array}\right] <0 \end{aligned}$$
(28)

Moreover, the state feedback controller gains are achieved as:

$$\begin{aligned} K_{sf}^i=V_jP^{-1} \end{aligned}$$

where

$$\begin{aligned}{} & {} \breve{\Xi }_{1 i j}=\left[ \begin{array}{cccc}\breve{\Phi } &{} \quad \sqrt{\varphi _{l}}\left[ \breve{M}_{1}, \breve{M}_{1}\right] &{} \quad \sqrt{\varphi _{m}}\left[ \breve{M}_{3}, \breve{M}_{3}\right] &{} \quad \breve{\Gamma }_{1} \\ * &{} \quad \breve{Z}_{1}-2 \breve{\textrm{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad \breve{\textrm{Z}}_{1}-2 \breve{\textrm{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad \breve{\Gamma }_{2}\end{array}\right] ,\\{} & {} \breve{\Xi }_{2 i j}=\left[ \begin{array}{cccc}\breve{\Phi } &{} \quad \sqrt{\varphi _{l}}\left[ \breve{M}_{1}, \breve{M}_{1}\right] &{} \quad \sqrt{\varphi _{m}}\left[ \breve{M}_{4}, \breve{M}_{4}\right] &{} \quad \breve{\Gamma }_{1} \\ * &{} \quad \breve{\textrm{Z}}_{1}-2 \check{\textrm{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad \breve{\textrm{Z}}_{1}-2 \breve{\textrm{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad \breve{\Gamma }_{2}\end{array}\right] ,\\{} & {} \breve{\Xi }_{3 i j}=\left[ \begin{array}{cccc}\breve{\Phi } &{} \quad \sqrt{\varphi _{l}}\left[ \breve{M}_{2}, \breve{M}_{2}\right] &{} \quad \sqrt{\varphi _{m}}\left[ \breve{M}_{3}, \breve{M}_{3}\right] &{} \quad \breve{\Gamma }_{1} \\ * &{} \quad \breve{Z}_{1}-2\breve{\textrm{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad \breve{Z}_{1}-2 \breve{\textrm{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad \breve{\Gamma }_{2}\end{array}\right] ,\\{} & {} \breve{\Xi }_{4 i j}=\left[ \begin{array}{cccc}\breve{\Phi } &{} \quad \sqrt{\varphi _{l}}\left[ \breve{M}_{2}, \breve{M}_{2}\right] &{} \quad \sqrt{\varphi _{m}}\left[ \breve{M}_{4}, \breve{M}_{4}\right] &{} \quad \breve{\Gamma }_{1} \\ * &{} \quad \breve{Z_{1}}-2 \breve{\textrm{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad \breve{\textrm{Z}}_{1}-2 \breve{\textrm{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad \breve{\Gamma }_{2}\end{array}\right] \\{} & {} \Pi =\left[ \begin{array}{ll}\Pi _{1}&\quad \Pi _{2}\end{array}\right] ,\\{} & {} \Pi _{1}=\left[ \begin{array}{cc}\varepsilon _{1} B_{\textrm{u g}} H F &{} \quad 0 \\ 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ \varepsilon _{1} \sqrt{\varphi _{l}} B_{\textrm{u g}} H F &{} \quad 0 \\ 0 &{} \quad \varepsilon _{2 \sqrt{\varphi }} \delta B_{\textrm{u g}} H F \\ \varepsilon _{1} \sqrt{\varphi _{l}} B_{\textrm{u g}} H F &{} \quad 0 \\ 0 &{} \quad \varepsilon _{2} \sqrt{\varphi _{m}} \delta B_{u g} H F \\ \varepsilon _{1} D_{l i} H F &{} \quad 0\end{array}\right] ,\\{} & {} \Pi _{2}=\left[ \begin{array}{cc}0 &{} \quad 0 \\ \beta \left( E V_{j}\right) ^{T} &{} \quad \left( E V_{j}\right) ^{T} \\ 0 &{} \quad 0 \\ (1-\beta )\left( E V_{j}\right) ^{T} &{} \quad -\left( E V_{j}\right) ^{T} \\ 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ 0 &{} \quad 0\end{array}\right] ,\\{} & {} \Lambda ={\text {diag}}\left( -\varepsilon _{1} I,-\varepsilon _{2} I,-\varepsilon _{1} I,-\varepsilon _{2} I,-\varepsilon _{1} I,-\varepsilon _{2} I\right) ,\\{} & {} \breve{\Phi }={\text {diag}}\left( \breve{\textrm{P}}_{1}+\breve{\textrm{P}}_{2}, 0,-\breve{\textrm{P}}_{1}, 0,-\breve{\textrm{P}}_{2},-\gamma ^{2} I\right) ,\\{} & {} +{\text {sym}}\left[ N_{1}^{T} \breve{Y}_{f}+\breve{M}_{1} N_{2}+\breve{M}_{2} N_{3}+\breve{M}_{3} N_{4}+\breve{M}_{4} N_{5}\right] ,\\{} & {} \breve{\Gamma }_{2}={\text {diag}}\left( \begin{array}{lllll}-\breve{Z}_{11}&\quad -\breve{Z}_{12}&\quad -\breve{Z}_{21}-\breve{Z}_{22}&\quad -I&\quad -I\end{array}\right) ,\\{} & {} \breve{Y}_{f}=\left[ \begin{array}{llllll}A_{i} P&\quad B_{u i} V_{j} \beta&\quad 0&\quad B_{u i} V_{j}(1-\beta )&\quad 0&\quad B_{\omega i}\end{array}\right] \\{} & {} \breve{Y}_{g}=\left[ \begin{array}{llllll}0&\quad B_{u i} V_{j}&\quad 0&\quad -B_{u i} V_{j}&\quad 0&\quad 0\end{array}\right] ,\\{} & {} \breve{Z}_{1 m}=\left[ \begin{array}{llllll}C_{1 i} P&\quad \beta D_{1 i} V_{j}&\quad 0&\quad (1-\beta ) D_{1 i} V_{j}&\quad 0&\quad 0\end{array}\right] ,\\{} & {} \breve{Z}_{2 m}=\left[ \begin{array}{llllll}C_{2 i} P&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\end{array}\right] ,\\{} & {} \breve{Z}_{1}=\left[ \begin{array}{cc}\breve{Z}_{11} &{} \quad 0 \\ 0 &{} \quad \breve{Z}_{12}\end{array}\right] , \breve{P}=\left[ \begin{array}{ll}P &{} \quad 0 \\ 0 &{} \quad P\end{array}\right] ,\\{} & {} \breve{Z}_{2}=\left[ \begin{array}{cc}\breve{Z}_{21} &{} \quad 0 \\ 0 &{} \quad \breve{Z}_{22}\end{array}\right] . \end{aligned}$$

Proof

The following conditions are defined as:

$$\begin{aligned} \begin{aligned}&\breve{Z}_{1}=Z_{1}^{-1},\ \breve{Z}_{2}=Z_{2}^{-1} \\&P=Q^{-1},\ V=K_{s f} P,\ {\bar{P}}=P^{T} Q P \\&\breve{M}_{1}=P M_{1} P, \quad \breve{M}_{2}=P M_{2} P \\&\breve{M}_{3}=P M_{3} P, \quad \breve{M}_{4}=P M_{4} P \\&\Theta ={\text {diag}}\left( P_{n} I P P P P I_{\textrm{s}}\right) ,n=6,s=8. \end{aligned} \end{aligned}$$

After replacing the corresponding matrix in (25) and (26), followed by pre-multiplying and post-multiplying (25) and (26) by diagonal matrix \(\mathrm {\Theta }\). (16) and (17) are then obtained by replacing \({\breve{Z}}_k-2\breve{P}\) to \(-\breve{P}{\breve{Z}}_k^{-1}\breve{P}\), where \( k=1, 2 \). Thus, Theorem 2 is obtained.

Remark 2

\(\Delta Kx(t)<\Delta u_{\max }\) is the bound of gain perturbations \(\Delta K(t)\). Considering the fragility of the controller, the gain perturbation \(\Delta K(t)\) is introduced into Theorems 2–3 to improve the anti-interaction ability of the suspension controller, but the gain perturbations are not infinite. Referring to [34], the bound is assumed as \(\Delta Kx(t)<\Delta u_{\max }\).

3.3 The output feedback control design

The measured output vector is defined as follows:

$$\begin{aligned} y(t)=C x(t) \end{aligned}$$
(29)

where

$$\begin{aligned} C=\left[ \begin{array}{llll} 1 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 1 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 1 \end{array}\right] . \end{aligned}$$

According to the relationship between state feedback and output feedback, the following equality holds [35]:

$$\begin{aligned} K_{s f}=K_{s o f} C=VP^{-1} \end{aligned}$$
(30)

The following equations are also defined as:

$$\begin{aligned} \begin{aligned}&P=S P_{N} S^{T}+R P_{R} R^{T} \\&V=V_{R} R^{T} \\&R=C^{\dagger }+S L \end{aligned} \end{aligned}$$

where \(K_{s f}\) denotes the feedback control gains, \(K_{s o f}\) denotes the output feedback control gain, \(P_{N}, P_{R}\) are positive definite matrices, S is the null space of C, L is an arbitrary matrix.

Based on (25)–(30), a non-fragile output feedback controller is presented in the following theorem.

Theorem 3

Considering the closed-loop system in (13), for given scalars \(\gamma \), \(0<\varphi _{l}<\varphi _{\textrm{u}}\), \(\varphi _{m}=\varphi _{\textrm{u}}-\varphi _{l}\), \(\beta \in [0,1]\), \(\delta ^{2}=\beta (1-\beta )\) and \(\Delta K x(\textrm{t})<\Delta u_{\text{ max } }\), the closed-loop system in (13) is EMSS, if there exist positive definite matrices \({\bar{Q}}\), \( {\bar{P}}_{1}\), \({\bar{P}}_{2}\), \({\bar{Z}}_{1}\), \({\bar{Z}}_{2}\), and general matrices \({\bar{M}}_{1}\), \({\bar{M}}_{2}\), \({\bar{M}}_{3}\), \({\bar{M}}_{4}\), such that the following conditions hold true for \(i,\ j=1, 2, 3, 4\).

$$\begin{aligned} \left[ \begin{array}{cc} {\bar{E}}_{1 i j} &{} \quad {\bar{\Pi }} \\ * &{} \quad \Lambda \end{array}\right]<0, \quad \left[ \begin{array}{cc} {\bar{\Xi }}_{2 i j} &{} \quad {\bar{\Pi }} \\ * &{} \quad \Lambda \end{array}\right] <0 \end{aligned}$$
(31)
$$\begin{aligned} \left[ \begin{array}{cc} {\bar{\Xi }}_{3 i j} &{} \quad {\bar{\Pi }} \\ * &{} \quad \Lambda \end{array}\right]<0, \quad \left[ \begin{array}{cc} {\bar{\Xi }}_{4 i j} &{} \quad {\bar{\Pi }} \\ * &{} \quad \Lambda \end{array}\right] <0 \end{aligned}$$
(32)
$$\begin{aligned} \left[ \begin{array}{c} -\left( S P_{N} S^{T}+R P_{R} R^{T}\right) \nonumber \\ * \end{array}\right. \\ \left. \begin{array}{c} \sqrt{\rho }\left( S P_{N} S^{T}+R P_{R} R^{T}\right) \left\{ C_{2 i}\right\} _{q}^{T}\\ -I \end{array}\right] <0 \end{aligned}$$
(33)
$$\begin{aligned} \left[ \begin{array}{cc} -I &{} \quad \frac{\sqrt{\rho } R V_{R i}^{T}}{u_{\max }-\Delta u_{\max }} \\ * &{} \quad S P_{N} S^{T}+R P_{R} R^{T} \end{array}\right] <0 \end{aligned}$$
(34)

Moreover, the output feedback controller gains are obtained as:

$$\begin{aligned} K_{s o f}^{i}=V_{R j} P_{R}^{-1} \end{aligned}$$

where

$$\begin{aligned}{} & {} {\bar{\Xi }}_{1 i j}=\left[ \begin{array}{cccc}{\bar{\Phi }} &{} \quad \sqrt{\varphi _{l}}\left[ {\bar{M}}_{1}, {\bar{M}}_{1}\right] &{} \quad \sqrt{\varphi _{m}}\left[ {\bar{M}}_{3}, {\bar{M}}_{3}\right] &{} \quad {\bar{\Gamma }}_{1} \\ * &{} \quad {\bar{Z}}_{1}-2 {\bar{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad {\bar{Z}}_{2}-2 {\bar{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad {\bar{\Gamma }}_{2}\end{array}\right] ,\\{} & {} {\bar{\Xi }}_{2 i j}=\left[ \begin{array}{cccc}{\bar{\Phi }} &{} \quad \sqrt{\varphi _{i}}\left[ {\bar{M}}_{1}, {\bar{M}}_{1}\right] &{} \quad \sqrt{\varphi _{m}}\left[ {\bar{M}}_{4}, {\bar{M}}_{4}\right] &{} \quad {\bar{\Gamma }}_{1} \\ * &{} \quad {\bar{Z}}_{1}-2 {\bar{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad {\bar{Z}}_{2}-2 {\bar{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad {\bar{\Gamma }}_{2}\end{array}\right] ,\\{} & {} {\bar{\Xi }}_{3 i j}=\left[ \begin{array}{cccc}{\bar{\Phi }} &{} \quad \sqrt{\varphi _{l}}\left[ {\bar{M}}_{2}, {\bar{M}}_{2}\right] &{} \quad \sqrt{\varphi _{m}}\left[ {\bar{M}}_{3}, {\bar{M}}_{3}\right] &{} \quad {\bar{\Gamma }}_{1} \\ * &{} \quad {\bar{Z}}_{1}-2 {\bar{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad {\bar{Z}}_{2}-2 {\bar{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad {\bar{\Gamma }}_{2}\end{array}\right] ,\\{} & {} {\bar{\Xi }}_{4 i j}=\left[ \begin{array}{cccc}{\bar{\Phi }} &{} \quad \sqrt{\varphi _{l}}\left[ {\bar{M}}_{2}, {\bar{M}}_{2}\right] &{} \quad \sqrt{\varphi _{m}}\left[ {\bar{M}}_{4}, {\bar{M}}_{4}\right] &{} \quad {\bar{\Gamma }}_{1} \\ * &{} \quad {\bar{Z}}_{1}-2 {\bar{P}} &{} \quad 0 &{} \quad 0 \\ * &{} \quad * &{} \quad {\bar{Z}}_{2}-2 {\bar{P}} &{} \quad 0 \\ * &{} \quad * &{} \quad * &{} \quad {\bar{\Gamma }}_{2}\end{array}\right] ,\\{} & {} {\bar{\Pi }}=\left[ \begin{array}{ll}{\bar{\Pi }}_{1}&\quad {\bar{\Pi }}_{2}\end{array}\right] ,\\{} & {} {\bar{\Pi }}_{1}=\left[ \begin{array}{cc}\varepsilon _{1} B_{\textrm{u g}} H F &{} \quad 0 \\ 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ \varepsilon _{1} \sqrt{\varphi _{l}} B_{\textrm{u g}} H F &{} \quad 0 \\ 0 &{} \quad \varepsilon _{2 \sqrt{\varphi }} \delta B_{\textrm{u g}} H F \\ \varepsilon _{1} \sqrt{\varphi _{l}} B_{\textrm{u g}} H F &{} \quad 0 \\ 0 &{} \quad \varepsilon _{2} \sqrt{\varphi _{m}} \delta B_{u g} H F \\ \varepsilon _{1} D_{l i} H F &{} \quad 0\end{array}\right] ,\\{} & {} {\bar{\Pi }}_{2}=\left[ \begin{array}{cc}0 &{} \quad 0 \\ \beta \left( E V_{R j} R^{T}\right) ^{T} &{} \quad \left( E V_{R j} R^{T}\right) ^{T} \\ 0 &{} \quad 0 \\ (1-\beta )\left( E V_{R j} R^{T}\right) ^{T} &{} \quad -\left( E V_{R j} R^{T}\right) ^{T} \\ 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ 0 &{} \quad 0\end{array}\right] ,\\{} & {} {\bar{\Phi }}={\text {diag}}\left( {\bar{P}}_{1}+{\bar{P}}_{2}, 0,-{\bar{P}}_{1}, 0,-{\bar{P}}_{1},-\gamma ^{2} I\right) ,\\{} & {} +{\text {sym}}\left[ N_{1}^{T} {\bar{Y}}_{f}+{\bar{M}}_{1} N_{2}+{\bar{M}}_{2} N_{3}+{\bar{M}}_{3} N_{4}+{\bar{M}}_{4} N_{5}\right] ,\\{} & {} {\bar{\Gamma }}_{2}={\text {diag}}\left( -{\bar{Z}}_{11}-{\bar{Z}}_{12}-{\bar{Z}}_{21}-{\bar{Z}}_{22} \quad -I-I\right) ,\\{} & {} \begin{aligned} {\bar{Y}}_{f}=&{\left[ A_{i}\left( S P_{N} S^{T}+R P_{R} R^{T}\right) \quad B_{1 {\dot{i}}} V_{R j} R^{T} \beta \quad 0\right. } \\ {}&\left. B_{u i} V_{R j} R^{T}(1-\beta ) \quad 0 \quad B_{\omega }\right] , \end{aligned}\\{} & {} {\bar{Y}}_{g}=\left[ \begin{array}{llllll}0&\quad B_{u i} V_{R j} R^{T}&\quad 0&\quad -B_{u i} V_{R j} R^{T}&\quad 0&\quad 0\end{array}\right] ,\\{} & {} {\bar{Z}}_{2 m}=\left[ C_{2 i}\left( S P_{N} S^{T}+R P_{R} R^{T}\right) \quad 0 \quad 0 \quad 0 \quad 0 \quad 0\right] ,\\{} & {} {\bar{Z}}_{1}=\left[ \begin{array}{cc}{\bar{Z}}_{11} &{} \quad 0 \\ 0 &{} \quad {\bar{Z}}_{12}\end{array}\right] , {\bar{Z}}_{2}=\left[ \begin{array}{cc}{\bar{Z}}_{21} &{} \quad 0 \\ 0 &{} \quad {\bar{Z}}_{22}\end{array}\right] ,\\{} & {} {\bar{P}}=\left[ \begin{array}{cc}S P_{N} S^{T}+R P_{R} R^{T} &{} \quad 0 \\ 0 &{} \quad S P_{N} S^{T}+R P_{R} R^{T}\end{array}\right] . \end{aligned}$$

3.4 Algorithm

To find a better gain matrix with a more advantageous performance, the following Algorithm 1 is presented to further obtain a better solution based on the two-step method [4]. The two-step method can effectively calculate the optimal output feedback controller based on the state feedback controller without redundant iteration. Besides, the first step is to solve Theorem 2 to obtain the transitional arbitrary matrix L, and the second step is to solve Theorem 3 on the basis of first step to finally obtain the output feedback gain directly.

figure a

Remark 3

It is noteworthy that the value of Matrix S also has a great influence on \(K_{sof}\), and its value should be adjusted appropriately in the process of solving. If the performance of the optimized control gain matrix \(K_{sof}\) is better than before, then the procedure is stopped.

4 Simulation results

In this section, some numerical simulations on a quarter-car ASS model are executed to estimate and verify the performance of the designed control algorithm. Table 3 lists the relevant parameters of the quarter-car ASS model.

Table 3 Vehicle parameters and values
Full size table

In order to more highlight the effectiveness of the presented control method, the control methods in [16, 17, 34] introduced for comparison. Given that the authors in [34] presented a non-fragile controller without time delay, or the ease of expression, this set of the comparison is represented as Cases 1- 4 with different controller parameter perturbation as shown in Table 4. The aim of this comparison is to clarify the effectiveness with consideration of time delay in the ASSs. The authors in [16] presented an output feedback controller with time delay which is not stochastic. In order to highlight the effectiveness of the stochastic method, we compare the presented controller with the controller in [16], which is reflected as Case 1. The authors in [17]proposed a fuzzy controller without considering non-fragile. Thus, we compare the proposed controller with the controller in [17]to emphasize the importance of the non-fragile control.

Remark 4

It is known that the state feedback system requires the measurement of every component of the state. However, in practical applications, it is not always possible to access all state variables, and only partial information is available through measured outputs. Compared with the state feedback control system, the output feedback control system is a low-cost solution which does not require full information of the state variables. However, the difference of the control effect with the two control methods is not obvious and cannot be easily figured out in the simulation stage, so the comparisons are not conducted in this work.

Table 4 Control perturbation cases in stimulation
Full size table

With mincx solver in the LMI toolbox, the following local control gains and compared gains are obtained as:

Case 1 :

$$\begin{aligned} \begin{aligned}&K=10^{4} \times [-1.2089-4.1497-0.0079] \\&K 1=2500 \times [5.2122-0.6415-0.2503] \\&K 2=10^{4} \times [1.7417\ \ 0.5445\ \ 0.0399 -0.0314] \end{aligned} \end{aligned}$$

Case 2:

$$\begin{aligned} \begin{aligned}&K=10^{4} \times [-1.7650-5.5251-0.0185] \\&K 1=2500 \times [4.4865-1.3724-0.1413] \\&K 3=10^{4} \times [1.6026-0.1181-0.2097-0.0333] \end{aligned} \end{aligned}$$

Case 3:

$$\begin{aligned} \begin{aligned}&K=10^{4} \times [-1.6826-5.4481-0.0110] \\&K 1=2500 \times [3.1293-2.4439-0.1658] \\&K 3=10^{4} \times [1.6026-0.1181-0.2097-0.0333] \end{aligned} \end{aligned}$$

Case 4:

$$\begin{aligned} \begin{aligned}&K=10^{4} \times [-1.5368-5.0442-0.0015] \\&K 1=2500 \times [2.4183-1.6881-0.1200] \\&K 3=10^{4} \times [1.6026-0.1181-0.2097-0.0333] \end{aligned} \end{aligned}$$
Fig. 4
figure 4

Frequency responses of vehicle body acceleration in Case 1, Case 2, Case 3, and Case 4

Full size image
Fig. 5
figure 5

Frequency responses of relative suspension travel in Case 1, Case 2, Case 3, and Case 4

Full size image
Fig. 6
figure 6

Frequency responses of suspension relative dynamic load in Case 1, Case 2, Case 3, and Case 4

Full size image

4.1 Frequency responses

Fig. 7
figure 7

Sprung mass acceleration under bump excitation in Case 1, Case 2, Case 3, and Case 4

Full size image
Fig. 8
figure 8

Relative suspension travel under bump excitation in Case 1, Case 2, Case 3, and Case 4

Full size image
Fig. 9
figure 9

Relative dynamic load under bump excitation in Case 1, Case 2, Case 3, and Case 4

Full size image
Fig. 10
figure 10

Quarter-car test rig

Full size image

The frequency response is used to show the interference attenuation performance in this section.

Fig. 11
figure 11

Block diagram of the experimental test with quarter car test rig

Full size image

The controller designed in this paper is K, which is represented by a red solid line. And the compared controller in [34] is K1, which is represented by a green dotted line. And the compared controllers in [16, 17] are K2 and K3, which are denoted by a yellow dash-dotted line and the black scribed line describes the uncontrolled passive suspension.

Fig. 12
figure 12

Experimental sprung mass acceleration under sinusoidal bump excitation in Case 1, Case 2, Case 3, and Case 4

Full size image
Fig. 13
figure 13

Experimental relative suspension travel under sinusoidal bump excitation in Case 1, Case 2, Case 3, and Case 4

Full size image
Fig. 14
figure 14

Experimental relative dynamic load under sinusoidal bump excitation in Case 1, Case 2, Case 3, and Case 4

Full size image

Figure 4 plots the frequency response of the sprung mass acceleration in Cases 1−4. We can see that with the controller K, the acceleration values of the ASSs are lower than with the other controllers evidently. It means the proposed controller in this paper can greatly improve the ride comfort.

Figures 5 and 6 plot the relative suspension travel and dynamic load. It can be seen that controller K provides a significant improvement near the natural frequency of the sprung mass mode.

Remark 5

The main purpose of this work is to maximumly improve the ride comfort of the suspension system, and at the same time meeting the mechanical constraints of the suspension dynamic travel and dynamic load. Although the Bode diagram of the relative dynamic load of the designed controller is not excellent, the main control target of this work is satisfied as well as the corresponding mechanical constraints.

4.2 Bump responses

The effectiveness of the proposed controller is verified by using a bumped road profile [36], as shown below:

$$\begin{aligned} z_{\textrm{r}}(t)=\left\{ \begin{array}{ll} \frac{A}{2}\left( 1-\cos \left( \frac{2 \pi v}{l} t\right) \right) ,&{} \quad \text{ if } \ 0 \le t \le \frac{l}{v} \\ 0, &{} \quad \text{ if } \frac{l}{v}<t \end{array}\right. \end{aligned}$$
(35)

where A denotes the height of the bump and l denotes the length of the bump. The parameters are set as \(A=0.05 \mathrm {~m}\) and \(l= 3 \mathrm {~m}\), and the forward velocity of vehicle is set as \(v=15 \mathrm {~m} / \textrm{s}\). The time-domain response results of Cases 1−4 are shown in Figs. 7, 8 and 9, respectively.

As shown in Fig. 7, the controller K can quickly reduce the sprung mass acceleration evidently, compared with other the controllers. It validates the effectiveness and importance of non-fragile control and stochastic method.

Figures 8 and 9 indicate that the maximum value of relative suspension travel and the maximum value of relative dynamic load are less than one, respectively. According to the conditions in (14), the ASSs satisfies the requirements of safety performance constraints.

4.3 Root mean square

Furthermore, the root mean square (RMS) values of body vertical acceleration are listed in Tables 5 and 6. As shown in Table 5, compared with the passive suspension, the RMS values of body vertical acceleration for the compared controller K1, K2 and designed controller K can be reduced by 57.31%, 44.11%, and 86.38% under Case 1, respectively. This shows that the designed controller can improve vehicle ride quality while taking time delay and safety performance constraints into account. Moreover, Table 6 shows the RMS values of body vertical acceleration under different controller parameter perturbations. This reveals that the controller parameter perturbation can cripple the performance of the ASS. Meanwhile, Table 6 also validates the effectiveness and robustness of the proposed controller.

Table 5 Root mean square 1
Full size table
Table 6 Root mean square 2
Full size table

5 Experimental results

For the sake of validating the significance and performance of the presented non-fragile \(H_\infty \) controller, experimental tests are carried out by a quarter-car test bench.

Table 7 Parameters of quarter car test rig
Full size table

As shown in Fig. 10, the test rig is mainly composed of a computer with an embedded controller, a data acquisition board, an emergency button, a power amplifier, and an active suspension emulator. The active suspension emulator elements mainly contain a servo motor to push the road, a payload to simulate the vehicle load-bearing, a vehicle body mass, a tire mass, and an actuator. Figure 11 shows the block diagram of the experimental test with quarter car test rig. The parameters of this test rig are listed in Table 7. Owing to the existence of white noise and the limitations of the motor, the random road contour cannot be provided by the servo motor. Since the sine wave road profile is usually used in the experiment to interpret the performance of controllers [37], the following sine wave road profile is employed for the experiments.

$$\begin{aligned} z_{\textrm{r}}(t)=A \sin \left( \frac{2 \pi v}{l} t\right) \end{aligned}$$
(36)

The parameters are set as \(A=0.005\) m, \(l=5\) m, and the forward velocity of vehicle is set as \(v=36\) km/s.

Remark 6

The output feedback control of the active suspension system is implemented in Simulink numerical environment. The stochastic network-induced delay and the nonlinear factors are fully considered for solving the feedback gains. Meanwhile, a delay block is used outside the controller to represent the network-induced delay in actuator-to-system link and an IT-2 T–S fuzzy model is introduced to describe the nonlinear characteristics of active suspension systems. In addition, road input is established in Simulink environment. The servo motor generates corresponding forces according to the road block to push the road upwards.

The local control gains of the experiment are shown in Table 8.

Table 8 Control gains in experiment
Full size table

Moreover, the experimental comparison gains of the controllers in [17] are as follows:

\(K 3=[70.785,-29.679,-12.852,-0.5105]\)

The experimental results are shown in Figs. 12, 13 and 14. Similar to the simulation study, the controller in [17] are taken as the compared controller to demonstrate the effectiveness of the designed controller. Figures 12, 13 and 14 indicate that the designed controller is more to improve the ride comfort compared with the controllers in [17] and passive suspension.

6 Conclusions

In this research, a non-fragile IT-2 fuzzy \(H_\infty \) controller for the uncertain ASSs with the stochastic network-induced delay is presented. According to the experimental results, the designed controller was more effective to demands of driving safety, handling stability and ride comfort than the comparative cases. Moreover, some useful conclusions are summarized as follows:

  1. (1)

    The IT-2 T–S fuzzy model built in this paper fully considers the parameter uncertainties of the suspension system, and reasonably reflects the dynamic characteristics of the ASSs.

  2. (2)

    In view of a large amount of output feedback calculation and the unsatisfactory system response, the optimal output feedback control method designed in this paper not only ensures the control performance, but also reduces the computational burden. Moreover, by introducing control gain perturbations, the control performance is further improved.

  3. (3)

    In the process of establishing Lyapunov function, the upper and lower bounds and existence of network-induced delay information are considered. The proposed approach effectively reduces the conservatism of the controller.

Future work can be considered to investigate the asynchronous constraints between the fuzzy system and the fuzzy controller. Moreover, the influencing factors of suspension frequency characteristics can be also considered in the future work.