1 Introduction

Due to increased applications of micro- and nano-scale beam, plate and shell-type structures in micro- or nano-electromechanical systems (MEMS/NEMS), the study of micro- and nano-scale structures has attracted a widespread interest in scientific community. Conducting experiments on micro- and nano-scale structures is expensive and hard to control. Hence, in literature a great deal of attention has been devoted for developing theoretical models to characterize the behavior of micro- and nano-scale structures. Theoretically atomistic models are the most accurate, but are computationally expensive and time consuming for complex structures. Compared to the atomistic approach, the models based upon continuum mechanics are widely used due to their computational efficiency and simplicity. However, it is worthwhile to note that, the models based on classical continuum mechanics cannot capture small size effects associated with micro- and nano-scale structures. To overcome this drawback, it would be practicable to use size-dependent continuum mechanics models such as nonlocal elasticity theory [1,2,3,4,5], strain gradient theory [6], couple stress theory [7, 8] and modified couple stress theory [9]. Among these models, the nonlocal elasticity theory initiated by Eringen and Edelen [1,2,3,4,5] is widely used by researchers due to its simplistic nature.

Many well-known beam theories including those of Euler-Bernoulli [10], Timoshenko [10], Reddy [10] and Levinson [11, 12] have been extended for the case of micro- and nano-scale beams using Eringen’s nonlocal elasticity model. The important works available in the literature in this connection are: the nonlocal version of Euler-Bernoulli Beam theory [13,14,15,16], Timoshenko Beam Theory [17, 18] and other shear deformation beam theories [19, 20]. In refs. [13, 14], the bending and free vibration analyses of microtubules by using nonlocal Euler–Bernoulli beam theory are presented. In ref. [15], the bending, vibration and buckling study of nonlocal Euler-Bernoulli beams with four classical boundary conditions is presented. Next, in ref. [16], the analogy between nonlocal and local Euler-Bernoulli nanobeams is discussed. However, it is worth mentioning that, the Euler-Bernoulli beam theory is suitable only for the analysis of slender beams as it neglects the effects of shear deformation. Whereas, a single variable nonlocal beam theory proposed in this paper could incorporate the effects of shear deformation in its formulation. Further, the governing equation and the expressions for the bending moment and shear force of the beam theory proposed here are strikingly similar to those of nonlocal Euler-Bernoulli beam theory.

In a paper by Wang et al [17], the bending solutions of micro- and nanobeams based on the Eringen nonlocal theory and Timoshenko beam theory is presented. The Eringen’s theory takes into account the small-scale effects whereas the effects of transverse shear deformation are accounted for in Timoshenko’s beam theory. In [18], the free vibration analysis solutions for micro- and nanobeams modeled after Eringen’s nonlocal theory and Timoshenko beam theory is presented. The solutions based on nonlocal Timoshenko beam theory account for a better representation of the bending and vibration behaviour of short, stubby, micro- and nanobeams where the small-scale effect and transverse shear deformation are significant. It is important to note that, the beam theory presented in this work can also incorporate the effects of shear deformation in its formulation. Further, the bending solutions obtained by using the present beam theory (based on classical elasticity) [21] are more accurate than Timoshenko beam theory results in comparison to two-dimensional theory of elasticity solutions. In case of clamped ends, using present theory one could define three different types of clamped end boundary conditions, namely, Type 1, Type 2 and Type 3, as discussed under section: Boundary conditions of this paper. Using these boundary conditions, one could obtain three different solutions for the case of beams with clamped ends. Further, the results obtained by using Type 1, Type 2 and Type 3 clamped end boundary conditions are more or less same as those obtained by Elementary theory (Euler-Bernoulli beam theory), First-order shear deformation theory (Timoshenko beam theory) and Higher-order shear deformation theory (Levinson beam theory), respectively.

Some of the important research papers available in the literature on bending, buckling and vibration analyses of micro- and nano-scale beams are: Papers by Reddy [19], Aydogdu [20], Niu et al [22], Thai [23], Thai and Vo [24]. Further, free vibrations study of micro- and nano-scale beams is also reported by Xu [25], Ruiz et al [26], Ke et al [27], Chakraverty and Behera [28].

In [19, 20, 22], the results pertaining to bending, vibration and buckling analyses of nanobeams are obtained by using the nonlocal version of Euler-Bernoulli, Timoshenko, Reddy and Levinson beam theories. In ref. [23], the bending, vibration and buckling analyses of nanobeams have been carried out by using a two variable refined beam theory. Further, in ref. [24], a nonlocal sinusoidal shear deformation beam theory with application to bending, buckling, and vibration study of nanobeams is presented. The discussions pertaining to nonlocal Euler-Bernoulli and Timoshenko beam theories have been already presented in the preceding paragraphs. Reddy and Levinson nonlocal beam theories are the higher-order shear deformation beam theories with two unknown functions. The formulation of beams using Reddy and Levinson theories result in two coupled governing differential equations. Also, the beam theories proposed in [23, 24] involve two coupled governing differential equations in terms of two unknown functions. Alternatively, the beam theory presented in this paper involves only one governing differential equation and one unknown variable.

In [25,26,27,28], the free vibration study of nanobeams has been carried out by using the nonlocal Euler-Bernoulli beam theory. However, the formulation of vibration problems by using Euler-Bernoulli beam theory does not include the effects of shear deformation. It is to be noted that, the effects of shear is important not only in case of study of thick beams, but in case of study of slender beams vibrating at higher modes. Whereas, using the beam theory presented in this paper one could incorporate the effects of both shear deformation and rotary inertia in formulating the beam vibration problems.

The objective of this work is to present a simple, yet accurate nonlocal beam theory for the bending of micro- and nano-scale rectangular beams based on Refined Plate Theory (RPT) [29] and a single variable rectangular beam theory based on classical elasticity [21]. The beam theory proposed in [21] is based on classical continuum mechanics and is suitable only for macro-scale beams. Whereas, the nonlocal beam theory presented in this paper is based on Eringen’s nonlocal elasticity theory. The small size effects which need to be considered in case of micro- and nano-scale beams are incorporated in the beam formulation by using Eringen’s differential constitutive relations.

Further, the nonlocal beam theory proposed here contains only one fourth-order governing differential equation involving a single variable. The efforts involved in obtaining the solutions for beam problems using the present theory are only marginally higher in comparison to that involved in case of Euler-Bernoulli Beam theory [13,14,15,16]. Moreover, the governing equation and the expressions for the bending moment and shear force of the present theory are strikingly similar to those of nonlocal Euler-Bernoulli Beam Theory (EBT). But, it needs to be noted that, the formulation of present theory involves both the bending as well as shear deformations, whereas, the formulation of Euler-Bernoulli Beam Theory involves only the bending deflection. The effects of shear deformation cannot be ignored in case of short or thick beams.

2 Beam under consideration

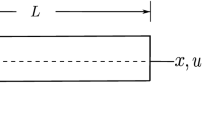
Consider a beam of rectangular cross-section having length L, width b and height h. The beam geometry is defined in O-x-y-z Cartesian right-handed coordinate system as shown in figure 1.

Figure 1
figure 1

Geometry of a rectangular beam.

Full size image

The beam geometry occupies a region:

$$ 0 \le x \le L , - \frac{b}{2} \le y \le \frac{b}{2} , - \frac{h}{2} \le z \le \frac{h}{2} $$
(1)

The beam is made of linearly elastic, homogeneous, isotropic material. The material properties of the beam are: Modulus of elasticity E, Modulus of rigidity G and Poisson’s ratio μ. The E, G and μ are related by \( E = 2 G \left( {1 + \mu } \right) \).

In accordance with Eringen’s nonlocal elasticity theory [1,2,3,4,5], the material properties important to incorporate small scale effects into beam analysis are: Material constant appropriate to each material e0 and internal characteristic length a. A detailed discussion on Eringen’s nonlocal elasticity approach is presented in the following section.

Beam can be subjected to any physically meaningful boundary conditions at x = 0 and x = L. Beam would be subjected to loads only in the transverse direction, i.e., along z-direction.

3 Eringen’s theory of nonlocal elasticity

According to Eringen’s theory of nonlocal elasticity [1,2,3,4,5], the stress at a reference point \( {\mathbb{X}} \) in the body depends not only on the strain at \( {\mathbb{X}} \) but also on strains at all other points of the body. Accordingly, the nonlocal stress tensor \( \sigma_{ij} \left( {\mathbb{X}} \right) \) at a point \( {\mathbb{X}} \) can be expressed as follows [4]:

$$ \sigma_{ij} \left( {\mathbb{X}} \right) = \mathop \int \limits_{V}^{{}} \alpha \left( {\left| {{\mathbb{X}}^{\prime } - {\mathbb{X}}} \right|, \tau } \right) t_{ij} \left( {{\mathbb{X}}^{\prime } } \right) dV\left( {{\mathbb{X}}^{\prime } } \right)\quad \left( {i, j = x, y, z} \right) $$
(2)

where integration is carried over volume V of the beam. In Eq. (2), \( t_{ij} \left( {{\mathbb{X}}^{\prime } } \right) \) is the local stress tensor at any point \( {\mathbb{X}}^{\prime } \) and, the kernel function \( \alpha \left( {\left| {{\mathbb{X}}^{\prime } - {\mathbb{X}}} \right|, \tau } \right) \) represents the nonlocal modulus which incorporates nonlocal effects into the constitutive relations. \( \left| {{\mathbb{X}}^{\prime } - {\mathbb{X}}} \right| \) is the Euclidean distance, and \( \tau \) is a constant which depends on the internal and external characteristic lengths and can be expressed as follows [4]:

$$ \tau = \frac{{e_{0} a}}{L} $$
(3)

In Eq. (3), e0 is a constant appropriate to each material, a is an internal characteristic length (e.g., length of C-C bond, lattice parameter, granular distance, etc.), and L is an external characteristic length (e.g., crack length, wavelength, sample size, etc.).

Next, in accordance with generalized Hooke’s law, the local stress tensor \( t_{ij} \left( {{\mathbb{X}}^{\prime } } \right) \) at a point \( {\mathbb{X}}^{\prime } \) can be related to strain tensor \( \varepsilon_{kl} \left( {{\mathbb{X}}^{\prime } } \right) \) at that point as follows:

$$ t_{ij} \left( {{\mathbb{X}}^{\prime } } \right) = D_{ijkl} \varepsilon_{kl} \left( {{\mathbb{X}}^{\prime } } \right)\quad \left( {i,j,k,l = x, y, z} \right) $$
(4)

where D ijkl is the elastic modulus tensor.

Generally, the solutions to nonlocal elasticity problems are difficult mathematically, due to involvement of the integro-partial differential equations (e.g., Eq. (2)). However, it has been shown that, the integro-partial differential equations of the nonlocal elasticity theory are reducible to partial differential equations for a special class of physically admissible kernels [4]. Accordingly, constitutive equations of the nonlocal elasticity theory can be expressed in the following differential form:

$$ \left( {1 - \tau^{2} L^{2} \nabla^{2} } \right) \sigma_{ij} \left( {\mathbb{X}} \right) = D_{ijkl} \varepsilon_{kl} \left( {\mathbb{X}} \right) $$
(5)

Where \( \nabla^{2} \) is the Laplacian operator.

Furthermore, it can be noted that, by setting \( \tau \to 0 \) in Eq. (5), one would get the Hooke’s law of classical elasticity.

4 Assumptions made in the theory

The assumptions made are as follows:

  1. 1.

    Beam is made of linearly elastic, homogeneous, isotropic material.

  2. 2.

    Displacements along x, y and z-directions are u, v and w, respectively. The displacements involved are very small compared to beam thickness and, therefore, strains involved are infinitesimal. Also, since no loading is considered in y-direction, the displacement v is ignored. Hence, to obtain non-zero strains, the following linear strain-displacement relations are used:

    $$ \varepsilon_{x} = \frac{\partial u}{\partial x} $$
    (6)
    $$ \gamma_{zx} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} $$
    (7)
  3. 3.

    In general, the normal stresses \( \sigma_{y} \) and \( \sigma_{z} \) can be ignored as they are small in comparison to \( \sigma_{x} \), i.e., \( \sigma_{y} \ll \sigma_{x} \) and \( \sigma_{z} \ll \sigma_{x} \). Also, the shear stresses \( \tau_{xy} \) and \( \tau_{yz} \) can be ignored. Therefore, based on the Eringen’s nonlocal elasticity theory [1,2,3,4,5] and referring to the Eq. (5), the differential constitutive relation between bending stress \( \sigma_{x} \) and bending strain \( \varepsilon_{x} \) can be written as:

    $$ \sigma_{x} - \left( {e_{0} a} \right)^{2} \frac{{d^{2} \sigma_{x} }}{{dx^{2} }} = E \varepsilon_{x} $$
    (8)

    Similarly too, the differential constitutive relation between transverse shear stress \( \tau_{zx} \) and transverse shear strain \( \gamma_{zx} \) can be written as:

    $$ \tau_{zx} - \left( {e_{0} a} \right)^{2} \frac{{d^{2} \tau_{zx} }}{{dx^{2} }} = G \gamma_{zx} $$
    (9)
  4. 4.

    The lateral displacement w consists of two components: Bending component w b and shear component w s . Both the components are functions of x only. Accordingly, by referring to [29,30,31,32,33], the expression for lateral displacement w could be written as follows:

    $$ w = w_{b} \left( x \right) + w_{s} \left( x \right) $$
    (10)
  5. 5.

    The axial displacement u consists of bending component u b and shear component u s . The u b and u s are functions of x and z only. Therefore, the expression for lateral displacement u could be written as follows [29,30,31,32,33]:

    $$ u = u_{b} \left( {x, z} \right) + u_{s} \left( {x, z} \right) $$
    (11)
    1. a.

      The bending component u b could be considered as analogous to the axial displacement of Euler-Bernoulli beam theory. Hence, the expression for u b could be written as follows [29,30,31,32,33]:

      $$ u_{b} = - z \frac{{dw_{b} }}{dx} $$
      (12)

      The displacement components u b and w b together do not contribute towards transverse shear strain \( \gamma_{zx} \) and, therefore, to transverse shear stress \( \tau_{zx} \).

    2. b.

      The shear component u s of axial displacement u is such that [29,30,31,32,33]:

      • it gives rise, in conjunction with w s , to transverse shear strain \( \gamma_{zx} \) in such a way that the transverse shear stress \( \tau_{zx} \) varies parabolically across the thickness of the beam in such a manner that transverse shear stress \( \tau_{zx} \) is zero at \( z = - h/2 \) and at z = h/2, and

      • its contribution towards normal strain \( \epsilon_{x} \) is such that, in the bending moment M x there is no contribution form the component u s .

  6. 6.

    Body forces are assumed to be zero. But, if the body forces are significant, then the body forces can be taken into account while prescribing the lateral load on the beam.

5 Expressions for displacements of the present nonlocal beam theory

The expressions for displacements of the present nonlocal beam theory are obtained by suitably adapting the displacement field of a two variable Refined Plate Theory (RPT) reported in ref. [29]. Referring to the assumptions of RPT and the assumptions of the present beam theory discussed in the preceding section, the axial and lateral displacements are assumed to be consist of bending and shear components. Accordingly, the displacement field of RPT [29] for the case of beams can be written as follows:

$$ \begin{aligned} u & = u_{b} \left( {x, z} \right) + u_{s} \left( {x, z} \right) \\ & = - z \frac{{dw_{b} }}{dx} + h\left[ {\frac{1}{4}\left( {\frac{z}{h}} \right) - \frac{5}{3}\left( {\frac{z}{h}} \right)^{3} } \right]\frac{{dw_{s} }}{dx} \\ \end{aligned} $$
(13)
$$ w = w_{b} \left( x \right) + w_{s} \left( x \right) $$
(14)

It can be noted that, the expressions for displacements u and w given by Eqs. (13) and (14), respectively, contain two unknowns, i.e., the bending component w b and the shear component w s . However, with some efforts, it is possible to express the shear component w s in terms of the bending component w b . The further discussions presented this section will communicate the steps involved in writing the shear component w s in terms of the bending component w b .

Using the Eq. (13) in Eq. (6), one obtains the expression for normal strain \( \epsilon_{x} \) as follows:

$$ \epsilon_{x} = - z\frac{{d^{2} w_{b} }}{{dx^{2} }} + h\left[ {\frac{1}{4}\left( {\frac{z}{h}} \right) - \frac{5}{3}\left( {\frac{z}{h}} \right)^{3} } \right]\frac{{d^{2} w_{s} }}{{dx^{2} }} $$
(15)

Next, by using the Eqs. (13) and (14) in Eq. (7), one obtains the expression for shear strain \( \gamma_{zx} \) as follows:

$$ \gamma_{zx} = \left[ {\frac{5}{4} - 5 \left( {\frac{z}{h}} \right)^{2} } \right]\frac{{dw_{s} }}{dx} $$
(16)

Referring to Eq. (16), it can be noted that, the displacement components u b and w b together do not contribute towards the transverse shear strain \( \gamma_{zx} \).

The differential constitutive relation between the bending stress σ x and the bending strain \( \epsilon_{x} \) is given by Eq. (8). Now, using the differential constitutive relation given by Eq. (8), one can obtain the expression for bending moment M x as follows:

For the case of beams, the bending moment M x can be defined as:

$$ M_{x} = \mathop \int \limits_{A}^{{}} \sigma_{x} z dA $$
(17)

where integration is carried over cross-sectional area A of the beam.

Multiplying by z on both sides of Eq. (8) and integrating, one can write Eq. (8) in the following form:

$$ \mathop \int \limits_{A}^{{}} \sigma_{x} z dA - \left( {e_{0} a} \right)^{2} \mathop \int \limits_{A}^{{}} z\frac{{d^{2} \sigma_{x} }}{{dx^{2} }}dA = \mathop \int \limits_{A}^{{}} E z\varepsilon_{x} dA $$
(18)

Now, using the definition of bending moment M x given by Eq. (17) and the expression for \( \varepsilon_{x} \) given by Eq. (15) in Eq. (18), one obtains

$$ M_{x} - \left( {e_{0} a} \right)^{2} \frac{{d^{2} M_{x} }}{{dx^{2} }} = - EI \frac{{d^{2} w_{b} }}{{dx^{2} }} $$
(19)

Where \( I = bh^{3} /12 \) is the moment of inertia of the considered beam of rectangular cross-section.

In case of beams, the relationship between the bending moment M x and the applied transverse distributed load q(x) can be written as follows:

$$ \frac{{d^{2} M_{x} }}{{dx^{2} }} = - q\left( x \right) $$
(20)

Using Eq. (20) in Eq. (19), one obtains

$$ M_{x} = - EI \frac{{d^{2} w_{b} }}{{dx^{2} }} - \left( {e_{0} a} \right)^{2} q\left( x \right) $$
(21)

Referring to Eq. (21), one can note that, the contribution of shear component u s towards normal strain \( \epsilon_{x} \) is such that, in the bending moment M x there is no contribution form the component u s .

The differential constitutive relation between the transverse shear stress \( \tau_{zx} \) and the transverse shear strain \( \gamma_{zx} \) is stated by Eq. (9). Now, using the differential constitutive relation given by Eq. (9), one can obtain the expression for shear force V x as follows:

For the case of beams, the shear force V x can be defined as:

$$ V_{x} = \mathop \int \limits_{A}^{{}} \tau_{zx} dA $$
(22)

where integration is carried over cross-sectional area A of the beam. Integrating Eq. (9) over cross-section of the beam, Eq. (9) can be written in the following form:

$$ \mathop \int \limits_{A}^{{}} \tau_{zx} dA - \left( {e_{0} a} \right)^{2} \mathop \int \limits_{A}^{{}} \frac{{d^{2} \tau_{zx} }}{{dx^{2} }}dA = \mathop \int \limits_{A}^{{}} G \gamma_{zx} dA $$
(23)

Now, using the definition of shear force given by Eq. (22) and the expression for \( \gamma_{zx} \) given by Eq. (16) in Eq. (23), one obtains

$$ V_{x} - \left( {e_{0} a} \right)^{2} \frac{{d^{2} V_{x} }}{{dx^{2} }} = \frac{5 E b h}{{12 \left( {1 + \mu } \right)}}\frac{{dw_{s} }}{dx} $$
(24)

Where I = bh3/12 is the moment of inertia of the considered beam of rectangular cross-section.

In case of beams, the relationship between the shear force V x and the applied transverse distributed load can be written as:

$$ \frac{{d^{2} V_{x} }}{{dx^{2} }} = - \frac{dq\left( x \right)}{dx} $$
(25)

Using Eq. (25) in Eq. (24), one obtains

$$ V_{x} = \frac{5 E b h}{{12 \left( {1 + \mu } \right)}}\frac{{dw_{s} }}{dx} - \left( {e_{0} a} \right)^{2} \frac{dq\left( x \right)}{dx} $$
(26)

Referring to Eq. (26), one can note that, in the shear force V x there is no contribution from the displacement components u b and w b .

In case of beams, the gross equilibrium equations in terms of the bending moment, shear force and the applied transverse distributed load can be written as:

$$ \frac{{dM_{x} }}{dx} - V_{x} = 0 $$
(27)
$$ \frac{{dV_{x} }}{dx} + q\left( x \right) = 0 $$
(28)

Now, substituting for M x and V x from Eqs. (21) and (26), respectively, in Eq. (27), one can conclude that,

$$ w_{s} = - \frac{{h^{2} \left( {1 + \mu } \right)}}{5 }\frac{{d^{2} w_{b} }}{{dx^{2} }} $$
(29)

It can be noted that, Eq. (29) establishes the relationship between the shear component w s and the bending component w b of lateral displacement w.

Now, substituting for w s from Eq. (29) in Eqs. (13) and (14), respectively, one obtains the expressions for axial displacement u and lateral displacement w in terms of bending component w b as follows:

$$ u = - z \frac{{dw_{b} }}{dx} - \frac{{h^{3} \left( {1 + \mu } \right)}}{5}\left[ {\frac{1}{4}\left( {\frac{z}{h}} \right) - \frac{5}{3}\left( {\frac{z}{h}} \right)^{3} } \right]\frac{{d^{3} w_{b} }}{{dx^{3} }} $$
(30)
$$ w = w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }} $$
(31)

Equations (30) and (31) would be considered as the displacement field expressions of the present beam theory. It is important to note that, the expressions for axial displacement u and the lateral displacement w given by Eqs. (30) and (31), respectively, contain only one unknown variable, i.e., the bending component w b of the lateral displacement w.

6 Expressions for strains, stresses, bending moment and shear force of the present nonlocal beam theory

6.1 Expressions for strains

Using the Eq. (30) in Eq. (6), one can write the expression for normal strain \( \epsilon_{x} \) as follows:

$$ \epsilon_{x} = - z\frac{{d^{2} w_{b} }}{{dx^{2} }} - \frac{{h^{3} \left( {1 + \mu } \right)}}{5}\left[ {\frac{1}{4}\left( {\frac{z}{h}} \right) - \frac{5}{3}\left( {\frac{z}{h}} \right)^{3} } \right]\frac{{d^{4} w_{b} }}{{dx^{4} }} $$
(32)

Next, by using Eqs. (30) and (31) in Eq. (7), one obtains the expression for shear strain \( \gamma_{zx} \) as γfollows:

$$ \gamma_{zx} = - h^{2} \left( {1 + \mu } \right)\left[ {\frac{1}{4} - \left( {\frac{z}{h}} \right)^{2} } \right]\frac{{d^{3} w_{b} }}{{dx^{3} }} $$
(33)

6.2 Expression for bending moment

Using the Eq. (21), the expression for bending moment M x can be written as:

$$ M_{x} = - E I \frac{{d^{2} w_{b} }}{{dx^{2} }} - \left( {e_{0} a} \right)^{2} q\left( x \right) $$
(34)

6.3 Expression for shear force

Next, using Eq. (29) in Eq. (26), one can write the expression for shear force V x as follows:

$$ V_{x} = - E I \frac{{d^{3} w_{b} }}{{dx^{3} }} - \left( {e_{0} a} \right)^{2} \frac{dq\left( x \right)}{dx} $$
(35)

7 Governing differential equation of the present nonlocal theory for rectangular beams

In this section, the governing differential equation of the present beam theory will now be derived.

Next, substituting for M x and V x from Eqs. (34) and (35), respectively, in Eq. (27), one can note that the gross equilibrium Eq. (27) is satisfied identically.

Finally, substituting for V x from Eq. (35) in Eq. (28), one obtains

$$ EI \frac{{d^{4} w_{b} }}{{dx^{4} }} + \left( {e_{0} a} \right)^{2} \frac{{d^{2} q\left( x \right)}}{{dx^{2} }} = q\left( x \right) $$
(36)

Equation (36) would be considered as the governing differential equation of the present nonlocal theory for rectangular beams. It can be seen that, the governing Eq. (36) contains only one unknown variable, i.e., the bending component w b of lateral displacement. Using the governing Eq. (36), one could obtain the solution for bending component w b . Next, using the Eq. (31), one could obtain the solution for lateral displacement w.

Also, it is worth mentioning that, the governing differential Eq. (36) is strikingly similar to that of nonlocal version of EBT [34] based on Eringen’s nonlocal elasticity theory. However, it is worthwhile to note the following important differences between Present theory and EBT:

  • The formulation of present theory involves both the bending as well as shear deformation, whereas, the formulation of EBT involves only bending deflection. Thus, the formulation of thick or short beams using EBT would result in the underestimation of deflections and overestimation of frequencies and buckling loads.

  • Using the present theory one could predict the transverse shear strain (\( \gamma_{zx} \)) and stress (\( \tau_{zx} \)) in a straight forward manner using the constitutive relation between the transverse shear stress and strain. Whereas, in case of EBT, the transverse shear strain (\( \gamma_{zx} \)) and stress (\( \tau_{zx} \)) obtained by using the constitutive relation between the transverse shear stress and strain is always zero. The transverse shear stress (\( \tau_{zx} \)) in case of EBT can only be obtained by using the theory of elasticity equilibrium equations or by consideration of the equilibrium of the forces acting on the beam.

  • Also, one could observe the considerable differences between the prescribed boundary conditions of the present theory with respect to EBT. The boundary conditions associated with the present theory have been presented in the following section.

8 Boundary conditions

In this section, few commonly used boundary conditions in case of beam analysis would be discussed. For the sake of illustration, the boundary conditions for the beam end x = 0 would be discussed. The boundary conditions at beam end x = L could be prescribed in similar lines as those prescribed in case of beam end x = 0.

8.1 Beam end is simply supported

If beam end x = 0 is simply supported, then the following boundary conditions are used:

$$ \left[ w \right]_{x = 0} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = 0} = 0 $$
(37)

and

$$ \left[ {M_{x} } \right]_{x = 0} = \left[ { - EI \frac{{d^{2} w_{b} }}{{dx^{2} }} - \left( {e_{0} a} \right)^{2} q\left( x \right)} \right]_{x = 0} = 0 $$
(38)

8.2 Beam end is free

If beam end x = 0 is free, then the following boundary conditions are used:

$$ \left[ {M_{x} } \right]_{x = 0} = \left[ { - EI \frac{{d^{2} w_{b} }}{{dx^{2} }} - \left( {e_{0} a} \right)^{2} q\left( x \right)} \right]_{x = 0} = 0 $$
(39)

and

$$ \left[ {V_{x} } \right]_{x = 0} = \left[ { - EI \frac{{d^{3} w_{b} }}{{dx^{3} }} - \left( {e_{0} a} \right)^{2} \frac{dq\left( x \right)}{dx}} \right]_{x = 0} = 0 $$
(40)

8.3 Beam end is clamped

If beam end x = 0 is clamped, using present beam theory it would be possible to prescribe three different types of boundary conditions at the clamped end. Therefore, henceforth in this paper, the three types of clamped end boundary conditions discussed in this paper would be identified as Type 1, Type 2 and Type 3, respectively. In all three types, the deflection w at the clamped end is taken as zero, whereas, the slope conditions would be different. Also, it is worthwhile to note that, the Type 1 and Type 3 clamped end boundary conditions are prescribed analogous to those prescribed by Timoshenko and Goodier [35]. Further, one could also find the Type 3 clamped end boundary conditions in case of beam and plate theories proposed by Levinson [11, 36].

8.3a Clamped end boundary condition: Type 1

In case of Type 1 clamped end, the displacement and slope boundary conditions are stated as follows:

$$ \left[ w \right]_{x = 0} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = 0} = 0 $$
(41)

and

$$ \left[ {\frac{dw}{dx}} \right]_{x = 0} = \left[ {\frac{{dw_{b} }}{dx} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{3} w_{b} }}{{dx^{3} }}} \right]_{x = 0} = 0 $$
(42)

It may be noted that, the deflection curve w(x) represents the deflection of elastic axis of the beam. The boundary condition (42) signifies that in this type of clamped condition, the rotation of elastic axis at clamped end is not permitted.

8.3b Clamped end boundary condition: Type 2

In case of Type 2 clamped end, the displacement and slope boundary conditions are stated as follows:

$$ \left[ w \right]_{x = 0} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = 0} = 0 $$
(43)

and

$$ \left[ {\frac{{dw_{b} }}{dx}} \right]_{x = 0} = 0 $$
(44)

The slope boundary condition (44) signifies that in this type of clamped end, the bending rotation is not allowed, whereas, the shear rotation is allowed.

8.3c Clamped end boundary condition: Type 3

In case of Type 3 clamped end, the displacement boundary condition remains same as in the earlier cases, but now the slope \( \left[ {\frac{\partial u}{\partial z}} \right]_{z = 0} \) is taken as zero at the clamped edge. This slope, using Eq. (30), can be expressed in terms of derivatives of w b . As a result, in case of Type 3 clamped end, the boundary conditions can be stated as follows:

$$ \left[ w \right]_{x = 0} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = 0} = 0 $$
(45)

and

$$ \left[ {\frac{{dw_{b} }}{dx}} \right]_{x = 0} = - \frac{{h^{2} \left( {1 + \mu } \right)}}{20}\left[ {\frac{{d^{3} w_{b} }}{{dx^{3} }}} \right]_{x = 0} $$
(46)

Using Eq. (33), Eq. (46) can also be written as follows:

$$ \left[ {\frac{{dw_{b} }}{dx}} \right]_{x = 0} = \frac{ 1}{{20 \left[ {\frac{1}{4} - \left( {\frac{z}{h}} \right)^{2} } \right]}}\left[ {\gamma_{zx} } \right]_{x = 0} $$
(47)

As can be seen from boundary condition (46), the rotation of elastic axis of the beam is permitted at the Type 3 clamped end. Due to the rotation of elastic axis, the effect of shear deflection at free end is significant as compared to the effect of shear deflection obtained if the clamped conditions were to be prescribed by Eq. (41) and Eq. (42), wherein rotation of elastic axis at the clamped end was not permitted. Therefore, henceforth in this paper, Eqs. (43) and (44) or Eqs. (45) and (46) will be utilized for prescribing clamped end boundary conditions.

Moreover, it is worth mentioning that, a detailed study on shear force inconsistencies at the clamped ends/edges of beams, plates and shells has been presented in a paper by Groh and Weaver [37]. It has been reported that, in case of a certain higher-order shear deformation beam and plate theories, one would obtain zero shear forces at the clamped ends/edges when constitutive equations of the corresponding theories are used. However, it is well-known that, from simple equilibrium considerations of the forces one would get non-zero shear forces at the clamped ends/edges. Whereas, in case of present theory, one could obtain correct shear forces by using the clamped end boundary conditions prescribed by Eqs. (43) and (44) or by Eqs. (45) and (46).

9 Comments on the present nonlocal beam theory

The noteworthy features of the nonlocal beam theory presented here could be listed as follows:

  1. 1.

    The theory involves only one governing differential equation (Eq. (36)) in terms of a single unknown function (w b ). Whereas, many other shear deformation theories available in the literature, involves two or more governing equations and unknown variables [19].

  2. 2.

    The present nonlocal beam theory is strikingly similar to nonlocal version of EBT [34] in many aspects (e.g., governing differential equation and the expressions for bending moment and shear force).

  3. 3.

    The displacement field of the theory gives rise to a realistic parabolic variation of transverse shear stress across the beam cross-section.

  4. 4.

    Theory proposed here is a displacement based theory. The governing equation of the theory is obtained by utilizing the gross equilibrium equations of beams in terms of bending moment, shear force and the applied loading.

10 Illustrative examples: bending of micro- and nano-scale rectangular beams

In this section, three illustrative examples of beam bending using present nonlocal beam theory will now be presented. The expressions for lateral deflections of simply supported, cantilever and clamped-clamped micro- and nano-scale rectangular beams are presented.

10.1 Simply supported beam carrying a uniformly distributed load

Consider a rectangular beam of length L as shown in figure 1. The beam is subjected to simply supported boundary conditions at x = 0 and x = L. The beam carries a uniformly distributed load of intensity q0 over the beam span L.

For the case of a beam simply supported at x = 0 and x = L, the boundary conditions could be written as follows: At x = 0,

$$ \left[ w \right]_{x = 0} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = 0} = 0 $$
(48)

and

$$ \left[ {M_{x} } \right]_{x = 0} = \left[ { - EI \frac{{d^{2} w_{b} }}{{dx^{2} }} - \left( {e_{0} a} \right)^{2} q\left( x \right)} \right]_{x = 0} = 0 $$
(49)

At x = L,

$$ \left[ w \right]_{x = L} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = L} = 0 $$
(50)

and

$$ \left[ {M_{x} } \right]_{x = L} = \left[ { - EI \frac{{d^{2} w_{b} }}{{dx^{2} }} - \left( {e_{0} a} \right)^{2} q\left( x \right)} \right]_{x = L} = 0 $$
(51)

Using the governing Eq. (36) and the boundary conditions given by Eqs. (48)–(51), one could obtain the solution for bending component w b . The expression obtained for w b is as follows:

$$ w_{b} = \frac{{q_{0} L^{4} }}{24 E I}\left\{ {\begin{array}{*{20}c} {\left( {\frac{x}{L}} \right)^{4} - 2\left( {\frac{x}{L}} \right)^{3} + \left( {\frac{x}{L}} \right)} \\ {} \\ { + 12 \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}\left[ {\left( {\frac{x}{L}} \right) - \left( {\frac{x}{L}} \right)^{2} } \right]} \\ \end{array} } \right\} $$
(52)

Next, using the obtained expression for w b in Eq. (31), one would obtain the expression for lateral deflection w as follows:

$$ w = \frac{{q_{0} L^{4} }}{24 E I}\left\{ {\begin{array}{*{20}c} {\left( {\frac{x}{L}} \right)^{4} - 2\left( {\frac{x}{L}} \right)^{3} + \left( {\frac{x}{L}} \right)} \\ {} \\ { + \frac{{12 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} \left[ {\left( {\frac{x}{L}} \right) - \left( {\frac{x}{L}} \right)^{2} } \right]} \\ {} \\ { + 12 \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}\left[ {\left( {\frac{x}{L}} \right) - \left( {\frac{x}{L}} \right)^{2} + \frac{{2 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} } \right]} \\ \end{array} } \right\} $$
(53)

Equation (53) is the expression for lateral deflection w obtained using the present nonlocal beam theory for the case of a simply supported beam carrying a uniformly distributed load of intensity q0. It can be seen that, in Eq. (53) by ignoring the terms pertaining to micro-scale effects, one could obtain the deflection expression for simply supported beams derived using the classical elasticity theory [11, 21].

The expression for maximum lateral deflection, i.e., w at x = L/2 can be written as:

$$ \left[ w \right]_{{x = \frac{L}{2}}} = \frac{{q_{0} L^{4} }}{24 E I}\left\{ {\begin{array}{*{20}c} {\frac{5}{16} + \frac{{3\left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} } \\ {} \\ { + 12 \frac{{\left( {e_{0} a} \right)^{2} }}{{L^{2} }}\left[ {\frac{1}{4} + \frac{{2 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} } \right]} \\ \end{array} } \right\} $$
(54)

10.2 Cantilever beam carrying a uniformly distributed load

The geometry of cantilever beam under consideration is as shown in figure 1. The beam is clamped at x = 0 and the other end i.e., x = L is free. The beam carries a uniformly distributed load of intensity q0.

As discussed under sub-section 8.3, using present theory it would be possible to prescribe three types of boundary conditions at the clamped ends, namely, Type 1, Type 2 and Type 3. As Type 1 boundary conditions do not incorporate the effects of shear deformation into the deflections predicted, here, only Type 2 and Type 3 boundary conditions would be used to obtain beam deflections. The steps involved in obtaining the expression for lateral deflection w using Type 3 clamped end boundary conditions will now be discussed. The expression for lateral deflection w using Type 2 boundary conditions could be obtained following a similar pattern. For the case of a cantilever beam discussed here, the boundary conditions to be used are:

At x = 0,

$$ \left[ w \right]_{x = 0} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = 0} = 0 $$
(55)

and

$$ \left[ {\frac{{dw_{b} }}{dx} + \frac{{h^{2} \left( {1 + \mu } \right)}}{20}\frac{{d^{3} w_{b} }}{{dx^{3} }}} \right]_{x = 0} = 0 $$
(56)

At x = L,

$$ \left[ {M_{x} } \right]_{x = L} = \left[ { - EI \frac{{d^{2} w_{b} }}{{dx^{2} }} - \left( {e_{0} a} \right)^{2} q\left( x \right)} \right]_{x = L} = 0 $$
(57)

and

$$ \left[ {V_{x} } \right]_{x = L} = \left[ { - EI \frac{{d^{3} w_{b} }}{{dx^{3} }} - \left( {e_{0} a} \right)^{2} \frac{dq\left( x \right)}{dx}} \right]_{x = L} = 0 $$
(58)

Using the governing Eq. (36) and the boundary conditions prescribed by Eqs. (55)–(58), one could obtain the solution for bending component w b . The expression for w b obtained could be written as:

$$ w_{b} = \frac{{q_{0} L^{4} }}{24 E I}\left\{ {\begin{array}{*{20}c} {\left( {\frac{x}{L}} \right)^{4} - 4\left( {\frac{x}{L}} \right)^{3} + 6 \left( {\frac{x}{L}} \right)^{2} } \\ {} \\ { + \frac{{6 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} \left[ {2 + \left( {\frac{x}{L}} \right)} \right]} \\ {} \\ { - \left( {e_{0} a} \right)^{2} \frac{24}{{L^{2} }}\left[ {\frac{1}{2}\left( {\frac{x}{L}} \right)^{2} + \frac{{\left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} } \right]} \\ \end{array} } \right\} $$
(59)

Now, using the solution for w b in Eq. (31), one would obtain the expression for lateral deflection w as follows:

$$ w = \frac{{q_{0} L^{4} }}{24 E I}\left\{ {\begin{array}{*{20}c} {\left( {\frac{x}{L}} \right)^{4} - 4\left( {\frac{x}{L}} \right)^{3} + 6 \left( {\frac{x}{L}} \right)^{2} } \\ {} \\ { + \frac{{6 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} \left[ {5 \left( {\frac{x}{L}} \right) - 2 \left( {\frac{x}{L}} \right)^{2} } \right]} \\ {} \\ \end{array} } \right\} $$
(60)

Equation (60) is the expression for lateral deflection w obtained using the present nonlocal theory for the case of a cantilever beam carrying a uniformly distributed load of intensity q0. One could obtain the beam deflection expression of classical elasticity theory [11, 29] by ignoring the terms associated with small-scale effects in Eq. (60).

The expression for maximum lateral deflection, i.e., w at x = L can be written as:

$$ \left[ w \right]_{x = L} = \frac{{q_{0} L^{4} }}{24 E I}\left[ { 3 + \frac{{18 \left( { 1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} - \left( {e_{0} a} \right)^{2} \frac{12}{{L^{2} }}} \right] $$
(61)

10.3 Clamped-clamped beam carrying a uniformly distributed load

Consider a rectangular beam of length L as shown in figure 1. The beam is clamped at x = 0 and x = L. The beam carries a uniformly distribute load of intensity q0 over the beam span L.

The steps involved in obtaining the expression for lateral deflection w using Type 3 clamped end boundary conditions will now be discussed. The expression for lateral deflection w using Type 2 boundary conditions could be obtained following a similar pattern. For the case of a beam clamped at x = 0 and x = L, the boundary conditions to be used are:

At x = 0,

$$ \left[ w \right]_{x = 0} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = 0} = 0 $$
(62)

and

$$ \left[ {\frac{{dw_{b} }}{dx} + \frac{{h^{2} \left( {1 + \mu } \right)}}{20}\frac{{d^{3} w_{b} }}{{dx^{3} }}} \right]_{x = 0} = 0 $$
(63)

At x = L,

$$ \left[ w \right]_{x = L} = \left[ {w_{b} - \frac{{h^{2} \left( {1 + \mu } \right)}}{5}\frac{{d^{2} w_{b} }}{{dx^{2} }}} \right]_{x = L} = 0 $$
(64)

and

$$ \left[ {\frac{{dw_{b} }}{dx} + \frac{{h^{2} \left( {1 + \mu } \right)}}{20}\frac{{d^{3} w_{b} }}{{dx^{3} }}} \right]_{x = L} = 0 $$
(65)

Using the governing Eq. (36) and the boundary conditions prescribed by Eqs. (62)–(65), one could obtain the expression for bending component w b as follows:

$$ w_{b} = \frac{{q_{0} L^{4} }}{24 E I}\left\{ {\begin{array}{*{20}c} {} \\ {\left( {\frac{x}{L}} \right)^{4} - 2\left( {\frac{x}{L}} \right)^{3} + \left( {\frac{x}{L}} \right)^{2} } \\ {} \\ { + \frac{{3 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} \left[ {\left( {\frac{x}{L}} \right) - \left( {\frac{x}{L}} \right)^{2} } \right]} \\ {} \\ { + \frac{{2 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} \left[ {1 + \frac{{3 \left( {1 + \mu } \right)}}{5}\left( {\frac{h}{L}} \right)^{2} } \right]} \\ \end{array} } \right\} $$
(66)

Next, using the obtained solution for w b in Eq. (31), the expression for lateral deflection w could be written as:

$$ w = \frac{{q_{0} L^{4} }}{24 E I}\left\{ {\begin{array}{*{20}c} {\left( {\frac{x}{L}} \right)^{4} - 2\left( {\frac{x}{L}} \right)^{3} + \left( {\frac{x}{L}} \right)^{2} } \\ {} \\ { + 3 \left( {1 + \mu } \right)\left( {\frac{h}{L}} \right)^{2} \left[ {\left( {\frac{x}{L}} \right) - \left( {\frac{x}{L}} \right)^{2} } \right]} \\ \end{array} } \right\} $$
(67)

Equation (67) is the expression for lateral deflection w obtained using the present nonlocal beam theory for the case of a clamped-clamped beam carrying a uniformly distributed load of intensity q0. It can be noted that, there are no terms pertaining to micro-scale effects are present in the Eq. (67). This observation is also noted by Reddy and Pang [38] in case of analysis of clamped-clamped beams carrying uniformly distributed loads based on Eringen’s nonlocal elasticity theory.

The expression for maximum lateral deflection, i.e., w at x = L/2 could be written as:

$$ \left[ w \right]_{{x = \frac{L}{2}}} = \frac{{q_{0} L^{4} }}{24 E I}\left[ {\frac{1}{16} + \frac{{3 \left( {1 + \mu } \right)}}{4}\left( {\frac{h}{L}} \right)^{2} } \right] $$
(68)

11 Results and discussions

In this section, the lateral deflection parameter (\( \bar{w} \)) obtained for the case of simply supported, cantilever and clamped-clamped beams have been presented in the form of plots. The lateral deflection parameter (\( \bar{w} \)) used herein is defined as:

$$ \bar{w} = \frac{100 E I}{{q_{0} L^{4} }} \times \left[ w \right]_{max} $$
(69)

The lateral deflection parameter (\( \bar{w} \)) versus nonlocal parameter (K) plots pertaining to the case of simply supported, cantilever and clamped-clamped beams are given in figures 2–4. In figures 2 through 4, the lateral deflection parameters (\( \bar{w} \)) have been plotted for the following cases:

$$ \frac{h}{L} = 0.1, \, 0.2\quad {\text{and}}\quad K = \left( {e_{0} a} \right)^{2} = \, 0, \, 1, \, 2, \, 3, \, 4 $$

The Poisson’s ratio (μ) of the beam material is assumed to be 0.3. The length of the beam under consideration is taken as 10 nm.

Figure 2
figure 2

Plot of lateral deflection (\( \bar{w} \)) versus nonlocal parameter (K) for the case of a simply supported beam carrying a uniformly distributed load.

Full size image

Figures 2–4 also present the deflection results obtained by other nonlocal beam theories based on Eringen’s nonlocal elasticity theory. The deflections pertaining to Euler-Bernoulli beam theory (EBT), Timoshenko beam theory (TBT) and Reddy beam theory (RBT) plotted in figure 2 have been taken from a paper by Thai [23]. And, EBT and TBT deflections plotted in figures 3 and 4 have been calculated by present authors using the deflection expressions provided in ref. [38].

Figure 3
figure 3

Plot of lateral deflection (\( \bar{w} \)) versus nonlocal parameter (K) for the case of a cantilever beam carrying a uniformly distributed load.

Full size image
Figure 4
figure 4

Plot of lateral deflection (\( \bar{w} \)) versus nonlocal parameter (K) for the case of a clamped-clamped beam carrying a uniformly distributed load.

Full size image

11.1 Discussions on deflection results

With reference to the lateral deflection (\( \bar{w} \)) results presented in figures 2–4, the following points need to be noted:

  1. 1.

    Referring to plots pertaining to lateral deflection parameter (\( \bar{w} \)) for the case of a simply supported beam carrying a uniformly distributed load presented in figure 2, the following points need to noted:

    • The results obtained by using the present nonlocal beam theory are more or less same as those predicted by nonlocal version of Timoshenko and Reddy beam theories. Whereas, EBT underestimates the beam deflections in comparison to present, Timoshenko and Reddy beam theories. Also, the error in predicted deflections will increase as the h/L ratio increases. In case of h/L = 0.1 and K = 4, the predicted error is –2.33 % in comparison to present theory, whereas, the predicted error is – 8.69 %, in case of h/L = 0.2 and K = 4.

    • Further, the efforts involved in obtaining the solutions for beam problems by using the present theory are only marginally higher in comparison to that involved in case of Euler-Bernoulli Beam theory [13,14,15,16].

  2. 2.

    Referring to plots pertaining to lateral deflection parameter (\( \bar{w} \)) for the case of a cantilever beam carrying a uniformly distributed load presented in figure 3, the following points need to be noted:

    • The present beam theory results are same as those of TBT results when Type 2 clamped end boundary conditions are used. Further, the present beam theory results are marginally on higher side in comparison to TBT results when Type 3 clamped end boundary conditions are used.

    • The EBT results are not satisfactory in comparison to the present beam theory and TBT results. The EBT underestimates the beam deflections. Also, the error in predicted deflections will increase as the h/L ratio increases. In case of Type 2 boundary conditions, for h/L = 0.1 and K = 4, the predicted error is – 1.22 % in comparison to present theory, whereas, the predicted error is –4.72 %, in case of h/L = 0.2 and K = 4. And, in case of Type 2 boundary conditions, for h/L = 0.1 and K = 4, the predicted error is –1.82 % in comparison to present theory, whereas, the predicted error is –6.91 %, in case of h/L = 0.2 and K = 4.

  3. 3.

    Referring to plots pertaining to lateral deflection parameters (\( \bar{w} \)) for the case of a clamped-clamped beam carrying a uniformly distributed load presented in figure 4, the following points need to be noted:

    • The parameters associated with the small-scale effects do not have any influence on the beam deflections. The deflection results obtained are same as those one could obtain in case of clamped-clamped beam analysis using classical elasticity theory.

    • The present beam theory results are same as those of TBT results when Type 2 clamped end boundary conditions are used.

      Also, it is worthwhile to note that, for the case of clamped-clamped beams, the formulation of present theory (in case of Type 3 clamped end boundary conditions) based on classical elasticity theory would predict deflections as same as those of two-dimensional theory of elasticity solution [39] and Levinson beam theory [12].

    • EBT underestimates the deflections in comparison to the deflections obtained in case of present beam theory and TBT. Also, the error in predicted deflections will increase as the h/L ratio increases. In case of Type 2 boundary conditions, for h/L = 0.1 and K = 4, the predicted error is – 11.10 % in comparison to present theory, whereas, the predicted error is –33.30 %, in case of h/L = 0.2 and K = 4. And, in case of Type 2 boundary conditions, for h/L = 0.1 and K = 4, the predicted error is –13.49 % in comparison to present theory, whereas, the predicted error is –38.43 %, in case of h/L = 0.2 and K = 4.

12 Concluding remarks

In this paper, a single variable nonlocal theory for bending of micro- and nano-scale rectangular beams has been proposed. The noteworthy features of the theory presented here are:

  1. 1.

    The theory involves only one governing differential equation in terms of a single variable.

  2. 2.

    The governing differential equation and the expressions for bending moment and shear force of the present nonlocal beam theory are strikingly similar to those of nonlocal version of Euler-Bernoulli beam theory based on Eringen’s nonlocal elasticity theory.

  3. 3.

    The displacement field of the present theory gives rise to a realistic parabolic distribution of transverse shear stress across the beam cross-section.

  4. 4.

    The deflection results obtained for lateral deflection parameters by using the present nonlocal beam theory are quite accurate in comparison to the deflections obtained by other nonlocal version of first-order and higher-order beam theories.

In conclusion, a single variable shear deformable nonlocal beam theory presented in this paper could be utilized in an accurate, simplistic manner for the bending analysis of micro- and nano-scale rectangular beams.


Nomenclature

A:

Cross-sectional area of beam

a :

Internal characteristic length

b :

Beam width

D ijkl :

Elastic modulus tensor

E :

Modulus of elasticity

e 0 :

Material constant appropriate to each material

G :

Modulus of elasticity in shear

h :

Beam height

I :

Moment of inertia

i, j, k, l:

Suffixes (Represent rank of a tensor)

K :

Material parameter

L :

Beam length

M x :

Moment due to bending stress σ x

O-x-y-z:

Cartesian coordinate system

\( {\mathbb{X}},{\mathbb{X}}^{\prime } \) :

Reference points

\( \left| {{\mathbb{X}}^{\prime } - {\mathbb{X}}} \right| \) :

Euclidean distance

q 0 :

Intensity of a uniformly distributed lateral load

q(x):

Intensity of a distributed lateral load

\( t_{ij} \left( {{\mathbb{X}}^{\prime } } \right) \) :

Local stress tensor at any point \( {\mathbb{X}}^{\prime } \)

u, v, w:

Displacements in x, y, and z-directions, respectively

u b , w b :

Bending components of displacements u and w, respectively

u s , w s :

Shear components of displacements u and w, respectively

V :

Volume of the beam under consideration

V x :

Shear force due to shear stress \( \tau_{zx} \)

\( \bar{w} \) :

Non-dimensional maximum lateral deflection

x, y, z:

Cartesian coordinates

\( \alpha \) :

Kernel function

\( \gamma_{zx} \) :

Shear strain

\( \epsilon_{kl} \left( {{\mathbb{X}}^{\prime }} \right) \) :

Strain tensor at any point \( {\mathbb{X}}^{\prime } \)

\( \epsilon_{x} \) :

Normal strain

\( \mu \) :

Poisson’s ratio

\( \gamma_{zx} \) :

Shear strain

\( \sigma_{ij} \left( {\mathbb{X}} \right) \) :

Nonlocal stress tensor at a reference point \( {\mathbb{X}} \)

σ x , σ y , σ z :

Normal stresses

τ :

Constant

τ xy , τ yz , τ zx :

Shear stresses

∇2:

Laplacian operator