1 Introduction

The objective in second-order static structural analysis is to determine the balance of internal and external forces throughout the deformed configuration of a structure until plastic hinge formation occurs. Such analysis is a transcendental problem that requires an iterative solution. Second-order static structural analysis has three main parts: static equilibrium, kinetic analysis, and kinematic analysis (figure 1). The static equilibrium part evaluates internal force using the external forces throughout the deflected geometry (the deflection curve and cross section).

Figure 1
figure 1

Iterative flow chart of second-order static structural analysis.

Full size image

The kinetic part is curvature calculation from internal forces using the material constitutive law and section integration. The kinematic part determines the deflection by satisfying the compatibility requirements between the strain (curvatures) and displacements [1]. Kinematic analysis can be classified into two main areas. The first type of analysis depends on solutions using differential equations under geometric assumptions. The second type of analysis depends on geometric considerations as in elastica or as in curvature-based deflection methods, where geometrically precise deflection calculations are obtained in terms of the curvature without geometric assumptions [2].

Accurate deflection calculations in finite strain play an important role in ultimate or in post-collapse analysis, where in-plane stresses are considered. The solution time, convergence, and accuracy will be problems if the fundamental kinematic theories are not well selected according to the expected deflection. When a solution is obtained analytically, the reliability and limits of the solution and the deflection depend on geometric assumptions in kinematic theory. Otherwise, physically unrealistic deflections are unavoidable, particularly for large strain, large deflection, and large rotations. For the second type of analysis, the most well-known analytical solution is based on elliptical integrations, which are not capable of analyzing distributed loads, variable stiffness members, or material nonlinearity [3]. Moreover, solutions with elliptic integrals are very sensitive to even small errors in the calculation [4].

The finite element method (FEM) is the most widely used numerical structural analysis method [1]. FEM is based on conventional kinematic theories with geometric assumptions. Failure or convergence problems are unavoidable when considering high deflections beyond a certain limit, even with a large number of mesh elements and high CPU time. Therefore, there is a need for more powerful methods for more reliable deflection calculations and modeling to satisfy the increasing requirements of structural analysis.

The analytical solutions for beams that consider material and geometric nonlinearities are limited [5]. Solutions are available for nonlinear elastic material models, such as Ludwick type [6] and Ramberg–Osgood type materials [7]. Some forms of moment–curvature models attempted to simulate elasto-plastic behavior with hyperbolic-tangent [8] or logarithmic type nonlinearities [9]. Gao [10] reported an analytical solution for elasto-plastic finite strain in wide plates.

This study examined a new advanced step by adapting elasto-plastic behavior to curvature-based kinematic displacement theory (KDT) [11]. In KDT, deflection is generated precisely without making any geometric assumptions or using differential equations of the deflection curve. A new analytical solution is proposed for elasto-plastic prismatic/non-prismatic rectangular cross-sectioned beams subjected to a tip moment. The curvature values are used geometrically to form the deflection curve. The aim is to have a plain and comprehensible presentation. Therefore, the compatibility conditions and lateral torsional buckling are restrained by assuming planar deflection. In addition, internal forces are selected as a uniform moment distribution to avoid the need for an iterative procedure for second-order theory and governing equations for the shear effect. The analytical results of the applications were compared with results from the Abaqus FEM software package, and there was a coherent correlation within the limits of the software for large strain.

2 Fundamentals of curvature-based kinematic planar deflection calculation

Let the axes in curvilinear coordinates be the directions of the normal vectors of the principal planes of a structure. This makes it possible to describe the planar displacement of the structure with the deflection of its major reference axis α with a general regular skew curve [12]. Briefly, the structure is generated by cross sections in which the centroids C move along reference axis α. The plane of the cross section is normal to α, as shown in figure 2, where s is the curve length [12].

Figure 2
figure 2

Planar deflection curve of a structure.

Full size image

All cross sections of the structure are in equilibrium with the external and internal forces until fracture occurs. Resultant forces have to be in equilibrium with the stress distribution over the cross section. Constitutive laws are used to express the strain distribution. Strain distribution over a cross section is always linear and proportional to its curvature value, even for a nonlinear stress distribution. Therefore, this equilibrium can be represented by the curvature value of the cross section, regardless of elastic or inelastic behavior (figure 3).

Figure 3
figure 3

Strain and stress distribution over the cross section.

Full size image

The physical meaning of the curvature is the rate of change in the slope of the major axis, as expressed in (1). The curvature values of the cross sections of the beam-column are uniform for the segment length ds. The resultant forces on the segment are constant, or the segment is infinitesimal [11]. The shape of the segment for uniform curvature distribution is indicated by the arc of a circle with radius r (figure 4). The radius is equal to the absolute inverse ratio of the curvature, as expressed in (2). θ and θ+dθ respectively denote the initial and terminal points of the slope angle of the segment of the deflection curve with the x-axis (figure 4).

$$ \kappa = {\text{d}}\theta /{\text{d}}s $$
(1)
$$ r = \left| {1/\kappa } \right|. $$
(2)
Figure 4
figure 4

Segment of a deflection curve.

Full size image

The solution to (1) is very simple when curvilinear coordinates are used. If the curvature value over a segment is given, the only unknown dθ can be obtained from (1). Using dθ, the deflection curve calculation turns into a basic geometry problem. If the location and slope of the initial point, the length, and the radius of the arc in (2) are known, the terminal point of the segment can be determined easily using geometric considerations [11]. Briefly, the segment is expressed with an arc with center angle, curve length, chord length, and radius of dθ, ds, dc, and r, respectively.

However, the curvature on the structure is not always constant. Therefore, the main question is how the different arcs can be connected to compose a deflection curve, or how the deflection curve can be represented for a non-uniform curvature distribution. The deflection curve is a regular skew curve that is differentiable and needs to meet the continuity conditions [13, 14]. If the deflection curve is differentiable, the slope angle of the deflection curve in curvilinear coordinates can be evaluated from (1) just by integration. If the integration begins from a specific reference point where the slope angle is known, the slope angle of the terminal point can be derived from (1) by integrating as follows [15]:

$$ \theta \left( s \right) = \theta \left( 0 \right) + {\text{ }}\int\limits_{0}^{s} {\kappa \left( {\bar{s}} \right){\text{d}}\bar{s}}. $$
(3)

This integration only requires curvature values of the ds segments. Therefore, if the curvature distribution is known, the slope angles of the deflection curve can be obtained without any geometric assumptions. The relation between curvature (or strain) and displacement in curvilinear coordinates is considered as the exact solution:

$$ \frac{{{\text{d}}x}}{{{\text{d}}s}} = \cos \theta \left( {{s}} \right) $$
(4)
$$ \frac{{{\text{d}}z}}{{{\text{d}}s}} = \sin \theta \left( {{s}} \right). $$
(5)

Finally, the analytical expression for a deflection vector between the s curvilinear lengths away from the reference point on a deflection curve can be obtained by substituting (3) into (4) and (5) and integrating. The following expression is obtained (figure 1) [15]:

$$ {\varvec{\alpha }}\left( s \right) = x\left( s \right)\user2{i} + z\left( s \right)\user2{k} = {\text{ }}\int\limits_{0}^{s} {\cos \theta \left( {\bar{s}} \right){\text{d}}\bar{s}\user2{i}} + {\text{ }}\int\limits_{0}^{s} {\sin \theta \left( {\bar{s}} \right){\text{d}}\bar{s}\user2{k}} , $$
(6)

where i and k are the unit vectors of the rectangular Cartesian coordinate system.

The deflection curve of the entire structure can be constructed with these circular arc segments according to curvature-based kinematic theory [11]. The deflection calculation becomes just a kinematic geometric problem if the curvatures can be discrete and expressed by a function or a distribution. If the curvature distribution can be formulated for any complicated structure, the deflection curve can be evaluated using the displacement vectors (figure 5).

Figure 5
figure 5

Relative locations according to the reference point of the deflection curve.

Full size image

Fundamentally, deflection calculation is based on the differential equation of the deflection curve, as given in (1) and figure 3. The main goal is to determine the values of dz and dx. Small deflection theory assumes that lateral deflection is so small that the difference between dx and ds is zero. Additionally, the tangent angle at any point is assumed to be constant for an infinitesimal element length, which is so small that it yields its tangent value. The main assumptions in small deflection theory are summarized as follows (figure 4):

$$ {\text{d}}s = {\text{d}}x\quad{\text{and}}\quad\theta = \frac{{{\text{d}}z}}{{{\text{d}}x}}. $$

Therefore, the displacement based on small deflection theory can be determined as follows:

$$ \kappa = {\text{d}}\theta /{\text{d}}s \approx \frac{{{\text{d}}^{2} z}}{{{\text{d}}x^{2} }}. $$

The following is also assumed:

$$ {\text{d}}s \ne {\text{d}}c = \sqrt {{\text{d}}x^{2} + {\text{d}}z^{2} } \quad{\text{and}}\quad\theta \ne \arctan {\text{d}}z/{\text{d}}x = \varphi . $$

If we consider large deflection theory, the main assumptions are that the curvilinear length of the infinitesimal element is equal to the length of the displacement vector, and that the tangent angle is constant for an infinitesimal element length. Therefore, displacement under large deflection theory can be determined as follows:

$$ \kappa = {\text{d}}\theta /{\text{d}}s \approx \frac{{{\text{d}}^{2} z/{\text{d}}x^{2} }}{{\left( {1 + \left( {{\text{d}}z/{\text{d}}x} \right)^{2} } \right)^{3/2} }}. $$

From a geometric perspective, it is impossible to say that curvilinear length is equal to the magnitude of the incremental displacement vector dc between adjacent nodes. Therefore, there will always be numerical error if the segment length is not infinitesimal. Additionally, the slope angle at the initial point of the segment is not constant during the displacement of the segment. This means the deflection is linear between two adjacent points. However, the change in the slope angle is already defined with the curvature value in (1). With this simple KDT, it is possible to extend the analytical or numerical solutions of elastica or exact geometric solution of beams to distributed loads, variable stiffness members, or material nonlinearity under full geometric nonlinearity.

Even though Green or Jaumann strain components are powerful with Lagrangian formulation in nonlinear FEA, they fundamentally still include geometric assumptions. Therefore, a large number of mesh elements are necessary in the case of large rotation and large displacement. Another advantage of KDT is that the segment length is not important when the curvature value is constant over the segment, even if rotation and displacement are large (figure 5).

Particular solutions with the geometric use of the curvature in deflection studies have been reported. The well-known applications in the bending of beams are those with uniform curvature distributions, where the deflection curve forms with parts of a circle [16]. Tayyar and Bayraktarkatal [17] reported a numerical iterative method for the non-uniform curvature distributions of stiffened plates considering second-order theory and local plate buckling while neglecting the shear effect. This method provides an opportunity to form the most complex deflection curves easily via curvatures of the individual segments. Exact planar kinematic displacement theory for a non-uniform curvature distribution was first reported with the application of a tapered rectangular elastic cantilever beam subjected to a tip moment [11]. An analytical method for the deflection calculations using curvature values was originally reported with the application of an elastic rectangular tapered beam subjected to a tip moment [15]. Numerical analysis of an elastic perfectly plastic stiffened panel with KDT was presented by Bayraktarkatal and Tayyar [18] and Tayyar et al [19].

3 Analytical method for elastic perfectly plastic material behavior

The analysis is composed of two parts. In the kinetic part, the moment–curvature relationship of the cross section is determined by section integration from the resultant forces and material model. In the kinematic part, the deflection calculation is evaluated from the curvature functions obtained in the kinetic part. Kinetic analysis is considered for tapered and prismatic conditions. A uniform moment distribution is preferred for comprehensibility, and it is possible to derive any function for moment distribution over the deflection curve for use in the curvature equation to achieve a more sophisticated calculation.

3.1 Moment curvature relationship of elasto-plastic rectangular cross section

Under the assumptions of the Bernoulli–Navier hypothesis, the strain distribution over the cross section is linear, even when material and geometric nonlinearities take effect. All equilibrium equations are evaluated over the cross section. The strain distribution can be expressed as follows:

$$ \varepsilon \left( z \right) = \kappa \left( {z_{N} - z} \right), $$
(7)

where z N represents the shift between the neutral axis and curve axis (figure 3).

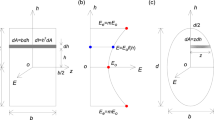
Figure 6 shows the typical stress–strain diagram of an elastic perfect plastic material, where σ 0 represents the tension yield stress, and ε 0 represents the tension yield strain. The strain–stress relationship for the elasto-plastic, homogenous, isotropic material assumes that the absolute values for the stress and strain in the tension and compression sides are the same.

Figure 6
figure 6

Stress/strain diagram of the elasto-plastic material.

Full size image

The stress distribution can be derived using the following expression, where E represents the Young’s modulus, and z cr represents the absolute critical distance from the neutral axis, where an inelastic behavior is started:

$$ \sigma = \left\{ {\begin{array}{*{20}l} {E \kappa \left( {z_{N} - z} \right)} \hfill & {\left| \kappa \right| < \varepsilon_{0} / \left| { z_{N} - z} \right|} \hfill \\ {\sigma_{0 } Sign\left( {\kappa \left( {z_{N} - z} \right)} \right)} \hfill & {\left| {\kappa } \right| \ge \varepsilon_{0} / \left| { z_{N} - z} \right|} \hfill \\ \end{array} } \right.. $$
(8)

Figure 7 shows the elastic, primary plastic, and secondary plastic stages of the strain and stress distribution over a rectangular cross section before plastic hinge (fully plastic) occurs. h represents the height of the cross section, and b represents the width.

Figure 7
figure 7

Strain/stress distribution of an elasto-plastic rectangular cross section.

Full size image

The equilibrium of the internal and external forces at any cross section is obtained from equilibrium equations over the cross-section area A. The first equation shows the relationship between the resultant normal forces, and the second equation shows the relationship between the moments at the cross section:

$$ N = \mathop {\iint }\limits_{A} \sigma {\text{d}}y {\text{d}}z $$
(9)
$$ M = \mathop {\iint }\limits_{A} \sigma z {\text{d}}y {\text{d}}z . $$
(10)

The maximum moment capacity can be expressed as follows when the cross section is fully plastic:

$$ M_{0} = b h^{2} \sigma_{0} /4. $$
(11)

Equation (9) can be satisfied only if z N equals zero when the action of normal forces and local buckling does not exist. Therefore, the neutral axis and curve axis is fixed at the centroid of the cross sections when a homogeneous material is considered. The moment equation can be expressed by substituting (8) into (10) as follows:

$$ M = \left\{ {\begin{array}{*{20}l} { - EI \kappa } \hfill & \quad {\left| \kappa \right| < 2 \varepsilon_{0} /{\text{h}}} \hfill \\ {M_{0} - \frac{{\sigma_{0 }^{3} b}}{{3 E^{2} \kappa^{2} }}} \hfill & \quad {\left| \kappa \right| \ge 2 \varepsilon_{0} /{\text{h}}} \hfill \\ \end{array} } \right. $$
(12)

where I represents second moment area. The curvature function can be evaluated from (12) and expressed as follows, where \( \kappa \) < 0, M > 0, and M < M 0:

$$ \kappa = \left\{ {\begin{array}{*{20}l} {\kappa_{e} = - \frac{ M}{ E I}} \hfill & {\left| M \right| < 2 \sigma_{0} I/{\text{h}}} \hfill \\ {\kappa_{p} = - \sqrt {\frac{{ b \sigma_{0}^{3} }}{{3 E^{2} \left( { M_{0} - M} \right)}} } } \hfill & {\left| M \right| \ge 2 \sigma_{0} I/{\text{h}}} \hfill \\ \end{array} } \right.. $$
(13)

3.2 Displacement equations of elasto-plastic cantilever prismatic beams

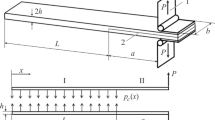
A cantilever beam subjected to a tip moment M with total beam length L is considered (figure 8). The width of the rectangular-beam cross section is b, and the height of the cross section is h. The reference point is selected as the clamped edge, where the slope angle is zero.

Figure 8
figure 8

Prismatic cantilever beam.

Full size image

Equation (3) can be expressed as follows by substituting (13) under a uniform bending moment, where the curvature will be constant throughout the curve.

$$ \theta \left( s \right) = \left\{ {\begin{array}{*{20}c} {\kappa_{e} s \quad \left| \kappa \right| < 2 \varepsilon_{0} / {\text{h}}} \\ {\kappa_{p} s\quad \left| \kappa \right| \ge 2 \varepsilon_{0} / {\text{h}}} \\ \end{array} } \right. . $$
(14)

The displacement vectors can be expressed as follows by substituting (14) into (6):

$$ \varvec{\alpha}\left( s \right) = \left\{ {\begin{array}{*{20}l} {\mathop \int \limits_{0}^{\varvec{s}} \begin{array}{*{20}c} {\cos \left( {\kappa_{e} {\bar{{s}}}} \right)d{\bar{{s}}}\, \varvec{i}} \\ \end{array} + \mathop \int \limits_{0}^{\varvec{s}} \sin \left( {\kappa_{e} {\bar{{s}}}} \right)d{\bar{{s}}}\,\varvec{j} \quad \left| \kappa \right| < 2 \varepsilon_{0} /{\text{h}}} \\ {\mathop \int \limits_{0}^{\varvec{s}} \begin{array}{*{20}c} {\cos \left( {\kappa_{p} {\bar{{s}}}} \right)d{\bar{{s}}}\, \varvec{i}} \\ \end{array} + \mathop \int \limits_{0}^{\varvec{s}} \sin \left( {\kappa_{p} {\bar{{s}}}} \right)d{\bar{{s}}}\,\varvec{j} \quad \left| \kappa \right| \ge 2 \varepsilon_{0} /{\text{h}}} \\ \end{array} } \right. . $$
(15)

3.2a Application for cantilever prismatic beams: The dimensions and main properties are selected as L = 1000 mm, E = 206,000 N/mm2, σ 0  = 1300 N/mm2, b = 20 mm, and h = 50 mm. No strain hardening effect after yield stress is taken into account. The analytical solutions could be obtained easily using (15). Figure 9 shows the deflection curve of the axis from the analytical solution of the elasto-plastic material properties.

Figure 9
figure 9

Deflection curves of the elasto-plastic cantilever beam.

Full size image

The in-plane deformation results were compared with results from Abaqus FEM software. The FEM results were obtained using the four-node quadrilateral membrane element M3D4R, as shown in figure 10. The highest deviation is approximately 4.2% when the tip displacement dz/L is 0.6155 and M/M p is 0.989. Unfortunately, the nonlinear FEM solution failed beyond this range, and convergence could not be achieved. In contrast, the KDT-based nonlinear solution generates results for ratios of up to M/M p  = 1. The shape of the deflection curve turns into a circle, which becomes increasingly smaller when it is close to a plastic hinge, as shown in figure 9.

Figure 10
figure 10

Tip deflection of the elasto-plastic cantilever beam.

Full size image

3.3 Displacement equations of tapered beams

A tapered cantilever beam under a uniform moment M and total beam length L is considered (figure 11). The width of the rectangular beam cross section is b, and heights of the beam cross section are H and H min at the clamped edge and free end, respectively (figure 11). The height of the cross section at any arc length can be expressed by (16), where s is the curve length.

Figure 11
figure 11

Tapered rectangular beam.

Full size image
$$ h\left( s \right) = H - \Delta h\frac{s}{L}. $$
(16)

The effect of tip moment is different in each cross section. The applied M moment can form a plastic hinge by the loss of height of the cross section. Therefore, the critical variable needs to be the height or its curve length instead of the moment. The critical curve length for a given tip moment where plastic hinge formation occurs by a decrease in cross section height is represented by s cr , which can be obtained by substituting (16) into (13):

$$ s_{cr} = \frac{L}{\Delta h}\left( {H - \sqrt {\frac{6 M}{{b \sigma_{0 } }} } } \right) . $$
(17)

Equation (10) is represented in parametric form. The reference point is selected as the clamped edge, where the slope angle is zero. Equation (3) can be expressed as follows by substituting (17) into (13) and then into (3) under a uniform bending moment:

$$ \theta \left( s \right) = \left\{ {\begin{array}{*{20}l} {\theta_{E} \left( s \right) = - \frac{{6 M s \left( {H + h\left( s \right)} \right)}}{{b E H^{2} h\left( s \right)^{2} }}} \hfill & { s < s_{cr} } \hfill \\ {\theta_{P} \left( s \right) = - \frac{{2 L \sigma_{0} }}{\sqrt 3 E \varDelta h}\left[ {G\left( 0 \right) - G\left( s \right)} \right]} \hfill & {s_{cr} < s} \hfill \\ \end{array} } \right.,\quad {\text{where }}G\left( {\text{s}} \right) = \ln \left( {b h\left( s \right) \sigma_{0} + \sqrt {4b \sigma_{0} \left( {b\frac{{h\left( s \right)^{2} \sigma_{0} }}{4} - M} \right)} } \right). $$
(18)

The displacement vector can be expressed by substituting (18) into (6):

$$ \varvec{\alpha}\left( s \right) = \left\{ {\begin{array}{*{20}l} {\mathop \int \limits_{0}^{\varvec{s}} \begin{array}{*{20}c} {\cos \theta_{P} \left( {\bar{s}} \right){\text{d}}\bar{s} \varvec{i}} \\ \end{array} + \mathop \int \limits_{0}^{\varvec{s}} \begin{array}{*{20}c} {\sin \theta_{P} \left( {\bar{s}} \right){\text{d}}\bar{s} \varvec{k}} \\ \end{array} } \hfill & { s_{cr} \le 0} \hfill \\ {\mathop \int \limits_{0}^{{s_{cr} }} \begin{array}{*{20}c} {\cos \theta_{E} \left( {\bar{s}} \right){\text{d}}\bar{s} \varvec{i}} \\ \end{array} + \mathop \int \limits_{{s_{cr} }}^{\varvec{s}} \begin{array}{*{20}c} {\cos \theta_{P} \left( {\bar{s}} \right){\text{d}}\bar{s} \varvec{i}} \\ \end{array} + \mathop \int \limits_{0}^{{s_{cr} }} \sin \theta_{E} \left( {\bar{s}} \right){\text{d}}\bar{s}\varvec{k} + \mathop \int \limits_{{s_{cr} }}^{\varvec{s}} \sin \theta_{P} \left( {\bar{s}} \right){\text{d}}\bar{s}\varvec{k}} \hfill & {0 < s_{cr} < s \le L.} \hfill \\ {\mathop \int \limits_{0}^{\varvec{s}} \begin{array}{*{20}c} {\cos \theta_{E} \left( {\bar{s}} \right){\text{d}}\bar{s}\varvec{i}} \\ \end{array} + \mathop \int \limits_{0}^{\varvec{s}} \sin \theta_{E} \left( {\bar{s}} \right){\text{d}}\bar{s}\varvec{k} } \hfill & { s_{cr} > L\quad or \quad s \le s_{cr} } \hfill \\ \end{array} } \right. $$
(19)

3.3a Application to cantilever tapered beams: The dimensions are selected as L = 1000 mm, b = 20 mm, H = 50 mm, and H min = 40 mm. The same material properties are applied to the tapered beam. M is taken as M p at the tip of the tapered beam. The analytical solutions of the elastic and elasto-plastic material property are obtained using (19). FEM results were obtained using Abaqus software, and figure 12 plots the results of the deflected shape. The highest deviation was found to be 0.1% at the free edge under the given conditions.

Figure 12
figure 12

Deflection curve of the tapered elasto-plastic cantilever beam at the plastic moment.

Full size image

4 Conclusion

The in-plane deformation of a planar curvature calculation for rectangular cross-sections has been explained, and kinematic analysis was derived for a prismatic/non-prismatic elasto-plastic cantilever beam under a uniform moment distribution. Nonlinear material behavior was coupled using KDT. The analytical results of the applications were compared with those from Abaqus FEM software, revealing coherent correlation within the limits of the software.

The advantage of precise modeling of the deflection curve provided high accuracy in the finite strain. This preliminary concept can be extended to a range of complicated problems. Uniform moments were selected, but there was no restriction in using a moment distribution over the deflection curve. For a non-uniform moment distribution, the resultant forces of each point on the deflection curve will depend on the deflected shape being evaluated. If needed, this second-order calculation can be determined iteratively.