1 Introduction

Nanofluids attracted the attention of researchers and engineers because of their striking thermophysical properties. Their origin can be traced back to 1993, when Masuda et al [1] dispersed powders of alumina, silica and titania in water to study the enhancement of thermal conductivity. In 1995, Choi and Eastman [2] coined the term ‘nanofluids’ and proposed a similar concept for engineering conventional heat transfer fluids for improved heat transfer applications. They presented the theoretical results and promising advantages of copper nanoparticles in water. Nanofluids, as the name suggests, are fluids with dispersed nanoparticles, which are preferred to the conventional heat transfer fluids. Unlike the conventional fluids, they are devoid of settling, deposition and clogging of flow channels and observed to have excellent heat transfer properties. These advantages are the result of the synergistic effect of the base fluids and the dispersed nanoparticles. In particular, graphene-based nanofluids are known for their high thermal conductivity. In applications, where magnetic field is used to control the fluid flow and heat transfer, fluids with higher thermal conductivity are used to enhance heat transfer through conduction. The prime reason for using graphene-based nanofluids in MHD studies is their higher thermal conductivity which enhances heat transfer. Several experiments and theoretical examinations on the synthesis and properties of graphene-based nanofluids are available, whereas numerical investigations on the flow over different geometries are limited. In particular, theoretical studies of graphene nanofluids under slip conditions are yet to be explored and exploited, besides many applications of nanofluids slip flow such as porous media applications, liquid coating, lubrication, MEMS, bio-MEMS etc. [3,4,5]. In this paper, we show that MHD flow of graphene oxide (GO) nanofluid under slip condition, enhances heat transfer through conduction.

The commonly used graphene nanofluids in literature are GO nanofluids and composite graphene nanofluids with ethylene glycol and water as base fluids [6]. Azimi et al [7] evaluated heat transfer analytically when GO nanofluid flows unsteadily within moving plates. They have conducted a comparative analysis by disperising GO, alumina, titania and silver nanoparticles and it is interpreted that silver nanofluid has the highest Nusselt number and it increases with volume fraction. Gul et al [8] examined the 2D flow in an upright channel. In this study, they concluded that GO with ethylene glycol has stronger thermal efficiency than water-based GO. Ullah et al [9] examined the 3D flow where the fluid is pressed between vertical channels. Both investigations emphasise the impacts of strong magnetic effects on the nanofluid flow when the medium is considered to be porous and it is concluded that magnetic field parameter controlled the fluid flow. Barai et al [6] noticed that the commonly used graphene nanofluids in literature are GO nanofluids and composite graphene nanofluids with ethylene glycol and water as base fluids. Also, the analytical investigation by Javanmard et al [10] focussed on the flow between concentric pipes with varying ratios under the impact of magnetic effects. But, in this case, the effects of Brownian motion and thermophoresis parameters are ignored and the results show that the magnetic field parameter reduces the temperature. Jamshed et al [11] examined the Sutterby nanofluid flow over a stretching and slippery surface including the impacts caused by radiative heat flux using hybrid copper and graphene nanoparticles. From the results obtained, the temperature field is observed to enhance with an increase in the volume fraction of copper and GO nanoparticles, while the mass fraction field is observed to increase with an increase in activation energy. The slip flow of titanium dioxide and GO nanofluids using Levenberg–Marquardt scheme in neural networks was studied by Khan et al [12]. The influence of flow variables on velocity, temperature and concentration profiles are discussed and the absolute error values are found to range between \(10^{-1}\) and \(10^{-8}\).

The studies on stretching geometries such as the one using Cattaneo–Christov model on hybrid graphene nanofluid flow with silver particles flowing above a cylinder stretching linearly is examined by Mamatha et al [13]. In this analysis, it is noticed that the graphene nanofluid has a better thermal performance and lesser impact of Lorentz force compared to silver nanofluid under the influence of magnetic field. Rehman et al [14] reported that the velocity and temperature profiles increased respectively with volume fraction and Eckert number, when the dynamic viscosity of the flow along a stretching cylinder is studied. This study was computed using optimal homotopy analysis method and emphasised the importance of viscous dissipation in the flow of nanofluids. Sarkar et al [15] analysed the MHD flow of the non-Newtonian Sisko nanofluid over a linearly stretching cylinder under the influence of velocity slip, chemical reaction and thermal radiation. From the graphical outcomes, it is concluded that the fluid temperature is elevated with radiation parameter and thermal Biot number and nanoparticle concentration decreases with activation energy parameter. Also, the entropy is found to increase with magnetic field. Ali et al [16] assessed the effectiveness of Hall currents and power-law slip condition on the hydromagnetic convective flow of an electrically conducting power-law fluid over an exponentially stretching sheet under a strong variable magnetic field and thermal radiation. From the investigation, it was concluded that Hall current enhances the velocity profiles and reduces skin friction coefficients and the temperature for the shear-thinning fluid is relatively higher than the corresponding temperature of the shear-thickening fluid. Ali et al [17] also studied the hydrothermal prominence of a mixed convective flow of a hybrid nanoliquid with single-walled and multi-walled carbon nanotubes and magnetite nanoparticles over a convectively heated extending curved surface under the influence of a uniform transverse magnetic field. Among various conclusions, the depletion of temperature profile with curvature parameter is to be noted. Rehman and Salleh [18] presented an analytic solution for the stagnation point flow of unsteady GO nanofluids with ethylene glycol and water as the base fluids with MHD effects and concluded that the unsteady parameter and Eckert number respectively reduce the velocity profiles and Nusselt number for both nanofluids. Das et al [19] numerically examined the magneto-nanofluid flow with copper, aluminium oxide and titanium dioxide particles over a curved stretching surface in the presence of viscous dissipation by adopting convective boundary conditions. It was observed that the fluid flow is controlled and temperature is increased with the magnetic parameter. Das et al [20] theoretically investigated the Darcy–Forchheimer flow of a magneto-couple stress fluid over an inclined exponentially stretching sheet using Stokes couple stress model. Two different kinds of thermal boundary conditions, namely, the prescribed exponential order surface temperature (PEST) and prescribed exponential order heat flux, are considered in the heat transfer analysis. It is found that the temperature profiles are generally increased with larger magnetic field and are consistently higher for the PEST case. Ali et al [21] examined the Cattaneo–Christov double diffusions theory in magneto-cross nanomaterial flow conveying gyrotactic micro-organisms over an extending horizontal cylinder and plate under velocity slippage, and activation energy with chemical reaction. From the results, it is visualised that flat plate offers less temperature than cylindrical surface when the flow occurs.

Other notable investigations, such as the numerical examination of the MHD flow of non-Newtonian nanofluid in a pipe by Ellahi [22] documented the decrease in fluid motion with the MHD. Ellahi et al [23] investigated the combined effects of MHD heat transfer flow under the influence of slip over a moving flat plate. The obtained results show that the temperature increases by increasing the values of MHD parameter. Ellahi et al [24] examined peristaltically moving Jeffrey fluid under the combined effects of slip and porosity under low Reynolds number and long wavelength. It is noticed that in the respective domain the velocity of the fluid declines for the slip parameter. Bhatti et al [25] studied the flow of blood in a catheterised tapered artery by considering the hybrid Sutterby nanofluid in the presence of gold (Au) and copper (Cu) nanoparticles in the presence of an intense external magnetic field. It is found that the Sutterby fluid parameter opposes the flow negligibly, whereas the Hartmann number strengthens the flow field. In addition, the trapping mechanism demonstrated that the fluid parameters influence the size and frequency of the bolus even though no impacts on non-tapered arteries were observed. Shehzad et al [26] investigated the multilayer coatings fully developed with steady Newtonian and non-Newtonian fluids through parallel inclined plates. The main observation in this study is that temperature and both axial and transverse velocity profiles increased with Jeffrey parameter in the region filled with Jeffrey fluid.

In spite of the computational studies on fluid flow, literature lacks the investigations on MHD flow of GO nanofluid over cylindrical geometries. Moreover, GO nanofluids in lower concentrations are experimentally observed to exhibit Newtonian behaviour [6, 27,28,29]. The intent of this paper is to model the Newtonian flow of GO nanofluids with water as the base fluid. The flow is considered over a linearly stretching cylinder in the presence of magnetic field under the slip condition with a view to investigate the aforesaid underexplored research area and to document the significance of dispersing GO nanoparticles in water when magnetic field is introduced.

2 Governing equations of the problem

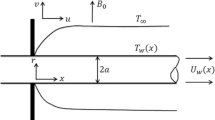
The flow of GO nanoparticles of size 1–100 nm dispersed in water is considered along a cylinder radius R aligned horizontally whose radial and axial directions are taken as (r, z). The following assumptions are made to model the flow over a cylinder:

  • We assume the flow to be steady and axisymmetric.

  • Let the u component of velocity be along the radial direction and w component be along the axial direction.

  • A uniform magnetic field \(B_0\) is applied along the radial direction.

  • The induced magnetic field and thus the induced electric field are ignored.

  • The body force due to gravity, Lorentz force, the effect of viscous dissipation, Brownian motion and thermophoresis are taken into consideration.

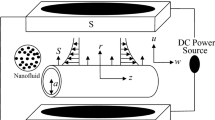
The representative picture of the flow is given in figure 1. With the above assumptions the appropriate governing equations [30] at the boundary layer are written using the nanofluid model proposed by Buongiorno [31],

$$\begin{aligned} \dfrac{\partial (ru)}{\partial r} + \dfrac{\partial (rw)}{\partial z}&= 0 \end{aligned}$$
(1)
$$\begin{aligned} u\dfrac{\partial w}{\partial r} + w\dfrac{\partial w}{\partial z}&= - \dfrac{\sigma _{nf}B_0^2}{\rho _{nf}}w + \dfrac{\mu _{nf}}{\rho _{nf}}\bigg (\dfrac{\partial ^2w}{\partial r^2} + \dfrac{\partial w}{r\partial r}\bigg ) \nonumber \\&\quad + \dfrac{g}{\rho _{nf}}((\rho \beta )_{nf}(1-C_\infty )(T-T_\infty )\nonumber \\&\quad +(\rho _{sp}-\rho _{bf})(C-C_\infty )) \end{aligned}$$
(2)
$$\begin{aligned} u\dfrac{\partial T}{\partial r} + w\dfrac{\partial T}{\partial z}&= \dfrac{\kappa _{nf}}{(\rho C_p)_{nf}}\bigg (\dfrac{\partial ^2 T}{\partial r^2} + \dfrac{\partial T}{r\partial r}\bigg )\nonumber \\ {}&\quad + \dfrac{\mu _{nf}}{(\rho C_p)_{nf}}\bigg (\dfrac{\partial w}{\partial r}\bigg )^2 \nonumber \\&\quad + \tau \bigg (D_B\dfrac{\partial C}{\partial r}\dfrac{\partial T}{\partial r} + \dfrac{D_T}{T_\infty }\bigg (\dfrac{\partial T}{\partial r}\bigg )^2\bigg ) \end{aligned}$$
(3)
$$\begin{aligned} u\dfrac{\partial C}{\partial r} + w\dfrac{\partial C}{\partial z}&= D_B\bigg (\dfrac{\partial ^2 C}{\partial r^2} + \dfrac{\partial C}{r\partial r}\bigg )\nonumber \\ {}&\quad + \dfrac{D_T}{T_\infty }\bigg (\dfrac{\partial ^2 T}{\partial r^2} + \dfrac{\partial T}{r\partial r}\bigg ). \end{aligned}$$
(4)
Fig. 1
figure 1

Schematic representation of the flow over a stretching cylinder.

Full size image

The corresponding boundary conditions are [32]

$$\begin{aligned}&u=0,\quad w(r,z)=\dfrac{U_0 z}{l}+S_w\nu _{bf}\dfrac{\partial w}{\partial r},\nonumber \\ {}&T=T_w, \quad C=C_w, \quad \text {at }r=R,\nonumber \\&w\rightarrow 0, \quad T\rightarrow T_\infty \quad \text {and} \quad C\rightarrow C_\infty \quad \text {as } r\rightarrow \infty . \end{aligned}$$
(5)

The symbols \(T_w\) and \(T_\infty \) are the fluid temperatures at the wall and at free stream respectively, and \(C_w\) and \(C_\infty \) are the concentrations of the nanofluid at the wall and at free stream, \(W(z)={U_0z}/{l}\) is the stretching velocity, \(S_w\) is the velocity slip factor, \(U_0\) and l are the reference velocity and the characteristic length, respectively.

The thermophysical properties of nanofluids defined in [8, 33] are taken as

$$\begin{aligned}&\mu _{nf}=\dfrac{\mu _{bf}}{(1-\Phi )^{2.5}}, \quad \rho _{nf}=(1-\Phi )\rho _{bf}+\Phi \rho _{sp},\\&\alpha _{nf}=\dfrac{\kappa _{nf}}{(\rho C_p)}_{nf},\\&{(\rho C_p)}_{nf}=(1-\Phi ){(\rho C_p)}_{bf}+\Phi {(\rho C_p)}_{sp},\\&{(\rho \beta )}_{nf}=(1-\Phi ){(\rho \beta )}_{bf}+\Phi {(\rho \beta )}_{sp}, \quad \\&\dfrac{\kappa _{nf}}{\kappa _{bf}}=\dfrac{\kappa _{sp}+2\kappa _{bf}+2\Phi (\kappa _{bf}-\kappa _{sp})}{\kappa _{sp}+2\kappa _{bf}-\Phi (\kappa _{bf}-\kappa _{sp})}, \quad \\&\dfrac{\sigma _{nf}}{\sigma _{bf}}=\dfrac{\sigma _{sp}+2\sigma _{bf}+2\Phi (\sigma _{bf}-\sigma _{sp})}{\sigma _{sp}+2\sigma _{bf}-\Phi (\sigma _{bf}-\sigma _{sp})}. \end{aligned}$$

The suffixes bf, nf, sp denote base fluid, nanofluid and solid particle and the quantities \(\mu \), \(\rho \), \(C_p\), \(\alpha \), \(\beta \) and \(\kappa \) denote dynamic viscosity, density, specific heat capacity, thermal diffusivity, thermal expansion and thermal conductivity coefficient, respectively. The values of the thermophysical properties of GO and water are presented in table 1.

Table 1 Values of thermophysical properties [34,35,36,37,38,39].
Full size table

The idea of similarity transformation broadly refers to the transformation of the given problem to a similar and simpler problem using the variables called similarity variables. In this study, it displays the physical similarity within the given problem such as the similarities of velocity, temperature and concentration profiles. These variables are used to reduce the number of independent variables of the problem under consideration. The similarity variables used here are defined as follows:

$$\begin{aligned}&\eta =\dfrac{r^2-R^2}{2R}{\sqrt{\dfrac{U_0 }{\nu _{bf} l}}}, \quad \psi (\eta )=\sqrt{\dfrac{U_0 \nu _{bf}}{l}}Rzf(\eta ), \quad \nonumber \\&u=\dfrac{-R}{r}\sqrt{\dfrac{U_0\nu _{bf}}{l}}f(\eta ) \quad \nonumber \\&w=\dfrac{U_0z}{l}f'(\eta ), \quad \theta (\eta )=\dfrac{T-T_\infty }{T_f-T_\infty }, \quad \nonumber \\&\phi (\eta )=\dfrac{C-C_\infty }{C_f-C_\infty }. \end{aligned}$$
(6)

Using these variables, eqs (1)–(4) are written as

$$\begin{aligned}&A_1(1+2\alpha \eta )f''' + 2A_1\alpha f'' + \lambda (A_2\theta + A_3N_r\phi )\nonumber \\&\quad + ff'' - f'^2 - A_4Ha^2f' = 0 \end{aligned}$$
(7)
$$\begin{aligned}&(1+2\alpha \eta )\theta '' + 2\alpha \theta ' + A_5PrEc(1+2\alpha \eta )f''^2 \nonumber \\&\quad + A_6((1+2\alpha \eta )(N_b\theta '\phi ' + N_t\theta '^2) + Prf\theta ') = 0 \end{aligned}$$
(8)
$$\begin{aligned}&(1+2\alpha \eta )\phi '' + 2\alpha \phi '\nonumber \\ {}&\quad + \dfrac{N_t}{N_b}((1+2\alpha \eta )\theta '' + 2\alpha \theta ') + Scf\phi ' = 0. \end{aligned}$$
(9)

The corresponding boundary conditions are transformed as

$$\begin{aligned}&\text {at }\eta =0, \quad f(0)=0, \quad f'(0)=1+Sf'',\nonumber \\ {}&\quad \theta =1, \quad \phi =1\nonumber \\&\text {as } \eta \rightarrow \infty , \quad f'=0,\quad \theta =0, \quad \phi =0. \end{aligned}$$
(10)

The constant coefficients and the non-dimensional numbers used, namely the mixed convection parameter \(\lambda \), the curvature parameter \(\alpha \), Prandtl number Pr, buoyancy ratio \(N_r\), Eckert number Ec, heat capacity ratio \(\tau \), Brownian motion parameter \(N_b\), thermophoresis parameter \(N_t\), Hartmann number Ha and slip parameter S are defined as

$$\begin{aligned}&A_1=\dfrac{\rho _{bf}(1-\Phi )^{-2.5}}{((1-\Phi )\rho _{bf}+\Phi \rho _{sp})},\\&A_2=\dfrac{(1-\Phi ) + \Phi ({(\rho \beta _{sp})}/{(\rho \beta _{bf}))}}{(1-\Phi )\rho _{bf}+\Phi \rho _{sp}},\quad Ha=\dfrac{\sigma _{bf}B_0^2l}{\rho _{bf}U_0}, \quad \\&A_3=\dfrac{\kappa _{sp}+2\kappa _{bf}-\Phi (\kappa _{bf}-\kappa _{sp})}{\kappa _{sp}+2\kappa _{bf}+2\Phi (\kappa _{bf}-\kappa _{sp})}, \\&N_r=\dfrac{(\rho _p-\rho _{bf})(C_f-C_\infty )}{(\beta _t)_{bf}(1-C_\infty )(T_f-T_\infty )}, \quad \\&A_4=\bigg (\dfrac{\rho _{bf}}{(1-\Phi )\rho _{bf}+\Phi \rho _{sp}}\bigg )\\ {}&\qquad \quad \times \bigg (\dfrac{\sigma _{sp}+2\sigma _{bf}+2\Phi (\sigma _{bf}-\sigma _{sp})}{\sigma _{sp}+2\sigma _{bf}-\Phi (\sigma _{bf}-\sigma _{sp})}\bigg ), \quad \\&\tau =\dfrac{(\rho C_p)_{sp}}{(\rho C_p)_{nf}}, \quad \\&A_5=\dfrac{\nu _{bf}\big (\kappa _{sp}+2\kappa _{bf}-\Phi (\kappa _{bf}-\kappa _{sp})\big )}{\kappa _{bf}\big (\kappa _{sp}+2\kappa _{bf}+2\Phi (\kappa _{bf}-\kappa _{sp}\big )}\\&\qquad \quad \times ((1-\Phi )(\rho C_p)_{bf}+\Phi (\rho C_p)_{sp}),\\&A_6=\bigg ((1-\phi )+\dfrac{\phi (\rho C_p)_{sp}}{(\rho C_p)_{bf}}\bigg )\\ {}&\qquad \quad \times \bigg (\dfrac{\kappa _{sp}+2\kappa _{bf}-\Phi (\kappa _{bf}-\kappa _{sp})}{\kappa _{sp}+2\kappa _{bf}+2\Phi (\kappa _{bf}-\kappa _{sp})}\bigg ), \\&Pr=\dfrac{\mu _{bf} C_{p_{bf}}}{\kappa },\quad \\&N_b=\dfrac{\tau D_B (C_f-C_\infty )(\rho C_p)_{bf}}{\kappa _{bf}}, \\&N_t=\dfrac{\tau D_T (T_f-T_\infty )(\rho C_p)_{bf}}{\kappa _{bf}T_\infty }, \quad Sc=\dfrac{\nu _{bf}}{D_B}, \quad \\&Ec=\dfrac{U_0^2 z^2}{l^2C_p(T_f-T_\infty )}, \lambda =\dfrac{gl^2\beta }{U\infty ^2 z}(T_f-T_\infty ),\\&\alpha =\sqrt{\dfrac{\nu l}{U_0 R^2}}, S=S_w\sqrt{\dfrac{U_0\nu _{bf}}{l}}. \end{aligned}$$

The quantities of practical importance, namely local Nusselt number Nu, local Sherwood number Sh and skin friction \(C_f\) are derived as follows:

$$\begin{aligned}&Nu(Re\,z/l)^{-1/2}= -\theta '(0),\nonumber \\&Sh(Re\,z/l)^{-1/2}= -\phi '(0),\nonumber \\&C_f(Re\,z/l)^{1/2}= C_1f''(0), \end{aligned}$$
(11)

where \(Re={U_0 z}/{\nu _{bf}}\) is the local Reynolds number and \(C_1=2(1-\Phi )^{-2.5}\big ((1-\Phi ) + \Phi {\rho _{sp}}/{\rho _{bf}}\big )^{-1}\) is a constant. We propose an assessment for the generated entropy and derive the entropy generation numbers in the next section.

3 Entropy generation analysis

The generated entropy depends on three parts, namely the entropy generated due to temperature term, entropy caused by viscous dissipation term and that due to concentration term. Hence, the entropy generation rate \(S_G\) can be written as [40]

$$\begin{aligned} S_G&=\dfrac{\kappa _{nf}}{T_\infty ^2}\bigg (\dfrac{\partial T}{\partial r}\bigg )^2 + \dfrac{\mu _{nf}}{T_\infty }\bigg (\dfrac{\partial w}{\partial r}\bigg )^2 + \dfrac{RD_B}{C_\infty }\bigg (\dfrac{\partial C}{\partial r}\bigg )^2 \nonumber \\&\quad + \dfrac{RD_B}{T_\infty }\bigg (\dfrac{\partial T}{\partial r}\bigg )\bigg (\dfrac{\partial C}{\partial r}\bigg ), \end{aligned}$$
(12)

where the first term on the RHS gives the thermodynamic irreversibility induced by temperature, the second term is the irreversibility induced by viscous dissipation and the last two terms are ascribed to concentration. The characteristic entropy generation rate \(S_{G_0}\) is given by \(S_{G_0}={\kappa _{nf}(T_f-T_\infty )^2}/{(T_\infty L)^2}\). From \(S_G\) and \(S_{G_0}\), the dimensionless entropy generation number is given by \(N_S={S_G}/{S_{G_0}}\).

Using the similarity variables, \(N_S\) can also be written as

$$\begin{aligned} N_S&=(1+2\alpha \eta )\dfrac{Re}{\chi }\bigg (\theta '^2 + B_1\dfrac{EcPr}{\Omega _T}f''^2 \nonumber \\&\quad + B_2M_m\dfrac{\Omega _C}{\Omega _T}\phi '\bigg (\dfrac{\Omega _C}{\Omega _T}\phi '+\theta '\bigg )\bigg ) \end{aligned}$$
(13)
$$\begin{aligned}&=N_{S_h}+N_{S_f}+N_{S_m}, \end{aligned}$$
(14)

where \(N_{S_h}\) is the irreversibility by heat transfer, \(N_{S_f}\) is the irreversibility by fluid friction and \(N_{S_m}\) is the irreversibility caused by mass transfer. The non-dimensional constant parameter in (13) is defined as \(\chi ={zl}/{L^2}\) and the constants are given by \(B_1=(1-\phi )^{-2.5}{\kappa _{bf}}/{\kappa _{nf}}\) and \(B_2={\kappa _{bf}}/{\kappa _{nf}}\).

The predominant cause for entropy generation is determined from Bejan number, \(Be={N_{S_h}}/{N_S}\). Eliciting from the entropy distribution ratio given by Bejan [41], Paoletti et al [42] proposed that if \(Be>0.5\), then the irreversibility influenced by heat transfer is the major cause of entropy generation, if \(Be<0.5\), then the entropy generation is influenced by magnetic field, fluid friction and mass transfer irreversibility and if \(Be=0.5\), then contribution to the generated entropy comes equally from all the irreversibilities, fluid friction, heat transfer and mass transfer.

4 Numerical solution

The successive linearisation method used in [43,44,45] is adapted to solve the ODEs (7)–(9) and (10).

We expand the functions \(f(\eta )\), \(\theta (\eta )\) and \(\phi (\eta )\) as

$$\begin{aligned} f&=f_i + \sum _{m=0}^{i-1}f_m, \nonumber \\ \theta&=\theta _i + \sum _{m=0}^{i-1}\theta _m, \quad \phi =\phi _i + \sum _{m=0}^{i-1}\phi _m, \end{aligned}$$
(15)

where \(f_i(\eta )\), \(\theta _i(\eta )\) and \(\phi _i(\eta )\) are unknown and we get the functions \(f_m(\eta )\), \(\theta _m(\eta )\) and \(\phi _m(\eta )\) by linearising and recursively iterating the linear equations to the order of SLM approximation. We apply spectral collocation method to iterate the functions using Chebyshev polynomials and Gauss Lobato collocation points. Also, a one-to-one correspondence is applied to these points and the domain such that \([0,\infty ]\) is transformed to \([-1,1]\), using the scaling parameter L.

Table 2 Comparison of \(\theta '(0)\) calculated by the present method for \(S=0\), \(Ha=0\), \(Ec=0\) and \(A_i=1\), \(\forall i=1,2,\ldots ,6\) with ref. [46].
Full size table
Fig. 2
figure 2

Variations of \(f'\) with (a) \(\alpha \), (b) \(\lambda \), (c) Ha and (d) S.

Full size image

The linearised equations with boundary conditions obtained by substituting (15) in (7)–(9) and (10) are

$$\begin{aligned}&a_{1,i-1}f_i''' + a_{2,i-1}f_i'' + a_{3,i-1}f_i' + a_{4,i-1}f_i + a_{5,i-1}\theta _i \nonumber \\&\quad + a_{6,i-1}\phi _i = p_{i-1} \end{aligned}$$
(16)
$$\begin{aligned}&b_{1,i-1}f_i'' + b_{2,i-1}f_i + b_{3,i-1}\theta _i'' + b_{4,i-1}\theta _i' + b_{5,i-1}\phi _i'\nonumber \\&\quad = q_{i-1} \end{aligned}$$
(17)
$$\begin{aligned}&c_{1,i-1}f_i + c_{2,i-1}\theta _i'' + c_{3,i-1}\theta _i' + c_{4,i-1}\phi _i'' + c_{5,i-1}\phi _i' \nonumber \\&\quad = r_{i-1} \end{aligned}$$
(18)

such that

$$\begin{aligned}&\text {at }\eta =0, \quad f_i(0)=0, \quad f_i'(0)=1,\nonumber \\ {}&\quad \theta _i(0)=1, \quad \phi _i(0)=1\nonumber ,\\&\text {as } \eta \rightarrow \infty , \quad f_i'=0,\quad \theta _i=0, \quad \phi _i=0. \end{aligned}$$
(19)
Fig. 3
figure 3

Variations of \(\theta \) with (a) \(\alpha \), (b) \(\lambda \), (c) Ha and (d) S.

Full size image
Fig. 4
figure 4

Variations of \(\phi \) with (a) \(\alpha \), (b) \(\lambda \), (c) \(N_b\), (d) \(N_t\), (e) Ha and (f) S.

Full size image
Fig. 5
figure 5

Influence of (a) \(\alpha \) on \(N_S\), (b) \(\alpha \) on Be, (c) \(\lambda \) on \(N_S\), (d) \(\lambda \) on Be, (e) Ec on \(N_S\) and (f) Ec on Be.

Full size image
Fig. 6
figure 6

Influence of (a) Ha on \(N_S\), (b) Ha on Be, (c) S on \(N_S\) and (d) S on Be.

Full size image
Table 3 Nusselt number, Sherwood number and skin friction values.
Full size table

The coefficients in the above equations are given by

$$\begin{aligned} a_{1,i-1}&=A_1(1+2\alpha \eta ), \quad a_{2,i-1}=2A_1\alpha + \sum _{m=0}^{i-1}f_m, \\ a_{3,i-1}&=-2\sum _{m=0}^{i-1}f_m' - A_4Ha, \\ a_{4,i-1}&=\sum _{m=0}^{i-1}f_m'', \quad a_{5,i-1}=A_2\lambda , a_{6,i-1}=A_3\lambda N_r, \\ b_{1,i-1}&=2A_5PrEc(1+2\alpha \eta )\sum _{m=0}^{i-1}f_m'',\\ b_{2,i-1}&=A_6Pr\sum _{m=0}^{i-1}\theta _m', b_{3,i-1}=(1+2\alpha \eta ), \quad \\ b_{4,i-1}&=2\alpha + A_6(1+2\alpha \eta )N_b\sum _{m=0}^{i-1}\phi _m' \\&\quad + 2A_6(1+2\alpha \eta )N_t\sum _{m=0}^{i-1}\theta _m' + A_6Pr\sum _{m=0}^{i-1}f_m, \quad \\ b_{5,i-1}&=A_6(1{+}2\alpha \eta )N_b\sum _{m=0}^{i-1}\theta _m', \quad c_{1,i-1}{=}Sc\sum _{m=0}^{i-1}\phi _m',\\ c_{2,i-1}&=\dfrac{N_t}{N_b}(1+2\alpha \eta ), \\ c_{3,i-1}&=\dfrac{N_t}{N_b}2\alpha , \quad c_{4,i-1}=(1+2\alpha \eta ), \\ c_{5,i-1}&=2\alpha + Sc\sum _{m=0}^{i-1}f_m, \\ p_{i-1}&=-\bigg [A_1(1+2\alpha \eta )\sum _{m=0}^{i-1}f_m''' + 2A_1\alpha \sum _{m=0}^{i-1}f_m'' \\&\quad + A_2\lambda \sum _{m=0}^{i-1}\theta _m + A_3\lambda N_r\sum _{m=0}^{i-1}\phi _m \\&\quad + \sum _{m=0}^{i-1}f_m\sum _{m=0}^{i-1}f_m'' {-} \bigg (\sum _{m=0}^{i-1}f_m'\bigg )^2\\&\quad {+} A_4Ha\sum _{m=0}^{i-1}f_m' \bigg ] \end{aligned}$$
$$\begin{aligned} q_{i-1}=&-\bigg [(1+2\alpha \eta )\sum _{m=0}^{i-1}\theta _m'' + 2\alpha \sum _{m=0}^{i-1}\theta _m' \\&+ A_5PrEc(1+2\alpha \eta )\bigg (\sum _{m=0}^{i-1}f_m'' \bigg )^2 \\&+ A_6(1+2\alpha \eta )N_b\sum _{m=0}^{i-1}\theta _m'\sum _{m=0}^{i-1}\phi _m'\\&+ A_6(1+2\alpha \eta )N_b\bigg (\sum _{m=0}^{i-1}\theta _m'\bigg )^2 \\&+ A_6Pr\sum _{m=0}^{i-1}f_m\sum _{m=0}^{i-1}\theta _m' \bigg ], \\ r_{i-1}=&-\bigg [(1+2\alpha \eta )\sum _{m=0}^{i-1}\phi _m'' + 2\alpha \sum _{m=0}^{i-1}\phi _m'\\&+ \dfrac{N_t}{N_b}(1+2\alpha \eta )\sum _{m=0}^{i-1}\theta _m'' \\&+ \dfrac{N_t}{N_b}2\alpha \sum _{m=0}^{i-1}\theta _m' + Sc\sum _{m=0}^{i-1}f_m\sum _{m=0}^{i-1}\phi _m'\bigg ]. \end{aligned}$$

If we assume \(\lim _{i\rightarrow \infty }f_i=\lim _{i\rightarrow \infty }\theta _i=\lim _{i\rightarrow \infty }\phi _i=0\), we obtain \(f(\eta )\approxeq \sum _{m=0}^{M}f_m(\eta )\), \(\theta (\eta )\approxeq \sum _{m=0}^{M}\theta _m(\eta )\), \(\phi (\eta )\approxeq \sum _{m=0}^{M}\phi _m(\eta )\), where M is the order of SLM approximation. The Gauss Lobato collocation points are defined as \(\xi _j=\cos {\pi j}/{N},\) \(j=0,1,2,\ldots ,N\) and the space \([0,\infty ]\) is mapped to these collocation points by \(\eta =L({\xi +1})/{2}\). Hence, the unknown functions are approximated as

$$\begin{aligned}&f_i(\xi )\approxeq \sum _{k=0}^{N}f_i(\xi _k)T_k(\xi _j), \quad \theta _i(\xi )\approxeq \sum _{k=0}^{N}\theta _i(\xi _k)T_k(\xi _j), \nonumber \\&\phi _i(\xi )\approxeq \sum _{k=0}^{N}\phi _i(\xi _k)T_k(\xi _j), \end{aligned}$$
(20)

where \(T_k(\xi )=\cos \big (k\cos ^{-1}(\xi )\big )\) is the Chebyshev polynomial. Furthermore, the derivatives are given by

$$\begin{aligned}&\dfrac{\textrm{d}^rf_i}{\textrm{d}\eta ^r}=\sum _{k=0}^{N}D_{kj}^rf_i(\xi _k), \quad \dfrac{\textrm{d}^r\theta _i}{\textrm{d}\eta ^r}=\sum _{k=0}^{N}D_{kj}^r\theta _i(\xi _k), \nonumber \\&\dfrac{\textrm{d}^r\phi _i}{\textrm{d}\eta ^r}=\sum _{k=0}^{N}D_{kj}^r\phi _i(\xi _k), \quad \end{aligned}$$
(21)

where \(j=0\) to N. Here \(\mathcal {D}={DL}/{2}\) is called the Chebyshev spectral matrix of differentiation. We substitute approximations (20) and derivatives (21) in (16) to obtain a matrix equation of the form

$$\begin{aligned} \mathcal {A}\mathcal {Y}_i=\mathcal {R}_{i-1}, \end{aligned}$$
(22)

associated with the boundary conditions

$$\begin{aligned}&f_i(\xi _N)=\sum _{k=0}^{N}D_{0k}f_i(\xi _k)=0, \nonumber \\&S\sum _{k=0}^{N}D^{2}_{Nk}f_i(\xi _k)-\sum _{k=0}^{N}D_{Nk}f_i(\xi _k)=0\nonumber , \\&\theta _i(\xi _0)=\theta _i(\xi _N)=0, \quad \phi _i(\xi _0)=\phi _i(\xi _N)=0. \end{aligned}$$
(23)

The initial approximations are chosen as \(f_0=(1-\textrm{e}^{-\eta })/{(1+S)}\), \(\theta _0=\textrm{e}^{-\eta }\) and \(\phi _0=\textrm{e}^{-\eta }\) to satisfy (19) and recursively iterate the matrix equation to the order of approximation by substituting the boundary conditions at the collocation points. Matlab is used for iteration and precise values are obtained approximately after the fifth iteration. Thus, the solution is obtained and the results are tabulated.

5 Results

Convergence of the results are obtained at fifth order of SLM approximation. The results for the case of \(S=Ha=Ec=0\), from the present study are compared with the results from Grubka and Bobba [46] in table 2 and the values are observed to be in good agreement.

Equations (22) and (23) are solved for dimensionless velocity f, temperature \(\theta \) and concentration \(\phi \) and the effects of implanted parameters on them are graphically represented in this section. Since the Newtonian model of the nanofluid is taken into account, lower volume fraction value of \(\Phi =0.01\) is considered. The values of Prandtl number is fixed throughout the paper to be \(Pr=6.5\). For the other parameters, we use \(\alpha =0.5\), \(N_b=2\times 10^{-4}\), \(N_t=10^{-3}\), \(Ec=0.01,\) \(\lambda =0.5\), \(Sc=170 \), \(N_r=2\) and \(S=0.8\) unless specified otherwise. The practical range of parameter values of the nanofluids are chosen for calculations adapting Malashetty et al [47] and Behseresht et al [48].

Figure 2 depicts the variations of velocity profiles with \(\alpha \), \(\lambda \), Ha and S. Clearly, \(f'\) increases with increasing values of \(\alpha \), that is, the curvature parameter has a positive impact on the nanofluid velocity (figure 2a). This demonstrates the significance of a cylinder over a flat surface. Similarly, increase in \(\lambda \) values has an increasing effect on the velocity (figure 2b) because bigger the values of \(\lambda \), greater is the impact of buoyancy forces on the fluid flow and hence the fluid moves with greater velocity, whereas increasing the Ha indicates a stronger magnetic field which strengthens the Lorentz force and the velocity of the fluid is controlled (figure 2c). Likewise, it is clearly observed that increase in slip parameter diminishes the values of velocity (figure 2d).

Figure 3 shows the impacts of various parameters on temperature profiles. It is clearly seen that \(\theta \) increases with increasing \(\alpha \) (figure 3a), while it reduces with increasing \(\lambda \) (figure 3b). Similar to the case of velocity, the curved cylindrical surface is preferred to flat geometries in view of the fluid temperature. Increasing Ha indicates a stronger magnetic field which strengthens the Lorentz force and hence the temperature of the fluid is supposed to be controlled. But, higher thermal conductivity of the chosen nanofluid enhances the fluid temperature by conduction, in spite of a strengthened Lorentz force (figure 3c). Similarly, an increase in slip parameter enhances temperature (figure 3d).

Figure 4 depicts the variations of \(\phi \) with \(\alpha \), \(\lambda \), \(N_b\), \(N_t\), Ha and S. Clearly, \(\phi \) increases with increasing \(\alpha \) values, just like \(f'\) and \(\theta \) (figure 4a). Similarly, increasing \(\lambda \) values has an increasing effect on concentration values (figure 4b). Figure 4c shows that an increase in \(N_b\) necessarily thins the concentration boundary layer resulting in reduced concentration, whereas a rise in \(N_t\) enhances the thermophoretic diffusion and hence concentration increases (figure 4d). Likewise, an increase in fluid concentration is observed with Ha (figure 4e). This is because, the GO nanoparticles aid in an enhanced diffusion in the presence of magnetic field. Figure 4f shows that \(\phi \) increases with S.

The impacts of \(\alpha \), \(\lambda \) and Ec on \(N_S\) and Be are shown in figure 5. The increasing values of \(\alpha \) necessarily has an increasing effect on dimensionless entropy generation number (figure 5a). This causes Be to increase near the surface and decrease further (figure 5b) implying that the heat transfer is the predominant cause of entropy generation near the surface and fluid friction and mass transfer dominate the entropy at the free stream, whereas the entropy generation increases at the surface and decreases eventually, with the values of \(\lambda \) (figure 5c). Evidently, there is an increase in Be near the surface which decreases away from the surface implying that the irreversibilities due to fluid friction and mass transfer are responsible for the increased entropy generation number both at the surface and at the free stream (figure 5d).

Figures 5c and 5d show the effects of Ec on \(N_S\) and Be. Increasing Ec increases the viscous dissipation, which successively increases heat generation and hence there is a rise in entropy generation (figure 5e). Consequently, Be decreases indicating that fluid friction and mass transfer are primarily responsible for the increased entropy generation when values of Ec are increased (figure 5f).

Figure 6 depicts the effects of Ha and S on \(N_S\) and Be. Clearly, the increasing Ha results in \(N_S\) to decrease near the surface which slightly increases away from the surface (figure 6a). Similarly, Be decreases near the surface and increases away from the surface denoting the influence of heat transfer on the generated entropy at the surface and at the free stream (figure 6b). Similarly, the entropy generation number decreases near the surface and slightly increases away from the surface in accordance with S (figure 6c), thus causing a raised Be profile (figure 6d). This implies that the increased entropy values are influenced by the increasing entropy caused by fluid friction and mass transfer near the surface and heat transfer at the free stream.

Table 3 represents the values for Nu, Sh and \(C_f\) for varying values of different parameters. Nusselt number is the ratio of heat transfer due to convection to heat transfer due to conduction at the surface. Clearly, the increasing values of \(\alpha \) and \(\lambda \) increase Nu and hence the quality of convective heat transfer is increased. Similarly, as \(N_t\) increases, thermophoretic diffusion increases and it has an increasing effect on Nu resulting in an increased convective heat transfer, while increasing values of Ec, \(N_b\), Ha and S cause a decrease in the values of Nu. This implies that the convective heat transfer is reduced and that by conduction is increased. As Ec increases, velocity of the nanofluid increases and hence convective heat transfer decreases, thus resulting in a reduced Nu. Also, a raised \(N_b\) value indicates an enhanced Brownian motion and hence an enhanced heat transfer due to conduction. Likewise, as Ha increases, magnetic field is strengthened and the heat transfer due to convection is controlled and conductive heat transfer is enhanced owing to the high thermal conductivity of GO nanoparticles. And, an increased slip parameter also causes an increased conductive heat transfer. Similarly, when \(\alpha \), \(\lambda \), Ec and \(N_b\) are increased, Sh also increases, resulting in an increase in convective mass transfer, whereas when \(N_t\) increases, the thermophoretic diffusivity increases, and hence Sh decreases. This implies that the quality of diffusive mass transfer is enhanced. Likewise, Ha and S have an enhancing effect on mass diffusivity due to favourable thermophysical properties of GO nanofluids, thus resulting in a reduced Sh. Considering the values of skin friction drag, the parameters \(\alpha \), \(N_b\) and Ha preferably have a reducing effect on \(C_f\), while \(\lambda \), Ec, \(N_t\) and S have an increasing effect on \(C_f\).

6 Conclusion

From the results obtained in this paper, the following conclusions on water-based GO nanofluids on lower concentrations are made.

  • Velocity can be enhanced by enhancing the curvature parameter, mixed convection parameter and Eckert number and by decreasing slip parameter.

  • Heat transfer can be enhanced by enhancing curvature parameter, Eckert number and slip parameter and by decreasing the mixed convection parameter.

  • Mass transfer can be increased by increasing the values of curvature parameter, thermophoresis parameter and slip parameter and reducing Brownian motion parameter, Eckert number, mixed convection parameter and Schmidt number.

  • The irreversibility caused by entropy generation near the surface is influenced by heat transfer but it is predominantly due to fluid friction.

  • Hartmann number enhances conductive heat transfer and diffusive mass transfer and reduces skin friction. Eckert number enhances conductive heat transfer, convective mass transfer and skin friction.

Thus, the curvature parameter of the cylindrical surface is preferred to the flat geometries in view of enhancing velocity, heat and mass transfer. Also, the influence caused by viscous dissipation on the generated entropy by considering GO nanofluids with water as the base fluid is significant. Results from the impacts of magnetic field parameter on temperature and concentration profiles signify the contribution of higher thermal conductivity of GO nanoparticles in MHD studies.

In particular, this investigation contributes to industrial applications such as cooling of electronic devices, energy storage, food processing, drying technology, annealing of copper wires, polymer sheet extrusion etc. The current study focusses on the Newtonian behaviour of GO nanofluid and can be further extended by exploring the shear thinning behaviour of the nanoparticles when dispersed in base fluids in higher concentrations.