Magnetohydrodynamic Heat Transfer of Nanofluids Past a Stretching Cylinder with Non-Uniform Heat Source/Sink and Chemical Reaction

Abstract

In this investigation, we intend to present the magnetohydrodynamic (MHD) heat and mass transfer of nanofluids along a stretching cylinder in the presence of non-uniform heat source/sink and chemical reaction under the prescribed surface heat flux boundary conditions on the cylinder surface. The governing partial differential equations are approximated by a system of non-linear locally similarity ordinary differential equations which are solved numerically using fifth-order Runge–Kutta–Fehlberg (RKF45) integration scheme shooting method. Present results are compared with the previously published results in some limiting cases and the results are found to be in an excellent agreement. Three different kinds of nanoparticles, namely copper (Cu), alumina (${\hbox {Al}}_2{\hbox {O}}_3$) and titanium dioxide (${\hbox {TiO}}_2$) with water as base fluid are considered here. The numerical results for the dimensionless velocity, temperature and nanoparticle volume fraction as well as on local skin-friction coefficient, local Nusselt number and Sherwood number have been constructed and illustrated graphically to reveal some interesting physical phenomena. The results of the present paper show that the flow velocity and temperature on the stretching cylinder and also skin-friction coefficient are strongly influenced by the curvature parameter.

Introduction

In the past few years, much interest was focused on hydromagnetic flow and heat transfer of nanofluid past stretching cylinder due to enormous industrial and chemical processes, transportation, electronics and biomedical applications such as cylindrical heat pipes, advanced nuclear systems, biological sensors and powder technology. The nanoparticles in the base fluids such as water, oil and ethylene glycol are used in many industrial processes such as in chemical, power generation and heating or cooling processes are poor heat transfer fluid due to its poor heat transfer properties with low thermal conductivity. One can use by suspending the solid nanoparticle into the base fluid in order to increase the thermal conductivity of the base fluid. Choi [1] proposed a new type of fluid i.e. mixture of the base fluids with the solid nanoparticle called Nanofluid. It was reported that nanofluids have good stability properties, no problems of sedimentation, erosion and pressure drop and dramatically higher thermal conductivities due to the presence of tiny size of the particles. A comprehensive literature on the topic of nanofluid flow has been discussed by Das et al. [2] and Kaka and Pramuanjaroenkij [3]. Das et al. [4] observed that the thermal conductivity for a nanofluid increases with increasing temperature of the fluid. They have also observed that nanofluids containing ${\hbox {Al}}_2{\hbox {O}}_3$ and CuO in the base fluid water have higher stabilizing effects.

The flow over a stretching cylinder is considered to be two-dimensional if the radius of the cylinder is large compared to the boundary layer thickness. On the other hand, for a thin cylinder, the radius of the cylinder may be of the same order as that of the boundary layer thickness. In this case, the flow may be considered as axisymmetric instead of two-dimensional flow. The study of hydrodynamic flow and heat transfer of nanofluids over stretching cylinder has gained considerable attention due to its applications in fiber technology, extrusion processes, glass production, electronic cooling, solar collectors and geothermal power generation. Wang [5] investigated the steady flow of a incompressible viscous fluid due to a stretching hollow cylinder. Mixed convection boundary layer flow of a and incompressible viscous fluid over a permeable vertical cylinder with prescribed heat flux has been studied by Bachok and Ishak [6]. Ishak et al. [7] investigated magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Elbashbeshy et al. [8] studied laminar boundary layer flow of an incompressible viscous fluid along a stretching horizontal cylinder embedded in a porous medium in the presence of a heat source or sink with suction/injection. Lin and Shih [9] analyzed the buoyancy effect of laminar boundary layer flow and heat transfer along a vertically moving cylinder with constant velocity and found that the similarity solutions could not be obtained due to the curvature effect of the cylinder. Mukhopadhyay [10] analyzed the magnetohydrodynamic (MHD) boundary layer slip flow along a stretching cylinder. Ashornejad et al. [11] discussed flow and heat transfer of the fluid filled with nanoparticle due to a stretching cylinder in the presence of magnetic field. Aydin and Kaya [12] studied MHD mixed convection of a viscous dissipating fluid about a vertical slender cylinder. The unsteady MHD flow of heat and mass transfer of Cu–water and ${\hbox {TiO}}_2$–water nanofluids over stretching sheet with a non-uniform heat source/sink by considering viscous dissipation and chemical reaction is investigated by Dessie and Kishan [13]. Sheikholeslami [14] studied the nanofluid flow and heat transfer over a stretching porous cylinder. The two-dimensional unsteady boundary layer stagnation-point flow of a nanofluid over a heated stretching sheet is investigated by El-Aziz [15]. Das et al. [16] studied the MHD boundary layer slip flow and heat transfer of nanofluid past a vertical stretching sheet with the effect of non-uniform heat generation or absorption. Boundary layer flow of a conducting dusty fluid due to linearly stretching cylinder immersed in a porous media in the presence of thermal radiation was considered by Manjunatha et al. [17] using two-phase model,. Malik et al. [18] presented a numerical study of Sisko fluid flow and heat transfer over stretching cylinder with variable thermal conductivity. Williamson fluid flow and heat transfer over a stretching cylinder with linear thermal conductivity and heat generation/ absorption effects were analyzed by Malik et al. [19]. Majeed et al. [20] investigated the flow due to stretching cylinder with Soret and Dufour effects. Heat transfer over a stretching cylinder due to variable prandtl number influenced by internal heat generation/absorption was explained by Majeed et al. [21]. Majeed et al. [22] also examined the mixed convection stagnation point flow over a stretching cylinder with sinusoidal surface temperature. Javed et al. [23] studied the unsteady MHD oblique stagnation point flow with heat transfer over an oscillating flat plate. Mustafa et al. [24] focused on magnetohydrodynamic stagnation point flow of a ferrofluid over a stretchable rotating disk. Mahmood et al. [25] discussed the hydromagnetic Hiemenz flow of micropolar fluid over a nonlinearly stretching/shrinking sheet. Pal et al. [26] discussed the stagnation-point flow and heat transfer of radiative nanofluids over a stretching/shrinking sheet in a porous medium with a non-uniform heat source/sink. Pal et al. [27] also studied Soret and Dufour effects on MHD convectiveradiative heat and mass transfer of nanofluids over a vertical non-linear stretching/shrinking sheet.

The effects of chemical reaction in the boundary layer flow has numerous applications in fibrous insulation and many other chemical engineering problems. Najib et al. [28] studied the effect of chemical reaction on stagnation point flow and mass transfer past a stretching/shrinking cylinder. The steady mixed convection boundary layer flow due to a permeable stretching cylinder with prescribed heat flux in porous medium with heat generation/absorption is investigated by Khalili et al. [29]. The effects of chemical reaction on MHD flow and heat transfer of a nanofluid near the stagnation point over a permeable stretching surface with non-uniform heat source/sink was studied by Gireesha and Rudraswamy [30]. Rudraswamy and Gireesha [31] studied the influence of chemical reaction and thermal radiation on MHD boundary layer flow and heat transfer of a nanofluid over an exponentially stretching sheet. Bandari and Gorfie [32] presented the study on boundary layer flow of nanofluids over a stretching sheet subjected to magnetic field, thermal radiation, viscous dissipation, chemical reaction and Ohmic effects.

In regards the above mentioned applications, the current study is mainly motivated by the need to understand the effects of magnetohydrodynamic heat and mass transfer of nanofluids over stretching cylinder in presence of non-uniform heat source/sink and chemical reaction. Three different kinds of nanoparticles, namely copper (Cu), alumina (${\hbox {Al}}_{2}{\hbox {O}}_{3}$), titanium dioxide (${\hbox {TiO}}_{2}$) in the base fluid water are considered. The well-known Runge–Kutta–Fehlberg method based shooting technique is employed to study the effects of solid volume fraction, curvature parameter, magnetic parameter, non-uniform heat source/sink parameters, chemical reaction parameter, Schmidt number of the nanofluid over stretching cylinder by using the thermophysical properties of Cu, ${\hbox {Al}}_{2}{\hbox {O}}_{3}$ and ${\hbox {TiO}}_{2}$ nanoparticles (see Table 1) in the base fluid (water).

Fig. 1

Physical model and coordinate system of problem considered

Formulation of the Problem

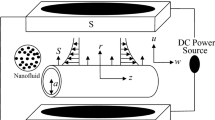
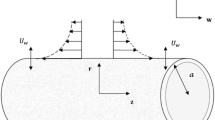
Consider the steady axisymmetric flow of an incompressible viscous fluid along a accelerating stretching cylinder in the presence of uniform magnetic field (see Fig. 1). The x-axis is measured along the axis of the cylinder and the r-axis is measured in the radial direction. It is assumed that the uniform magnetic field of intensity $B_0$ acts in the radial direction. The magnetic Reynolds number is assumed to be small so that the induced magnetic field is negligible in comparison with the applied magnetic field. Further, it is assumed that the cylinder is being stretched in the axial direction with velocity $u_w=cx$ and the surface of the cylinder is subjected to a prescribed heat flux $q_w=bx$, where a and b are constants. Under these assumptions the boundary layer equations governing the flow, heat transfer and concentration in the presence of non-uniform heat source or sink are as follows:

$$\begin{aligned}&\frac{\partial {}}{\partial {x}}(ru)+\frac{\partial {}}{\partial {r}} (rv)= 0, \end{aligned}$$

(1)

$$\begin{aligned}&{u}\frac{\partial {u}}{\partial {x}}+{v}\frac{\partial {u}}{\partial {r}} =\frac{\mu _{nf}}{\rho _{nf}}\left( \frac{\partial ^2u}{\partial {r}^2}+\frac{1}{r}\frac{\partial {u}}{\partial {r}}\right) -\frac{\sigma {B_0}^2}{\rho _{nf}}u, \end{aligned}$$

(2)

$$\begin{aligned}&{u}\frac{\partial {T}}{\partial {x}}+{v}\frac{\partial {T}}{\partial {r}}=\alpha _{nf}{\left( \frac{\partial ^2T}{\partial {r}^2}+\frac{1}{r}\frac{\partial {T}}{\partial {r}}\right) }-\frac{1}{{(\rho C_p)}_{nf}}q''', \end{aligned}$$

(3)

$$\begin{aligned}&{u}\frac{\partial {C}}{\partial {x}}+{v}\frac{\partial {C}}{\partial {r}}=D_m{\left( \frac{\partial ^2C}{\partial {r}^2}+\frac{1}{r}\frac{\partial {C}}{\partial {r}}\right) }-K_0(C-C_\infty ) \end{aligned}$$

(4)

subject to the boundary conditions (see Qasim et al. [33]):

$$\begin{aligned}&u = u_w(x)=c x, ~v = 0,\,\kappa _f\frac{\partial {T}}{\partial {r}}= -q_w(x), ~ C=C_w~~~~~~ ~~at~ r = a, \end{aligned}$$

(5)

$$\begin{aligned}&u \rightarrow 0, ~T = T_{\infty },~~C = C_{\infty }~~ ~~~~~~~~~~as~ r \rightarrow \infty , \end{aligned}$$

(6)

where x and r are the coordinates measured in the radial and axial direction of the cylinder, and u and v are the velocity components in the x and r directions, respectively. Further, T is the temperature, C is the concentration in the boundary layer. It is assumed that the temperature and concentration at the stretching/shrinking sheet take the constant values $T_w$ and $C_w$ while those of the ambient nanofluid takes the constant value $T_\infty$ and $C_\infty$, respectively at the free stream flow with assuming that $T_w>>T_\infty$ and $C_w>>C_\infty$. Also, $\sigma$ is the electrical conductivity, $D_m$ is the species diffusivity, $q'''$ is the non uniform heat source respectively. Further, $\rho _{nf}$ is the effective density of the nanofluid, $\mu _{nf}$ is the coefficient of viscosity of the nanofluid, $\alpha _{nf}$ is the thermal diffusivity of the nanofluid, $(\rho C_p)_{nf}$ is the heat capacitance of the nanofluid, which are defined as follows:

$$\begin{aligned} \alpha _{nf}= & {} \frac{\kappa _{nf}}{(\rho {C_p})_{nf}} ,~~~\rho _{nf}=(1-\phi )\rho _f+\phi \rho _s,\nonumber \\ ~\mu _{nf}= & {} \frac{\mu _f}{(1-\phi )^{2.5}},~(\rho {\beta })_{nf}=(1-\phi )(\rho {\beta })_f+\phi (\rho {\beta })_s, \nonumber \\ ~(\rho {C_p})_{nf}= & {} (1-\phi )(\rho {C_p})_f+\phi (\rho {C_p})_s, ~\frac{\kappa _{nf}}{\kappa _f}=\frac{(\kappa _s+2 \kappa _f)-2 \phi (\kappa _f-\kappa _s)}{(\kappa _s+2 \kappa _f)+\phi (\kappa _f-\kappa _s)}, \end{aligned}$$

(7)

$\phi$ is the solid volume fraction of the nanoparticle, $\rho _f$ is the reference density of the base fluid, $\rho _s$ is the reference density of the nanoparticle, $\mu _f$ is the reference viscosity of the base fluid, ${C_p}_f$ is the reference capacitance of the base fluid, ${C_p}_s$ is the reference capacitance of the nanoparticle, $\kappa _f$ is the thermal conductivity of the base fluid, and $\kappa _s$ is the thermal conductivity of the nanoparticle.

The non uniform heat source/sink $q'''$ is modeled as (Pal and Mondal [34]):

$$\begin{aligned} q'''=\left( \frac{\kappa _{nf} u_w(x)}{x {\nu }_f}\right) \left[ A^*(T_w-T_\infty )F'(\eta )+(T-T_\infty )B^* \right] \end{aligned}$$

(8)

where $A^*$ and $B^*$ are parameters of the coefficients of space and temperature-dependent heat source/sink, respectively. The case $A^* >0$ and $B^* >0$ corresponds to internal heat generation while $A^* <0$ and $B^* <0$ correspond to internal heat absorption.

We now look for a similarity solution of the Eqs. (1)–(4) with boundary conditions (5), (6) by employing the following dimensionless functions in the following form (see Qasim et al. [33]):

$$\begin{aligned} \psi= & {} \left( 2\nu _f x u_w\right) ^{1/2}a f(\eta ),~\eta =\frac{r^2-a^2}{2a}\left( \frac{u_w}{\nu _f x}\right) ^{1/2},\nonumber \\ ~\theta (\eta )= & {} T_\infty +\frac{q_w}{\kappa _f}\left( \frac{\nu _f x}{u_w}\right) ^{1/2}, ~C^{*}(\eta )=\frac{C-C_\infty }{C_w-C_\infty }~ \end{aligned}$$

(9)

where $\nu _f$ is the kinematic viscosity of the fluid and $\psi$ is the free stream function that satisfies the continuity equation (Eq. (1)) with $u=\frac{1}{r}\frac{\partial {\psi }}{\partial {r}}$, $v= -\frac{1}{r} \frac{\partial {\psi }}{\partial {x}}$.

Substituting Eqs. (7)–(9) into Eqs. (2) and (4), we get the following nonlinear ordinary differential equations:

$$\begin{aligned}&(1+2\gamma \eta )F'''+2\gamma F''+{\phi _1 \phi _2}(FF''-F'^2)-\phi _1MF'=0, \end{aligned}$$

(10)

$$\begin{aligned}&(1+2\gamma \eta ){\theta }''+2\gamma {\theta }'+{\phi _3 Pr }\left( \frac{\kappa _{f}}{\kappa _{nf}}\right) \left( F \theta '-F' \theta \right) +\left( A^{*}F'+B^{*}\theta \right) =0, \end{aligned}$$

(11)

$$\begin{aligned}&(1+2\gamma \eta ){C^{*}}''+2\gamma {C^{*}}'+Sc(F{C^{*}}'- \varGamma C^{*}) =0, \end{aligned}$$

(12)

with the corresponding boundary condition as obtained from Eqs. (5), (6) in the form:

$$\begin{aligned}&F(\eta )=0,~~ F'(\eta )= 1, ~~ \theta (\eta )= -1, ~~C^{*}(\eta )=1 ~at~~\eta =0, \end{aligned}$$

(13)

$$\begin{aligned}&F'(\eta )\rightarrow 0,~~\theta (\eta )\rightarrow 0, ~~C^{*}(\eta ) \rightarrow 0~as~\eta \rightarrow \infty . \end{aligned}$$

(14)

The non-dimensional constants appearing in Eqs.(10)–(14) are Prandtl number Pr, magnetic field parameter M, curvature parameter $\gamma$, Schmidt number Sc, chemical reaction parameter $\varGamma$ which are defined as

$$\begin{aligned} Pr =\frac{\nu _f}{\alpha _f},~~M=\frac{\sigma B_0^2}{c\rho _f},\,\gamma = \left( \frac{\nu _f}{ca^2}\right) ^{1/2},\,Sc=\frac{\nu _f}{D_m},\,\varGamma =\frac{K_0}{c}.~ ~~~~~ \end{aligned}$$

(15)

Also, we have

$$\begin{aligned} \phi _1=(1-\phi )^{2.5},~ \phi _2=1-\phi +\phi \left( \frac{\rho _s}{\rho _f}\right) , ~\phi _3=1-\phi +\phi \frac{(\rho C_p)_s}{(\rho C_p)_f}. \end{aligned}$$

(16)

The important physical quantities in this study are skin-friction or shear stress coefficient $C_f$, local Nusselt number $Nu_x$, and Sherwood number $Sh_x$, which are defined by

$$\begin{aligned} C_{f}= & {} \frac{ \mu _{nf}}{\rho _f u_w^{2}}{\left( {\frac{\partial u}{\partial r}}\right) }_{r=a},~~ Nu_x = \frac{-x \kappa _{nf}}{\kappa _f(T_w-T_\infty )}\left( -\frac{\partial T}{\partial y}\right) _{y=0},~~\nonumber \\ Sh_x= & {} -\frac{x}{C_w-C_\infty }\left( {\frac{\partial u}{\partial y}} \right) _{y=0}.~~ \end{aligned}$$

(17)

Using (11) in (18) skin-friction coefficient, local Nusselt number and Sherwood number can be expressed as

$$\begin{aligned} Re_x^{1/2}C_{f} = \frac{1}{(1-\phi )^{2.5}}F''(0),~~ Re_x^{-1/2}Nu_x = -\frac{\kappa _{nf}}{\kappa _f}\theta '(0),~~ Re_x^{-1/2}Sh_x = -{C^{*}}'( 0),~~~~~~~~~~~~~~~~~ \end{aligned}$$

(18)

where $Re_x = u_w(x)x/\nu _f$ is the local Reynolds number.

Numerical Method of Solution

Thus the non-linear ordinary differential Eqs. (10)–(12) subjected to boundary conditions (13)–(14) have been solved by using fifth-order Runge–Kutta–Fehlberg method along with shooting technique since Runge–Kutta fourth order method (RK4) requires a significant amount of computation for the smaller step size and the RK4 method must be repeated if it is determined that the agreement is not good enough, whereas the novelty of the Runge–Kutta–Fehlberg method (denoted RKF45) is that it has a procedure to determine automatically the proper step size to be used. At each step, two different approximations for the solution are made and compared. If the two answers are in close agreement, the approximation is accepted. If the two answers do not agree to a specified accuracy, the step size is reduced. If the answers agree to more significant digits than required, the step size is increased. Also, RKF45 method is based on the discretization of the problem domain and the calculation of unknown boundary conditions i.e. the domain of the problem is discretized and the boundary conditions for $\eta =\infty$ are replaced by $f'(\eta _{max})=0$,  $\theta (\eta _{max})=0$ and $C^*(\eta _{max})=0$, whereas $\eta _{max}$ is sufficiently large value of $\eta$ (corresponding to step size) at which the boundary condition (14) for $f(\eta )$ is satisfied. In the present work we have set $\eta =14$. To solve the problem we first converted governing non-linear partial differential Eqs. (2)–(4) subject to boundary conditions (5), (6) were first transformed into a set of nonlinear ordinary differential equations (10)–(12) with boundary conditions (13), (14). Here, similarity transformation is used before being solved numerically by the Runge–Kutta–Fehlberg method with shooting techniques (see Pal and Mondal [35]). In this approach Eqs. (10)–(12) are transformed to set of first order differential equations by assuming $(F, F', F'', \theta , \theta ', C^{*}, {C^{*}}')= (F_1, F_2, F_3, F_4, F_5, F_6, F_7)$ as given below:

$$\begin{aligned} \left( \begin{array}{l} F_1' \\ F_2' \\ F_3' \\ F_4' \\ F_5' \\ F_6' \\ F_7' \\ \end{array} \right) = \left( \begin{array}{l} F_2 \\ F_3 \\ \{-\phi _1 \phi _2 (F_1 F_3-{F_2}^2)+\phi _1 M F_2-2\gamma F_3\}/(1+2\gamma \eta ) \\ F_5 \\ \{-\phi _3 Pr (F_1 F_5-F_2 F_4)-2 \gamma F_5\}/(1+2\gamma \eta )\\ F_6 \\ \{-Sc (F_1 F_7- \varGamma F_6)-2\gamma F_7\}/(1+2\gamma \eta ) \\ \end{array} \right) \end{aligned}$$

with the boundary conditions

$$\begin{aligned} \left( \begin{array}{l} F_1 \\ F_2 \\ F_4 \\ F_6 \\ \end{array} \right) =\left( \begin{array}{l} 0 \\ 1 \\ -1 \\ 1 \\ \end{array} \right) \begin{array}{l} at~ \eta =0, \end{array} ~~ \left( \begin{array}{l} F_2 \\ F_4 \\ F_6 \\ \end{array} \right) =\left( \begin{array}{l} 0 \\ 0 \\ 0 \\ \end{array} \right) \begin{array}{l} as~ \eta \rightarrow \infty . \end{array} \end{aligned}$$

where

$$\begin{aligned} \left( \begin{array}{l} \phi _1 \\ \phi _2 \\ \phi _3 \\ \end{array} \right) = \left( \begin{array}{l} (1-\phi )^{2.5} \\ \phi _2=1-\phi +\phi (\rho _s/\rho _f) \\ \phi _3=1-\phi +\phi {(\rho C_p)_s/(\rho C_p)_f}\\ \end{array} \right) \end{aligned}$$

Here prime denotes differentiation with respect to $\eta$. The value of $\eta _{\infty }$ varies from 1 to 14 depending upon the physical parameter that governs our problem.

The values of $F_3(0)$, $F_5(0)$ and $F_7(0)$ are not prescribed, so we start to solve the problem numerically with the initial guess value $F_3(0)\,=\,d_{10}$, $F_5(0)\,=\,d_{20}$ and $F_7(0)\,=\,d_{30}$. Let $\gamma _1$, $\gamma _2$ and $\gamma _3$ be the correct values of $F_3(0)$, $F_5(0)$ and $F_7(0)$, respectively. The seven ordinary differential equations are then solved by fifth-order Runge–Kutta–Fehlberg method and denote the values $F_3(0)$, $F_5(0)$ and $F_7(0)$ at $\eta \,=\,\eta _{\infty }$ by $F_3(d_{10},d_{20},d_{30}, \eta _{\infty })$, $F_5(d_{10},d_{20},d_{30}, \eta _{\infty })$ and $F_7(d_{10},d_{20},d_{30}, \eta _{\infty })$, respectively. It is important to note that the “Infinity” in the above expression represents the edge of the boundary-layer. Since $F_3$, $F_5$, $F_7$ are clearly function of $\gamma _1$, $\gamma _2$ and $\gamma _3$ they are expanded around $\gamma _1-d_{10}$, $\gamma _2-d_{20}$ and $\gamma _3-d_{30}$, respectively using in Taylor series expansion method by retaining only the linear terms. Thus, after solving the system of Taylor series expansions for $\delta {\gamma _1}$= $\gamma _1-d_{10}$, $\delta {\gamma _2}\,=\,\gamma _2-d_{20}$ and $\delta {\gamma _3}$= $\gamma _3-d_{30}$, we avail the new estimate $d_{11}\,=\,d_{10}$+ $\delta d_{10}$, $d_{21}\,=\,d_{20}$+ $\delta d_{20}$ and $d_{31}\,=\,d_{30}$+ $\delta d_{30}$. Now, we repeat the entire process starting with $F_1(0)$, $F_2(0)$, $d_{11}$, $F_4(0)$, $d_{21}$, $F_6(0)$ and $d_{31}$ as initial conditions. Iteration of the whole outlined process is repeated with the latest estimates of $\gamma _1$, $\gamma _2$, and $\gamma _3$ until prescribed boundary conditions are satisfied. Finally $d_{1n}=d_{1(n-1)}+\delta d_{1(n-1)}$, $d_{2n}=d_{2(n-1)}+\delta d_{2(n-1)}$ and $d_{3n}=d_{3(n-1)}+\delta d_{3(n-1)}$ for $n=1,2,3\ldots$ are obtained which seemed to be the most desired approximate initial values of $F_3(0)$, $F_5(0)$ and $F_7(0)$. In this way we can determine all the seven initial conditions. Now it is possible to solve the resultant system of five simultaneous equations by fifth-order Runge–Kutta–Fehlberg integration scheme so that velocity, temperature and concentration fields for a particular set of physical parameters can easily be obtained.

Results and Discussions

In this paper, we have analyzed the magnetohydrodynamic heat and mass transfer of nanofluids over stretching cylinder in the presence of non-uniform heat source/sink and chemical reaction. Computed results are presented in tabular forms and effects are shown in graphical form. The thermophysical properties of base fluid water and different kind of nanoparticles are provided in Table-1 [2–4]. We have extracted interesting insights regarding the influence of various physical parameters that govern our problem. In addition,we have validated the numerical method used in this study and compared the present results with the available results in the literature for $-F''(0)$ and $-\theta '(0)$ which are presented in Tables 2 and 3. The results are found in a very good agreement. It is observed from these table that the present results coincide very well with the results of Bachok [37], Qasim et al. [33] for $-F''(0)$ and Yih et al. [38], Ali et al. [39] and Aurangzaib et al. [40] for different values of $\gamma$ and Pr, which confirm that the numerical method used in this paper is perfect and accurate. Therefore, we are confident that our results are highly accurate to analyze this boundary layer flow problem.

Table 1 Thermophysical properties of fluid and nanoparticles ( Oztop and Abu-Nada [36])

Table 2 Comparison of results for $-F''(0)$ when $\phi = \gamma = M = A^{*} = B^{*}= Sc = S = 0$ for stretching cylinder

Table 3 Comparison of results for $-\theta '(0)$ when $\phi = M = A^* = B^* = Sc = \gamma = S = 0$ for stretching cylinder

The thermophysical properties of the base fluids water and the three nanoparticles are listed in Table-1. The variation of velocity, temperature and concentration profiles considering several parameters for different values of nanoparticle volume fraction $\phi$ is shown in Figs. 2, 3 and 4 for Cu–water nanofluid over stretching cylinder. It is seen that the velocity, temperature and concentration profiles increase but having significant effect for temperature profile by increasing the value of the solid volume fraction $\phi$. It is also observed that the hydrodynamic and thermal boundary layer increase with increase of nanoparticle volume fraction parameter. This agrees with the physical behavior that when the solid volume fraction of nanoparticles increases the thermal conductivity and then the thermal and hydrodynamic boundary layer thickness increases. Variability of the volume fraction of the nanoparticles allows for tuning to maximize spectral absorption of thermal radiation throughout the fluid volume. Enhancement in the thermal conductivity can lead to efficiency improvements, via more effective fluid heat transfer. Vast enhancements in convective surface area due to the extremely small particle size, which makes nanofluid based thermal radiation systems attractive for thermochemical processes. The effects of curvature parameter $\gamma$ on the velocity, temperature and concentration profiles for Cu–water nanofluids over stretching cylinder in the presence of uniform magnetic field are shown in Figs. 5, 6 and 7. It is observed from these figures that when $\gamma \, =\, 0$ then the outer surface of the cylinder behaves like a flat plate. Thus it is noted from Fig. 5 that for an increase in the curvature parameter $\gamma$, the velocity profile and momentum boundary layer thickness decrease first and then increase. This may be due to the fact that for an increase in the curvature parameter $\gamma$, the radius and surface area of the cylinder decrease and consequently less resistive force occurs for the fluid and as a result the velocity profile increases. Similar behavior is observed for temperature profiles as shown in Fig. 6. This is due to the fact that by increasing the curvature parameter, threr is decrease in the radius of cylinder and consequently less particles stick to the surface which are responsible for heat transfer through conduction. Therefore, the temperature profile decreases near the surface of the cylinder. It is also observed that the temperature profile is higher in case of flat plate when compared with the cylinder. Figure 7 is drawn to study the effect of curvature parameter $\gamma$ on the concentration profiles. It is also observed in this figure that for larger curvature parameter, the concentration boundary layer thickness first decreases and then increases. The effects of magnetic field on the velocity, temperature and concentration of Cu–water nanofluid at the cylinder surface are shown in Figs. 8, 9, 10. It is examined from Fig. 8 that the velocity profile decreases with increasing the values of the magnetic parameter M. This is because application of a transverse magnetic field normal to the flow direction gives rise to a resistive drag-like force known as Lorentz force acting in a direction opposite to that of the flow. This has a tendency to reduce fluid transport phenomena and increase the fluid temperature. Figures 9 and 10 are drawn to analyze the influence of magnetic parameter M on the dimensionless temperature and nanoparticle concentration. It is found from these figures that the dimensionless temperature and concentration profiles are significantly affected by increasing the magnetic parameter. It is well known that the Lorentz force is a resistive force which opposes the fluid motion, so due to obstruction in the motion of the fluid, heat is produced and as a result the thermal boundary layer thickness and concentration boundary layer thickness increase with enhancement of the magnetic field.

Fig. 2

Variation of velocity profile with different value of $\phi$ for Cu–water nanofluid

Fig. 3

Variation of temperature profile with different value of $\phi$ for Cu–water nanofluid

Fig. 4

Variation of concentration profile with different value of $\phi$ for Cu–water nanofluid

Fig. 5

Variation of velocity profile with different value of $\gamma$ for Cu–water nanofluid

Fig. 6

Variation of temperature profile with different value of $\gamma$ for Cu–water nanofluid

Fig. 7

Variation of concentration profile with different value of $\gamma$ for Cu–water nanofluid

Fig. 8

Variation of velocity profile with different value of M for Cu–water nanofluid

Fig. 9

Variation of temperature profile with different value of M for Cu–water nanofluid

Fig. 10

Variation of concentration profile with different value of M for Cu–water nanofluid

Figures 11, 12 display the effects of non-uniform heat source/sink parameters $A^{*}$ and $B^{*}$ on temperature profiles of Cu–water nanofluid over stretching cylinder. From Fig. 11, it is observed that the thermal boundary layer generates energy, which causes the temperature profiles to increase with the increasing values of $A^{*}> 0$. The effect of temperature dependent heat source/sink parameter $B^{*}$ on heat transfer is demonstrated in Fig. 12. This figure illustrates that energy is released for increasing values of $B^{*} > 0$ which causes the temperature to increase. Hence, non-uniform heat source/sink parameter is better suited for heating/cooling purposes. The influence of chemical reaction parameter $\varGamma$ on concentration field of Cu–water nanofluid over the stretching cylinder surface is sketched in Fig. 13. It is observed from this figure that the concentration profile decreases with an increase in the chemical reaction parameter. In fact, with the increase in chemical reaction, the parameter rate of destructive chemical reaction increases, which is responsible in the reduction in the concentration profile.

Fig. 11

Variation of temperature profile with different value of $A^{*}$ for Cu–water nanofluid

Fig. 12

Variation of temperature profile with different value of $B^{*}$ for Cu–water nanofluid

Fig. 13

Variation of concentration profile for different values of $\varGamma$ for Cu–water nanofluid

Figure 14 plots the effect of Schmidt number Sc on concentration profile of Cu–water nanofluid at the stretching cylinder surface. It is observed from this figure that both concentration and boundary layer thickness decrease with increasing the values of the Schmidt number Sc. It is due to the fact that Schmidt number Sc is the ratio of momentum diffusivity to mass diffusivity as a result higher values of Schmidt number Sc correspond to small mass diffusivity.

Fig. 14

Variation of concentration profile for different values of Sc for Cu–water nanofluid

The variations of the skin-friction coefficient and local Sherwood number with increase in the values of solid volume fraction $\phi$ for different values of curvature parameter $\gamma$ for three different types of nanofluid (Cu–water, ${\hbox {Al}}_2{\hbox {O}}_3$–water, and ${\hbox {TiO}}_2$–water) over stretching cylinder are shown in Figs. 15, 16, respectively. It is observed that the effect of increasing the solid volume fraction $\phi$ is to decrease the skin-friction coefficient but to increase the local Sherwood number for all the three types of nanofluids. It is also noticed that the value of skin-friction coefficient decreases with increasing the value of curvature parameter $\gamma$ for all the three types of nanofluids but reverse effect is observed for Sherwood number. Figs. 17, 18 depict the effect of increasing the value of $\gamma$ for different values of $\phi$ on the skin-friction coefficient and local Nusselt number for all the three different types of nanofluid (Cu–water, ${\hbox {Al}}_2{\hbox {O}}_3$–water and ${\hbox {TiO}}_2$–water) over stretching cylinder. It is observed that the skin-friction coefficient decreases with increasing solid volume fraction $\phi$ for all the three types of nanofluids. Further, the effect of increasing the $\gamma$ on local Nusselt number has no significant effect for the flow over a stretching cylinder.

Fig. 15

Variation of skin-friction coefficient with $\phi$ for different values of $\gamma$ for different types of nanofluids

Fig. 16

Variation of Sherwood number with $\phi$ for different values of $\gamma$ for different types of nanofluids

Fig. 17

Variation of skin-friction coefficient with $\gamma$ for different values of $\phi$ for different types of nanofluids

Fig. 18

Variation of the local Nusselt number with $\gamma$ for different values of $\phi$ for different types of nanofluids

Conclusion

In this paper, an analysis has been carried out to study the magnetohydrodynamic heat and mass transfer of nanofluids over stretching cylinder in the presence of non-uniform heat source/sink and chemical reaction with prescribed heat flux boundary condition on temperature. Three different kinds of nanoparticle, namely ${\hbox {Cu}}, {\hbox {Al}}_2{\hbox {O}}_3, {\hbox {TiO}}_2$ in the base fluid (water) is considered here. The governing non-linear partial differential equations were transformed into a set of ordinary differential equation using similarity transformation before being solved numerically by the Runge–Kutta–Fehlberg method with shooting techniques. Numerical calculations were carried out for different values of solid volume fraction $\phi$, curvature parameter $\gamma$, magnetic parameter M, non-uniform heat source/sink parameters $A^{*}$ and $B^{*}$, chemical reaction parameter $\varGamma$, Schmidt number Sc and their effects are analyzed graphically on flow, heat and mass transfer characteristics. Some of the important findings of our analysis obtained by the graphical representation are listed below:

(i) Velocity, temperature and concentration profiles of Cu–water nanofluid over stretching cylinder increase with increase in the values of $\phi$ and curvature parameter $\gamma$.

(ii) Temperature and concentration profiles increase but velocity profile decreases with increase in the magnetic parameter M for Cu–water nanofluid over stretching cylinder.

(iii) Temperature profile of Cu–water nanofluid over stretching cylinder increases with the increase in values of non-uniform heat souece/sink parameter $A^{*}$ and $B^{*}$.

(iv) Concentration profile of Cu–water nanofluid over stretching cylinder decreases with the increase in the chemical reacction parameter $\varGamma$ and Schmidt number Sc.

(v) Cu–water posses lower skin-friction coefficient and local Sherwood number compared to other two nanofluids, ${\hbox {Al}}_2{\hbox {O}}_3$–water and ${\hbox {TiO}}_2$–water.

(vi) Skin-friction coefficient decreases with increasing the value of $\phi$ as well as the value of $\gamma$ but local Sherwood number decreases with increasing the value of $\phi$ for all the three types of nanofluids (${\hbox {Cu}}, {\hbox {Al}}_2{\hbox {O}}_3, {\hbox {TiO}}_2$–water) over stretching cylinder. Finally, all the numerical results coincide very well with the previously published results.