Unsteady MHD Casson fluid flow with heat transfer passed over a porous rigid plate with stagnation point flow: Two-parameter Lie scaling approach

Abstract

This study examined the steady flow of Casson fluid over a rigid porous plate in an infinite region with magnetohydrodynamic (MHD), thermal radiation and heat source-sink effects. Under the influence of stagnation point flow and thermal transport, the physical model is strengthened. The model consists of nonlinear partial differential equations (PDEs), which are controlled after applying approximation of the boundary layer (BL). The significance of this flow model here is that these PDEs have been turned into ordinary differential equations (ODEs) by means of two-parameter Lie scaling transformations. These ODEs are rectified using the MATLAB bvp4c technique. Convergence analysis of these ODEs demonstrate the consistency of the model. Dimensionless parameters are: Casson fluid parameter $\beta$, Hartmann number $M_{t}$, Darcy ratio K, thermal radiation $\Delta _{t}$ and heat source-sink parameter $Q_{t}$. These parameters are analysed using graphs for fluid flow, temperature and physical quantities. These quantities are analysed using graphs and a table. All the prominent parameters increased the flow of fluid, but thermal transport was decreased for different parameters.

1 Introduction

Many researchers studied non-Newtonian fluid properties in several models because of the absence of Newton’s law of viscosity. Casson fluid model is a common non-Newtonian fluid model describing complete liquid rheology in liquids such as blood, ketchup, crude oil, shampoo, etc. Blood behaves as a Newtonian fluid when flowing through a large-diameter tube, but behaves as a non-Newtonian fluid when flowing in a small-diameter tube and then it behaves like the Casson fluid. Casson fluid properties of a porous stretch sheet were analysed by Nanjundaswamy et al [1]. El-Aziz and Afify [2] combined the entropy production and Hall effects for the Casson fluid over a stretching board. Mahdy analysed [3] Casson fluid rheology with heat transfer in a stretching cylindrical device. Bachok et al [4] discussed the instability of the nanofluid boundary layer (BL) over a permeable stretching-shrinking wall. Tie-Gang et al [5] found a shrinking sheet with a concentration profile to have viscous effects.

In 1665–1666, the historical background of differential equations (DEs) began with calculus. Many mathematicians, including Leibniz, Bernoulli, Ricatti and Clairaut, presented numerous types of DEs. They gave outstanding results from those DEs. The 18th century was the beginning of PDEs history. The 19th century showed many discoveries in the form of PDEs, which were very useful. During the period 1880–1900, Lie discovered a systematic method to solve DEs. Reduction, analysis and DE classification are revolutionary aspects of Lie’s theory. The modern theory of DE is known to be incomplete without Lie’s contribution. Such an approach has a great capacity to be effectively applied on non-linear DEs. The DEs remain unchanged under the approach of the Lie group, called a symmetry group. These symmetries are groupings of continuous transformations. The cornerstones of the hydrodynamic method include the law of conservation of mass, momentum and energy. The Reynolds transport theorem establishes these rules. Normally, one-parameter scaling transformation is added to the equations governing framework. The invariance conditions of the control system of the equations generated by the hydrodynamic method were determined using those transformations. Scaling analysis is connected from one space to another space–time with the physical process solution. In addition, the investigators figure out the invariants by applying one-parameter scaling transformations to the governing equations but it is difficult to measure the invariants in the presence of more than two independent variables. Uddin et al [6, 7] have used the two-parameter scaling transformations to evaluate the effects of magnetohydrodynamics (MHD) on various non-Newtonian fluids for more than two independent variables. MHD has many uses in the study of heat transfer. Moreover, crystal melting, chemical processing, space heatings and power generation are heat transfer applications in automotive and manufacture industries. The Lorentz forces generate electric current under a strong magnetic field. These forces increase the flow of energy due to the increase in temperature of the fluid particles. Sadiq [8] has investigated the effects of isotropic slip on the MHD nanofluid on a rigid layer.

In different fields including aerodynamics and engineering, stagnation point flow applications have occurred. In 1991, Hiemenz analysed the flow of stagnation. The fluid flow has split into two parts. Besides, the fluid flow was moving far from the region’s centre. The oblique stagnation point flow was discussed by Tilley and Weidman [9]. Wang [10] spoke about the shrinking sheet stagnation results. The stagnation flow for the disc was implemented by Wang [11]. Wang [12] later noticed the effects of stagnation on a plate with the isotropic slip. Several researchers [13,14,15] have spoken of the movement of stagnating points. Three-dimensional stagnation point flow has been discussed in [16,17,18,19,20]. We find several approaches and techniques in literature for solving PDEs and ODEs [21, 22]. We observed in this regard that Yang and Gao [23] proposed a new transformation of the Sumudu to solve heat equations. Yang [24, 25] used an integral transform approach for evaluating thermocouples to test a steady-state heat equation. Yang and co-workers [26,27,28,29,30,31] also provided numerous results for solving various types of heat equations with various geometries. Besides, Saima et al [32] discussed two integral transform techniques for perturbed equation structures.

Mahato and Das [33] considered an inconsistent radiative Casson fluid model with different thermal consequences. Gautam et al [34] used a vertical plate for the Carreau fluid model, under the influence of mixed convective, Soret and Doufer. For three-dimensional flow with a modified Fourier law, Carreau fluid model is regarded by Ramadevi et al [35]. Mustafa et al [36] investigated various solutions of stable solutions of Newtonian fluid flow. The effects of the Cattaneo–Christov heat flux and stagnation point flow model are described in a Sutterby fluid model by Azher et al [37]. Kumar et al [38] used a vertical plate for the Jeffrey fluid model with entropy generation results. Iqbal et al [39] have done a numerical analysis under the influence of entropy and melting heat transfer. Afify and El-Aziz [40] provided a Lie group study of the non-Newtonian nanofluid spread over a stretching surface.

The unsteady, laminar and two-dimensional work with the stagnation point flow is recently investigated by using two-parameter scaling transformations. According to the literature, the researchers did not recognise this form of flow. This flow incorporated a rigid plate with a porous medium and a stagnation point flow. The dimensionless parameters, such as the Hartmann number, the Darcy number, thermal radiation and heat-sink, demonstrated the rheological properties of the Casson fluid in the Lie group analysis. We reached from PDEs to ODEs by way of two-parameter transformations. Graphical findings are tested using the code bvp4c via MATLAB. Physical quantities for the combinations of various parameters have been discussed using graphs and a table. Model convergence is seen using the graph with the highest infinity value. Even the testing of this model has been shown. Finally, details of discussion and conclusion are given.

2 Mathematical description

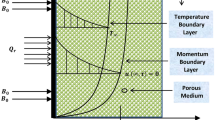
Figure 1 represents the porous medium of the MHD Casson fluid model with the two-dimensional, laminar and unsteady stagnation point flow. Even the MHD Casson model experiences the unpredictable effects of thermal radiation and source-sink heat. We have chosen the following system $({\bar{x}}, {\bar{y}})$ with velocity components $({\bar{u}},{\bar{v}}).$ The magnetic field is applied parallel to ${\bar{y}}$-axis with $B_{0}/{\sqrt{t}}.$

Fig. 1

Stagantion point flow geometry.

The Casson fluid model is [1,2,3]

$$\begin{aligned} \tau _{ij}=\left\{ \begin{array}{c} 2\left( \mu _{B}+\dfrac{p_{y}}{\sqrt{2\pi }}\right) e_{ij},\ \ \ \ \ \pi >\pi _{c} \\ 2\left( \mu _{B}+\dfrac{p_{y}}{\sqrt{2\pi }}\right) e_{ij},\ \ \ \ \ \pi <\pi _{c} \end{array} \right. , \end{aligned}$$

(1)

where $\tau _{ij}$, Cauchy stress tensor, is elaborated as$\ \pi =e_{ij}e_{ij}$ ($e_{ij}$ is the (i, j)th component of the deformation rate), $\pi$ is the product term$,\ \pi _{c}$ is the critical value, $\mu _{B}$ is the plastic dynamic viscosity and $p_{y}$ is the yield stress. The dimensional forms of the momentum and thermal boundary layer equations are denoted as ${\bar{u}}$ and ${\bar{T}}.$ The laws are arrived in the form of eqs (2)–(8):

$$\begin{aligned}&\frac{\partial {\bar{u}}}{\partial {\bar{x}}}+\frac{\partial \bar{ v}}{\partial {\bar{y}}}=0, \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial {\bar{u}}}{\partial {\bar{t}}}+{\bar{u}}\frac{ \partial {\bar{u}}}{\partial {\bar{x}}}+{\bar{v}}\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\nonumber \\&\quad =-\frac{1}{\rho }\frac{\partial {\bar{p}}}{\partial {\bar{x}}} +\nu \left( 1+\frac{1}{\beta }\right) \frac{\partial ^{2}{\bar{u}}}{\partial {\bar{y}}^{2}}-\frac{\sigma _{e}B_{0}^{2}{\bar{u}}}{\rho t}\nonumber \\&\qquad -\nu \left( 1+\frac{1}{\beta }\right) \frac{{\bar{u}}}{k_{1}t}. \end{aligned}$$

(3)

For the free stream velocity, ${\bar{u}}={\bar{u}}_{e}({\bar{x}},{\bar{t}} )$, eq. (3) is reduced as

$$\begin{aligned}&\frac{\partial {\bar{u}}_{e}}{\partial {\bar{t}}}+{\bar{u}}_{e} \frac{\partial {\bar{u}}_{e}}{\partial {\bar{x}}}\nonumber \\&\quad =-\frac{1}{\rho } \frac{\partial {\bar{p}}}{\partial {\bar{x}}}-\frac{\sigma B_{0}^{2}}{ \rho t}\left( {\bar{u}}_{e}\right) -\nu \left( 1+\frac{1}{\beta }\right) \frac{{\bar{u}}_{e}}{k_{1}t}, \end{aligned}$$

(4)

and from eqs (3) and (4), we obtained the momentum equation by omitting the pressure term

$$\begin{aligned}&\frac{\partial {\bar{u}}}{\partial {\bar{t}}}+{\bar{u}}\frac{ \partial {\bar{u}}}{\partial {\bar{x}}} +{\bar{v}}\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\nonumber \\&\quad =\frac{\partial {\bar{u}}_{e}}{ \partial {\bar{t}}}+{\bar{u}}_{e}\frac{\partial {\bar{u}}_{e}}{ \partial {\bar{x}}}+\nu \left( 1+\frac{1}{\beta }\right) \frac{\partial ^{2}{\bar{u}}}{\partial {\bar{y}}^{2}}\nonumber \\&\qquad -\frac{\sigma _{e}B_{0}^{2}\left( {\bar{u}} -{\bar{u}}_{e}\right) }{\rho t}-\nu \left( 1+\frac{1}{\beta }\right) \frac{\left( {\bar{u}}-{\bar{u}} _{e}\right) }{k_{1}t}, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial {\bar{T}}}{\partial {\bar{t}}}+{\bar{u}}\frac{ \partial {\bar{T}}}{\partial {\bar{x}}}+{\bar{v}}\frac{\partial {\bar{T}}}{\partial {\bar{y}}}\nonumber \\&\quad =\frac{k_{t}}{\rho C_{P}}\frac{\partial ^{2}{\bar{T}}}{\partial {\bar{y}}^{2}}-\frac{1}{\rho C_{P}t}\frac{ \partial q_{r}}{\partial {\bar{y}}}+\frac{Q_{0}^{\prime }}{\rho C_{p}t} \left( {\bar{T}}-{\bar{T}}_{\infty }\right) , \end{aligned}$$

(6)

where the radiative heat flux as given in [21, 22] may be adopted. Thus,

$$\begin{aligned} - \frac{\partial q_{r}}{\partial {\bar{y}}}=4\gamma ^{2}\left( {\bar{T}}- {\bar{T}}_{\infty }\right) ,\quad \gamma ^{2}=\int _{0}^{\infty }\left( \alpha _{\lambda }\frac{\partial B}{\partial T}\right) \mathrm {d}\lambda , \end{aligned}$$

where $\alpha _{\lambda }$ is the absorption coefficient, B is the Planck’s function, $\lambda$ is the frequency. The unsteady boundary conditions (BCs) with stagnation point flow according to [4, 5] are

$$\begin{aligned}&{\bar{u}}({\bar{t}},{\bar{x}},{\bar{y}}) =0,\ \ \ {\bar{v}}( {\bar{t}},{\bar{x}},{\bar{y}})=0, \nonumber \\&{\bar{T}}({\bar{t}}, {\bar{x}},{\bar{y}})={\bar{T}}_{p}+({\bar{T}}_{p}-{\bar{T}} _{\infty })\frac{{\bar{x}}}{t^{2}},\ \ \ \mathrm {at}\ \ \ {\bar{y}}=0, \end{aligned}$$

(7)

$$\begin{aligned}&{\bar{u}}({\bar{t}},{\bar{x}},{\bar{y}}) ={\bar{u}}_{e},\ \ \ {\bar{v}}({\bar{t}},{\bar{x}},{\bar{y}})=0, \nonumber \\&{\bar{T}}( {\bar{t}},{\bar{x}},{\bar{y}})\rightarrow {\bar{T}}_{\infty }\ \ \ \mathrm {as}\ \ \ {\bar{y}}\rightarrow \infty , \end{aligned}$$

(8)

where ${\bar{t}}$ is the unsteadiness$,\ {\bar{u}}$ is the axial velocity$,\ \beta =\frac{\mu _{B \sqrt{2\pi _{c}}}}{P_{y}}$ is the Casson fluid parameter, $\rho$ is the fluid density$,\ \sigma _{e}$ is the electrical conductivity, $B_{0}$ is the magnetic field intensity$,\ k_{1}$ is the Darcy coefficient,$\ k_{t}$ is the thermal conductivity, $C_{P}$ is the specific heat at constant pressure, ${\bar{T}}$ is the fluid temperature$,\ {\bar{T}}_{p}$ is the plate fluid temperature$,\ {\bar{T}}_{\infty }$ is the free stream fluid temperature$,\ \gamma$ is the term due to thermal radiation,  $Q_{0}^{\prime }<0$ represents the heat sink$,\ Q_{0}^{\prime }>0$ represents the heat source$,\ \eta$ is the similarity parameter, $U_{p}$ is the plate velocity, $u_{e}$ is the stagnation velocity and $L_{p}$ is the plate length. We define the dimensionless quantities with Reynolds number $\text{ Re }={U_{p}L_{p}}/{\nu }$ as

$$\begin{aligned} x&=\frac{{\bar{x}}}{L_{p}},\ \ \ y=\frac{{\bar{y}}}{L_{p}}\text{ Re}^{ {1}/{2}},\ \ \ u=\frac{{\bar{u}}}{U_{p}}, \nonumber \\ v&=\frac{{\bar{v}}}{ U_{p}}\text{ Re}^{{1}/{2}},\ \ \ t=\frac{U_{p}{\bar{t}}}{L_{p}}, \nonumber \\ T&=\frac{{\bar{T}}-{\bar{T}}_{\infty }}{{\bar{T}}_{p}-{\bar{T}} _{\infty }},\ \ \ u_{e}=\frac{{\bar{u}}_{e}}{U_{p}}. \end{aligned}$$

(9)

Equations (2)–(8) are in dimensionless form after using eq. (9)

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\nonumber \\&\quad =\frac{\partial u_{e}}{\partial t}+u_{e}\frac{\partial u_{e}}{ \partial x}+\left( 1+\frac{1}{\beta }\right) \frac{\partial ^{2}u}{\partial y^{2}}\nonumber \\&\qquad -\left( M_{t}^{2}+\left( 1+\frac{1}{\beta }\right) K\right) \frac{ \left( u-u_{e}\right) }{t}, \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{1}{\Pr }\frac{\partial ^{2}T}{\partial y^{2}}+\frac{ \left( \Delta _{t}+Q_{t}\right) }{t}T \end{aligned}$$

(12)

and the BCs with the stagnation point effect are

$$\begin{aligned} u= & {} 0,\ \ \ v=0,\ \ \ T=\frac{x}{t^{2}}\ \ \ \text {at}\,\,\,\,y=0, \end{aligned}$$

(13)

$$\begin{aligned} u= & {} u_{e},\ \ \ v=0,\ \ \ \vartheta \rightarrow 0,\,\,\,\, \text {as}\,\,\,\, y\rightarrow \infty . \end{aligned}$$

(14)

The physical parameters in eqs (10)–(14) are defined as

$$\begin{aligned} \Pr= & {} \frac{\rho C_{P}}{k_{t}},\ \ \ M_{t}^{2}=\frac{\sigma _{e}B_{0}^{2}L_{p}}{\rho U_{p}},\ \ \ K=\frac{\nu L_{p}}{k_{1}U_{p}}, \\ \Delta _{t}= & {} \frac{4\gamma ^{2}L_{p}}{\rho C_{P}U_{p}},\ \ \ Q_{t}=\frac{ Q_{0}L_{p}}{\rho C_{P}U_{p}}, \end{aligned}$$

where $\Pr$ is the Prandtl number, $M_{t}$ is the Hartmann number, K is the Darcy parameter, $Q_{t}$ is the heat source-sink parameter and $\Delta _{t}$ is the thermal radiation. The stream function is chosen $\psi (x,y,t)$ as

$$\begin{aligned} u=\frac{\partial \psi }{\partial y},\ \ \ v=-\frac{\partial \psi }{\partial x }, \end{aligned}$$

(15)

which satisfies eq. (10) easily. Equations (11)–(14) in terms of $\psi$ are

$$\begin{aligned}&\frac{\partial ^{2}\psi }{\partial t\partial y}+\frac{\partial \psi }{\partial y}\frac{\partial ^{2}\psi }{\partial x\partial y}-\frac{\partial \psi }{\partial x}\frac{\partial ^{2}\psi }{\partial y^{2}}\nonumber \\&\quad =\frac{\partial u_{e}}{\partial t}+u_{e}\frac{\partial u_{e}}{\partial x}+\left( 1+\frac{1}{ \beta }\right) \frac{\partial ^{3}\psi }{\partial y^{3}} \nonumber \\&\qquad -\left( M_{t}^{2}+\left( 1+\frac{1}{\beta }\right) K\right) \frac{1}{t}\left( \frac{ \partial \psi }{\partial y}-u_{e}\right) , \end{aligned}$$

(16)

$$\begin{aligned}&\frac{\partial T}{\partial t}+\frac{\partial \psi }{\partial y}\frac{\partial T}{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial T}{ \partial y}=\frac{1}{\Pr }\frac{\partial ^{2}T}{\partial y^{2}}+\frac{\left( \Delta _{t}+Q_{t}\right) }{t}T\nonumber \\ \end{aligned}$$

(17)

with

$$\begin{aligned} \frac{\partial \psi }{\partial y}= & {} 0,\ \ \ \frac{\partial \psi }{\partial x }=0,\ \ \ T=\frac{x}{t^{2}}\ \ \ \text {at} \,\,\, y=0, \end{aligned}$$

(18)

$$\begin{aligned} \frac{\partial \psi }{\partial y}= & {} u_{e},\ \ \ T\rightarrow 0\ \ \ \text { as}\,\,\, y\rightarrow \infty . \end{aligned}$$

(19)

3 Two-parameter Lie scaling transformations

To minimise the intensity of higher-order PDEs, Lie scaling transformations have been used. We have employed two-parameter scaling transformations for analysing the continuous symmetries of the PDEs and reduce the three independent variables $t,\ x$ and y into one independent symmetry variable $\eta .$ All the independent and dependent variables following the two-parameter scaling transformations are scaled as follows [6, 7]:

$$\begin{aligned} {\tilde{t}}= & {} tA^{\mu _{1}},\ \ \ {\tilde{x}}=xB^{\nu _{1}},\nonumber \\ {\tilde{\psi }}= & {} \psi A^{\mu _{2}}B^{\nu _{2}},\ \ \ {\tilde{y}}=yA^{\mu _{3}}B^{\nu _{3}}, \nonumber \\ {\tilde{\vartheta }}= & {} TA^{\mu _{4}}B^{\nu _{4}},\ \ \ {\tilde{u}} _{e}=u_{e}A^{\mu _{5}}B^{\nu _{5}}, \end{aligned}$$

(20)

where $A,\ B,\ \mu _{i},\ \nu _{i}(i=1{-}5)$ are arbitrary constants. Nonlinear PDEs (16) and (17) by time-dependent BCs (18) and (19) are resolved using the scaling transformations of two-parameters specified in eq (20). Equation (20) made eqs (16)–(19) as

$$\begin{aligned}&\frac{\partial ^{2}{\tilde{\psi }}}{\partial {\tilde{y}}\partial {\tilde{t}}}A^{\mu _{3}-\mu _{2}+\mu _{1}}B^{\nu _{3}-\nu _{2}}\nonumber \\&\qquad +\frac{\partial {\tilde{\psi }}}{\partial {\tilde{y}}}\frac{\partial ^{2} {\tilde{\psi }}}{\partial {\tilde{x}}\partial {\tilde{y}}}A^{2\mu _{3}-2\mu _{2}}B^{\nu _{1}+2\nu _{3}-2\nu _{2}}\nonumber \\&\qquad -\frac{\partial \tilde{ \psi }}{\partial {\tilde{x}}}\frac{\partial ^{2}{\tilde{\psi }}}{ \partial {\tilde{y}}^{2}}A^{\mu _{3}-2\mu _{2}+\mu _{4}}B^{\nu _{1}-2\nu _{2}+\nu _{3}+\nu _{4}} \nonumber \\&\quad =\frac{\partial {\tilde{u}}_{e}}{\partial {\tilde{t}}}A^{\mu _{1}-\mu _{5}}B^{-\nu _{5}}\nonumber \\&\qquad +{\tilde{u}}_{e}\frac{\partial {\tilde{u}}_{e}}{ \partial {\tilde{x}}}A^{-2\mu _{5}}B^{\nu _{1}-2\nu _{5}}\nonumber \\&\qquad +\left( 1+\frac{1 }{\beta }\right) \frac{\partial ^{3}{\tilde{\psi }}}{\partial {\tilde{y}} ^{3}}A^{3\mu _{3}-\mu _{2}}B^{3\nu _{3}-\nu _{2}} \nonumber \\&\qquad -\left( M_{t}^{2}+\left( 1+\frac{1}{\beta }\right) K\right) \frac{1}{ {\tilde{t}}}A^{\mu _{1}+\mu _{3}-\mu _{2}}B^{\nu _{3}-\nu _{2}}\frac{ \partial {\tilde{\psi }}}{\partial {\tilde{y}}}\nonumber \\&\qquad +\left( M_{t}^{2}+K\right) \frac{1}{{\tilde{t}}}A^{\mu _{1}-\mu _{5}}B^{-\nu _{5}} {\tilde{u}}_{e}, \end{aligned}$$

(21)

$$\begin{aligned}&\frac{\partial {\tilde{\vartheta }}}{\partial {\tilde{t}}}A^{\mu _{1}-\mu _{4}}B^{-\nu _{4}} \nonumber \\&\qquad +\frac{\partial {\tilde{\psi }}}{\partial {\tilde{y}}}\frac{\partial {\tilde{\vartheta }}}{\partial {\tilde{x}}} A^{\mu _{3}-\mu _{2}-\mu _{4}}B^{\nu _{1}-\nu _{2}+\nu _{3}-\nu _{4}}\nonumber \\&\qquad -\frac{ \partial {\tilde{\psi }}}{\partial {\tilde{x}}}\frac{\partial \tilde{ \vartheta }}{\partial {\tilde{y}}}A^{\mu _{3}-\mu _{2}-\mu _{4}}B^{\nu _{1}-\nu _{2}+\nu _{3}-\nu _{4}} \nonumber \\&\quad =\frac{1}{\Pr }\frac{\partial ^{2}{\tilde{\vartheta }}}{\partial {\tilde{y}}^{2}}A^{2\mu _{3}-\mu _{4}}B^{2\nu _{3}-\nu _{4}}\nonumber \\&\qquad +\frac{\left( \Delta _{t}+Q_{t}\right) }{{\tilde{t}}}{\tilde{\vartheta }}A^{\mu _{1}-\mu _{4}}B^{-\nu _{4}}, \end{aligned}$$

(22)

with the shifted boundary conditions

$$\begin{aligned}&\frac{\partial {\tilde{\psi }}}{\partial {\tilde{y}}}A^{\mu _{3}-\mu _{2}}B^{\nu _{3}-\nu _{2}}=0, \nonumber \\&\frac{\partial {\tilde{\psi }}}{ \partial {\tilde{x}}}A^{-\mu _{2}}B^{\nu _{1}-\nu _{2}}=0, \end{aligned}$$

(23)

$$\begin{aligned}&{\tilde{\vartheta }}A^{-\mu _{4}}B^{-\nu _{4}}=\frac{{\tilde{x}}}{ {\tilde{t}}^{2}}A^{-2\mu _{1}}B^{-\nu _{1}}. \end{aligned}$$

(24)

$$\begin{aligned}&\frac{\partial {\tilde{\psi }}}{\partial {\tilde{y}}}A^{\mu _{3}-\mu _{2}}B^{\nu _{3}-\nu _{2}}={\tilde{u}}_{e}A^{-\mu _{5}}B^{-\nu _{5}}. \end{aligned}$$

(25)

Following [6, 7], we get the linear combination of $\mu _{i}$ and $\nu _{i}$ as on comparing the powers of the arbitrary constants A and B in eqs (21) and (22)

$$\begin{aligned}&\mu _{1}+\mu _{3}-\mu _{2}=-2\mu _{2}+2\mu _{3} \nonumber \\&\qquad \qquad \qquad \quad \, =3\mu _{3}-\mu _{2}=\mu _{1}-\mu _{4}, \end{aligned}$$

(26)

$$\begin{aligned}&\nu _{3}-\nu _{2}=\nu _{1}-2\nu _{2}+2\nu _{3}=3\nu _{3}-\nu _{2}, \end{aligned}$$

(27)

and from the BCs (23)–(25), we get the values as

$$\begin{aligned} \mu _{2}= & {} -\frac{1}{2}\mu _{1},\ \ \ \mu _{3}=\frac{1}{2}\mu _{1},\ \ \nonumber \\ \mu _{4}= & {} -2\mu _{1},\ \ \ \mu _{5}=-\mu _{1}, \end{aligned}$$

(28)

$$\begin{aligned} \nu _{1}= & {} \nu _{2},\ \ \ \nu _{3}=0,\ \ \ \nu _{4}=\nu _{1},\ \ \ \nu _{5}=\nu _{1}. \end{aligned}$$

(29)

Equation (20) now can be written in terms of one arbitrary constant after using eqs (28) and (29)

$$\begin{aligned} {\tilde{t}}= & {} tA^{\mu _{1}}, \nonumber \\ {\tilde{x}}= & {} xB^{\nu _{1}},\ \ \ {\tilde{\psi }}=\psi A^{-\frac{1}{2}\mu _{1}}B^{\nu _{1}},\ \ \ \tilde{y}=yA^{\frac{1}{2}\mu _{1}}, \nonumber \\ {\tilde{\vartheta }}= & {} TA^{-2\mu _{1}}B^{\nu _{1}},\ \ \ {\tilde{u}} _{e}=u_{e}A^{-\mu _{1}}B^{\nu _{1}}. \end{aligned}$$

(30)

4 Absolute invariants

Equations (20) and (30) gave us the following relation:

$$\begin{aligned} \frac{{\tilde{y}}}{{\tilde{t}}^{{1}/{2}}}=\frac{y}{t^{{1}/{2}}}. \end{aligned}$$

(31)

The first absolute invariant from eq. (31) is

$$\begin{aligned} \eta ={\tilde{y}}{\tilde{t}}^{-{1}/{2}} \end{aligned}$$

(32)

and the remaining absolute invariants are followed from eqs (20) and (30):

$$\begin{aligned} f(\eta )=\frac{{\tilde{\psi }}}{{\tilde{t}}^{-{1}/{2}}{\tilde{x}}} ,\ \ \ \vartheta (\eta )=\frac{{\tilde{t}}^{2}}{{\tilde{x}}}\tilde{ \vartheta },\ \ \ {\tilde{u}}_{e}=B\frac{{\tilde{x}}}{{\tilde{t}}}. \end{aligned}$$

(33)

4.1 Reduced governing system

The nonlinear PDEs (21)–(25) become ODEs with stagnation point effect after using eqs (32) and (33), where prime denotes the derivative with respect to $\eta .$

$$\begin{aligned}&\left( 1+\frac{1}{\beta }\right) f^{\prime \prime \prime }(\eta )+\left( f(\eta )+\frac{1}{2}\eta \right) f^{\prime \prime }(\eta )\nonumber \\&\quad +f^{\prime }(\eta )\left( 1-f^{\prime }(\eta )-\left( M_{t}^{2}+\left( 1+\frac{1}{\beta } \right) K\right) \right) \nonumber \\&\quad +\left( M_{t}^{2}+\left( 1+\frac{1}{\beta }\right) K\right) =0, \end{aligned}$$

(34)

$$\begin{aligned}&\frac{1}{\Pr }\vartheta ^{\prime \prime }(\eta )+2\vartheta (\eta )+\frac{1}{ 2}\eta \vartheta ^{\prime }(\eta )\nonumber \\&\quad -f^{\prime }(\eta )\vartheta (\eta )+f(\eta )\vartheta ^{\prime }(\eta )\nonumber \\&\quad +\left( \Delta _{t}+Q_{t}\right) \vartheta (\eta )=0, \end{aligned}$$

(35)

$$\begin{aligned}&f(\eta )=0,\ \ \ f^{\prime }(\eta )=0,\ \ \ \vartheta (\eta )=1\ \ \ \text {at}\ \ \ \eta =0,\nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned}&f^{\prime }(\eta )=1,\ \ \ \vartheta (\eta )=0\ \ \ \text {as}\ \ \ \eta \rightarrow \infty . \end{aligned}$$

(37)

5 Physical quantities

Skin friction coefficient $C_{f}$ and local Nusselt number $Nu_{x}$ are

$$\begin{aligned}&C_{f}=\frac{\left( \mu _{B}+\frac{P_{y}}{\sqrt{2\pi _{c}}}\right) }{\rho \left( {\bar{u}}\right) ^{2}}\left. \left( \frac{\partial {\bar{u}}}{ \partial {\bar{y}}}\right) \right| _{{\bar{y}}=0}, \end{aligned}$$

(38)

$$\begin{aligned}&Nu_{x}=\frac{{\bar{x}}}{T_{p}-T_{\infty }}\left. \left( -\frac{\partial T }{\partial {\bar{y}}}\right) \right| _{{\bar{y}}=0}. \end{aligned}$$

(39)

We get the dimensionless physical quantities by using eqs (9), (38) and (39)

$$\begin{aligned} (\text{ Re}_{x})^{-1}C_{f}= & {} A^{-{3}/{2}}\left( \text{ Re }\right) ^{-{3 }/{2}}\nonumber \\&\times \left( 1+\frac{1}{\beta }\right) \left. \frac{\partial ^{2}f(\eta )}{\partial \eta ^{2}}\right| _{\eta =0}, \end{aligned}$$

(40)

$$\begin{aligned} Nu_{x}(\text{ Re}_{x})^{-2}= & {} -A^{-{5}/{2}}(\text{ Re})^{-{3}/{2}}\left. \frac{\partial \vartheta (\eta )}{\partial \eta }\right| _{\eta =0}, \end{aligned}$$

(41)

Fig. 2

Action of $\beta$ on the fluid flow.

Fig. 3

Action of $M_{t}$ on the fluid flow.

where A is the unsteady parameter and mathematically

$$\begin{aligned} \text{ Re}_{x}=\frac{u_{p}{\bar{x}}}{\nu }. \end{aligned}$$

Fig. 4

Action of K on the fluid flow.

Fig. 5

Action of $\hbox {Pr}$ on the thermal flow.

Fig. 6

Action of $\Delta _{t}$ on the thermal flow.

Fig. 7

Action of ${Q}_{t}$ on the thermal flow.

Fig. 8

Action of $\beta$ on the thermal flow.

Fig. 9

Action of ${M}_{t}$ on the thermal flow.

Fig. 10

Action of K on the thermal flow

Fig. 11

Action of $\beta$ on ${C}_{f}$.

Fig. 12

Action of ${M}_{t}$ on ${C}_{f}$.

Fig. 13

Consistency flow for the convergence.

Table 1 Variations of $Nu _{x}$ for different parameters.

6 Results and discussion

6.1 Convergence analysis

The validation of the system of eqs (34)–(37) is obtained when $\beta \rightarrow \infty ,\ M_{t}=0$ and $K=0$ [5]. This will give a good agreement to our result which is obtained from the two-parameter scaling transformations. Numerical solution of the unsteady two-dimensional MHD Casson fluid under the influence of porous medium, thermal radiation and heat source-sink parameters is obtained in MATLAB via the bvp4c. Bvp4c is a language of finite difference that incorporates three steps of the Lobatto IIIa formula. It is a collocation algorithm, and a $C^{11}$ continuous approach is given by the collocation polynomial, which is uniformly reliable to the fourth order in [a, b]. Selection of mesh and the regulation of errors are based on the continuous solution residual. Moreover, in figure 13, we achieved the consistent behaviour for this model. The bvp4c cannot be solved at infinite interval, and solving the bvp4c in a very large finite interval is impractical. Instead, this approach addresses a sequence of issues posed at the smaller interval $\left[ 0,\eta \right]$ to check that the solution has consistent behaviour when $\eta \rightarrow \infty .$

In figures 2–12, for the rigid plate with stagnation point flow, graphs are plotted for $f^{\prime }(\eta ),$ $\vartheta (\eta )$ and $C_{f}$. These layers satisfy boundary conditions depending on time. In figure 2, the Casson fluid parameter $\beta$ improves the fluid’s motion. Furthermore, the power of the magnetic field tends to decrease the fluid’s motion but in figure 3, the Lorentz force in the case of a rigid plate has the opposite action and the fluid’s motion is increased with higher values of Hartmann number $M_{t}$ (see [8]). The fluid’s motion is also improved in the porous medium, and the thickness of the boundary layer is increased in figure 4 due to Darcy resistance K. Variations in the thermal profile are traced in figures 5–10. The effects of thermal flow vs. Prandtl number $\Pr$, thermal radiation as well as heat source-sink parameter $Q_{t}$ are demonstrated in figures 5–7. The thermal profile is a decreasing feature for $\Pr$ but not for $\Delta _{t}$ and $Q_{t}$. The thermal layer is reduced by these parameters. In addition, much of the energy was transferred into the porous plate with time effects during the radiation and sourcing-sinking process. Figures 8–10 show the thermal flow vs. $\beta$, $M_{t}$ and K. With an increase in these numbers, the thermal profile decreases. The thermal transport is slowed down by the effects of Casson fluid parameter, Lorentz force and porous medium. Figures 11 and 12 display an improvement in $\beta$ and $M_{t}$ values for $C_{f}$. There are two regions plotted for $C_{\!f}$ vs. $\beta$ and $M_{t}$ in these two diagrams. The first region has improved behaviour and the second region has reduced behaviour. The variations of $Nu_{x}$ for $\beta ,$ $\Delta _{t},\ Q_{t},\ M_{t}$ and K are shown in table 1. The $Nu_{x}$ function increases for $\beta ,\ Q_{t},\ M_{t}$ and K while the $\Delta _{t}$ function decreases.

7 Conclusion

The unsteady, laminar and two-dimensional work on the stagnation point flow is being studied using two-parameter scaling transformations. This flow included a large, porous plate with a stagnation point flow. Through two-parameter transformations, we reached from PDEs to ODEs. In the Lie group analysis, dimensionless parameters, such as the Hartmann number, Darcy number, thermal radiation and heat sink showed the rheological properties of the Casson liquid. The main points are: under the influence of Darcy resistance, Hartmann number and Casson parameter the velocity profile increases. Thermal flow increases with $\Delta _{t}$ and $Q_{t}$. The $\Pr$, resistance of Darcy, the Casson parameter and the Hartmann number reduce the thermal profile.