1 Introduction

Exact solutions to Einstein–Maxwell (EM) system of field equations play an important role in the study of self-gravitating spherically symmmetric charged fluid distributions. Ever since the discovery of the Reissner–Nordström solution, many investigators have contributed to the study of EM system which includes the pioneering works of Papapetrou [1], Majumdar [2], Bonner [3, 4], Stettner [5], Bekenstein [6] and Cooperstock and Cruz [7]. A detailed review of exact solutions to Einstein–Maxwell systems and their physical acceptability can be found in the compilation work of Ivanov [8]. A large class of interior solutions, corresponding to the exterior Reissner–Nordström space–time, have been developed to model a wide variety of stellar distributions such as neutron stars, strange stars and stellar objects composed of quark–diquark mixtures [9,10,11,12,13,14,15,16,17]. Stellar models have also been developed for charged core–envelope-type configurations [18,19,20]. Mak and Harko [21] and Komathiraj and Maharaj [22] have obtained solutions for charged strange quark stars admitting a linear equation of state (EOS). Thirukkanesh and Maharaj [23] have analysed the role of anisotropy on the physical behaviour of a given charged distribution admitting a linear EOS. Varela et al [24] have analysed features of a charged anisotropic fluid distribution admitting linear as well as nonlinear EOS. Takisa and Maharaj [25] have obtained a new class of solutions for a charged quark matter distribution. Feroze and Siddiqui [26] and Maharaj and Takisa [27] have independently developed charged stellar models by assuming a quadratic EOS. Thirukkanesh and Ragel [28, 29] have obtained new solutions for charged fluid spheres by specifying the polytropic index leading to masses and energy densities which have been shown to be consistent with observational data. Maharaj et al [30] have presented a new family of exact solutions to the Einstein–Maxwell system for an anisotropic charged matter on the Finch and Skea [31] background space–time. A class of charged anisotropic stellar solutions have been developed and studied by Murad and Fatema [32]. Hansraj et al [33] have analysed all static-charged dust sphere models in general relativity. Recently, Sunzu and Danford [34] have generated two new classes of exact solutions to the Einstein–Maxwell system of field equations describing an anisotropic and charged stellar body which accommodates a quark matter like linear EOS.

The main objective of the present work is to contribute to this rich family of solutions by generating new solutions which can be used as viable models of realistic astrophysical objects. While generating the solutions, one needs to ensure that the gravitational, electromagnetic and matter variables remain finite, continuous, well-behaved and the speed of sound remains less than the speed of light within the distribution. For a charged fluid sphere, the interior solution must be matched to the exterior Riessner–Nordström metric across the boundary. We present here a different family of solutions to the coupled Einstein–Maxwell system where all the above requirements are fulfilled. This has been done by choosing a rational form for one of the gravitational potentials and also the fall-off behaviour of the charged fluid distribution. This particular approach is similar to the method adopted earlier by Maharaj and Leach [35] which was, in fact, a generalisation of the superdense stellar model developed by Tikekar [36]. In our approach, the solutions are generated by reducing the condition of pressure isotropy to a recurrence relation with real and rational coefficients so that the system can be solved by mathematical induction. We have performed a systematic analysis of the new family of solutions to examine their physical viability.

The paper is organised as follows: In §2, we have presented the EM field equations for a static spherically symmetric charged fluid distribution. The nonlinear system was then transformed into a more tractable set of equations. By assuming a particular form for one of the metric potentials and also by specifying the electric field intensity, we have obtained the condition of pressure isotropy in terms of the undetermined gravitational potential in §3. We have assumed a series solution for the resultant equation which yielded a recurrence relation. We have managed to solve the system from the first principles in §4. In §5, we have presented polynomials and product of polynomials with algebraic functions as the first solution. The general solution containing the integral form was eventually integrated to yield elementary functions by placing specific restrictions on the model parameters. We have demonstrated that it is possible to regain many solutions found earlier by adopting this technique. Finally, we have provided two different classes of exact solutions to the EM system in simple closed forms. In §6, we have discussed features of the class of solutions and showed that the solutions might be used to model realistic compact stellar systems. The results are summarised in §7.

2 Einstein–Maxwell system

For a static spherically symmetric relativistic charged fluid distribution, we assume the line element in coordinates \((t,r,\theta ,\phi )\) as

$$\begin{aligned} \mathrm {d}s^{2}= & {} -\mathrm {e}^{2\nu (r)}\mathrm {d}t^{2}+\mathrm {e}^{2\lambda (r)}\mathrm {d}r^{2}\nonumber \\&+r^{2}(\mathrm {d}\theta ^{2}+\sin ^{2}\theta \, \mathrm {d}\phi ^{2}), \end{aligned}$$
(1)

where \(\nu (r)\) and \(\lambda (r)\) are arbitrary functions of the radial coordinate r. The Einstein–Maxwell field equations for the line element (1) are then obtained (in system of units having 8\(\pi G = c = 1\)) as

$$\begin{aligned}&\frac{1}{r^{2}}(1-\mathrm {e}^{-2\lambda })+\frac{2\lambda ^\prime }{r}\mathrm {e}^{-2\lambda }=\rho +\frac{1}{2}E^{2}, \end{aligned}$$
(2a)
$$\begin{aligned}&\frac{-1}{r^{2}}(1-\mathrm {e}^{-2\lambda })+\frac{2\nu ^\prime }{r}\hbox {e}^{-2\lambda }=p-\frac{1}{2}E^{2}, \end{aligned}$$
(2b)
$$\begin{aligned}&\mathrm {e}^{-2\lambda }\left( \nu ^{\prime \prime }+{\nu ^\prime }^2+\frac{\nu ^\prime }{r}-\nu ^\prime \lambda ^\prime -\frac{\lambda ^\prime }{r}\right) =p+\frac{1}{2}E^{2}, \end{aligned}$$
(2c)
$$\begin{aligned}&\frac{1}{r^{2}}\mathrm {e}^{-\lambda }(r^{2}E)^\prime =\sigma , \end{aligned}$$
(2d)

where prime (\({'}\)) denotes differentiation with respect to r. The energy density \(\rho \) and the pressure p are measured relative to the co-moving fluid 4-velocity \(u^{a}=\mathrm {e}^{-\nu }\delta ^{a}_{0}\). The electric field intensity E and the proper charge density \(\sigma \) appear in the system through the energy–momentum tensor corresponding to the electro-magnetic field and the Maxwell equations.

A different but equivalent form of the field equations can be generated if we introduce a new independent variable x and introduce new functions y and Z:

$$\begin{aligned} x=Cr^{2},~~~A^{2}y^{2}(x)=\mathrm {e}^{2\nu (r)},~~~Z(x)=\mathrm {e}^{-2\lambda (r)}, \end{aligned}$$
(3)

proposed by Durgapal and Bannerji [37], where A and C are constants. Under the transformation (3), system (2) becomes

$$\begin{aligned}&\frac{1-Z}{x}-2\dot{Z} = \frac{\rho }{C}+\frac{E^{2}}{2C}, \end{aligned}$$
(4a)
$$\begin{aligned}&4Z\frac{\dot{y}}{y}+\frac{Z-1}{x} = \frac{p}{C}-\frac{E^{2}}{2C}, \end{aligned}$$
(4b)
$$\begin{aligned}&4Zx^{2}\ddot{y}+2\dot{Z}x^{2}\dot{y}+\left( \dot{Z}x-Z+1-\frac{E^{2}x}{C}\right) y = 0, \end{aligned}$$
(4c)
$$\begin{aligned}&\frac{4Z}{x}(x\dot{E}+E)^{2} = \frac{\sigma ^{2}}{C}, \end{aligned}$$
(4d)

where dots (\(\cdot \)) denote differentiation with respect to the variable x. System (4) determines the gravitational behaviour of a charged perfect fluid. Consequently, we have a nonlinear system of four independent equations in six unknown variables, namely, \(\rho \), p, E, \(\sigma \), y and Z. The advantage of this system lies in the fact that a solution, upon suitable substitutions of Z and E, can be obtained by integrating the second-order differential equation (4c) which is linear in y.

3 Integration procedure

We solve the Einstein–Maxwell system (4) by making explicit choices for the metric function Z and the electric field intensity E. For the metric function Z we write

$$\begin{aligned} Z=\frac{(1+k x)}{(1+mx)},~~~k\ne m, \end{aligned}$$
(5)

where k and m are real constants. Note that the choice (5) ensures that the metric function \(\mathrm {e}^{2\lambda }\) is regular and continuous in the interior because of the freedom provided by parameters k and m. It is important to note that the particular choice of Z is physically reasonable and contains some special cases of known relativistic star models. \(m=1\) case corresponds to the Maharaj and Komathiraj [38] charged stellar model which is a generalisation of the stellar models developed previously by Finch and Skea [31] and Hansraj and Maharaj [39]. A similar form of Z has also been utilised in refs [26, 27, 40] for the construction of a charged anisotropic stellar model admitting a polytropic EOS.

Substitution of (5) in (4c) yields

$$\begin{aligned}&4(1+kx)(1+mx)\ddot{y}+2(k-m)\dot{y}\nonumber \\&\quad +\left[ m(m-k)-\frac{E^{2}(1+mx)^{2}}{Cx}\right] y=0. \end{aligned}$$
(6)

It is convenient at this point to introduce the following transformation:

$$\begin{aligned} z=1+mx. \end{aligned}$$
(7)

This transformation enables us to rewrite the second-order differential equation (6) in a simpler form

$$\begin{aligned}&4z(kz+m-k)\frac{\mathrm {d}^{2}\tilde{y}}{\mathrm {d}z^{2}}+2(k-m)\frac{\mathrm {d}\tilde{y}}{\mathrm {d}z}\nonumber \\&\quad +\left[ (m-k)-\frac{E^{2}z^{2}}{C(z-1)}\right] \tilde{y}=0, \end{aligned}$$
(8)

in terms of the new dependent and independent variables \(\tilde{y}=y(z)\) and z, respectively. To integrate (8), it is necessary to specify the electric field intensity E. Even though a variety of choices for E is possible, only a few of them are physically reasonable and can generate closed form solutions. We reduce (8) to an integrable form by letting

$$\begin{aligned} \frac{E^{2}}{C}= & {} \alpha \frac{(z-1)}{z^{2}}-\beta \frac{(z-1)}{z^{3}}\nonumber \\= & {} \alpha \frac{ mx}{(1+mx)^{2}}-\beta \frac{ mx}{(1+mx)^{3}}, \end{aligned}$$
(9)

where \(\alpha \) and \(\beta \) are constants. The form \(E^{2}\) in (9) is physically acceptable as E remains regular and continuous throughout the sphere. Note that \(E=0\) at \(r=0\). Some special cases of (9) have earlier been studied by Takisa and Maharaj [40] and John and Maharaj [41] and can also be reduced to the uncharged stellar model developed by Maharaj and Mkhwanazi [42]. Substituting (9) in eq. (8), we obtain

$$\begin{aligned}&4z^{2}(kz+m-k)\frac{\mathrm {d}^{2}\tilde{y}}{\mathrm {d}z^{2}}+2z(k-m)\frac{\mathrm {d}\tilde{y}}{\mathrm {d}z}\nonumber \\&\quad +[(m-k-\alpha )z+\beta ]\tilde{y}=0, \end{aligned}$$
(10)

which is the master equation for the system of equations (4). For \(\alpha =\beta =0\), the differential equation (10) reduces to

$$\begin{aligned} 4z(kz+m-k)\frac{\mathrm {d}^{2}\tilde{y}}{\mathrm {d}z^{2}}+2(k-m)\frac{\mathrm {d}\tilde{y}}{\mathrm {d}z}+(m-k)\tilde{y}=0,\nonumber \\ \end{aligned}$$
(11)

which is the limiting case and corresponds to an uncharged sphere.

4 General series solution

It is difficult to obtain a closed form solution of eq. (10). However, one can transform it to a differential equation which can be integrated by the method of Frobenius. This can be done in the following way.

We introduce a new function u(z) such that

$$\begin{aligned} \tilde{y}(z)=z^{d}u(z), \end{aligned}$$
(12)

where d is a constant. A similar kind of transformation was utilised earlier by Komathiraj and Maharaj [43] for generating charged stellar models. With the help of (12), differential equation (10) can be written as

$$\begin{aligned}&4z^{2}(kz+m-k)\frac{\mathrm {d}^{2}u}{\mathrm {d}z^{2}}\nonumber \\&\quad +2z[4d(kz+m-k)+(k-m)]\frac{\mathrm {d}u}{\mathrm {d}z}\nonumber \\&\quad -\left\{ [k-m+\alpha -4kd(d-1)]z\right. \nonumber \\&\quad \left. +2d(2d-3)(k-m)-\beta \right\} u=0. \end{aligned}$$
(13)

A substantial simplification of the equation can be achieved if we set

$$\begin{aligned} 2d(2d-3)(k-m)=\beta . \end{aligned}$$
(14)

Equation (13) then reduces to

$$\begin{aligned} 4z(z-c)\frac{\mathrm {d}^{2}u}{\mathrm {d}z^{2}}+ & {} 2[4d(z-c)+c]\frac{\mathrm {d}u}{\mathrm {d}z}\nonumber \\- & {} [c+\tilde{\alpha }-4d(d-1)]u=0, \end{aligned}$$
(15)

where we have set

$$\begin{aligned} c=\frac{k-m}{k},~~~~~k \tilde{\alpha }=\alpha . \end{aligned}$$
(16)

As the point \(z=c\) is a regular singular point of (15), there exists two linearly independent solutions of the form of power series with centre \(z=c\). Therefore, we can write the solution of differential equation (15) by the method of Frobenius as

$$\begin{aligned} u=\sum _{i=0}^{\infty }c_{i}(z-c)^{i+b},~~~ c_{0}\ne 0 , \end{aligned}$$
(17)

where \(c_{i}\) are the coefficients of the series and b is a constant.

For a legitimate solution, we need to determine the coefficients \(c_{i}\) as well as the parameter b. Substituting (17) in differential equation (15), we obtain the indicial equation

$$\begin{aligned} 2cc_{0}b(2b-1)=0 \end{aligned}$$

and the recurrence formula

$$\begin{aligned} c_{i+1}=-\frac{\{4(i+b)(i+b-1+2d)-T\}}{2c(i+b+1)(2i+2b+1)}c_{i}, \end{aligned}$$
(18)

with \(i\ge 0\) and \(T=c+\tilde{\alpha }-4d(d-1)\). As \(c_{0}\ne 0\), \(c=k-m\ne 0\), we must have \(b=0\) or \(b={1}/{2}\). The coefficients \(c_{1},~c_{2},\, c_{3},\ldots \) can be written in terms of the leading coefficient \(c_{0}\) and we can generate the expression as

$$\begin{aligned} c_{i+1}=\prod _{p=0}^{i}-\frac{4(p+b)(p+b-1+2d)-T}{2c(p+b+1)(2p+2b+1)}c_{0}. \end{aligned}$$
(19)

It is also possible to establish the result (19) rigorously by using the principle of mathematical induction.

We generate two linearly independent solutions to (15) with the help of (17) and (19). For \(b=0\), we obtain the first solution

$$\begin{aligned} u_{1}=c_{0}\left[ 1+\sum _{i=0}^{\infty }\prod _{p=0}^{i}-\frac{\psi }{\eta }(z-c)^{i+1}\right] , \end{aligned}$$

where \(\psi =4p(p-1+2d)-[c+\tilde{\alpha }-4d(d-1)]\) and \(\eta =2c(p+1)(2p+1).\) For \(b={1}/{2}\), we obtain the second solution

$$\begin{aligned} u_{2}=c_{0}(z-c)^{{1/2}}\left[ 1+\sum _{i=0}^{\infty }\prod _{p=0}^{i}-\frac{\alpha }{\beta }(z-c)^{i+1}\right] , \end{aligned}$$

where \(\alpha =(2p+1)(2p-1+4d)-[c+\tilde{\alpha }-4d(d-1)]\) and \(\beta =c(2p+3)(2p+2).\) We, therefore, have a general solution to (15) as the functions \(u_{1}\) and \(u_{2}\) are linearly independent. In terms of the original variable \(x=Cr^{2}\), the functions are obtained as

$$\begin{aligned} y_{1}= & {} c_{0}(1+mx)^{d}\left[ 1+\sum _{i=0}^{\infty }\prod _{p=0}^{i}-\frac{\psi _1}{\eta _1}\right. \nonumber \\&\left. \times \left[ \frac{m(1+kx)}{k}\right] ^{i+1}\right] , \end{aligned}$$
(20)
$$\begin{aligned} y_{2}= & {} c_{0}(1+mx)^{d}\left[ \frac{m(1+kx)}{k}\right] ^{{1}/{2}}\nonumber \\&\times \left[ 1+\sum _{i=0}^{\infty }\prod _{p=0}^{i}-\frac{\alpha _1}{\beta _1}\left[ \frac{m(1+kx)}{k}\right] ^{i+1}\right] , \end{aligned}$$
(21)

where

$$\begin{aligned} \psi _1= & {} 4kp(p-1+2d)-[k-m+\alpha -4kd(d-1)],\\ \eta _1= & {} 2(k-m)(p+1)(2p+1),\\ \alpha _1= & {} k(2p+1)(2p-1+4d)\\&-\,[k-m+\alpha -4kd(d-1)],\\ \beta _1= & {} (k-m)(2p+3)(2p+2). \end{aligned}$$

Thus, the general solution to differential equation (6), for the choice of the electric field (9), is given by

$$\begin{aligned} y(x)=A_{1}y_{1}(x)+A_{2}y_{2}(x), \end{aligned}$$
(22)

where \(A_{1}\) and \(A_{2}\) are arbitrary constants. Using (4) and (22), we write the exact solution to the Einstein–Maxwell system in the form

$$\begin{aligned}&\mathrm {e}^{2\lambda }=\frac{1+mx}{1+kx}, \end{aligned}$$
(23a)
$$\begin{aligned}&\mathrm {e}^{2\nu }=A^{2}y^{2}, \end{aligned}$$
(23b)
$$\begin{aligned}&\frac{\rho }{C}=\frac{(m-k)(3+mx)}{(1+mx)^{2}}-\alpha \frac{mx}{2(1+mx)^{2}}\nonumber \\&~~~~~~~+\,\beta \frac{mx}{2(1+mx)^{3}}, \end{aligned}$$
(23c)
$$\begin{aligned}&\frac{p}{C}=4\frac{(1+kx)}{(1+mx)}\frac{\dot{y}}{y}+\frac{k-m}{(1+mx)}\nonumber \\&~~~~~~~+\alpha \frac{mx}{2(1+mx)^{2}}-\beta \frac{mx}{2(1+mx)^{3}}, \end{aligned}$$
(23d)
$$\begin{aligned}&\frac{E^{2}}{C}=\alpha \frac{mx}{(1+mx)^{2}}-\beta \frac{mx}{(1+mx)^{3}}. \end{aligned}$$
(23e)

As the choice of the metric function (5) together with the electric field intensity (9) have not been considered earlier, to the best of our knowledge, the class of solutions (23) have not been reported previously. One interesting feature of the new family of solutions is that by setting \(\alpha =0\) and \(\beta =0~(d=0~\text {or}~d={3}/{2})\), it is possible to switch off the effect of charge onto the system. Secondly, solution (22) has been expressed in terms of a series of real arguments and not complex arguments which one might encounter when mathematical software packages are used.

5 Terminating series

It is interesting to observe that the series in (20) and (21) terminates for specific values of the parameters \(k,~m,~\alpha \) and d. It is, therefore, possible to generate solutions in terms of elementary functions by imposing specific restrictions on \(k,~m,~\alpha \) and d. The solutions may be found in terms of polynomials and algebraic functions. We use recurrence relation (18), rather than the series (20) and (21), to find the elementary solutions.

5.1 Elementary solutions

If we fix \(b=0\) in (18), and set \(c+\tilde{\alpha }-4d(d-1)=4n(n-1+2d)\), for integer values of n, we obtain

$$\begin{aligned} c_{i+1}=4\frac{(n-i)(n+i-1+2d)}{c(2i+1)(2i+2)}c_{i},~i\ge 0, \end{aligned}$$
(24)

where n is a fixed integer. Obviously, \(c_{n+1}=0\). Consequently, the remaining coefficients \(c_{n+2},~c_{n+3},~c_{n+4},\ldots \) vanish. Equation (24) may be solved to yield

$$\begin{aligned} c_{i}= & {} \left( \frac{4}{c}\right) ^{i}\frac{n!(n+i-2+2d)!}{(2i)!(n-i)!(n-2+2d)!}c_{0},~0\le i\le n.\nonumber \\ \end{aligned}$$
(25)

Using (17) (when \(b=0\)) and (25), we obtain

$$\begin{aligned} u(z)=c_{0}\sum _{i=0}^{n}\left( \frac{4}{c}\right) ^{i}\frac{n!(n+i-2+2d)!}{(2i)!(n-i)!(n-2+2d)!}(z-c)^{i}, \end{aligned}$$
(26)

where

$$\begin{aligned} c+\tilde{\alpha }-4d(d-1)=4n(n-1+2d). \end{aligned}$$

On substituting \(b={1}/{2}\) in (18) and by setting \(c+\tilde{\alpha }-4d(d-1)=(2n+1)(2n-1+4d)\), we obtain

$$\begin{aligned} c_{i+1}=\frac{4(n-i)(n+i+2d)}{c(2i+3)(2i+2)}c_{i},\quad i\ge 0, \end{aligned}$$
(27)

where n is a fixed integer. Obviously, \(c_{n+1}=0\) and the subsequent coefficients \(c_{n+2},\) \(c_{n+3},\) \(c_{n+4},\ldots \) vanish. Equation (27) yields

$$\begin{aligned} c_{i}= & {} \left( \frac{4}{c}\right) ^{i}\frac{(n)!(n+i-1+2d)!}{(2i+1)!(n-i)!(n-1+2d)!}c_{0},\nonumber \\&0\le i\le n. \end{aligned}$$
(28)

Using (17) (when \(b={1}/{2}\)) and (28), we obtain

$$\begin{aligned} u(z)=c_{0}(z-c)^{{1}/{2}}\sum _{i=0}^{n}\left( \frac{4}{c}\right) ^{i}\frac{(n)!(n_1+i)!}{(2i{+}1)!(n{-}i)!n_1!}(z-c)^{i}, \end{aligned}$$
(29)

where

$$\begin{aligned} n_1=(n-1+2d) \end{aligned}$$

and

$$\begin{aligned} c+\tilde{\alpha }-4d(d-1)=(2n+1)(2n-1+4d). \end{aligned}$$

The polynomial (26) and the product of the polynomial and algebraic function (29) generate a particular solution of the differential equation (15) for appropriate values of the parameters \(c,\tilde{\alpha }\) and d.

5.2 General solutions

It is possible to obtain solutions to (15) by restricting the values of \(c,~\tilde{\alpha }\) and d so that only elementary functions survive. The elementary functions are expressible as polynomials and product of polynomials with algebraic functions. Using (26), we express the first category of general solutions to differential equation (15) in the form

$$\begin{aligned}&u(z)=\sum _{i=0}^{n}\left( \frac{4}{c}\right) ^{i}\frac{n!(n+i-2+2d)!}{(2i)!(n-i)!(n-2+2d)!}(z-c)^{i}\nonumber \\&\quad \times \left[ B_{1}+B_{2}\int \frac{z^{({1}/{2})-2d}(z-c)^{-{1}/{2}}}{\{\sum _{i=0}^{n}\left( \frac{4}{c}\right) ^{i}\frac{n!(n_2+i)!}{(2i)!(n-i)!n_2!}(z{-}c)^{i}\}^{2}}\mathrm {d}z\right] ,\nonumber \\ \end{aligned}$$
(30)

where

$$\begin{aligned} n_2=(n-2+2d) \end{aligned}$$

and

$$\begin{aligned} c+\tilde{\alpha }-4d(d-1)=4n(n-1+2d). \end{aligned}$$

Using (29), the second category of general solutions to (15) is obtained as

$$\begin{aligned}&u(z)=(z-c)^{{1}/{2}}\nonumber \\&\quad \times \,\sum _{i=0}^{n}\left( \frac{4}{c}\right) ^{i} \frac{n!(n_1+i)!}{(2i+1)!(n-i)!n_1!}(z-c)^{i}\nonumber \\&\quad \times \left[ B_{1}+B_{2}\right. \nonumber \\&\quad \times \,\left. \int \frac{z^{({1}/{2})-2d}(z-c)^{-{3}/{2}}}{\{\sum _{i=0}^{n}\left( \frac{4}{c}\right) ^{i}\frac{n!(n_1+i)!}{(2i+1)!(n-i)!n_1!}(z-c)^{i}\}^{2}}\mathrm {d}z\right] ,\nonumber \\ \end{aligned}$$
(31)

where

$$\begin{aligned} c+\tilde{\alpha }-4d(d-1)=(2n+1)(2n-1+4d). \end{aligned}$$

In (30) and (31), \(B_{1}\) and \(B_{2}\) are integration constants. In terms of the original variable \(x=Cr^{2}\), it is possible to write (30) in the form

$$\begin{aligned}&y(x)= (1+mx)^{d}\sum _{i=0}^{n}\left( \frac{4k}{k-m}\right) ^{i}\frac{n!(n_2+i)!}{(2i)!(n-i)!n_2!}t^{i}\nonumber \\&\quad \times \left[ C_{1}+C_{2}\right. \nonumber \\&\quad \times \,\int \left. \frac{(1+mx)^{({1}/{2})-2d}[(1+kx)]^{-{1}/{2}}}{\left\{ \sum _{i=0}^{n}\left( \frac{4k}{k-m}\right) ^{i}\frac{n!(n_2+i)!}{(2i)!(n-i)!n_2!}[\frac{m(1+kx)}{k}]^{i}\right\} ^{2}}\mathrm {d}x\right] ,\nonumber \\ \end{aligned}$$
(32)

where

$$\begin{aligned} k-m+\alpha -4kd(d-1)=4kn(n-1+2d). \end{aligned}$$

Equation (31) in terms of \(x=Cr^{2}\), takes the form

$$\begin{aligned}&y(x)=C_3\sum _{i=0}^{n}\left( \frac{4k}{k-m}\right) ^{i}\frac{n!(n_1+i)!}{(2i+1)!(n-i)!n_1!}t^{i}\nonumber \\&\quad \times \left[ C_{1}+C_{2}\right. \nonumber \\&\quad \times \,\left. \int \frac{(1+mx)^{({1}/{2})-2d}[(1+kx)]^{-{3}/{2}}}{\left\{ \sum _{i=0}^{n}\left( \frac{4k}{k-m}\right) ^{i}\frac{n!(n_1+i)!}{(2i+1)!(n-i)!n_1!}t^{i}\right\} ^{2}}\mathrm {d}x\right] , \end{aligned}$$
(33)

where

$$\begin{aligned}&k-m+\alpha -4kd(d-1)=k(2n+1)(2n-1+4d),\\&C_3=(1+mx)^{d}(1+kx)^{{1}/{2}} \end{aligned}$$

and

$$\begin{aligned} t=m(1+kx)/k. \end{aligned}$$

Thus, we have generated two classes of solutions (32) and (33) to the differential equation (6) for the assumed electric field (9) by using the infinite series solution (22). It should be stressed that the class of solutions can be used to study stellar properties in the presence as well as absence of charge. By setting \(\alpha =0\) and \(\beta =0~(d=0 ~\text {or}~{3}/{2})\) in (32) and (33), one obtains solutions for an uncharged sphere.

We are now in a position to integrate eqs (32) and (33) for specific values of the parameters \(k,~m,~\alpha , d\) and n.

For \(n=0\), eq. (32) becomes

$$\begin{aligned} y(x)= & {} (1+mx)^{d}\nonumber \\&\left[ C_{1}+C_{2}\int \frac{1}{(1+mx)^{2d-({1}/{2})}(1+kx)^{{1}/{2}}}\mathrm {d}x\right] ,\nonumber \\ \end{aligned}$$
(34)

where

$$\begin{aligned} k-m+\alpha -4kd(d-1)=0. \end{aligned}$$

Also for \(n=0\), eq. (33) takes the form

$$\begin{aligned}&y(x)=C_3\nonumber \\&\quad \times \, \left[ C_{1}+C_{2}\int \frac{1}{(1+mx)^{2d-({1}/{2})}(1+kx)^{{3}/{2}}}\mathrm {d}x\right] ,\nonumber \\ \end{aligned}$$
(35)

where

$$\begin{aligned} 2k-m+\alpha -4kd^{2}=0. \end{aligned}$$

By setting \(k=-{1}/{2},~ m=1,~ \alpha =0 \) and \(d={3}/{2}~(\text {or}~ \beta =0)\) in (34), we obtain

$$\begin{aligned} y(x)=a_{1}(1+x)^{{3}/{2}}+a_{2}(2-x)^{{1}/{2}}(5+2x), \end{aligned}$$

where we have assumed \(a_{1}=C_{1}\) and \(a_{2}=-({2\sqrt{2}}/{27})C_{2}\). Thus, we have regained the Durgapal and Bannerji solution [37].

If we set \(k={1}/{2},~ m=1,~ \alpha =0 \) and \(d=0~(\text {or}~ \beta =0)\) in (35), we obtain

$$\begin{aligned} y(x)= & {} (2+x)^{{1}/{2}}(a_{1}+a_{2}\ln [(1+x)^{{1}/{2}}{+}(2+x)^{{1}/{2}}])\\&-a_{2}(1+x)^{{1}/{2}}, \end{aligned}$$

where we have assumed \(a_{1}={C_{1}}/{\sqrt{2}}\) and \(a_{2}=4C_{2}\). This class of solutions was found earlier by Maharaj and Mikhwanazi [42].

Further, by setting \(~k={1}/{3},~m=1,~\alpha ={1}/{3}\) and \(d=0~(\text {or}~ \beta =0)\) in (35), we obtain

$$\begin{aligned} y(x)= & {} (3+x)^{{1}/{2}}(a_{1}+a_{2}\ln [(1+x)^{{1}/{2}}{+}(3+x)^{{1}/{2}}])\\&-a_{2}(1+x)^{{1}/{2}}, \end{aligned}$$

where we have assumed \(a_{1}={C_{1}}/{\sqrt{3}}\) and \(a_{2}=6C_{2}\). This particular solution corresponds to the charged stellar model of John and Maharaj [41]. Note that a minor error appearing in the John and Maharaj paper [41] has been addressed in this work.

5.3 New family of solutions

We now aim to generate new closed form solutions for y which can subsequently be used to model realistic stars. To achieve our objective, we set \(k=-{1}/{2},~ m=2\) and \(\alpha =1\). Then, making use of (34), it is possible to obtain two categories of solutions for (i) \(d={3}/{2}\, (\beta =0)\) and (ii) \(d=-{1}/{2}~(\beta =-10).\)

Case I: \(d={3}/{2}~(\beta =0)\)

In this case (34) becomes

$$\begin{aligned} y(x)=a_{1}(1+2x)^{{3}/{2}}+a_{2}(2-x)^{{1}/{2}}(7+4x), \end{aligned}$$
(36)

where we have set

$$\begin{aligned} a_{1}=C_{1},\quad a_{2}=-\frac{2}{75}C_{2}. \end{aligned}$$

Subsequently, the general solution to the Einstein–Maxwell system (23) can be expressed as

$$\begin{aligned}&\mathrm {e}^{2\lambda }=\frac{2(1+2x)}{2-x}, \end{aligned}$$
(37a)
$$\begin{aligned}&\mathrm {e}^{2\nu }=A^{2}\{a_{1}(1+2x)^{{3}/{2}}\nonumber \\&~~~~~~~~+\,a_{2}(2-x)^{{1}/{2}}(7+4x)\}^{2}, \end{aligned}$$
(37b)
$$\begin{aligned}&\frac{\rho }{C}=\frac{15+8x}{2(1+2x)^{2}}, \end{aligned}$$
(37c)
$$\begin{aligned}&\frac{p}{C}=\frac{g_1(x)}{g_2(x)}, \end{aligned}$$
(37d)
$$\begin{aligned}&\frac{E^{2}}{C}=\frac{2x}{(1+2x)^{2}}, \end{aligned}$$
(37e)

where

$$\begin{aligned} g_1(x)&=a_{1}(2-x)^{{1}/{2}}(1+2x)^{{1}/{2}}(19+18x-40x^{2})\\&\quad +a_{2}(-34-111x-96x^{2}+80x^{3}) \end{aligned}$$

and

$$\begin{aligned} g_2(x)&=2(2-x)^{{1}/{2}}(1+2x)^{2}[a_{1}(1+2x)^{{3}/{2}}\\&\quad +a_{2}(2-x)^{{1}/{2}}(7+4x)]. \end{aligned}$$

Case II: \(d=-\frac{1}{2}~(\beta =-10)\)

In this case (34) becomes

$$\begin{aligned} y(x)= & {} a_{1}(1+2x)^{-{1}/{2}}+a_{2}\left[ -2\sqrt{2-x}(17+4x)\right. \nonumber \\&\left. -75\sqrt{2}(1+2x)^{-{1}/{2}}\arcsin \left( \sqrt{\frac{2(2-x)}{5}}\right) \right] ,\nonumber \\ \end{aligned}$$
(38)

where we have set \(a_{1}=C_{1},~a_{2}=\frac{1}{8}C_{2}.\)

The simple form of our class of solutions facilitates the analysis of matter and gravitational variables of realistic stellar objects as can be seen in the following sections.

6 Physical analysis

For a physically viable model, the class of solutions obtained by our approach should satisfy certain regularity and physical requirements [44]. In this section, we analyse the features of our solutions and examine whether the solutions can be used for describing realistic stars.

Note that we should restrict our solutions only to those values of k and m for which the energy density \(\rho \), pressure p and the electric field intensity E remain finite and positive. In addition, k and m should be so chosen that the gravitational potential \(\mathrm { e}^{2\lambda }\) remains positive because the other metric function \(\mathrm {e}^{2\nu }\) is obviously positive. In (23a) and (23b), we note that \( \mathrm {e}^{2\lambda }\) and \(\mathrm {e}^{2\nu }\) are continuous in the stellar interior. They are also regular at the centre for all values of the parameters \(k,m,\alpha \) and \(d~(\text {or}~\beta )\).

That pressure of a realistic star must vanish at a finite boundary \(r=R\) implies that

$$\begin{aligned}&4(1+kCR^{2})\left[ \frac{\dot{y}}{y}\right] _{R}+k-m+\frac{\alpha mCR^{2}}{2(1+mCR^{2})}\nonumber \\&\quad -\frac{\beta mCR^{2}}{2(1+mCR^{2})^{2}}=0, \end{aligned}$$

where y is given by (22). The above equation puts a restriction on the constants \(A_{1}\) and \(A_{2}\).

The unique solution to the Einstein–Maxwell system for \(r > R\) is given by the Riessner–Nordström line element

$$\begin{aligned} \mathrm {d}s^{2}= & {} -\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right) \mathrm {d}t^{2}\nonumber \\&+\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right) ^{-1}\mathrm {d}r^{2}\nonumber \\&+\,r^{2}(\mathrm {d}\theta ^{2}+\sin ^{2}\theta \,\mathrm {d}\phi ^{2}), \end{aligned}$$
(39)

where M and Q are the total mass and the charge of the star. Matching of the line elements (1) and (39), across the boundary \(r=R\), yields the relationships between the constants \(A_{1},A_{2},k,m\) and R as follows:

$$\begin{aligned}&1-\frac{2M}{R}+\frac{Q^{2}}{R^{2}}=A^{2}[A_{1}y_{1}(CR^{2})+A_{2}y_{2}(CR^{2})]^{2},\\&\left( 1-\frac{2M}{R}+\frac{Q^{2}}{R^{2}}\right) ^{-1}=\frac{1+mCR^{2}}{1+kCR^{2}}. \end{aligned}$$

For the particular solution, using (37c), we obtain the central density

$$\begin{aligned} \rho _{0}=\rho (r=0)=\frac{15}{2}C, \end{aligned}$$

which implies that \(C>0\). To obtain bounds on other parameters, we evaluate the pressure at two different points. Using eq. (37d) at the centre of the star (\(r=0\)), we obtain the central pressure

$$\begin{aligned} p_{0}=p(x=0)=\frac{C(19a_{1}-17\sqrt{2}a_{2})}{2(a_{1}+7\sqrt{2}a_{2})}. \end{aligned}$$

Obviously, we must have

$$\begin{aligned} \frac{(19a_{1}-17\sqrt{2}a_{2})}{(a_{1}+7\sqrt{2}a_{2})} >0, \end{aligned}$$
(40)

as \(({C}/{2})>0\).

At the boundary of the star (\(r=R\)), we impose the condition that the pressure vanishes, i.e., \(p_{R}=p(x=CR^{2})=0\), which yields

$$\begin{aligned}&a_{1}\sqrt{(2-CR^{2})(1+2CR^{2})}(19+18CR^{2}-40C^{2}R^{4})\nonumber \\&\quad +\,a_{2}(-34-111CR^{2}-96C^{2}R^{4}+80C^{3}R^{6})=0.\nonumber \\ \end{aligned}$$
(41)

Equation (41) determines the radius R of the star.

From (37c), we note that the density is always positive and

$$\begin{aligned} \frac{\mathrm {d}\rho }{\mathrm {d}r}=-\frac{4C^{2}r(13+4Cr^{2})}{(1+2Cr^{2})^{3}} <0. \end{aligned}$$
(42)

We must also have

$$\begin{aligned} \frac{\mathrm {d}p}{\mathrm {d}r}=-\frac{C^{2}r[-8a_{1}^{2}~f(r){+}a_{1}a_{2}~g(r){+}8a_{2}^{2}~h(r)]}{\sqrt{(2-Cr^{2})}(1+2Cr^{2})^{{7}/{2}}n_1}<0, \end{aligned}$$
(43)

where

$$\begin{aligned} n_1=[a_{1}(1+2Cr^{2})^{{3}/{2}}+a_{2}\sqrt{2-Cr^{2}}(7+4Cr^{2})]^{2}. \end{aligned}$$

To fulfill the causality condition \(0<{\mathrm{d}p}/{\mathrm{d}\rho }<1\), we must have

$$\begin{aligned} 0<\frac{-8a_{1}^{2}~f(r)+a_{1}a_{2}~g(r)+8a_{2}^{2}~h(r)}{H(r)}<1, \end{aligned}$$
(44)

throughout the interior of the star where

$$\begin{aligned} f(r)= & {} \sqrt{2-Cr^{2}}(1+2Cr^{2})^{{7}/{2}}(-12+5Cr^{2}),\nonumber \\ g(r)= & {} (1+2Cr^{2})^{2}(513-28Cr^{2}\nonumber \\&-848C^{2}r^{4}+320C^{3}r^{6}),\nonumber \\ h(r)= & {} \sqrt{(2-Cr^{2})(1+2Cr^{2})}(-24-34Cr^{2}\nonumber \\&-153C^{2}r^{4}-72C^{3}r^{6}+80C^{4}r^{8}), \nonumber \\ H(r)= & {} 4\sqrt{(2-Cr^{2})(1+2Cr^{2})}\nonumber \\&\times (13+4Cr^{2})[a_{1}(1+2Cr^{2})^{{3}/{2}}\nonumber \\&+\,a_{2}\sqrt{2-Cr^{2}}(7+4Cr^{2})]^{2}. \end{aligned}$$
(45)

It is not difficult to note that, at the centre of the star \((x=0)\), the causality condition puts a constraint

$$\begin{aligned} 0<\frac{96\sqrt{2}a_{1}^{2}+513a_{1}a_{2}-192\sqrt{2}a_{2}^{2}}{52\sqrt{2}(a_{1}+7\sqrt{2}a_{2})^{2}}<1. \end{aligned}$$
(46)

Using the matching conditions, we also obtain

$$\begin{aligned}&1-\frac{2M}{R}+\frac{Q^{2}}{R^{2}}=A^{2}[a_{2}(2-\textit{CR}^{2})^{{1}/{2}}(7+4\textit{CR}^{2})\nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~\quad +\,a_{1}(1+2\textit{CR}^{2})^{{3}/{2}}]^{2}, \end{aligned}$$
(47)
$$\begin{aligned}&\left( 1-\frac{2M}{R}+\frac{Q^{2}}{R^{2}}\right) ^{-1}=\frac{2(1+2\textit{CR}^{2})}{2-\textit{CR}^{2}}. \end{aligned}$$
(48)

Equation (47) determines the values of the constants in terms of the total mass M, radius R and the charge Q. From eq. (48), we obtain the total mass of the star as

$$\begin{aligned} M=\frac{\textit{CR}^{3}(5+14\textit{CR}^{2})}{4(1+2\textit{CR}^{2})^{2}}. \end{aligned}$$

As all the parameters on the right-hand side of this equation have positive values, the mass of the star is finite and positive.

Fig. 1
figure 1

Behaviour of gravitational potential \(\mathrm {e}^{\lambda }\).

Full size image
Fig. 2
figure 2

Behaviour of gravitational potential \(\mathrm {e}^{\nu }\).

Full size image

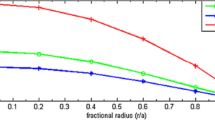
To analyse physical behaviour of a star, we have set \(a_{1}=1,~R=1,~C=0.6\) which are consistent with the bounds (40)–(46). Using these values in eq. (41), we have obtained \(a_{2}=0.229275\). In figures 1 and 2, we have plotted the gravitational potentials which have been shown to be well behaved. The behaviour of the energy density and the isotropic pressure are shown in figures 3 and 4, respectively. We note that the energy density and pressure are positive and monotonically decreasing within the stellar interior and the pressure vanishes at the boundary. In figure 5, we have shown the fall-off behaviour of the electric field intensity E. In figure 6, we have plotted \({\mathrm {d}p}/{\mathrm {d} \rho }\) on the interval \(0\le r \le 1\). We note that \({\mathrm {d}p}/{\mathrm {d} \rho }\) is always positive and less than unity, i.e., causality condition is not violated. It, therefore, can be concluded that there exists a particular set of model parameters for which solution (37) satisfies all the requirements of a realistic star.

Another interesting feature of our model is that it allows us to generate a barotropic relationship between the energy density and pressure. It is difficult to obtain a closed form thermodynamics relationship between density and pressure, in general, from the interior solutions [45]. However, our solution has the nice feature of providing a barotropic EOS. To demonstrate this, we first note from (37c) that the variable x can be expressed completely in terms of the energy density \(\rho \) in the form

$$\begin{aligned} x=\frac{2(C-\rho )\pm \sqrt{2C(11\rho +2C)}}{4\rho }=f(\rho ), \end{aligned}$$
(49)

where \(f(\rho )\) denotes the function of \(\rho \).

Fig. 3
figure 3

Radial variation of density \(\rho \).

Full size image
Fig. 4
figure 4

Radial variation of pressure p.

Full size image
Fig. 5
figure 5

Radial variation of electric field \(E^2\).

Full size image

Consequently, the pressure p in (37d) can be obtained in terms of density \(\rho \) as

$$\begin{aligned} p = C\frac{f_1(\rho )}{f_2(\rho )}, \end{aligned}$$

where

$$\begin{aligned} f_1&=a_{1}[2-f(\rho )]^{{1}/{2}}[1+2f(\rho )]^{1/2}\\&\quad \times [19+18f(\rho )-40f(\rho )^{2}]\\&\quad +a_{2}[-34-111f(\rho )-96f(\rho )^{2}+80f(\rho )^{3}],\\ f_2&=2\{[2-f(\rho )]^{{1}/{2}}[1+2f(\rho )]^{2}[a_{1}[1+2f(\rho )]^{{3}/{2}} \\&\quad +a_{2}[2-f(\rho )]^{{1}/{2}}[7+4f(\rho )]\}. \end{aligned}$$
Fig. 6
figure 6

Radial variation of square of sound speed \({\mathrm {d}p}/{\mathrm {d}\rho }\).

Full size image

7 Discussion

In this paper, we have presented a new technique to generate a large family of solutions to the EM system by making use of Durgapal and Bannerji [37] transformation equations together with a particular fall-off behaviour of the electric field intensity. A large class of solutions obtained previously have been shown to be contained in our general class of solutions. Moreover, we have demonstrated that for the specific set of model parameters, it is possible to obtain closed-form solutions from the general series solution. Note that different families of the solutions depend crucially on transformation (12). It should be stressed here that even though the integral forms in (32) and (33) parametrized by d do not permit one to regain the previously obtained charge-independent solutions, it can be done at a later stage. Once the integrations in (32) and (33) are obtained in closed forms for specific model parameters, the charged and uncharged solutions in terms of elementary functions can be obtained independently. This technique has been used to regain the Durgapal and Bannerji [37] and Maharaj and Mkhwanazi [42] stellar solutions and also John and Maharaj [41] charged fluid solution. We have also provided two separate closed-form solutions to the EM system. The simple form of the solution facilitates the analysis of the physical behaviour of a charged fluid sphere effectively. Interestingly, our solution has also been shown to provide a barotropic equation of state. It should, however, be pointed out that we have generated closed-form solutions for some specific values of the model parameters. It will be interesting to explore the possibility of generating new class solutions for values of model parameters which have not been covered in this paper. This, however, will be taken up elsewhere.