Numerical study of entropy generation and melting heat transfer on MHD generalised non-Newtonian fluid (GNF): Application to optimal energy

Abstract

This paper concerns an application to optimal energy by incorporating thermal equilibrium on MHD-generalised non-Newtonian fluid model with melting heat effect. Highly nonlinear system of partial differential equations is simplified to a nonlinear system using boundary layer approach and similarity transformations. Numerical solutions of velocity and temperature profile are obtained by using shooting method. The contribution of entropy generation is appraised on thermal and fluid velocities. Physical features of relevant parameters have been discussed by plotting graphs and tables. Some noteworthy findings are: Prandtl number, power law index and Weissenberg number contribute in lowering mass boundary layer thickness and entropy effect and enlarging thermal boundary layer thickness. However, an increasing mass boundary layer effect is only due to melting heat parameter. Moreover, thermal boundary layers have same trend for all parameters, i.e., temperature enhances with increase in values of significant parameters. Similarly, Hartman and Weissenberg numbers enhance Bejan number.

1 Introduction

It is well known that some fluids do not adhere to classical Newtonian viscosity description. These are classified as non-Newtonian fluids. One special class of fluids is of considerable practical importance in the field of science and technology. In these fluids, viscosity depends on shear stress or flow rate. Moreover, viscosity of most non-Newtonian fluids, such as polymers, is usually a nonlinear decreasing function of generalised shear rate. This is known as shear-thinning behaviour. Tangent hyperbolic fluid model exhibits rheological characteristics of such fluids (Ai and Vafai [1]). The tangent hyperbolic fluid is used extensively for different laboratory experiments. Friedman et al [2] used tangent hyperbolic fluid model for large-scale magneto-rheological fluid damper coils.

The study of boundary layer flows over a stretching sheet has been considerably increased because of their tremendous applications in different fields of science and engineering. Some of the examples include hot rolling, continuous stretching, aerodynamic extrusion of plastic sheets, polymer industries etc. Revolutionary study in this context was conducted by Sakaidis [3]. Crane [4] and Gupta and Gupta [5] have analysed continuous moving surface problem with constant surface temperature. Many contributions to this problem including stretching velocity and study of heat transfer are available in literature (see [6, 7]).

Fig. 1

Engineering flow structure.

The first analysis on induced magnetic field was done by Vishnyakov and Pavlov [8]. In their analysis, viscous fluids have been considered. Theory of magnetohydrodynamics (MHD) concerns with inducing current in a moving conductive fluid in the presence of magnetic field, which creates force on electrons of conductive fluid and also changes magnetic field itself. A survey of MHD studies can be found in [9]. Singh and Gupta [10] have discussed MHD-free convective flow of a viscous fluid through a porous medium bounded by an oscillating porous plate in slip flow regime with mass transfer.

In thermodynamics, the measure of disorder is called entropy. According to the second law of thermodynamics for an isolated system, system spontaneously grows toward thermodynamic equilibrium and attains minimum entropy. On the other hand, for a non-isolated system, there is a possibility of a decrease in entropy of a system, which may transfer the same amount of entropy to surroundings. Heat transfer and viscous dissipation play vital roles in changing the behaviour of entropy of a system. Study of entropy generation is a field of interest among researchers. Different sources such as heat transfer and viscous dissipation are responsible for the generation of entropy [11, 12]. Bejan [13] investigated entropy generation rate in a circular duct with forced heat flux at the boundary and its extension to determine optimum Reynolds number as a function of Prandtl number. Sahin [14] introduced second law analysis to a viscous fluid in circular duct with isothermal boundary conditions. Falahat [15] discussed entropy generation of nanofluids in helical tube and laminar flow. In another paper, Sahin [16] presented the effect of variable viscosity on entropy generation rate for a heated circular duct. In more recent papers, Mahmud and Fraser [17, 18] used second law analysis to convective heat transfer problems and to non-Newtonian fluid flow between two parallel plates. Saouli and Saouli [19] studied entropy generation in a liquid film falling along an inclined heated plate. Some recent articles for readers’ interest are cited in refs [20, 21].

For any engineering system, an optimal and efficient system is desired. In order to examine the efficiency of the system, one has to study the facts contributing to energy loss. In thermodynamics, this energy loss is measured by measuring the entropy generation and irreversibility ratio. These two parameters play vital roles to analyse the process through which engineering system attains its thermal equilibrium. The present entropy generation analysis is carried out for melting heat transfer of MHD GNF model. Moreover, conducting equations of two-dimensional tangent hyperbolic fluid are modelled. With the help of dimensionless parameters, entropy generation analysis is discussed numerically with the assistance of the shooting method.

2 Problem development

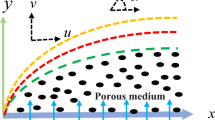
Assume a steady incompressible flow of a tangent hyperbolic fluid over a stretching sheet situated at the initial line, i.e. on x-axis $(y=0)$. Consider that the fluid is under the influence of a magnetic field of strength $B_{0}$ that is applied in positive y-direction normal to the plate. Moreover, melting at a steady rate is incorporated with constant property. The x- and y-axes are taken along and perpendicular to the sheet, respectively, and the flow is being confined to the region $y\ge 0$. The velocity of stretching sheet is considered to be $u_{w}(x)=ax$, where a is a positive stretching sheet constant. The temperature of the melting surface $T_{m}$ and ambient temperature $T_{\infty }$ have been chosen such that $T_{\infty }>T_{m}$. The induced magnetic field due to magnetic Reynolds number is taken to be small enough and negligible when compared to the applied magnetic field. Physical flow situation is presented in figure 1.

The governing equations of the boundary layer flow, heat and mass transfer of a tangent hyperbolic fluid are [22]:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$

(1)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \left( 1-n\right) \frac{\partial ^{2}u}{\partial y^{2}}\nonumber \\&\qquad \qquad \qquad \quad +\,\sqrt{2}\nu n\Gamma \left( \frac{\partial u}{\partial x}\frac{\partial ^{2}u}{\partial y^{2}}\right) - \frac{\sigma B_{0}^{2}}{\rho }u, \end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k}{\rho C_{p}}\frac{\partial ^{2}T}{\partial y^{2}}, \end{aligned}$$

(3)

where u and v are velocity components in x- and y-directions, respectively. n is the behaviour index. It represents Newtonian behaviour of fluid for $n=1$, shear thinning when $n>1$ and shear thickening when $n<1$. T is the fluid temperature, $C_{p}$ is the specific heat, k is the thermal conductivity, $\rho$ is the fluid density, $\nu =\mu {/}\rho$ (ratio of viscosity to density of fluid) is the kinematic viscosity. The associated boundary conditions are

$$\begin{aligned}&u=u_{w}(x)=ax,{ \ \ }v=0,{ \ \ }T=T_{w}{ \ \ \mathrm{at} }\,y=0, \nonumber \\&u\rightarrow 0,{ \ \ }\frac{\partial u}{\partial y}\rightarrow 0, { \ \ }T\rightarrow T_{\infty }{ \ \ \ \mathrm{as} }\,y\rightarrow \infty , \end{aligned}$$

(4)

with

$$\begin{aligned} \left. k\left( \frac{\partial T}{\partial y}\right) \right| _{y\text { }= \text { }0}=\rho \left[ \lambda +c_{s}(T_{m}-T_{0})\right] v(x,0). \end{aligned}$$

(5)

In the above equations, $\lambda$ is the latent heat of fluid and $c_{s}$ is the heat capacity of the solid surface. The boundary conditions defined in eq. (4) explain that the heat conducted to the melting surface is equal to the heat of melting plus sensible heat required in rising solid temperature $T_{0}$ to its melting temperature $T_{m}$. The boundary layer equations (1)–(3) admit solution of the form:

$$\begin{aligned}&u=axf^{\prime }(\eta ),{ \ \ }v=\sqrt{a\nu }f\left( \eta \right) {, \ \ }\eta =\sqrt{\frac{a}{\nu }}y, \nonumber \\&\theta (\eta )=\frac{T-T_{w}}{T_{\infty }-T_{w}}.\text { } \end{aligned}$$

(6)

Equation (1) is automatically satisfied, and (2)–(3) become

$$\begin{aligned}&(1-n)f^{{\prime \prime \prime }}+ff^{{\prime \prime }}-( f^{{\prime \prime }}) ^{2}\nonumber \\&\quad +nW_{e}f^{{\prime \prime }}f^{{\prime \prime \prime }}-M^{2}f^{{\prime }}=0, \end{aligned}$$

(7)

$$\begin{aligned}&\theta ^{{\prime \prime }}+\Pr f\theta ^{{\prime }}=0 \end{aligned}$$

(8)

and the corresponding boundary conditions (4) are

$$\begin{aligned}&{\ }f^{{\prime }}\left( 0\right) =1,{ \ \ }\theta \left( 0\right) =0,{ \ \ }\Pr f\left( 0\right) +M_{1}\theta ^{\prime }\left( 0\right) =0, \nonumber \\&f^{\prime \prime }\rightarrow 0,{ \ \ }\theta \rightarrow 1\text { as } \eta \rightarrow \infty , \end{aligned}$$

(9)

where primes denote differentiation with respect to $\eta ,\Pr$ is the Prandtl number, Weissenberg number, $W_{e}$ is the fluid parameter, M is the Hartman number and $M_{1}$ is the dimensionless melting parameter. It is a combination of Stefan numbers $c_{f}(T_{\infty }-T_{w})/\lambda$ and $c_{s}(T_{w}-T_{0})/\lambda$ for liquid and solid phases, respectively. Mathematically, we have

$$\begin{aligned} W_{e}= & {} \sqrt{\frac{2a}{\nu }}ax\Gamma ,{ \ \ \ }\Pr =\frac{k}{\rho C_{p}} ,\nonumber \\ M_{1}= & {} \frac{c_{f}(T_{\infty }-T_{w})}{\lambda +c_{s}(T_{w}-T_{0})}, \nonumber \\ M^{2}= & {} \frac{\sigma B_{0}^{2}}{\rho a}. \end{aligned}$$

(10)

The skin friction coefficient $C_{f}$ and local Nusselt number $\hbox {Nu}_{x}$ are

$$\begin{aligned}&C_{f}=\frac{\tau _{w}}{\rho u_{w}^{2}}\text {, }\nonumber \\&\mathrm {Nu}_{x}=\frac{xq_{w}}{ k(T_{\infty }-T_{w})}, \end{aligned}$$

(11)

in which expressions of wall skin friction $\left( \tau _{w}\right)$ and wall heat flux $\left( q_{w}\right)$ are given by

$$\begin{aligned}&\tau _{w}=\left. \left( 1-n\right) \frac{\partial u}{\partial y}+\frac{ n\Gamma }{\sqrt{2}}\frac{\partial ^{2}u}{\partial y^{2}}\right| _{y=0}, \nonumber \\&q_{w}=-\left. \left( k+\frac{16\sigma ^{*}T_{\infty }^{3}}{ 3k^{*}}\right) \frac{\partial T}{\partial y}\right| _{y=0}. \end{aligned}$$

(12)

With the help of dimensionless variables (10), we have

$$\begin{aligned}&C_{f}\left( \mathrm{Re}_{x}\right) ^{-1/2}{=}\left. \left( 1-n\right) f^{\prime \prime }\left( \eta \right) {+}\frac{n}{2}W_{e}\left( f^{\prime \prime }\left( \eta \right) \right) ^{2}\right| _{\eta =0}\text {,} \nonumber \\&\mathrm{Nu}_{x}\mathrm{Re}_{x}^{-1/2}=-\theta ^{\prime }(0), \end{aligned}$$

(13)

where $\mathrm{Re}_{x}=ax^{2}{/}\nu$ is the local Reynolds number.

3 Entropy generation analysis

The following expression indicates entropy generation:

$$\begin{aligned} E_{G}=\frac{k}{T_{\infty }}\left[ \left( \frac{\partial T}{\partial x} \right) ^{2}+\left( \frac{\partial T}{\partial y}\right) ^{2}\right] +\tau L. \end{aligned}$$

(14)

Entropy generation due to fluid friction is a non-dimensional quantity denoted as $N_{s}$. It is the ratio of actual entropy generation rate $E_{G}$ to characteristic entropy transfer rate $E_{G_{0}}$ and is given as

$$\begin{aligned}&E_{G_{0}}=\frac{k\Delta T}{l^{2}T_{\infty }^{2}},\quad \Lambda =\frac{\Delta T}{ T_{\infty }}, \end{aligned}$$

(15)

$$\begin{aligned}&N_{s}=\frac{E_{G}}{E_{G_{0}}}=\left( \frac{\partial T}{\partial y}\right) ^{2}+\frac{\gamma }{\Lambda }\left( \frac{\partial u}{\partial n}\right) ^{2}. \end{aligned}$$

(16)

In eq. (16), first term on the right side represented as $N_{h}$ is entropy due to heat transfer and second one is due to viscous dissipation termed as $N_{f}$, i.e.,

$$\begin{aligned} N_{s}=N_{h}+N_{f}. \end{aligned}$$

(17)

Ratio between entropy generation due to fluid friction and Joule dissipation to total entropy generation due to heat transfer is known as irreversibility ratio. It is defined as

$$\begin{aligned} r=\frac{N_{f}}{N_{h}}=\frac{({\gamma }{/}{\Lambda })\left( {\partial u}/{\partial n}\right) ^{2}}{\left( {\partial T}/{\partial y}\right) ^{2}}. \end{aligned}$$

(18)

It is worth mentioning that heat transfer irreversibility dominates in the region $0 \le r < 1$ and fluid friction with magnetic effects dominates when $r > 1$. Moreover, heat transfer and combined effect of friction and magnetic field is in equilibrium when $r = 1$. Another irreversibility parameter is Bejan number $B_{e}$. It is defined as

$$\begin{aligned} B_{e}=\frac{1}{1+r}. \end{aligned}$$

(19)

It has a range from 0 to 1. The combined effect of fluid friction and magnetic field is prominent when $B_{e}\rightarrow 0$. For $B_{e}\rightarrow 1$, it is the case for entropy generation due to the dominant effect of heat transfer irreversibility. Equilibrium occurs when $B_{e}=1/2$, i.e., when entropy generation crops up due to the same effects of heat transfer and fluid friction.

4 Computational procedure

The solution of eqs (7)–(8) along with boundary conditions (9) is computed by employing a numerical technique known as shooting method. Here, we convert nonlinear equations into a system of five first-order ordinary differential equations by labelling variables as $f=y_{1},$ $f^{{\prime }}=y_{1}^{{\prime }}=y_{2},$ $f^{{\prime \prime }}=y_{2}^{{\prime }}=y_{3},$ $\theta =y_{4},$ $\theta ^{{\prime }}=y_{4}^{{\prime }}=y_{5}.$ This yields the following mathematical expressions:

$$\begin{aligned}&\left( \begin{array}{l} y_{1}^{\prime } \\ y_{2}^{\prime } \\ y_{3}^{\prime } \\ y_{4}^{\prime } \\ y_{5}^{\prime } \end{array} \right) =\left( \begin{array}{c} y_{2} \\ y_{3} \\ \dfrac{1}{1-n+nW_{e}y_{2}^{2}}(y_{3}^{2}+M^{2}y^{2}-y^{1}y^{3}) \\ y_{5} \\ -\Pr y_{1}y_{5} \end{array} \right) , \\&\left( \begin{array}{l} y_{1}(0) \\ y_{2}(0) \\ y_{3}(0) \\ y_{4}(0) \\ y_{5}(0) \end{array} \right) =\left( \begin{array}{c} \dfrac{-M_{1}\theta ^{\prime }(0)}{\Pr } \\ 1 \\ f^{\prime \prime }(0) \\ 0 \\ \theta ^{\prime }(0) \end{array} \right) . \end{aligned}$$

Then, we solve it by Runge–Kutta method of order 5. The iterative process will be terminated when error involved is $<10^{-6}$.

5 Description of results

The flow and heat transfer in tangent hyperbolic fluid has been solved numerically using shooting method. The expressions of velocity and temperature have been used to compute entropy generation and Bejan number. Figures 2–6 depict the effects of various material parameters, such as Prandtl number $\Pr$, melting parameter $M_{1}$, Weissenberg number $W_{e}$ and magnetic parameter M, on velocity profile $f^{\prime }( \eta )$. Figure 2 shows that an increase in $W_{e}$ decreases the boundary layer thickness because the fluid parameter causes a resistance in the velocity of fluid, i.e. fluid velocity is remarkably affected by this physical parameter. For the case of shear thinning fluids, fluid parameter plays a role in increasing fluid flow which leads to a decrease in boundary layer thickness. Same trend can be seen for power law index n and Prandtl number $\Pr$ (see figures 3 and 4). It is depicted that $\Pr$ contributes in lowering the velocity profile. The influence of melting parameter $M_{1}$ on velocity profile is illustrated in figure 5. It causes an increase in boundary layer thickness. Figure 6 shows the influence of increasing magnetic parameter M. It decreases the fluid velocity leading to an enhanced boundary layer thickness. Figures 7–10 describe the impact of several physical numbers on temperature profile $\theta (\eta )$. In figure 7, it can be observed that $W_{e}$ influences in enhancing temperature. The temperature profile has similar behaviour in comparison to other parameters like n, $M_{1}$ and magnetic parameter M.

Fig. 2

Impact of $W_{e}$ on $f^{\prime }\left( \eta \right)$.

Fig. 3

Variation of n on $f^{\prime }\left( \eta \right) \!.$

Fig. 4

Behaviour of $\Pr$ on $f^{\prime }\left( \eta \right) \!.$

Fig. 5

Impact of $M_{1}$ on $f^{\prime }\left( \eta \right) \!.$

Fig. 6

Influence of M on $f^{\prime }\left( \eta \right)$.

Fig. 7

Effect of $W_{e}$ on $\theta \left( \eta \right) \!.$

Fig. 8

Impact of n on $\theta \left( \eta \right) \!.$

Fig. 9

Behaviour of M on $\theta \left( \eta \right) \!.$

Fig. 10

Influence of $M_{1}$ on $\theta \left( \eta \right) \!.$

Fig. 11

Variation of $W_{e}$ on $(\mathrm{Re}_{x})^{{1}/{2}}C_{f}$ against M.

Fig. 12

Effect of n on $(\mathrm{Re}_{x})^{{1}/{2}}C_{f}$ against M.

Fig. 13

Variation of n on $(\mathrm{Re}_{x})^{{1}/{2}}\mathrm{Nu}_{x}$ against M.

Figures 11–13 show the effects of parameters on skin friction coefficient and local Nusselt number. The effect of Weissenberg number $W_{e}$ on skin friction is seen in figure 11. It explains that skin friction is an increasing function of applied magnetic field and opposite trend is seen against $W_{e}$. Moreover, from figure 12, it is depicted that skin friction decreases by rising power law index. Figure 13 shows the effect of power law index on Nusselt number when plotted against applied magnetic field. It can be seen that both M and n play roles in decreasing Nusselt number.

5.1 Analysis of thermal equilibrium

$N_{s}$ and $B_{e}$ are the two significant non-dimensional parameters in entropy generation analysis. Entropy generation number $N_{s}$ consists of two major factors, $N_{h}$ (due to heat transfer) and $N_{f}$ (due to viscous dissipation). Graphical illustrations of entropy generation and Bejan numbers can be seen in figures 14–19. Figures 14–16 demonstrate the effect of power law index, applied magnetic field and fluid parameter on $N_{s}$. It is depicted that the parameters n and $W_e$ contribute in decreasing $N_s$ due to the fact that, more shear thinning behaviour of fluid has more energy loss. However, theapplied magnetic field, being a resistance force, contributes in up-surging it. Effects of pertinent parameters n, M and $W_{e}$ on irreversibility parameter are displayed in figures 17–19. Analysis of these graphs concludes that all the three significant parameters contribute in enlarging Bejan number. $B_{e}\rightarrow 1$ is significant in the sense that it shows the dominant role of viscous dissipation. It is observed that viscous dissipation gets dominant where boundary layer ends.

Further, table 1 gives values of Nusselt number for different influential parameters. From this table, we noticed that Nusselt number increases with an increase in Hartman, Weissenberg and index numbers. Table 2 represents the behaviour of entropy number $N_{s}$, entropy due to heat generation $N_{h}$ and entropy due to viscous dissipation $N_{f}$ with respect to significant parameters. It is clear from the table that $\Pr$ is related directly with $N_{h},N_{s}$ and $N_{f}$ and inversely related to index n, Weissenberg number $W_{e}$, Hartman number M and dimensionless parameter $\Lambda$.

Fig. 14

Result of power index n on $N_s.$

Fig. 15

Outcome of M on $N_s$.

Fig. 16

Influence of $W_{e}$ on $N_{s}$.

Fig. 17

Effect of power index n on $B_{e}$.

Fig. 18

Variation of M on $B_{e}$.

Fig. 19

Impact of $W_{e}$ on $B_{e}$.

Table 1 Numerical results analysis of $-\theta ^{\prime }(0)$ for physical parameters n, M and $W_e.$

Table 2 Computational analysis for entropy generation.

6 Summary

The present analysis explained boundary layer flow of hyperbolic tangent fluid with combined effects of MHD and melting heat transfer. The main findings of the present analysis are:

• The rate of transport reduces with increase in Prandtl number $\Pr$ and hence viscous boundary layer diminishes.

• The effect of index n, Weissenberg $W_{e}$ and Hartman M numbers on viscous and thermal boundary layers is the same.

• Velocity and temperature profile decrease with an increase in magnetic, index and Weissenberg numbers.

• Results of M, n and $W_{e}$ are the same for entropy generation number, but reverse in the case of Bejan number.

• Melting parameter contributes in lessening the entropy of flow.

• There is an increase in skin friction coefficient when n and $W_{e}$ increase.

• Influence of n and $W_{e}$ on $B_{e}$ and $N_{s}$ is quite opposite.

• Thermal equilibrium is attained within the boundary layer.

• Dominant effects of viscous dissipation exist at free stream.