1 Introduction

Many studies show that Einstein–Maxwell field equations can describe structures and properties of charged gravitating matter. The field equations are therefore very useful in relativistic astrophysics to model compact objects such as neutron stars, gravastars, dark energy stars, black holes, and quark stars. Due to their importance in modelling relativistic matter, they attract the attention of many researchers. In the paper by Sunzu et al [1] new models for quark stars with charge and anisotropy using field equations are described. In the work by Mak and Harko [2], models of relativistic compact objects in isotropic coordinates of Einstein’s field equations for the interior of compact bodies in hydrostatic equilibrium are found. Anisotropic charged models with astrophysical significance were generated in the paper by Sunzu et al [3]. On the other hand, Schwarzschild [4] constructed within the framework of Einstein’s general relativity the simplest model of astrophysical relevance for a perfect fluid. Chaisi [5] generated new solutions to the anisotropic Einstein’s field equations which are important in the study of highly dense stellar bodies. Exact solutions to the field equations in static space–times which are realistic to compact anisotropic spheres whose properties are relevant to some stellar objects were obtained by Thirukkanesh and Maharaj [6]. Chaisi and Maharaj [7] formulated models for dense spheres that generate surface redshifts and masses which correspond to realistic stellar bodies such as Her X-1 and Vela X-1.

In modelling most of the relativistic bodies, the pressure anisotropy is an essential aspect to be considered. The pressure anisotropy affects the physical properties, stability and structure of relativistic matter. The paper by Sharma et al [8] suggests that anisotropy is a crucial component in the description of dense objects with strange matter. Gleiser and Dev [9] generated results which indicate that pressure anisotropy may significantly affect the physical structure of the relativistic object which may cause several observational effects. They highlighted that relativistic bodies may be more stable if the pressure anisotropy exists near its core. The stability of stellar bodies is improved for positive measure of anisotropy when compared to configurations of isotropic stellar bodies. Many investigations show that the presence of anisotropic pressures in a charged matter improve the stability of the configuration under radial adiabatic perturbations when compared to isotropic matter (Dev and Gleiser [10]). Other treatments that include the presence of both electric field and anisotropy in the stellar object are those indicated in [1, 3, 11,12,13,14,15]. However, most of charged models always have anisotropy. Models with vanishing anisotropy are needed in order to regain isotropic models.

Compact stellar bodies can be modelled by several kinds of equations of states. These include linear, quadratic, polytropic, and Van der Waals equations of state. Thirukkanesh and Ragel [16] found exact solutions for non-charged anisotropic spheres with the polytropic equation of state for particular choices of the polytropic index. In addition to that, Maharaj and Mafa Takisa [17] obtained exact solutions for field equations with the electromagnetic field and anisotropic pressure present using general polytropic equation of state. Thirukkanesh and Ragel [18] formulated a system of field equations with Van der Waals equation of state in spherically symmetric static space–time to describe anisotropic compact matter and obtained a new class of solution by choosing one of the gravitational potentials. Moreover, exact models for Einstein–Maxwell field equations describing charged anisotropic matter found by using a quadratic equation of state include those by Maharaj and Mafa Takisa [19] and Feroze and Siddiqui [20]. Recent treatments with linear equation of state include anisotropic charged compact star models generated by Ngubelanga et al [21], static anisotropic exact models found by Govender and Thirukkanesh [22], relativistic stellar models describing highly compact objects obtained by Kileba Matondo and Maharaj [23] and core envelope star model generated by Mafa Takisa and Maharaj [24]. Other exact models for anisotropic and charged matter with linear equation of state include results generated by Mafa Takisa and Maharaj [17] on compact exact regular solution and quark star models generated by Thirukkanesh and Maharaj [6]. However, most anisotropic exact models do not regain isotropic compact models as a special case. We have considered bag equation to find exact solutions for Einstein–Maxwell field equations that describe the properties of quark matter. It is important to note that the anisotropic models generated in this paper have isotropic properties after setting anisotropic parameters to vanish. We also regain previous anisotropic and isotropic models on quark matter obtained by other researchers.

The objective of this paper is to find new solutions to the Einstein–Maxwell field equations for charged anisotropic matter in static spherical symmetry space–time using linear equation of state consistent with quark matter. In order to achieve this objective, our work is arranged in the following manner: In the next section, we formulate the model, transform the field equations and make choice for suitable measure of anisotropy and one of the gravitational potentials. In §3, we generate a first exact model and find the exact solution that generalizes the results previously obtained by other researchers. In §4, we generate an exact nonsingular model. In §5, we present the discussion of the graphical plots and the generated relativistic stellar masses.

2 The model

We formulate models that describe the interior of the stellar objects. We consider the space–time geometry to be static and spherically symmetric with the line element

$$\begin{aligned} \mathrm {d}s^{2}=-\mathrm {e}^{2\nu (r)}\mathrm {d}t^{2}+ \mathrm {e}^{2\lambda (r)} \mathrm {d}r^{2}+r^{2}\begin{matrix}(\mathrm {d} \theta ^{2}+\mathrm {sin}^{2}\theta \, \mathrm {d}\phi ^{2})\end{matrix}, \end{aligned}$$
(1)

where \(\nu (r) \) and \(\lambda (r)\) are variables defining the gravitational potentials. The Reisser–Nordstrom line element describes the exterior space–time and is given by

$$\begin{aligned} \mathrm {d}s^{2}= & {} -\left( 1-\dfrac{2M}{r} + \dfrac{Q^{2}}{r^{2}}\right) \mathrm {d}t^{2}\nonumber \\&+\,\left( 1-\dfrac{2M}{r} + \dfrac{Q^{2}}{r^{2}}\right) ^{-1}\mathrm {d}r^{2}\nonumber \\&+\,r^{2}(\mathrm{d} \theta ^{2}+\sin ^{2}\theta \,\mathrm {d}\phi ^{2}), \end{aligned}$$
(2)

where M and Q represent total mass and charge as measured by an observer at infinity. The energy–momentum tensor for a charged anisotropic matter is given by

$$\begin{aligned} \tau _{ij}= & {} \mathrm {diag}\left( -\rho -\frac{1}{2}E^{2},p_{\mathrm{r}} -\frac{1}{2}E^{2} , p_{\mathrm{t}} + \frac{1}{2}E^{2},\right. \nonumber \\&\left. p_{t} +\frac{1}{2}E^{2}\right) , \end{aligned}$$
(3)

where \(\rho \) is the energy density, \(p_{\mathrm {r}}\) is the radial pressure, \( p_{\mathrm {t}}\) is the tangential pressure and E is the electric field inside the charged star.

A more detailed discussion on the space–time geometry and the Einstein–Maxwell field equations with matter and charge in general relativity is given in [25,26,27,28,29] and are given as

$$\begin{aligned}&\dfrac{1}{r^{2}}\begin{matrix} (1-\mathrm {e}^{-2\lambda })\end{matrix}+\dfrac{2\lambda ^{\prime }}{r}\mathrm {e}^{-2\lambda }=\rho +\frac{1}{2}E^{2}, \end{aligned}$$
(4a)
$$\begin{aligned}&\dfrac{-1}{r^{2}}(1-\mathrm {e}^{-2\lambda })+\frac{2\nu ^{\prime }}{r}\mathrm {e}^{-2\lambda }=p_\mathrm{r} -\frac{1}{2}E^{2}, \end{aligned}$$
(4b)
$$\begin{aligned}&\mathrm {e}^{-2\lambda }\left( \nu ^{\prime \prime }+\nu ^{{\prime }^{2}}-\nu ^{\prime }\lambda ^{\prime } + \dfrac{\nu ^{\prime }}{r}-\dfrac{\lambda ^{\prime }}{r}\right) =p_\mathrm{t} +\frac{1}{2}E^{2}, \end{aligned}$$
(4c)
$$\begin{aligned}&\sigma = \dfrac{1}{r^{2}} \mathrm {e}^{-\lambda }(r^{2}E)^{\prime }, \end{aligned}$$
(4d)

where \( \sigma \) is a proper charged density. In system (4), prime defines the differentiation of the variables with respect to radial coordinate r. We shall consider a linear relationship between the radial pressure and the energy density as

$$\begin{aligned} p_{\mathrm {r}}= \frac{1}{3}(\rho -4B), \end{aligned}$$
(5)

where B is the bag constant. Equation (5) is well known as the Bag equation and is consistent with strange matter like quark stars. The mass function contained within the charged sphere is given by

$$\begin{aligned} m(r)=\frac{1}{2}\int _{0}^{r}\omega ^{2} \rho \,\mathrm {d}\omega . \end{aligned}$$
(6)

The fundamental line element (1) and the field equations (4) can be transformed to a simple form by introducing the new functions given by

$$\begin{aligned} x=Cr^{2}, \quad Z(x)=\mathrm {e}^{-2\lambda (r)}, \quad A^{2}y^{2}(x)=\mathrm {e}^{2v(r)}, \end{aligned}$$
(7)

where C and A are arbitrary constants. The transformation in system (7) was suggested by Durgapal and Bannerji [30]. Therefore, the Einstein–Maxwell field equations (4) and the equation of state can be written in the following form:

$$\begin{aligned}&\rho =3p_{\mathrm {r}}+4B, \end{aligned}$$
(8a)
$$\begin{aligned}&\dfrac{p_{\mathrm {r}}}{C}=Z\dfrac{\dot{y}}{y} -\dfrac{\dot{Z}}{2}-\dfrac{B}{C}, \end{aligned}$$
(8b)
$$\begin{aligned}&p_{\mathrm {t}}=p_{\mathrm {r}} +\Delta , \end{aligned}$$
(8c)
$$\begin{aligned}&\Delta =4CxZ\dfrac{\ddot{y}}{y}+C(6Z+2x\dot{Z})\dfrac{\dot{y}}{y}\nonumber \\&\qquad +\,\,C\left( 2\left( \dot{Z} + \dfrac{B}{C}\right) +\dfrac{Z-1}{x}\right) , \end{aligned}$$
(8d)
$$\begin{aligned}&\dfrac{E^{2}}{2C}=\dfrac{1-Z}{x}-3Z\dfrac{\dot{y}}{y}-\dfrac{\dot{Z}}{2}-\dfrac{B}{C}, \end{aligned}$$
(8e)
$$\begin{aligned}&\sigma =2\sqrt{\frac{CZ}{x}}(x\dot{E} +E). \end{aligned}$$
(8f)

The mass function (6) becomes

$$\begin{aligned} M(x)=\frac{1}{4C^{{3}/{2}}}\int _{0}^{x}\sqrt{\omega } \rho \, \mathrm {d}\omega . \end{aligned}$$
(9)

System (8) has six equations in eight variables \( ( \rho , p_{\mathrm {r}}, p_{\mathrm {t}}, E, Z, y, \sigma , \Delta )\). In order to find exact solutions of system (8), we specify two of the quantities and generate an ordinary differential equation in only one dependent variable. For our models we have chosen to specify the metric function y and the measure of anisotropy \( \Delta \). The metric function y is specified to be

$$\begin{aligned} y= (\begin{matrix}a + x^{m}\end{matrix})^{n}, \end{aligned}$$
(10)

where a, m and n are arbitrary constants. The choice of metric function (10) is very crucial in modelling relativistic matter. It is observed to be finite, regular and continuous throughout the interior of the stellar objects. This choice of metric function was also adopted by Komathiraj and Maharaj [31] and Sunzu et al [1].

On the other hand, our choice for measuring anisotropy is a polynomial function of degree four in the form of

$$\begin{aligned} \Delta = \alpha _{0} x^{3}+\alpha _{1}x^{4}, \end{aligned}$$
(11)

where \(\alpha _{0} \) and \( \alpha _{1} \) are arbitrary constants. This choice is an extension of the choice made by Maharaj et al [11] and Sunzu et al [3] which was a general cubic polynomial. However, our choice of anisotropy does not contain linear and quadratic terms which are present in the choice of anisotropy made in these papers. We can therefore obtain particular anisotropic charged models generated by Maharaj et al [11] when linear and quadratic terms in their anisotropy are zero. When \(\alpha _{0}=\alpha _{1}=0 \), we have \(\Delta =0\) and in this case we have isotropic pressures. With our choice of anisotropy \(\Delta \), metric function y and the linear equation of state used, we regain the previous isotropic models obtained by Mak and Harko [32], Komathiraj and Maharaj [31], and Misner and Zapolsky [33]. We therefore see that these choices are likely to give new results that generalized other models.

Substituting eqs (10) and (11) in eq. (8d) we obtain

$$\begin{aligned}&\dfrac{\left( 1-\dfrac{2xB}{C}+\dfrac{x^{3}(\alpha _{0} +\alpha _{1}x)}{C}\right) \left( a+x^{m}\right) }{2x(nmx^{m}+x^{m}+a)} \nonumber \\&\quad = \dot{Z} + \left( \dfrac{1}{2x} +\dfrac{m(4(mn+1) -3m)x^{m-1}}{2(a+(1+nm)x^{m})} \right. \nonumber \\&\qquad \left. +\,\dfrac{2m(n-1)x^{m-1}}{a+x^{m}}\right) Z. \end{aligned}$$
(12)

Equation (12) is a general equation governing the model for stellar object with charge corresponding to the choice of the metric function and the measure of anisotropy made in eqs (10) and (11) respectively. Knowing the values of m and n, eq. (12) can be linear and tractable. By integrating eq. (12) the variable Z is known and we can therefore find the remaining variables \( \rho , p_{\mathrm {r}}, p_{\mathrm {t}}\) and \( E^{2} \) using system (8). However, in doing so, we need to specify the constants m and n and find exact solutions to our models.

3 Generalized singular model

In this section, we find the exact solution for system (8) by specifying the value of \( m = {1}/{2}\) and \( n =1\). Substituting these values in eq. (12) we obtain the following gravitational potentials and matter variables:

$$\begin{aligned}&\mathrm {e}^{2\nu }=A^{2}(a+\sqrt{x})^{2}, \end{aligned}$$
(13a)
$$\begin{aligned}&\mathrm {e}^{2\lambda }=\dfrac{3(2a+3\sqrt{x})}{3(\sqrt{x}+ 2a)-\dfrac{Bx}{C}(4a+3\sqrt{x}) +\dfrac{N(x)}{C}}, \end{aligned}$$
(13b)
$$\begin{aligned}&\rho =\dfrac{3C(6a^{2}+10\sqrt{x}+3\sqrt{x})}{2\sqrt{x}(a +\sqrt{x})(2a+3\sqrt{x})^{2}} \nonumber \\&\qquad +\,\dfrac{B(16a^{3}+47a^{2}\sqrt{x}+48ax+18x^{{3}/{2}}) -3L(x)}{2(a+\sqrt{x})(2a+3\sqrt{x})^{2}}, \end{aligned}$$
(13c)
$$\begin{aligned}&p_{\mathrm {r}} = \dfrac{C(6a^{2}+10\sqrt{x}+3\sqrt{x})}{2\sqrt{x}(a+ \sqrt{x})(2a+3\sqrt{x})^{2}} \nonumber \\&\qquad - \dfrac{B(\frac{16}{3}a^{3}+27a^{2}\sqrt{x}+40ax+18x^{{3}/{2}})+L(x)}{2(a +\sqrt{x})(2a+3\sqrt{x})^{2}}, \end{aligned}$$
(13d)
$$\begin{aligned}&p_{\mathrm {t}}= \dfrac{C(6a^{2}+10\sqrt{x}+3\sqrt{x})}{2\sqrt{x}(a +\sqrt{x})(2a+3\sqrt{x})^{2}} \nonumber \\&\qquad -\dfrac{B(\frac{16}{3}a^{3}+27a^{2}\sqrt{x}+40ax+18x^{{3}/{2}}-{G}(x))}{2(a+\sqrt{x})(2a+3\sqrt{x})^{2}}, \end{aligned}$$
(13e)
$$\begin{aligned}&\Delta = \alpha _{0}x^{3} + \alpha _{1}x^{4}, \end{aligned}$$
(13f)
$$\begin{aligned}&E^{2}=\dfrac{C(-2a^{2}-2a\sqrt{x}) +Bx(a^{2}+2a\sqrt{x})-T(x)}{\sqrt{x}(\sqrt{x} +a)(2a+3\sqrt{x})^{2}}.\nonumber \\ \end{aligned}$$
(13g)

In this case, the line element (1) becomes

$$\begin{aligned} \mathrm {d}s^{2}= & {} -A^{2}(a+\sqrt{x})^{2}\mathrm {d}t^{2}+\left( \dfrac{3(2a+3\sqrt{x})}{3(\sqrt{x}+2a) -({Bx}/{C})(4a+3\sqrt{x})+({N(x)}/{C})}\right) \mathrm {d}r^{2}\nonumber \\&+r^{2}(\mathrm {d} \theta ^{2}+\sin ^{2}\theta \, \mathrm {d}\phi ^{2}). \end{aligned}$$
(14)

For simplicity we have set

$$\begin{aligned} N(x)= & {} \alpha _{0}\left( \frac{2}{9}ax^{4}+\frac{1}{5}x^{{9}/{2}}\right) \\&+\, \alpha _{1}\left( \frac{2}{11}ax^{5}+\frac{1}{6}x^{{11}/{2}}\right) , \\ {L}(x)= & {} \alpha _{0}\left( \frac{16}{9}a^{3}x^{3}+\frac{82}{15}a^{2}x^{{7}/{2}}+\frac{82}{15}ax^{4} +\frac{9}{5}x^{{9}/{2}}\right) \\&+\,\alpha _{1}\left( \frac{20}{11}a^{3}x^{4}+\frac{379}{66}a^{2}x^{{9}/{2}}+\frac{65}{11}ax^{5}\right. \\&\left. +\,2x^{{11}/{2}}\right) , \\ {G}(x)= & {} \alpha _{0}\left( \frac{56}{9}a^{3}x^{3}+\frac{398}{15}a^{2}x^{{7}/{2}}+\frac{548}{15}ax^{4}\right. \\&\left. +\,\frac{81}{5}x^{{9}/{2}}\right) +\,\alpha _{1}\left( \frac{68}{11}a^{3}x^{4}+\frac{1733}{66}a^{2}x^{{9}/{2}}\right. \\&\left. +\,\frac{397}{11}ax^{5}+16x^{{11}/{2}}\right) , \\ T(x)= & {} \alpha _{0}\left( \frac{8}{3}a^{3}x^{{7}/{2}}+\frac{154}{15}a^{2}x^{4}+\frac{196}{15}ax^{{9}/{2}}\right. \\&\left. +\,\frac{27}{5}x^{5}\right) +\alpha _{1}\left( \frac{28}{11}a^{3}x^{{9}/{2}}+\frac{213}{22}a^{2}x^{5}\right. \\&\left. +\,\frac{134}{11}ax^{{11}/{2}}+5x^{6}\right) . \end{aligned}$$

If we set \( \alpha _{1} = 0 \) the anisotropy \(\Delta = \alpha _{0}x^{3}\) and the line element (1) becomes

$$\begin{aligned}&\mathrm {d}s^{2} =-A^{2}\left( a+\sqrt{x}\right) ^{2}\mathrm {d}t^{2}\nonumber \\&\quad +\left( \dfrac{3\left( 2a+3\sqrt{x}\right) }{3\left( \sqrt{x}+2a\right) -\dfrac{Bx}{C}\left( 4a+3\sqrt{x}\right) +\dfrac{N_{0}(x)}{C}}\right) \mathrm {d}r^{2} \nonumber \\&\qquad +\,r^{2}\left( \mathrm {d} \theta ^{2}+\sin ^{2}\theta \, \mathrm {d}\phi ^{2}\right) , \end{aligned}$$
(15)

where

$$\begin{aligned} N_{0}(x) = \alpha _{0}\left( \frac{2}{9}ax^{4}+\frac{1}{5}x^{{9}/{2}}\right) . \end{aligned}$$

The line element (15) is similar to the one obtained by Maharaj et al [11] at the vanishing point of linear and quadratic terms in their anisotropy. When \( \alpha _{0} = \alpha _{1} = 0\) in our model, the anisotropy \( \Delta = 0 \). In this, we obtain isotropic model with gravitational potentials and matter variables similar to the one generated by Komathiraj and Maharaj [31]. In this case, the line element describing the corresponding isotropic model is given by

$$\begin{aligned} \mathrm {d}s^{2}=&-A^{2}(a+\sqrt{x})^{2}\mathrm {d}t^{2}\nonumber \\&+ \dfrac{3(2a+3\sqrt{x})}{3(\sqrt{x}+2a) -({Bx}/{C})(4a+3\sqrt{x})} \mathrm {d}r^{2} \nonumber \\&+r^{2}(\mathrm {d} \theta ^{2}+\sin ^{2}\theta \,\mathrm {d}\phi ^{2}). \end{aligned}$$
(16)

If we further substitute \(a=0\) in eq. (16) we obtain the gravitational potentials, and matter variables similar to those obtained by Mak and Harko [32] with the line element

$$\begin{aligned} \mathrm {d}s^{2}= & {} -A^{2}Cr^{2}\mathrm {d}t^{2}+\left( \frac{3}{1-Br^{2}}\right) \mathrm {d}r^{2}\nonumber \\&+\,r^{2}(\mathrm {d}\theta ^{2}+\sin ^{2}\theta \,\mathrm {d}\phi ^{2}). \end{aligned}$$
(17)

Finally when \(B=0\), we regain the Misner and Zapolsky [33] particular results for the equation of state \(p=({1}/{3})\rho \). It is important to note that the singularity in this model is also present in other models whose results are regained by us. We can therefore say that, models obtained in this section contain results that have been obtained by other researchers as special cases. This is an important aspect for any realistic stellar model.

4 Generalized nonsingular model

In this section, we find the exact solutions of system (8) by introducing other values of m and n. Substituting \(m=1\) and \(n = 2\) into eq. (12), the model becomes nonsingular and we regain results for the second model generated by Komathiraj and Maharaj [31] and we can obtain particular second anisotropic model for Maharaj et al [11].

Under this model, the gravitational potentials and matter variables become

$$\begin{aligned}&\mathrm{e}^{2\nu }=A^{2}(a+x)^{4}, \end{aligned}$$
(18a)
$$\begin{aligned}&\mathrm {e}^{2\lambda }=315(a+x)^{2}(a+3x) \left[ 9(35a^{3}+35a^{2}x\right. +21ax^{2}+5x^{3}) \nonumber \\&-\, \dfrac{2B}{C}(105a^{3}x+189a^{2}x^{2}+35ax^{3}+35x^{4})\left. + \dfrac{315H(x)}{C} \right] ^{-1}, \end{aligned}$$
(18b)
$$\begin{aligned}&p_{\mathrm {r}} = \dfrac{C(140a^{4}+434a^{3}x+318a^{2}x^{2}+150ax^{3}+30x^{4})}{35(a+x)^{3}(a+3x)^{2}} \nonumber \\&-\,\dfrac{ B(70a^{5}+994a^{4}x+3708a^{3}x^{2} +\frac{16780}{3}a^{2}x^{3}+\frac{11770}{3}ax^{4}+1050x^{5})}{105(a+x)^{3}(a+3x)^{2}} \nonumber \\&-\,\dfrac{\Omega (x)}{105(a+x)^{3}(a+3x)^{2}}, \end{aligned}$$
(18c)
$$\begin{aligned}&\rho =\dfrac{3C(140a^{4}+434a^{3}x+318a^{2}x^{2}+150ax^{3}+30x^{4})}{35(a+x)^{3} (a+3x)^{2}}-\dfrac{3\Omega (x)}{105(a+x)^{3}(a+3x)^{2}} \nonumber \\&-\,\dfrac{ 3B(70a^{5}+994a^{4}x+3708a^{3}x^{2} +\frac{16780}{3}a^{2}x^{3}+\frac{11770}{3}ax^{4}+1050x^{5})}{105(a+x)^{3}(a+3x)^{2}} +4B\qquad \qquad \qquad \qquad \qquad \qquad \qquad \; \end{aligned}$$
(18d)
$$\begin{aligned}&p_{\mathrm {t}} =\dfrac{C(140a^{4}+434a^{3}x+318a^{2}x^{2}+150ax^{3}+30x^{4})}{35(a+x)^{3}(a+3x)^{2}}+\dfrac{\Gamma (x)}{105(a+x)^{3}(a+3x)^{2}} \nonumber \\&-\,\dfrac{ B(70a^{5}+994a^{4}x+3708a^{3}x^{2} +\frac{16780}{3}a^{2}x^{3}+\frac{11770}{3}ax^{4}+1050x^{5})}{105(a+x)^{3}(a+3x)^{2}}, \end{aligned}$$
(18e)
$$\begin{aligned}&\Delta =x^{3}(\alpha _{0}+\alpha _{1}x), \end{aligned}$$
(18f)
$$\begin{aligned}&E^{2} =-\,\dfrac{B(168a^{4}x+1296a^{3}x^{2}+6528a^{2}x^{3}+7280ax^{4}+2520x^{5}) +630\xi (x)}{315(a+x)^{3}(a+3x)^{2}} \nonumber \\&+\,\dfrac{C(196a^{3}x+1452a^{2}x^{2}+1356ax^{3}+420x^{4})}{35(a+x)^{3}(a+3x)^{2}}. \end{aligned}$$
(18g)

The line element (1) corresponding to this model becomes

$$\begin{aligned} \mathrm {d}s^{2}=&-A^{2}(a+x)^{4}\mathrm {d}t^{2} + 315(a+x)^{2}(a+3x)\nonumber \\&\times \, \left[ 9(35a^{3}+35a^{2}x+21ax^{2} +5x^{3}) \right. \nonumber \\&-\, \dfrac{2B}{C}(105a^{3}x+189a^{2}x^{2}+35ax^{3}+35x^{4})\nonumber \\&\left. +\,\dfrac{315H(x)}{C}\right] ^{-1}\mathrm {d}r^{2} +\,r^{2}(\mathrm {d} \theta ^{2}+\sin ^{2}\theta \, \mathrm {d}\phi ^{2}). \end{aligned}$$
(19)

For simplicity we have set

$$\begin{aligned} \Omega (x)= & {} \alpha _{0}\left( \frac{70}{3}a^{5}x^{3}+\frac{3710}{33}a^{4}x^{4}+\frac{2310}{13}a^{3}x^{5}\right. \\&\left. +\,\frac{17206}{143}a^{2}x^{6}+\frac{1701}{26}ax^{7}\right) \\&+\,\alpha _{1}\left( \frac{525}{22}a^{5}x^{4}+\frac{3255}{26}a^{4}x^{5}+\frac{32403}{143}a^{3}x^{6}\right. \\&\left. +\,\frac{41517}{221}a^{2}x^{7}+\frac{2415}{34}ax^{8}+\frac{315}{34}x^{9}\right) ,\\ \Gamma (x)= & {} \alpha _{0}\left( \frac{245}{3}a^{5}x^{3}+\frac{27475}{33}a^{4}x^{4}+\frac{38640}{13}a^{3}x^{5}\right. \\&\left. +\,\frac{673484}{143}a^{2}x^{6} +\frac{88389}{26}ax^{7}+945x^{8}\right) \\&+\,\alpha _{1}\left( \frac{1785}{22}a^{5}x^{4}+\frac{21315}{26}a^{4}x^{5}\right. \\&+\,\frac{418047}{143}a^{3}x^{6}+\frac{1025913}{221}a^{2}x^{7}\\&\left. +\,\frac{115395}{34}ax^{8}+\frac{31815}{34}x^{9}\right) \\ \xi (x)= & {} \alpha _{0}\left( \frac{1}{3}a^{5}x^{3}+\frac{265}{99}a^{4}x^{4}+\frac{1150}{143}a^{3}x^{5}\right. \\&\left. +\,\frac{7012}{715}a^{2}x^{6}+\frac{115}{26}ax^{7}+ \frac{9}{5}x^{8}\right) \\&+\,\alpha _{1}\left( \frac{7}{22}a^{5}x^{4}+\frac{719}{286}a^{4}x^{5}+\frac{417}{55}a^{3}x^{6}\right. \\&\left. +\,\frac{150527}{14365}a^{2}x^{7}+\frac{17677}{2465}ax^{8}+\frac{57}{34}x^{9}\right) \\ H(x)= & {} \alpha _{0}\left( \frac{a^{3}x^{4}}{9}+\frac{3a^{2}x^{5}}{11}+\frac{ax^{6}}{13}+\frac{x^{7}}{15}\right) \\&+\, \alpha _{1}\left( \frac{a^{3}x^{5}}{11}+\frac{3a^{2}x^{6}}{13}+\frac{3ax^{7}}{15}+\frac{x^{8}}{17}\right) . \end{aligned}$$

The mass function (9) corresponding to this model becomes

(20)

If we set \( \alpha _{1} = 0 \) in our model above, line element (1) becomes

$$\begin{aligned} \mathrm {d}s^{2}=&-A^{2}\left( a+x\right) ^{4}\mathrm {d}t^{2}+ 315\left( a+x\right) ^{2}(a+3x)\nonumber \\&\times \,\Big [9(35a^{3} +35a^{2}x+21ax^{2} +5x^{3})\nonumber \\&-\, \dfrac{2B}{C}(105a^{3}x+189a^{2}x^{2}+35ax^{3}+35x^{4})\nonumber \\&+\, \dfrac{315\omega (x)}{C}\Big ]^{-1}\mathrm {d}r^{2} \nonumber \\&+\,r^{2}(\mathrm {d} \theta ^{2}+\sin ^{2}\theta \, \mathrm {d}\phi ^{2}), \end{aligned}$$
(21)

where for simplicity we have set

$$\begin{aligned} \omega (x) = \alpha _{0}\left( \frac{a^{3}x^{4}}{9}+\frac{3a^{2}x^{5}}{11}+\frac{ax^{6}}{13}+\frac{x^{7}}{15}\right) . \end{aligned}$$

The line element (21) is similar to the one obtained by Maharaj et al [11] when linear and quadratic terms of their anisotropy are set to vanish. When \( \alpha _{0} = \alpha _{1} = 0 \), system (18) becomes isotropic. In this case, we regain exact isotropic model generated by Komathiraj and Maharaj [31]. For this isotropic model, the line element becomes

$$\begin{aligned} \mathrm {d}s^{2}=&-A^{2}(a+x)^{4}\mathrm {d}t^{2}+ 315(a+x)^{2}(a+3x)\nonumber \\&\times \,\left[ 9(35a^{3}+35a^{2}x+21ax^{2} +5x^{3})\right. \nonumber \\&-\left. \dfrac{2B}{C}(105a^{3}x+189a^{2}x^{2}+35ax^{3}{+}35x^{4}) \right] ^{-1}\mathrm {d}r^{2}\nonumber \\&+\,r^{2}(\mathrm {d} \theta ^{2}+\sin ^{2}\theta \, \mathrm {d}\phi ^{2}). \end{aligned}$$
(22)

The line element (22) is the same as the one obtained in second isotropic model by Komathiraj and Maharaj [31]. The same results were also regained in Maharaj et al [11] for their second model when \( \Delta = 0 \). We can state that our model generated in this section regains isotropic and particular anisotropic models as special cases.

Fig. 1
figure 1

The energy density \(\rho \) against the radial distance r.

Full size image
Fig. 2
figure 2

The radial pressure \(p_{\mathrm{r}}\) against the radial distance r.

Full size image
Fig. 3
figure 3

The tangential pressure \( p_{\mathrm{t}} \) against the radial distance r.

Full size image
Fig. 4
figure 4

The measure of anisotropy \(\Delta \) against the radial distance r.

Full size image
Fig. 5
figure 5

The electric field \(E^{2}\) against the radial distance r.

Full size image

5 Discussion

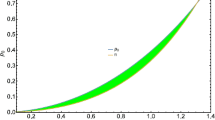
In this section, we show that the exact solutions of the field equations in §4 are well behaved throughout the interior of the stellar object. We consider the behaviour of the matter variables and the electric field. The Python programming language was used to generate graphs for \( a = 0.3 \), \( B = 0.2 \), \( C = 2 \), \(\alpha _{0} = 0.01 \), \( \alpha _{1} = 0.02 \), and \( A =1. \) The graphs generated are for the matter variables energy density \(\rho \) (figure 1), radial pressure \( p_{\mathrm {r}}\) (figure 2), tangential pressure \( p_{\mathrm {t}} \) (figure 3), measure of anisotropy \( \Delta \) (figure 4), the electric field \( E^{2} \) (figure 5), the mass M (figure 6) and the speed of sound v (figure 7). All the figures are plotted against the radial coordinate r. These quantities are regular and well behaved inside the stellar objects. The energy density \(\rho \), the radial pressure \( p_{\mathrm {r}} \) and the tangential pressure \( p_{\mathrm {t}} \) are decreasing functions as we approach the boundary from the core of stellar object yielding \(\rho ^{\prime }\le 0\), \(p_{\mathrm {r}}^{\prime }\le 0\) and \(p_{\mathrm {t}}^{\prime }\le 0\). It is evident and physical to have maximum values of these variables at the centre of the star as their gradients are greatest at the core regions. Recent papers with similar graphical profiles include those of Maharaj et al [11, 34]. The measure of anisotropy \( \Delta \) is finite, regular, continuous and increases from the core to the surface of the stellar objects. It is observed to be zero at the centre of the stellar objects. This is physical as we expect the tangential pressure to be equal to the radial pressure at the centre. It is also shown that the anisotropy \(\Delta \ge 0\) throughout the stellar interior which implies that \(p_{\mathrm {t}}\ge p_{\mathrm {r}}\). This is also the case in the recent work by Ngubelanga et al [35]. The electric field \( E^{2} \) is finite and regular at the core. It increases from the core and then decreases after reaching a maximum value and this profile is similar to the one obtained in Maharaj et al [11, 34]. The mass in figure 6 is a monotonic increasing function with the radial distance r. It is indicated in figure 7 that the speed of sound is constant and less than unity. This is physical as we expect the speed of sound to be less than the speed of light. It is constant \((v={1}/{3})\) because we have used a linear quark equation of state.

Fig. 6
figure 6

The mass M against the radial distance r.

Full size image
Fig. 7
figure 7

The speed of sound \( v={\mathrm {d}p_{\mathrm{r}}}/{\mathrm {d}\rho }\) against the radial distance r.

Full size image
Table 1 Relativistic stellar masses obtained for various parameter values.
Full size table

We also indicate that using exact nonsingular model in §4, relativistic stellar masses consistent with observations and previously found by other researchers can be generated. This is an important aspect for any realistic physical models. In doing so, we transform the mass function in eq. (20) using the following transformation:

$$\begin{aligned}&\tilde{\alpha }_{0}= \alpha _{0}R^{2},\quad \tilde{\alpha }_{1}= \alpha _{1}R^{2},\quad \, \tilde{a}=aR^{2},\quad \\&\tilde{B}= BR^{2},\quad \, \tilde{C}=CR^{2}. \end{aligned}$$

In this, R takes the same unit as the variable x, and is renormalized by a factor of 43.245 for realistic stellar objects to be generated. We have obtained the mass \(M=2.86M_{\odot }\) with radius \(r=9.46\) km which is consistent with the stellar object found by Mak and Harko [32], the mass \(M=1.67M_{\odot }\) with radius of 9.4 km which is consistent with the star PSR J1903\(+\)327 as studied in the paper by Gangopadhyay et al [36], the mass \(M=1.60M_{\odot }\) with radii of 7.60 km and 7.61 km generated by Sunzu et al [1], the mass \(M=1.433M_{\odot }\) with radius \(r=7.07\) km discussed by Dey et al [37] and is consistent with the star SAX J1808.4-3658, and the stellar object with mass \(M=0.94M_{\odot }\) and radii of 7.07 km found by Thirukkanesh and Maharaj [6] and Mafa Takisa and Maharaj [17]. The stellar object with mass \(M=1.97M_{\odot }\) and radii of 10.30 km is consistent with pursar PSR J1614-2230 as highlighted in Mafa Takisa and Maharaj [24] and Gangopadhyay et al [36]. Parameter values for these stellar masses and radii are given in table 1.

6 Conclusion

New exact models which describe interior solutions for the Einstein–Maxwell field equations have been generated. The solution generated are for the charged anisotropic stellar objects with linear equation of state consistent with quark matter. We have made new choice for the measure of anisotropy and one of the gravitational potentials. In our charged anisotropic models, we have regained previous isotropic models and particular anisotropic exact solutions as a special case. Models generalized in our work are those generated by Komathiraj and Maharaj [31], Mak and Harko [32] and the treatments by Misner and Zapolsky [33] and particular anisotropic models generated by Maharaj et al [11]. The plots generated show that all the matter variables are well behaved. The stellar objects generated have masses and radii consistent with those obtained by Mak and Harko [32], Gangopadhyay et al [36], Sunzu et al [1], Dey et al [37], Thirukkanesh and Maharaj [6] and Mafa Takisa and Maharaj [24]. Models generated in this paper are significant in describing structures and properties of anisotropic stellar objects such as the pursar PSR J1903\(+\)327, PSR J1614-2230, and the star SAX J1808.4-3658. Other results can be obtained by studying our models. This may be achieved by considering different forms for gravitational potentials, equation of states and measure of anisotropy.